2013-14材料力学试卷A答案及评分标准
2013-2014学年第2学期《材料力学》复习要点_参考简答题答案

2013-2014学年第2学期《材料力学》复习要点_参考简答题答案2013-2014学年第2学期《材料力学》复习要点——参考简答题答案1、什么是变形固体?材料力学中关于变形固体的基本假设是什么?【解答】:在外力作用下,一切固体都将发生变形,故称为变形固体。
材料力学中对变形固体所作的基本假设:连续性假设:认为整个物体体积内毫无空隙地充满物质。
均匀性假设:认为物体内的任何部分,其力学性能相同。
各向同性假设:认为在物体内各个不同方向的力学性能相同。
小变形假设:认为固体在外力作用下发生的变形比原始尺寸小得很多,因此在列平衡方程求约束力或者求截面内力时,一般按构件原始尺寸计算。
2、什么是截面法?简要说明截面法的四个基本步骤。
【解答】:用一个假想截面,将受力构件分开为两个部分,取其中一部分为研究对象,将被截截面上的内力以外力的形式显示出来,根据保留部分的平衡条件,确定该截面内力大小、内力性质(轴力、剪力、扭转还是弯矩,符号的正负)的一种方法。
截面法贯穿于材料力学的始终,一定要反复练习,熟练掌握。
截面法的四个基本步骤:(1)截:在需要确定内力处用一个假想截面将杆件截为两段。
(2)取:取其中任何一段为研究对象(舍弃另一段)。
(3)代:用被截截面的内力代替舍弃部分对保留部分所产生的作用。
(4)平:根据保留部分的平衡条件,确定被截截面的内力数值大小和内力性质。
3、什么是材料的力学性能?低碳钢拉伸试验要经历哪四个阶段?该试验主要测定低碳钢的哪些力学性能指标?【解答】:材料的力学性能是指:在外力作用下材料在变形和破坏方面所表现出的各种力学指标。
如强度高低、刚度大小、塑性或脆性性能等。
低碳钢拉伸试验要经历的四个阶段是:弹性阶段、屈服阶段、强化阶段、颈缩断裂阶段。
低碳钢拉伸试验主要测定低碳钢的力学性能指标有:屈服极限、强度极限、延伸率、断面收缩率等。
4、什么是极限应力?什么是许用应力?轴向拉伸和压缩的强度条件是什么(内容、表达式)?利用这个强度条件可以解决哪三类强度问题?【解答】:材料失效时所达到的应力,称为极限应力。
材料力学试题

材料的力学性能课程期末试卷A卷标准答案(即评分标准)一、填空(每空1分,共10分)1、应力强度因子反映了裂纹尖端区域应力场的强度,它综合反映了__________和裂纹位置、__________对裂纹尖端应力场强度的影响。
2、对于材料的静拉伸实验,在整个拉伸过程中的变形分为弹性变形、塑性变形和__________三个阶段,塑性变形又可分为__________、均匀塑性变形和____________三个阶段。
3、材料塑性的评价,在工程上一般以光滑圆柱试样的拉伸伸长率和__________作为塑性性能指标。
常用的伸长率指标有__________、最大应力下总伸长率和最常用的__________三种。
4、根据外加应力的类型及其与裂纹扩展面的取向关系,裂纹扩展的基本方式有______________、滑开型(Ⅱ型)裂纹扩展和______________三类。
答案:1、外加应力;长度。
2、断裂、屈服、不均匀集中塑性变形。
3、断面收缩率;最大应力下非比例伸长率;断后伸长率。
4、张开型(Ⅰ型)裂纹扩展、撕开型(Ⅲ型)裂纹扩展。
\二、判断题:(每题1分,共10分)()1、磨损包括三个阶段,这三个阶段中均能观察到摩擦现象,最后发生疲劳韧脆性断裂。
()2、应力状态软性系数越大,最大切应力分量越大,表示应力状态越软,材料越易于产生塑性变形;反之,应力状态软性系数越小,表示应力状态越硬,则材料越容易产生脆性断裂。
()3、断裂δ判据是裂纹开始扩展的断裂判据,而不是裂纹失稳扩展的断裂判据,显然,按这种判据设计构件是偏于保守的。
()4、测量陶瓷、铸铁的冲击吸收功时,一般采用夏比U型缺口试样,很少采用X型及无缺口冲击试样。
()5、应力腐蚀断裂速度远大于没有应力时的腐蚀速度,又远小于单纯力学因素引起的断裂速度。
()6、工程设计和材料选用中一般以工程应力、工程应变为依据;但在材料科学研究中,真应力与真应变具有更重要的意义。
()7、同一材料用不同的硬度测定方法所测得的硬度值是不相同的,且完全不可以互相转换。
材料力学A期末考试题及答案

材料力学A期末考试题及答案一、选择题(每题2分,共20分)1. 材料力学中,以下哪项不是应力的分类?A. 正应力B. 剪应力C. 拉应力D. 扭应力答案:C2. 在拉伸试验中,材料的屈服强度是指:A. 材料开始发生塑性变形的应力B. 材料发生断裂的应力C. 材料弹性极限的应力D. 材料达到最大应力的点答案:A3. 根据胡克定律,当材料受到拉伸时,其应力与应变的关系是:A. 线性关系B. 非线性关系C. 无关系D. 指数关系答案:A4. 梁的弯曲应力公式中,应力与下列哪项无关?A. 弯矩B. 截面惯性矩C. 材料的弹性模量D. 梁的长度答案:D5. 以下哪种材料不属于各向同性材料?A. 木材B. 钢材C. 玻璃D. 碳纤维复合材料答案:D6. 材料力学中,泊松比是描述材料在受到轴向拉伸时:A. 横向应变与轴向应变的比值B. 轴向应变与横向应变的比值C. 剪切应变与轴向应变的比值D. 剪切应变与横向应变的比值答案:A7. 材料的疲劳破坏通常发生在:A. 最高应力点B. 最低应力点C. 应力集中区域D. 材料的中心答案:C8. 梁在纯弯曲时,其横截面上的正应力分布规律是:A. 线性分布B. 抛物线分布C. 指数分布D. 对数分布答案:B9. 材料力学中,剪切模量与弹性模量的关系是:A. 互为倒数B. 互为平方根C. 互为常数倍D. 互为对数关系答案:C10. 材料力学中,以下哪项不是材料的基本力学性能?A. 弹性B. 塑性C. 韧性D. 硬度答案:D二、简答题(每题10分,共40分)1. 简述材料力学中的三种基本变形类型。
答案:材料力学中的三种基本变形类型包括拉伸和压缩、剪切和扭转、弯曲。
2. 描述材料的弹性模量和剪切模量的定义及其物理意义。
答案:弹性模量(E)定义为材料在弹性范围内应力与应变的比值,反映了材料抵抗轴向变形的能力。
剪切模量(G)定义为材料在剪切应力作用下剪切应力与剪切应变的比值,反映了材料抵抗剪切变形的能力。
材料力学试AB及其参考答案

南阳理工学院课程考试参考答案与评分标准考试课程:材料力学学年学期:2012-2013-2试卷类型:A 考试时间:120分钟一、名词解释:(每题2分,共10分)1. 内力:构件内由于发生变形而产生的相互作用力,或由于外力作用使构件内部产生的附加相互作用力。
2. 刚度:构件抵抗变形的能力。
3. 主单元体:在描述点的应力状态的单元体上,其各个表面只有正应力,没有切应力时,称为主单元体。
4. 线应变:单位长度上的变形量。
5. 许用应力:材料实际允许承受的最大应力值,它是极限应力除以安全系数得到的。
二、简答题:(每题5分,共20分)1.简述材料力学中对变形固体所作的三个基本假设。
2.简述胡克定律及主应力状态下广义胡克定律的一般表达式。
3.画出塑性材料拉伸时的应力-应变曲线,并说明分为哪几个阶段。
4.提高梁弯曲强度的措施有哪些?1. 答:材料力学中对变形固体所作的三个基本假设分别是:连续性假设,均匀性假设,各向同性假设。
连续性假设:认为整个物体体积内毫无空隙地充满物质;均匀性假设:认为物体内的任何部分,其力学性能相同;各向同性假设:认为在物体内各个不同方向的力学性能相同。
2.答:胡克定律,σ=Eε和τ=Gγ。
主应力状态下广义胡克定律的一般表达式为,ε1=[σ1-μ(σ2+σ3)]/——ε2=[σ2-μ(σ1+σ3)]/E,ε3=[σ3-μ(σ2+σ1)]/E。
3.答:低碳钢拉伸时分为如下变形阶段:弹性变形阶段,塑性变形阶段,强化阶段,局部变形阶段。
4. 答:提高梁弯曲强度的措施有:(1)降低最大弯矩,改变力的分布及作用点,改变支座的位置;(2)提高抗弯截面系数,改变截面形状使更多的材料承受较高的应力,调整截面承受弯矩的位置;(3)采用变截面梁,使承受弯矩较大的部位具有较大的抗弯截面系数。
三、画图题1.如图所示的等直杆横截面横截面面积A=400mm2,作轴力图。
(6分)2. 图中轴A端受固定端约束,B、C处受图示力偶作用,已知M B=30KN•m M C=20KN•m。
《材料力学》(A卷)答案及评分标准

《材料力学》(A卷)答案及评分标准广东工业大学考试试卷(开闭卷)( A B卷)课程名称:材料力学课程代码:成绩:考试时间:第周星期(年月日)题号一二三四五六七八九十总分得分评分人一、填空题 (共20分)1.外力是根据坐标标架来规定正负号的,内力则是根据变形的原则来规定正负号的,对于轴力,通常规定拉为(0.5分)正,对于剪力,通常规定绕隔离体顺时针方向为(0.5分)正,对于梁构件中的弯矩,通常规定下部受拉为(0.5分)正。
2.材料力学中,杆件变形的基本形式有:(0.5分) 轴向拉伸或轴向压缩、 (0.5分) 剪切、(0.5分) 扭转、(0.5分) 弯曲这四种。
3.内力在一点处的集度称为(0.5分) 应力,它的单位是(0.5分)2/Mpa N mm 或,它分为:①垂直于横截面的(0.5分) 正应力σ,②相切于横截面的(0.5分) 剪应力τ。
4.胡克定律的公式ΔL=NL/EA 反映出:当杆件应力不超过某一限度时,其轴向变形与(0.5分) 轴力和(0.5分) 杆长成正比,与(0.5分) 横截面面积成反比,比例系数为材料的柔度,即1/E 。
(要求:填写中文)5.刚度是抵抗变形能力的一种量度,由两方面决定,一是跟所选的材料有关,另一个则是由构件的几何性质来决定的,因此,如果材料已选定,则构件的设计实际上就是构件截面的形状和尺寸设计。
要提高构件的刚度,对于轴力杆件,只需提高其(0.5分) 横截面面积,对于弯曲杆件,只需提高其(0.5分) 截面惯性距。
6.在梁横截面上由弯矩引起的应力是(0.5分)正应力,它的分布规律是(1.5分)中性轴为零、边缘最大、沿截面呈线性分布。
7.弯矩图的横坐标表示(1分) 横截面位置,纵坐标表示(1分) 该横截面上的弯矩值。
8.在受扭构件横截面上的内力是(1分) 扭矩,由扭矩引起的最大剪应力发生在(1分) 最大扭矩截面的边缘上。
9.矩形截面梁的最大剪应力发生在(2分) 最大的剪力截面的中性轴上。
(完整版)材料力学试题(AB卷)
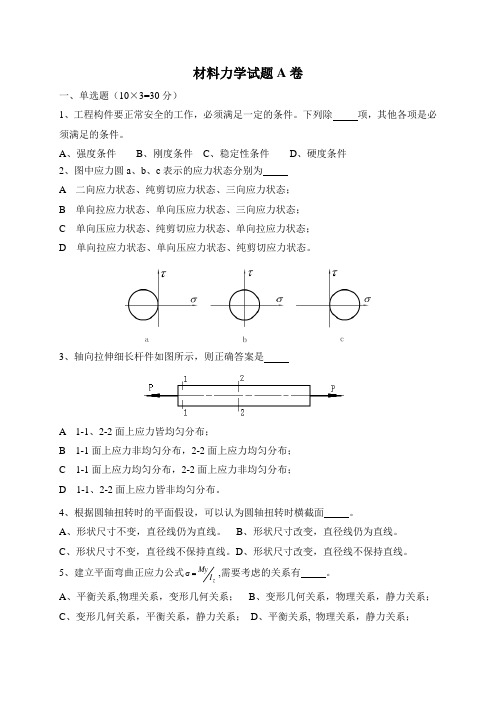
材料力学试题A 卷一、单选题(10×3=30分)1、工程构件要正常安全的工作,必须满足一定的条件。
下列除 项,其他各项是必须满足的条件。
A 、强度条件B 、刚度条件C 、稳定性条件D 、硬度条件 2、图中应力圆a 、b 、c 表示的应力状态分别为 A 二向应力状态、纯剪切应力状态、三向应力状态; B 单向拉应力状态、单向压应力状态、三向应力状态; C 单向压应力状态、纯剪切应力状态、单向拉应力状态; D 单向拉应力状态、单向压应力状态、纯剪切应力状态。
3、轴向拉伸细长杆件如图所示,则正确答案是A 1-1、2-2面上应力皆均匀分布;B 1-1面上应力非均匀分布,2-2面上应力均匀分布;C 1-1面上应力均匀分布,2-2面上应力非均匀分布;D 1-1、2-2面上应力皆非均匀分布。
4、根据圆轴扭转时的平面假设,可以认为圆轴扭转时横截面 。
A 、形状尺寸不变,直径线仍为直线。
B 、形状尺寸改变,直径线仍为直线。
C 、形状尺寸不变,直径线不保持直线。
D 、形状尺寸改变,直径线不保持直线。
5、建立平面弯曲正应力公式zI My =σ,需要考虑的关系有 。
A 、平衡关系,物理关系,变形几何关系;B 、变形几何关系,物理关系,静力关系;C 、变形几何关系,平衡关系,静力关系;D 、平衡关系, 物理关系,静力关系;6、利用积分法求梁的变形,不需要用到下面那类条件来确定积分常数。
A 、平衡条件。
B 、边界条件。
C 、连续性条件。
D 、光滑性条件。
7、图示交变应力的循环特征r 、平均应力m σ、应力幅度a σ分别为 。
A -10、20、10; B 30、10、20; C -1/3、20、10; D -1/3、10、20 。
8、压杆临界力的大小 。
A 与压杆所承受的轴向压力大小有关;B 与压杆的柔度大小有关;C 与压杆材料无关;D 与压杆的柔度大小无关。
9、利用图乘法计算弹性梁或者刚架的位移,要求结构满足三个条件。
材料力学试卷完整三套打包含答案
《材料力学》试卷(A卷)考试形式:开()、闭(√)卷注:学生在答题前,请将密封线内各项内容准确填写清楚,涂改及模糊不清者、试卷作废。
A、构件不发生断裂破坏;B、构件原有形式下的平衡是稳定的;C、构件具有足够的抵抗变形的能力;D、构件具有足够的强度、刚度和稳定性。
2、下列关于平面弯曲正应力公式的应用范围的说法,哪种是正确的:A、细长梁、弹性范围内加载;B、弹性范围内加载、载荷加在对称面或主轴平面内;C、细长梁、弹性范围内加载、载荷加在对称面或主轴平面内;D、细长梁、载荷加在对称面或主轴平面内。
3、外径为D,内径为d的空心圆截面,其抗扭截面系数等于;A、316PDWπ=B、331616PD dWππ=-C、344116PD dWDπ⎛⎫=-⎪⎝⎭D、344132PD dWDπ⎛⎫=-⎪⎝⎭4、正多边形截面有多少根形心主惯性轴:A、一根B、无穷多根C、一对D、三对5、细长压杆,常用普通碳素钢制造,而不用高强度优质钢制造,这是应为:A、普通碳素钢的强度极限高;B、钢强度优质钢的比例极限低。
C、普通碳素钢便宜;D、普通碳素钢价格便宜,而弹性模量和高强度优质钢差不多;6、在连接件挤压实用计算的强度条件[]Pcc c cF A σσ=≤中,A C 是指连接件的:A 、横截面面积;B 、有效挤压面积;C 、实际挤压部分面积;D 、最大挤压力所在的横截面面积。
7、图示应力状态,用第三强度理论校核时,其相当应力为: A 、3r στ=、3r στ=C 、33r στ=D 、 32r στ=8、有A 、B 两种不同材质的杆件,受到相同的轴向拉力,若两杆的抗拉刚度相同,长度一样,则两杆内各点:A 、应力不同,但应变相同;B 、应力不同,应变也不一样;C 、应力相同,应变不相同;D 、应力相同,应变也一样。
9、两根圆轴,一为实心轴,一为空心轴,若它们的长度、横截面面积、、所用材料及所受扭矩均相同,则有结论: A 、ϕϕ=空实; B 、ϕϕ>空实;C 、ϕϕ<空实; D 、有待具体计算,才能作出ϕϕ空实与的比较。
《材料力学》A卷参考答案.doc
XX学院2014-2015学年第二学期期末考试A卷参考答案及评分标准试卷编号:课程名称:材料力学课程归属:土木工程系适用专业(班级):土木工程出卷人:学科部主任:一、填空题(每空1分,共10分)1.剪切弯曲2.弹性阶段强化阶段3.04.变截面梁5.弯曲变形6.27.[一、2)2 + 02 - $3)2 + ($3 - $1 广 I 8.F二、单项选择题(每小题2分,共20分)9-13 ABDDC 14-18 BDBBD三、简述题(共14分)19.答:线弹性和小变形(4分)。
叠加在本质上是几何和,如不同方向的位移、正应力和切应力、正应变和切应变间的叠加(2分);但同一方向的多个位移、同一方向的多个正应变、正应力、切应力在规定了其符号后,叠加是代数求和(2分)。
20.答:1)、减小梁的跨度,增加支承约束;(2分)2)、调整加载方式,改善结构设计;(2 分)3)、增大截面惯性矩,改变截面形状。
(2分)四、作图题(共15分)21.略22.略五、计算题(共41分)23.(1)弹性模量E是表征材料抵抗弹性变形的能力;(2分)(2)E(./E s;(2 分)(3)E s/E c : (2 分)(4)=3\.5MPa(2 分):= 4.2MPa(2 分)•J c24.(1)c Ali = 5MPa(2 分)(7liC = 20MPa(2 分)(y(D = 7.5MPci(2 分)(2)A/.w = -0.03Smm(3 分),225.(1)M心= J = "l.25KN m(1 分)iTldX 8hh2W、=——= 648xlQ-6m3(1 分)cr inax=也些=1 JAMPa > [b] = 1 OMPa(2 分)max ▼ j r- 」此梁强度不够(1分)(2)[q] = 2.07 KN/m(3 分)(3)h = 2\(2 分)b - 144mm(2 分)26.计算挺杆柔度九=J宇=92.9 (2 分)人=« = 128.5 (2 分).I4>九,可见挺杆为大柔度压杆(2分)可以用欧拉公式FI= —— = 6.3xlO37V (2 分)Frr3VF 〃=工=3.58>〃“,安全。
材料力学清考试卷A答案
《材料力学》课程清考试卷 (A)2013-2014学年第2学期专业: 班级: 姓名: 学号:题号一二三四五六七总分得分评卷人一、填空题 (本大题共15空,每空 1 分,共 15 分)1、构件在外荷载作用下具有抵抗破坏的能力为材料的( );具有一定的抵抗变形的能力为材料的( );保持其原有平衡状态的能力为材料的( )。
强度、刚度、稳定性2、现代工程中常用的固体材料种类繁多,物理力学性能各异。
所以,在研究受力后物体(构件)内部的力学响应时,除非有特别提示,一般将材料看成由( )、( )、( )的介质组成。
连续性、均匀性、各向同性。
3、构件所受的外力可以是各式各样的,有时是很复杂的。
材料力学根据构件的典型受力情况及截面上的内力分量可分为( )、( )、( )、( )四种基本变形。
拉伸或压缩、剪切、扭转、弯曲。
4、轴力是指通过横截面形心垂直于横截面作用的内力,而求轴力的基本方法是( )。
截面法5、空心圆轴外径为D,内径为d=D/2,两端受扭转力偶 作用,则其横截面上切应力呈( )分布,最大切应力为( ),最小切应力为( )6、图(a)、图(b)所示两圆轴的材料、长度相同,扭转时两轴表面上各点的剪应力相同,此时作用于两端的扭转力偶之比m a:m b=( 1/8 )二、选择题 (本大题共 5题,每小题 4 分,共20 分)1、危险截面是( )所在的截面。
A、最大面积B、最小面积C、最大应力D、最大内力2、长度、横截面面积相同的两杆,一杆为钢杆,另一杆为铜杆,在相同拉力作用下,下述结论正确的是( )。
(A) 钢=铜 , ΔL钢<ΔL铜 (B) 钢=σ铜 , ΔL钢>ΔL铜 (C) 钢>铜 , ΔL钢<ΔL铜 (D) 钢<σ铜 , ΔL钢>ΔL铜3、圆轴受扭如图所示,已知截面上A点的剪应力为5MPa,则B点的剪应力是( B )。
(A) 5MPa (B) 10MPa (C) 15MPa (D) 04、如图所示高度等于宽度两倍(h=2b)的矩形截面梁,承受垂直方向的载荷,若仅将竖放截面改为平放截面,其它条件都不变,则梁的强度( )A、提高到原来的2倍题二、4图B、提高到原来的4倍C、降低到原来的1/2倍D、降低到原来的1/4倍5、 已知图示二梁的抗弯截面刚度EI相同,若二者自由端的挠度相等,则P1/P2=( )A、2题二、5图B、4C、8D、16三、判断题 (正确的在括号中打“√”、错误的打“×”,本大题共10 题,每小题 1分,共 10分)1、材料力学研究的主要问题是微小弹性变形问题,因此在研究构件的平衡与运动时,可不计构件的变形。
2013-14(1)材料力学考试卷A问题详解及评分实用标准
工业大学2013/2014学年 第一学期试卷A 答案及评分标准课程 材料力学 ___________________________ 班级_______________________________________________________________ 题序 一 二 三 四 五 六 七 八 九 十 总评 计分1.(15分)图示轴向拉压杆横截面面积A =1000mm 2,E =200GPa, P =10kN ,纵向分布载荷q =10kN/m ,a =1m 。
求:(1)画轴力图;(2)各段的应力;(3)最大切应力(绝对值); (4)最大正应变(绝对值);(5)杆的总伸长。
解:(1)轴力图(m ) 3(2)各段的应力左半段:0=σ 1右半段:)10(1010001000≤≤=⋅==x xMPa qx A F N σ 2 (3)最大切应力:MPa 52/max max ==στ 3 (4)最大正应变(绝对值):5max max 105/-⨯==E σε 2(5)杆的总伸长:mm dx EAx F l N 025.0)(1==∆⎰42.(20分) 直径为d 的圆轴,许用切应力[τ]=30MPa ,剪切弹性模量G =80GPa 。
(1) 画出扭矩图; (2) 选择轴的直径;(3) 以计算所得的直径求最大单位长度扭转角; (4) 以计算所得的直径求两端的相对扭转角;解:(1) 画出扭矩图5(2) 选择轴的直径][/16/3max max max τπτ≤⋅==d T W T P 3mm T d 71.46][/163max =⋅≥τπ 2取 d =47mm 1(3) 以计算所得的直径求最大单位长度扭转角)/(100.8)/(1057.1/12max m m rad GI T o p --⨯=⨯=='ϕ 3(4) 以计算所得的直径求两端的相对扭转角;)(1074.3)(1053.6108032105.04.010*******.06.010*******.03.013439439439o i pii rad d d d GI lT --⨯=⨯=⨯⨯⨯⨯⨯⨯-⨯⨯⨯⨯⨯⨯+⨯⨯⨯⨯⨯⨯==∑πππϕ 63.(20分)T 型截面铸铁梁的荷载与截面尺寸如下图所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
工业大学2013/2014学年 第一学期试卷A 答案及评分标准
课程 材料力学 ___________________________
班级_______________________________________________________________ 题序 一 二 三 四 五 六 七 八 九 十 总评 计分
1.(15分)图示轴向拉压杆横截面面积A =1000mm 2
,E =200GPa, P =10kN ,纵向分布载荷q =10kN/m ,a =1m 。
求:(1)画轴力图;(2)各段的应力;(3)最大切应力(绝对值); (4)最大正应变(绝对值);(5)杆的总伸长。
解:(1)轴力图
(m ) 3
(2)各段的应力
左半段:0=σ 1
右半段:)10(101000
1000
≤≤=⋅==
x xMPa qx A F N σ 2 (3)最大切应力:MPa 52/max max ==στ 3 (4)最大正应变(绝对值):5max max 105/-⨯==E σε 2
(5)杆的总伸长:mm dx EA
x F l N 025.0)
(1
==∆⎰
4
2.(20分)直径为d的圆轴,许用切应力[τ]=30MPa,剪切弹性模量G=80GPa。
(1)画出扭矩图;
(2)选择轴的直径;
(3)以计算所得的直径求最大单位长度扭转角;
(4)以计算所得的直径求两端的相对扭转角;
解:(1)画出扭矩图
5
(2)选择轴的直径
]
[
/
16
/3
max
max
max
τ
π
τ≤
⋅
=
=d
T
W
T
P
3
mm
T
d71
.
46
]
[
/
16
3
max
=
⋅
≥τ
π 2 取d=47mm 1 (3)以计算所得的直径求最大单位长度扭转角
)
/
(
10
0.8
)
/
(
10
57
.1
/1
2
max
m
m
rad
GI
T o
p
-
-⨯
=
⨯
=
='ϕ 3 (4)以计算所得的直径求两端的相对扭转角;
)
(
10
74
.3
)
(
10
53
.6
10
80
32
10
5.0
4.0
10
80
32
10
5.0
6.0
10
80
32
10
5.0
3.0
1
3
4
3
9
4
3
9
4
3
9
o
i p
i
i
rad
d
d
d
GI
l T
-
-⨯
=
⨯
=
⨯
⨯
⨯
⨯
⨯
⨯
-
⨯
⨯
⨯
⨯
⨯
⨯
+
⨯
⨯
⨯
⨯
⨯
⨯
=
=∑
π
π
π
ϕ
6
3.(20分)T 型截面铸铁梁的荷载与截面尺寸如下图所示。
已知I z =763cm 4,且
y 1=52mm,许用拉应力MPa t 30][=σ , 许用压应力MPa c 160][=σ。
试校核梁的正应力强度。
解:
∑∑==0,0y B
F M
,得
014192=⋅+⋅-⋅RA F ,F RA =2.5kN, F RB =10.5kN 5
弯矩图
5
][26.271076352100.44
61max
,t z B B t MPa I y M σσ
<=⨯⨯⨯=⋅= 2 ][13.4610763)5220120(100.44
62max
,c z B B
c MPa I y M σσ
<=⨯-+⨯⨯=⋅= 2 ][83.281076388105.2462max
,t z C C t MPa I y M σσ
<=⨯⨯⨯=⋅= 2
][04.1710
76352105.24
61max
,c z C C c MPa I y M σσ
<=⨯⨯⨯=⋅= 2 梁符合强度要求。
2
4.(15分)单元体应力状态如下图所示。
求:(1)指定斜截面上的应力;(2)主应力大小、方位;(3)将主平面标在单元体图上。
解:解析法:
MPa MPa MPa xy y x 300,200,200-=-==τσσ,060=α, 2 (1)指定斜截面上的应力
Mpa x y
x y
x 80..1592sin 2cos 2
2
=--+
+=
ατασσσσσα 3
Mpa x y
x 20.3232cos 2sin 2
=+-=
ατασστα 3
(2)主应力大小、方位; MPa x y
x y
x 56.360)2
(
2
2
2max =+-++=
τσσσσσ 3
MPa x y
x y
x 56.360)2
(
2
22min -=+--+=
τσσσσσ 2
MPa MPa MPa 56.360,0,56.360321-===σσσ 2 5.122tan 0=--
=y
x x
σστα,0015.28=α,或0015.118=α 3
(3)主平面单元体
2
应力圆
6 MPa R 56.36030020022=+= 3
MPa MPa MPa 56.360,0,56.360321-===σσσ 3
5.1200
300
2tan 0==
α,0015.28=α,或0015.118=α 3 MPa R 80.159)2120cos(00=-=ασα, 2 MPa R 20.323)2120sin(00=-=ατα 2
2
5.(15分)等截面圆轴上安装二齿轮C、D。
其直径D
1=200mm,D
2
=300mm。
已
知C轮上作用切向力P
1
=20kN,材料的许用应力[σ]=60MPa。
(1)用第三强度理论确定轴的直径;(2)画出危险点的应力状态。
解:(1)轴AB受力如图:
3
由∑=0
x
M,得100P1=150P2,P2=13.33kN。
M
C
= M B =2kN.m,
∑=0
y
M,F RB=4.44kN, F RA=15.56kN
∑=0
z
M,F HB=8.89kN, F HA=4.44kN 3 力图:
3
m kN M M M Cz Cy C .23.322=+=,m kN M M M Dz Dy D .98.22
2=+=
截面C 是危险截面。
][.38002
2
3σσ=≤=
+=W
m
N W
T M C r mm m d 4.860864.010
603800
323
6
==⨯⨯⨯≥π 3 (2)危险点的应力状态
3
6.(15分)图示A 端固定,B 端铰支的超静定梁,受H =0.01l 处重物Q 的自由落体冲击。
试求动荷系数K α,若A 端改为铰支(其他不变),动荷系数是变大还是缩小?
解:基本静定系,满足几何相容性条件w B =0. 2
11)(x F x M B =,222)2/()(Qx x l F x M B -+=
22112/)(,)(x l F x M x F x M B B +=∂∂=∂∂,221)
(,0)(x Q
x M Q x M -=∂∂=∂∂ 3
由卡氏第二定理:
0)6
5
38(1)
()()()(1
22
/0
2112
/0
1=-=
∂∂⋅+∂∂⋅=⎰⎰
Q F EI dx F x M EI x M dx F x M EI x M w B B l B l B
16
5Q
F B = 3 静位移
EI Ql dx Q x M EI x M dx Q x M EI x M w l l C 7687)()()()(3
122
/0
2112
/0
1=∂∂⋅+∂∂⋅=
⎰⎰
3 217538411211Ql
EI
w H K C d ++=+
+= 2 若A 端改为铰支(其他不变),则静位移
c l C
w EI
Ql dx x EI Qx w >=⋅='⎰482223
12
/0
, 故动荷系数缩小。
2。
