平面直角坐标系重点难点题
初一数学平面直角坐标系30道必做题(含答案和解析及考点)

初一数学平面直角坐标系30道必做题(含答案和解析及考点)1、如图是小刚画的一张脸,他对妹妹说“如果我用(1,3)表示左眼,用(3,3)表示右眼,那么嘴的位置可以表示成.答案:(2,1).解析:略.考点:函数——平面直角坐标系——点的位置与坐标.2、如图所示,小颖从家到达莲花中学要穿过一个居民小区,若小区的道路均是正南或正东方向,小颖走下面哪条线路不能到达学校().A.(0,4)(0,0)(4,0)B.(0,4)(4,4)(4,0)C.(0,4)(1,4)(1,1)(4,1)(4,0)D.(0,4)(3,4)(4,2)(4,0)答案:D.解析:(3,4)(4,2)所走路线为斜线,不符合题意,不能正常到达学校.考点:函数——平面直角坐标系.3、如图,围棋盘放置在某个平面直角坐标系内,白棋②的坐标为(-7,-4),白棋④的坐标为(-6,-8),那么,黑棋的坐标应该分别是.答案:(-6,-6),(-4,-7).解析:黑棋①的坐标是(-6,-6),黑棋③的坐标是(-4,-7).考点:函数——平面直角坐标系——点的位置与坐标.4、如果点A(x,y)在第三象限,则点B(-x,y-1)在().A. 第一象限B. 第二象限C. 第三象限D. 第四象限答案: D.解析:∵点A(x,y)在第三象限,∴{x<0y<0.∴-x>0,y-1<0.∴点B(-x,y-1)在第四象限.考点:函数——平面直角坐标系——点的位置与坐标.5、如图的坐标平面上有P、Q两点,其坐标分别为(5,a)、(b,7).根据图中P、Q两点的位置,判断点()落在第象限.答案:四.解析:由图象可知,b<5,a<7.∴6-b>0,a-10<0.∴点(6-b,a-10)落在第四象限.考点:函数——平面直角坐标系——点的位置与坐标.6、已知A(-2,0),B(a,0)且AB=5,则B点坐标为.答案:(3,0)或(-7,0).解析:由题知︱a+2︱=5,∴a=3或-7.∴B点坐标为(3,0)或(-7,0).考点:函数——平面直角坐标系——坐标与距离.7、若点A(-2,n)在x轴上,则点B(n-1,n+1)在().A. 第一象限B. 第二象限C. 第三象限D. 第四象限答案:B.解析:略.考点:函数——平面直角坐标系——点的位置与坐标.8、点P(m+3,m+1)在直角坐标系的x轴上,则点P的坐标为().A.(1,-2)B.(2,0)C.(4,0)D.(0,-4)答案:B.解析:∵点P(m+3,m+1)在直角坐标系的轴上.∴m+1=0.∴m=-1.∴点P的坐标为(2,0).考点:函数——平面直角坐标系——点的位置与坐标.9、已知点M(3a-8,a-1).(1)若点M在第二象限,并且a为整数,则点M的坐标为.(2)若点N的坐标为(3,-6),并且直线MN∥x轴,则点M的坐标为.答案:(1)(-2,1).(2)(-23,-6).解析:(1)若点M在第二象限,3a<0,a-1>0.∴1<a<8,又a为整数.3∴a=2.∴M(-2,1).(2)若点N的坐标为(3,-6),并且直线MN∥x轴.∴a-1=-6,即a=7.∴点M(-23,-6).考点:函数——平面直角坐标系——点的位置与坐标.10、若点P(-1,a),Q(b,2),且PQ∥x轴,则a ,b .答案:a=2.b≠-1.解析:∵PQ∥x轴.∴PQ两点的纵坐标相同.∴a=2.又∵P、Q应为不重合的两点.∴b≠-1.考点:函数——平面直角坐标系——点的位置与坐标.11、点P(a,b)是平面直角坐标系内的点,请根据点的坐标判断点P的特征:(1)若a=b,则P点在.(2)若a+b=0,则P点在.答案:(1)一三象限坐标轴夹角平分线上.(2)二四象限坐标轴夹角平分线上.解析:(1)略.(2)略.考点:函数——平面直角坐标系——点的位置与坐标.12、若点M在第一、三象限的角平分线上,且点M到x轴的距离为2,则点M的坐标是().A.(2,2)B.(-2,-2)C.(2,2)或(-2,-2)D.(2,-2)或(-2,2)答案:C.解析:略.考点:函数——平面直角坐标系——坐标与距离.13、已知点(3-2k2,4k-3)在第一象限的角平分线上,则k= .答案:1.解析:略.考点:函数——平面直角坐标系——点的位置与坐标.14、若点M(5-a,2a-6)在第四象限,且点M到x轴与y轴的距离相等,试求(a-2)2014-a-2015的值.答案:0.解析:由题意得,5-a+2a-6=0.解得a=1.所以,(a-2)2014-a-2015=(1-2)2014-1-2015=1-1=0.考点:函数——平面直角坐标系——坐标与距离.15、若点P位于y轴左方,距y轴3个单位长,位于x轴上方,距x轴四个单位长,则点P的坐标是.答案:(-3,4).解析:略.考点:函数——平面直角坐标系——特殊点的坐标.16、在平面直角坐标系中,点P(-3,6)关于y轴的对称点的坐标为.答案:(3,6).解析:根据关于谁对称,谁不变,可知,点P(-3,6)关于y轴的对称点的坐标为(3,6). 考点:几何变换——图形的对称——关于x轴、y轴对称的点的坐标.17、在平面直角坐标系中,点P(-1,2)关于y轴的对称点为.答案:(1,2).解析:由关于谁对称谁不变,可知点P(-1,2)关于y轴的对称点为(1,2).考点:几何变换——图形的对称——关于x轴、y轴对称的点的坐标.18、在平面直角坐标系中,点P(-1,2)关于x轴的对称点在第象限.答案:三.解析:点P(-1,2)满足点在第二象限的条件.关于x轴的对称点的横坐标与P点的横坐标相同,是-2.纵坐标互为相反数,是-3.则P关于x 轴的对称点是(-2,-3),在第三象限.考点:几何变换——图形的对称——关于x轴、y轴对称的点的坐标.19、平面直角坐标系中,将线段OA向左平移2个单位,平移后,点O 、A的对应点分别为点O1 、A1,则点O1 、A1的坐标分别是().A.(0,0),(1,4)B.(0,0),(3,4)C.(-2,0),(1,4)D.(-2,0),(-1,4)答案:D.解析:∵线段OA向左平移2个单位,点O(0,0),A(1,4).∴点O1,A1的坐标分别是(-2,0),(-1,4).考点:几何变换——图形的平移——坐标与图形变化:平移.20、已知三角形的三个顶点坐标分别是(-2,1),(2,3),(-3,-1),把△ABC运动到一个确定位置,在下列各点坐标中,()是平移得到的.A.(0,3),(0,1),(-1,-1)B.(-3,2),(3,2),(-4,0)C.(1,-2),(3,2),(-1,-3)D.(-1,3),(3,5),(-2,1)答案:D.解析:由(-2,1)→(-1,3),(2,3)→(3,5),(-3,-1)→(-2,1)可以看作点向右平移1个单位长度,向上平移2个单位长度,而图形的平移是相同的,所以D对,A、B、C错.考点:函数——平面直角坐标系——点的位置与坐标.几何变换——图形的平移——点的平移.21、线段CD是由线段AB平移得到的,点A(-1,4)的对应点为,则点B(-4,-1)的对应点D坐标为().A.(2,9)B.(5,3)C.(1,2)D.(-9,-4)答案:C.解析:略.考点:函数——平面直角坐标系——点的位置与坐标.22、已知点A(0,0),B(3,0),点C在y轴上,且△ABC的面积为6,则点C的坐标是.答案:(0,4)或(0,-4).解析:由题意可知1AC·AB=6.2∴AC=4.∴点C的坐标是(0,4)或(0,-4).考点:函数——平面直角坐标系——坐标与面积.23、如图所示,半圆AB平移到半圆CD的位置时所扫过的面积为().A.3B.3+πC.6D.6+π答案:C.解析:扫过面积即为矩形ABDC的面积.∴扫过面积=2×3=6.考点:函数——平面直角坐标系——坐标与面积.24、在正方形网格上有一个△ABC ,网格上最小正方形的边长为1.(1) 把△ABC 平移,使点A 移动到点A’的位置,画出平移后的△A’B’C’,写出结论:__________.(2)△A’B’C’的面积为__________.(3)若点A 的坐标是(-5,2),点C’为坐标是(0,-2),在图中画出平面直角坐标系,点B’的坐标是__________.答案:(1) 结论:A’B’∥AB (答案不唯一).(2)△A’B’C’的面积是为5. (3)点B’的坐标是(-3,-3).解析:(1)平移后的△A’B’C’如图所示,结论:A’B’∥AB (答案不唯一).(2)观察图形可知,△A’B’C’内接在一个长为4,宽为3的长方形中.S △A’B’C’=4×3 −12×1×3−12×1×3−12×2×4=5. ∴△A’B’C’的面积是为5.(3)平面直角坐标系如图所示,点B’的坐标是(-3,-3).考点:三角形——三角形基础——三角形面积及等积变换.几何变换——图形的平移——平移的性质——坐标与图形变化:平移——作图:平移变换.25、定义:f (a,b )=(b,a ),g (m,n )=(-m,-n ).例如f (2,3)=(3,2),g (-1,-4)=(1,4).则g[f (-5,6)] 等于 . 答案:(-6,5).解析:根据所给定义,g[f (-5,6)]=g (6,-5)=(-6,5). 考点:式——探究规律——定义新运算.函数——平面直角坐标系.26、在平面直角坐标系中,对于平面内任一点(m ,n ),规定以下两种变换①f (m ,n )=(m ,-n ),如f (2,1)=(2,-1);②g (m ,n )=(-m ,-n ),如g (2,1)=(-2,-1).按照以上变换有:f[g (3,4)]=f (-3,-4)=(-3,4),那么g[f (-3,2)] 等于( ). A.(3,2) B.(3,-2) C.(-3,2) D.(-3,-2) 答案:A.解析:∵f (-3,2)=(-3,-2).∴g[f (-3,2)]=g (-3,-2)=(3,2). 考点:式——探究规律——定义新运算.27、观察下列有规律的点的坐标:A 1(1,1),A 2(2,-4),A 3(3,4),A 4(4,-2),A 5(5,7),A 6(6,−43),A 7(7,10),A 8(8,-1)依此规律,A 11的坐标为 ,A 12的坐标为 . A.(12,16),(12,−23) B.(11,15),(11,−23)C.(11,16),(11,−23) D.(11,16),(12,−23)答案:D. 解析:略.考点:函数——平面直角坐标系——点的位置与坐标.28、如图,边长为1,2的长方形ABCD 以右下角的顶点为中心旋转90°,此时A 点的坐标为 ;依次旋转2011次,则顶点A 的坐标为 . A.(3,3),(3027,0) B.(3,3),(3017,0) C.(3,2),(3027,0) D.(3,2),(3017,0) 答案:D. 解析:略.考点:式——探究规律.方程与不等式.函数——平面直角坐标系.29、一个粒子在第一象限内及x 轴、y 轴上运动,在第1min 内它从原点运动到(1,0),而后接着按如图所示方式在与x 轴、y 轴平行的方向上来回运动,且每分钟移动1个单位长度,那么,在2011min 后,求这个粒子所处的位置坐标.A.(41,13)B.(41,14)C.(44,13)D.(44,14) 答案:C.解析:弄清粒子的运动规律,并求出靠近2011min 后粒子所在的特殊点的坐标,最后确定所求点的坐标.对于这种运算数较大的题目,我们首先来寻找规律,先观察横坐标与纵坐标相同的点:(0,0),粒子运动了0min. (1,1),粒子运动了1×2=2(min ),向左运动. (2,2),粒子运动了2×3=6(min ),向下运动.(3,3),粒子运动了3×4=12(min),向左运动.(4,4),粒子运动了4×5=20(min),向下运动.……于是点(44,44)处粒子运动了44×45=1980(min).这时粒子向下运动,从而在运动了2011后,粒子所在的位置是(44,44-31),即(44,13).考点:函数——平面直角坐标系.30、在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位.其行走路线如图所示.①填写下列各点的坐标:A1(,),A3(,),A12(,).②写出点A4n的坐标为(是正整数).③指出蚂蚁从点A100到A101的运动方向为.A. ①(1,1),(1,0),(5,0);②(2n,0);③ 从下到上.B. ①(1,1),(1,0),(6,0);②(2n,0);③ 从上到下.C. ①(0,1),(1,0),(5,0);②(2n,0);③ 从上到下.D. ①(0,1),(1,0),(6,0);②(2n,0);③ 从下到上.答案:D.解析:略.考点:函数——平面直角坐标系——点的位置与坐标——坐标与距离.。
精编7年级数学下册难点探究专题平面直角坐标系中的变化规律(带答案解析)

难点探究专题:平面直角坐标系中的变化规律——掌握不同规律,以不变应万变◆类型一 沿坐标轴方向运动的点的坐标规律探究1.如图,动点P 在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2)……按这样的运动规律,经过第2016次运动后,动点P 的坐标是________.2.(2017·阿坝州中考)如图,在平面直角坐标系中,一动点从原点O 出发,沿着箭头所示方向,每次移动1个单位,依次得到点P 1(0,1),P 2(1,1),P 3(1,0),P 4(1,-1),P 5(2,-1),P 6(2,0),…,则点P 2017的坐标是________.◆类型二 绕原点呈“回”字形运动的点的坐标规律探究3.在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点.如图,由里向外数第2个正方形开始,分别是由第1个正方形各顶点的横坐标和纵坐标都乘2,3,…得到的,请你观察图形,猜想由里向外第10个正方形四条边上的整点个数共有( )A .10个B .20个C .40个D .80个第3题图 第4题图4.(2017·温州中考)我们把1,1,2,3,5,8,13,21,…这组数称为斐波那契数列,为了进一步研究,依次以这列数为半径作90°圆弧P 1P 2︵,P 2P 3︵,P 3P 4︵,…得到斐波那契螺旋线,然后顺次连接P 1P 2,P 2P 3,P 3P 4,…得到螺旋折线(如图),已知点P 1(0,1),P 2(-1,0),P 3(0,-1),则该折线上的点P 9的坐标为( )A .(-6,24)B .(-6,25)C.(-5,24) D.(-5,25)◆类型三图形变化中的点的坐标探究5.(2017·河南模拟)如图,点A(2,0),B(0,2),将扇形AOB沿x轴正方向做无滑动的滚动,在滚动过程中点O的对应点依次记为点O1,点O2,点O3…,则O10的坐标是()A.(16+4π,0) B.(14+4π,2)C.(14+3π,2) D.(12+3π,0)6.如图,在直角坐标系中,第一次将三角形OAB变换成三角形OA1B1,第二次将三角形OA1B1变换成三角形OA2B2,第三次将三角形OA2B2变换成三角形OA3B3.已知A(1,3),A1(2,3),A2(4,3),A3(8,3),B(2,0),B1(4,0),B2(8,0),B3(16,0).(1)观察每次变换后的三角形有何变化,找出规律,按此变换规律再将三角形OA3B3变换成三角形OA4B4,则A4的坐标是__________,B4的坐标是__________;(2)若按(1)中找到的规律将三角形OAB进行了n次变换,得到三角形OA n B n,比较每次变换中三角形顶点坐标有何变化,找出规律,推测点A n的坐标是__________,点B n的坐标是__________.参考答案与解析1.(2016,0)解析:结合图象可知,当运动次数为偶数次时,P点运动到x轴上,且横坐标与运动次数相等.∵2016为偶数,∴运动2016次后,动点P的坐标是(2016,0).2.(672,1)解析:由已知得P7(2,1),P13(4,1),所以P6n+1(2n,1).因为2017÷6=336……1,所以P2017(336×2,1),即P2017(672,1).3.C解析:每个正方形四个顶点一定为整点,由里向外第n个正方形每条边上除顶可见,第n个正方形每条边上除顶点外还有(n-1)个整点,四条边上除顶点外有4(n-1)个整点,加上4个顶点,共有4(n-1)+4=4n(个)整点.当n=10时,4n=4×10=40,即由里向外第10个正方形的四条边上共有40个整点.故选C.4.B解析:由题意,P5在P2的正上方,推出P9在P6的正上方,且到P6的距离为21+5=26,所以P9的坐标为(-6,25),故选B.5.C6.(1)(16,3)(32,0)(2)(2n,3)(2n+1,0)解析:(1)∵A1(2,3),A2(4,3),A3(8,3),∴A4的横坐标为24=16,纵坐标为3.故点A4的坐标为(16,3).又∵B1(4,0),B2(8,0),B3(16,0),∴B4的横坐标为25=32,纵坐标为0.故点B4的坐标为(32,0).(2)由A1(2,3),A2(4,3),A3(8,3),可以发现它们各点坐标的关系为横坐标是2n,纵坐标都是3.故点A n的坐标为(2n,0).由B1(4,0),B2(8,0),B3(16,0),可以发现它们各点坐标的关系为横坐标是2n+1,纵坐标都是0.故点B n的坐标为(2n+1,0).。
七年级平面直角坐标系动点规律问题(经典难题)
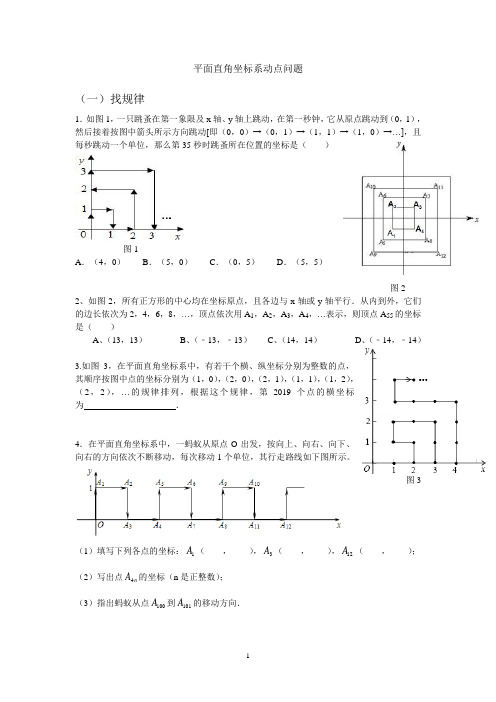
平面直角坐标系动点问题(一)找规律1.如图1,一只跳蚤在第一象限及x 轴、y 轴上跳动,在第一秒钟,它从原点跳动到(0,1),然后接着按图中箭头所示方向跳动[即(0,0)→(0,1)→(1,1)→(1,0)→…],且每秒跳动一个单位,那么第35秒时跳蚤所在位置的坐标是( )图1A .(4,0)B .(5,0)C .(0,5)D .(5,5)图22、如图2,所有正方形的中心均在坐标原点,且各边与x 轴或y 轴平行.从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A 1,A 2,A 3,A 4,…表示,则顶点A 55的坐标是( ) A 、(13,13) B 、(﹣13,﹣13) C 、(14,14) D 、(﹣14,﹣14)3.如图3,在平面直角坐标系中,有若干个横、纵坐标分别为整数的点,其顺序按图中点的坐标分别为(1,0),(2,0),(2,1),(1,1),(1,2),(2,2),…的规律排列,根据这个规律,第2019个点的横坐标为 .4.在平面直角坐标系中,一蚂蚁从原点O 出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其行走路线如下图所示。
图3(1)填写下列各点的坐标:1A (____,____),3A (____,____),12A (____,____); (2)写出点n A 4的坐标(n 是正整数); (3)指出蚂蚁从点100A 到101A 的移动方向.5.观察下列有序数对:(3,﹣1)(﹣5,)(7,﹣)(﹣9,)…根据你发现的规律,第100个有序数对是 .6、观察下列有规律的点的坐标:依此规律,A 11的坐标为 ,A 12的坐标为 .7、以0为原点,正东,正北方向为x 轴,y 轴正方向建立平面直角坐标系,一个机器人从原点O 点出发,向正东方向走3米到达A 1点,再向正北方向走6米到达A 2,再向正西方向走9米到达A 3,再向正南方向走12米到达A 4,再向正东方向走15米到达A 5,按此规律走下去,当机器人走到A 6时,A 6的坐标是 .8、如图,将边长为1的正三角形OAP 沿x 轴正方向连续翻转2019次,点P 依次落在点201921,,,P P P 的位置,则点2019P 的横坐标为 .9、如图,在平面直角坐标系上有个点P (1,0),点P 第1次向上跳动1个单位至点P 1(1,1),紧接着第2次向左跳动2个单位至点P 2(﹣1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…,依此规律跳动下去,点P 第100次跳动至点P 100的坐标是 .点P 第2019次跳动至点P 2019的坐标是 .图4 图5 10、如图5,已知A l (1,0),A 2(1,1),A 3(﹣1,1),A 4(﹣1,﹣1),A 5(2,﹣1),….则点A 2019的坐标为 .1PAOyxP1. 如图,一个粒子在第一象限内及x 、y 轴上运动,在第一分钟内它从原点运动到()1,0,而后它接着按图所示在x 轴、y 轴平行的方向上来回运动,且每分钟移动1个长度单位,那么,在1989分钟后这个粒子所处的位置是( ).A .()35,44B .()36,45C .()37,45D .()44,352. 如果将点P 绕定点M 旋转180︒后与点Q 重合,那么称点P 与点Q 关于点M 对称,定点M 叫做对称中心,此时,点M 是线段PQ 的中点,如图,在直角坐标系中,ABO △的顶点A 、B 、O 的坐标分别为()1,0、()0,1、()0,0,点1P ,2P ,3P ,…中相邻两点都关于ABO △的一个顶点对称,点1P 与点2P 关于点A 对称,点2P 与点3P 关于点B 对称,点3P 与点4P 关于点O 对称,点4P 与点5P 关于点A 对称,点5P 与点6P 关于点B 对称,点6P 与点7P 关于点O 对称,…对称中心分别是A ,B ,O ,A ,B ,O ,…且这些对称中心依次循环,已知1P 的坐标是()1,1.试写出点2P 、7P 、100P 的坐标.3. 如图,在平面直角坐标系中,四边形各顶点的坐标分别为:()0,0A ,()7,0B ,()9,5C ,()2,7D .(1)求此四边形的面积.(2)在坐标轴上,你能否找到一点P ,使50PBC S =△?若能,求出P 点坐标;若不能,请说明理由.4. 如图①,已知OABC 是一个长方形,其中顶点A 、B 的坐标分别为()0,a 和()9,a ,点E在AB 上,且13AE AB =,点F 在OC 上,且13OF OC =.点G 在OA 上,且使GEC △的面积为20,GFB △的面积为16,试求a 的值.图②5. 如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如()1,0,()2,0,()2,1,()1,1,()1,2,()2,2……根据这个规律,第2019个点的横坐标为_______.6. 在平面直角坐标系xOy 中,我们把横、纵坐标都是整数的点叫做整点.已知点()0,4A ,点B 是x 轴正半轴上的整点,记AOB △内部(不包括边界)的整点个数为m ,当3m =时,点B 的横坐标的所有可能值是_______;当点B 的横坐标为4n (n 为正整数)时,m =________(用含n 的代数式表示).7. 如图,把自然数按图的次序排在直角坐标系中,每个自然数都对应着一个坐标.如1的对应点是原点()0,0,3的对应点是()1,1,16的对应点是()1,2-,那么2019的对应点的坐标是_______.8.如图,长方形BCDE 的各边分别平行于x 轴或y 轴,物体甲和物体乙由点()2,0A 同时出发,沿长方形BCDE 的边作环绕运动,物体甲按逆时针方向以每秒1个单位长度的速度匀速运动,物体乙按顺时针方向以每秒2个单位长度的速度匀速运动,求两个物体开始运动后的第2019次相遇地点的坐标.9. 在平面直角坐标系中,如图①,将线段AB 平移至线段CD ,连接AC 、BD . (1)直接写出图中相等的线段、平行的线段; (2)已知()3,0A -、()2,2B --,点C 在y 轴的正半轴上.点D 在第一象限内,且5ACD S =△,求点C 、D 的坐标;(3)如图②,在平面直角坐标系中,已知一定点,()1,0M ,两个动点(),21E a a +、(),23F b b -+,请你探索是否存在以两个动点E 、F 为端点的线段EF 平行于线段OM 且等于线段OM .若存在,求以点O 、M 、E 、F 为顶点的四边形的面积,若不存在,请说明理由.图②10 . 如图,AOCD 是放置在平面直角坐标系内的梯形,其中O 是坐标原点.点A 、C 、D 的坐标分别为()0,8,()5,0,()3,8,若点P 在梯形内,且PAD POC S S =△△,PAO PCD S S =△△,求P 点的坐标.11. 操作与研究(1)对数轴上的点P 进行如下操作:先把点P 表示的数乘以13,再把所得数对应的点向右平移1个单位,得到点P 的对应点'P B .点A ,B 在数轴上,对线段AB 上的每个点进行上述操作后得到线段''A B ,其中点A ,B 的对应点分别为'A ,'B .如图①,若点A 表示的数是3-,则点'A 表示的数是______;若点'B 表示的数是2,则点表示的数是______;已知线段AB 上的点E 经过上述操作后得到的对应点'E 与点E 重合,则点E 表示的数是_________.(2)如图②,在平面直角坐标系xOy 中,对正方形ABCD 及其内部的每个点进行如下操作:把每个点的横、纵坐标都乘以同一个实数a ,将得到的点先向右平移m 个单位,再向上平移n 个单位()0,0m n >>,得到正方形''''A B C D 及其内部的点,其中点A ,B 的对应点分别为'A ,'B .已知正方形ABCD 内部的一个点F 经过上述操作后得到的对应点'F 与点F 重合,求点F 的坐标.图①A B'-1-2-3-412340图②(二)几何综合问题1、已知点A 的坐标是(3,0)、AB=5,(1)当点B 在X 轴上时、求点B 的坐标、(2)当AB//y 轴时、求点B 的坐标2、如图,已知A 、B 两村庄的坐标分别为(2,2)、(7,4),一辆汽车在x 轴上行驶,从原点O 出发.(1)汽车行驶到什么位置时离A 村最近?写出此点的坐标. (2)汽车行驶到什么位置时离B 村最近?写出此点的坐标. (3)请在图中画出汽车行驶到什么位置时,距离两村的和最短?4.如图,在平面直角坐标系中,点A ,B 的坐标分别为(-1,0),(3,0),现同时将点A ,B 分别向上平移2个单位,再向右平移1个单位,分别得到点A ,B 的对应点C ,D ,连接AC ,BD ,CD .(1)求点C ,D 的坐标及四边形ABDC 的面积ABDC S 四边形D C 3-1BA O x y PDCBAOx y (2)在y 轴上是否存在一点P ,连接PA ,PB ,使PAB S ∆=ABDC S 四边形,若存在这样一点,求出点P 的坐标,若不存在,试说明理由.(3)点P 是线段BD 上的一个动点,连接PC ,PO ,当点P 在BD 上移动时(不与B ,D 重合)给出下列结论:①DCP BOP CPO ∠+∠∠的值不变,②DCP CPOBOP∠+∠∠的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.5.已知:在平面直角坐标系中,四边形ABCD 是长方形, ∠A =∠B =∠C =∠D =90°,AB ∥CD ,AB =CD =8cm ,AD =BC =6cm ,D 点与原点重合,坐标为(0,0). (1)写出点B 的坐标.(2)动点P 从点A 出发以每秒3个单位长度的速度向终点B 匀速运动, 动点Q 从点C 出发以每秒4个单位长度的速度沿射线CD 方向匀速运动,若P ,Q 两点同时出发,设运动时间为t 秒,当t 为何值时,PQ ∥BC ?(3)在Q 的运动过程中,当Q 运动到什么位置时,使△ADQ 的面积为9? 求出此时Q 点的坐标.6.如图在平面直角坐标系中,A(a,0),B(b,0),(﹣1,2).且|2a+b+1|+=0.(1)求a、b的值;(2)①在y轴的正半轴上存在一点M,使S△COM=S△ABC,求点M的坐标.②在坐标轴的其他位置是否存在点M,使S△COM=S△ABC仍成立?若存在,请直接写出符合条件的点M的坐标.7.如图,在下面的直角坐标系中,已知A(0,a),B(b,0),C(b,4)三点,其中a,b 满足关系式.(1)求a,b的值;(2)如果在第二象限内有一点P(m,),请用含m的式子表示四边形ABOP的面积;(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积与△ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.8.在平面直角坐标系中,点A(a,b)是第四象限内一点,AB⊥y轴于B,且B(0,b)是y轴负半轴上一点,b2=16,S△AOB=12.(1)求点A和点B的坐标;(2)如图1,点D为线段OA(端点除外)上某一点,过点D作AO垂线交x轴于E,交直线AB于F,∠EOD、∠AFD的平分线相交于N,求∠ONF的度数.(3)如图2,点D为线段OA(端点除外)上某一点,当点D在线段上运动时,过点D作直线EF交x轴正半轴于E,交直线AB于F,∠EOD,∠AFD的平分线相交于点N.若记∠ODF=α,请用α的式子表示∠ONF的大小,并说明理由.。
平面直角坐标系重难点题型(四大题型)(原卷版)

专题05 平面直角坐标系重难点题型(四大题型)【题型1 两点间距离】【题型2 求平面直角坐标系中动点问题的面积】【题型3 平面直角坐标系中规律题探究】【题型4 等腰三角形个数讨论问题】【题型1 两点间距离】1.在平面直角坐标系中,有A(﹣2,a+1),B(a﹣1,4),C(b﹣2,b)三点.(1)当AB∥x轴时,求A、B两点间的距离;(2)当CD⊥x轴于点D,且CD=1时,求点C的坐标.2.已知平面直角坐标系内的三点:A(a﹣1,﹣2),B(﹣3,a+2),C(b﹣6,2b).(1)当直线AB∥x轴时,求A,B两点间的距离;(2)当直线AC⊥x轴,点C在第二、四象限的角平分线上时,求点A和点C 的坐标.3.先阅读一段文字,再回答下列问题:已知在平面内两点坐标P1(x1,y1),P2(x2,y2),其两点间距离公式为P1P2=,同时,当两点所在的直线在坐标轴上或平行于x轴或垂直于x轴时,两点距离公式可简化成|x1﹣x2|或|y2﹣y1|.(1)已知A(3,5),B(﹣2,﹣1),试求A,B两点的距离;(2)已知A,B在平行于y轴的直线上,点A的纵坐标为6,点B的纵坐标为﹣4,试求A,B两点的距离;(3)已知一个三角形各顶点坐标为A(0,6),B(﹣3,2),C(3,2),找出三角形中相等的边?说明理由.4.先阅读一段文字,再回答下列问题:已知在平面内两点坐标P1(x1,y1),P2(x2,y2),其两点间距离公式为:p1p2=,例如:点(3,2)和(4,0)的距离为.同时,当两点所在的直线在坐标轴上或平行于x轴或平行于y轴距离公式可简化成:p1p2=|x1﹣x2|或p1p2=|y1﹣y2|.(1)已知A、B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为2,则A,B两点的距离为;(2)线段AB平行于x轴,且AB=3,若点B的坐标为(2,4),则点A的坐标是;(3)已知A(3,5),B(﹣4,4),A,B两点的距离为;(4)已知△ABC三个顶点坐标为A(3,4),B(0,5),C(﹣1,2),请判断此三角形的形状,并说明理由.5.先阅读下列一段文字,再解答问题:已知在平面内有两点P1(x1,y1),P2(x2,y2),其两点间的距离公式为;同时,当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点距离公式可简化为|x2﹣x1|或|y2﹣y1|.(1)已知点A(2,4),B(﹣2,1),则AB=;(2)已知点C,D在平行于y的直线上,点C的纵坐标为3,点D的纵坐标为﹣2,则CD=;(3)已知点M和(1)中的点A有MA∥x轴,且MA=3,则点M的坐标为;(4)已知点P(3,1)和(1)中的点A,B,则线段P A,PB,AB中相等的两条线段是.6.先阅读下列一段文字,再回答后面的问题:已知在平面直角坐标系内两点P1(x1,y1),P2(x2,y2),其两点间的距离P1P2=,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|.(1)已知A(1,3),B(﹣3,﹣5),试求A,B两点间的距离;(2)已知线段MN∥y轴,MN=4,若点M的坐标为(2,﹣1),试求点N 的坐标.7.先阅读下列一段文字,再回答后面的问题.已知在平面内两点P1(x1,y1),P2(x2,y2),这两点间的距离P1P2=,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|.(1)已知A(2,4),B(﹣3,﹣8),试求A,B两点间的距离;(2)已知A,B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为﹣1,试求A,B两点间的距离.8.阅读材料:两点间的距离公式:如果平面直角坐标系内有两点A(x1,y1)、B(x2,y2),那么A、B两点的距离AB=,则AB2=(x1﹣x2)2+(y1﹣y2)2.例如:若点A(4,1),B(3,2),则AB=,若点A(a,1),B(3,2),且AB=,则.根据实数章节所学的开方运算即可求出满足条件的a的值.根据上面材料完成下列各题:(1)若点A(﹣2,3),B(1,2),则A、B两点间的距离是.(2)若点A(﹣2,3),点B在x轴上,且A、B两点间的距离是5,求B 点坐标.9.在平面直角坐标系中,有A(﹣2,a+1),B(a﹣1,4),C(b﹣2,b)三点.(1)当点C在y轴上时,求点C的坐标;(2)当AB∥x轴时,求A,B两点间的距离;(3)当CD⊥x轴于点D,且CD=1时,求点C的坐标.10.先阅读下列一段文字,在回答后面的问题.已知在平面内两点P1(x1,y1)、P2(x2,y2),其两点间的距离公式,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|.(1)已知A(2,4)、B(﹣3,﹣8),试求A、B两点间的距离;(2)已知A、B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为﹣1,试求A、B两点间的距离.(3)已知一个三角形各顶点坐标为A(0,6)、B(﹣3,2)、C(3,2),你能判定此三角形的形状吗?说明理由.【题型2 求平面直角坐标系中动点问题的面积】11.如图所示,在平面直角坐标系中,已知A(0,1),B(2,0),C(4,3).(1)在平面直角坐标系中画出△ABC,则△ABC的面积是;(2)若点D与点C关于原点对称,则点D的坐标为;(3)已知P为x轴上一点,若△ABP的面积为4,求点P的坐标.12.如图,在平面直角坐标系中,已知A(a,0),B(b,0),其中a,b满足.(1)填空:a=,b=;(2)若在第三象限内有一点M(﹣2,m),用含m的式子表示△ABM的面积;(3)在(2)条件下,线段BM与y轴相交于C(0,﹣),当时,点P是y轴上的动点,当满足△PBM的面积是△ABM的面积的2倍时,求点P的坐标.13.如图,在平面直角坐标系内,已知点A的坐标为(3,2),点B的坐标为(3,﹣4),点P为直线AB上任意一点(不与A、B重合),点Q是点P 关于x轴的对称点.(1)在方格纸中标出A、B,并求出△ABO的面积;(2)设点P的纵坐标为a,求点Q的坐标;(3)设△OP A和△OPQ的面积相等,且点P在点Q的上方,求出此时P点坐标.14.如图,在平面直角坐标系中,已知A(a,0),B(b,0),其中a,b满足a2+2a+1+|3a+b|=0.(1)填空:a=,b=;(2)若存在一点M(﹣2,m)(m<0),点M到x轴距离,到y轴距离,求△ABM的面积(用含m的式子表示);(3)在(2)条件下,当m=﹣1.5时,在y轴上有一点P,使得△MOP的面积与△ABM的面积相等,请求出点P的坐标.15.如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(3,c)三点,其中a、b、c满足关系式:|a﹣2|+(b﹣3)2+=0.(1)求a、b、c的值;(2)如果在第二象限内有一点P(m,),请用含m的式子表示四边形ABOP 的面积;(3)在(2)的条件下,是否存在负整数m,使四边形ABOP的面积不小于△AOP面积的两倍?若存在,求出所有满足条件的点P的坐标,若不存在,请说明理由.16.如图,已知在平面直角坐标系中,点A在y轴上,点B、C在x轴上,S△ABO =8,OA=OB,BC=10,点P的坐标是(﹣6,a),(1)求△ABC三个顶点A、B、C的坐标;(2)连接P A、PB,并用含字母a的式子表示△P AB的面积(a≠2);(3)在(2)问的条件下,是否存在点P,使△P AB的面积等于△ABC的面积?如果存在,请求出点P的坐标;若不存在,请说明理由.17.如图,在平面直角坐标系中,A(a,0),B(b,0),C(﹣1,2),且|a+2|+=0.(1)求a,b的值;(2)①在x轴的正半轴上存在一点M,使△COM的面积=△ABC的面积,求出点M的坐标;②在坐标轴的其它位置是否存在点M,使△COM的面积=△ABC的面积恒成立?若存在,请直接写出符合条件的点M的坐标.18.如图,直线AB与x轴,y轴分别相交于点A(6,0),B(0,8),M是OB上一点,若将△ABM沿AM折叠,则点B恰好落在x轴上的点B'处.求:(1)点B'的坐标;(2)△ABM的面积.19.如图在直角坐标系中,已知A(0,a),B(b,0)C(3,c)三点,若a,b,c满足关系式:|a﹣2|+(b﹣3)2+=0.(1)求a,b,c的值.(2)求四边形AOBC的面积.(3)是否存在点P(x,﹣x),使△AOP的面积为四边形AOBC的面积的两倍?若存在,求出点P的坐标,若不存在,请说明理由.20.已知:在平面直角坐标系中,A(0,1),B(2,0),C(4,3)(1)求△ABC的面积;(2)设点P在x轴上,且△ABP与△ABC的面积相等,求点P的坐标.21.如图,在平面直角坐标系中,A(2,2),B(﹣1,0),C(3,0)(1)求△ABC面积;(2)在y轴上存在一点D,使得△AOD的面积是△ABC面积的2倍,求出点D的坐标;(3)在平面内有点P(3,m),是否存在m值,使△AOP的面积等于△ABC 面积的2倍?若存在,直接写出m的值;若不存在,请说明理由.22.在平面直角坐标系中,△ABC的顶点坐标分别为A(2,0),B(0,4),C(﹣3,2).(1)如图1,求△ABC的面积.(2)若点P的坐标为(m,0),①请直接写出线段AP的长为(用含m的式子表示);②当S△P AB =2S△ABC时,求m的值.(3)如图2,若AC交y轴于点D,直接写出点D的坐标为.23.如图,在平面直角坐标系中,点A(﹣3b,0)为x轴负半轴上一点,点B (0,4b)为y轴正半轴上一点,其中b满足方程:3(b+1)=6.(1)求点A、B的坐标;(2)点C为y轴负半轴上一点,且△ABC的面积为12,求点C的坐标;(3)在(2)的条件下,在x轴上是否存在点P,使得△PBC的面积等于△ABC的面积的一半?若存在,求出相应的点P的坐标;若不存在,请说明理由.【题型3 平面直角坐标系中规律题探究】24.如图,动点P按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次运动到点(2,0),第3次运动到点(3,2),…,按这样的运动规律,则第2021次运动到点()A.(2021,1)B.(2021,2)C.(2020,1)D.(2021,0)25.有一组数,按照下列规律排列:1,2,3,6,5,4,7,8,9,10,15,14,13,12,11,16,17,18,19,20,21,……数字5在第三行左数第二个,我们用(3,2)点示5的位置,那点这组成数里的数字100的位置可以表示为()A.(14,9)B.(14,10)C.(14,11)D.(14,12)26.如图,在平面直角坐标系中,A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2).把一条长为2012个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A﹣B﹣C﹣D﹣A﹣…的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是()A.(1,﹣1)B.(﹣1,1)C.(﹣1,﹣2)D.(1,﹣2)27.如图,在平面直角坐标系上有个点P(1,0),点P第一次向上跳动1个单位至P1(1,1),紧接着第二次向左跳动2个单位至点P2(﹣1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…,依此规律跳动下去,点P第100次跳动至点P100的坐标是()A.(﹣24,49)B.(﹣25,50)C.(26,50)D.(26,51)28.如图,一个机器人从O点出发,向正东方向走3m到达A1点,再向正北方向走6m到达A2点,再向正西方向走9m到达A3点,再向正南方向走12m到达A4点,再向正东方向走15m到达A5点.按如此规律走下去,当机器人走到A6点时,离O点的距离是()A.10m B.12m C.15m D.20m29.如图,将正整数按有图所示规律排列下去,若用有序数对(n,m)表示n 排从左到右第m个数.如(4,3)表示9,则(10,3)表示.30.如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(0,1),(0,2),(1,2),(1,3),(0,3),(﹣1,3)…,根据这个规律探索可得,第90个点的坐标为.31.如图所示点A0(0,0),A1(1,2),A2(2,0),A3(3,﹣2),A4(4,0),…根据这个规律,探究可得点A2017坐标是.32.如图所示,一个机器人从O点出发,向正东方向走3m到达A1点,再向正北方向走6m到达A2点,再向正西方向走9m到达A3点,再向正南方向走12m 到达A4点,再向正东方向走15m到达A5点,按如此规律走下去,相对于点O,机器人走到A6时是位置.33.如图,在平面直角坐标系上有点A(1,0),点A第一次跳动至点A1(﹣1,1),第四次向右跳动5个单位至点A4(3,2),…,依此规律跳动下去,点A第100次跳动至点A100的坐标是.【题型4 等腰三角形个数讨论问题】34.如图,在平面直角坐标系中,点A的坐标是(6,6),点B在坐标轴上,且△OAB是等腰直角三角形,则点B的坐标不可能是()A.(0,6)B.(6,0)C.(12,0)D.(0,﹣6)35.如图,在平面直角坐标系中,A,B两点的坐标分别为(﹣4,0),(0,3),连接AB,点P在第二象限,以点P,A,B为顶点的等腰直角三角形有个,任意写出其中一个点P坐标为.36.如图,在平面直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3.(1)观察每次变换前后的三角形的变化规律,若将△OA3B3变换成△OA4B4,则A4的坐标是,B4的坐标是.(2)若按第(1)题找到的规律将△OAB进行n次变换,得到△OA n B n,比较每次变换中三角形顶点坐标有何变化,找出规律,推测A n的坐标是,B n的坐标是.(3)若按第(1)题找到的规律将△OAB进行n次变换,得到△OA n B n,则△OA n B n的面积S为37.如图,方格纸中小正方形的边长均为1个单位长度,A、B均为格点.(1)在图中建立直角坐标系,使点A、B的坐标分别为(3,3)和(﹣1,0);(2)在(1)中x轴上是否存在点C,使△ABC为等腰三角形(其中AB为腰)?若存在,请直接写出所有满足条件的点C的坐标.38.如图,在平面直角坐标系中,已知点A(﹣2,0),B(2,0).(1)画出等腰三角形ABC(画一个即可);(2)写出(1)中画出的三角形ABC的顶点C的坐标.。
专题03 平面直角坐标系(专题详解)(解析版)

专题03 平面直角坐标系专题03 平面直角坐标系 (1)7.1 平面直角坐标系 (2)知识框架 (2)一、基础知识点 (2)知识点1 有序数对 (2)知识点2 平面直角坐标系 (2)知识点3 点的坐标特点 (3)二、典型题型 (6)题型1 有序数对 (6)题型2 平面直角坐标系的概念 (6)题型3 点的坐标的特征 (6)一、点的位置与坐标 (7)二、点的坐标与距离 (8)三、点的坐标与平行于坐标轴的直线(数形结合思想) (8)四、点的坐标与图形的面积 (9)(1)知坐标,求面积 (9)(2)知面积,求坐标(方程思想) (10)(3)分类讨论 (12)三、难点题型 (14)题型1 确定点所在的象限 (14)题型2 点到坐标轴的距离 (14)题型3 探究平面直角坐标系坐标的变化规律 (15)7.2 坐标系的简单运用 (17)知识框架 (17)一、基础知识点 (17)知识点1 用坐标表示地理位置 (17)知识点2 用坐标表示平移 (18)二、典型题型 (20)题型1 用坐标表示地理位置 (20)题型2 用坐标表示平移 (21)一、点的平移 (21)(1)已知点和平移方式,求对应点 (21)(2)已知点和对应点,求平移方式 (21)二、图形的平移 (22)三、难点题型 (23)题型1 动点问题 (23)7.1 平面直角坐标系知识框架{基础知识点{有序数对平面直角坐标系点的坐标的特点典型题型{ 有序数对平面直角坐标系的概念点的坐标的特征{ 点的位置与坐标点的坐标与距离点的坐标与平行于坐标轴的直线(数形结合思想)点的坐标与图形的面积{知坐标,求面积知面积,求坐标(方程思想)分类讨论难点题型{确定点所在的象限点到坐标轴的距离探究平面直角坐标系坐标的变化规律 一、基础知识点知识点1 有序数对1)我们把有顺序的两个数a 与b 组成的数对,用于表示平面中某一确定位置的,叫作有序数对,记作(a ,b )注:①(a ,b )与(b ,a )表达的含义不同,注意有序数对的顺序②在表达有序数对时,一般行在前,列在后。
(完整版):平面直角坐标系经典例题解析

【平面直角坐标系重点考点例析】考点一:平面直角坐标系中点的特征例1 在平面直角坐标系中,点P(m,m-2)在第一象限内,则m的取值范围是.思路分析:根据第一象限的点的坐标,横坐标为正,纵坐标为正,可得出m的范围.解:由第一象限点的坐标的特点可得:20 mm>⎧⎨->⎩,解得:m>2.故答案为:m>2.点评:此题考查了点的坐标的知识,属于基础题,解答本题的关键是掌握第一象限的点的坐标,横坐标为正,纵坐标为正.例1 如果m是任意实数,则点P(m-4,m+1)一定不在()A.第一象限B.第二象限C.第三象限D.第四象限思路分析:求出点P的纵坐标一定大于横坐标,然后根据各象限的点的坐标特征解答.解:∵(m+1)-(m-4)=m+1-m+4=5,∴点P的纵坐标一定大于横坐标,∵第四象限的点的横坐标是正数,纵坐标是负数,∴第四象限的点的横坐标一定大于纵坐标,∴点P一定不在第四象限.故选D.点评:本题考查了点的坐标,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(—,+);第三象限(-,—);第四象限(+,-).例2 如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2012次相遇地点的坐标是()A.(2,0) B.(﹣1,1)C.(﹣2,1)D.(﹣1,﹣1)分析:利用行程问题中的相遇问题,由于矩形的边长为4和2,物体乙是物体甲的速度的2倍,求得每一次相遇的地点,找出规律即可解答.解答:解:矩形的边长为4和2,因为物体乙是物体甲的速度的2倍,时间相同,物体甲与物体乙的路程比为1:2,由题意知:①第一次相遇物体甲与物体乙行的路程和为12×1,物体甲行的路程为12×=4,物体乙行的路程为12×=8,在BC边相遇;②第二次相遇物体甲与物体乙行的路程和为12×2,物体甲行的路程为12×2×=8,物体乙行的路程为12×2×=16,在DE边相遇;③第三次相遇物体甲与物体乙行的路程和为12×3,物体甲行的路程为12×3×=12,物体乙行的路程为12×3×=24,在A点相遇;…此时甲乙回到原出发点,则每相遇三次,两点回到出发点,∵2012÷3=670…2,故两个物体运动后的第2012次相遇地点的是:第二次相遇地点,即物体甲行的路程为12×2×=8,物体乙行的路程为12×2×=16,在DE边相遇;此时相遇点的坐标为:(﹣1,﹣1),故选:D.点评:此题主要考查了行程问题中的相遇问题及按比例分配的运用,通过计算发现规律就可以解决问题.例2 如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P第2013次碰到矩形的边时,点P的坐标为()A.(1,4) B.(5,0)C.(6,4) D.(8,3)思路分析:根据反射角与入射角的定义作出图形,可知每6次反弹为一个循环组依次循环,用2013除以6,根据商和余数的情况确定所对应的点的坐标即可.解:如图,经过6次反弹后动点回到出发点(0,3),∵2013÷6=335…3,∴当点P第2013次碰到矩形的边时为第336个循环组的第3次反弹,点P的坐标为(8,3).故选D.点评:本题是对点的坐标的规律变化的考查了,作出图形,观察出每6次反弹为一个循环组依次循环是解题的关键,也是本题的难点.对应训练2.如图,在平面直角坐标系中,A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2).把一条长为2012个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A﹣B﹣C﹣D﹣A﹣…的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是()A .(1,﹣1)B . (﹣1,1)C . (﹣1,﹣2)D . (1,﹣2)分析: 根据点的坐标求出四边形ABCD 的周长,然后求出另一端是绕第几圈后的第几个单位长度,从而确定答案.解答: 解:∵A(1,1),B (﹣1,1),C (﹣1,﹣2),D (1,﹣2),∴AB=1﹣(﹣1)=2,BC=1﹣(﹣2)=3,CD=1﹣(﹣1)=2,DA=1﹣(﹣2)=3, ∴绕四边形ABCD 一周的细线长度为2+3+2+3=10, 2012÷10=201…2,∴细线另一端在绕四边形第202圈的第2个单位长度的位置, 即点B 的位置,点的坐标为(﹣1,1). 故选B .点评: 本题利用点的坐标考查了数字变化规律,根据点的坐标求出四边形ABCD 一周的长度,从而确定2012个单位长度的细线的另一端落在第几圈第几个单位长度的位置是解题的关键.例2 如图,在平面直角坐标系xOy 中,点P (-3,5)关于y 轴的对称点的坐标为( ) A .(—3,—5) B .(3,5) C .(3.—5) D .(5,—3) 答:B考点二:函数的概念及函数自变量的取值范围 例3 在函数1x y x+=中,自变量x 的取值范围是 . 思路分析:本题主要考查自变量的取值范围,函数关系中主要有二次根式和分式两部分.根据二次根式的意义,被开方数x+1≥0,根据分式有意义的条件,x≠0.就可以求出自变量x 的取值范围. 解:根据题意得:x+1≥0且x≠0 解得:x≥-1且x≠0. 例3 函数y=31x x +-中自变量x 的取值范围是( ) 思路分析:根据被开方数大于等于0,分母不等于0列式计算即可得解. 解:根据题意得,x+3≥0且x —1≠0, 解得x≥—3且x≠1. 故选D .点评:本题考查了函数自变量的范围,一般从三个方面考虑: (1)当函数表达式是整式时,自变量可取全体实数; (2)当函数表达式是分式时,考虑分式的分母不能为0; (3)当函数表达式是二次根式时,被开方数非负. 对应训练 3.函数2y x =+中自变量x 的取值范围是( )A .x >—2B .x≥2 C.x≠—2 D .x≥-2 3.A考点三:函数图象的运用例4 一天晚饭后,小明陪妈妈从家里出去散步,如图描述了他们散步过程中离家的距离S (米)与散步时间t (分)之间的函数关系,下面的描述符合他们散步情景的是( )A .从家出发,到了一家书店,看了一会儿书就回家了B .从家出发,到了一家书店,看了一会儿书,继续向前走了一段,然后回家了C .从家出发,一直散步(没有停留),然后回家了D .从家出发,散了一会儿步,到了一家书店,看了一会儿书,继续向前走了一段,18分钟后开始返回思路分析:根据图象可知,有一段时间内时间在增加,而路程没有增加,意味着有停留,与x 轴平行后的函数图象表现为随时间的增多路程又在增加,由此即可作出判断.解:A 、从家出发,到了一家书店,看了一会儿书就回家了,图象为梯形,错误;B 、从家出发,到了一家书店,看了一会儿书,继续向前走了一段,然后回家了,描述不准确,错误;C 、从家出发,一直散步(没有停留),然后回家了,图形为上升和下降的两条折线,错误;D 、从家出发,散了一会儿步,到了一家书店,看了一会儿书,继续向前走了一段,18分钟后开始返回从家出发,符合图象的特点,正确. 故选D .点评:考查了函数的图象,读懂图象是解决本题的关键.首先应理解函数图象的横轴和纵轴表示的量,再根据函数图象用排除法判断.例5 如图,ABCD 的边长为8,面积为32,四个全等的小平行四边形对称中心分别在ABCD 的顶点上,它们的各边与ABCD 的各边分别平行,且与ABCD 相似.若小平行四边形的一边长为x ,且0<x≤8,阴影部分的面积的和为y ,则y 与x 之间的函数关系的大致图象是( )A .B .C .D .思路分析:根据平行四边形的中心对称性可知四块阴影部分的面正好等于一个小平行四边形的面积,再根据相似多边形面积的比等于相似比的平方列式求出y 与x 之间的函数关系式,然后根据二次函数图象解答. 解:∵四个全等的小平行四边形对称中心分别在ABCD 的顶点上,∴阴影部分的面积等于一个小平行四边形的面积, ∵小平行四边形与ABCD 相似,∴2()328y x =, 整理得212y x =,又0<x≤8,纵观各选项,只有D 选项图象符合y 与x 之间的函数关系的大致图象. 故选D .点评:本题考查了动点问题的函数图象,根据平行四边形的对称性与相似多边形的面积的比等于相似比的平方求出y与x的函数关系是解题的关键.例8已知一个矩形纸片OACB,将该纸片放置在平面直角坐标洗中,点A(11,0),点B(0,6),点P为BC 边上的动点(点P不与点B、C重合),经过点O、P折叠该纸片,得点B′和折痕OP.设BP=t.(Ⅰ)如图①,当∠BOP=30°时,求点P的坐标;(Ⅱ)如图②,经过点P再次折叠纸片,使点C落在直线PB′上,得点C′和折痕PQ,若AQ=m,试用含有t 的式子表示m;(Ⅲ)在(Ⅱ)的条件下,当点C′恰好落在边OA上时,求点P的坐标(直接写出结果即可).考点:翻折变换(折叠问题);坐标与图形性质;全等三角形的判定与性质;勾股定理;相似三角形的判定与性质.分析:(Ⅰ)根据题意得,∠OBP=90°,OB=6,在Rt△OBP中,由∠BOP=30°,BP=t,得OP=2t,然后利用勾股定理,即可得方程,解此方程即可求得答案;(Ⅱ)由△OB′P、△QC′P分别是由△OBP、△QCP折叠得到的,可知△OB′P≌△OBP,△QC′P≌△QCP,易证得△OBP∽△PCQ,然后由相似三角形的对应边成比例,即可求得答案;(Ⅲ)首先过点P作PE⊥OA于E,易证得△PC′E∽△C′QA,由勾股定理可求得C′Q的长,然后利用相似三角形的对应边成比例与m= 16t2-116t+6,即可求得t的值.点评:此题考查了折叠的性质、矩形的性质以及相似三角形的判定与性质等知识.此题难度较大,注意掌握折叠前后图形的对应关系,注意数形结合思想与方程思想的应用.对应训练4.甲、乙两队举行了一年一度的赛龙舟比赛,两队在比赛时的路程s(米)与时间t(分钟)之间的函数关系图象如图所示,请你根据图象判断,下列说法正确的是()A.甲队率先到达终点B.甲队比乙队多走了200米路程C.乙队比甲队少用0。
关于平面直角坐标系的最难规律题

关于平面直角坐标系的最难规律题关于平面直角坐标系的最难规律题引言:在数学学习中,平面直角坐标系是一种重要且基础的概念。
通过平面直角坐标系,我们可以将点和图形在平面上准确地表示出来,从而帮助我们解决各种数学问题。
然而,平面直角坐标系中的规律题常常具有一定的难度,需要我们深入理解和灵活运用相关概念。
本文将就平面直角坐标系中的最难规律题展开讨论,并为读者提供相关解题思路和个人见解。
第一部分:基本概念与解题技巧1. 坐标系简介:平面直角坐标系由横轴(x轴)和纵轴(y轴)组成,它们相交于原点O,形成四个象限。
横轴和纵轴上的刻度用数值表示,可以表示出每个点的具体位置。
2. 解题技巧的重要性:解决平面直角坐标系中的规律题需要我们熟练掌握相关的解题技巧。
根据对称性质,我们可以在不完全画出一个图形的情况下,推断出其对称部分的坐标。
我们还可以利用距离公式和直线方程等概念,更加灵活地解决问题。
3. 规律题的分类:在平面直角坐标系中,规律题主要可分为直线的性质、图形的对称性以及点的位置等方面。
对于每一类规律题,我们要理明其特点和解题思路,并逐一进行深入讨论。
在此,我们将聚焦于最具挑战性的规律题类型,以期拓展我们的数学思维和应用能力。
第二部分:直线的最难规律题1. 点与线的位置关系:考虑如下问题:已知一直线和一个点P(x, y),如何判断点P是否在直线上?这是一个常见且具有一定难度的问题。
解决该问题需要我们理解直线方程表达式、点的坐标以及直线上点的特点。
我们可以通过代入点的坐标到直线方程中,来判断点是否满足直线方程。
如果满足,则点位于直线上。
2. 直线的平行与垂直关系:平面直角坐标系中,直线的平行与垂直关系也是一个重要且常见的规律题。
解决该类题目需要我们掌握直线的斜率概念以及平行和垂直的性质。
两个直线平行的条件是它们的斜率相等,而两个直线垂直的条件是它们的斜率之积为-1。
通过计算直线的斜率,我们可以判断它们的平行与垂直关系。
期末难点特训(三)和平面直角坐标系有关的压轴题-【微专题】七年级数学下册常考点微专题提分精练

七下期末难点特训(三)和平面直角坐标系有关的压轴题1. 在平面直角坐标系xOy 中,对于P ,Q 两点给出如下定义:若点P 到x 、y 轴的距离中的最大值等于点Q 到x 、y 轴的距离中的最大值,则称P ,Q 两点为“等距点”.下图中的P ,Q 两点即为“等距点”.(1)已知点A 的坐标为(﹣3,1),①在点E (0,3),F (3,﹣3),G (2,﹣5)中,为点A 的“等距点”的是 ;②若点B 的坐标为B (m ,m +6),且A ,B 两点为“等距点”,则点B 的坐标为 ;A .(3,9)B .(﹣9,﹣3)C .(﹣3,3)D .不能确定(2)若1T (﹣1,﹣k ﹣3),2T (4,4k ﹣3)两点为“等距点”,求k 的值.2. 平面直角坐标系中,(),0A a ,()0,B b ,a ,b 均为整数,且满足b =C 在y 轴负半轴上且10ABC S =△,将线段AB 平移到DE ,其中点A 的对应点是点D .(1)请直接写出点A ,B ,C 的坐标;(2)如图(1),若点D 的坐标为()1,0-,点(),F m n 为线段DE 上一点,且ACF △的面积大于12,求m 的取值范围;(3)如图(2),若DE 与y 轴的交点G 在B 点上方,点P 为y 轴上一动点,请直接写出EBO ∠,BPD ∠,PDA ∠之间的数量关系.3. 如图所示,在平面直角坐标系中,如图①,将线段AB 平移至线段CD ,点A 在x 轴的负半轴,点C 在y 轴的正半轴上,连接AC 、BD .(1)若(3,0)A -、(2,2)B --,(0,2)C ,直接写出点D 的坐标;(2)如图②,在平面直角坐标系中,已知一定点(2,0)M ,两个动点(,21)E a a +、(,23)F b b -+.请你探索是否存在以两个动点E 、F 为端点的线段EF 平行于线段OM 且等于线段OM ,若存在,求点E 、F 的坐标;若不存在,请说明理由;(3)如图③,在直线EF 上有两点A 、C ,分别引两条射线AB 、CD .110BAF ∠=︒,60DCF ∠=︒,射线AB 、CD 分别绕A 点,C 点以1度/秒和3度/秒的速度同时顺时针转动,设时间为t ,在射线CD 转动一周的时间内,是否存在某时刻,使得CD 与AB 平行?若存在,求出所有满足条件的时间t .4. 如图,在平面直角坐标系中,AB x ⊥轴,垂足为A ,BC y ⊥轴,垂足为C ,已知(,0)A a ,(0,)C c ,其中a ,c 满足关系式2(6)0a -+=,点P 从O 点出发沿折线OA AB BC --的方向运动到点C 停止,运动的速度为每秒2个单位长度,设点P 的运动时间为t 秒.(1)在运动过程中,当点P 到AB 的距离为2个单位长度时,t =________秒;(2)在点P 的运动过程中,用含t 的代数式表示P 点的坐标;(3)当点P 在线段AB 上的运动过程中,射线AO 上一点E ,射线OC 上一点F (不与C 重合),连接PE ,PF ,使得70EPF ∠=︒,求AEP ∠与PFC ∠的数量关系.5. 在平面直角坐标系中,(),0A a ,()1,B b ,a ,b 满足0a b +=,连接AB 交y 轴于C .(1)直接写出=a ______,b =______;(2)如图1,点P 是y 轴上一点,且三角形ABP 的面积为12,求点P 的坐标;(3)如图2,直线BD 交x 轴于()4,0D ,将直线BD 平移经过点A ,交y 轴于E ,点(),Q x y 在直线AE 上,且三角形ABQ 的面积不超过三角形ABD 面积的13,求点Q 横坐标x 的取值范围.6. 在平面直角坐标系中,点A ,C 均在x 轴上,点B 在第一象限,直线AB 上所有点的坐标(),x y 都是二元一次方程2x y -=-的解,直线BC 上所有点的坐标(),x y 都是一元一次方程28x y +=的解.(1)求B 点的坐标时,小明是这样想的:先设B 点坐标为()m n ,,因为B 点在直线AB 上,所以()m n ,是方程2x y -=-的解;又因为B 点在直线BC 上,所以()m n ,也是方程28x y +=的解,从而m ,n 满足228m n m n -=-⎧⎨+=⎩,据此可求出B 点坐标为______.再求出A 点坐标为______;C 点坐标为______.(均直接写出结果)(2)若线段BC 上存在一点D ,使12OCD ABC S S =△△(O 为原点),求D 点坐标(3)点(),3E a -是坐标平面内的动点,若满足13ABE ABC S S ≤△△,求a 的取值范围.7. 如图1,在平面直角坐标系中,已知(),0A a ,()0,B b ,(),C a c .其中a 、b 、c 满足关系式()226a b -=--,()250c -≤.(1)=a _______;b =_______;c =______.(2)如果在第四象限内有一点()1,P m ,使得APO △的面积是ABC 面积的一半,求点P 的坐标.(3)如图2,过点A 作AD AB ⊥,交BC 延长线于点D ,且AB AD =,点(),36M m m -+在直线AB 上,点Q 是x 轴上异于点A 的一个动点,是否存在DQM 为等腰直角三角形,若存在,请直接写出点Q 的坐标.8. 如图,在平面直角坐标系中,已知A (a ,0),B (0,b ),C (a ,c ).其中a 、b 、c 满足关系式|a ﹣2|=﹣(b ﹣6)2,(c ﹣5)2≤0.(1)a =______,b =______,c =______;(2)如果在第四象限内有一点P (1,m ),使得△APO 的面积是△ABC 面积的一半,求点P 的坐标.(3)过点A 作AD ⊥AB ,交BC 延长线于点D ,且AB =AD ,点M (m ,﹣3m +6)在直线AB 上,点Q 是x 轴上异于点A 的一个动点,是否存在△DQM 为等腰直角三角形,若存在,请直接写出点Q 的坐标.9. 如图1,在平面直角坐标系中,已知点(),A a b ,(),B a b a --,且a ,b 满足:0a +=.(1)求点A ,B 的坐标;(2)如图1,将AB 平移到A B '',使点B 的对应点B '落在x 轴的正半轴上,在y 轴上有一点P ,且20ABP ∠=︒,试判断PB A ''∠与B PB '∠之间的数量关系,并说明理由;(3)如图2,线段AB 与y 轴交于点M ,将AB 平移到A B '',连接MA ',MB ',点B 的对应点(),0B n ',若2024A B M S ''≤≤△,求n 的取值范围.10. 如图,在平面直角坐标系中,A 、B 、C 三个点的坐标分别为()4,0-A 、()0,4B 、()3,4C ,D 为OA 中点,BD 与AC 相交于点E .(1)则点D 坐标为_______,BC =________;(2)点(),F a b 在直线BD 上,且2BF DF =,求b 的值;(3)点(),0M m 在x 轴上,若MCE △的面积大于BCE 的面积,直接写出m 的取值范围_______.11. 在如图所示的平面直角坐标系xOy 中,BC ⊥y 轴于点C ,OA =12,BC =OC =6,点B 在第三象限.设动点P 从A 点出发沿x 轴正方向以每秒3个单位长度匀速移动,同时动点Q 从O 点出发沿y 轴负方向以每秒32个单位长度匀速移动,连接PB ,QB .(1)直接写出点A 、B 的坐标;(2)当△PAB 的面积是△QBC 的面积的4倍时,求点P 的坐标;(3)若S △OPB 、S △QBC 分别表示△OPB 、△QBC 的面积,说明S △OPB 与S △QBC 的数量关系.12. 在平面直角坐标系中,已知M (0,4),N (3,2),线段MN 平移得到线段PQ ,使点M 的对应点为P ,点N 的对应点为Q ,若点P 的坐标为()2,1--,点Q 的坐标为(),a b ,(1)=a ___________,b =___________;(2)若点E 为x 轴正半轴上的一个动点,探究MNE ∠、NEQ ∠和EQP ∠之间的数量关系并证明;(注:MNE ∠、NEQ ∠和EQP ∠均为大于0︒且小于180︒的角)(3)将线段MN 向下平移得到线段AB ,从使得点N 的对应点B 落在x 轴上,点M 的对应点A 落在y 轴上,动点C 从点B 出发,以每秒钟移动3个单位长度的速度沿x 轴向左运动,动点D 从点A 出发,以每秒钟移动2个单位长度的速度沿y 轴向下运动,直线BD 与直线AC 交于点F ,设点F 的坐标为(),m n .动点C 和动点D 同时出发且它们的运动时间为t 秒.①在01t <<时,试探究ADF △与BCF △的面积关系,并说明理由;②若在点C 、D 的运动过程中,ABF △的面积为7,请直接写出m 的值.13. 在平面直角坐标系中,如果点P (a ,b )满足a +1>b 且b +1>a ,则称点P 为“自大点”:如果一个图形的边界及其内部的所有点都不是“自大点”,则称这个图形为“自大忘形”.(1)判断下列点中,哪些点是“自大点”,直接写出点名称 ;P1(1,0)P 2P 3(﹣12,13)P 4(﹣1)(2)如果点N (2x +3,2)不是“自大点”,求出x 的取值范围.(3)如图,正方形ABCD 的初始位置是A (0,6),B (0,4),C (2,4),D (2,6),现在正方形开始以每秒1个单位长的速度向下(y 轴负方向)平移,设运动时间为t 秒(t >0),请直接写出当正方形成为“自大忘形”时,t 的取值范围: .七下期末难点特训(三)和平面直角坐标系有关的压轴题【1题答案】【答案】(1)①E ,F ;②C(2)1或2【解析】【分析】(1)①找到x 、y 轴距离最大为3的点即可;②先分析出直线上的点到x 、y 轴距离中有3的点,再根据“等距点”概念进行解答即可;(2)先分析出直线上的点到x 、y 轴距离中有4的点,再根据“等距点”概念进行解答即可.【小问1详解】解:①∵点A (-3,1)到x 、y 轴的距离中最大值为3,又∵点E (0,3)和点F (3,-3)到x 、y 轴的距离中最大值为3,∴与A 点是“等距点”的点是E 、F ;②∵点B 的坐标为(m ,m +6),且有m <m +6,又∵点A 与点B 为“等距点”,点A (-3,1)到x 、y 轴的距离中最大值为3,∴m +6=3,解得m =-3,即B 点的坐标为(-3,3),故选:C .故答案为:①E 、F ;②C ;【小问2详解】解:1(1,3)T k ---,()24,43T k -两点为“等距点”,①若|4k -3|≤4时,则4=-k -3或-4=-k -3,解得k =-7(舍去)或k =1;②若|4k -3|>4时,则|4k -3|=|-k -3|,解得k =2或k =0(舍去).根据“等距点”的定义知,k =1或k =2符合题意.即k 的值是1或2.【点睛】本题考查了直角坐标系中的坐标中的知识,理解读懂“等距点”的定义是解题的关键.【2题答案】【答案】(1)()4,0A ,()0,2B ,()0,3C -(2)1455m -≤<- (3)当点P 在点B 的下方时,180EBO BPD ADP ∠=∠+︒-∠;当点P 在B 的上方、AD 的延长线与y 轴的交点的下方时,360EBO PDA BPD ∠+∠+∠=︒;当点P 在AD 的延长线与y 轴的交点T 上方时,PDA EBO BPD ∠=∠+∠.【解析】【分析】(1)由非负性可求a ,b 的值,由三角形的面积公式可求点C 坐标;(2)由平移的性质可得AB DE =,AB DE ∥,5AD BE ==,由面积关系可求m ,n 的数量关系,即可求解;(3)分三种情况讨论,由平移的性质,平行线的性质以及角的数量关系可求解.【小问1详解】解:b =- 40a ∴- ,240a - ,24a ∴ ,a ,b 均为整数,4a ∴=,2b =,(4,0)A ∴,(0,2)B ,4∴=OA ,2OB =,10ABC S ∆= ,∴1102BC OA ⨯⨯=,5BC ∴=,点C 在y 轴负半轴上,∴点C 坐标为(0,3)-;【小问2详解】解:如图,连接BE ,BF ,OF ,将线段AB 平移到DE ,AB DE ∴=,AB DE ∥,5AD BE ==,∴四边形ABED 的面积2510=⨯=,152ABF ABEDS S ∆∴==四边形,ABF ADF ABO BFO DFO ABFD S S S S S S ∆∆∆∆∆=+=++ 四边形,111155422()12222n m n ∴+⨯⨯=⨯⨯+⨯⨯-+⨯⨯,12m n --∴=,12ACF AFO AOC OCF S S S S ∆∆∆∆=++> ,∴1114433()12222n m ⨯⨯+⨯⨯+⨯⨯->,145m ∴<-;∵F 为线段DE 上一点,∴5,m ≥- ∴145.5m -≤-<【小问3详解】解:如图,当点P 在点B 的下方时,延长EB 交PD 于F ,将线段AB 平移到DE ,AB DE ∴∥,AD BE ∥,ADP BFD ∴∠=∠,180180PFB BFD PDA ∴∠=︒-∠=︒-∠,EBO BPD BFP ∠=∠+∠ ,180EBO BPD PDA ∴∠=∠+︒-∠,180EBO PDA BPD ∴∠+∠-∠=︒;如图,当点P 在B 的上方、AD 的延长线与y 轴的交点下方时,延长DP 交BE 于点F ,将线段AB 平移到DE ,AD BE ∴∥,180PDA BFD ∴∠+∠=︒,180BFP PDA ∴∠=︒-∠,EBO BFP BPF ∠=∠+∠ ,180180EBO PDA BPD ∴∠=︒-∠+︒-∠,360EBO PDA BPD ∴∠+∠+∠=︒;如图,当点P 在AD 的延长线与y 轴的交点T 上方时,EBO BEG EGB ∠=∠+∠ ,又BE AD ∥,BEG GDT ∴∠=∠,由对顶角得EGB TGD ∠=∠,PTD TGD TDG ∠=∠+∠ ,PTD EBO ∴∠=∠,PDA PTD TPD ∠=∠+∠ ,PDA EBO BPD∴∠=∠+∠综上所述:当点P 在点B 的下方时,180EBO BPD ADP ∠=∠+︒-∠;当点P 在B 、与AD 的延长线与y 轴的交点之间时,360EBO PDA BPD ∠+∠+∠=︒;当点P 在AD 的延长线与y 轴的交点T 上方时,PDA EBO BPD ∠=∠+∠.【点睛】本题是三角形综合题,考查了平移的性质,三角形面积公式,利用分类讨论思想解决问题是解题的关键.【3题答案】【答案】(1)(1,0)D(2)存在,3,42E ⎛⎫ ⎪⎝⎭, 1,42F ⎛⎫- ⎪⎝⎭(3)存在,t 为5秒或95秒【解析】【分析】(1)根据平移变换只改变图形的位置不改变图形的形状可知对应线段平行且相等,对应点的连线平行且相等;(2) 根据()()0,02,0EF OM EF OM O M =∥,,,,得出21232a b a b +=-+-=,,解答即可.(3) 分①AB 与CD 在EF 的两侧,分别表示出ACD ∠与BAC ∠,然后根据内错角相等两直线平行,列式计算即可得解;②CD 旋转到与AB 都在EF 的右侧,分别表示出DCF ∠与BAC ∠,然后根据同位角相等两直线平行,列式计算即可得解;③CD 旋转到与AB 都在EF 的左侧,分别表示出DCF ∠与BAC ∠,然后根据同位角相等两直线平行,列式计算即可得解.【小问1详解】解:设(,)D x y ,将线段AB 平移至线段CD ,(3,0)A -、(2,2)B --,(0,2)C ,02(3)x ∴-=---,220y -=--,1x ∴=,0y =,(1,0)D ∴;【小问2详解】解:存在,理由://EF OM ,EF OM =,(0,0)O ,(2,0)M ,∴点E 与F 的纵坐标相等,横坐标的差的绝对值为2,四边形OMEF 是平行四边形,即2123a b +=-+,||2a b -=,解得:12a =-,32b =或32a =,12b =-,∴点E 的坐标为1(2-,0),F 的坐标为3(2,0)或点E 的坐标为3(2,4),F 的坐标为1(2-,4),当1(2E -,0),3(2F ,0)时,O 、M 、E 、F 四点均在x 轴上,不能构成平行四边形,舍去;(E ∴32,4),1(2F -,4);【小问3详解】解:存在.分三种情况:如图①,AB 与CD 在EF 的两侧时,110BAF ∠=︒ ,60DCF ∠=︒,18060312031203ACD t t t ∴∠=︒-︒-︒⨯=︒-︒⨯=︒-︒,1101110BAC t t ∠=︒-︒⨯=︒-︒,要使//AB CD ,则ACD BAF ∠∠=,即1203110t t ︒-︒=︒-︒,解得5t =,此时(18060)340︒-︒÷︒=,040t ∴<<,②CD 旋转到与AB 都在EF 的右侧时,110BAF ∠=︒ ,60DCF ∠=︒,3603603003DCF t t ∴∠=︒-︒-︒=︒-︒,110BAC t ∠=︒-︒,要使//AB CD ,则DCF BAC ∠∠=,即3003110t t ︒-︒=︒-︒,解得95t =,此时(36060)3100︒-︒÷︒=,40100t ∴<<;③CD 旋转到与AB 都在EF 的左侧时,110BAF ∠=︒ ,60DCF ∠=︒,3(18060180)3300DCF t t ∴∠=︒-︒-︒+︒=︒-︒,110BAC t ∠=︒-︒,要使//AB CD ,则DCF BAC ∠∠=,即3300110t t ︒-︒=︒-︒,解得95t =,此时110t >,95110< ,∴此情况不存在.综上所述,t 为5秒或95秒时,CD 与AB 平行.【点睛】本题考查了坐标与图形变化-平移,平行线的判定,三角形的面积,熟记平移变化只改变图形的位置不改变图形的形状,读懂题意并熟练掌握平行线的判定方法,要注意分情况讨论是解题的关键.【4题答案】【答案】(1)2s 或8s ;(2)当0≤t ≤3时,P (2t ,0);当3≤t ≤7时,P (6,6−2t );当7≤t ≤10时,P (20−2t ,−8);(3)∠PFC +∠PEA =160°或∠PFC −∠AEP =20°.【解析】【分析】(1)由非负数的性质得a −6=0,c +8=0,解得a =6,c =−8,由此即可解决问题;(2)分三种情形:①当0≤t ≤3时,②当3≤t ≤7时,③当7≤t ≤10时,分别求解即可;(3)分两种情形分别画出两个图形,根据三角形外角的性质和三角形内角和定理进行求解即可.【小问1详解】解:∵a ,c 满足关系式2(6)0a -+=,∴a −6=0,c +8=0,∴a =6,c =−8,∴A (6,0),B (6,−8).当点P 到AB 的距离为2个单位长度时,运动路程s =6−2=4或s =6+8+2=16,∴4÷2=2s 或16÷2=8s ,故答案为:2s或8s;【小问2详解】①当0≤t≤3时,点P在OA上,此时,P(2t,0);②当3≤t≤7时,点P在AB上,此时PA=2t−6,由于点P在第四象限,纵坐标小于0,则P(6,6−2t);③当7≤t≤10时,点P在BC上,此时PB=2t−OA−AB=2t−14,PC=BC−PB=6−(2t−14)=20−2t,∴P(20−2t,−8);【小问3详解】当点P在线段AB上时,分两种情况:①如图3中,结论:∠PEA+∠PFC=160°,理由如下:连接OP,∵∠PFC=∠FPO+∠FOP,∠AEP=∠EOP+∠EPO,∴∠PEA+∠PFC=∠FPO+∠FOP+∠EOP+∠EPO=∠AOF+∠EPF=90°+70°=160°;②如图4中,结论:∠PFC−∠AEP=20°,理由如下:设PM 交OC 于G ,∵∠AEP +∠EGO =90°,∠EGO =∠PGF =110°−∠PFC ,∴∠AEP +110°−∠PFC =90°,∴∠PFC −∠AEP =20°,综上所述,∠PFC +∠PEA =160°或∠PFC −∠AEP =20°.【点睛】本题是三角形综合题,考查了图形与坐标性质、非负数的性质、三角形的外角性质、直角三角形的性质等知识,综合性强,解题的关键是学会用分类讨论的思想思考问题,属干中考常考题型.【5题答案】【答案】(1)-3,4(2)-3,4 (3)-4≤x ≤-2且x ≠-3【解析】【分析】(1)根据非负数的性质构建方程组,解方程组求出a ,b ;(2)过点B 作BM x ⊥轴于M ,设OC m =,由三角形面积关系得出111()222OA OC OC BM OM AM BM ⋅++⋅=⋅,求出3m =,过点B 作BN y ⊥轴于N ,由三角形面积关系得出1131222CP CP ⨯⨯+=,求出CP 即可;(3)连接DQ ,过点Q 作QR x ⊥轴,分点Q 在第二象限,点Q 在第三象限时,两种情况,分别列出方程,解之即可.【小问1详解】解: |210|0a b -+=,又0,|210|0a b -+ ,∴102100a b a b +-=⎧⎨-+=⎩,解得:34a b =-⎧⎨=⎩,故答案为:-3,4.【小问2详解】过点B 作BM x ⊥轴于M ,设OC m =,三角形AOC 的面积+四边形OCBM 的面积=三角形ABM 的面积,∴111()222OA OC OC BM OM AM BM ⋅++⋅=⋅,即1113(4)144222m m ⨯++⨯=⨯⨯,解得:3m =,点C 的坐标为(0,3),过点B 作BN y ⊥轴于N ,三角形ABP 的面积=三角形ACP 的面积+三角形BCP 的面积,∴111222OA CP BN CP ⋅+⋅=,即1131222CP CP ⨯⨯+=,6CP ∴=,∴点P 的坐标为(0,3)-或(0,9).【小问3详解】点B 向左平移4个单位长度,向下平移4个单位长度到点A ,∵点D 向左平移4个单位长度后的对应点正好在y 轴上,∴点D 平移后的对应点恰好是点(0,4)E -,连接DQ ,过点Q 作QR x ⊥轴,如图所示:AE BD ∥,∴三角形ADQ 的面积=三角形ABQ 的面积,当三角形ABQ 的面积13=三角形ABD 的面积时,1433B QR y ==,当点Q 在第三象限时,∴14141(3)(4)()4323232x x +⨯++-=⨯⨯,解得:2x =-,当点Q 在第二象限时,∴11411634(3)()22323x x ⨯⨯+-⨯=-⨯,解得:4x =-,∴当三角形ABQ 的面积不超过三角形ABD 面积的13时,点Q 的横坐标x 的取值范围是42x -- ,且3x ≠-.【点睛】本题属于三角形综合题,考查了三角形的面积,非负数的性质,平行线的性质等知识,解题的关键是学会用分类讨论的思想思考问题,学会利用参数构建方程解决问题.【6题答案】【答案】(1)(2,4),(-2,0),(4,0)(2)(52,3)(3)-7≤a≤-3且a≠-5【解析】【分析】(1)解方程组可求出B点坐标,解方程可求出A和C的坐标;(2)求出三角形ABC的面积=12,则可求出D点的纵坐标,代入2x+y=8求出x,可得答案;(3)设直线BA交直线y=-3于点F,过点B作x轴的垂线分别交x轴,直线y=-3于M,N,根据S△ABM+S梯形AMNF=S△FBN求出FN=7,得出S△ABE≤4,令S△ABE=4,得出方程|a+5|=2,解出a=-7或-3,则可得出答案.【小问1详解】解:∵m,n满足2 28m nm n-=-⎧⎨+=⎩,解得:24mn=⎧⎨=⎩,∴B(2,4),∵点A在x轴上,又在直线AB上,令y=0,则x-0=-2,∴x=-2,∴A(-2,0),同理,令y=0,∴2x+0=8,∴x=4,∴C(4,0),故答案为:(2,4),(-2,0),(4,0);【小问2详解】∵B(2,4),A(-2,0),C(4,0);∴AC=4+2=6,∴S△ABC=12AC×4=12×6×4=12,∵S△OCD=12S△ABC,∴S △OCD =12OC •y D =6,∴y D =3,代入2x +y =8得,x =52,∴D (52,3);【小问3详解】设直线BA 交直线y =-3于点F ,过点B 作x 轴的垂线分别交x 轴,直线y =-3于M ,N ,∵S △ABM +S 梯形AMNF =S △FBN ,∴12×4×4+12(4+FN )×3=12×FN ×7,∴FN =7,∴F (-5,-3),∵S △ABE ≤13S △ABC ,∴S △ABE ≤4,令S △ABE =4,∵S △BEF -S △AEF =S △ABE ,∴12|a +5|×7-12|a +5|×3=4,∴|a +5|=2,解得a =-7或-3,∵S △ABE ≤4,∴-7≤a ≤-3且a ≠-5.【点睛】本题是三角形综合题,考查了二元一次方程组的解法,坐标与图形的性质,三角形的面积公式,熟练掌握坐标与图形的性质是解题的关键.【7题答案】【答案】(1)2,6,5(2)(1,52 -)(3)存在,点Q的坐标为(-3,0)或(22,0)或(-18,0)【解析】【分析】(1)根据非负数的性质,即可解答;(2)根据△APO的面积是△ABC面积的一半列方程,即可解答;(3)存在,分三种情况:当∠DQM=90°时,点Q与A重合,此种情况不成立,有∠DMQ=90°和∠MDQ=90°,分情况正确画图,证明三角形全等,求出m的值,即可解答.【小问1详解】解:∵|a-2|=-(b-6)2,∴|a-2|+(b-6)2=0,∴a=2,b=6,∵(c-5)2≤0,(c-5)2≥0,∴c-5=0,∴c=5,故答案为:2,6,5;【小问2详解】∵a=2,b=6,c=5,∴A(2,0),B(0,6),C(2,5),∴AC∥y轴,AC=5,OB=6,AO=2,∵P(1,m),使得△APO的面积是△ABC面积的一半,∴S△APO=12S△ABC,∴12•2•(-m)=12×12×5×2,∴m=52 -,∴P(1,52 );【小问3详解】存在,①如图2,∠DMQ=90°,△MDQ是等腰直角三角形,过点M作GH∥x轴,过点D作DG⊥GH于G,过点Q作QH⊥GH于H,∵点M(m,-3m+6)在直线AB上,∴FM=m,QH=3m-6,∵AB⊥AD,∴∠BAD=∠BAO+∠DAE=90°,∵∠BAO+∠ABO=90°,∴∠DAE=∠ABO,∵AB=AD,∠AOB=∠AED=90°,∴△ABO≌△DAE(AAS),∴AE=OB=6,DE=OA=2,∵△DQM是等腰直角三角形,∴同理得△QHM≌△MGD(AAS),∴MG=QH=3m-6,∵OE=FG,∴2+6=m+3m-6,∴m=72,∴OQ=FH=HM-FM=DG-FM=2+3m-6-m=2m-4=7-4=3,∴Q(-3,0);②如图3,∠MDQ=90°,△MDQ是等腰直角三角形,过点D作DG⊥x轴于E,过点M作MG⊥DG于G,同理得△BOA≌△AED,△MGD≌△DEQ,∴DE=MG=OA=2,OE=2+6=8,∴OE=8=m+2,∴m=6,∴OQ=OE+EQ=OE+DG=8+2+3m-6=3m+4=22,∴Q(22,0);③如图4,∠MDQ=90°,△MDQ是等腰直角三角形,过点D作DE⊥x轴于E,过M作MG∥y轴,过点D作DG⊥MG于G,同理得:OA=DE=DG=2,∴m=2+6+2=10,∴OQ=EQ-OE=MG-OE=2+3m-6-8=18,∴Q(-18,0);综上,点Q的坐标为(-3,0)或(22,0)或(-18,0).【点睛】本题是三角形的综合题,考查了坐标与图形性质及非负数的性质,等腰直角三角形的性质和判定,三角形全等的性质和判定等知识,解决本题的关键是作辅助线构建三角形全等.【8题答案】【答案】(1)2,6,5(2)P(1,﹣52)(3)存在,点Q的坐标为(﹣3,0)或(22,0)或(﹣18,0)【解析】【分析】(1)根据非负数的性质,即可解答;(2)根据△APO的面积是△ABC面积的一半列方程,即可解答;(3)存在,分三种情况:当∠DQM=90°时,点Q与A重合,此种情况不成立,有∠DMQ=90°和∠MDQ=90°,分情况正确画图,证明三角形全等,求出m的值,即可解答.【小问1详解】解:∵|a﹣2|=﹣(b﹣6)2,∴|a﹣2|+(b﹣6)2=0,∴a=2,b=6,∵(c﹣5)2≤0,(c﹣5)2≥0,∴c﹣5=0,∴c=5,故答案为:2,6,5;【小问2详解】∵a=2,b=6,c=5,∴A(2,0),B(0,6),C(2,5),∴AC∥y轴,AC=5,OB=6,AO=2,∵P(1,m),使得△APO的面积是△ABC面积的一半,∴S△APO=12S△ABC,∴12•2•(﹣m)=12×12×5×2,∴m=﹣52,∴P(1,﹣52);【小问3详解】存在,①如图2,∠DMQ=90°,△MDQ是等腰直角三角形,过点M作GH∥x轴,过点D作DG⊥GH于G,过点Q作QH⊥GH于H,∵点M(m,﹣3m+6)在直线AB上,∴FM=m,QH=3m﹣6,∵AB⊥AD,∴∠BAD=∠BAO+∠DAE=90°,∵∠BAO+∠ABO=90°,∴∠DAE=∠ABO,∵AB=AD,∠AOB=∠AED=90°,∴△ABO≌△DAE(AAS),∴AE=OB=6,DE=OA=2,∵△DQM是等腰直角三角形,∴同理得△QHM≌△MGD(AAS),∴MG=QH=3m﹣6,∵OE=FG,∴2+6=m+3m﹣6,∴m=72,∴OQ=FH=HM﹣FM=DG﹣FM=2+3m﹣6﹣m=2m﹣4=7﹣4=3,∴Q(﹣3,0);②如图3,∠MDQ=90°,△MDQ是等腰直角三角形,过点D作DG⊥x轴于E,过点M作MG⊥DG于G,同理得△BOA≌△AED,△MGD≌△DEQ,∴DE=MG=OA=2,OE=2+6=8,∴OE=8=m+2,∴m=6,∴OQ=OE+EQ=OE+DG=8+2+3m﹣6=3m+4=22,∴Q(22,0);③如图4,∠MDQ=90°,△MDQ是等腰直角三角形,过点D 作DE ⊥x 轴于E ,过M 作MG ∥y 轴,过点D 作DG ⊥MG 于G ,同理得:OA =DE =DG =2,∴m =2+6+2=10,∴OQ =EQ ﹣OE =MG ﹣OE =2+3m ﹣6﹣8=18,∴Q (﹣18,0);综上,点Q 的坐标为(﹣3,0)或(22,0)或(﹣18,0).【点睛】本题是三角形的综合题,考查了坐标与图形性质及非负数的性质,等腰直角三角形的性质和判定,三角形全等的性质和判定等知识,解决本题的关键是作辅助线构建三角形全等.【9题答案】【答案】(1)()4,2A -、()4,6B(2)当点P 在AB 上方时,20PB A B PB '''∠-∠=︒;当点P 在AB 下方时,20B PB PB A '''∠-∠=︒(3)24n ≤≤【解析】【分析】(1)由非负数的性质求出a =-4,b =2,则可得出答案;(2)①当点P 在AB 上方时,如图1,过点P 作PQ ∥AB ,②当点P 在AB 下方时,如图2,过点P 作PQ ∥AB ,由平行线的性质可得出答案;(3)如图3,过点A 作AC ⊥x 轴于C 、过点B 作BD ⊥x 轴于点D ,过点A '、B '构造矩形A 'GEF ,设M (0,m ),根据S 梯形ACDB =S 梯形ACOM +S 梯形OMDB 得出12×8×(2+6)=12×(2+m )+12×4×(6+m ),求出m =4,求出S △A ′B ′M =2n +16,解不等式组可得出答案.【小问1详解】解:0a +=,∴4020a b +=⎧⎨-=⎩,解得:42a b =-⎧⎨=⎩,∴()4,2A -、()4,6B ;【小问2详解】解:①当点P 在AB 上方时,如图1,过点P 作PQ AB ∥,∵由平移得:AB A B ''∥∴PQ A B ''∥∴QPB PB A '''∠=∠,20QPB PBA ∠=∠=︒∴20PB A QPB B PB QPB B PB PBA B PB ''''''∠=∠=∠+∠=∠+∠=∠+︒∴20PB A B PB '''∠-∠=︒②当点P 在AB 下方时,如图2,过点P 作PQ AB ∥,同①可证:20B PB B PQ QPB PB A PBA PB A ''''''∠=∠+∠=∠+∠=∠+︒∴20B PB PB A '''∠-∠=︒;【小问3详解】解:如图3,过点A 、B 构造梯形ABDC ,过点A '、B '构造矩形A GEF ',设()0,M m∵ACDB ACOM OMDBS S S =+梯形梯形梯形∴()()()111826246222m m ⨯⨯+=⨯++⨯⨯+解得:4m =如图3,过点A '、B '构造矩形A GEF ',∴A B M A GB MEB A FMA GEF S S S S S '''''''=---矩形△△△△()1118884488222n n =⨯-⨯⨯-⨯⋅-⨯⋅-64162324n n---+216n =+∵2024A B M S ''≤≤△∴201624n ≤+≤∴24n ≤≤;【点睛】本题是三角形综合题,考查了平方根与绝对值的非负性质、三角形面积计算、平面直角坐标系与点的坐标、平移的性质、平行线的性质等知识,熟练掌握平移的性质、平行线的性质是解题的关键.【10题答案】【答案】(1)()2,0, 3.D BC -=(2)43b =或 4.b =- (3)7m <-或 1.m >-【解析】【分析】(1)先由A 的坐标结合D 为OA 的中点可得D 的坐标,由B ,C 的坐标可得BC 的长度;(2)如图,当F 在线段BD 上时,过F 作FN AM ⊥于N ,连接OF ,由2BF DF =,:1:3,DOF BOD S S = 而()2,4,,,OD OB F a b == 再建立方程求解即可;当F 在BD 的延长线上时,如图,当F 在线段BD 的延长线上时,可得D 是线段BF 的中点,再利用中点坐标公式可得答案;(3)如图,过(),E x y 作EN AM ⊥于,N 作EK OB ⊥于,K 过C 作CH AM ⊥于,H 由,DOE BOE BOD S S S += 可得24,y x =+ 同理:由ACH AEH ECH S S S =+ 可得:7416,y x -= 再联立两个方程求解68,,55E ⎛⎫ ⎪- ⎪⎝⎭再求解11818||3|4|2255BCE E B B S C y y ∆=⋅-=⨯⨯-=,MCE AMC AME S S S ∆∆∆=-6|4|5m =+,再建立不等式,利用绝对值的含义解不等式即可.【小问1详解】解:(4,0)- A ,4,OA ∴=∵D 为OA 中点,2,OA ∴=∴()2,0,D -∵()()0,4,3,4,B C BC x ∴∥轴, 3.BC =【小问2详解】如图,当F 在线段BD 上时,过F 作FN AM ⊥于N ,连接OF ,90FND BOD ︒∴∠=∠=,∵2BF DF =,∴:2,BOF DOF S S =∴:1:3,DOF BOD S S = 而()2,4,,,OD OB F a b ==1212,13242b ⨯∴=⨯⨯ 解得:4.3b = 当F 在线段BD 的延长线上时,如图,∵2,BF DF =∴D 是线段BF的中点,∴4+20,b =⨯解得:4,b =- 综上:43b =或 4.b =-【小问3详解】如图,过(),E x y 作EN AM ⊥于,N 作EK OB ⊥于,K 过C 作CH AM ⊥于,H ,DOE BOE BOD S S S +=()1112442,222y x ∴⨯⨯+⨯⨯-=⨯⨯ 整理得:24,y x =+同理:由ACH AEH ECH S S S =+ 可得:7416,y x -=∴24,7416y x y x ⎧=+⎪⎨-=⎪⎩解得:65,85x y ⎧=-⎪⎪⎨⎪=⎪⎩即68,,55E ⎛⎫ ⎪- ⎪⎝⎭ 11818||3|4|2255BCE E B C S B y y ∆=⋅-=⨯⨯-=∴,∵(),0,M m|4||4|AM m m ∴=--=+,MCE AMC AMES S S ∆∆∆=-∴11||||22C E AM y AM y =⋅-⋅118|4|4|4|225m m =⨯+⨯-⨯+⨯6|4|5m =+∵MCE △的面积大于BCE 的面积,618|4|55m ∴+>,解得:7m <-或 1.m >-【点睛】本题考查的是坐标与图形,中点坐标公式的应用,图形面积与坐标之间的关系,二元一次方程组的解法,一元一次不等式的解法,熟练的求解(3)中的点E 的坐标是解本题的关键.【11题答案】【答案】(1)A (-12,0),B (-6,-6)(2)点P (-4,0)或(12,0)(3)2OPB QBCS S ∆∆=【解析】【分析】(1)根据OA =12可得 A 坐标,OC =6可得 C 坐标,再由BC ⊥y 轴,BC =OC =6可得B 坐标;(2)设运动时间为t 秒,然后分0<t <4、t =4、t >4三种情况建立方程求解即可;(3)由运动可得OP =|12-3m |、QC =|6-32m |=12|12-3m |可得OP =2QC ,再结合△OPB 与△QBC 分别以OP ,OC 为底、高为6即可解答.【小问1详解】解:∵OA =12,BC =OC =6,∴A (-12,0),C (0,-6)∵BC ⊥y 轴于点C ,点B 在第三象限,∴B (-6,-6).【小问2详解】解:设运动时间为t 秒,当点Q 在O 、C 之间,点P 在A 、O 之间时,即0<t <4,∵△PAB 的面积是△QBC 的面积的4倍,∴113364(6)6222t t ⋅⋅⋅=⨯-⋅,解得:t =83, ∴点P 的横坐标为83×3-12=-4,∴点P (-4,0);当t =4时,不符合题意;当t >4时,∵△PAB 的面积是△QBC 的面积的4倍,∴113364(6)6222t t ⋅⋅=⨯-⋅,解答t =8,∴点P 的横坐标为83×8-12=12,∴点P (12,0);综上,点P (-4,0)或(12,0).【小问3详解】解:设运动时间为m ,由题意知,OP =|12-3m |,QC =|6-32m |=12|12-3m |,∴OP =2QC ,∵△OPB 与△QBC 分别以OP ,OC 为底,高为6,∴2OPB QBC S S ∆∆=.【点睛】本题主要考查了三角形的面积的计算方法、坐标与图形的性质等知识点,用方程和分类讨论的思想解决问题是解答本题的关键.【12题答案】【答案】(1)1,3a b ==-(2)NEQ EQP MNE ∠=∠+∠或360MNE NEQ EQP ∠+∠+∠=︒或PQF MNE NEQ ∠=∠-∠(3)①ADF BCF S S =△△;②m 的值为2-或5.【解析】【分析】(1)由由()0,4M 平移到()2,1P --确定平移的方式,从而可得答案;(2)分三种情况讨论:如图,当E 在NQ 的左边时,连接NQ ,如图,当E 在NQ 的右边,直线MN 的左边时,(包括E 在这两条直线上),如图,当E 在直线MN 的右边时,记直线MN 与EQ 的交点为F ,再根据平行线的性质,三角形的内角和定理与三角形的外角的性质可得答案;(3)①当01t <<时,如图,由题意可得:()()0,2,3,0,A B2,3,22,33,AD t BC t OD t OC t ===-=- 记四边形OCFD 的面积为m ,再分别表示两个三角形的面积即可得到答案;②由7,ABF S = 可得,C D 都在负半轴上,再分两种情况讨论:交点F 在第三象限,如图,证明2,3n m = 即2,,3F m m ⎛⎫ ⎪ ⎪⎝⎭ 作A ,F 作x 轴的平行线,过F ,B 作y 轴的平行线,交点分别即为L ,P ,Q ,则四边形LFQP 为矩形,再利用面积列方程,如图,当交点F 在第一象限,同理利用面积列方程即可.【小问1详解】解:由()0,4M 平移到()2,1,P -- 而()3,2N 平移到(),,Q a b∴321,253,a b =-==-=-【小问2详解】如图,当E 在NQ 的左边时,连接NQ ,由平移可得:,MN PQ ∥180,MNQ PQN EQP MNE ENQ EQN ∴∠+∠=︒=∠+∠+∠+∠180,NEQ ENQ EQN ∠+∠+∠=︒,NEQ EQP MNE ∴∠=∠+∠如图,当E 在NQ 的右边,直线MN 的左边时,(包括E 在这两条直线上),同理可得:180,180,MNQ PQN QNE NEQ NQE ∠+∠=︒∠+∠+∠=︒ 360,MNE NEQ EQP ∴∠+∠+∠=︒如图,当E 在直线MN 的右边时,记直线MN 与EQ 的交点为F ,同理:,PQF NFE ∠=∠ ,NFE MNE NEQ ∠=∠-∠ ∴PQF MNE NEQ∠=∠-∠【小问3详解】①当01t <<时,如图,由题意可得:()()0,2,3,0,A B 2,3,22,33,AD t BC t OD t OC t ===-=- 记四边形OCFD 的面积为m ,()123333,2ADF AOC S S m t m t m ∴=-=⨯⨯--=--()132233,2BCF BOD S S m t m t m =-=⨯⨯--=-- ∴.ADF BCF S S =②7,ABF S = 则,C D 都在负半轴上,交点F 在第三象限,如图,同理可得:,ADF BCF S S = 而(),,F m n()()1123,22t m t n ∴⨯-=⨯- 解得:2,3n m = 即2,,3F m m ⎛⎫ ⎪ ⎪⎝⎭7,ABF S = 作A ,F 作x 轴的平行线,过F ,B 作y 轴的平行线,交点分别即为L ,P ,Q ,则四边形LFQP 为矩形,()()()2112123223237,322323m m m m m m ⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪∴---⨯⨯-⨯-⨯--⨯-⨯-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭解得:2,m =-如图,当交点F 在第一象限,同理可得:()21211222337,323223m m m m m m ⎛⎫ ⎪---⨯⨯-⨯-= ⎪⎝⎭ 解得:5,m =综上:m 的值为2-或5.【点睛】本题考查的是坐标与图形,坐标系内图形的平移,平行线的性质,三角形的内角和定理的应用,三角形的外角的性质,利用割补法求解图形的面积,一元一次方程的应用,整式的乘法运算,本题的综合程度高,清晰的分类讨论是解本题的关键.【13题答案】【答案】(1)2P ,3P ;(2)1x - 或0x ;(3)1t 或7t 【解析】【分析】(1)根据点(,)P a b 满足1a b +>且1b a +>,则称点P 为“自大点”, a ,b 满足11b a -<-<,根据关系式逐个判断即可;(2)先求出点(23,2)N x +是“自大点”时x 的取值范围,再求点(23,2)N x +不是“自大点”时x 的取值范围即可;(3)根据“自大点”的纵横坐标满足的关系列出关系式求出t 的范围即可.【小问1详解】点(,)P a b 满足1a b +>且1b a +>,则称点P 为“自大点”,a ∴,b 满足11b a -<-<,1(1,0)P ,011-=-,故1(1,0)P 不是“自大点”,2P ,11-<,故2P 是“自大点”,31(2P -,1)3,111()132-<--<,故31(2P -,1)3是“自大点”,4(1,P -,(1)1--=4(1,P -不是“自大点”,故答案为:2P ,3P ;【小问2详解】如果点(23,2)N x +是“自大点”,则12(23)1x -<-+<,解得,10x -<<,故当1x - 或0x 时,点(23,2)N x +不是“自大点”,x ∴的取值范围是1x - 或0x ;【小问3详解】正方形ABCD 的初始位置是(0,6)A ,(0,4)B ,(2,4)C ,(2,6)D ,∴平移之后的坐标分别为(0,6)t -,(0,4)B t -,(2,4)C t -,(2,6)D t -,当A 点平移后的点是“自大点时”, 161t -<-<,解得,57t <<,故A 点平移后的点不是“自大点时”, 5t 或7t ,同理,当B 点和D 点平移后的点不是“自大点时”, 3t 或5t ,同理,当C 点平移后的点不是“自大点时”, 1t 或3t ,∴当平移后的正方形边界及其内部的所有点都不是“自大点”时,1t 或7t ,故答案为:1t 或7t .【点睛】本题主要考查正方形的性质,坐标与图形的平移变化,根据题意,准确找出“自大点”的纵横坐标满足的关系是解答此题的关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平面直角坐标系练习题选择题:1、下列各点中,在第二象限的点是()A.(2,3)B.(2,-3) C.(-2,3) D.(-2, -3)2、已知点M(-2,b)在第三象限,那么点N(b, 2 )在()A.第一象限B.第二象限C.第三象限D.第四象限3、若点P(a,b)在第四象限,则点M(b-a,a-b)在()A. 第一象限B. 第二象限C. 第三象限D. 第四象限4、已知点P(a,b),且ab>0,a+b<0,则点P在()A.第一象限B.第二象限C.第三象限D.第四象限5、如果点P(a,b)在第二象限内,那么点P(ab,a-b)在()A、第一象限B、第二象限C、第三象限D、第四象限6、若点P(x ,y)的坐标满足xy=0(x≠y),则点P在()A.原点上B.x轴上C.y轴上D.x轴上或y轴上7、平面直角坐标中,和有序实数对一一对应的是()A.x轴上的所有点B.y轴上的所有点C.平面直角坐标系内的所有点D.x轴和y轴上的所有点8、将点A(-4,2)向上平移3个单位长度得到的点B的坐标是()A. (-1,2)B. (-1,5)C. (-4,-1)D. (-4,5)9、线段CD是由线段AB平移得到的,点A(–1,4)的对应点为C(4,7),则点B(-4,–1)的对应点D的坐标为()A.(2,9)B.(5,3)C.(1,2)D.(– 9,– 4)10、点P(m+3,m+1)在x轴上,则P点坐标为()A.(0,-2)B.(2,0)C.(4,0)D.(0,-4)11、点P的横坐标是-3,且到x轴的距离为5,则P点的坐标是()A. (5,-3)或(-5,-3)B. (-3,5)或(-3,-5)C. (-3,5)D. (-3,-5)12、已知点P(x,y)在第四象限,且│x│=3,│y│=5,则点P的坐标是()A.(-3,5)B.(5,-3)C.(3,-5)D.(-5,3)13、点P(x,y)位于x轴下方,y轴左侧,且x=2 ,y=4,点P的坐标是()A.(4,2)B.(-2,-4)C.(-4,-2)D.(2,4)14、点P(0,-3),以P为圆心,5为半径画圆交y轴负半轴的坐标是()A.(8,0)B.(0,-8)C.(0,8)D.(-8,0)15、点E(a,b)到x轴的距离是4,到y轴距离是3,则有()A.a=3, b=4 B.a=±3,b=±4 C.a=4, b=3 D.a=±4,b=±316、将某图形的横坐标都减去2,纵坐标保持不变,则该图形()A.向右平移2个单位B.向左平移2 个单位C.向上平移2 个单位D.向下平移2 个单位17、如果点M到x轴和y轴的距离相等,则点M横、纵坐标的关系是()A.相等B.互为相反数C.互为倒数D.相等或互为相反数18、已知正方形ABCD的三个顶点坐标为A(2,1),B(5,1),D(2,4),现将该正方形向下平移3个单位长度,再向左平移4个单位长度,得到正方形A'B'C'D',则C'点的坐标为()A. (5,4)B. (5,1)C. (1,1)D. (-1,-1)19、若点M在第一、三象限的角平分线上,且点M到x轴的距离为2,则点M的坐标是()A.(2,2)B.(-2,-2)C.(2,2)或(-2,-2)D.(2,-2)或(-2,2)20、已知P(0,a)在y轴的负半轴上,则Q(21,1a a---+)在( )A、y轴的左边,x轴的上方B、y轴的右边,x轴的上方C 、y 轴的左边,x 轴的下方D 、y 轴的右边,x 轴的下方21、三角形ABC 三个顶点的坐标分别是A (-4,-1),B (1,1),C (-1,4),将三角形ABC 向右平移2个单位长度,再向上平移3个单位长度,则平移后三个顶点的坐标是( ) A .(2,2),(3,4),(1,7) B .(-2,2),(4,3),(1,7) C .(-2,2),(3,4),(1,7) D .(2,-2),(3,3),(1,7)22、已知△ABC 的面积为3,边BC 长为2,以B 原点,BC 所在的直线为x 轴,则点A 的纵坐标为( )A 、3B 、-3C 、6D 、±3 23、点M (a ,a-1)不可能在( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限 二、填空题:1、在电影票上,如果将“8排4号”记作(8,4),那么(10,15)表示____________。
2、点A (-3,5)在第_____象限,到x 轴的距离为______,到y 轴的距离为_______;关于原点的对称点坐标为_________,关于x 轴的对称点坐标为_________,关于y 轴的对称点坐标为_________。
3、已知x 轴上点P 到y 轴的距离是3,则点P 坐标是_____________。
4、一只蚂蚁由(0,0)先向上爬4个单位长度,再向右爬3个单位长度,再向下爬2个单位长度后,它所在位置的坐标是_________。
5、点P (m +3, m +1)在x 轴上,则m = ,点P 坐标为 。
6、已知点P(m ,2m -1)在y 轴上,则P 点的坐标是 。
7、一个长方形在平面直角坐标系中三个顶点的坐标为(-1,-1)、(-1,2)、(3,-1),则第四个顶点的坐标为8、已知点A (2,-3),线段AB 与坐标轴没有交点,点B 的坐标可以是 (写出一个即可) 9、点E 与点F 的纵坐标相同,横坐标不同,则直线EF 与y 轴的关系是 10、直线a 平行于x 轴,且过点(-2,3)和(5,y ),则y=11、若P (x ,y )是第四象限内的点,且2,3x y ==,则点P 的坐标是12、已知点P在第二象限,它的横坐标与纵坐标的和为1,点P的坐标是______(写出一个点即可).13、已知:A(3,1),B(5,0),E(3,4),则△ABE的面积为________.14、点A(1-a,5),B(3,b)关于y轴对称,则a+b=_______.15、已知点P(m,n)到x轴的距离为3,到y轴的距离等于5,则点P的坐标是。
16、已知点P的坐标(2-a,3a+6),且点P到两坐标轴的距离相等,则点P的坐标是.17、已知点A(3a+5,a-3)在二、四象限的角平分线上,则a=_____.18、在平面直角坐标系内,已知点(1-2a,a-2)在第三象限的角平分线上,则a=,点的坐标为。
19、已知点P(0,a)在y轴的负半轴上,则点Q(-2a-1,-a+1)在第象限.20、将点P(-3,y)向下平移3个单位,向左平移2个单位后得到点Q(x,-1),则xy=___________。
三、解答题:1、如图所示的直角坐标系中,三角形ABC的顶点坐标分别是A(0,0)、B(6,0)、C(5,5)。
求:(1)求三角形ABC的面积;(2)如果将三角形ABC向上平移3个单位长度,得三角形A1B1C1,再向右平移2个单位长度,得到三角形A2B2C2。
分别画出三角形A1B1C1和三角形A2B2C2。
并试求出A2、B2、C2的坐标?2、已知点P(a+1,2a-1)关于x轴的对称点在第一象限,求a的取值范围. ACAx yBA3、在如图所示的平面直角坐标系中表示下面各点:A(0,3);B(1,-3);C(3,-5);D(-3,-5);E(3,5);F(5,7);G(5,0)(1)A点到原点O的距离是。
(2)将点C向x轴的负方向平移6个单位,它与点重合。
(3)连接CE,则直线CE与y轴是什么关系?(4)点F分别到x、y轴的距离是多少?4、在直角坐标系中,已知点A(-5,0),点B(3,0),C点在y轴上,且△ABC的面积为12,试确定点C的坐标。
5、写出如图中△ABC 各顶点的坐标且求出此三角形的面积。
6、如图,△AOB 中,A 、B 两点的坐标分别为(-4,-6),(-6,-3),求△AOB 的面积。
7、如图,在直角坐标系中,第一次将三角形OAB 变换成三角形OA 1B 1,第二次将三角形OABC1xyOA 1B 1变成三角形OA 2B 2,第三次将三角形OA 2B 2变成三角形OA 3B 3,已知123(1,3),(2,3),(4,3),(8,3)A A A A ,123(2,0),(4,0),(8,0),(16,0)B B B B 。
(1)、观察每次变换前后的三角形有何变化,找出规律,按此规律再将三角形OA 3B 3变换成三角形44OA B ,则3B 的坐标是 ,4B 的坐标是 。
(2)若按第(1)题找到的规律将三角形OAB 进行了n 次变换,得到三角形OA n B n ,比较每次变换中三角形顶点坐标有何变化,找出规律,推测n A 的坐标是 ,n B 的坐标是 。
8、如图,在△ABC 中,三个顶点的坐标分别为A(-5,0),B(4,0),C(2,5),将△ABC 沿x 轴正方向平移2个单位长度,再沿y 轴沿负方向平移1个单位长度得到△EFG 。
(1)求△EFG 的三个顶点坐标。
(2)求△EFG 的面积。
9、如图,在平面直角坐标系中,点A ,B 的坐标分别为(-1,0), (3,0),现同时将点A ,B 分别向上平移2个单位,再向右平移 1个单位,分别得到点A ,B 的对应点C ,D ,连接AC ,BD ,CD .(1)、求点C ,D 的坐标及平行四边形ABDC 的面积ABDC S 四边形(2)、在y 轴上是否存在一点P ,连接PA ,PB ,使PAB S =2ABDC S 四边形,若存在这样一点,求出点P 的坐标,若不存在,试说明理由.PD CBAOxy(3)、点P 是线段BD 上的一个动点,连接PC ,PO ,当点P 在BD 上移动时(不与B ,D 重合)给出下列中有且只有一个是正结论:①DCP BOP CPO ∠+∠∠的值不变,②DCP CPOBOP∠+∠∠的值不变,其确的,请你找出这个结论并求其值.10、如图:三角形ABC 三个顶点A 、B 、C 的坐标分别为A (1,2)、B (4,3)、C (3,1).(1)把三角形A 1B 1C 1向右平移4个单位,再向下平移3个单位,恰好得到三角形ABC ,试写出三角形A 1B 1C 1三个顶点的坐标; (2)求出三角形 A 1B 1C 1的面积11、在直角坐标系中,我们把横、纵坐标都为整数的点叫做整点,设坐标轴的单位长度为1cm,整点P从原点O出发,速度为1cm/s,且整点P作向上或向右运动(如图1所示).运动时间(s)与整点个数的关系如下表:根据上表中的规律,回答下列问题:(1)、当整点P从点O出发4s时,可以得到的整点的个数为________个.(2)、当整点P从点O出发8s时,在直角坐标系(图2)中描出可以得到的所有整点,并顺次连结这些整点.(3)、当整点P从点O出发________s时,可以得到整点(16,4)的位置.图1(试验图)图2。
