满足置信度的计算修改版
置信度置信区间公式表-互联网类

置信度置信区间公式表-互联网类哎呀,说起置信度和置信区间公式表,这在互联网领域里可真是个有点让人挠头但又特别重要的东西呢!咱们先来讲讲啥是置信度。
简单说,它就是你对某个结论或者估计的相信程度。
比如说,你预测明天会下雨,但是你心里有多大把握呢?这就是置信度。
那置信区间呢,就是根据一些数据和计算,得出一个可能的范围,在这个范围内,你认为真实的值大概率会在里面。
就拿我之前遇到的一件事儿来说吧。
我有个朋友在一家互联网公司做数据分析,他们公司要推出一款新的 APP,想预估一下上线第一个月的用户数量。
这时候就用到置信度和置信区间啦。
他们收集了大量类似 APP 的数据,通过复杂的计算和分析,得出了一个置信区间。
比如说,他们估计新 APP 第一个月的用户数量有 95%的可能性会在 10万到 20 万之间。
这就是置信区间。
在互联网世界里,置信度和置信区间公式表的应用那是相当广泛。
比如说电商平台预测商品的销量,社交平台预估用户的活跃度,或者是在线教育平台估计课程的报名人数等等。
咱们来看看具体的公式。
常见的置信区间公式有很多种,比如对于正态分布总体均值的置信区间公式,如果总体标准差已知,那就是:均值 ±(Zα/2 × 标准差/√n);如果总体标准差未知,那就得用样本标准差代替,公式变成:均值 ±(tα/2 × 样本标准差/√n)。
这里的Zα/2 和tα/2 可都是根据置信度来确定的数值哦。
再比如说,在互联网广告投放中,要评估广告效果。
假如我们想知道某个广告的点击率是不是真的比原来有显著提高。
通过收集一定数量的点击数据,利用置信区间的计算,就能判断这个提高是偶然的波动,还是确实有了实质性的变化。
还有啊,在做用户调研的时候。
比如要了解用户对某个新功能的满意度,通过发放问卷收集数据。
然后利用置信区间的分析,就能更准确地把握用户的真实态度,而不是被一些表面的数据所迷惑。
总之,置信度和置信区间公式表就像是互联网世界里的一把精准尺子,能帮助我们在海量的数据中找到更可靠、更有价值的信息,做出更明智的决策。
置信度(置信区间计算方法)

) ( 0.0199 ,
0.3069 )
(二) 两个正态总体的情形
为取自总体 N ( 1 12 ) 的样本, ( X 1 , X 2 , , X n )
( Y1 , Y2 ,, Ym )
为取自总体 N ( 2 22 ) 的样本, 分别表示两样本的均值与方差
X , S1 ; Y , S 2
( X Y ) z 2
S1
S2 (7) n m
2 2
(4) 1 , 2 未知, 但 n = m , 1 2的置信区间
2 2
令 Zi = Xi -Yi , i = 1,2,…, n, 可以将它们看成来
自正态总体 Z ~ N ( 1 2 , 12 + 22) 的样本
nm2
P
( X Y ) ( 1 2 ) 1 n 1 m (n 1) S1 (m 1) S 2
2 2
nm2
t 1 2
1 2
的置信区间为
1 n 1 m (n 1) S1 (m 1) S 2 nm2
2
-2
(4)
2
1
• 2
2
4
6
8
•
10
2
2
例1 某工厂生产一批滚珠, 其直径 X 服从 正态分布 N( 2), 现从某天的产品中随机 抽取 6 件, 测得直径为 15.1 , 14.8 , 15.2 , 14.9 , 14.6 , 15.1
(1) 若 2=0.06, 求 的置信区间 (2) 若 2未知,求 的置信区间 (3) 求方差 2的置信区间.
置信度置信区间计算方法-置信区间公式表

置信度置信区间计算方法-置信区间公式表置信度置信区间计算方法置信区间公式表在统计学中,置信度和置信区间是非常重要的概念,它们帮助我们在样本数据的基础上对总体参数进行估计,并给出估计的可靠性范围。
接下来,让我们深入探讨一下置信度和置信区间的计算方法以及相关的公式表。
首先,我们来理解一下什么是置信度。
置信度通常用百分数表示,比如 95%、99%等。
它表示在多次重复抽样的情况下,得到的置信区间包含总体参数真值的概率。
例如,95%的置信度意味着,如果我们进行多次抽样并计算置信区间,大约有 95%的置信区间会包含总体参数的真实值。
而置信区间则是一个范围,它基于样本数据计算得出,旨在估计总体参数可能的取值范围。
常见的总体参数包括总体均值、总体比例等。
那么,如何计算置信区间呢?这就需要用到相应的公式。
对于总体均值的置信区间计算,当总体标准差已知时,使用以下公式:\\overline{x} \pm z_{\alpha/2} \frac{\sigma}{\sqrt{n}}\其中,\(\overline{x}\)是样本均值,\(z_{\alpha/2}\)是对应于置信度的标准正态分布的分位数(例如,对于95%的置信度,\(\alpha =005\),\(z_{\alpha/2} =196\)),\(\sigma\)是总体标准差,\(n\)是样本容量。
当总体标准差未知,且样本容量较大(通常认为\(n \geq 30\))时,可以用样本标准差\(s\)代替总体标准差\(\sigma\),使用近似的公式:\\overline{x} \pm z_{\alpha/2} \frac{s}{\sqrt{n}}\而当样本容量较小(\(n < 30\))且总体服从正态分布时,需要使用 t 分布来计算置信区间,公式为:\\overline{x} \pm t_{\alpha/2, n 1} \frac{s}{\sqrt{n}}\其中,\(t_{\alpha/2, n 1}\)是自由度为\(n 1\)、对应于置信度的 t 分布的分位数。
置信度(置信区间计算方法)

推导
选取枢轴量 T X ~ T (n 1)
S
n X 由P t (n 1) 确定t ( n 1) 2 S 2 n
这时, T2 T1 往往增大, 因而估计精度降低.
确定后, 置信区间 的选取方法不唯一,
ch73
常选最小的一个.
75
处理“可靠性与精度关系”的原 则
先
求参数 置信区间 保 证 可靠性
再
提 高 精 度
ch73
76
求置信区间的步骤
寻找一个样本的函数
— 称为枢轴量 它含有待估参数, 不含其它未知参数, 它的分布已知, 且分布不依赖于待估参 数 (常由 的点估计出发考虑 ). 例如 X~N ( , 1 / 5)
P(T1 T2 ) 1
则称 [ T1 , T2 ]为 的置信水平为1 - 的
置信区间或区间估计. T1 置信下限 T2 置信上限
ch73
几点说明
置信区间的长度 T2 T1 反映了估计精度 T2 T1 越小, 估计精度越高.
反映了估计的可靠度, 越小, 越可靠. 越小, 1- 越大, 估计的可靠度越高,但
( 引例中 a 1.96, b 1.96 )
由 a g ( X1, X 2 , X n , ) b 解出 T1 , T2
得置信区间 ( T1 , T2 ) 引例中
( T1 , T2 ) ( X 1.96 1 , X 1.96 1 ) 5 5
ch73 78
置信区间常用公式
耐久性试验的时间-样件数-置信度计算
2
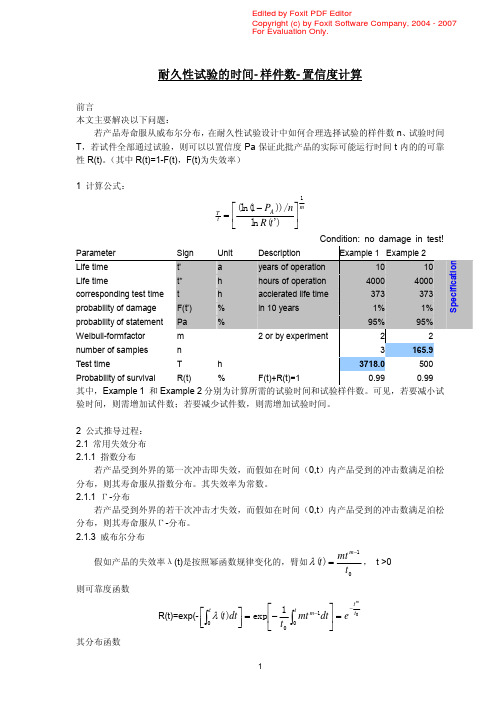
− − n t0 r t0 n − r L(t 0 ) = ∑ [ 1 − e ] [ e ] r r =0 c Tm Tm
(1)
确定在运行 t 时间可靠度 R 的情况下, R(t)= e
− tm t0
(2)
确定置信度 Pa,则使用方风险应为 1-Pa。即需
L(t 0 ) = 1 − Pa
若令合格判定数 c=0,则由(1)式可得
Tm t0
(3)
L(ห้องสมุดไป่ตู้ 0 ) = [e
−
]n
1
(4)
则联合(2)、(3)、(4) 可得
T t
(ln(1 − PA )) / n m = ln R(t ' )
(5)
[参考书目] [1] 茆试松等 编著,可靠性统计,华东师范大学出版社,1984 年 3 月第一版
1
Parameter Life time Life time corresponding test time probability of damage probability of statement Weibull-formfactor number of samples Test time Probability of survival
− Tm t0
未失效的概率为 P(t≥T)= e
− Tm t0
n 个产品在[0,T]内失效 r 个的概率为
− n t0 P(X=r)= 1 e − r Tm
r
−T e t 0
m
n−r
在确定 T、n、c 下的抽样方案的接收概率为
T t
(ln(1 − PA )) / n m = ln R(t ' )
置信度_可靠度_存活率

AERI ·CAE
置信度—可靠度—样本数
• 样本数由实际操作中时间、经济等因素限制,一般 采谱试验由3个驾驶员分别试验5次,这样得到15 个样本。
• 在样本数一定的情况下,试验的置信度由试件的可 靠度决定,可靠度高的例如R=95%,其置信度限 定在50%;可靠度低的例如R=90%,在15个样本 条件下其置信度就会达到80%。
C 1 Rn C : 置信度 R:可靠度 n:样本数
12
AERI ·CAE
置信度—可靠度—样本数
•当可靠度一定时,需要获得较高的置信度,就必须 增加样本数。
R 90% 90% 90% 90% 50% 70% 80% 90% 99% 99.999%
n
1
3
7 11 15 22 44
109
•当置信度一定时,检验的产品的可靠度越高,所 需检验的样本数越大。
R 50% 60% 70% 80% 90% 95% 96% 97% 98% 99% 99.9%
C 50% 50% 50% 50% 50% 50% 50% 50% 50% 50% 50%
n
1 1 2 3 7 14 17 23 34 69 693 13
靠度相当于置信度。
在X轴上随着b1的增大,置信度和可靠度都减小, 但是,置信度小表示估计越准确; 可靠度小表示产品性能不可靠。
0
b1
b1’
9
AERI ·CAE
置信度—可靠度
道路模拟试验 • 道路模拟试验就是对整车和零部件的某些关键点
位进行有针对性的疲劳试验,保证几天或几个星 期道路模拟试验在整车或零部件上的累积损伤总 量等于在实际道路条件下几年产生的累积损伤总 量,使得整车开发在系统上和零部件上的缺陷在 早期设计阶段就能被诊断并加以改进和优化。
置信区间的计算公式
置信区间的计算公式置信区间是统计学中一种重要的概念,它是用来估计一个总体参数的一种统计技术。
置信区间是一个可以把一个总体参数的可能取值范围限定在一定范围内的统计技术。
置信区间的计算公式是:置信区间=(样本均值-置信度α/2的标准误差,样本均值+置信度α/2的标准误差)。
置信度α是一个介于0到1之间的数字,它表示置信区间的置信程度,一般来说,α越大,置信区间越宽,置信程度越低;α越小,置信区间越窄,置信程度越高。
标准误差是一个衡量样本均值与总体均值之间差异的量,它是样本均值的可信度的度量。
置信区间的计算公式是:置信区间=(样本均值-置信度α/2的标准误差,样本均值+置信度α/2的标准误差)。
置信区间的计算可以帮助我们更好地了解总体参数的可能取值范围,从而更好地掌握总体参数的变化趋势。
置信区间的计算公式是一种统计技术,它可以帮助我们更好地了解总体参数的可能取值范围,从而更好地掌握总体参数的变化趋势。
置信区间的计算公式是:置信区间=(样本均值-置信度α/2的标准误差,样本均值+置信度α/2的标准误差)。
置信度α是一个介于0到1之间的数字,它表示置信区间的置信程度,标准误差是一个衡量样本均值与总体均值之间差异的量,它是样本均值的可信度的度量。
置信区间的计算公式是一种重要的统计技术,它可以帮助我们更好地了解总体参数的可能取值范围,从而更好地掌握总体参数的变化趋势。
置信区间的计算公式是:置信区间=(样本均值-置信度α/2的标准误差,样本均值+置信度α/2的标准误差)。
置信度α和标准误差是置信区间计算公式的两个重要参数,它们可以帮助我们更好地了解总体参数的可能取值范围,从而更好地掌握总体参数的变化趋势。
置信度置信区间计算方法-置信区间公式表
置信度置信区间计算方法-置信区间公式表置信度置信区间计算方法置信区间公式表在统计学中,置信度和置信区间是非常重要的概念。
它们帮助我们在对总体参数进行估计时,给出一个可能包含真实参数值的范围,以及我们对这个范围的确定程度,也就是置信度。
首先,让我们来理解一下什么是置信度。
置信度通常用百分数表示,比如 95%或 99%。
它反映了我们在多次重复抽样和估计的过程中,得到的置信区间能够包含真实总体参数值的比例。
比如说,95%的置信度意味着如果我们进行 100 次抽样和估计,大约有 95 次得到的置信区间能够包含真实的总体参数值。
而置信区间则是一个可能包含总体参数真实值的范围。
这个范围的宽窄取决于我们所选择的置信度、样本数据的特征以及样本量的大小。
接下来,我们重点介绍几种常见的置信区间计算方法和相应的公式。
对于正态总体均值的置信区间计算,当总体方差已知时,我们使用的公式是:\\bar{X} \pm Z_{\alpha/2} \frac{\sigma}{\sqrt{n}}\其中,\(\bar{X}\)是样本均值,\(Z_{\alpha/2}\)是标准正态分布的双侧分位数(对应于置信度\(1 \alpha\)),\(\sigma\)是总体标准差,\(n\)是样本量。
例如,如果我们有一个样本均值为 50,总体标准差为 10,样本量为 100,并且想要计算 95%置信度下的置信区间,那么首先找到\(Z_{\alpha/2}\),对于 95%的置信度,\(\alpha = 005\),\(\alpha/2 = 0025\),对应的\(Z_{\alpha/2} \approx 196\)。
然后代入公式计算:\50 \pm 196 \times \frac{10}{\sqrt{100}}= 50 \pm 196\得到的置信区间就是 4804, 5196。
当总体方差未知时,我们用样本方差\(s\)来代替总体方差\(\sigma\),此时使用的是\(t\)分布,公式变为:\\bar{X} \pm t_{\alpha/2}(n 1) \frac{s}{\sqrt{n}}\其中,\(t_{\alpha/2}(n 1)\)是自由度为\(n 1\)的\(t\)分布的双侧分位数。
置信度可靠度计算公式
置信度可靠度计算公式置信度和可靠度是统计学和概率论中非常重要的概念,它们在很多领域都有着广泛的应用。
先来说说置信度吧。
想象一下,你是一个糖果厂的质量检测员,每天都要从生产线上随机抽取一些糖果来检测它们的重量是否符合标准。
假设你抽取了 100 颗糖果,测量出它们的平均重量为 10 克,并且计算出了样本的标准差。
这时候,你想知道整个生产线生产的糖果的平均重量在某个范围内的可能性有多大,这个范围和可能性就是置信度。
比如说,你通过计算得出,有 95%的置信度可以认为生产线生产的糖果的平均重量在 9.8 克到 10.2 克之间。
这意味着,如果你多次进行这样的抽样和计算,大约有 95%的情况下,真正的总体平均重量会落在这个区间内。
那可靠度又是怎么回事呢?咱们还是拿糖果厂举例。
假设厂里的一台包装机器,在长时间的运行中,它不出故障正常工作的概率就是可靠度。
如果这台机器在一年中能正常工作 90%的时间,那它的可靠度就是 90%。
再来讲讲置信度的计算公式。
假设我们有一个样本均值为\( \bar{x} \) ,样本标准差为 \( s \) ,样本大小为 \( n \) ,我们要计算一个置信区间,比如常见的 95%置信区间。
这时候,我们使用的公式就是\( \bar{x} \pm z_{\alpha/2} \frac{s}{\sqrt{n}} \) ,其中 \( z_{\alpha/2} \)是与置信水平相关的一个值。
比如说对于 95%的置信水平,\( z_{\alpha/2} \approx 1.96 \) 。
可靠度的计算就稍微复杂一些啦。
如果是一个简单的系统,只有两个部件,一个可靠度是 \( R_1 \) ,另一个是 \( R_2 \) ,并且它们是串联的,那么整个系统的可靠度就是 \( R = R_1 \times R_2 \) 。
如果是并联的,可靠度就是 \( R = 1 - (1 - R_1)(1 - R_2) \) 。
置信度与置信区间的概念与计算
置信度与置信区间的概念与计算置信度和置信区间是统计学中重要的概念,用于描述对总体参数的估计结果的可靠程度。
本文将介绍置信度与置信区间的概念,以及如何计算置信区间。
一、置信度的概念在统计学中,置信度是指估计结果在一定置信水平下的可信程度。
置信度通常用一个百分比表示,比如95%的置信度意味着我们可以有95%的信心相信估计结果的准确性。
置信度越高,估计结果越可信。
二、置信区间的概念置信区间是指统计学上用来估计总体参数的一个范围,在给定的置信水平下,总体参数的真值有一定的可能性落在这个范围内。
置信区间通常由一个点估计值加减一个允许误差得到,表示估计结果的不确定性。
三、计算置信区间的方法常见的计算置信区间的方法有以下几种:点估计法、频率学派方法和贝叶斯方法。
1. 点估计法点估计法是指使用样本数据得到总体参数的估计值。
根据中心极限定理,当样本容量足够大时,样本均值的分布将近似服从正态分布。
在点估计法中,我们可以使用样本均值作为总体均值的点估计,样本标准差作为总体标准差的点估计。
2. 频率学派方法频率学派方法基于大样本理论,通过构造置信区间来估计总体参数。
常见的应用频率学派方法计算置信区间的方法有z检验和t检验。
在这些方法中,我们需要指定置信水平和样本容量,通过计算得到一个范围,该范围就是置信区间。
3. 贝叶斯方法贝叶斯方法是一种基于概率模型和贝叶斯定理的统计推断方法。
在贝叶斯方法中,我们需要先设定一个先验分布,然后根据样本数据得到后验分布。
根据后验分布,我们可以计算出置信区间。
四、示例为了更好地说明置信度和置信区间的计算方法,我们以一个简单的例子来说明。
假设我们想估计某个城市的平均气温,我们随机抽取了30天的气温数据,并计算得到样本均值为25摄氏度,样本标准差为3摄氏度。
根据频率学派方法,假设置信水平为95%,我们可以使用t分布来计算置信区间。
根据t分布表,自由度为29,对应的临界值为2.045。
计算得到置信区间为:(25 - 2.045 * (3 / √30), 25 + 2.045 * (3 / √30))根据点估计法,置信区间为(24.40, 25.60)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
随机测量数据的置信度
1、关于置信度的计算方法
置信度是表征测量结果可信赖程度的一个参数,用置信区间和置信概率来表示。
置信区间[-a ,+a] 是鉴定测量系统的设计误差指标,对于已有的检测系统,随机误差δ服从正态分布,标准误差σ已知。
区间[- a ~ +a]与P(δ)曲线构成的面积就是测量误差在[-a ~ +a] 区间出现的置信概率。
如下图所示:
置信概率计算
置信概率等于在置信区间对概率密度函数的定积分;随机误差出现的概率就是测量数据出现的概率;
由于服从正态分布的概率密度函数具有对称性,随机误差概率公式为:
置信区间可用标准偏差的倍数K 来表示,K 称为置信因子,即:
可以推出:
0()()()(||)2()a a a a a p a a p d p X dX p a p d μμδδδδδδ
++---≤≤+===≤=
⎰⎰⎰a K σ
=2222200202()22()a a a p d e d e d δσδσδδδδσ
-+-==⎰⎰⎰
令 ,因 ,积分由0 到a 变为由0 到K :
上式是一个计算比较复杂的积分,可以通过查表获得积分值。
2、按题目要求计算得出标准差
题目要求置信概率在97%以上,误差在1cm 以内,即a=1cm ,要使置信概率在97%以上,则根据正态分布概率表可以差得K=2.17,从而σ=a/K=0.460。
即设计的系统的标准差应该在0.460以下。
t δσ=a K σ=()()()22
0||||t K p a p t K e dt K δϕ-≤=≤==⎰。
