面积23
【新】北师大版三年级数学下册《面积单位》教案教学设计(优质完整)

北师大版三年级数学下册《面积单位》教案教学设计面积单位。
(教材第51~52页)1.使学生结合具体测量活动,体会统一面积单位的必要性。
2.体会平方厘米、平方分米、平方米等面积单位,并对它们的大小形成正确的表象。
3.使学生能正确选择合适的面积单位表示面积的大小,提高学生运用所学知识解决问题的能力。
重点:体会平方厘米、平方分米、平方米等面积单位,并对它们的大小形成正确的表象。
难点:能选择合适的面积单位表示面积的大小。
1平方厘米和1平方分米的正方形纸、插座、粉笔盒、一米长的绳子4条、实物投影仪、画好的不同大小方格子的正方形和长方形、面积相等的正方形、长方形、三角形和圆。
1.旧知复习。
师:什么是面积?生:物体的表面或封闭图形的大小就是它们的面积。
师:比较下面方格中哪个图形的面积大,为什么?出示:生:正方形的面积最大,因为它含有16个小方格,其余图形的面积都相等,都含有12个小方格。
2.游戏导入。
师:老师这儿有一张长方形的纸和一张正方形的纸,下面请男同学闭上眼睛,女同学观察。
师:正方形含有多少个小方格?生:9个。
师:下面请女同学闭上眼睛,男同学观察。
师:长方形含有多少个小方格?生:18个。
老师收起长方形和正方形后,让学生都睁开眼睛。
师:下面你们说说长方形和正方形谁大?大部分学生会说长方形大,然后教师出示长方形和正方形,有的学生可能会说不公平,画的小方格不一样大。
集体交流后得出的结论:要比较图形的大小,必须看它们含有相同大小的小方格的多少。
师:大家说的小方格,实际上就是面积单位。
每个人画的小方格不一样大,比起来就比较麻烦,因此我们要统一小方格的大小,也就是统一面积单位。
【设计意图:注重学生的认知冲突,揭示和呈现矛盾,巧设悬念,以激趣为基点,层层深入,激发学生强烈的求知欲望】3.点明课题。
这节课,我们就一起来学习常用的面积单位。
(板书课题:面积单位)1.测量数学书封面的面积。
师:同学们手中有面积都相等的长方形、正方形、三角形和圆,请你们任选一种,测量一下数学书封面的面积。
初中数学竞赛奥数培优资料第二辑专题23 面积的计算

专题23面积的计算○阅○读○与○思○考计算图形的面积是几何问题中一种重要题型,计算图形的面积必须掌握如下与面积有关的重要知识:1.常见图形的面积公式;2.等积定理:等底等高的两个三角形面积相等;3.等比定理:(1)同底(或等底)的两个三角形面积之比等于等于对应高之比;同高(或等高)的两个三角形面积之比等于等于对应底之比.(2)相似三角形的面积之比等于对应线段之比的平方.熟悉下列基本图形、基本结论:例题与求解【例1】如图,△ABC内三个三角形的面积分别为5,8,10,四边形AEFD的面积为x,则x=________.(黄冈市竞赛试题)解题思路:图中有多对小三角形共高,所以可将面积比转化为线段之比作为解题突破口.例1图【例2】如图,在△ABC中,已知BD和CE分别是两边上的中线,并且BD⊥CE,BD=4,CE=6,那么△ABC的面积等于()(全国初中数学联赛) A.12B.14C.16D.18解题思路:由中点想到三角形中位线,这样△ABC与四边形BCDE面积存在一定的关系.例2图【例3】如图,依次延长四边形ABCD 的边AB ,BC ,CD ,DA 至E ,F ,G ,H ,使BE AB =CF BC =DG CD =AH DA=m ,若S 四边形EFGH =2S 四边形ABCD ,求m 的值.解题思路:添加辅助线将四边形分割成三角形,充分找出图形面积比与线段比之间的关系,建立关于m 的方程.例3图【例4】如图,P ,Q 是矩形ABCD 的边BC 和CD 延长线上的两点,PA 与CQ 相交于点E ,且∠PAD =∠QAD ,求证:S 矩形ABCD =S △APQ .解题思路:图形含全等三角形、相似三角形,能得到相等的线段、等积式,将它们与相应图形联系起来,促使问题的转化.例4图【例5】如图,在Rt △ABC 中,∠A =90°,AB =8,AC =6,若动点D 从点B 出发,沿线段BA 运动到点A 为止,移动速度为每秒2个单位长度.过点D 作DE ∥BC 交AC 于点E ,设动点D 运动的时间为x 秒,AE 的长为y .(1)求出y 关于x 的函数关系式,并写出自变量x 的取值范围;(2)当x 为何值时,△BDE 的面积S 有最大值,最大值为多少?(江西省中考试题)解题思路:对于(1)利用△ADE ∽△ABC 可得y 与x 的关系式;对于(2)先写出S 关于x 的函数关系式,再求最大值.例5图【例6】如图,设P 为△ABC 内任意一点,直线AP ,BP ,CP 交BC ,CA ,AB 于点D ,E ,F .求证:(1)PD AD +PE BE +PFCF=1;(2)PA AD +PB BE +PC CF=2解题思路:过点A ,P 分别作BC 的垂线,这样既可得到平行线,产生比例线段,又可以与面积联系起来,把PAAD转化为面积比,利用面积法证明.例6图○能○力○训○练A级1.如图,ABCD 中,AE ∶BE =1∶2,S △AEF =6cm 2,则S △CDF 的值为________.(济南市中考试题)2.如图,正六边形ABCDEF 的边长为23cm ,P 为正六边形内任一点,则点P 到各边距离之和为_______.第1题图第2题图第3题图3.如图,P 是边长为8的正方形ABCD 外一点,PB =PC ,△PBD 的面积等于48,则△PBC 的面积为_____________.(北京市竞赛试题)4.如图,已知△BOF ,△AOF ,△BOD ,△COE 的面积分别为30,40,35,84,则△ABC 的面积为________.(浙江省竞赛试题)5.如图,已知AD 是Rt △ABC 斜边BC 上的高,DE 是Rt △ADC 斜边上的高,如果DC ∶AD =1∶2,S △DCE =a ,那么S △ABC 等于()(金华市中考试题)A .4aB .9aC .16aD .25a第4题图第5题图第6题图6.如图,已知M 是ABCD 边AB 的中点,CM 交BD 于点E ,则图中阴影部分面积与ABCD 的面积之比为()(山西省中考试题)A .16B .14C .13D .5127.如图,在△ABC 中,DE ∥BC ,DE 分别交AB ,AC 于点D ,E ,若S △ADE =2S △DCE ,则S △ADES △ABC等于()(浙江省宁波市中考试题)A .14B .12C .23D .498.如图,△ABC 是边长为6cm 的等边三角形,被一平行于BC 的矩形所截,AB 被截成三等分,则图中阴影部分面积面积为()cm 2.(广东省竞赛试题)A .4B .23C .33D .43第7题图第8题图第9题图9.如图,平面上有两个边长相等的正方形ABCD 和A ′B ′C ′D ′,且正方形A ′B ′C ′D ′的顶点A ′在正方形ABCD 的中心,当正方形A ′B ′C ′D ′绕A ′转动时,两个正方形重合部分的面积必然是一个定值.这个结论对吗?证明你的判断.(“希望杯”邀请赛试题)10.如图,设凸四边形ABCD 的一组对边AB ,CD 的中点分别为K ,M .求证:S 四边形ABCD =S △ABM +S △DCK..第10题图11.如图1,AB ,CD 是两条线段,M 是AB 的中点,S △DMC ,S △DAC ,S △DBC 分别表示△DMC ,△DAC ,△DBC 的面积,当AB ∥CD 时,有S △DMC =S △DAC +S △DBC2………..①.(1)如图2,若图1中AB 与CD 不平行时,①式是否成立?请说明理由.(2)如图3,若图1中AB 与CD 相交于点O 时,问S △DMC 与S △DAC 和S △DBC 有何相等关系?试证明你的结论.(安徽省中考试题)12.如图,在△ABC 中,∠ACB =90°,∠ABC =30°,将△ABC 绕顶点C 顺时针旋转,旋转角为θ(0°<θ<180°),得到△A ′B ′C ′.(1)如图1,当AB ∥CB ′时,设A ′B ′与CB 相交于点D ,证明:△A ′CD 是等边三角形;(2)如图2,连接A ′A ,B ′B ,设△ACA ′和△BCB ′的面积分别为S △ACA ′和S △BCB ′.求证:S △ACA ′∶S △BCB ′=1∶3.(3)如图3,设AC 的中点为E ,A ′B ′的中点为P ,AC =a ,连接EP ,当θ=_____时,EP 长度最大,最大值是____________.(安徽省中考试题)B级1.如图,A 在线段BG 上,ABCD 和DEFG 都是正方形,面积分别为7cm 2和11cm 2,则△CDE 的面积等于___________cm 2.(武汉市竞赛试题)2.如图,P 为正方形ABCD 内一点,PA =PB =10,并且P 到CD 边的距离也等于10,那么正方形ABCD 的面积是_______________.(北京市竞赛试题)3.如图,四边形ABCD 中,点E ,F 分别在BC ,DC 上,DF FC =1,CEBE =2,若△ADF 的面积为m ,四边形AECF 的面积为n (n >m ),则四边形ABCD 的面积为___________.(全国初中数学联赛试题)第1题图第2题图第3题图第4题图4.如图,图形ABCD 中,AB ∥CD ,AC 和BD 相交于点O ,若AC =5,BD =12,中位线长为132,△AOB 的面积为S 1,△OCD 的面积为S 2,则S 1+S 2=_________.(山东省竞赛试题)5.如图,分别延长△ABC 的三边AB ,BC ,CA 至A ′,B ′,C ′,使得AA ′=3AB ,BB ′=3BC ,CC ′=3AC ,若S △ABC =1,则S △A ′B ′C ′等于().A .18B .19C .24D .27(山东省竞赛试题)6.如图,若ABCD 是2×2的正方形,E 是AB 的中点,F 是BC 的中点,AF 与DE 相交于点I ,BD 和AF 相交于点H ,那么四边形BEIH 的面积是()A .13B .52C .715D .815(江苏省竞赛试题)第5题图第6题图第7题图7.如图,矩形ABCD 中,E 是BC 上的一点,F 是CD 上的点,已知S △ABE =S △ADF =13S ABCD ,则S △AEF S △CEF的值等于()(北京市竞赛试题)A.2B.3C.4D.58.(1)探究:如图1,在ABCD的形外分别作等腰直角三角形ABF和等腰直角三角形ADE,∠FAB =∠EAD=90°,连接AC,EF.在图中找一个与△FAE全等的三角形,并加以证明.(2)应用:以ABCD的四条边为边,在其形外分别作正方形,如图2,连接EF,GH,IJ,KL,若ABCD的面积为5,则图中阴影部分四个三角形的面积之和为____________.(长春市中考试题)9.如图,在梯形ABCD中,AD∥BC,AB=AD=DC=2cm,BC=4cm,在等腰△PQR中,∠QPR=120°,底边QR=6cm,点B,C,Q,R在同一条直线l上,且C,Q两点重合,如果等腰△PQR以1cm/s 的速度沿直线l箭头所示方向匀速运动,t秒时梯形ABCD与等腰△PQR重合部分的面积记为S cm2.(1)当t=4时,求S的值;(2)当4≤t≤10时,求S与t的函数关系式,并求出S的最大值.(广州市中考试题)第9题图10.有一根直尺的短边长为2cm,长边长为10cm,还有一块锐角为45°的直角三角纸板,它的斜边长为12cm,如图1将直尺的短边DE放置与直角三角纸板的斜边AB重合,且点D与点A重合将直尺沿AB方向平移,如图2,设平移的长为x cm(0≤x≤10),直尺与三角形纸板重叠部分(图中阴影部分)的面积S cm2.x时,S=________;(1)当x=0时,S=________,当10(2)当0<x≤4时,求S关于x的函数关系式;(3)当4<x<10时,求S关于x的函数关系式,并求出S的最大值.(徐州市中考试题)11.如图,设H 是等腰三角形ABC 的三边上的高线的交点,在底边BC 保持不变的情况下,让顶点A 至底边BC 的距离变小(仍保持三角形为等腰三角形),这时HBC ABC S S ∆∆⋅的值变大、变小、还是不变?证明你的结论.(全国初中数学联赛试题)第11题图12.(1)请你在图1中作一条直线,使它将矩形ABCD 分成面积相等的两部分;(2)如图2,点M 是矩形ABCD 内一定点,请你在图2中过点M 作一条直线,使它将矩形ABCD 分成面积相等的两部分;(3)如图3,在平面直角坐标系中,直角梯形OBCD 是某市将要筹建的高新技术开发区用地示意图,其中DC ∥OB ,OB =6,BC =4,CD =4.开发区综合服务管理委员会(其占地面积不计)设在点P (4,2)处.为了方便驻区单位,准备过点P 修一条笔直的道路(路的宽不计),并且使这条路所在的直线l 将直角梯形OBCD 分成面积相等的两部分.你认为直线l 是否存在?若存在,求出直线l 的表达式;若不存在,请说明理由.(陕西省中考试题)专题23面积的计算例1.22提示:连接AF .例2.选C 提示:连接DE .例3.12-提示:连接GA ,HB ,EC ,FD ,AC ,BD ,则(1)(1)HAE HAB ABD S m S m mS =+=+∙△△△,同理(1)FCG BCD S m m S =+△△,故+(1)HAE FCG ABCD S S m m S =+∙△△,同理+(1)EBF GDH ABCD S S m m S =+△△.例4.提示:过E 作EF ∥BC 交AB 于F ,△AEF ≌△ADE ≌△ADQ ,又△AED ∽△PEC ,则AD DEPC CE=,积AD ·CE =PC ·DE .例5.提示:(1)362y x =-+(0≤x ≤4)(2)22336(2)622S x x x =-+=--+,当x =2时,S 最大值=6.例6.(1)如图,分别过P ,A 作BC 的垂线,垂足为P 1,A 1.11111212PBCABCBC PP S PP PDS AA AD BC AA === △△则.同理PCA ABC S PE BE S =△△,=PABABCS PF CF S △△,故++=1BPC PCA PABABCS S S PD PE PF AD BE CF S ++=△△△△.(2)=3()2PD PB PC PD PE PFAD BE CF AD BE CF++-++=.A 级1.54cm2.18cm3.324.3155.C6.C7.D 8.C9.提示:当正方形ABCD 与正方形A ’B ’C ’D ’的对应边平行时,两者重合部分面积为正方形面积的14;转动后,两者重合面积仍为定值.10.提示:过A 、K 、B 分别作CD 的垂线.11.(1)结论仍然成立,证明略.(2)2DBC DACDMC S S S -=△△△12.(1)略(2)△ACA ’∽△BCB ’2213ACA BCB S AC S BC''==△△(3)120°,32aB级12.2563.3122n m +4提示:S 梯形ABCD=2+5.B 6.C 7.D 8.(1)略(2)109.提示:(1)当t =4时,Q 与B 重合,P 与D 重合,如图a ,重合部分是△BDC ,S △BDC=122⨯⨯=.(2)①当4≤t ≤6时,如图b ,BQ =t -4,CR =6-4,由△PQR ∽△BQM ∽△CRN ,得22(),CRN PQR S CR S PQ == PQRBQM S S ∆∆=(PQ BQ )2=(324-t )2,∴S =S △PQR -S △BQM -S △CRN =235)532+--t .当t =5时,S 最大值=325.②当6<t ≤10时,如图c ,BR =10-t ,BK ⊥RK ,且∠KRB =30°,所以BK =21BR =21(10-t ),KR =23(10-t ),S =21BK ·KR =83(10-t )2.当t =6时,S 最大值=23.综合①②,当t =5时,S 最大值=325.10.提示:(1)S =2cm 2;S =2cm 2.(2)当0<x ≤4时,如图a ,DG =AD =x ,AE =EF =x +2,S =2)(DEDG EF ⨯+=2x +2cm 2.(3)当4<x <10时,应分两种情况进行讨论:①当4<x <6时,如图b ,DG =AD =x ,EF =BE =12-x -2=10-x ,S =S △ABC -S △ADG -S △BEF =-x 2+10x-14=-(x -5)2+11,故当x =5时,S 最大值=11.②当6≤x <10时,如图c ,BD =DG =12-x ,EF =BE =10-x ,S =22-x ,当x =6时,S 最大值=10.综上所述,4<x <10时,S 的最大值为11cm 2.11.∵∠HBD =∠HAE ,∴Rt △BDH ∽Rt △ADC .∴HD DC BD AD =.又BD =DC =21BC ,∴AD ·HD =BD ·DC =41BC 2.∴S △ABC ·S △HBC =(21AD ·BC )(21HD ·BC )=161BC 4.而BC 是不变的,∴当点A 至BC 的距离变小时,乘积S △ABC ·S △HBC 保持不变.12.(1)(2)略(3)如图,存在符合条件的直线l .过点D 作DA ⊥OB 于A ,则点P (4,2)为矩形ABCD 的对称中心.∴过点P 的直线只要平分△DOA 的面积即可.易知,在OD 边上必存在点H ,使得直线PH 将△DOA 的面积平分,从而,直线PH 平分梯形OBCD 的面积,直线PH 即为所求直线l .设直线PH 的表达式为y =kx +b ,且点P (4,2),∴2=4k +b ,即b =2-4k ,∴y =kx +2-4k .∵直线OD 的表达式为y =2x ,∴⎩⎨⎧=-+=x y k kx y 242,解得⎪⎪⎩⎪⎪⎨⎧--=--=k k y k k x 284242,∴点H 的坐标为(k k --242,kk --284).∴PH 与线段AD 的交点F 的坐标为(2,2-2k ),∴0<2-2k <4,∴-1<k <1.∴S △DHF =21(4-2+2k )·(2-k k --242)=21×21×2×4,解得k =2313-(k =2313--不合题意,舍去).∴b =8-213,∴直线l 的表达式为y =2313-x +8-213.。
如右下图已知三角形ABC是直角三角形
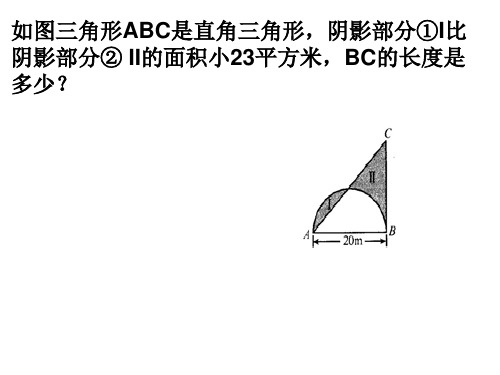
解:半圆面积为3.14×(20÷2)2× =314× ,
,
=157(平方厘米), 三角形ABC的面积为:157+23=180(平方厘米). BC的长为:180×2÷20, =360÷20, =18(厘米). 答:BC的长度是18米. 分析:从图中可以看出阴影部分Ⅰ加上空白部分的面积是 半圆的面积,阴影部分Ⅱ加上空白部分的面积是三角形ABC 的面积.又已知Ⅰ的面积比Ⅱ的面积小23平方厘米,故半 圆面积比三角形ABC的面积小23平方厘米.利用圆和三角形 的面积公式即可求解. 点评:此题考查了学生三角形以及圆的面积公式及其应用, 同时考查了学生观察图形的能力.
Hale Waihona Puke
求不规则图形面积的五种方法

求不规则图形面积的五种方法
一、相加法:临方法是将不规则图形分解转化成几个基本规测图形,分别计算它们的面积,然后相加求出整个图形的面积。
二、相减法:这种方法是将所求的不规则图形的面积看成是若千个基本规则图形的面积之差.
三、直接求法:这种方法是根据已知条件,从整体出发直接求出不规则图形面积
四、重新组合法:这种方法是将不规则图形拆开,根据具体情况和计算上的需要,重新组合成一个新的图形,设法求出这个新图形面积即可4个角处,这时采用相减法就可求出其面积了.
五、割补法:这种方法是把原图形的受部分切割下来补在图形中的另部分使之成为基本规则图形,从而使问题得到解决。
小学数学六年级《圆的面积—外方内圆外圆内方》教学设计23

外方内圆(阴影部分的面积)教学目标:1、认识“外方内圆”图形的特点,会根据要求画出“外方内圆”图形;2、利用圆的面积计算公式解决生活中“外方内圆”的实际问题,培养学生灵活运用知识的能力;3、体验数学与生活的联系,感受平面图形的学习价值。
教学重、难点:会解决“外方内圆”的实际问题。
正确理解图形中圆和正方形之间的关系(在正方形里画一个最大的圆,正方形的边长等于圆的直径)。
教学准备:三角板、圆规等教学工具。
课时安排:1课时教学过程:一、课前三分钟口语训练二、导入课题同学们,在前边的学习中我们已经学了有关圆的知识,现在老师就考考大家,看谁答得又对又快。
圆的面积?圆环的面积?真棒!看来大家都掌握得很好,那么作为奖励现在老师要和大家分享几张漂亮的图片。
1、出示第一张图片,这些图片中你发现了那些平面图形?2、出示第二张图片,观察这三张图片,它们漂亮吗?它们有什么特点?3、出示第三张图片,再观察这张图片有什么特点?4、像这种正方形里边有一个最大的圆的图形我们把他称之为“外方内圆”。
那么,像这种“外方内圆”的设计在我国的建筑上经常能看到,你们见过吗?在哪见的?(电视上、比较古老的房子上……)那么,今天我们就来学习有关“外方内圆”的实际问题的解法。
三、探究新知1、动手画“外方内圆”的图形,观察这个图形它有什么能特点?那么你能不能画一个这样的图形?这种图形它隐含着什么数学问题呢? ppt 出示例题题目: 上图中圆的半径是1m ,你能求出正方形和圆之间部分的面积吗?2、学生读题目,找出题中的已知条件和问题。
已知条件:正方形里有一个最大的圆,圆的半径是1米。
问题:求阴影部分的面积。
3、小组合作学习,求出正方形和圆之间部分的面积。
4、学生汇报展示5、集体纠正本题是在正方形里画一个最大的圆,求正方形和圆之间部分的面积,通过画图我们知道:阴影部分的面积=正方形的面积—圆的面积。
要求正方形的面积必须知道正方形的边长,正方形的边长知道吗?如何求?因为在正方形里画最大的圆,正方形的边长=圆的直径的长度,所以 正方形边长a=d=2r=2×1=2(m ) 正方形的面积s= a ²= 2²=4(m ²) 而圆的面积s=πr ²=3.14x1²=3.14(m²) 所以正方形和圆之间部分的面积=正方形的面积—圆的面积 =4—3.14=0.86(m ²) 答:正方形和园之间部分的面积是0.86m ²。
满堂脚手架面积计算方法

满堂脚手架面积计算方法:满堂脚手架,按实际塔设的水平投影面积计算,不扣除附墙柱、柱所占面积,其基本层高以3.6m以上至5。
2m为准.凡超过3。
6m、在5.2m以内的天棚抹灰及装饰装修,应计算满堂脚手架基本层;层高超过5.2m,每增加1.2m计算一个增加层,增加层的层数=(层高—5。
2m)/1.2m,按四舍五入取整数。
室内凡计算了满堂脚手架者,其内墙面装饰不再计算装饰架,只按每100㎡墙面垂直投影面积增加改架工1.28工日。
使用了满堂脚手架后,3。
6米以上的内墙装饰不再另行计算装饰脚手架,而内墙的砌筑脚手架仍按里脚手架规定计算.满堂脚手架的使用视其高度而定,当天棚净高在3。
6M以下者,不管天棚采用何种装饰工艺,均不计算装饰脚手架。
当天棚净高在3。
6M至5.2M之间时,天棚的装饰脚手架按满堂脚手架本层定额计算,当天棚净高在5。
2M上时,天棚的装饰脚手架要计算基本层和增加层两个定额项目。
对于常见的现浇砼有梁板,实际施工过程中模板下侧钢管及扣件为模板支撑,不是满堂脚手架。
计算有梁板结构脚手架工程量时应按计算规则区分柱、梁构件计算并套用相应的脚手架定额。
计算方法室内天棚装饰(包括抹平扫白)满堂脚手架,按室内净面积计算,即室内结构净长乘以结构净宽以面积计算,附墙柱、垛、内部独立柱所等占面积不予扣除。
满堂脚手架工程量=室内净长度×室内净宽度.说明一、凡工业与民用建(构)筑物所需垂直运输,均按本定额执行。
二、建筑物垂直运输以建筑物的檐高及层数两个指标划分定额子目。
凡檐高达到上一级而层数未达到时,以檐高为准;如层数达到上一级而檐高未达到时,以层数为准。
三、建筑物檐高系指建筑物自设计室外地面标高至檐口滴水标高。
无组织排水的滴水标高为屋面板顶,有组织排水的油水标高为天沟板底。
地下室和屋顶有围护结构的楼梯间、电梯间、塔楼、望台等,计算建筑面积,不计算高度、层数。
四、建(构)筑物垂直运输定额中的塔式起重机,应另计算场外运输费。
欧洲国家面积排名
欧洲国家面积排名
欧洲国家面积排名,此数据包括殖民地,数字代表平方公里。
1、俄罗斯:1712万
2、丹麦:221万
3、法国:67万
4、乌克兰:56万
5、西班牙:50万
6、瑞典:45万
7、挪威:38万
8、德国:35万
9、芬兰:33万
10、波兰:31万
11、意大利:30万
12、英国:26万
13、罗马尼亚:23万
14、白俄罗斯:20万
15、希腊:13万
16、保加利亚:11万
17、冰岛:10万
18、匈牙利:9.3万
19、葡萄牙:9.2万
20、奥地利:8.3万
21、捷克:7.8万
22、塞尔维亚:7.7万
23、爱尔兰:7.02万
24、立陶宛:6.5万
25、拉脱维亚:6.4万
26、克罗地亚:5.6万
27、波黑:5.1万
28、斯洛伐克:4.9万
29、爱沙尼亚:4.5万
30、荷兰:4.2万
31、瑞士:4.1万
32、比利时:3.05万
33、摩尔多瓦:2.9万
34、阿尔巴尼亚:2.8万
35、马其顿:2.5万
36、斯洛文尼亚:2.02万
37、黑山:1.3万
38、科索沃:1.08万
39、卢森堡:2586
40、安道尔:468
41、马耳他:316
42、列支敦士登:160
43、圣马力诺:61
44、摩纳哥:2
45、梵蒂冈:0.44。
北师大版三年级数学下册《面积单位》说课课件
北师大版小学数学三年级下册
大家好,今天我说课的内容是北师大版小学数学三年 级下册的《 面积》单元的课时内容《面积单位》。下面我 将从说教材、说学情、说教学目标、说教学重难点、说教 法、说教学过程和板书设计及教学反思这八个方面展开。 接下来开始我的说课。恳请大家批评指正。
一、说教材
参考答案 1、(1)平方厘米 (2)平方分米 (3)平方米 2、电视机大约15平方分米。 电冰箱的占地面积大约1平方米。 电脑的面积大约是2平方分米。 电灯的面积大约是4平方分米。
板块四、课堂总结 在这节课中,你们学到了什么知识? 生1:我们知道了面积的单位有平方米、平方分米、平方厘米,它们 都可以用字母表示。 生:2:测量较小物体的面积用平方厘米作单位,测量稍大物体的面积 用平方分米作单位,测量较大物体的面积用平方米作单位。 生3:1平方厘米<1平方分米<1平方米。
《面积单位》是北师大版小学数学五年级下册《面积》单元的 课时内容。本课是让学生经历动手操作,交流各自测量结果,在对 彼此不同的测量结果的质疑与反思中,体会统一面积单位的必要性; 在这个基础上,认识1平方厘米、1平方分米与1平方米面积单位, 并让学生说一说自己身边哪些物体的面积大约是1平方厘米、1平方 分米与1平方米,使每个面积单位变得直观具体、看的见,摸得着。 学生有了对面积单位的体验后,让他们再估算并测量身边事物的面 积大小。
八、教学反思
1.学生的空间观念处于初步发展阶段,因此学生容易把物体表面的 面积与周长混淆,对于面积和周长这两个概念,部分学生的认识处于 模糊状态,由此对面积单位和长度单位,不能很好地区分。因此在教 学中教师要尽量多地让学生动手去触摸和感知物体的面,体会面和 边的不同,从而对“面积”的意义加深理解。
三角形面积的性质及相关定理
三角形面积的性质及相关定理三角形是几何学中最基本的图形之一,其面积的计算对于解决各种几何问题具有重要的意义。
在本文中,我们将探讨三角形面积的性质以及与之相关的定理。
一、三角形面积的性质1. 任意三角形的面积是非负的:根据几何学的定义,一个图形的面积是其所占据的平面空间的量度。
因此,三角形的面积必然是非负的,即大于等于零。
2. 三角形面积可以通过底边与高的乘积来计算:三角形的面积可以使用以下公式来计算:面积 = 底边 ×高 / 2。
其中,底边为任意一条边,高是从底边到对应顶点所画的垂直线段的长度。
3. 三角形的面积与底边是正相关的:当三角形的高不变时,面积与底边呈正比关系。
也就是说,底边越长,三角形的面积越大;底边越短,三角形的面积越小。
二、三角形面积的相关定理1. 海伦公式:对于任意三角形,可以使用海伦公式来计算其面积。
海伦公式的表达式为:面积= √[s × (s-a) × (s-b) × (s-c)],其中s是三角形的半周长,a、b、c分别表示三角形的三边长。
2. 直角三角形的面积定理:对于直角三角形,其面积可以通过直角边的乘积再除以2来计算。
即面积 = 直角边1 ×直角边2 / 2。
3. 正弦定理:正弦定理是三角形面积计算的常用定理之一。
它的表达式为:面积= a × b × sin(θ) / 2,其中a和b为两个边长,θ为它们夹角的正弦值。
4. 海涅定理:海涅定理是另一种用于计算三角形面积的公式。
对于已知三角形的三个顶点坐标(x1, y1)、(x2, y2)和(x3, y3),可以使用以下公式来计算面积:面积 = 1/2 * |(x1y2 + x2y3 + x3y1 - x1y3 -x2y1 - x3y2)|。
三、实例应用为了更好地理解三角形面积的性质和相关定理,我们来看几个具体的应用实例。
1. 例题一:已知三角形的底边长为6cm,高为4cm,求其面积。
多边形的面积23公式长方形周长=长宽×2面积=长×宽
第五单元多边形的面积23、公式:长方形:周长=(长+宽)×2 面积=长×宽字母公式:C=2 (a+b) S=ab a=S÷b练习:已知正方形边长a=4.2厘米,求它的面积S和周长C.正方形:周长=边长×4 面积=边长×边长字母公式:C=4a a= C÷4 S=练习:一个长方形的长是12厘米,宽是8厘米,求它的面积S和周长C.平行四边形:面积=底×高字母公式:S=ah h=S÷a练习:一个平行四边形的底是15分米,高是8分米,它的面积是多少?三角形:面积=底×高÷2 ——【底=面积×2÷高;高=面积×2÷底】字母公式:S=ah÷2 h=2S÷a a=2S÷h练习:一个三角形的底是8厘米,高是底的一半,它的面积是()梯形:面积=(上底+下底)×高÷2字母公式:S=(a+b)h÷2 a=2S÷h-b b=2S÷h-a a+b=2S÷h h=2S÷(a+b)练习:梯形的上底是16厘米,下底是24厘米,高是下底的一半,这个梯形的面积是多少?24、平行四边形面积公式推导:剪拼、平移平行四边形可以转化成一个长方形;25、三角形面积公式推导:旋转两个完全一样的三角形可以拼成一个平行四边形,长方形的长相当于平行四边形的底;平行四边形的底相当于三角形的底;长方形的宽相当于平行四边形的高;平行四边形的高相当于三角形的高;长方形的面积等于平行四边形的面积,平行四边形的面积等于三角形面积的2倍,因为长方形面积=长×宽,所以平行四边形面积=底×高。
因为平行四边形面积=底×高,所以三角形面积=底×高÷226、梯形面积公式推导:旋转27、三角形、梯形的第二种推导方法老师已讲,自己看书两个完全一样的梯形可以拼成一个平行四边形,知道就行。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
郑州市郑东新区昆丽河小学 谢蕾蕾
甲、乙两人又相约比赛扫地,乙让甲先选, 甲、乙两人围着这两块场地的边线跑一圈, 甲在心里嘀咕,“既然他们的周长一样,那它们 甲输了,于是对乙说:“不行,我跑的路线比你 里面的面积也应该是一样大。我还是扫上面的 的要长一些。” 大家同意吗? 吧!”这种想法对吗?
甲
B A 乙
下面的图形有面积吗?指一指。
(
)
(
)
(
) (
)
下面的图形,哪些有面积?谁的面积最大? 谁的面积最小?
①
②
③
观察法
④
⑤
⑥
上下两个图形被蓝色部分遮住了,猜测一下, 谁的面积大一些?
思考:下列图形的周长和面积有什么关系?
①
②
③
周长变大,面积也变大
思考:下列图形的周长和面积有什么关系?
结论:正方形的面积大
... ...
硬币
三角形 结论:正方形的面积大 测量法
3.如图,用方砖铺满空地,哪块空地用的方砖最少?
通过这节课,你学到了什么?
①
②
③
周长变大,面积变小了
思考:下列图形的周长和面积有什么关系?
①
②
③
周长不变,面积变小了
下列两幅图,你能用肉眼比较出它们面积的大 小吗?
重叠法
结论:正方形的面积大
活动要求
1.议一议:怎样比较?用哪些工具? 2.做一做:选择工具和比较的方法,比一比。 3.说一说:你的比较方法。
学具袋
测量法
