无单元技术在压力管道屈曲失稳分析中的应用
含缺陷海底管道屈曲稳定性的数值模拟

含缺陷海底管道屈曲稳定性的数值模拟赵冬岩;余建星;岳志勇;段梦兰【摘要】针对几种常见的缺陷形式,利用有限元软件进行屈曲稳定性分析,并对海底管道整体腐蚀和局部腐蚀两类缺陷进行了仿真计算,拟合得到了较为简单的含缺陷海底管道临界我荷的近似计算公式,可供工程设计人员进行相关设计和评估时参考使用,同时也为制定新的含缺陷海底管道屈曲稳定性设计规范提供了参考依据.【期刊名称】《天津大学学报》【年(卷),期】2009(042)012【总页数】5页(P1067-1071)【关键词】海底管道;屈曲;初始缺陷;临界载荷【作者】赵冬岩;余建星;岳志勇;段梦兰【作者单位】天津大学建筑工程学院港口与海洋工程教育部、天津市重点实验室,天津,300072;海洋石油工程股份有限公司,天津,300451;天津大学建筑工程学院港口与海洋工程教育部、天津市重点实验室,天津,300072;北京大学力学与工程科学系,北京,100871;中国石油大学(北京)海洋油气研究中心,北京,102249【正文语种】中文【中图分类】P751海底管道在工作过程中,所受的载荷主要包括由于管道内部原油温度较高引起的温度应力、平铺在海底的裸露管道受到的静水压力、埋设在海底的管道受到的土壤压力、输油时候的内压力、自重以及端部连接处其他海底管道施加的轴向压力等,这些载荷又可以简化为轴向压力和径向内外压力.根据工程中的实践经验,海底管道的屈曲多为轴向或径向受压导致的屈曲.因此对海底管道屈曲稳定性问题,只需简化为两类力学模型考虑:①轴向受压圆柱壳的屈曲模型;②径向外压作用下圆柱壳的屈曲模型.文献[1-3]指出在轴向对称载荷作用下的圆柱壳,其动力屈曲失稳荷载和静力屈曲失稳荷载大小基本相同.因此在分析管道屈曲失稳时,一般只需考虑静力屈曲.关于圆柱壳在轴向或径向压力作用下的屈曲问题,相关的研究已经很多,得到了一系列圆柱壳稳定性的经典结果.依据小挠度屈曲理论得到的这些结果,有些与实验符合很好(如受径向压力作用下的圆柱壳),也有一些与实验值出现了较大的差异(如受轴向压力作用的圆柱壳),早期实验值大部分在理论值的1/2~1/5之间.为了解释这种现象,前人从理论与实验两方面进行了探索,提出了非线性大挠度屈曲理论[4-5]和前屈曲一致性理论[6],并指出初始缺陷是导致实验结果与经典理论解存在差异的主要因素.由于海底管道在制造和使用过程中不可避免地会出现缺陷,例如:制造精度引起的管线截面的不圆度和不直度;由于海水、输送介质的腐蚀,造成海底管道局部管段壁厚变薄;拖网渔船渔具和坠落物的碰撞(如锚砸)等机械性损伤.因此在考虑海底管道的屈曲问题时,应考虑管道缺陷的影响.上述缺陷可以分为几何型缺陷(如截面不圆等)和体积型缺陷(如腐蚀引起的局部管段和局部位置壁厚变薄等)两大类.其中几何型缺陷的问题在文献[7-9] 中均有论述,本文不再详述.但体积型缺陷由于考虑局部质量损失,目前尚无很好的解决办法.工程上使用的海底管道屈曲稳定性的设计方法,仍然是参照完好管道的经典理论解,含缺陷的海底管道屈曲稳定性还没有海底管道工程界普遍认可的方法.笔者针对海底管道的局部管段变薄、局部位置变薄等体积型缺陷,利用大型有限元软件Ansys进行建模计算.由于常用的海底管道,其截面半径是壁厚的10倍以上,因此在 Ansys计算中可以当作薄壳结构来处理.1.1 完好圆柱壳稳定性的若干经典结果如图1所示建立柱坐标系统,取圆柱壳的轴向为x方向,壳体横截面的环向为θ方向,径向为z方向.图中:a为圆柱壳横截面半径,m;h为圆柱壳壁厚,m;l 为圆柱壳长度,m.由于海底管道所受的屈曲载荷主要为轴压或径向外压作用,因此只考虑圆柱壳受轴压和径向外压作用两种情况.对完好圆柱壳模型,考虑小挠度屈曲问题,由线性屈曲理论可以得到圆柱壳在基本载荷作用下的临界载荷值[10-11].对端部简支圆柱壳受轴压作用情况,临界载荷的经典理论解为式中:E为圆柱壳材料弹性模量;ν为泊松比,无量纲.圆柱壳屈曲失稳时有轴对称屈曲和非轴对称屈曲2种形式,且2种屈曲形式的临界载荷是相同的,实际观察到的多为非轴对称屈曲.根据小挠度理论求得的屈曲临界载荷σcr又称为经典线性临界载荷,这里注意到临界载荷与壳体长度无关,而实验却指出,临界载荷是随管长l的增加而降低的[12].另外式(1)对短壳(管长小于管线截面半径的圆柱壳为短壳,其余的则为中长壳)不适用.对端部简支圆柱壳受径向外压力作用的情况,由唐奈尔(Donnell)简化模型得到的临界载荷为1.2 完好管道稳定性数值模拟分析对完好管道情况,分别采用 Ansys软件中的特征值屈曲分析方法和非线性屈曲分析方法求解管道的屈曲临界载荷,将计算结果与经典理论解比较,可以求得无量纲临界载荷.海底管道参数取自某实际工程,其中管外径为0.219,1,m,有效输油内径为0.199,71,m,管线弹性模量为2.03×1011Pa,钢管密度为7.8×103kg/m3. 管道可以看作圆柱壳模型,用壳单元进行整体的有限元模拟,对局部损伤位置采用网格更细的体单元,边界条件为两端简支边条件,损伤缺陷的描述参见第2.1和2.2节.1)轴向压力作用圆柱壳受力模型如图2所示.设由 Ansys中的特征值方法求得的临界载荷为σ,非线性方法求得的临界载荷为σ1.与经典线性理论得到的临界载荷σcr相比,误差分别为,计算结果如表1所示.可以看到,经典理论解偏大,这与别人的实验结果是一致的.另外,在 Ansys计算中使用非线性方法比特征值方法得到的临界载荷更小,这是因为使用非线性方法计算临界载荷时,为了诱使管线发生屈曲,而给管线施加了与其屈曲模态形状一致的初始位移缺陷(位移缺陷大小约为特征值屈曲变形分析中求得的位移的0.002倍)缘故,说明临界载荷对初始缺陷是比较敏感的.经典理论解得到的临界载荷与管长没有关系,而Ansys计算结果指出,随着管长增加,临界载荷略有降低.例如取管长la= 时的临界载荷为基值,将管长增大,分别求得相应的临界载荷,并与基值对比,得到无量纲的临界载荷随管长变化的关系曲线,如图3所示,这点与实验一致.求得管道梁型屈曲的临界应力已经小于壳型屈曲的临界应力.因此,当管道较长时,不仅要考虑管道壳型屈曲,还要考虑管线梁型屈曲.由于在海底管道工程中,壳型屈曲的危害比梁型屈曲的危害大,因此主要研究管道壳型屈曲问题,而未考虑长管线的梁型失稳.2)径向压力作用圆柱壳受力模型如图4所示.设由 Ansys中的特征值方法求得的临界载荷为q,非线性方法求得的临界载荷为 q1,与经典线性理论得到的临界载荷 qcr的误差分别为和计算结果如表1所示.由 Ansys中特征值屈曲分析方法求得的临界载荷同经典理论解很接近,实验结果也表明径向外压作用下的圆柱壳,其经典理论解误差较小.但注意到使用 Ansys中的非线性方法得到的结果比经典理论解小很多,这也是因为在使用 Ansys软件计算时,已经考虑了初始缺陷影响的缘故.从前面的分析可以看到,使用非线性屈曲分析方法得到的临界载荷值比较小,在使用时偏安全.对于实际结构求解屈曲应力时,为安全起见,建议使用非线性方法求解.但在海底管道工程中,如果分别对每个管道建立力学模型求解,则会非常麻烦.工程上目前进行海底管道屈曲稳定性设计时,一般采用经典临界载荷乘以安全系数的方法,这样处理既保证了安全,又可以使计算过程简单.对含缺陷的海底管道问题,目前还没有合适的求解临界载荷值的方法.本文针对几种常见缺陷形式,利用 Ansys软件中的特征值方法(因为该方法得到的结果和经典理论解比较接近,便于工程应用的延续性)进行仿真计算,求得含缺陷管道的无量纲临界载荷λ(含缺陷管道的临界载荷值与完好管道临界载荷值的比值)与缺陷参数之间的关系,从而为工程上提供较为简单的含缺陷管线临界载荷的近似简单计算公式.2.1 管道整体腐蚀缺陷受到海水及输送介质腐蚀等原因引起的管道某管段壁厚变薄的现象,考虑到腐蚀深度是渐进变化的,腐蚀缺陷一般是轴对称的,因此可以设缺陷形式为此处的μ为壁厚变薄参数,即在坐标x处的管道壁厚为 h + w*( x),如图5所示,在数值计算时取管线长度l≥ 2a(一般认为当 l < 2a时,计算结果变化较大;当l≥ 2a时得到的结果变化很小,而海底管线一般较长,因此取 l = 2a计算即可).1)轴向压力作用使用Ansys软件计算,可以求得无量纲的临界载荷值,对应于大小不同的缺陷,可以得到不同的结果,如图6所示,其中λ为无量纲临界载荷(含缺陷圆柱壳临界载荷和完好圆柱壳临界载荷比值).在0.4μ≤ 时,拟合得到无量纲临界载荷近似为2)径向压力作用使用Ansys软件数值计算,同样可以求得一组无量纲的临界载荷值,如图7所示.在0.4μ≤ 时,拟合得到无量纲临界载荷近似为2.2 管道表面局部损伤缺陷平铺或浅埋在海底表面的管道容易受到拖网渔具、锚砸等机械性损伤或擦伤,从而引起管道表面局部位置壁厚变薄缺陷.在 Ansys建模中,缺陷形状可以看作是圆球与圆柱相交,其相交面在圆柱面上围成的面积,如图8所示.图中b为缺陷宽度,r为圆球半径,缺陷最深处的管道壁厚为(1 − μ)h.1)轴向压力作用取管道长度2l=a,图9中给出了不同缺陷宽度下,无量纲临界载荷λ与壁厚变薄参数μ的关系.从图9可以看到,在缺陷较小时,管道的屈曲临界载荷下降不大,此时管道的屈曲变形是整体变形,当缺陷的宽度和深度都达到一定范围后(如b>0.5a, μ>0.4),管道的屈曲临界载荷迅速降低,此时管道的屈曲变形已不再是整体变形而是缺陷所在位置处发生的局部变形,此类局部屈曲失稳危害很大,在工程应用中应该特别小心此类缺陷.可见,对这种荷载作用下的缺陷,重要的是确定屈曲临界载荷迅速降低时的缺陷的宽度和深度,具体的无量纲临界载荷λ与壁厚变薄参数μ的关系已不重要.数值计算表明,对 b<0.7a,μ<0.6的缺陷,管道的屈曲形状为整体变形(管道整体变扁),并没有出现局部屈曲,因此不会引起临界载荷较大的下降.取b = 0.7a,无量纲临界载荷λ与参数μ的关系如图10所示.2)径向压力作用对 0.7b a= 的缺陷,在0.6μ≤ 时,拟合得到无量纲临界载荷近似为对b<a0.7的缺陷,其临界应力下降更缓慢.(1)对海底管道整体腐蚀缺陷,轴向压力作用下其临界屈曲载荷近似为径向压力作用下临界屈曲载荷近似为(2)对海底管道局部损伤缺陷,轴向压力下临界屈曲载荷对缺陷不敏感;径向压力下,临界屈曲载荷近似为【相关文献】[1] Lee L H N,Ariman T,Chen C C. On buckling of buried pipelines by seismic excitation[C]//ASME. Pressure Vessel and Piping. San Francisco,1980:80-C2/PVP-75. [2] Chen C C,Ariman T,Lee L H N. Elastic buckling analysis of buried pipelines under seismic loads[C]// ASME. Pressure Vessel and Piping. San Francisco,1980:80-C2/PVP-76. [3] Lee L H N,Ariman T,Chen C C. Elastic-plastic buckling of buried pipelines by seismic excitations [J]. International Journal of Soil Dynamics and Earthquake Engineering,1984,3(4):168-173.[4] Timoshenko S P,Gere J M. Theory of Elastic Stability [M]. New York:McGraw-Hill,1961.[5] Bleich F. Buckling Strength of Metal Structures [M]. New York:McGraw-Hill,1952. [6] Vlasov V Z. Thin-walled elastic beams [G]//Office of Technical Services. Israel Program for Scientific Translations. Washington D C:US Department of Commerce,1961:38-46.[7] Column Research Committee of Japan. Handbook of Structural Stability [M]. Tokyo:Corona Publishing Company Limited,1971.[8]余轩凌. 含缺陷海底石油管道的弹性稳定性分析[D].北京:北京大学力学与工程科学系,2003. Yu Xuanling. The Elastic Stability Analysis of Subsea Pipeline with Imperfections[D]. Beijing:Department of Mechanics and Engineering,Peking University,2003(in Chinese). [9]岳志勇. 海底输油管线的抗震设计方法与含缺陷管道的稳定性研究[D]. 北京:北京大学力学与工程科学系,2004. Yue Zhiyong. The Anti-Earthquake Design Method of Subsea Pipeline and the Stability Study of Subsea Pipeline with Imperfections[D]. Beijing:Department of Mechanics and Engineering,Peking University,2004(in Chinese).[10]武际可,苏先樾. 弹性系统的稳定性[M]. 北京:科学出版社,1994. Wu Jike,Su Xianyue. The Elastic System Stability[M]. Beijing:Science Press,1994(in Chinese).[11]周承倜. 薄壳弹塑性稳定性理论 [M]. 北京:国防工业出版社,1979. Zhou Chengti. The Elastic-Plastic Stability Theory of Thin Shell[M]. Beijing:Defense Industry Press,1979 (in Chinese).[12]吴连元. 板壳稳定性理论 [M]. 武汉:华中理工大学出版社,1996. Wu Lianyuan. The Stability Theory of Plate and Shell [M]. Wuhan:Huazhong University of Science & Technology Press,1996(in Chinese).。
压力管道应力强度非概率可靠性分析

压力管道应力强度非概率可靠性分析
邵世飞;周昌玉;常乐
【期刊名称】《南京工业大学学报(自然科学版)》
【年(卷),期】2016(038)003
【摘要】对压力管道进行应力强度分析时不确定参数的分布函数较难获取.为弥补数据的不确定信息,首先,运用非概率可靠性方法计算压力管道一次应力与二次应力的非概率可靠性,其次,通过调整功能函数与不确定参数的位置关系进一步研究区间可靠性与凸模可靠性的计算特点.压力管道应力强度计算结果表明:凸模可靠性较区间可靠性,在非概率可靠性计算区间扩张方面更有优势,而且可以根据工程实际问题作出灵活响应.区间可靠性较凸模可靠性更为保守,在数据不足的情况下,区间可靠性可保证安全.
【总页数】6页(P44-49)
【作者】邵世飞;周昌玉;常乐
【作者单位】南京工业大学机械与动力工程学院,江苏南京211800;南京工业大学机械与动力工程学院,江苏南京211800;南京工业大学机械与动力工程学院,江苏南京211800
【正文语种】中文
【中图分类】TE8
【相关文献】
1.结构系统概率-模糊-非概率混合可靠性分析 [J], 尼早;邱志平
2.非随机过程的地震激励下埋地压力管道的非概率可靠性分析 [J], 张鹏;王艺环;秦国晋
3.概率模型和非概率模型在结构可靠性分析中的比较 [J], 胡海波;李苏平
4.基于断裂力学的起重机结构概率-非概率疲劳可靠性分析 [J], 李建明;丁谦
5.基于概率-非概率混合模型和贝叶斯网络的汽车起重机起重臂屈曲可靠性分析 [J], 屈福政;孙奇;谢正义
因版权原因,仅展示原文概要,查看原文内容请购买。
加劲式压力钢管外压稳定性有限元屈曲分析

p n tc r ie . h EM sf a il a o u k i g a ay i o t fn rr g p n t c . h n u n e fv r u n t l e so k a e gv n T e F i e sb e w y f rb c l n l ss fsi e e n e s k T e if e c so ai si i a n f i o l o i d fc s p p h c n s n t fn rr g s e o rt a o d o e so k wee a s ic s e . ee t, i e ti k e s a d si e e n i n c i c lla fp n t c r l d s u s d f i z i o Ke o d : x e n l r s u e sa i t; i i l me t u k i g a ay i; n t ld f c; o d d s l c me tc r e si e e n y W r s e t r a e s r t b l y f t ee n c l n l ss i i a e e t l a - ip a e n u v ; tf n rr g p i n e b n i f i
Absr t t ac :Theexe n lp esur t b l y o nd r r un e t c sa ke sue i n i e i esg The eg n v l n tr a r s e sa ii fu e g o d p nso k i y is n e gne rng d in t ie aue a d
摘
要 :埋 藏 式 压 力 钢 管 抗外 压 稳 定 是 1 程 设 计 中 的关 键 问 题 。 在 考 虑 钢 管 的初 始 缺 陷 、 塑性 行 为 以及 大 变 形 的 基 二
加劲环式压力管道非线性有限元分析及稳定性计算
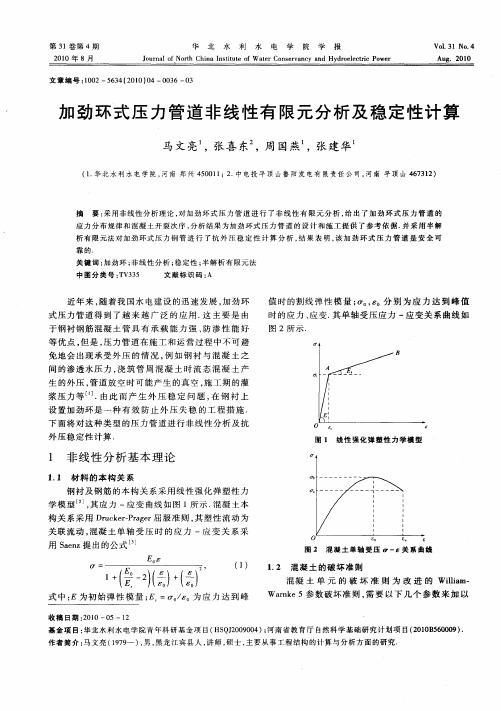
l
:
F
=
—
s ≥0 ,
第 3 卷 第 4期 1
21 0 0年 8月
华
北
水
利
水 电
学
院
学
报
Vo _ No. l 31 4
Au g.201 0
J ur a fNo t i a I siu e o ae n e v n y a d Hy o l ti we o n lo rh Ch n n ttt fW trCo s r a c n dreecrc Po r
生 的外 压 , 管道放 空 时可能 产生 的真 空 , 工期 的灌 施 浆 压力 等 …. 由此 而 产 生 外 压 稳 定 问 题 , 钢 衬 上 在
设 置加 劲环 是一 种有 效 防止 外 压 失稳 的工 程 措 施 .
下 面 将 对 这 种 类 型 的 压 力 管 道 进 行 非 线 性 分 析 及 抗
Wan e5参 数破 坏准 则 , 要 以下 几 个参 数 来 加 以 rk 需
基金项 目: 华北 水利 水 电 学 院 青 年 科研 基金 项 目( S J09 0 ) 河 南 省 教 育 厅 自然 科 学 基 础 研 究 计 划 项 目(0 0 5 00 ) H Q2 0 04 ; 2 1B 6 09 . 作者简 介: 马文 亮 ( 99 ) 男 , 17 一 , 黑龙 江宾 县人 , 师 , 士 , 要 从 事 工 程 结 构 的计 算 与 分 析 方 面 的研 究 . 讲 硕 主
深海管道非线性屈曲理论计算方法

深海管道非线性屈曲理论计算方法
余建星;李智博;杜尊峰;傅明炀;卞雪航;杨源
【期刊名称】《海洋工程》
【年(卷),期】2013(0)1
【摘要】针对深海管道在侧向静水压条件下发生局部屈曲压溃的情况,研究了关于管道前屈曲阶段变形响应和压溃压力的计算方法。
假定管道前屈曲阶段发生沿轴向均匀一致的椭圆度变形,建立基于圆环的力学模型,考虑几何大变形和材料的弹塑性本构关系,利用虚功原理建立平衡方程。
通过选用合适的位移离散函数对方程组数值离散,并利用牛顿法进行数值求解,得到含椭圆度缺陷的管道截面的变形响应和压溃压力。
通过试验、有限元分析和规范对理论计算结果进行了对比验证,证明该方法精度可靠,与事实吻合。
最后,计算了初始椭圆度缺陷对不同径厚比管道的压溃压力的影响。
【总页数】7页(P54-60)
【关键词】深海管道;压溃压力;非线性屈曲;初始椭圆度
【作者】余建星;李智博;杜尊峰;傅明炀;卞雪航;杨源
【作者单位】天津大学建筑工程学院
【正文语种】中文
【中图分类】P751
【相关文献】
1.基于广义梁理论的非线性材料薄壁受压构件屈曲荷载计算方法 [J], 朱浩川;姚谏
2.基于非线性环理论的管道上卷弯曲屈曲分析 [J], 廖洪千;王立权;李怀亮;刘军;李松羽
3.深海管道在冲击载荷作用下的局部屈曲特性研究 [J], 杨政龙;余建星;陈海成;余杨;段晶辉
4.外压作用下深海腐蚀缺陷管道的屈曲失稳机理 [J], 龚顺风;徐勤贵;周家伟;王喜鹏;刘承斌
5.后挖沟深度对深海海底管道屈曲影响数值分析 [J], 李修波;刘可安;王华昆;王鸿飞
因版权原因,仅展示原文概要,查看原文内容请购买。
基于量纲分析的管道临界屈曲应变准则研究

基于量纲分析的管道临界屈曲应变准则研究
张华;赵新伟;罗金恒;张广利;宫少涛
【期刊名称】《焊管》
【年(卷),期】2008(031)006
【摘要】管道的局部屈曲通常被认为是一种失效,在基于应变的管道设计方法中,临界屈曲应变是一个重要指标.针对现有公式的不足,分析了临界屈曲应变的主要影响因素,采用量纲分析法,利用收集到的试验数据拟合建立了新的临界屈曲应变预测公式.与现有临界屈曲应变公式计算结果相比,该公式具有较高的预测精度.
【总页数】4页(P90-93)
【作者】张华;赵新伟;罗金恒;张广利;宫少涛
【作者单位】中国石油天然气集团公司管材研究所,西安,710065;中国石油天然气集团公司管材研究所,西安,710065;中国石油天然气集团公司管材研究所,西
安,710065;中国石油天然气集团公司管材研究所,西安,710065;中国石油天然气集团公司管材研究所,西安,710065
【正文语种】中文
【中图分类】TE88
【相关文献】
1.基于灰色关联度法的管道临界屈曲应变影响因素分析 [J], 张华;赵新伟;罗金恒;张广利;张奕
2.基于应变设计管道局部屈曲应变极限值的计算 [J], 李璞;陶燕丽;周建
3.基于应变准则对管道横向滑坡响应规律的研究 [J], 王黎明;署恒木;黄小光
4.考虑变形硬化的管道塑性弯曲屈曲临界应变预测 [J], 郑茂盛; 刘姣姣; 王怡; 魏利平; 滕海鹏; 胡军
5.穿越走滑断层海底管道局部屈曲研究及应变响应预测 [J], 李杨;余建星;余杨;韩梦雪;李牧之;于佳晖
因版权原因,仅展示原文概要,查看原文内容请购买。
压力钢管安全鉴定的创新技术和应用案例
压力钢管安全鉴定的创新技术和应用案例随着工业技术的不断发展,压力钢管在许多领域中广泛应用,如石油、天然气开采、城市供水、化工等。
然而,由于长期使用和不可避免的环境因素,压力钢管可能会发生磨损、腐蚀、断裂等问题,给生产和人员安全造成潜在威胁。
为了确保压力钢管的安全运行,进行安全鉴定成为一项重要任务。
本文将介绍压力钢管安全鉴定的一些创新技术和应用案例。
第一节:无损检测技术无损检测技术被广泛应用于压力钢管的安全鉴定中,它可以在不破坏材料的情况下,通过检测材料内部和表面的缺陷来评估压力钢管的可靠性。
1. 超声波检测技术超声波检测技术是一种常用的无损检测方法,在压力钢管的安全鉴定中得到了广泛应用。
通过发射超声波脉冲,利用超声波在不同介质中传播速度的变化来检测压力钢管中的缺陷,如腐蚀、裂纹等。
2. 磁粉检测技术磁粉检测技术是一种通过涂覆磁性粉末并应用磁场的方法来检测压力钢管表面和近表面的缺陷。
当有缺陷存在时,磁粉会集中在缺陷处,形成可观察到的磁粉堆积。
3. 射线检测技术射线检测技术主要包括X射线和γ射线检测。
这两种技术通过射线在材料内部的吸收和散射来检测压力钢管中的缺陷,如气孔、裂纹等。
第二节:智能监测技术传统的安全鉴定方法在进行安全评估时,通常需要停机维修,导致生产效率低下。
而智能监测技术可以实现对压力钢管的在线监测,提高生产效率和安全性。
1. 无线传感器技术无线传感器技术可以在压力钢管上布设传感器,实时监测压力、温度、应变等信息,通过无线通信将数据传输到监控系统,实现远程监测和预警。
2. 数据分析和大数据技术通过对传感器收集到的数据进行分析和挖掘,结合大数据技术,可以建立智能监测模型,实现对压力钢管运行状态的预测和故障诊断。
第三节:应用案例1. 油气管道安全监测系统某油气公司引入智能监测技术,利用无线传感器布设在油气管道上,实现对温度、压力和颤振等参数的在线监测,并通过数据分析和大数据技术,建立了预警模型,有效预防了压力钢管爆裂和泄漏事故的发生。
样条无单元法在薄板弹性稳定分析中的应用
3
2 l O
= 0+ i , = a N , i = 0, 2, ,v; h h / 1, … J 7
y =Y j h o+ h , =b M, /
=o, , , , l2 …
图 1 样 条 结 点 离 散
Fg 1 Dip re pi n t i. se dsl s nek os
中 图分 类号 :T 3 14 U 1 . 文献标 志码 :A
薄板 的稳 定 问题一 直是 工程界 比较 关注 的 问题 .将 工 程 界应 用 最 为广 泛 的有 限单 元 法 用 于解 决 该 问题 时 ,根据 收敛 性准则 ,位移插 值 函数要 满足 c类 连续 性 ,这 给 单元 的构 造 带来 相 当大 的 困难 . 许 多 学者 致力 于矩 形 、三 角形 、四边形 的非协 调 元 的建 立 以及 如何 提 高 其精 度 的 研究 ,近年 来 发 展
薄板的挠度函数可采用三次 样条函数乘积的线性组合:
收稿 日期 : 0 6一 6— 3 2 0 o 2
基 金项 目:国家 自 科学 基金 资助项 目 (9700 ;广西 自然 科学 基金资 助项 目 ( 然 1822 ) 桂科 自 0303 39 1)
作者 简介 :李秀梅 (98 ,女 ,博 士研 究生 ,副教 授 ,研 究方 向 :高层 建筑 结构计 算方 法. 16 一)
c^+ ^ + ,l f l
,
}
是样条结点的位移参数 , 也是样条无单元法分析薄板弯曲问题 的基本未知量 , 它是( 3 Ⅳ+ )X( + ) 3 阶
列 阵.
[ () ]=[ 一 z 。 ) (
。 ) (
。 ) … (
+ ) , 。 ] (
无单元技术在压力管道屈曲失稳分析中的应用
1
加肋柱壳应变状态分析
如将肋看成厚曲梁,就必须放弃Kirchhoff假设,对剪切变形单独考虑。其实,有限元方法对厚梁、 厚板、厚壳的处理是方便的,但有限元不易构造高阶的位移模式,使得这些厚的结构体变薄时产生闭锁现 象,得出虚假结论,尽管有缩减积分、杂交模型等方法来处理,但始终不令人满意。本文采用无单元法来 处理厚曲梁是因为考虑剪切变形时, 无单元法可以构造高阶的完备的多项式, 注意各位移分量之间的关系, 可以使由厚变薄的曲梁消除剪切及薄膜闭锁,因而对厚、薄曲梁乃至直梁具有通用性。处理厚曲梁的无单 元技术可以推广到厚板、厚壳中,可以像肋一样得到适应厚、薄壳分析的一般性理论方法。只是限于本文 工程实际及稳定性分析的针对性,这里不用厚壳而针对薄壳进行分析。无单元技术对壳体结构的描述与分 析不像有限元法那样受到局限,可以发挥可构造高阶连续形函数的优点,不必顾虑协调性,避开了有限元 法分析壳体时的困难,且自由度少,列式简便,本文提出的构造新的形函数的办法,运算量少,边界条件 易处理。 1.1 肋 的 应 变 状 态 分 析 取图1所示一段曲梁, 1 2 3 设 放在坐标系xoy中,建立a a a 正交坐标活动标架, AB为深曲梁且只在xoy面内变形。 1 2 3 x=Rcos(S/R),y=Rsin(S/R),z=z, a =t, a =s, a =z。 中线上一点C用矢量表示为
[ε ]s
(11)
简记
{ε l }s + {ε 0 }s + {ε N }s
上述三项分为线性项、缺陷项及非线性项。对第二、第三项任意取舍以反应不同的几何变形状态。 为便于消除加劲肋的剪切闭锁,需分析加劲肋的内力虚功方程,找出t+R→0时,消除剪切与薄膜变形 能的内在机制,为此用与正交曲线坐标重合的局部笛卡尔坐标系ei来衡量各物理量,便于找出本构关系, 设ui是在ei中位移,则(无求和约定) u i =
管道的屈曲分析讲解
逆解法
(1)假设管道失稳时的弯曲形状为 波浪形
y
f x
?
管道的挠曲线方程即为 y ? f sin ?x ?
? —称为管道的失稳波长。
联立上述两式,可得
? ? A(? )4 ?
?
P轴
?
2B(? ?
)2 ?
C
?
0
整理,得
P轴
?
? C( ? ?
)2 ?
A(? ?
)-2
?
2B
当
dP
d?
?
0时,对应的轴向力P轴即为失稳时的临界轴向 力Pcr
(2? 4.49341)2 L2
?
80.73
EI L2
临界荷载方程
求出了A、B、C、D,即可得到挠曲线方程 为
?
?
y
?
q k 2 P轴
?
?? ???
cos kx
cos
kL 2
?
k 2 L2 8
? 1?
k 2 x2 2
阶小数,可忽略不计。即认为 Ku=0,则
? ? ? 4 EI
K0D
适用于直线管道(或曲率半 径R0 ? 1000D的弯曲管道)。
Pcr ? 2 K0 DEI
与土壤压缩抗力系数K 0有较大关系
土壤的压缩抗力系数K0
土壤性质 密度小的土壤
中等密度的土壤
土壤名称
泥煤土 流砂 软湿土 新填砂 压实砂 砾石 湿粘土
第四章 管道的屈曲分析
? 屈曲也称为失稳,是指结构丧失了保持其原有平 衡形状的能力。
? 由于管道的薄壁、细长的结构特性,在其受力和 变形条件稍有恶化时,容易产生屈曲破坏。
? 管道产生屈曲的原因,通常有外压作用下的弹性 失稳、机械作用或管道本身缺陷造成的局部屈曲、 弯曲屈曲和象“压杆”一样的纵向屈曲等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0 (0 ) r = rA + u, u = (u + tθ )a 0 + wn m = [R /(T + t )](u + tθ )g 2 + wg 1 + zg 3
式中:θ为剪应变引起的法线转角。 因仅在xoy面内考虑曲梁变形,故z不予考虑。而
设u=u gi,令变形后矢量:Gi=r,I, Gij=Gi·Gj。由张量分析定义,应变为
摘要:本文将加肋的水工压力管道看成厚曲梁与柱壳的组合体,考虑肋壳的相互作用,推导了厚曲梁及柱壳的非 线性几何方程。应用无单元技术建立曲梁的位移形状函数,消除了有限元法计算板壳时的闭锁现象。推导出了加 肋柱壳的稳定性分析及静态和动态分析的一般性数学表达式。基于上述理论及水工压力管道实际工作状态,建立 了分析压力管道屈曲失稳的模型。 关键词:加肋柱壳;稳定性;位移模式;无单元新技术 中图分类号:TU433 文献标识码:A
2
(9)
本文水工压力管道加肋S方向位移u=0,同时将上述分解成线性与非线性部分,为
2 w 1 t 1 tR ε s + 1 tθ , s + w, s 2 + θ ,s R + 2 = = {ε }RL + {ε }RN = R + R t 2 rts w + θ 0 ,s
g ii u i , ε j =
1 g ii g ii
ε ij ,σ ij = g ii g ii σ ij , 因
σ ij δε ij = σ ij δε ij ,所以
www.bzfxw.com
v
ext = ∫ σ ij δε ij = ∫∫ δw R
Eε 22δε 22 2Gkε 12δε 12 2GKε 21δε 21 + + g 22 g 22 ( g 22 )
[ε ]s
(11)Βιβλιοθήκη 简记{ε l }s + {ε 0 }s + {ε N }s
上述三项分为线性项、缺陷项及非线性项。对第二、第三项任意取舍以反应不同的几何变形状态。 为便于消除加劲肋的剪切闭锁,需分析加劲肋的内力虚功方程,找出t+R→0时,消除剪切与薄膜变形 能的内在机制,为此用与正交曲线坐标重合的局部笛卡尔坐标系ei来衡量各物理量,便于找出本构关系, 设ui是在ei中位移,则(无求和约定) u i =
水
2005 年 7 月 文章编号:0559-9350(2005)07-0880-06
利
学
报
第 36 卷 第7期
SHUILI
XUEBAO
无单元技术在压力管道屈曲失稳分析中的应用
孟闻远1,2,卓家寿1,籍东3
(1.河海大学 土木工程学院,江苏 南京 210098; 2.华北水利水电学院,河南 郑州 100031) 450008; 3.华睿投资集团有限公司,北京
水工压力管道正常工作时一般承受较大的内水压力, 但在施工期或非正常无水状态下承受较大的 外压力(如灌浆压力、突然停水后的负压力等)。在外压力作用下,压力管道时有失稳破坏,如我国湖 南镇水电站和黄龙滩水电站、 云南绿水江水电站、 广东泉水水电站。 在国外也有压力管道破坏的事故, 如加拿大的Kemao水电站、 巴西的Nilo-pecanha水电站、 美国的泰乌姆及美国最大的抽水蓄能电站Bath County水电站等。随着国内外水电站建设事业的迅速发展,特别是大量的高水头、大容量抽水蓄能电 站的兴建,压力管道越来越趋向于大型化、巨型化,这就给压力管道的设计提出了更加复杂的课题。 [1~10] ,在分析方法、强度分析、结构优化 20世纪50年代以来,国内外对水电站压力管道有大量的研究 与设计、材料与结构模型试验等方面有较大的发展,如钢衬钢筋混凝土压力管道的成功应用及其分析 [6] [7] [8] [9] 理论、设计方法的出现等。马善定 、董哲仁 、路振刚和董毓新 、刘东常 等对水电站压力管道的 设计和分析理论均有新的发展。但现有压力管道外压稳定性分析理论存在着缺陷,主要表现在计算模 [1,11] 是解析方法和以有限 型不够准确,计算方法受到局限。目前压力管道稳定性设计分析的主要方法 元分析为主的数值计算方法。 事实上, 真正用解析方法对此类复杂的组合壳体进行分析是无能为力的, 于是有研究者将实物模型进行降维简化以求得解析表达式, 这些方法都是在假设条件下以牺牲真实受 力变形状态为代价来推导简化公式,他们在垂直轴线方向取单位宽度的圆环来分析,把肋看成刚性支 承,即使考虑肋的作用,也是将肋看成附加部分壳体尺寸的圆环。随着计算理论及计算机技术的迅速 发展,有限元数值计算方法逐步应用于水工压力管道分析,但由于曲壳元所依据的理论及有限元列式 [12] 都非常复杂,因而往往难以构造出完备的阶次高、协调性好且易于计算的单元。后来,Ahmad等人 提出了三维弹性体的退化壳元,此单元虽然有很多优点,但退化成薄壳易产生剪切与薄膜闭锁,当然 对加肋也有类似结果。文献[9]在分析水工压力管道时,提出了半解析方法,但对肋的处理有待探讨。 实际工程上, 加肋由于受到围岩及混凝土在垂直肋所在平面方向的约束, 一般不易发生侧移失稳变形, 而仅在肋轴线形成的平面内变形。同时,不同工程的加肋截面不同,有工字型、槽形、角形等,而仅
SHUILI
XUEBAO
几何非线性等任何形态的壳。对柱壳省略高阶微量后,为
2 1 ∂w 1 w z ∂2w 1 ∂w ∂w 0 R ∂φ 2 R − 2 2 2 R ∂φ R ∂φ ∂φ 2 2 0 1 ∂w ∂ w ∂w ∂w = − z 2 + + ∂y y y 2 ∂ ∂ y ∂ z ∂ 2 w 1 ∂w 0 ∂w ∂w ∂w 0 1 ∂w ∂w + R ∂φ∂y R ∂y ∂φ ∂φ ∂y R ∂φ ∂y
(8)
式(8)为任意圆弧状深曲梁的非线性应变公式,可适用于其它工程问题的大变形分析,对之进行显式 0 化,不计n 方向应变w,t等,有
1 w 1 R t ε s = ε 22 + 1 u , s + tθ , s + + w, s 2 + (u , s + tθ , s ) 2 R 2 R+t R u rts = 2ε 12 = w, s + θ − R
1
加肋柱壳应变状态分析
如将肋看成厚曲梁,就必须放弃Kirchhoff假设,对剪切变形单独考虑。其实,有限元方法对厚梁、 厚板、厚壳的处理是方便的,但有限元不易构造高阶的位移模式,使得这些厚的结构体变薄时产生闭锁现 象,得出虚假结论,尽管有缩减积分、杂交模型等方法来处理,但始终不令人满意。本文采用无单元法来 处理厚曲梁是因为考虑剪切变形时, 无单元法可以构造高阶的完备的多项式, 注意各位移分量之间的关系, 可以使由厚变薄的曲梁消除剪切及薄膜闭锁,因而对厚、薄曲梁乃至直梁具有通用性。处理厚曲梁的无单 元技术可以推广到厚板、厚壳中,可以像肋一样得到适应厚、薄壳分析的一般性理论方法。只是限于本文 工程实际及稳定性分析的针对性,这里不用厚壳而针对薄壳进行分析。无单元技术对壳体结构的描述与分 析不像有限元法那样受到局限,可以发挥可构造高阶连续形函数的优点,不必顾虑协调性,避开了有限元 法分析壳体时的困难,且自由度少,列式简便,本文提出的构造新的形函数的办法,运算量少,边界条件 易处理。 1.1 肋 的 应 变 状 态 分 析 取图1所示一段曲梁, 1 2 3 放在坐标系xoy中,建立a a a 正交坐标活动标架, 设 AB为深曲梁且只在xoy面内变形。 1 2 3 x=Rcos(S/R),y=Rsin(S/R),z=z, a =t, a =s, a =z。 中线上一点C用矢量表示为
(4)
曲线坐标上基矢量gi为
g1 =
0 0 ∂rA ∂rA ∂r 0 ∂n 0 t 0 n , g t = + 1 a 0 , g 3 = e3 = = = + 2 1 2 2 2 ∂a ∂a ∂a ∂a R
(5)
两坐标体积分转换关系为 dv =
g ds dt dz , g = g 2 ⋅ ( g 3 × g1 ) = t / R + 1 ,梁上点在变形后的位置
收稿日期:2004-01-18 基金项目:国家自然科学金资助项目(50079005) 作者简介:孟闻远(1965-),男,河南郾城人,博士生,教授,研究方向为数值计算及结构分析等。 E-mail:meng-wenyuan@ 1
水
2005 年 7 月
利
学
报
第 36 卷 第7期
g dsdt
R 3 R = b ∫∫ E ε s δε s + GK rts δrts dsdt t + R t + R t/R →0
式中: b 为梁宽 在最小能量函数式中,系数相当于罚因子,作用于剪切与薄膜变形能。有关系:E>GK>>Et2,弯曲梁 变薄变直时,即t/R→0,剪切与薄膜闭锁消失,则应使γts=w,s+θ=0,εm=w/R=0,显然,R→∝时w/R→0可 以实现。而关键是要w,s+θ=0,即其位移模式是用多项式表达位移模式,则W须比θ高一阶,为保持θ的一 阶连续性,由式(9)与式(12)知,θ至少为2阶,而w为3阶,即w与θ的多项式阶数可分别表述为P及P+1阶 (P≥2)。P阶数高,列式复杂些,而闭锁消失。这是构造厚曲梁位移模式的内在依据。值得强调的是它可 以推广到厚板、厚壳中。为了消除肋闭锁现象及便于薄壳分析,本文采用无单元技术位移模式。这是因为 有限元在处理加肋壳时形式复杂,不易构造高阶完备的位移单元,导致一般厚肋(厚壳也是如此)变薄时无 法消除闭锁,进而产生错误结果,而无单元技术仅用节点,易于构造高阶的位移模式,这对厚肋与薄壳体
