叶盛标高数上
微积分Ⅱ教学大纲

微积分Ⅱ教学大纲内部编号:(YUUT-TBBY-MMUT-URRUY-UOOY-DBUYI-0128)《微积分Ⅱ》课程教学大纲课程编号:03034制定单位:信息管理学院制定人(执笔人):余达锦审核人:万建香制定(或修订)时间:2013年8月30日江西财经大学教务处《微积分Ⅱ》课程教学大纲一、课程总述本课程大纲是以2012年全校本科专业人才培养方案为依据编制的。
二、教学时数分配三、单元教学目的、教学重难点和内容设置第五章多元函数微分学【教学目的】1.了解空间坐标系的有关概念。
2.掌握二元函数定义、定义域的求法与表示法。
3.理解多元函数的偏导数与全微分的概念,熟练掌握多元复合函数与隐函数的偏导数的求法。
4.熟练掌握二元函数极值及条件极值的求法。
【重点难点】重点:多元函数的偏导数、极值及其在经济分析中的应用。
难点:多元复合函数的导数。
【教学内容】多元函数基本概念,多元函数的偏导数,多元函数的全微分,多元复合函数及隐函数求导法则,多元函数的极值,多元函数微分法在经济上的应用。
第六章不定积分【教学目的】1.了解原函数与不定积分的定义,掌握不定积分的性质,熟练掌握基本积分公式,换元积分法和分部积分法。
2.几种特殊类型函数的积分只作简单介绍。
【重点难点】重点:不定积分的定义、积分公式、换元积分法和分部积分法。
难点:换元积分法、有理函数的积分。
【教学内容】不定积分的概念和性质,积分基本公式,换元积分法,分部积分法。
第七章定积分【教学目的】1.了解定积分的概念和性质,掌握积分中值定理;熟练掌握牛顿—莱布尼兹公式,定积分的换元积分法和分部积分法。
2.会利用定积分计算平面图形的面积、旋转体的体积和一些简单的经济应用题。
3.会计算一些常见的收敛的广义积分。
【重点难点】重点:定积分的定义、定积分的计算和应用。
难点:定积分的应用。
【教学内容】定积分的概念,定积分的基本性质,定积分计算基本公式,定积分基本积分方法,广义积分,定积分的应用。
同济高等数学第六版上册市公开课金奖市赛课一等奖课件

第9页
已知 f ( x) 存在,且 f ( x) 0, y ln[ f ( x)],
求
d2y dx2 .
解
dy f ( x)
dx f ( x)
d 2 y f ( x) f ( x) [ f ( x)]2
dx2
f 2(x)
第10页
设ƒ(x)含有任意阶导数, 且 f '( x) e f ( x) , f (0) 1 , 则求 f (n)(0). 解 f '( x) e f ( x)
x0
x
f (n) ( x) lim f (n1) ( x x) f (n1) ( x)
x0
x
定义1 普通地,假如函数 y =ƒ(x)n-1 阶导数仍可导时, 则 函数 y =ƒ(x) n –1阶导数导数称为函数 y =ƒ(x)n 阶导数, 即
并记为
y(n) [ y(n1) ]
y(n) ,
y
''
(1
1 x)2
,
y
'''
(1
2! x)3
,
y(4)
(1
3! x)4
,
,
(
y )( n )
(1)n1
(n 1)! (1 x)n
尤其地
(ln
x )( n )
(1)n1
(n 1)! xn
第7页
(4) (sin x) cos x sin( x )
2
(sin x) [sin( x )]
f
(n)
(
x),
dny dx n
,
dn dx
f
n
.
第3页
注1 二阶和二阶以上导数为高阶导数.为了以便, 记 f (x) f (0)(x)
叶盛标神奇的特例法

以考纲为纲,以课本为本,以思维定势拿高分,以常考题型论输赢!叶盛标考研数学系列公开课之三神奇的特例法思维定势就是人们的一种思维倾向,它是人们在长期的思维过程中所形成的一种思维条件反射,亦称思维惯性。
我们平时脱口而出的“七七四十九,九九八十一”就是思维定势。
要对付考试,必须掌握思维定势。
常考题型是基本概念、基本理论、基本方法的具体化,是考点的具体化,是考纲的具体化。
要对付考试,必须掌握常考题型。
我的最大特点是:在表达思维定势和常考题型的时候使用了母语的力量,而母语的力量就是我们中华民族的力量, 我们中华民族的力量是不可战胜的!特例特法,瞬间搞定.(随时拿来随时用,特殊寓于一般中,ABCD 任我选,管他春夏与秋冬!)例1(全国1987数二)设()x f 在a x =处可导,则()()xx a f x a f x --+→0lim等于()()a f A '. ()B 2()a f '. ()C 0. ()D ()a f 2'.例2 设函数()x f 在a x =处二阶可导,则()()()='--+→ha f h a f h a f h 0lim()A ()2a f ''. ()B ()a f ''. ()C ()a f ''2. ()D ()a f ''-.例3(全国2004数三,数四)设()x f '在[]b a ,上连续,且()a f '>0,()b f '<0,则下列结论中错误的是()A 至少存在一点()b a x ,0∈,使得()0x f >()a f . ()B 至少存在一点()b a x ,0∈,使得()0x f >()b f . ()C 至少存在一点()b a x ,0∈,使得()0x f '=0.()D 至少存在一点()b a x ,0∈,使得()0x f =0.例4(全国2003数三)设()x f 为不恒等于零的奇函数,且()0f '存在,则函数()()xx f x g = ()A 在0=x 处极限不存在. ()B 有跳跃间断点0=x .()C 在0=x 处右极限不存在. ()D 有可去间断点0=x .例5(全国2002数二,数四)设函数()x f 连续,则下列函数中,必为偶函数的是 ()A ()⎰xdt t f 02. ()B ()⎰xdt t f 02.()C ()()[]⎰--xdt t f t f t 0. ()D ()()[]⎰-+xdt t f t f t 0例6(全国1993数二)若()()x f x f --=,在()+∞,0内()x f '>0,()x f ''>0,则()x f 在()0,∞-内 ()A ()x f '<0,()x f ''<0. ()B ()x f '<0,()x f ''>0. ()C ()x f '>0,()x f ''<0. ()D ()x f '>0,()x f ''>0.例7(全国1997数三,数四)若()()x f x f =-, ()+∞∞-,,在()0,∞-内()x f '>0,()x f ''<0 ,则()x f 在()+∞,0内有()A ()x f '>0,()x f ''<0. ()B ()x f '>0,()x f ''>0. ()C ()x f '<0,()x f ''<0. ()D ()x f '<0,()x f ''>0.例8(全国2006数二)设()x f 奇函数,除0=x 外处处连续 ,0=x 是其第一类间断点,则()⎰xdt t f 0是()A 连续的奇函数. ()B 连续的偶函数. ()C 在0=x 间断的奇函数. ()D 在0=x 间断的偶函数.例9(全国2005数一,数二)设()x F 是连续函数()x f 的一个原函数,”“N M ⇔表示“M 的充分必要条件是N ”,则必有()A ()x F 是偶函数⇔()x f 是奇函数. ()B ()x F 是奇函数⇔()x f 是偶函数.()C ()x F 是周期函数⇔()x f 是周期函数. ()D ()x F 是单调函数⇔()x f 是单调函数.例10(全国1999数一,数二)设()x f 是连续函数,()x F 是()x f 的原函数,则 ()A 当()x f 是奇函数时,()x F 必是偶函数. ()B 当()x f 是偶函数时,()x F 必是奇函数.()C 当()x f 是周期函数时,()x F 必是周期函数. ()D 当()x f 是单调增函数时,()x F 必是单调增函数.例11 若()x f 是以T 为周期的连续函数,则其原函数()A 是以T 为周期的函数. ()B 是周期函数, 但周期不是T .()C 不是周期函数. ()D 不一定是周期函数.例12(全国1996数二)设函数()x f 在区间()δδ+-,内有定义,若当()δδ+-∈,x 时,恒有(),2x x f ≤则0=x 必是()x f 的()A 间断点.()B 连续而不可导的点.()C 可导的点,且()00='f . ()D 可导的点,且()00≠'f .例13 (全国2004数三,数四)设()x f 在()+∞∞-,内有定义,且()a x f x =∞→lim ,()⎪⎩⎪⎨⎧=≠⎪⎭⎫ ⎝⎛=,,,000,1x x x f x g 则()A 0=x 必是()x g 的第一类间断点.()B 0=x 必是()x g 的第二类间断点.()C 0=x 必是()x g 的连续点.()D ()x g 在点0=x 处的连续性与a 的取值有关.例14(全国1990数二)设()()()⎪⎩⎪⎨⎧=≠=,0,0,0,x f x xx f x F 其中()x f 在0=x 处可导,()(),00,00=≠'f f 则0=x 是()x F 的()A 连续点. ()B 第一类间断点.()C 第二类间断点. ()D 连续点或间断点不能由此确定.例15(全国2008数三,数四)设函数()x f 在区间[]1,1-上连续,则0=x 是函数()()xdtt f x g x⎰=0的()A 跳跃间断点. ()B 可去间断点.()C 无穷间断点. ()D 振荡间断点.例16(全国2001数三,数四)设()x f 的导数在a x =处连续,又()1lim-=-'→ax x f ax ,则 ()A a x =是()x f 的极小值点. ()B a x =是()x f 的极大值点.()C ()()a f a ,是曲线()x f y =的拐点.()D a x =不是()x f 的极值点, ()()a f a ,也不是曲线()x f y =的拐点.例17(全国1990数一)已知()x f 在0=x 的某个邻域内连续,且()(),2cos 1lim,000=-=→xx f f x 则在点0=x 处()x f()A 不可导. ()B 可导且()00≠'f . ()C 取得极大值. ()D 取得极小值.例18(全国1996数一)设()x f 有二阶连续导数,且()()1lim,000=''='→xx f f x ,则 ()A ()0f 是()x f 的极大值. ()B ()0f 是()x f 的极小值. ()C ()()0,0f 是曲线()x f y =的拐点.()D ()0f 不是()x f 的极值, ()()0,0f 也不是曲线()x f y =的拐点.例19 设函数()x f 有连续导数,且()()11lim=-'+-→xx e x f x f ,则当()00=f 时, ()A ()0f 是()x f 的极大值. ()B ()0f 是()x f 的极小值.()C ()0f 不是()x f 的极值. ()D 不能判定()0f 是否为极值.。
厦大高分学子我的高分归结为八个字

厦大高分学子:我的高分归结为八个字时光若白驹之过隙,转眼间,我告别生涯已经有一段时间了。
但回想自己走过的那些日子,内心仍是百感交集。
无论如何,我坚持下来了,梦想中的院校大门最终还是向我敞开了。
总结这次,我觉得成功的关键在于8个字:踏实、恒心、计划、目标。
也正是这八个字伴随着我走过了整个生涯。
给自己找一个坚定的理由,然后就努力吧首先说说踏实和恒心吧,一个准备的人,这两样是绝对不能缺少的,如果你今天决定了,那么就要很执着的追逐下去,至少备考的这大半年要很执着,听海文的全程规划课时,梁伟伟对我们说过这样的话:“如果你今天坐在这里,并且决定了,那么请坚持下去;如果你以后准备放弃,那么请现在就放弃,什么都不要再准备了。
”这句话的意思大致就是,假如我们在准备了两个月后放弃,那么我们不仅没取得成果,而且我们失去了属于自己的这两个月的大好时光,可以说是一无所获;假如我们一直坚持下去了,即使没有成功,但在最后也会发现,我们收获了很多很多;但换句话说,如果我们真的踏踏实实的去努力了,我相信成功的几率是非常非常大的。
是一场没有硝烟的战斗,要想成功,就必须踏踏实实的干下去,不要抱有任何侥幸的心理。
做一个适合自己的计划,运用灵活的战屡战术来“达标”谈到“计划”和“目标”时,我希望所有准备的同学们首先要确定好一个合适的目标,然后为了目标执着的奋斗,同时,大家应该有一个属于自己的计划,一个朝着目标奋斗的计划,这种计划应该分为长期计划(比如说,每个阶段应该完成什么任务等)和短期计划(比如说每天的十几个小时的学习怎么划分)。
当然,一个好的计划应该不是死板的,而应该是灵活、有弹性的,这就是说,当计划制定好了后,执行计划是理所当然的,但这并不意味着盲目的执行,我们要不定期的和周围的同学交流交流,尤其是那种准备的比较充分的同学去交流,然后适时的改进自己的计划;同时,我们也可以经常去听听一些免费的讲座,根据老师的一些专业建议进行适当的调整,我备考的前期就经常去听一些好的讲座,比如说海文的全程规划,因为,我总觉得磨刀不误砍柴工,刀子快了,效率才会高。
同济大学高等数学第六版上导数的概念公开课一等奖优质课大赛微课获奖课件

法线方程为 y 2 1 ( x 1), 即 2x 8 y 15 0.
42
第22页
2.物理意义 非均匀改变量瞬时改变率.
变速直线运动:路程对时间导数为物体瞬时 速度.
v(t) lim s ds . t 0 t dt
交流电路:电量对时间导数为电流强度. i(t) lim q dq . t 0 t dt
在 x 1处不可导.
0
1
x
第26页
3. 函数 f ( x)在连续点的左右导数都 不存在
(指摆动不定) , 则 x0点不可导 .
比如,
f
(
x
)
x
sin
1 x
,
0,
x 0, x0
y
1
-1/π 0 1/π
x
在x 0处不可导.
第27页
4. 若f ( x0 ) , 且在点 x0的两个单侧导数 符号相反 , 则称点 x0为函数 f ( x)的尖点 (不可导点) .
★ 导数概念是概括了各种各样改变率而得出 一个更普通、更抽象概念, 它撇开了变量所代表 特殊意义, 而纯正从数量方面来刻画改变率本质
★ 点导数是因变量在点 x0处的变化率,它 反映了因变量随自变量的变化 而变化的快
慢程度.
★
y x
是y在以x0和x0
x为端点的区间上的
平均变化率
第9页
★ 如果函数 y f ( x)在开区间 I 内的每点 处都可导, 就称函数 f ( x)在开区间 I 内可导.
y f (x)
N
T
CM
极限位置即
o
x0
xx
MN 0, NMT 0. 设 M ( x0 , y0 ), N ( x, y).
2016-2017-1学期2016级本科高等数学A(上)分层课表
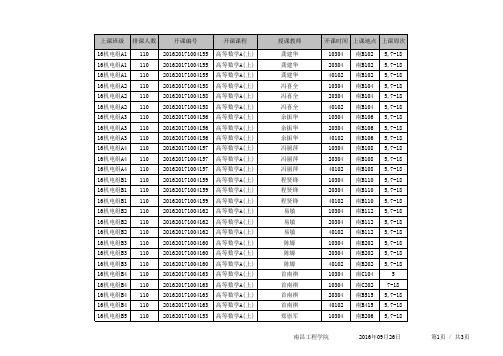
授课教师
龚建华 龚建华 龚建华 冯喜全 冯喜全 冯喜全 余振华 余振华 余振华 冯丽萍 冯丽萍 冯丽萍 程贤锋 程贤锋 程贤锋
易敏 易敏 易敏 陈嫄 陈嫄 陈嫄 首南祺 首南祺 首南祺 首南祺 郑崇军
开课时间 上课地点 上课周次
10304 20304 40102 10304 20304 40102 10304 20304 40102 10304 20304 40102 10304 20304 40102 10304 20304 40102 10304 20304 40102 10304 10304 20304 40102 10304
高等数学A(上) 高等数学A(上) 高等数学A(上) 高等数学A(上) 高等数学A(上) 高等数学A(上) 高等数学A(上) 高等数学A(上) 高等数学A(上) 高等数学A(上) 高等数学A(上) 高等数学A(上) 高等数学A(上) 高等数学A(上) 高等数学A(上) 高等数学A(上) 高等数学A(上) 高等数学A(上) 高等数学A(上) 高等数学A(上) 高等数学A(上) 高等数学A(上) 高等数学A(上) 高等数学A(上) 高等数学A(上) 高等数学A(上)
南B102 南B102 南B102 南B104 南B104 南B104 南B106 南B106 南B106 南B108 南B108 南B108 南B110 南B110 南B110 南B112 南B112 南B112 南B202 南B202 南B202 南C104 南C202 南B515 南B415 南B206
5,7-18 5,7-18 5,7-18 5,7-18 5,7-18 5,7-18 5,7-18 5,7-18 5,7-18 5,7-18 5,7-18 5,7-18 5,7-18 5,7-18 5,7-18 5,7-18 5,7-18 5,7-18 5,7-18 5,7-18 5,7-18
高中数学新课标人教A版必修第一二册教材解读〖第九章统计章整体解读〗精选全文完整版
可编辑修改精选全文完整版第九章统计统计学有多种不同的定义,综合来说,统计学是收集、处理、分析、解释数据并从数据中得出结论的科学.作为专门研究有效收集和分析数据的科学,可以说凡是一个实际问题涉及数据处理,都应该利用统计学方法去分析和解决.统计方法不仅有用,对于理解周围的世界经常也是不可或缺的,它提供了对许多现象获得新见解的方法.现在统计学已深入到科学、技术、工程和现代社会生活的各个方面.尤其当我们进入大数据时代和“互联网+”时代,作为研究数据分析的重要数学技术,统计学方法在相关领域的应用已成为数学应用的主要方法.统计素养已成为一名效率公民的基本素养.从新中国成立以来,在中学数学课程中,统计经历从无到有、从描述统计到推断统计、从选修变为必修的过程,其要求和地位都在不断提高.《课程标准2021年版》把“概率与统计”与“函数”“代数与几何”并列作为高中数学课程内容主线之一,并贯穿必修、选择性必修和选修整个数学课程.除了在初中统计基础上进一步学习数据收集和整理的方法、数据直观图表的表示方法、数据统计特征的刻画方法外,要求能用样本的统计特征推断总体的统计特征,包括单变量总体集中趋势参数、离散程度参数、取值规律和百分位数的估计,双变量总体的相关关系、一元线性回归模型和独立性的推断.相比初中统计以描述统计为主,高中统计以推断统计为主,更加强调数据的随机性.在统计的学习过程中,应让学生感悟在实际生活中进行科学决策的必要性和可行性;体会统计思维与确定性思维的差异、归纳推断与演绎证明的差异;通过实际操作、计算机模拟等活动,积累数据分析的经验.通过统计的学习,还应帮助学生建立正确的随机观念,养成通过数据来分析问题的习惯,学会抓住事物的主要因素等,发展数据分析、数学建模、逻辑推理、数学运算和数学抽象等数学学科核心素养,实现统计的教育价值.一、本章内容安排统计是通过数据分析来解决问题的,数据分析的过程体现了统计解决问题的基本思路.因此,让学生了解这个过程,对整体把握统计学科的特点,理解具体的数据分析方法和应用数据分析方法解决实际问题都是非常重要的.数据分析的过程存在多种不同的划分,《课程标准2021年版》对数据分析过程的划分如下:虽然在不同的数据分析过程划分中,划分的环节数、每个环节提法等不完全一致,但都遵循从收集数据到分析数据再到得出结论的基本过程.本章内容主要根据数据分析的基本过程进行安排,把学习内容分为三节.“9.1随机抽样”主要学习收集和整理数据的方法;“9.2样本估计总体”主要学习分析数据的方法,包括数据直观图表的表示方法和数据统计特征的刻画方法等,以及根据样本数据的统计特征估计总体的统计特征;“9.3统计案例公司员工的肥胖情况调查分析”是对前两节所学知识的综合应用.本章的知识结构如下:二、突出数据分析的基本过程,在过程中学习数据分析方法为了达到有效分析数据的目的,统计中会用到各种数据分析的方法,每个数据分析环节都有各自专属的数据分析方法,例如数据收集有随机抽样方法,数据分析有各种数字特征等,这些方法构成了统计研究和学习的主要内容.虽然很多具体的数据分析方法是针对数据分析过程中的某一个环节的,但其方法的合理性要放在整个数据分析过程中去理解.例如,一种抽样方法好坏要通过其抽取的数据对总体估计的效果进行评价,一个数字特征的选取合适与否取决于是否达到最终的统计目的等.因此,要理解数据分析方法的合理性,不能只针对某个环节孤立地进行学习,而应该放在数据分析的过程中进行学习.本章不管是抽样方法的学习,还是样本估计总体的学习,都尽可能通过具体案例的完整解决,让学生经历数据分析的基本过程,在基本过程中来学习数据分析的方法,理解数据分析的思路,并运用所学知识和方法解决实际问题.例如,简单随机抽样方法属于数据收集的内容,教科书并不是直接介绍简单随机抽样方法的定义和不同实现方法,而是设置了以下的问题:问题1家具厂要为树人中学高一年级制作课桌椅,事先想了解整个年级学生的平均身高,以便设定可调节课桌椅的标准高度.已知树人中学高一年级有712名学生,如果要通过简单随机抽样的方法调查高一年级学生的平均身高,应该怎么抽取样本?这是一个以估计总体均值为目的的抽样调查问题,但问题的解决需要经历数据分析的整个过程.在这个问题的解决过程中,不仅学习简单随机抽样方法的实现,还要通过总体均值和样本均值的比较,评价简单随机抽样方法的效果,体会简单随机抽样方法的特点.三、结合典型案例学习数据分析方法统计学是一门应用性很强的学科,它的概念和方法产生的动力基本都来自解决实际问题的需要.与建立在概念和定义基础上,通过演绎方式进行研究的数学其他分支不同,统计学是建立在数据基础上,通过归纳方式研究随机现象,通过数据分析解决问题.因此,统计的学习有别其他数学分支,需结合具体案例,由具体问题驱动学习,在问题的解决中体会数据的随机性,学习统计的概念和方法,积累数据分析的经验.而且结合具体案例还可以克服由于概念和方法的抽象性带来的理解困难.因此,结合具体案例介绍概念和方法是统计教科书编写的一个主要原则.由于统计的概念和方法都有各自的特点和适用范围,因而根据不同内容的特点,选择典型的案例就成为一个关键的问题.在中学阶段,案例的典型性不仅要体现统计概念、方法引入的必要性和解决问题的适切性,案例的背景还要符合学生的认知特点,有助于理解相关的概念和方法.教科书要尽量采用学生熟悉的案例背景,通过设计恰当的统计问题,在问题的解决中学习有关统计知识.例如,教科书在学习具体的抽样方法前,通过全国人口调查这个案例引入统计调查中涉及的一些基本概念.一方面,全国人口调查是学生比较熟悉的真实统计调查案例,让学生感受统计学科的重要性和应用性.另一方面全国人口调查不仅有普查,还有抽样调查,除了可以引入全面调查、抽样调查、总体、个体、样本、样本量等基本概念外,通过了解全国人口调查实施普查和抽样调查的背景及原因,可以进一步明确两种抽样方式的特点,以及抽样调查的必要性,帮助学生建立和完善有关统计调查的概观知识.这对后续进入具体随机抽样方法的学习是非常必要的.又如,教科书以同一个案例背景贯穿简单随机抽样和分层随机抽样的学习.在简单随机抽样问题1的基础上,教科书在随机分层抽样中设置了以下问题:问题2在树人中学高一年级的712名学生中,男生有326名、女生386名.能否利用这个辅助信息改进简单随机抽样方法,减少这种“极端”样本的出现,从而提高对整个年级平均身高的估计效果呢?教科书之所以采用“调查一个学校高一年级的平均身高”作为抽样调查的案例,主要考虑在通常情况下,对于一所学校的高一年级的学生数,既有进行抽样调查的必要性,又有进行全面调查的可行性,即获得总体均值是可行的,这使教科书后续比较样本均值与总体均值,进而评价随机抽样的效果显得比较自然.而两种抽样方法的学习使用同一案例背景,只是改变男生、女生人数这个条件,不仅有利于比较两种抽样方法的效果,而且有利于理解两种抽样方法的联系与区别.四、加强数据分析方法的形成过程,体现方法的合理性在数据分析方法中会用到很多数学的工具,如果不了解数学符号和公式背后的统计思想和数学原理,容易把统计学习变成纯粹的画图列表、公式计算等程序性操作,学生体会不到数据分析方法的合理性.方法引入的必要性,可以通过合适的案例背景来体现,而体现方法的合理性,则需要加强从直观想法到数学表达的转化过程,这个过程也是积累数据分析经验的过程.体现了方法的必要性和合理性,不仅使得知识的产生显得自然,也有利于学生更好地把握方法的本质.本章数据分析方法中,数学工具的使用主要是在用数字特征刻画数据的统计特征中.对于数字特征,主要是要理解其统计含义.有些数字特征的定义形式比较简单,其统计含义相对比较容易理解.例如,平均数刻画了一组数据平均水平,众数是一组数据最典型的代表,极差刻画了一组数据的波动范围等.但有些数字特征的数学表达相对复杂,其统计含义有时并不能一目了然,例如中位数、方差、标准差,尤其是分层抽样的方差公式.对于数字特征,往往是先有刻画数据某一方面的特征需要,再根据需要定义数字特征的.如果了解数字特征定义的目的是刻画数据哪一方面的特征,不仅有助于学生理解数字特征的统计含义,而且有利于理解数字特征定义的形式.例如,如果学生了解了中位数是把一组数据按大小分成个数相等两部分的那个数,就很容易理解中位数为什么要根据数据的个数,分奇偶两种情况进行定义.又如,方差和标准差都可以用来刻画一组数据离散程度,它们的公式初看起来都比较复杂,但了解了它们定义的过程,就容易理解它们在刻画数据离散程度上的特点,以及之所以定义成现在这种形式.为了让学生更好地理解方差和标准差的统计含义,积累数据分析的经验,教科书详细呈现了方差概念的形成过程.教科书首先通过比较两名射击运动员成绩稳定性,让学生体会定义数字特征刻画数据离散程度的必要性.通过分析,把刻画一组数据的离散程度问题逐步转化为刻画与平均数的“平均距离”大小的数学问题.在数学中,距离可以有多种定义,教科书先呈现学生最容易想到的“绝对值距离”,由于绝对值的数学性质不够好,为了避免含有绝对值,又引入“平方和距离”,以此作为刻画数据的离散程度的数字特征,即方差.这个从统计直观到数学表达逐步优化的数据分析过程,在数字特征的定义中具有一般意义,积累的经验有助于理解选择性必修中样本相关系数的定义.五、加强信息技术与统计的融合1.培养学生使用信息技术的意识和初步能力统计是通过数据分析解决问题的.在数据分析中经常会涉及数据的整理、可视化表示、计算等数据处理,尤其当样本量比较大时,工作量就会变得非常大.运用计算器、计算机等信息技术工具,不仅可以实现快速、准确地列表、画图、计算等数据处理,而且能使大量人工难以完成的数据处理变成可能.会使用信息技术处理数据是现代统计学习的重要组成部分.在高中统计的学习中,应该培养学生使用信息技术的意识和初步能力.为了给学生在统计学习中运用信息技术提供支持,在高中统计的起始章,教科书安排选学栏目“信息技术应用统计软件的应用”,集中介绍电子表格和R两款软件的基本统计功能,其中电子表格软件是使用比较普遍且具有一定统计功能的办公软件,而R软件则是统计专业人员中使用普遍且免费的专业统计软件.在后续统计的章节中,教科书结合有关内容,在适合使用的信息技术的地方,以边注的形式对给予提示.2.利用信息技术提高教学的效率和质量信息技术既是现代统计的组成部分,也是统计学习的有效辅助手段.通过合理使用信息技术,可以把学生从机械、烦琐的数据处理中解放出来,把更多精力集中于统计概念和方法的理解,从而提高教学的效率和质量.例如,绘制频率分布直方图涉及数据的分组、频率的计算、图形的绘制等大量工作,用统计软件可以快速绘制出不同组距和组数的直方图,节约重复计算、机械性操作的时间,把更多的精力花在直方图信息的提取上.又如,平均数、方差等特征数的计算,在学生已经知道如何计算的情况下,统计软件的使用就可以大大节约时间,进而把更多的精力花在理解特征数的统计含义上.3.通过随机模拟直观解释数据分析方法的合理性统计是研究数据收集和分析数据的科学,其研究重点是如何有效地收集和分析数据,所有数据分析方法都是为了达到这个目的.这里的“有效”既包括人力、物力、时间的节省,也包括估计精确度和可靠度的提高.在没有足够概率理论知识刻画估计的精确度和可靠度时,如何让学生了解样本和总体的关系,体会数据分析方法的科学性就成为统计内容呈现的重点.在中学统计中,信息技术一个很大的作用是可以实现随机模拟,它使大量重复试验成为可能.通过随机模拟,可以让学生体会样本数据的随机性和规律性,了解样本和总体之间的关系,这可以在很大程度上直观解释一些数据分析方法的合理性,弥补由于理论知识不足造成的理解困难.例如,在随机抽样的学习中,需要讨论样本量对于抽样估计效果的影响,以及评价简单随机抽样和分层随机抽样的估计效果,在理论上进行说明并不容易.因此,教科书通过随机模拟的方式,让学生直观观察的多次抽样的结果图1和图2,在此基础上归纳概括随机抽样方法的特点.。
盘点2011年高考数学中的“高观点”试题
壁的一周,点 ,Ⅳ在大圆内所绘出的图形大致是
( ) 是长为 2 1 设 I 的线段 , 求点集 D: Pl( , { P, d )
≤1所表 示 图形 的面积 ; }
@ @
解析 选 A.根据小圆与大 圆半径 1 的关系, : 2 找上 下左 右 四个点 ,根 据这 四个 点 的位 置 ,小 圆转
( Ⅲ)写出到两条线段 ‘ ’ 距离相等的点的集 ,f
合 Q:{ ( ‘ =dP, ) , 中 ‘=A 1=C , PI P, ) ( 1 } 其 d 2 B,2 D ABC D 是下 列 三组 点 中的一 组 .对 于 下 列 三组 点 ,,,
只需选做一种 ,满分分别是 : ) 0 2分,②6分,③8 分 ;若选择了多于一种的情形 ,则按照序号较小 的 解答 计 分 .
语言叙述“ 高观点” 的是试题 的表述带有浓烈 指 高等数学语言色彩 .这样的试题在 2 1 年高考数学 0 1
中俯 拾 即 是 .
1 . 3图形语言
例 3 (0 1 2 1 年高考江西卷 ・ 理 1)如 图 ,一个直 径 为 1的小 圆沿 M Ⅳ 是 小 圆 的一 条 固 定 直径 的两 个端 点 .那么 ,当小 圆这 样 滚 过大 圆 内
点评 本题的难点就在于集合语言的理解 ,有较
强的抽象性 ,要求考生对相关 的数学语言有较高层 次的理解 ,能够准确地将抽象的数学符号翻译成 自
己熟悉的数学语言 .类似的试题还有 2 1 年高考广 0 1 东卷 ・ 2 . 理 1
2 代数背景高观点 . 1 以某些数学分支 的基本概念为背景 ,引进新的 概念 ,设计信息迁移题 ,可 以考查学生的阅读理解
1 集合语言 . 1
叶盛标考研数学 2015《考前测试》卷
∞
(D ) 若 lim n→∞
∞ u n +1 < 1 ,则 ∑ u n 收敛. un n =1
(5) 设 A 为 m × n 矩阵,已知 R( A) = m ,且方程组 Ax = 0 有非零解,
则下列选项中不正确的是
( A) m < n . (C ) A 的列向量线性相关.
(B ) m ≥ n . (D ) Ax = β 有无穷多组解.
2
.
(10)
积为
[1]
⎧ x2 y2 ⎪ 曲线 ⎨ a 2 + b 2 = 1, ⎪ ⎩ Ax + By + Cz = 0
.
(C ≠ 0) 所围平面区域 D 的面
(11) 圆 x 2 + ( y − b )2 = a 2 (0 < a < b ) 绕 x 轴旋转一周所生成的形
如车胎的体积为 .
(12)[1] 设 u = u (x, y, z ) 具有二阶连续的偏导数,且满足
( A) 单调增加.
(B ) 单调减少.
(C ) 有极值.
(D ) 常数.
(2) 函数 z = z (x, y ) 由方程
⎛z⎞ x 2 + y 2 + z 2 = yf ⎜ ⎜ y⎟ ⎟ 所给出,则 ⎝ ⎠
(x
2
− y2 − z2
∂z ∂z )∂ + 2 xy = x ∂y
( A) 2 xz .
(B ) 2 yz .
9 1 9 2 2 ( ) ( X i − Y )2 服从 X , 若统计量 aX + b X + X + X + c ∑ ∑ i 1 2 3 4 5 i =5 i =5
考研数学与大纲配套的课本内容
考研数学与大纲配套的课本内容叶盛标考研培训中心编写同济大学高等数学第六版上册第一章函数与极限第十节三、一致连续性不考第二章导数与微分第四节二、由参数方程所确定的函数的导数数三不考;第五节四、微分在近似计算中的应用不考第三章微分中值定理与导数的应用第七节曲率数三不考第八节方程的近似解不考一、二分法(178)二、切线法(179)不考不定积分第五节积分表的使用不考定积分第五节反常积分的审敛法函数(超纲),叶老师要求都要掌握函数定积分的应用第二节三、平面曲线的弧长数一数二考第三节定积分在物理学上的应用数一数二考第三节齐次方程二、可化为齐次的方程不考第四节二、伯努利方程数一考第五节可降阶的高阶微分方程数一数二考第六节高阶线性微分方程三、常数变易法不考第九节欧拉方程数一考第十节常系数线性微分方程组解法举例不考同济大学高等数学第六版下册第八章空间解析几何与向量代数数一考第九章多元函数微分法及其应用第三节全微分二、全微分在近似计算中的应用不考第六节多元函数微分学的几何应用数一考第七节方向导数与梯度数一考第九节二元函数的泰勒公式(非重点)数一内容,可以不看一、二函数的泰勒公式(119)二、极值充分条件的证明非重点第十节最小二乘法不考第十章重积分第二节三、二重积分的换元法不考第三节三重积分数一考第四节重积分的应用数一考第五节含参变量的积分不考第十一章曲线积分与曲面积分数一考第十二章无穷级数数一数三考常数项级的概念和性质数一数三考柯西审敛原理不考常数项级数的审敛法数一数三考幂级数数一数三考函数展开成幂级数数一考函数的幂级数展开式的应用不考函数项级数的一致收敛性及一致收敛级数的基本性质不考傅里叶级数数一考一般周期函数的傅里叶级数数一考傅里叶级数的复数形式不考浙大概率论与数理统计(第四版)前六章数一、数三都要考的第七章参数估计1点估计重点,数一数三考2 基于截尾样本的最大似然估计不考3估计量的评选标准数一考4 区间估计数一考5 正态总体均值与方差的区间估计数一考6 (0—1)分布参数的区间估计不考7 单侧置信区间数一考第八章假设检验数一考5样本容量的选取数一考6 分布拟合检验不考7秩合检验不考8 假设检验问题的P值法不考第九章以后都不考的同济大学线性代数(第五版)第一章行列式第二章矩阵及其运算第三章矩阵的初等变换与线性方程组第四章向量组的线性相关性第五章相似矩阵及二次型第六章线性空间与线性变换数学一考到§3基变换与坐标变换。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
前言 只要两秒 强行带入 定型定法 以洛为主 单夹积导极限是微积分的基石;导数是微积分的关键;初等函数——公式搞定; 分段函数——分段搞定;上限函数——导数搞定。
第一章 函数、极限与连续 §0内容提要0、极限的定义(科学的ε语言——五句话) i)函数极限的定义(科学的ε语言——五句话)①0,()x x f x →的极限定义为:①(任给)0ε∀>;②(存在)0δ∃>;③当00x x δ<-<时;④总有()f x A ε-<成立;⑤则有0lim ()x x f x A →=。
前4句话与第5句话等价0,()x x f x -→的左极限定义为:①0ε∀>;②0δ∃>;③当00x x x δ-<<时;④总有()f x A ε-<成立;⑤则有000lim ()(0)x x f x A f x →-==-。
结论:0lim ()x x f x →存在00(0)(0)f x f x ⇔-=+,即左极限与右极限存在且相等②,()x f x →∞的极限定义为:①0ε∀>;②0X ∃>;③当x X >时;④总有()f x A ε-<成立;⑤则有lim ()x f x A →∞=。
前4句话与第5句话等价,()x f x →-∞的左极限定义为:①0ε∀>;②0X ∃>;③当x X <-时;④总有()f x A ε-<成立;⑤则有lim ()x f x A →-∞=。
ii)数列极限的定义(科学的ε语言——五句话)数列{}n x 的极限定义为:①0ε∀>;②0N ∃>;③当n N >时;④总有n x a ε-<成立;⑤则有lim n n x a →∞=。
前4句话与第5句话等价 1、两个重要极限0sin lim1x x x →=,1lim(1)lim(1)x x k x x ke e x x→∞→∞+=⇔+=这两个极限之所以重要,是因为几乎全部的基本初等函数求导公式都是由这两个重要极限推出的。
2、极限存在的两个准则:i)夹逼定理;ii)单调有界数列有极限. 3、连续与间断设函数()y f x =在点0x 的某邻域内有定义,如果0lim ()x x f x →存在,且00lim ()()x x f x f x →=,则称()y f x =在点0x 连续。
破坏“设”、“如果”、“且”三条件之一者谓之间断,0x 为间断点。
若左极限0(0)f x -及右极限0(0)f x +都存在,那么称0x 为()f x 的第一类间断点,否则为第二类间断点。
4、最值定理 5、保函数号定理0)(0,)(lim 0>⇒>=→x f A A x f x x证明:δδε<-<>∃>∀>=→00,0,0;0,)(lim 0x x A A x f x x 当 时,保号定理, 保命定理。
即εε+<<-A x f A )(,于是取0>=A ε,即证毕,)(0εε+<<-=A x f A 6、保极限号定理00)(,)(lim 0≥⇒>=→A x f A x f x x ,证明:反正即可。
7、介值定理 8、零点定理9、极限的四则运算注意:1lim lim 00=⋅→→xxx x x xx x 不存在,但是。
§1思维定势思维定势1 洛必达前,要用三处(高等数学、初等数学、特例法) 在春天就必须掌握的五个常用的麦克劳林公式)1,1(!)1()1(!2)1(1)1(];1,1()1(32)1ln();,()!2()1(!6!4!21cos );,()!12()1(!5!3sin );,(!!3!2121322642125332-++--++-++=+-+-+++-=++∞-∞+-++-+-=+∞-∞++-+++-=+∞-∞+++++=++ nnn n n n nnxx n n x x x n x x x x x n x x x x x n x x x x x n x x x e ααααααα 0,x →生产出系列等价无穷小I)0→x 时,;!3~!21;!2~1;~1322x x x e x x e x e x xx ------Iv)0→x 时,;2~)1ln(;~)1ln(2x x x x x --++ v)0→x 时,;!2)1(~1)1(;~1)1(2x x x x x ---+-+αααααα§2常考题型常考题型1强行带入,定顶星定法 例2求极限 )11ln 1(lim 1--→x x x 解:xx xx x x x x ln )1(ln 1lim )11ln 1(lim 11---=--→→ 2)1(~)11ln()1()1(~)11ln(,12--+----+→x x x x x x ,时中值定理, 边值搞定零点定理,边值搞定洛必达前, 要用三处。
(初处)21)1(2)1(lim )11ln()1()11ln(1lim 2211=--=-+--+--=→→x x x x x x x x 超越函数:不能用有限次加、减、乘、除、乘方、开方运算,得到函数值的函数,谓之超越函数,指数函数、对数函数、三角函数为超越函数。
例3求极限11)1232(lim +→++x x x x解:)1232(lim )1232(lim )1232(lim 1111++⋅++=++→→+→x x x x x x x x x x x e e e x x xx x x xx ==++⋅++=+∞→+∞→2123)12()32(lim )211()231(lim补充(全国2010,数一)极限)(]))(([lim 2=+-∞→x x b x a x xA 、1B 、eC 、ba e- D 、ab e-解:b a b a x x x x x e ee xbx a b x a x x --∞→∞→=⋅=+-=+-1)1()1(1lim ]))(([lim 2 例4 xx x tan 2)(sin lim π→解:xx x xxx x xx x xx eeex cos )1sin 1ln(2sin cos )1sin 1ln(2cot )ln(sin 2tan 2lim lim lim )(sin lim -+→⋅-+→→→===ππππ1lim lim lim sin cos 2cos 1sin 2cos )1sin 1ln(2====-→-→-+→xx x xx x xx x eeeπππ(1sin ~)1sin 1ln(--+x x )补充(全国2008数一、数二)求极限40sin )]sin(sin [sin limxxx x x -→ 解:3040)sin(sin sin lim sin )]sin(sin [sin lim xx x x x x x x x -=-→→ 20203)]cos(sin 1[cos lim 3cos )][cos(sin cos lim x x x x x x x x x -=⋅-=→→ 613sin 21lim 220==→x xx 另解:3040)sin(sin sin lim sin )]sin(sin [sin lim x x x x x x x x x -=-→→ 61!3limsin lim 2sin sin2sin cos 2lim 3303030==-=-+=→→→x x x x x x xx x x x x x 超越函数,不再超越。
洛必达前, 极限搞定。
幂指函数, 对数恒等。
零与非零, 泾渭分明。
高处 零与非零, 泾渭分明。
βαsin sin -2sin 2cos 2βαβα-+= ,sin )(取x b t t f ==解法三:3040)sin(sin sin lim sin )]sin(sin [sin limxx x x x x x x x -=-→→ 61!3lim )sin (cos lim 33030==-=→→x x x x x x x ξ 补充(全国2009数二、数三) 求极限xx x x x 40sin )]tan 1ln()[cos 1(lim+--→ 解:xx x x x x x x x x x x x 2tan 1sec 1lim 21)tan 1ln(lim 21sin )]tan 1ln()[cos 1(lim 202040+-=+-=+--→→→xxx x x x x x x 2020sec tan 1lim41)tan 1(sec tan 1lim 41-+=+-+=→→ 41tan tan lim 4120=-=→x x x x评注:求极限的最好办法:洛必达前,极限搞定。
补充:求极限xxx x ln 11)1(lim -+∞→解:)0()1(lim lim lim ,)1(lim 0ln 1111lim ln lim ln 1ln 11xx x x xx xx x xx xx x x e e e ex x x x -⇒====-+∞→+∞→+∞→+∞→+∞→+∞→而xx x xx x xx xx x x xx x xx xx eee x 1)'(11lim1)'1(11limln )1ln(limln 11111)1(lim ⋅--⋅--+∞→+∞→+∞→+∞→===-1ln ln 1limln 1ln 1limln 111limln 111lim1ln 111lim22ln 12121---⋅-⋅--⋅--⋅⋅-======+∞→+∞→+∞→+∞→+∞→e eeeeex x x x xx xx e x x x x xxx x x x xx x xx x xx注意:21ln 1ln ln 1ln 1)'()'(2xxx eex xxxx x xx x-⋅===-⋅ 另解:xe xxx xx x ex ln )1ln(lim ln 11ln 1)1(lim -+∞→+∞→=-111ln 1lim ln ln ln ln limln ln ln ln limln ln ln lim ----+∞→====→∞→∞→∞e eeeexxx x x xx x x x xx xx x x x补充处理:x x xxx e xe xx x xx x xx x eex ln ln lnln ln)1ln(limln )1ln(limln 11ln 1ln 1)1(lim ⋅--+∞→+∞→+∞→==-,拉氏弧形,不拉不行。
零与非零, 泾渭分明。
幂指函数, 对数恒等。
零与非零, 泾渭分明。
此处不能直接利用等价无穷小(∞→-)ln(1ln xxe),应作如下处理。
