揭阳2017届高三统一考试卷(文数)
广东省揭阳一中2017届高三(上)第一次段考试卷(文)(解析版)

广东省揭阳一中2017届高三(上)第一次段考试卷(文)一、选择题(共12小题,每小题5分,共60分.在四个选项中,只有一项符合题目要求)1.(5分)在△ABC中,角A,B,C所对的边分别为a,b,c,若C=60°,c=a,则()A.a>b B.a<bC.a=b D.a与b的大中关系不能确定2.(5分)已知数列{a n}是等差数列,且a1+a4+a7=2π,则tan(a3+a5)的值为()A.B.C.D.3.(5分)△ABC的三边长分别为|AB|=7,|BC|=5,|CA|=6,则•的值为()A.19 B.14 C.﹣18 D.﹣194.(5分)若一个等差数列前3项的和为34,最后3项的和为146,且所有项的和为390,则这个数列有()A.13项B.12项C.11项D.10项5.(5分)如果把直角三角形的三边都增加同样的长度,则这个新的三角形的形状为()A.锐角三角形B.直角三角形C.钝角三角形D.由增加的长度决定6.(5分)设{a n}是公差为正数的等差数列,若a1+a2+a3=15,a1a2a3=80,则a11+a12+a13=()A.120 B.105 C.90 D.757.(5分)在△ABC中,a=2,b=2,B=,则A等于()A.B.C.或D.或8.(5分)已知{a n}为等差数列,a1+a3+a5=105,a2+a4+a6=99,以S n表示{a n}的前n项和,则使得S n达到最大值的n是()A.21 B.20 C.19 D.189.(5分)若A、B是锐角三角形△ABC的两个内角,如果点P的坐标为P(cos B﹣sin A,sin B﹣cos A),则点P在直角坐标平面内位于()A.第一象限B.第二象限C.第三象限D.第四象限10.(5分)设函数f(x)(x∈R)满足f(x+π)=f(x)+sin x.当0≤x<π时,f(x)=0,则f()=()A.B.C.0 D.﹣11.(5分)已知方程(x2﹣2x+m)(x2﹣2x+n)=0的四个根组成一个首项为的等差数列,则|m﹣n|等于()A.1 B.C.D.12.(5分)数列{a n}满足a1=1,a n+a n+1=()n(n∈N*),记T n=a1+a2•4+a3•42+…+a n•4n﹣1,类比课本中推导等比数列前n项和公式的方法,可求得5T n﹣4n•a n=()A.n B.n2C.2n2D.n+1二、填空题(本大题共4小题,每小题5分,共20分)13.(5分)在△ABC中,角A,B,C所对应的边分别为a,b,c,已知b cos C+c cos B=2b,则=.14.(5分)设等差数列{a n}的前n项和为S n,S m﹣1=﹣2,S m=0,S m+1=3,则正整数m的值为.15.(5分)已知,则的值等于.16.(5分)设数列{a n}是以2为首项,1为公差的等差数列,数列{b n}是以1为首项,2为公比的等比数列,则b+b+b+…+b=.三、解答题(本大题共6小题,共70分,解答应写出必要文字说明,证明过程或演算过程.)17.(10分)△ABC中,内角A、B、C对应的边为a、b、c,且满足a•sin A+c•sin C﹣a•sin C=b•sin B(1)求B;(2)若A=75°,b=2,求a、c.18.(12分)已知A、B、C是△ABC的三个内角,a、b、c为其对应边,向量=(﹣1,),=(cos A,sin A),且•=1(1)求角A;(2)若c=,=,求△ABC的面积S.19.(12分)正项等比数列{a n},若2a1+3a2=1,a32=9a2a6.(1)求数列{a n}的通项公式;(2)设b n=log3a1+log3a2+log3a3+…log3a n,求数列{}的前n项和S n.20.(12分)设函数f(x)=cos(2x+)+sin2x.(Ⅰ)求函数f(x)的最大值和最小正周期;(Ⅱ)设A,B,C为△ABC的三个内角,若cos B=,f()=﹣,且C为锐角,求sin A.21.(12分)已知等差数列{a n}满足:a1=2,且a1、a2、a5成等比数列.(1)求数列{a n}的通项公式.(2)记S n为数列{a n}的前n项和,是否存在正整数n,使得S n>60n+800?若存在,求n 的最小值;若不存在,说明理由.22.(12分)已知数列{a n}的前n项和为S n,点在直线y=x+4上.数列{b n}满足b n+2﹣2b n+1+b n=0(n∈N*),且b4=8,前11项和为154.(1)求数列{a n}、{b n}的通项公式;(2)设是否存在m∈N*,使得f(m+9)=3f(m)成立?若存在,求出m的值;若不存在,请说明理由.参考答案一、选择题1.B【解析】在△ABC中,角A,B,C所对的边分别为a,b,c,若C=60°,c=a,则由正弦定理可得,解得sin A=.再由题意可得,a不是最大边,故A为锐角,故A=30°.再由三角形内角和公式可得B=90°,再由大角对大边可得a<b,故选B.2.C【解析】∵数列{a n}是等差数列,且a1+a4+a7=2π,∴a1+a4+a7=3a4=2π,∴a4=,∴tan(a3+a5)=tan(2a4)=tan=tan=,故选:C.3.D【解析】由题意,cos B==,∴•=5×5×(﹣)=﹣19.故选:D.4.A【解析】依题意a1+a2+a3=34,a n+a n﹣1+a n﹣2=146,∴a1+a2+a3+a n+a n﹣1+a n﹣2=34+146=180,又∵a1+a n=a2+a n﹣1=a3+a n﹣2,∴a1+a n==60,∴S n===390,∴n=13,故选A.5.A【解析】设增加同样的长度为x,原三边长为a、b、c,且c2=a2+b2,c为最大边;新的三角形的三边长为a+x、b+x、c+x,知c+x为最大边,其对应角最大.而(a+x)2+(b+x)2﹣(c+x)2=x2+2(a+b﹣c)x>0,由余弦定理知新的三角形的最大角的余弦=>0,则为锐角,那么它为锐角三角形.故选A.6.B【解析】{a n}是公差为正数的等差数列,∵a1+a2+a3=15,a1a2a3=80,∴a2=5,∴a1a3=(5﹣d)(5+d)=16,∴d=3,a12=a2+10d=35,∴a11+a12+a13=105,故选B.7.C【解析】△ABC中,∵a=2,b=2,B=,∴由正弦定理可得=,解得sin A=,∴A=,或A=,故选:C.8.B【解析】设{a n}的公差为d,由题意得a1+a3+a5=a1+a1+2d+a1+4d=105,即a1+2d=35,①a2+a4+a6=a1+d+a1+3d+a1+5d=99,即a1+3d=33,②由①②联立得a1=39,d=﹣2,∴S n=39n+×(﹣2)=﹣n2+40n=﹣(n﹣20)2+400,故当n=20时,S n达到最大值400.故选:B.9.B【解析】∵A,B为锐角三角形的两个内角,∴A+B>,∴A>﹣B>0,∴sin A>sin(﹣B)=cos B,∴cos B﹣sin A<0,同理可得sin B﹣cos A>0,故选B.10.A【解析】∵函数f(x)(x∈R)满足f(x+π)=f(x)+sin x.当0≤x<π时,f(x)=0,∴f()=f()=f()+sin=f()+sin+sin=f()+sin+sin+sin=sin+sin+sin==.故选:A.11.C【解析】设4个根分别为x1、x2、x3、x4,则x1+x2=2,x3+x4=2,由等差数列的性质,当m+n=p+q时,a m+a n=a p+a q.设x1为第一项,x2必为第4项,可得数列为,,,,∴m=,n=.∴|m﹣n|=.故选C.12.A【解析】由S n=a1+a2•4+a3•42+…+a n•4n﹣1①得4•s n=4•a1+a2•42+a3•43+…+a n﹣1•4n﹣1+a n•4n②①+②得:5s n=a1+4(a1+a2)+42•(a2+a3)+…+4n﹣1•(a n﹣1+a n)+a n•4n=a1+4×+42•2+…+4n•a n=1+1+1+…+1+4n•a n=n+4n•a n.所以5s n﹣4n•a n=n.故选A.二、填空题13. 2【解析】将b cos C+c cos B=2b,利用正弦定理化简得:sin B cos C+sin C cos B=2sin B,即sin(B+C)=2sin B,∵sin(B+C)=sin A,∴sin A=2sin B,利用正弦定理化简得:a=2b,则=2.故答案为:214.5【解析】由题意可得a m=S m﹣S m﹣1=0﹣(﹣2)=2,a m+1=S m+1﹣S m=3﹣0=3,∴等差数列{a n}的公差d=a m+1﹣a m=3﹣2=1,由通项公式可得a m=a1+(m﹣1)d,代入数据可得2=a1+m﹣1,①再由求和公式可得S m=ma1+d,代入数据可得0=ma1+,②联立①②可解得m=5,故答案为:5.15.3【解析】∵,∴;∵,∴.∴.故答案为:3.16.126【解析】∵数列{a n}是以2为首项,1为公差的等差数列,∴a n=2+(n﹣1)×1=n+1.则a1=2,a2=3,a3=4,a4=5,a5=6,a6=7,{b n}是以1为首项,2为公比的等比数列,则bn=1×2n﹣1=2n﹣1,∴b+b+b+…+b=b2+b3+b4+b5+b6+b7=2+4+8+16+32+64=126.故答案为:126.三、解答题17.解:(1)因为a•sin A+c•sin C﹣a•sin C=b•sin B,所以由正弦定理得,,即,由余弦定理得:cos B==,因为0°<B180°,所以B=45°. (2)因为sin A=sin75°=sin(30°+45°)=sin30°cos45°+cos30°sin45°==,所以由正弦定理得,====,则a=,c=.18.解:(1)∵=(﹣1,),=(cos A,sin A),∴•=sin A﹣cos A=2sin(A﹣)=1,∴sin(A﹣)=,∵0<A<π,∴﹣<A﹣<,∴A﹣=,∴A=;(2)∵=,=,变形整理可得b2=c2,∴b=c,又∵A=,∴△ABC为等边三角形,又c=,∴△ABC的面积S=×()2×=19.解:(1)依题意,a32=9a2a6=9a3a5,∴=q2=,解得:q=或q=﹣(舍),又∵2a1+3a2=1,即2a1+3a1=1,∴a1=,∴数列{a n}是首项、公比均为的等比数列,∴其通项公式a n=.(2)由(1)可知log3a n=log3=﹣n,∴b n=log3a1+log3a2+log3a3+…log3a n=﹣1﹣2﹣…﹣n=﹣,∴=﹣=﹣2(﹣),∴数列{}的前n项和S n=﹣2(1﹣+…+﹣)=﹣2(1﹣)=﹣.20.解:(1)f(x)=cos(2x+)+sin2x=,所以当sin2x=﹣1时,函数f(x)的最大值为,它的最小正周期为:=π;(2)因为==﹣,所以,因为C为锐角,所以;因为在△ABC中,cos B=,所以,所以=.21.解:(1)设等差数列{a n}的公差为d,∵a1=2,且a1、a2、a5成等比数列.∴=a1a5,即(2+d)2=2(2+4d),解得d=0或4.∴a n=2,或a n=2+4(n﹣1)=4n﹣2.(2)当a n=2时,S n=2n,不存在正整数n,使得S n>60n+800.当a n=4n﹣2时,S n==2n2,假设存在正整数n,使得S n>60n+800,即2n2>60n+800,化为n2﹣30n﹣400>0,解得n>40,∴n的最小值为41.22.解:(1)由题意,得,即.故当n≥2时,a n=S n﹣S n﹣1=n2+4n﹣(n﹣1)2﹣4(n﹣1)=2n+3.注意到n=1时,a1=S1=5,而当n=1时,n+4=5,∴a n=2n+3(n∈N*).又b n+2﹣2b n+1+b n=0,即b n+2﹣b n+1=b n+1﹣b n(n∈N*),∴{b n}为等差数列,于是.而b4=8,故b8=20,,∴b n=b4+3(n﹣4)=3n﹣4,即b n=b4+3(n﹣4)=3n﹣4(n∈N*).(2),①当m为奇数时,m+9为偶数.此时f(m+9)=3(m+9)﹣4=3m+23,3f(m)=6m+9∴3m+23=6m+9,(舍去);②当m为偶数时,m+9为奇数.此时,f(m+9)=2(m+9)+3=2m+21,3f(m)=9m﹣12,所以2m+21=9m﹣12,(舍去).综上,不存在正整数m,使得f(m+9)=3f(m)成立.。
广东省揭阳市高三数学一模试卷(文科) Word版含解析

2017年广东省揭阳市高考数学一模试卷(文科)一、选择题:共12小题,每小题5分,共60分.在每个小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合A={﹣1,0,1,2},集合B={y|y=2x﹣3,x∈A},则A∩B中元素的个数为()A.1 B.2 C.3 D.42.已知点A(0,1),B(3,2),向量,则向量=()A.(10,7)B.(10,5)C.(﹣4,﹣3)D.(﹣4,﹣1)3.若直线mx+2y+m=0与直线3mx+(m﹣1)y+7=0平行,则m的值为()A.7 B.0或7 C.0 D.44.已知命题p:∃x,y∈R,sin(x+y)=sinx+siny,命题,则下列判断正确的是()A.命题p∨q是假命题B.命题p∧q是真命题C.命题p∨(¬q)是假命题D.命题p∧(¬q)是真命题5.曲线与的交点横坐标所在区间为()A.B.C.D.6.阅读图的程序框图,运行相应的程序,当输入x的值为﹣36时,输出x的值为()A.0 B.1 C.3 D.157.如果实数x、y满足条件,那么2x﹣y的最大值为()A.2 B.1 C.﹣2 D.﹣38.清代著名数学家梅彀成在他的《增删算法统宗》中有这样一歌谣:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”其译文为:“远远望见7层高的古塔,每层塔点着的灯数,下层比上层成倍地增加,一共有381盏,请问塔尖几盏灯?”则按此塔各层灯盏的设置规律,从上往下数第4层的灯盏数应为()A.3 B.12 C.24 D.369.连续掷两次骰子,以先后得到的点数m,n为点P的坐标(m,n),那么点P 在圆x2+y2=17内部(不包括边界)的概率是()A.B.C.D.10.某工件的三视图如图所示,现将该工件通过切割,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工件的一个面内,则新工件的棱长为()A.B.1 C.2 D.11.已知抛物线y=ax2+2x﹣a﹣1(a∈R),恒过第三象限上一定点A,且点A在直线3mx+ny+1=0(m>0,n>0)上,则的最小值为()A.4 B.12 C.24 D.3612.已知函数f(x)=|sinx|(x∈[﹣π,π]),g(x)为[﹣4,4]上的奇函数,且,设方程f (f (x ))=0,f (g (x ))=0,g (g (x ))=0的实根的个数分别为m 、n 、t ,则m +n +t=( )A .9B .13C .17D .21二、填空题:本大题共4小题,每小题5分,共20分,请把正确的答案填写在答题卡相应的横线上.13.已知函数f (x )=ax 3+bx +1,若f (a )=8,则f (﹣a )= .14.已知数列{a n }对任意的n ∈N *都有a n +1=a n ﹣2a n +1a n ,若,则a 8= . 15.已知△ABC 的顶点都在球O 的球面上,AB=6,BC=8,AC=10,三棱锥O ﹣ABC的体积为40,则该球的表面积等于 .16.已知双曲线右焦点为F ,P 为双曲线左支上一点,点,则△APF 周长的最小值为 .三、解答题:解答应写出文字说明,证明过程或演算步骤.17.已知:复数z 1=2sinAsinC +(a +c )i ,z 2=1+2cosAcosC +4i ,且z 1=z 2,其中A 、B 、C 为△ABC 的内角,a 、b 、c 为角A 、B 、C 所对的边.(Ⅰ)求角B 的大小;(Ⅱ) 若,求△ABC 的面积.18.如图,在直三棱柱ABC ﹣A 1B 1C 1中,AB=BC=BB 1,AB 1∩A 1B=E ,D 为AC 上的点,B 1C ∥平面A 1BD ;(Ⅰ)求证:BD ⊥平面A 1ACC 1;(Ⅱ)若AB=1,且AC•AD=1,求三棱锥A ﹣BCB 1的体积.19.某地政府拟在该地一水库上建造一座水电站,用泄流水量发电.图是根据该水库历年的日泄流量的水文资料画成的日泄流量X(单位:万立方米)的频率分布直方图(不完整),已知X∈[0,120),历年中日泄流量在区间[30,60)的年平均天数为156,一年按364天计.(Ⅰ)请把频率分布直方图补充完整;(Ⅱ)已知一台小型发电机,需30万立方米以上的日泄流量才能运行,运行一天可获利润为4000元,若不运行,则每天亏损500元;一台中型发电机,需60万立方米以上的日泄流量才能运行,运行一天可获利10000元,若不运行,则每天亏损800元;根据历年日泄流量的水文资料,水电站决定安装一台发电机,为使一年的日均利润值最大,应安装哪种发电机?20.已知椭圆的离心率为,点M,N是椭圆C上的点,且直线OM与ON的斜率之积为﹣(Ⅰ)求椭圆C的方程;(Ⅱ)设动点P(x0,y0)满足=+2,是否存在常数λ,使得P是椭圆上的点.21.已知函数.(a∈R)(Ⅰ)若函数在区间上单调递减,求实数a的取值范围;(Ⅱ)试讨论函数f(x)在区间(0,+∞)内极值点的个数.[选修4-4:坐标系与参数方程]22.已知曲线C的参数方程为(θ为参数).以原点O为极点,x 轴的非负半轴为极轴建立极坐标方程.(1)求曲线C的极坐标方程;(2)若直线l:θ=α(α∈[0,π),ρ∈R)与曲线C相交于A,B两点,设线段AB的中点为M,求|OM|的最大值.[选修4-5:不等式选讲]23.设函数f(x)=a(x﹣1).(Ⅰ)当a=1时,解不等式|f(x)|+|f(﹣x)|≥3x;(Ⅱ)设|a|≤1,当|x|≤1时,求证:.2017年广东省揭阳市高考数学一模试卷(文科)参考答案与试题解析一、选择题:共12小题,每小题5分,共60分.在每个小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合A={﹣1,0,1,2},集合B={y|y=2x﹣3,x∈A},则A∩B中元素的个数为()A.1 B.2 C.3 D.4【考点】交集及其运算.【分析】有题目给出的已知条件,用列举法表示出集合B,取交集运算后答案可求.【解答】解:由A={﹣1,0,1,2},集合B={y|y=2x﹣3,x∈A}={﹣5,﹣3,﹣1,1}所以A∩B={﹣1,1}.所以A∩B中元素的个数为2.故选B.2.已知点A(0,1),B(3,2),向量,则向量=()A.(10,7)B.(10,5)C.(﹣4,﹣3)D.(﹣4,﹣1)【考点】平面向量的坐标运算.【分析】根据题意,由点A、B的坐标,计算可得向量的坐标,又由=+,代入坐标计算可得答案.【解答】解:根据题意,点A(0,1),B(3,2),则向量=(3,1),又由,则向量=+=(﹣4,﹣3);故选:C.3.若直线mx+2y+m=0与直线3mx+(m﹣1)y+7=0平行,则m的值为()A.7 B.0或7 C.0 D.4【考点】直线的一般式方程与直线的平行关系.【分析】由m(m﹣1)=3m×2,求出m值,再进行检验即可.【解答】解:∵直线mx+2y+m=0与直线3mx+(m﹣1)y+7=0平行,∴m(m﹣1)=3m×2,∴m=0或7,经检验都符合题意.故选:B.4.已知命题p:∃x,y∈R,sin(x+y)=sinx+siny,命题,则下列判断正确的是()A.命题p∨q是假命题B.命题p∧q是真命题C.命题p∨(¬q)是假命题D.命题p∧(¬q)是真命题【考点】复合命题的真假.【分析】分别判断出p,q的真假,从而判断出复合命题的真假即可.【解答】解:令x=0,y=,显然满足sin(x+y)=sinx+siny,故命题p是真命题;x∈[0,π],cosx=±,故命题q是假命题,故命题p∧(¬q)是真命题,故选:D.5.曲线与的交点横坐标所在区间为()A.B.C.D.【考点】函数的图象.【分析】方法一:分别画出与的图象,由图象,结合各选项即可判断.方法二:构造函数,利用函数零点存在定理,即可判断【解答】解:方法一:分别画出与的图象,如图所示,由图象可得交点横坐标所在区间为(,),方法二:设f (x )=()x ﹣x,∵f ()=()﹣<0,f ()=()﹣()>0,∴f ()f ()<0,根据函数零点存在定理可得点函数零点所在区间为(,),即交点横坐标所在区间为(,),故选:B6.阅读图的程序框图,运行相应的程序,当输入x 的值为﹣36时,输出x 的值为( )A.0 B.1 C.3 D.15【考点】程序框图.【分析】根据题意,按照程序框图的顺序进行执行,当|x|≤1时跳出循环,输出结果.【解答】解:当输入x=﹣36时,|x|>1,执行循环,x=6﹣2=4;|x|=4>1,执行循环,x=2﹣2=0,|x|=0<1,退出循环,输出的结果为x=1﹣1=0.故选:A7.如果实数x、y满足条件,那么2x﹣y的最大值为()A.2 B.1 C.﹣2 D.﹣3【考点】简单线性规划的应用.【分析】先根据约束条件画出可行域,再利用几何意义求最值,z=2x﹣y表示直线在y轴上的截距,只需求出可行域直线在y轴上的截距最大值即可.【解答】解:先根据约束条件画出可行域,当直线2x﹣y=t过点A(0,﹣1)时,t最大是1,故选B.8.清代著名数学家梅彀成在他的《增删算法统宗》中有这样一歌谣:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”其译文为:“远远望见7层高的古塔,每层塔点着的灯数,下层比上层成倍地增加,一共有381盏,请问塔尖几盏灯?”则按此塔各层灯盏的设置规律,从上往下数第4层的灯盏数应为()A.3 B.12 C.24 D.36【考点】等比数列的通项公式.【分析】由题意知第七层至第一层的灯的盏数构成一个以a1为首项,以2为公比的等比数列,由等比数列的求和公式可得a1,即可求出a4.【解答】解:依题意知,此塔各层的灯盏数构成公比q=2的等比数列,且前7项和S7=381,由,解得a1=3,故.故选:C.9.连续掷两次骰子,以先后得到的点数m,n为点P的坐标(m,n),那么点P 在圆x2+y2=17内部(不包括边界)的概率是()A.B.C.D.【考点】列举法计算基本事件数及事件发生的概率.【分析】基本事件总数N=6×6=36,再利用列举法求出点P在圆x2+y2=17内部(不包括边界)包含的基本事件个数,由此能求出点P在圆x2+y2=17内部(不包括边界)的概率.【解答】解:连续掷两次骰子,以先后得到的点数m,n为点P的坐标(m,n),基本事件总数N=6×6=36,点P在圆x2+y2=17内部(不包括边界)包含的基本事件有:(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),共8个,∴点P在圆x2+y2=17内部(不包括边界)的概率是p==.故选:D.10.某工件的三视图如图所示,现将该工件通过切割,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工件的一个面内,则新工件的棱长为()A.B.1 C.2 D.【考点】由三视图求面积、体积.【分析】依题意知该工件为圆锥,底面半径为,高为2,要使加工成的正方体新工件体积最大,则该正方体为圆锥的内接正方体.【解答】解:依题意知该工件为圆锥,底面半径为,高为2,要使加工成的正方体新工件体积最大,则该正方体为圆锥的内接正方体,设棱长为2x,则有,解得,故2x=1,即新工件棱长为1.故选B.11.已知抛物线y=ax2+2x﹣a﹣1(a∈R),恒过第三象限上一定点A,且点A在直线3mx+ny+1=0(m>0,n>0)上,则的最小值为()A.4 B.12 C.24 D.36【考点】基本不等式;二次函数的性质.【分析】抛物线y=ax2+2x﹣a﹣1(a∈R),恒过第三象限上一定点A,得到A(﹣1,﹣3),再把点A代入直线方程得到m+n=,再把“1”整体代入所求的式子,利用基本不等式求出最小值.【解答】解:抛物线y=ax2+2x﹣a﹣1(a∈R),恒过第三象限上一定点A,∴A(﹣1,﹣3),∴,又===12,当且仅当m=n时等号成立.故选:B12.已知函数f(x)=|sinx|(x∈[﹣π,π]),g(x)为[﹣4,4]上的奇函数,且,设方程f(f(x))=0,f(g(x))=0,g(g(x))=0的实根的个数分别为m、n、t,则m+n+t=()A.9 B.13 C.17 D.21【考点】正弦函数的图象.【分析】根据x∈[﹣π,π]时函数f(x)=|sinx|的值域为[0,1],由函数g(x)的图象与性质得出其值域为[﹣4,4],由方程f(x)=0的根得出方程f(f(x))=0根的个数m;求出方程f(g(x))=0的实根个数n;由方程g(x)=0的实根情况得出方程g(g(x))=0的实根个数t;从而求出m+n+t的值.【解答】解:因x∈[﹣π,π],所以函数f(x)=|sinx|的值域为[0,1],函数g(x)=的图象如图示,由图象知,其值域为[﹣4,4],注意到方程f(x)=0的根为0,﹣π,π,所以方程f(f(x))=0的根为方程f(x)=0或f(x)=﹣π,f(x)=π的根,显然方程f(x)=0有3个实根,因﹣π,π∉[0,1],所以f(x)=﹣π,与f(x)=π均无实根;所以方程f(f(x))=0的实根的个数为3,即m=3;方程f(g(x))=0的实根为方程g(x)=0或g(x)=﹣π,g(x)=π的根,方程g(x)=﹣π,g(x)=π各有3个根,同时方程g(x)=0也有3个根,从而方程f(g(x))=0根的个数为9,即n=9;方程g(x)=0有三个实根﹣3、0、3,方程g(g(x))=0的实根为方程g(x)=﹣3或g(x)=0或g(x)=3的根,方程g(x)=﹣3或g(x)=3各有3个根,同时方程g(x)=0也有3个根,从而方程g(g(x))=0根的个数为9,即t=9;综上,m+n+t=3+9+9=21.故选:D.二、填空题:本大题共4小题,每小题5分,共20分,请把正确的答案填写在答题卡相应的横线上.13.已知函数f(x)=ax3+bx+1,若f(a)=8,则f(﹣a)=﹣6.【考点】函数奇偶性的性质.【分析】本题利用函数的奇偶性,得到函数解析式f (﹣x )与f (x )的关系,从面通过f (﹣a )的值求出f (a )的值,得到本题结论. 【解答】解:∵函数f (x )=ax 3+bx +1,∴f (﹣x )=a (﹣x )3+b (﹣x )+1=﹣ax 3﹣bx +1, ∴f (﹣x )+f (x )=2, ∴f (﹣a )+f (a )=2. ∵f (a )=8, ∴f (a )=﹣6. 故答案为﹣6.14.已知数列{a n }对任意的n ∈N *都有a n +1=a n ﹣2a n +1a n ,若,则a 8= .【考点】数列递推式.【分析】由a n +1=a n ﹣2a n +1a n 得,利用等差数列的通项公式即可得出.【解答】解:由a n +1=a n ﹣2a n +1a n 得,故数列是,公差d=2的等差数列,,.故答案为:.15.已知△ABC 的顶点都在球O 的球面上,AB=6,BC=8,AC=10,三棱锥O ﹣ABC的体积为40,则该球的表面积等于 400π . 【考点】球的体积和表面积.【分析】求出△ABC 所在圆面的半径为,则由得三棱锥的高h=5,设球O 的半径为R ,则由h 2+52=R 2,得R=10,【解答】解:依题意知△ABC 为直角三角形,其所在圆面的半径为,设三棱锥O ﹣ABC 的高为h ,则由得h=5,设球O的半径为R,则由h2+52=R2,得R=10,故该球的表面积为400π.故答案为400π.16.已知双曲线右焦点为F,P为双曲线左支上一点,点,则△APF周长的最小值为4(1+).【考点】双曲线的简单性质.【分析】△APF的周长l=|AF|+|AP|+|PF|=|AF|+2a+|PF'|+|AP|,要△APF的周长最小,只需|AP|+|PF'|最小,如图,当A、P、F三点共线时取到,即可得出结论.【解答】解:由题意,点,△APF的周长l=|AF|+|AP|+|PF|=|AF|+2a+|PF'|+|AP|,要△APF的周长最小,只需|AP|+|PF'|最小,如图,当A、P、F三点共线时取到,故l=.故答案为:4(1+).三、解答题:解答应写出文字说明,证明过程或演算步骤.17.已知:复数z1=2sinAsinC+(a+c)i,z2=1+2cosAcosC+4i,且z1=z2,其中A、B、C为△ABC的内角,a、b、c为角A、B、C所对的边.(Ⅰ)求角B的大小;(Ⅱ)若,求△ABC的面积.【考点】三角形中的几何计算.【分析】(Ⅰ)根据复数相等得到2sinAsinC=1+2cosAcosC,根据两角和余弦公式和诱导公式,即可求出B的大小;(Ⅱ)由余弦定理可以及a+c=4,可得ac,再根据三角形的面积公式计算即可.【解答】解:(Ⅰ)∵z1=z2∴2sinAsinC=1+2cosAcosC﹣﹣﹣﹣①,a+c=4﹣﹣﹣﹣②,由①得2(cosAcosC﹣sinAsinC)=﹣1即,∴,∵0<B<π∴;(Ⅱ)∵,由余弦定理得b2=a2+c2﹣2accosB⇒a2+c2﹣ac=8,﹣﹣④,由②得a2+c2+2ac=16﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣⑤由④⑤得,∴=.18.如图,在直三棱柱ABC﹣A1B1C1中,AB=BC=BB1,AB1∩A1B=E,D为AC上的点,B1C∥平面A1BD;(Ⅰ)求证:BD⊥平面A1ACC1;(Ⅱ)若AB=1,且AC•AD=1,求三棱锥A﹣BCB1的体积.【考点】棱柱、棱锥、棱台的体积;直线与平面垂直的判定.【分析】(Ⅰ)连结ED,证明:BD⊥AC,A1A⊥BD,即可证明BD⊥平面A1ACC1;(Ⅱ)若AB=1,且AC•AD=1,利用体积公式求三棱锥A﹣BCB1的体积.【解答】(Ⅰ)证明:连结ED∵平面AB1C∩平面A1BD=ED,B1C∥平面A1BD,∴B1C∥ED,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣∵E为AB1中点,∴D为AC中点,∵AB=BC,∴BD⊥AC①,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣由A1A⊥平面ABC,BD⊂平面ABC,得A1A⊥BD②,由①②及A1A、AC是平面A1ACC1内的两条相交直线,得BD⊥平面A1ACC1.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(Ⅱ)解:由AB=1得BC=BB1=1,由(Ⅰ)知,又AC•DA=1得AC2=2,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣∵AC2=2=AB2+BC2,∴AB⊥BC,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣∴∴.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣19.某地政府拟在该地一水库上建造一座水电站,用泄流水量发电.图是根据该水库历年的日泄流量的水文资料画成的日泄流量X(单位:万立方米)的频率分布直方图(不完整),已知X∈[0,120),历年中日泄流量在区间[30,60)的年平均天数为156,一年按364天计.(Ⅰ)请把频率分布直方图补充完整;(Ⅱ)已知一台小型发电机,需30万立方米以上的日泄流量才能运行,运行一天可获利润为4000元,若不运行,则每天亏损500元;一台中型发电机,需60万立方米以上的日泄流量才能运行,运行一天可获利10000元,若不运行,则每天亏损800元;根据历年日泄流量的水文资料,水电站决定安装一台发电机,为使一年的日均利润值最大,应安装哪种发电机?【考点】频率分布直方图.【分析】(Ⅰ)根据频率,组距的关系求出a的,再画图即可,(Ⅱ)根据不同泄流量,分别安装运行一台小型发电机或一台小型发电机的利润,比较即可.【解答】解:(Ⅰ)在区间[30,60)的频率为,,设在区间[0,30)上,,则,解得,补充频率分布直方图如右;(Ⅱ)当日泄流量X≥30(万立方米)时,小型发电机可以运行,则一年中一台小型发电机可运行的天数为:(天);当日泄流量X≥60(万立方米)时,中型发电机可以运行,则一年中一台中型发电机可运行的天数为:(天);①若运行一台小型发电机,则一年的日均利润值为:(或)(元)②若运行一台中型发电机,则一年的日均利润值为:(或)(元)因为,故为使水电站一年的日均利润值最大,应安装中型发电机.20.已知椭圆的离心率为,点M,N是椭圆C上的点,且直线OM与ON的斜率之积为﹣(Ⅰ)求椭圆C的方程;(Ⅱ)设动点P(x0,y0)满足=+2,是否存在常数λ,使得P是椭圆上的点.【考点】直线与椭圆的位置关系.【分析】(Ⅰ)由椭圆的离心率为,求出a=2,由此能求出椭圆的标准方程.(Ⅱ)设M(x1,y1),N(x2,y2),则由=,得x0=x1+2x2,y0=y1+2y2,由点M,N在椭圆=1上,由直线OM与ON的斜率之积为﹣,由此能求出存在常数λ=5,使得P点在椭圆上.【解答】解:(Ⅰ)∵椭圆的离心率为,∴e=,解得,又b2=2,解得a=2,故椭圆的标准方程为=1.(Ⅱ)设M(x1,y1),N(x2,y2),则由=,得x0=x1+2x2,y0=y1+2y2,又点M,N在椭圆=1上,∴,,设k OM,k ON分别为直线OM,ON的斜率,由题意知:k OM•k ON==﹣,∴x1x2+2y1y2=0,∴=,因此,存在常数λ=5,使得P点在椭圆上.21.已知函数.(a∈R)(Ⅰ)若函数在区间上单调递减,求实数a的取值范围;(Ⅱ)试讨论函数f(x)在区间(0,+∞)内极值点的个数.【考点】利用导数研究函数的极值;利用导数研究函数的单调性.【分析】(Ⅰ)由题意可知f′(x)=﹣+≤0,a≥,则构造辅助函数,求导,根据函数函数的单调性即可求得最大值,即可求得实数a的取值范围;(Ⅱ)方法1:构造辅助函数,g(x)=,求导g′(x)=,根据函数的单调性即可求得g(x)最小值,根据函数的单调性及极值的判断求得函数的f (x)的极值点的个数;方法2:分类讨论,根据当a≤1时,根据函数的单调性f(x)在区间(0,+∞)递增,f(x)无极值,当a>1时,构造辅助函数,求导,根据函数的单调性与极值的关系,即可求得f(x)的极值个数.【解答】解:(Ⅰ)由题意可知:对∀x∈,f′(x)=﹣+≤0,即a≥,对∀x∈恒成立,令g(x)=,求导g′(x)=,当0<x<1时,g′(x)<0,当x>1,g′(x)>0,∴函数g(x)在[,1]上单调递减,在(1,e]上单调递增,∴g()=,g(e)=e e﹣1,由e e﹣1>,∴在区间上g(x)max=e e﹣1,∴a≥e e﹣1,(Ⅱ)解法1:由f′(x)=﹣+==,g(x)=,g′(x)=,当0<x<1时,g′(x)<0,当x>1时,g′(x)>0,∴函数g(x)在(0,1)单调递减,在(1,+∞)单调递增,g(x)min=g(1)=e,当a≤e时,g(x)≥a恒成立,f′(x)≥0,函数f(x)在区间(0,+∞)单调递增,f(x)无极值点,当a>e时,g(x)min≥g(1)=e<a,故存在x1∈(0,1)和x2∈(1,+∞),使得g(x1)=g(x2)=a,当0<x<x1,f′(x)>0,当x1<x<x2时,f′(x)<0,当x>x2,f′(x)>0,∴函数f(x)在(x1,x2)单调递减,在(0,x1)和(x2,+∞),∴x1为函数f(x)的极大值点,x2为函数f(x)的极小值点,综上可知;a≤e时,函数f(x)无极值点,当a>e时,函数f(x)有两个极值点.方法2:f′(x)=,设h(x)=e x﹣ax(x>0),则h(x)=e x﹣a,由x>0,e x>1,(1)当a≤1时,h′(x)>0,h(x)递增,h(x)>h(0)=1,则f′(x)>0,f(x)递增,f(x)在区间(0,+∞)内无极值;(2)当a>1时,由h′(x)=e x﹣a>0,则x>lna,可知h(x)在(0,lna)内递减,在(lna,+∞)单调递增,∴h(x)max=h(lna)=a(1﹣lna),①当1<a≤e时,h(x)>h(x)min≥0,则f′(x)>0,f(x)单调递增,f(x)在区间(0,+∞)内无极值;②当a>e时,h(x)min<0,又h(0)>0,x很大时,h(x)>0,∴存在x1∈(0,lna),x2∈(lna,+∞),使得h(x1)=0,h(x2)=0,即f′(x1)=0,f′(x2)=0,可知在x1,x1两边f′(x)符号相反,∴函数f(x)有两个极值点x1,x2,综上可知;a≤e时,函数f(x)无极值点,当a>e时,函数f(x)有两个极值点.[选修4-4:坐标系与参数方程]22.已知曲线C的参数方程为(θ为参数).以原点O为极点,x 轴的非负半轴为极轴建立极坐标方程.(1)求曲线C的极坐标方程;(2)若直线l:θ=α(α∈[0,π),ρ∈R)与曲线C相交于A,B两点,设线段AB的中点为M,求|OM|的最大值.【考点】简单曲线的极坐标方程;参数方程化成普通方程.【分析】(I)利用平方关系可得曲线C的普通方程,把x=ρcosθ,y=ρsinθ,代入即可得出.(II)联立θ=α和ρ2+2ρcosθ﹣2ρsinθ﹣2=0,得ρ2+2ρ(cosα﹣sinα)﹣2=0,设A(ρ1,α),B(ρ2,α),可得ρ1+ρ2=2(cosα﹣sinα)=2,即可得出.【解答】解:(I)曲线C的普通方程为(x+1)2+(y﹣1)2=4,由x=ρcosθ,y=ρsinθ,得ρ2+2ρcosθ﹣2ρsinθ﹣2=0.(II)联立θ=α和ρ2+2ρcosθ﹣2ρsinθ﹣2=0,得ρ2+2ρ(cosα﹣sinα)﹣2=0,设A(ρ1,α),B(ρ2,α),则ρ1+ρ2=2(cosα﹣sinα)=2,由|OM|=,得|OM|=,当α=时,|OM|取最大值.[选修4-5:不等式选讲]23.设函数f(x)=a(x﹣1).(Ⅰ)当a=1时,解不等式|f(x)|+|f(﹣x)|≥3x;(Ⅱ)设|a|≤1,当|x|≤1时,求证:.【考点】绝对值三角不等式;绝对值不等式的解法.【分析】(Ⅰ)当a=1时,不等式|f(x)|+|f(﹣x)|≥3x即|x﹣1|+|x+1|≥3x,分类讨论,即可解不等式|f(x)|+|f(﹣x)|≥3x;(Ⅱ)设|a|≤1,当|x|≤1时,|f(x2)+x|≤|a|(1﹣x2)+|x|≤1﹣x2+|x|,即可证明:.【解答】解:(I)当a=1时,不等式|f(x)|+|f(﹣x)|≥3x即|x﹣1|+|x+1|≥3x当x≤﹣1时,得1﹣x﹣x﹣1≥3x⇒x≤0,∴x≤﹣1﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣当﹣1<x<1时,得1﹣x+x+1≥3x,∴﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣当x≥1时,得x﹣1+x+1≥3x⇒x≤0,与x≥1矛盾,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣综上得原不等式的解集为=﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(II)证明:|f(x2)+x|=|a(x2﹣1)+x|≤|a(x2﹣1)|+|x|﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣∵|a|≤1,|x|≤1∴|f(x2)+x|≤|a|(1﹣x2)+|x|≤1﹣x2+|x|﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣=,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣当时取“=”,得证.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣2017年4月13日。
广东省揭阳2017届高三上学期第一次时期考试数学文试题Word版含答案

揭阳一中高三数学(文)上学期时期1考试(命题人:方少萍 审题人:杨敏)一、选择题:此题共12小题,每题5分,在每题给出的四个选项中,只有一项为哪一项符合题目要求的. 1.已知集合{0,1,2,3}A =,1{|2,}k B n n k A -==∈,那么A B =( )A .{1,2,3}B .{1,2}C .{1}D .{3}2.已知复数142iz i i+=-,那么复数z 的模为( )A .4B . 5C .6D .73.已知命题p :∃x 0∈R ,x 0-2>0,命题q :∀x ∈R ,x <x ,那么以下说法中正确的选项是( )A .命题p ∨q 是假命题B .命题p ∧q 是真命题C .命题p ∧(¬q )是真命题D .命题p ∨(¬q )是假命题4.设抛物线2:4C y x =的核心为F ,准线l 与x 轴的交点为R ,过抛物线C 上一点P 作准线l 的垂线,垂足为Q ,假设QRF ∆的面积为2,那么点P 的坐标为( ) A .(1,2)或(1,-2) B .(1,4)或(1,-4) C .(1,2) D .(1,4)5.某几何体的三视图如图(其中俯视图中的圆弧是半圆),那么 该几何体的表面积为( )A .92+14πB .82+14πC .92+24πD .82+24π6.函数311log (2),1()3,1x x x f x x -+-<⎧=⎨≥⎩,那么3(7)(log 12)f f -+=( )A .8B .15C .7D .167.某程序框图如下图,该程序运行后输出的k 的值是( )A .3B .4C .5D .68.设函数()sin(2)cos(2)44f x x x ππ=+++,那么( ) A .()y f x =在(0,)2π上单调递增,其图象关于直线4x π=对称 B .()y f x =在(0,)2π上单调递增,其图象关于直线2x π=对称C .()y f x =在(0,)2π上单调递减,其图象关于直线4x π=对称 D .()y f x =在(0,)2π上单调递减,其图象关于直线2x π=对称 9.已知数列{a n }的前n 项和为S n ,假设S n =2a n -4(n ∈N *),那么a n =( ) A .2n +1B .2nC .2n -1D .2n -210.设a =log 32,b =log 52,c =log 23,那么( )A .a >c >bB .b >c >aC .c >b >aD .c >a >b 11.πsin 22cos 2x x ⎛⎫-+ ⎪⎝⎭的最大值是( )A .-3B .-32C .32D .312.已知函数()y f x =的概念域为R ,当x <0时,()1f x >,且对任意的实数x 、y ∈R ,等式()()()f x f y f x y =+恒成立.假设数列{a n }知足a 1=f (0),且11()(2)n n f a f a +=--(*)n N ∈,那么a 2021的值为( )A .4029B .3029C .2249D .2209二、填空题:此题共4小题,每题5分.13.已知向量(,1)a x x =-,(1,2)b =,且a //b ,那么x = ___________ .14.设曲线x e x f xsin )(=在(0,0)处的切线与直线x +my +l=0平行,那么m = _____ . 15. 假设x ,y 知足约束条件2022020x y x y x y +-⎧⎪-+⎨⎪-+⎩≤≤≥,则3z x y =+的最大值为.16.假设偶函数(),y f x x R =∈,知足(2)()f x f x +=-,且当[0,2]x ∈时,2()2f x x =-,那么方程()sin ||f x x =在[-10,10]内的根的个数为 ___________ .三、解答题:解许诺写出文字说明、证明进程或演算步骤.17.(本小题总分值12分)在ΔABC 中,a ,b ,c 别离为内角A ,B ,C 的对边,且sin sin().3a Bb A π=-+(1)求A ;(2)若ΔABC 的面积234S c =,求sin C 的值.18.(本小题总分值12分)为了了解某学校高二年级学生的物理成绩,从中抽取n 名 学生的物理成绩(百分制)作为样本,按成绩分成 5组: [50,60),[60,70),[70,80),[80,90),[90,100], 频率散布直方图如下图,成绩落在[70,80)中的人数为20.(1)求a 和n 的值;(2)设成绩在80分以上(含80分)为优秀,已知样本中成绩落在[50,80)中的男、女生人数比为1:2,成绩落在[80,100]中的男、女生人数比为3:2,请完成下面的2×2列联表,并判定是不是有95%的把握以为物理成绩优秀与性别有关.参考公式和数据:))()()(()(22d b c a d c b a bc ad n K ++++-=19.(本小题总分值12分)如下图,在四棱锥P -ABCD 中,底面A BCD 是边长为a 的正方形,侧面PAD ⊥底面ABCD ,且PA =PD =22AD ,假设E ,F 别离为PC ,BD 的中点. (1)求证:EF ∥平面PAD ; (2)求证:平面PDC ⊥平面PAD ; (3)求四棱锥P -ABCD 的体积.20.(本小题总分值12分)已知圆心为C 的圆,知足以下条件:圆心C 位于x 轴正半轴上,圆C 与直线3x -4y +7=0相切,且被y 轴截得的弦长为23,圆C 的面积小于13. (1)求圆C 的标准方程;(2)设过点M (0,3)的直线l 与圆C 交于不同的两点A ,B ,以OA ,OB 为邻边作平行四边形OADB .是不是存在如此的直线l ,使得直线OD 与MC 恰好平行?若是存在,求出l 的方程;假设不存在请说明理由.21.(本小题总分值12分) 已知函数21()(22)(21)ln .2f x x a x a x =-+++ (1)假设曲线()y f x =在点(2, f (2))处的切线的斜率小于0,求f (x )的单调区间;(2)对任意的a ∈[32,52],函数g (x )=f (x )-λx 在区间[1,2]上为增函数,求λ的取值范围.请考生在(22)~(24)题中任选一题作答,若是多做,那么按所做的第一题记分. 22.(本小题总分值10分)选修4-1:几何证明选讲如图,AB 是O 的直径,AC 是O 的切线,BC 交O 于点E . (1)过E 做O 的切线,交AC 与点D ,证明:D 是AC 的中点;(2)假设3CE AO =,求ACB ∠的大小.23.(本小题总分值10分)选修4-4:坐标系与参数方程已知直线1:3x t l y t=⎧⎪⎨=⎪⎩(t 为参数),圆221:(3)(2)1C x y -+-=,以坐标原点为极点,x 轴的正半轴为极轴成立直角坐标系.(1)求圆1C 的极坐标方程,直线1l 的极坐标方程; (2)设1l 与1C 的交点为,M N ,求1C MN ∆的面积.24.(本小题总分值10分)选修4-5:不等式选讲 已知函数f (x )=|x -a |.(1)假设不等式f (x )≤3的解集为{x |-1≤x ≤5},求实数a 的值;(2)在(1)的条件下,假设f (x )+f (x +5)≥m 对一切实数x 恒成立,求实数m 的取值范围.P(K 2≥k)0.50 0.05 0.025 0.005k0.4553.841 5. 024 7.879(第22题图)揭阳一中高三数学(文)上学期时期1考试参考答案14.- 1 15. 103BBCAA CBDAD CA 13.-1 16.10 ∵sin sin()3a Bb A π=-+,17.解:(1)∴由正弦定理得sin sin sin sin()3A B B A π=-+,即sin sin()3A A π=-+,亦即13sin (sin cos )22A A A =-+, 化简得3tan 3A =- ∵(0,)A π∈,∴56A π=. ……………………(6分) (2)由(1)已得56A π=,那么1sin 2A =,由2311sin 424S c bc A bc ===,得3b c =, ∴22222252cos (3)23cos76a b c bc A c c c c c π=+-=+-=,那么7a c =, 由正弦定理得sin 7sin 14c A C a ==. ……………………(12分) 18.解: (1)连接EF ,AC ,∵四棱锥P -ABCD 中,底面ABCD 是边长为a 的正方形且点F 为对角线BD 的中点, ∴对角线AC 通过F 点,又点E 为PC 的中点,∴EF 为△PAC 的中位线,∴EF ∥PA .又PA ⊂平面PAD ,EF ⊄平面PAD ,∴EF ∥平面PAD .……………………(4分) (2)∵底面ABCD 是边长为a 的正方形,∴CD ⊥AD , 又侧面PAD ⊥底面ABCD ,侧面PAD ∩底面ABCD =AD , ∴CD ⊥平面PAD .又CD ⊂平面PCD ,∴平面PDC ⊥平面PAD . ……………………(8分) (3)过点P 作AD 的垂线PG ,垂足为点G ,∵侧面PAD ⊥底面ABCD ,PG ⊂平面PAD ,侧面PAD ∩底面ABCD =AD , ∴PG ⊥平面ABCD ,即PG 为四棱锥P -ABCD 的高, 又PA =PD =22AD 且AD =a ,∴PG =a2. ∴V 四棱锥P -ABCD =13S 正方形ABCD ·PG =13×a 2×a 2=16a 3. ……………………(12分)19.解:(1)由10a =1-(0.005+0.01+0.015+0.02)×10=0.5得 a =0.05, 则n =20100.05⨯= 40.. ……………………(5分)(2)优秀的男生为6人,女生为4人;不优秀的男生为10人,女生为20人.因此2×2列联表如下表:则2240(620410) 2.222 3.84116241030K ⨯⨯-⨯=≈<⨯⨯⨯, 因此没有95%的把握以为物理成绩优秀与性别有关.…………(12分)20.解: (1)设圆C :(x -a )2+y 2=r 2(a >0),由题意知⎩⎪⎨⎪⎧|3a +7|32+42=r ,a 2+3=r ,解得a =1或a =138,又S =πr 2<13,∴a =1,∴圆C 的标准方程为(x -1)2+y 2=4.………………………………(5分) (2)当斜率不存在时,直线l 为x =0,不知足题意.……………………(6分) 当斜率存在时,设直线l :y =kx +3,A (x 1,y 1),B (x 2,y 2), 又l 与圆C 相交于不同的两点,联立得⎩⎪⎨⎪⎧y =kx +3,x -12+y 2=4,消去y 得(1+k 2)x 2+(6k -2)x +6=0.∴Δ=(6k -2)2-24(1+k 2)=12k 2-24k -20>0,解得k <1-263或k >1+263. ………………………………(8分)x 1+x 2=-6k -21+k 2,y 1+y 2=k (x 1+x 2)+6=2k +61+k2, OD →=OA →+OB →=(x 1+x 2,y 1+y 2),MC →=(1,-3),假设OD →∥MC →,那么-3(x 1+x 2)=y 1+y 2,解得k =34 ………………(11分)显然k =34 ∉ (-∞,1-263)∪(1+263,+∞),假设不成立,∴不存在如此的直线l . ………………………………(12分)[来源:Z#xx#]男生 女生 合计 优秀 6 4 10 不优秀 10 20 30 合计16244021.解:(1)21(21)(1)()(22)(0)a x a x f x x a x x x+---'=-++=> 若曲线()y f x =在点(2, f (2))处的切线的斜率小于0, 则1(2)02f a '=-+<,即12a >, ∴2a +1>1 那么令()0f x '>,解得0<x <1或x >2a +1; 令()0f x '<,解得1<x <2a +1.∴()f x 的单调递增区间为(0,1),(2a +1,+∞),单调递减区间为(1,2a +1) .…(5分) (2)∵()()g x f x xλ=-在区间[1,2]上为增函数,∴()0g x '≥对任意的a ∈[32,52],x ∈[1,2]恒成立,∴221()(22)0a g x x a x xλ+'=-+++≥, 化简可得32(22)(21)0x a x a x λ-++++≥,即232(22)20x x a x x x λ-+-++≥,其中a ∈[32,52] ……………(7分)∵x ∈[1,2],∴2220x x -≤,∴只需2325(22)202x x x x x λ-+-++≥ 即32760x x x λ-++≥对任意x ∈[1,2]恒成立. 令32()76h x x x x λ=-++,x ∈[1,2], 则2()31460h x x x '=-+<在[1,2]上恒成立, ∴32()76h x x x x λ=-++在区间[1,2]上为减函数,∴min ()(2)80h x h λ==-≥,解得8λ≥. ……………………………(12分) 22.(1)证明:连接,OE AE ,∵AC 是O 的切线,DE 也是O 的切线,∴弦切角CAE DEA ∠=∠,∴ADE ∆是等腰三角形,AD DE =, ∵AB 是O 的直径,∴090AEB CEA ∠==∠.∴D 是AEC ∆的外心,即是AC 的中点.………………………………(5分)(2)解:不妨设AO =1,那么CE =3 在ABC ∆中,22sin 3AO ACB CE BE BE ∠==++………① 在ABE ∆中,cos 22BE BE EBA AO ∠==,即sin 2BEACB ∠=………② 联立①②,解得1sin sin -22ACB ACB ∠=∠=或(舍), ∴锐角030ACB ∠=. ………………………………(10分)23.解:(1)将cos sin x y ρθρθ=⎧⎨=⎩代入1C 展开整理得:223cos 4sin 60ρρθρθ--+=,∴圆1C 的极坐标方程为:223cos 4sin 60ρρθρθ--+=.∵直线1l 的方程消参得3yx=, 又∵tan y xθ=, ∴直线1l 的极坐标方程为tan 3,3πθθ==即(R ρ∈)……(5分)(2)∵直线1l 的一般方程为30x y -=,∴圆心C 1(3,2)到直线1l 的距离为|332|1231•-=+, |MN |=2121()32-=,∴11133224C MN S ∆=⨯⨯=. ……………………………………(10分) 24 .解:(1)由f (x )≤3得|x -a |≤3,解得a -3≤x ≤a +3.又已知不等式f (x )≤3的解集为{x |-1≤x ≤5},因此⎩⎪⎨⎪⎧a -3=-1,a +3=5,解得a =2. …………………………………(5分)(2) 解法一:当a =2时,f (x )=|x -2|.设g (x )=f (x )+f (x +5),于是g (x )=|x -2|+|x +3|=⎩⎪⎨⎪⎧-2x -1,x <-3,5,-3≤x ≤2,2x +1,x >2.因此当x<-3时,g(x)>5;当-3≤x≤2时,g(x)=5;当x>2时,g(x)>5.综上可得,g(x)的最小值为5.又f(x)+f(x+5)≥m,即g(x)≥m对一切实数x恒成立,因此m的取值范围为(-∞,5].…………………………………(10分)解法二:当a=2时,f(x)=|x-2|.设g(x)=f(x)+f(x+5).因为|x-2|+|x+3|≥|(x-2)-(x+3)|=5(当且仅当-3≤x≤2时等号成立)因此g(x)的最小值为5.又f(x)+f(x+5)≥m即g(x)≥m对一切实数x恒成立,因此m的取值范围为(-∞,5].…………………………………(10分)。
2017年4月广东省揭阳市高三数学联考(附答案)
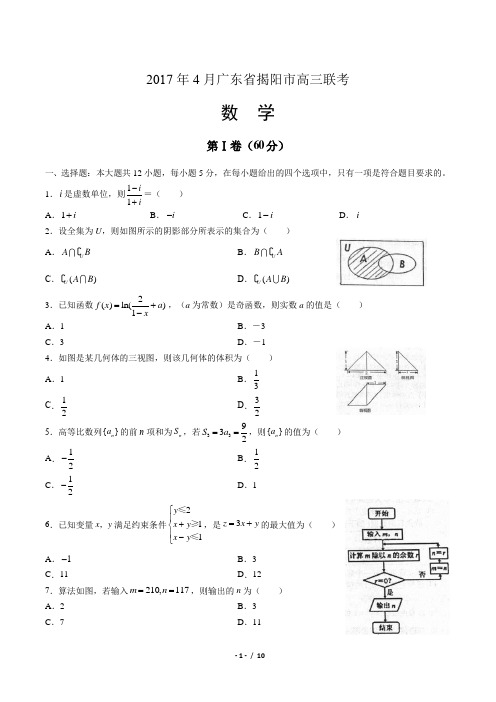
2017年4月广东省揭阳市高三联考数 学第Ⅰ卷(60分)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.i 是虚数单位,则11ii-+=( ) A .1i +B .i - C .1i - D .i 2.设全集为U ,则如图所示的阴影部分所表示的集合为( ) A .UA B B .UB AC .()UA BD .()UA B3.已知函数2()ln()1f x a x=+-,(a 为常数)是奇函数,则实数a 的值是( ) A .1B .-3C .3D .-14.如图是某几何体的三视图,则该几何体的体积为( )A .1B .13C .12D .325.高等比数列{}n a 的前n 项和为n S ,若33932S a ==,则{}n a 的值为( )A .12-B .12C .12- D .16.已知变量x ,y 满足约束条件211y x y x y ⎧⎪+⎨⎪-⎩≤≥≤,是3z x y =+的最大值为( )A .1-B .3C .11D .12 7.算法如图,若输入210,117m n ==,则输出的n 为( )A .2B .3C .7D .118.函数sin(())x f x A ωϕ=+(其中π0,2A ϕ><)的图像如图所示,为了得到()cos2g x x =的图像,则只需将()f x 的图像( )A .向右平移π6个单位长度B .向右平移π12个单位长度 C .向左平移π6个单位长度D .向左平移π12个单位长度9.如图,OA 是双曲线实半轴,OB 是虚半轴,F 是焦点,且30BAO ∠=︒,1(633)2ABF S =-△,则双曲线的标准方程是( )A .22139x y -=B .22193x y -=C .22133x y -=D .22133x y -= 10.已知点G 是ABC △的重心, 120A ∠=︒,2AB AC =-,则AG 的最小值是( )A .33B .22C .23D .3411.已知正方形123APP P 的边长为2,点B ,C 是边12P P 、23P P 的中点,AB ,BC ,CA 拆成一个三棱锥P -ABC (使1P ,2P ,3P 重合于点P )则三棱锥P -ABC 的外接球表面积为( ) A .9πB .8πC .6πD .4π12.已知212(0)(0)()e x a x x x f x x -⎧--⎪=⎨⎪⎩<≥,且函数()1y f x =-恰有3个不同的零点,则实数a 的取值范围是( )A .(1,]∞-+B .(2,0]-C .(2,]-+∞D .(0,1]第Ⅱ卷(90分)本卷包括必考题和选考题两部分。
广东揭阳市普通高中2017届高考高三数学3月模拟考试试

揭阳市普通高中2017届高考高三数学3月模拟考试试题(一)第I 卷(60分)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题 目要求的。
A .1+iB. -iC. 1-iD. i2.设全集为U,则如图所示的阴影部分所表示的集合为 A. B C A U B. A C B U C. )(B A C U <0} D. )(B A C UA 1 B.-3 C. 3 D.-14. 如图是某几何体的三视图,则该几何体的体积为5.高等比数列{a n }的前n 项和为S n ,若S 则{a n }的值为6. 已知变量x,y 满足约束条件⎪⎩⎪⎨⎧≤-≥+≤112y x y x y ,是z =3x +y 的最大值为A, -1 B.3 C.11D.127. 算法如图,若输入m=210,n = 117,则输出的n 为 A.2 B.3C,7 D.118. 函数f (x )= )sin(ϕω+x A (其中A>0, 2||πϕ<)的图象如图 所示,为了得到g(x=cos 2x的图象,则只需将f(x)的图象9.如图,OA是双曲线实半轴,OB是虚半轴,F是焦点,且10.已知点G是ΔABC的重心,A ∠ = 1200,= -2,则的最小值是A.4311.已知正方形AP 1P 2P 3的边长为2,点B,C是边P 1P 2,P 2P 3的中点,没AB,BC,CA拆成一个三棱锥P-ABC(使P 1,P 2,P 3重合于点P)则三棱锥P-ABC的外接球表面积为A. π9B. π8C. π6D. π412.已知f(x)= ⎪⎩⎪⎨⎧≥<---)0()0(2|1|2x e x x x a x ,且函数y=f(x)-1恰有3个不同的零点,则实数a 的取值范围是A. (-1,∞+]B. (-2,0]C. (-2,∞+]D. (0,1]第II 卷(90分)本卷包括必考题和选考题两部分。
广东省揭阳市高三数学第一次模拟考试试题 文

是输入x x=|x|-2x =2x -1否|x|>1?结束开始输出x 图1揭阳市2017年高中毕业班高考第一次模拟考试数学(文科)本试卷共4页,满分150分.考试用时120分钟.注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.答题前,考生务必将自己的姓名、准考证号填写在答题卡上.2.回答第Ⅰ卷时,选出每个小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮搽干净后,再选涂其他答案标号,写在本试卷上无效.3.回答第Ⅱ卷时,将答案写在答题卡上,答在本试题上无效.4.考试结束,将本试题和答题卡一并交回.第Ⅰ卷一、选择题:共12小题,每小题5分,共60分.在每个小题给出的四个选项中,只有一项是符合题目要求的.(1)已知集合}2,1,0,1{-=A ,集合={|23,}B y y x x A =-∈,则A B I 中元素的个数为(A )1 (B )2(C )3(D )4(2)已知点(01)A ,,(3,2)B ,向量(7,4)BC =--u u u r ,则向量AC =u u u r(A )(10,7) (B )(10,5) (C )(4,3)-- (D )(4,1)-- (3)若直线20mx y m ++=与直线3(1)70mx m y +-+=平行,则m 的值为(A )7(B )0或7 (C )0(D )4(4)已知命题:,,sin()sin sin p x y R x y x y ∃∈+=+,命题1cos 2:[0,cos 2xq x x π+∀∈=,则下列判断正确的是(A )命题p q ∨是假命题 (B )命题p q ∧是真命题(C )命题()p q ∨⌝是假命题 (D )命题()p q ∧⌝是真命题(5)曲线xy )31(=与12y x =的交点横坐标所在区间为(A ))31,0( (B ))21,31( (C ))32,21( (D ))1,32((6)阅读图1的程序框图,运行相应的程序,当输入x 的值为36-时,输出x 的值为(A )0 (B )1 (C )3 (D )15(7)如果实数x y 、满足条件⎪⎩⎪⎨⎧≤++≥+≥+-010101y x y y x , 那么2x y -的最大值为(A )2 (B )1 (C )2- (D )3-(8)清代著名数学家梅彀成在他的《增删算法统宗》中有这样一歌谣:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”其译文为:“远远望见7层高的古塔,每层塔点着的灯数,下层比上层成倍地增加,一共有381盏,请问塔尖几盏灯?”则按此塔各层灯盏的设置规律,从上往下数第4层的灯盏数应为(A )3 (B )12 (C )24 (D )36(9)连续掷两次骰子,以先后得到的点数m , n 为点P 的坐标(,)m n ,那么点P 在圆2217x y +=内部(不包括边界)的概率是(A )14 (B )16 (C )518(D )29(10)某工件的三视图如图2所示,现将该工件通过 切割,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工件的一个面内,则 新工件的棱长为 (A )12(B )1 (C ) 2 (D )22(11)已知抛物线221y ax x a =+--()a R ∈,恒过第三象限上一定点A ,且点A 在直线310mx ny ++=(0,0m n >>)上,则11m n+的最小值为 (A)4 (B) 12(C) 24 (D) 36(12)已知函数()=|sin |([,])f x x x ππ∈-,()g x 为]4,4[-上的奇函数,且⎩⎨⎧≤<-≤<-=)42(124)20(2)(x x x x x g ,设方程(())0f f x =,(())0f g x =,(())0g g x =的实根的个数分别为m 、n 、t ,则m n t ++=俯视图22222222图2A CBA 1C 1B 1DE图31105(日泄流量)x1210频率组距(A )9 (B)13 (C)17 (D) 21第Ⅱ卷本卷包括必考题和选考题两部分.第(13)题~第(21)题为必考题,每个试题考生都必须做答.第(22)题~第(23)题为选考题,考生根据要求做答.二、填空题:本大题共4小题,每小题5分,共20分,请把正确的答案填写在答题卡相应的横线上.(13)已知函数3()1f x ax bx =++,若()8f a =,则()f a -=_________.(14)已知数列{}n a 对任意的n N *∈都有112n n n n a a a a ++=-,若112a =,则8a = .(15)已知△ABC 的顶点都在球O 的球面上,AB=6,BC=8,AC=10,三棱锥O-ABC 的体积为403,则该球的表面积等于 .(16)已知双曲线22142x y -=右焦点为F ,P 为双曲线左支上一点,点2)A ,则△APF 周长的最小值为 .三、解答题:解答应写出文字说明,证明过程或演算步骤. (17)(本小题满分12分)已知:复数12sin sin ()z A C a c i =++,212cos cos 4 z A C i =++,且12z z =,其中A 、B 、C为△ABC 的内角,a 、b 、c 为角A 、B 、C 所对的边. (Ⅰ)求角B 的大小;(Ⅱ) 若22b =,求△ABC 的面积. (18)(本小题满分12分)如图3,在直三棱柱ABC —A 1B 1C 1中,AB=BC=BB 1,11AB A B E =I ,D 为AC 上的点,B 1C ∥平面A 1BD ;(Ⅰ)求证:BD ⊥平面11ACC A ;(Ⅱ)若1,AB =且1AC AD =⋅,求三棱锥A-BCB 1的体积. (19)(本小题满分12分)某地政府拟在该地一水库上建造一座水电站,用泄流水 量发电.图4是根据该水库历年的日泄流量的水文资料画成的 日泄流量X (单位:万立方米)的频率分布直方图(不完整), 已知)120,0[∈X ,历年中日泄流量在区间[30,60)的年平 均天数为156,一年按364天计.(Ⅰ)请把频率分布直方图补充完整;(Ⅱ)已知一台小型发电机,需30万立方米以上的日泄流 量才能运行,运行一天可获利润为4000元,若不运行,则每天亏损500元;一台中型发电机,需60万立方米以上的日泄流量才能运行,运行一天可获利10000元,若不运行,则每天亏损800元;根据历年日泄流量的水文资料,水电站决定安装一台发电机,为使一年的日均利润值最大,应安装哪种发电机? (20)(本小题满分12分)已知椭圆222:1(2)2x y C a a +=>的离心率为22,点,M N 是椭圆C 上的点,且直线OM 与ON 的斜率之积为12-.(Ⅰ)求椭圆C 的方程;(Ⅱ)设动点()00,P x y 满足2OP OM ON =+u u u r u u u u r u u u r ,是否存在常数λ,使得P 是椭圆2222x y a λ+=上的点.(21)(本小题满分12分)已知函数x e ax f x ln )(+=.()a R ∈ (Ⅰ)若函数在区间],1[e e上单调递减,求实数a 的取值范围; (Ⅱ)试讨论函数()f x 在区间(0,)+∞内极值点的个数.请考生在第(22)、(23)题中任选一题作答,如果多做,则按所做的第一个题目计分. (22)(本小题满分10分)选修4-4:坐标系与参数方程已知曲线C 的参数方程为12cos 12sin x y θθ=-+⎧⎨=+⎩(θ为参数).以原点O 为极点,x 轴的非负半轴为极轴建立极坐标系.(Ⅰ)求曲线C 的极坐标方程;(Ⅱ)若直线l :αθ=)),,0[(R ∈∈ρπα与曲线C 相交于A 、B 两点,设线段AB 的中点为M ,求||OM 的最大值.(23)(本小题满分10分)选修4-5:不等式选讲设函数)1()(-=x a x f .(Ⅰ)当1a =时,解不等式|()||()|3f x f x x +-≥; (Ⅱ)设1||≤a ,当1||≤x 时,求证:45|)(|2≤+x x f .揭阳市2017年高中毕业班高考第一次模拟考试数学(文科)参考答案及评分说明一、本解答给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.二、对计算题当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错误,就不再给分.三、解答右端所注分数,表示考生正确做到这一步应得的累加分数. 四、只给整数分数. 一、选择题: 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案BCBDBABCDBBD部分题目解析:(8)依题意知,此塔各层的灯盏数构成公比2q =的等比数列,且前7项和7381S =,由 71(12)381,12a -=-解得13a =,故34124a a q ==.(102,高为2,要使加工成的正方体新工件体积最大,则该正方体为圆锥的内接正方体,设棱长为2x 22222x x-=,解得12x =,故2x=1,即新工件棱长为1.(11)易得(1,3)A --,则13m n +=,又11m n+n n m m n m )(3)(3+++=)(36n mm n ++= 1266=⋅+≥nm m n ,当且仅当m n =时等号成立.(或111122122m n m n m nmn+≥⋅=≥=+.) (12)因[,]x ππ∈-,所以函数()f x 的值域为[0,1],函数()g x 的 图象如图示,由图象知,其值域为[4,4]-,注意到方程()0f x =的 根为0,π-,π,所以方程(())0f f x =的根为方程()0f x =或(),f x π=-()f x π=的根,显然方程()0f x =有3个实根,因 ,[0,1]ππ-∉,所以(),f x π=-与()f x π=均无实根;所以方程(())0f f x =的实根的个数为3,即3m =;方程(())0f g x =的实根为方程()0g x =或(),()g x g x ππ=-=的根,方程(),()g x g x ππ=-=各有3个根,同时方程()0g x =也有3个根,从而方程(())0f g x =根的个数为9,即9n =;方程()0g x =有三个实根-3、0、3,方程(())0g g x =的实根为方程3)(-=x g 或()0g x =或3)(=x g 的根,方程3)(-=x g 或3)(=x g 各有3个根,同时方程()0g x =也有3个根,从而方程(())0g g x =根的个数为9,即9t =,故m n t ++=21. (12)二、填空题:题号 1314 1516答案6-400π 4(12)+部分题目解析:(14) 由112n n n n a a a a ++=-得1112n n a a +-=,故数列1{}n a 是112a =,公差2d =的等差数列122(1)2n n n a =+-=,故8116a =. (15)依题意知△ABC 为直角三角形,其所在圆面的半径为152AC =,设三棱锥O-ABC 的高为h ,则由116840332h ⨯⨯⨯=得53h =,设球O 的半径为R ,则由2225h R +=得10R =, 故该球的表面积为400π.(16)易得点(6,0)F ,△APF 的周长l =||||||AF AP PF ++||2|'|||AF a PF AP =+++,要△APF 的周长最小,只需 |||'|AP PF +最小,如图,当A 、P 、F 三点共线时取到,故l 2||24(12)AF a =+=+. 三、解答题:(17)解:(Ⅰ)∵12z z =∴2sin sin 12cos cos A C A C =+----①,4a c +=----② --------------------------------2分由①得2(cos cos sin sin )1A C A C -=- 即1cos()cos()cos 2A CB B π+=-=-=-----------③ -----------------------------------4分∴1cos 2B =,∵0B π<< ∴EDB 1C 1A 1BCA3B π=-------------------------------------------------------------6分(Ⅱ) ∵22b =,由余弦定理得2222cos b a c ac B =+-⇒228a c ac +-=,--④-------------------------------------------------------------------------------8分由②得22216a c ac ++=------------⑤ 由④⑤得83ac =, -------------------------------------------------------------------------------------10分∴1sin 2ABC S ac B ∆==1832323⨯⨯=.-------------------------------------------------------12分 (18)解:(Ⅰ)连结ED ,----------------------------------------------------------------------------------1分∵平面AB 1C ∩平面A 1BD=ED ,B 1C ∥平面A 1BD , ∴B 1C ∥ED,----------------------------------------------------------------------------------------------3分 ∵E 为AB 1中点,∴D 为AC 中点,∵AB=BC , ∴BD ⊥AC ①, -------------------------------4分 法一:由A 1A ⊥平面ABC ,⊂BD 平面ABC ,得A 1A ⊥BD ②, 由①②及A 1A 、AC 是平面11ACC A 内的两条相交直线,得BD ⊥平面11ACC A .-------------------------------------------6分 【法二:由A 1A ⊥平面ABC ,A 1A ⊂平面11ACC A∴平面11ACC A ⊥平面ABC ,又平面11ACC A I 平面ABC=AC ,得BD ⊥平面11ACC A .】 (Ⅱ)由1AB =得BC=BB 1=1,由(Ⅰ)知AC DA 21=,又1=⋅DA AC 得22AC =,----------------------------------------8分∵2222BC AB AC +==,∴BC AB ⊥,---------------------------------------------------10分 ∴1122ABC S AB BC ∆=⋅= ∴11111113326A BCB ABC V S BB -∆=⋅=⨯⨯=.---------------------------------------------------------12分其它解法请参照给分.1701105(日泄流量)x1210901206030频率组距(19)解:(Ⅰ)在区间[30,60)的频率为73364156=------------------------------------------------1分 31==73070⨯频率组距,-------------------------2分 设在区间[0,30)上,a =频率组距, 则130)21011051701(=⨯+++a , 解得2101=a ,----------------------------------------3分 补充频率分布直方图如右;--------------------------5分(Ⅱ)当日泄流量X ≥30(万立方米)时,小型发电机可以运行,则一年中一台小型发电机可运 行的天数为:136430364312210-⨯⨯=(天);-----------------------------------------------------7分当日泄流量X ≥60(万立方米)时,中型发电机可以运行,则一年中一台中型发电机可运行 的天数为:11()30364156105210+⨯⨯=(天);------------------------------------------------------9分①若运行一台小型发电机,则一年的日均利润值为:11(312400052500)33573647⨯⨯-⨯=(或723500)(元)------------------------------10分②若运行一台中型发电机,则一年的日均利润值为:14(15610000208800)38283647⨯⨯-⨯=(或726800)(元)----------------------------11分 因为413828335777>,故为使水电站一年的日均利润值最大,应安装中型发电机.----12分 (20)解:(Ⅰ)由22=a c 得22222a c a b =-=,又22=b ,解得2=a ,故椭圆的标准方程为22142x y +=.--------------------------------------------------------------------4分(Ⅱ)设()()1122,,,M x y N x y ,则由2OP OM ON =+u u u r u u u u r u u u r,得0120122,2x x x y y y =+=+----------------------------------------------------------------------6分又点,M N 在椭圆22142x y +=上,∴2222112224,24x y x y +=+=设,OM ON k k 分别为直线,OM ON 的斜率,由题意知,212121-==⋅x x y y k k ON OM ,∴12122=0x x y y +,---------------------------------------------------8分222222000012122(2)2(2)4244x y x y x x y y ++++∴+=== 222211221212(2)4(2)4(2)20544x y x y x x y y ++++⋅+⋅==--------------------------------------11分 因此,存在常数5,λ=使得P点在椭圆22542x y +=上. ------------------------------------------12分 (21)解:(Ⅰ)由题意知:对∈∀x ],1[e e ,01)('≤+-=x e a x f x, 即xe a x ≥,对∈∀x ],1[e e恒成立,-----------------------------------------------------------------1分令2(1)(),()x xe x e g x g x x x -'==,当01x <<时,()0,g x '<当1x >时,()0,g x '>所以函数()g x 在)1,1[e上单调递减,在],1(e 上单调递增,----------3分由e e eg 11)1(+=,1)(-=e e e g ,ee e e 111+->,得区间],1[e e 上1max )(-=e e x g , 所以1-≥e e a . ------------------------------------------------------------------------------------------5分 (Ⅱ)解法1:1().xx x x xe a a e ax xf x e x xe e --'=-+==Q ----------------------------------------------6分 令2(1)(),()x xe x e g x g x x x -'==-------------------------------------------------------------------------7分且当01x <<时,()0,g x '<当1x >时,()0,g x '>所以函数()g x 在(0,1)单调递减,在(1,)+∞单调递增,-----------------------------------------8分min ()(1)g x g e ∴==,当a e ≤时,()g x a ≥恒成立,()0.f x '∴≥函数()f x 在区间(0,)+∞单调递增,()f x 无极值点----------------------------------------------9分当a e >时,min ()(1)g x g e a ==<,故存在1(0,1)x ∈和2(1,)x ∈+∞,使得12()()g x g x a == 当10x x <<时,()0,f x '>当12x x x <<时,()0,f x '<当2x x >时,()0,f x '>所以函数()f x 在12(,)x x 单调递减,在1(0,)x 和2(,)x +∞单调递增,所以1x 为函数()f x 的极大值点,2x 为函数()f x 的极小值点.--------------------------------11分综上可知:当a e ≤时,函数()f x 无极值点当a e >时,函数()f x 有两个极值点----------------------------------------------------------------12分【解法二:x x xe ax e x f -=)(')0(>x ,---------------------------------------------------------------------6分设ax e x h x -=)()0(>x ,则a e x h x -=)(',由0>x 得1>x e ,(1)当1≤a 时,0)('>x h ,)(x h 递增,1)0()(=>h x h ,得0)('>x f ,)(x f 递增,()f x 在区间(0,)+∞内无极值点;--------------------------------7分(2)当1>a 时,由0)('>-=a e x h x得a x ln >,可知)(x h 在)ln ,0(a 内递减,在),(ln ∞+a 内递增,所以)ln 1()(ln )(min a a a h x h -==, ①当e a ≤<1时,0)()(min ≥≥x h x h ,得0)('>x f ,)(x f 递增,()f x 在区间(0,)+∞内无极值点;--------------------------------9分②当e a >时,0)(min <x h ,又0)0(>h ,x 很大时0)(>x h ,所以存在∈1x )ln ,0(a ,),(ln 2∞+∈a x ,使得0)(1=x h ,0)(2=x h ,即0)('1=x f ,0)('2=x f ,可知在21,x x 两边)('x f 的符号相反,所以函数()f x 有两个极值点21,x x ,--------------------------------------------------------------11分综上可知:当a e ≤时,函数()f x 无极值点当a e >时,函数()f x 有两个极值点--------------------------------------------------------------12分】选做题:(22)解:(I )曲线C 的普通方程为222(1)(1)2x y ++-=,--------------------------------------2分由⎩⎨⎧==θρθρsin cos y x ,得22cos 2sin 20ρρθρθ+--=;---------------------------------------5分(II )解法1:联立αθ=和22cos 2sin 20ρρθρθ+--=,得22(cos sin )20ρραα+--=,------------------------------------------------------------------6分设),(1αρA 、),(2αρB ,则)4sin(22)cos (sin 221παααρρ-=-=+--------------8分由|2|||21ρρ+=OM , 得2|)4sin(|2||≤-=παOM ,---------------------------------9分当34πα=时,|OM |取最大值2.----------------------------------------------------------------10分【解法2:由(I )知曲线C 是以点P (1,1)-为圆心,以2为半径的圆,在直角坐标系中,直线l 的方程为x y ⋅=αtan ,则||PM =,---------------------------------------------------6分 ∵2222||||||2OM OP PM =-=-22tan 11tan αα=-+,-----------------------------8分 当(,)2παπ∈时,tan 0α<,21tan 2|tan |αα+≥,222|tan |||121tan OM αα=+≤+,当且仅当tan 1α=-,即34πα=时取等号,∴||OM ≤,即||OM 的最大值为2.-----------------------------------------------------------10分】(23)解:(I )当1a =时,不等式|()||()|3f x f x x +-≥即|1||1|3x x x -++≥当1x ≤-时,得113x x x ---≥0x ⇒≤,∴1x ≤------------------------------------------1分当11x -<<时,得113x x x -++≥23x ⇒≤,∴213x -<≤ -----------------------------2分当1x ≥时,得113x x x -++≥0x ⇒≤,与1x ≥矛盾,-------------------------------------3分综上得原不等式的解集为2{|1}{|1}3x x x x ≤--<≤U =2{|}3x x ≤------------------------5分 (II )|)1(||)(|22x x a x x f +-=+|||)1(|2x x a +-≤-----------------------------------------------6分∵1||≤a ,1||≤x∴2|()|f x x +||)1(||2x x a +-≤||12x x +-≤-------------------------------------------------7分4545)21|(|1||||22≤+--=++-=x x x , ----------------------------------------------------9分 当21||=x 时取“=”,得证. -----------------------------------------------------------------------10分。
2017届广东省揭阳市高三数学(文)一模试题答案
2017 届广东省揭阳市高三数学(文)一模试题答案一、选择题:共12 小题,每题 5 分,共 60 分.在每个小题给出的四个选项中,只有一项为哪一项切合题目要求的.1.已知会合 A={ ﹣1,0,1,2} ,会合 B={ y| y=2x﹣3,x∈A} ,则 A∩ B 中元素的个数为()A.1B.2C.3D.4【解答】解:由 A={ ﹣1,0,1,2} ,会合 B={ y| y=2x﹣3,x∈A} ={ ﹣5,﹣3,﹣1,1}所以 A∩B={ ﹣1,1} .所以 A∩B 中元素的个数为2.应选 B.2.已知点 A( 0, 1),B(3,2),向量,则向量=()A.(10, 7)B.(10,5)C.(﹣ 4,﹣ 3)D.(﹣ 4,﹣ 1)【解答】解:依据题意,点A(0,1),B(3,2),则向量=(3,1),又由,则向量= +=(﹣ 4,﹣ 3);应选: C.3.若直线 mx+2y+m=0 与直线 3mx+(m﹣1)y+7=0 平行,则 m 的值为()A.7B.0 或 7 C.0D.4【解答】解:∵直线 mx+2y+m=0 与直线 3mx+( m﹣1)y+7=0 平行,∴ m(m﹣1)=3m×2,∴ m=0 或 7,经查验都切合题意.应选: B.4 .已知命题 p : ? x , y ∈ R , sin ( x+y ) =sinx+siny ,命题,则以下判断正确的选项是()A.命题 p∨q 是假命题 B.命题 p∧q 是真命题C.命题 p∨(¬ q)是假命题D.命题 p∧(¬ q)是真命题【解答】解:令 x=0,y=,明显知足sin(x+y)=sinx+siny,故命题 p 是真命题;x∈[ 0,π] ,cosx=±,故命题 q 是假命题,故命题 p∧(¬ q)是真命题,应选: D.5.曲线与的交点横坐标所在区间为()A.B.C.D.【解答】解:方法一:分别画出与的图象,如下图,由图象可得交点横坐标所在区间为(,),方法二:设 f (x) =()x﹣x,∵ f() =()﹣<0,f()=()﹣()>0,∴f() f()< 0,依据函数零点存在定理可得点函数零点所在区间为(,),即交点横坐标所在区间为(,),应选: B6.阅读图的程序框图,运转相应的程序,当输入x 的值为﹣ 36 时,输出 x 的值为()A.0B.1C.3D.15【解答】解:当输入 x=﹣36 时,| x| >1,履行循环, x=6﹣2=4;| x| =4> 1,履行循环, x=2﹣ 2=0,| x| =0< 1,退出循环,输出的结果为 x=1﹣ 1=0.应选: A7.假如实数 x、 y 知足条件,那么2x﹣y的最大值为()A.2B.1C.﹣ 2 D.﹣ 3【解答】解:先依据拘束条件画出可行域,当直线 2x﹣y=t 过点 A(0,﹣ 1)时,t 最大是 1,应选 B.8.清朝有名数学家梅彀成在他的《增删算法统宗》中有这样一歌谣:“眺望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”其译文为:“远远看见 7 层高的古塔,每层塔点着的灯数,基层比上层成倍地增添,一共有381盏,请问塔尖几盏灯?”则按此塔各层灯盏的设置规律,从上往下数第 4 层的灯盏数应为()A.3B.12 C.24D.36【解答】解:依题意知,此塔各层的灯盏数组成公比q=2 的等比数列,且前7项和 S7=381,由,解得 a1,=3故.应选: C.9.连续掷两次骰子,以先后获得的点数m,n 为点 P 的坐标( m,n),那么点 P在圆 x2+y2=17 内部(不包含界限)的概率是()A.B.C.D.【解答】解:连续掷两次骰子,以先后获得的点数m,n 为点 P 的坐标( m,n),基本领件总数 N=6×6=36,点 P 在圆 x2+y2=17 内部(不包含界限)包含的基本领件有:(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),共 8个,∴点 P 在圆 x2+y2=17 内部(不包含界限)的概率是p= =.应选: D.10.某工件的三视图如下图,现将该工件经过切割,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工件的一个面内,则新工件的棱长为()A.B.1C.2D.【解答】解:依题意知该工件为圆锥,底面半径为,高为2,要使加工成的正方体新工件体积最大,则该正方体为圆锥的内接正方体,设棱长为 2x,则有,解得,故2x=1,即新工件棱长为1.应选 B..已知抛物线2+2x﹣a﹣1(a∈ R),恒过第三象限上必定点A,且点 A 在11y=ax直线 3mx+ny+1=0(m> 0, n> 0)上,则的最小值为()A.4B.12 C.24D.36【解答】解:抛物线 y=ax2+2x﹣a﹣1(a∈R),恒过第三象限上必定点A,∴A(﹣ 1,﹣ 3),∴,又===12,当且仅当 m=n 时等号成立.应选: B12.已知函数 f(x)=| sinx| (x∈[ ﹣π,π] ),g(x)为[ ﹣4,4] 上的奇函数,且,设方程f( f( x)) =0, f( g( x)) =0, g( g( x))=0的实根的个数分别为m、 n、 t,则 m n t=()+ +A.9B.13 C.17D.21【解答】解:因 x∈ [ ﹣π,π] ,所以函数 f( x)=| sinx| 的值域为 [ 0,1] ,函数 g(x)=的图象如图示,由图象知,其值域为 [ ﹣4,4] ,注意到方程 f (x) =0 的根为 0,﹣π,π,所以方程 f( f(x))=0 的根为方程 f (x)=0 或 f (x)=﹣π,f( x)=π的根,明显方程 f( x)=0 有 3 个实根,因﹣π,π?[ 0,1] ,所以 f(x)=﹣π,与 f( x)=π均无实根;所以方程 f( f(x))=0 的实根的个数为3,即 m=3;方程 f (g(x))=0 的实根为方程 g(x)=0 或 g(x)=﹣π,g(x)=π的根,方程 g(x)=﹣π,g(x)=π各有 3 个根,同时方程 g(x)=0 也有 3 个根,进而方程 f( g( x))=0 根的个数为 9,即 n=9;方程 g(x)=0 有三个实根﹣3、 0、3,方程 g(g(x)) =0 的实根为方程 g(x)=﹣3 或 g(x) =0 或 g(x) =3 的根,方程 g(x)=﹣3 或 g( x)=3 各有 3 个根,同时方程 g( x)=0 也有 3 个根,综上, m+n+t=3+9+9=21.应选: D.二、填空题:本大题共 4 小题,每题 5 分,共 20 分,请把正确的答案填写在答题卡相应的横线上.13.已知函数 f (x)=ax3+bx+1,若 f (a)=8,则 f (﹣ a)=﹣6.【解答】解:∵函数 f (x)=ax3+bx+1,∴f(﹣ x) =a(﹣ x)3+b(﹣ x) +1=﹣ax3﹣ bx+1,∴f(﹣ x) +f(x) =2,∴f(﹣ a) +f(a)=2.∵f(a)=8,∴f(a)=﹣6.故答案为﹣ 6.n *都有 an+1 n n+1 n8.14.已知数列 { a } 对随意的 n∈ N=a﹣2a a ,若,则 a =【解答】解:由 a n+1n﹣n+1 n 得,=a2a a故数列是,公差 d=2 的等差数列,,.故答案为:.15.已知△ ABC的极点都在球 O 的球面上, AB=6,BC=8,AC=10,三棱锥 O﹣ABC的体积为 40,则该球的表面积等于400π .【解答】解:依题意知△ ABC为直角三角形,其所在圆面的半径为,设三棱锥 O﹣ABC的高为 h,则由得h=5,设球 O 的半径为 R,则由 h2+52=R2,得 R=10,故该球的表面积为400π.故答案为 400π.16.已知双曲线右焦点为F,P为双曲线左支上一点,点,则△ APF周长的最小值为4(1+).【解答】解:由题意,点,△APF的周长l= AF AP PF= AF2a PF'AP APF的周长最小,只要|AP PF'| |+||+||| |++||+|| ,要△|+||最小,如图,当 A、P、F 三点共线时取到,故 l=.故答案为: 4(1+).三、解答题:解答应写出文字说明,证明过程或演算步骤.17.已知:复数 z1=2sinAsinC+(a+c)i,z2=1+2cosAcosC+4i,且 z1=z2,此中 A、B、C 为△ ABC的内角, a、 b、 c 为角 A、 B、 C 所对的边.(Ⅰ)求角 B 的大小;(Ⅱ)若,求△ ABC的面积.【解答】解:(Ⅰ)∵ z1=z2∴2sinAsinC=1+2cosAcosC﹣﹣﹣﹣①, a+c=4﹣﹣﹣﹣②,由①得 2( cosAcosC﹣ sinAsinC) =﹣1即,∴,∵ 0< B<π∴;(Ⅱ)∵,由余弦定理得b2 2c2﹣ 2accosB a2 c2﹣ac=8,﹣﹣④,=a +?+由②得 a2+c2+2ac=16﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣⑤由④⑤得,∴=.18.如图,在直三棱柱ABC﹣A1B1C1中, AB=BC=BB1,AB1∩A1B=E,D 为 AC 上的点, B1C∥平面 A1BD;(Ⅰ)求证: BD⊥平面 A1ACC1;(Ⅱ)若 AB=1,且 AC?AD=1,求三棱锥 A﹣ BCB1的体积.【解答】(Ⅰ)证明:连接 ED∵平面 AB1C∩平面 A1BD=ED, B1C∥平面 A1BD,∴B1C∥ ED,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣∵E 为 AB1中点,∴ D 为 AC中点,∵AB=BC,∴ BD⊥AC①,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣由 A1A⊥平面 ABC, BD? 平面 ABC,得 A1A⊥ BD②,由①②及 A1A、AC是平面 A1ACC1内的两条订交直线,得 BD⊥平面 A1ACC1.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(Ⅱ)解:由 AB=1 得 BC=BB1=1,由(Ⅰ)知,又AC?DA=1得AC2=2,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣222∵ AC=2=AB +BC,∴ AB⊥BC,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣∴∴.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣19.某地政府拟在该地一水库上建筑一座水电站,用泄流水量发电.图是依据该水库历年的日泄流量的水文资料画成的日泄流量X(单位:万立方米)的频次分布直方图(不完好),已知 X∈ [ 0,120),历年中日泄流量在区间 [ 30,60)的年均匀天数为 156,一年按 364 天计.(Ⅰ)请把频次散布直方图增补完好;(Ⅱ)已知一台小型发电机,需30 万立方米以上的日泄流量才能运转,运转一天可获收益为 4000 元,若不运转,则每日损失500 元;一台中型发电机,需60万立方米以上的日泄流量才能运转,运转一天可赢利10000 元,若不运转,则每天损失 800 元;依据历年日泄流量的水文资料,水电站决定安装一台发电机,为使一年的日均收益值最大,应安装哪一种发电机?【解答】解:(Ⅰ)在区间 [ 30, 60)的频次为,,设在区间 [ 0,30)上,,则,解得,增补频次散布直方图如右;(Ⅱ)当天泄流量 X≥30(万立方米)时,小型发电机能够运转,则一年中一台小型发电机可运行的天数为:(天);当天泄流量 X≥60(万立方米)时,中型发电机能够运转,则一年中一台中型发电机可运转的天数为:(天);①若运转一台小型发电机,则一年的日均收益值为:(或)(元)②若运转一台中型发电机,则一年的日均收益值为:(或)(元)由于,故为使水电站一年的日均收益值最大,应安装中型发电机.20.已知椭圆的离心率为,点M,N是椭圆C上的点,且直线 OM 与 ON 的斜率之积为﹣(Ⅰ)求椭圆 C 的方程;(Ⅱ)设动点 P(x0,y0)知足= +2,能否存在常数λ,使得P是椭圆上的点.【解答】解:(Ⅰ)∵椭圆的离心率为,∴ e=,解得,又 b2=2,解得 a=2,故椭圆的标准方程为=1.(Ⅱ)设 M (x ,y1),(,),则由=,1N x2y2得 x0=x1+2x2,y0=y1+2y2,又点 M,N 在椭圆=1 上,∴,,设 k OM,k ON分别为直线 OM,ON 的斜率,由题意知:k OM?k ON==﹣,∴ x1x2+2y1y2=0,∴=,所以,存在常数λ=5,使得P点在椭圆上.21.已知函数.(a∈R)(Ⅰ)若函数在区间上单一递减,务实数 a 的取值范围;(Ⅱ)试议论函数 f (x)在区间( 0,∞)内极值点的个数.+【解答】解:(Ⅰ)由题意可知:对 ? x∈,f ′(x)=﹣ +≤0,即 a≥,对 ? x∈恒成立,令 g(x) = ,求导 g′( x) =,当 0<x< 1 时, g′( x)< 0,当 x>1,g′(x)> 0,∴函数 g(x)在 [,1]上单一递减,在(1,e]上单一递加,∴ g()=,g(e)=e e﹣1,由 e e﹣1>,∴在区间上 g(x)max=e e﹣1,∴a≥ e e﹣1,(Ⅱ)解法 1:由 f ′( x) =﹣+ ==,g(x)=,g′(x)=,当 0<x< 1 时, g′( x)< 0,当 x>1 时, g′(x)> 0,∴函数 g(x)在( 0,1)单一递减,在( 1,+∞)单一递加,g(x)min=g(1)=e,当 a≤e 时, g(x)≥ a 恒成立, f (′ x)≥ 0,函数 f (x)在区间( 0,+∞)单一递加, f( x)无极值点,当 a>e 时, g(x)min≥g(1)=e<a,故存在 x1∈( 0,1)和 x2∈( 1,+∞),使得 g(x1) =g(x2)=a,当 0<x< x1,f (′x)> 0,当 x1<x<x2时, f ′(x)< 0,当 x> x2,f ′(x)> 0,∴函数 f(x)在( x1,x2)单一递减,在( 0, x1)和( x2,+∞),∴ x1为函数 f (x)的极大值点, x2为函数 f( x)的极小值点,综上可知; a≤ e 时,函数 f(x)无极值点,当 a>e 时,函数 f(x)有两个极值点.方法 2:f ′(x)=,设h(x)=e x﹣ax(x>0),则h(x)=e x﹣a,由x>0,e x> 1,(1)当 a≤1 时, h′(x)> 0,h(x)递加, h(x)> h(0)=1,则 f ′(x)> 0,f (x)递加, f(x)在区间( 0,+∞)内无极值;(2)当 a>1 时,由 h′( x) =e x﹣ a> 0,则 x>lna,可知 h(x)在( 0, lna)内递减,在( lna,+∞)单一递加,∴h( x)max=h( lna) =a(1﹣lna),①当 1<a≤e 时, h( x)> h(x)min≥0,则 f ′(x)> 0,f (x)单一递加, f(x)在区间( 0,+∞)内无极值;②当a>e 时, h(x)min<0,又 h(0)> 0,x 很大时, h(x)> 0,∴存在 x1∈( 0,lna), x2∈( lna,+∞),使得 h(x1)=0,h(x2)=0,即 f ′(x1)=0,f ′(x2)=0,可知在 x1,x1两边 f (′x)符号相反,∴函数 f(x)有两个极值点 x1, x2,综上可知; a≤ e 时,函数 f(x)无极值点,当 a>e 时,函数 f(x)有两个极值点.[ 选修 4-4:坐标系与参数方程 ]22.已知曲线 C 的参数方程为(θ为参数).以原点O为极点,x 轴的非负半轴为极轴成立极坐标方程.(1)求曲线 C 的极坐标方程;(2)若直线 l:θ=α(α∈[ 0,π),ρ∈R)与曲线 C 订交于 A, B 两点,设线段AB 的中点为 M,求 | OM| 的最大值.【解答】解:( I)曲线 C 的一般方程为( x+1)2+(y﹣ 1)2=4,由 x=ρcos,θy=ρsin,θ得ρ2+2ρcosθ﹣ 2ρsin﹣θ2=0.( II)联立θ=α和ρ2+2ρcosθ﹣2ρsin﹣θ2=0,得ρ2+2ρ(cosα﹣sin α)﹣ 2=0,设 A(ρ1,α),(ρ2,α),B则ρ,1+ρ2=2(cosα﹣sinα)=2由| OM| =,得| OM| =,当α=时,| OM| 取最大值.[ 选修 4-5:不等式选讲 ]23.设函数 f (x)=a(x﹣1).(Ⅰ)当 a=1 时,解不等式 | f(x)|+| f(﹣ x)| ≥3x;(Ⅱ)设 | a| ≤ 1,当 | x| ≤1 时,求证:.【解答】解:( I)当 a=1 时,不等式 | f(x)|+| f (﹣ x)| ≥3x 即| x﹣ 1|+| x+1|≥3x当 x≤﹣ 1 时,得 1﹣ x﹣ x﹣1≥3x? x≤ 0,∴ x≤﹣ 1﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣当﹣ 1<x< 1 时,得 1﹣x+x+1≥3x,∴﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣当 x≥1 时,得 x﹣1+x+1≥3x? x≤ 0,与 x≥1 矛盾,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣综上得原不等式的解集为=﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(II)证明: | f (x2)+x| =| a(x2﹣ 1) +x| ≤ | a( x2﹣ 1)|+| x| ﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣∵| a| ≤1, | x| ≤1∴ | f(x2)+x| ≤| a| (1﹣x2)+| x| ≤1﹣x2+| x| ﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣=,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣当时取“=,”得证.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣。
广东省揭阳一中、金山中学2017届高三上学期期中联考文数试卷及答案
广东省揭阳一中、汕头金山中学2017届高三上学期期中联考数学(文科)本试卷共4页,共23题,满分150分,考试时间为120分钟。
注意事项:1.答卷前,考生务必将自己的姓名、班级、座号写在答题卷密封线内。
2.非选择题必须用黑色字迹的铅笔或签字笔作答。
3.答案一律写在答题区域内,不准使用铅笔和涂改液,不按以上要求作答的答案无效。
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有 一项是符合题目要求的)1.若集合{}0≥=x x B ,且A B A = ,则集合A 可能是( )A.{}2,1 B.{}1≤x x C.{}1,0,1- D.R 2.复数iiz +=1的共轭复数在复平面上对应的点在( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 3.已知平面向量,a b 满足()5a a b ⋅+=,且2a =,1b =,则向量a 与b夹角的余弦值为( )A.23 B.23- C.21 D.21- 4.执行如图所示的程序框图,如输入的a 值为1,则输出的k 值为( )A.1B.2C.3D.45.在《张邱建算经》中有一道题:“今有女子不善织布,逐日所织的布同数递减,初日织五尺,末一日织一尺,计织三十日.”由此推断,该女子到第十日时,大约已经完成三十日织布总量的( ) A .33% B .49% C .62% D .88%6.某几何体的三视图如图所示,其中俯视图为扇形,则该几何体的体积为( )A.32πB.3πC.92πD.916π7.为了得到x y 2cos =,只需要将)32sin(π+=x y 作如下变换( )A.向右平移3π个单位 B.向右平移6π个单位 C.向左平移12π个单位 D.向右平移12π个单位8.若A 为不等式组⎪⎩⎪⎨⎧≤-≥≤200x y y x 表示的平面区域,则当a 从-2连续变化到1时,则直线a y x =+扫过A 中的那部分区域的面积为( ) A.1 B.32 C. 34 D. 749. 已知,A B 是球O 的球面上两点,60AOB ∠=︒,C 为该球面上的动点,若三棱锥O ABC -体积的最大值为O 的体积为( )A .81πB .128πC .144πD .288π10. 焦点在x 轴上的椭圆方程为)0(12222>>b a by a x =+,短轴的一个端点和两个焦点相连构成一个三角形,该三角形内切圆的半径为3b,则椭圆的离心率为( ) A.41 B.31 C.21 D.32则关于x 的方程(),()f x a a R =∈实根个 11.已知函数数不可能为( )A.2B.3C.4D.512.函数()sin(2)(,0)2f x A x A πθθ=+≤>部分图像如图所示,且0)()(==b f a f ,对不同的[]b a x x ,,21∈,若)()(21x f x f =,有3)(21=+x x f ,则( )A.)(x f 在)12,125(ππ-上是减函数B.)(x f 在)12,125(ππ-上是增函数C.)(x f 在)65,3(ππ上是减函数D.)(x f 在)65,3(ππ上是增函数()52log 1,(1)()(2)2,(1x x f x x x ⎧-⎪=⎨--+≥⎪⎩<)第II 卷(非选择题 共90分)二、填空题(本大题共4个小题,每小题5分,满分20分)13. 某单位有840名职工, 现采用系统抽样抽取42人做问卷调查, 将840人按1, 2, …, 840随机编号, 则抽取的42人中, 编号落入区间[481,720]的人数为 . 14.已知110,0,lg 2lg8lg 2,3x yx y x y>>+=+则的最小值是_______. 15.已知抛物线)0(22>p px y =上一点),1(m M 到其焦点的距离为5,双曲线122=-ay x 的左顶点为A ,若双曲线一条渐近线与直线AM 垂直,则实数a=_______.16.设函数x x x f 1)(2+=,x e x x g =)(,对任意),0(,21+∞∈x x ,不等式1)()(21+≤k x f k x g 恒成立,则正数k 的取值范围是________.三、解答题(本大题共6小题,共70分。
2017届广东省揭阳一中、金山中学高三三模联考文科数学试卷及答案 精品
2016—2017学年度两校三模联考数学科试题(文科)命题人:揭阳第一中学文科数学备课组本试卷共4页,21题,满分150分.考试时间为l20分钟. 注意事项:1.答卷前,考生务必将自己的姓名、班级、座号写在答题卷密封线内.2.非选择题必须用黑色字迹钢笔或签字笔作答.3. 答案一律写在答题区域内,不准使用铅笔和涂改液,不按以上要求作答的答案无效.一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.若复数2(32)(1)a a a i -++-是纯虚数,则实数a 的值为( )A. 1B. 2C. 1或 2D. -12.设集合{|A x y ==,{|2}x B y y ==,则A B = ( )A .02)(, B .[02], C .(1,2] D .02](, 3. 某校高三一班有学生54人,二班有学生42人,现在要用分层抽样的方法从两个班抽出16人参加军训表演,则一班和二班分别被抽取的人数是( )A. 8,8B. 10,6C. 9,7D. 12,44.已知()1,2=→a ,52=→b,且→a∥→b ,则b →为( )A.()2,4-B.()2,4C.()2,4-或()2,4-D.()2,4--或()2,45.“1k =”是“直线0x y k -+=与圆221x y +=相交”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分又不必要条件 6.一个算法的程序框图如图所示,该程序输出的结果为( ) A .89B .910 C .1011 D .11127.已知3x ≥,则11y x x=--的最小值为( ) A.2 B. 72C. 38.数列{}n a 的前n 项和为n S ,首项为a ,且21()n n n S a a n N +=-+∈.若实数x y ,满足100x y x y x a ⎧-+⎪+⎨⎪⎩,,,≥≥≤则2zx y =+的最小值是( )A .-1B .12C .5D .19.已知函数()f x 是定义在R 上的奇函数,且当(],0x ∈-∞时,2()x f x e ex a -=-+,则函数()f x 在1x =处的切线方程为( )A .0x y +=B .10ex y e -+-=C .10ex y e +--=D .0x y -=10.对于函数(),y f x x D =∈,若存在常数C ,对任意1x D ∈,存在唯一的2x D ∈C =,则称函数()f x 在D 上的几何平均数为C.已知(),[2,4]f x x D ==,则函数()f x 在D 上的几何平均数为正视图侧视图()A..3 C.2 D二.填空题:本大题共6小题,每小题5分,共30分,把答案填在答题卡相应横线上.(一)必做题(第11至13题为必做题,每道题目考生都必须作答.)11.在ABC∆中,a、b、c分别是角A、B、C所对的边,,13A a cπ===,则ABC∆的面积S= ______.12.椭圆2221(1)xy aa+=>上存在一点P,使得它对两个焦点1F,2F张角122F PFπ∠=13全面积为 .(二)选做题(14~15题,考生只能从中选做一题)14.(坐标系与参数方程)在极坐标中,已知点P()cos sin1ρθθ+=所表示的曲线上一动点⎪⎭⎫⎝⎛3,2πQ,则PQ的最小值为____________.15.(几何证明选讲)如图,以4AB=为直径的圆与△ABC的两边分别交于,E F两点,60ACB∠= ,则EF= .CAEF第15题三、解答题:本大题共6小题,共80分. 解答应写出必要的文字说明、证明过程或演算步骤. 16.(本小题满分12分)已知函数()sin()(0,0)f x x ωϕωϕπ=+><<的最小正周期为π,且函数()f x 的图象过点,12π⎛⎫- ⎪⎝⎭.(1)求ω和ϕ的值;(2)设()()()4g x f x f x π=+-,求函数()g x 的单调递增区间.17.(本小题满分12分)某校从参加高一年级期中考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[)50,40,[)60,50…[]100,90后得到如下部分频率分布直方图.观察图形的信息,回答下列问题: (1)求分数在[)70,80内的频率,并补全这个频率分布直方图;(2)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计本次考试的平均分;(3)用分层抽样的方法在分数段为[)80,60的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2人,求至多有1人在分数段[)80,70的概率.第17题18.(本小题满分14分)如图,在三棱柱111ABC A B C -中,AB AC ⊥,顶点1A 在底面ABC 上的射影恰为点B , 且12AB AC A B ===.(1)求证:11AC ⊥平面11AA B B ;(2)若P 为线段11B C 的中点,求四棱锥11P AA B B -的体积.19.(本小题满分14分)在等比数列{a n }中,)(0*N n a n ∈>,公比)1,0(∈q ,且252825351=++a a a a a a ,又a 3与a 5的等比中项为2.(1)求数列{a n }的通项公式;(2)设n n a b 2log =,求数列{b n }的前n 项和S n. (3)是否存在*,k N ∈使得1212n S S S k n+++< 对任意*n N ∈恒成立,若存在,求出k 的最小值,若不存在,请说明理由.20.(本小题满分14分)如图,抛物线21:8C y x =与双曲线22222:1(0,0)x y C a b a b-=>>有公共焦点2F ,点A 是曲线12,C C 在第一象限的交点,且25AF =.(1)求双曲线2C 的方程;(2)以1F 为圆心的圆M 与双曲线的一条渐近线相切, 圆N :22(2)1x y -+=.已知点(1P ,过点P 作互相垂 直且分别与圆M 、圆N 相交的直线1l 和2l ,设1l 被圆M 截 得的弦长为s ,2l 被圆N 截得的弦长为t . s t是否为定值? 请说明理由.21.(本小题满分14分)已知函数x x a x x f --+=2)ln()(在点0=x 处取得极值. (1)求实数a 的值;(2)若关于x 的方程b x x f +-=25)(在区间[0,2]上有两个不等实根,求b 的取值范围;(3)证明:对于任意的正整数n ,不等式211ln nn n n +<+.2013—2017学年度两校三模联考数学科 (文科)参考答案及评分说明一.选择题:BDCDA BBABA二.填空题:12. ,13.,三.解答题: 16.解:(1)由图可知222T ππωπ===,………………………………………………2分 又由()12f π=-得,sin(2)12πϕ⋅+=-,得sin 1ϕ=0ϕπ<<2πϕ∴=, …………4分(2)由(1)知:()sin(2)cos 22f x x x π=+= ………………………………6分因为()cos 2cos(2)cos 2sin 22g x x x x x π=+-=+)4x π=+ …………9分所以,222242k x k πππππ-≤+≤+,即3 (Z)88k x k k ππππ-≤≤+∈.………11分 故函数()g x 的单调增区间为3, (Z)88k k k ππππ⎡⎤-+∈⎢⎥⎣⎦.…12分17. 解:(1)分数在[)70,80内的频率为:1(0.0100.0150.0150.0250.005)10-++++⨯10.70.3=-=,故0.30.0310=,……2分 如图所示: ----4分(求频率2分,作图2分)(2)平均分为:450.1550.15650.15750.3850.25950.0571x =⨯+⨯+⨯+⨯+⨯+⨯=.------------6分(3)由题意,[)60,70分数段的人数为:0.15609⨯=人; ----------------7分[)70,80分数段的人数为:0.36018⨯=人; ----------------8分∵在[)80,60的学生中抽取一个容量为6的样本,∴[)60,70分数段抽取2人,分别记为,m n ;[)70,80分数段抽取4人,分别记为,,,a b c d ;设从样本中任取2人,至多有1人在分数段[)80,70为事件A ,则基本事件空间包含的基本事件有:(,)m n 、(,)m a 、(,)m b 、(,)m c 、(,)m d 、……、(,)c d 共15种, 则事件A 包含的基本事件有:(,)m n 、(,)m a 、(,)m b 、(,)m c 、(,)m d 、(,)n a 、(,)n b 、(,)n c 、(,)n d 共9种,---11分 ∴93()155P A ==. --------------------------------12分18.(1) 证明:1A B ⊥ 平面ABC , …………………1分 AC ⊂平面ABC ,1AC A B ∴⊥ …………………2分 又AC AB ⊥, ………………3分AB ⊂平面11AA B B , 1A B ⊂平面11AA B B ,1A B AB B = AC ∴⊥平面11AA B B …………5分又在三棱柱111ABC A B C -中,11AC AC // 11AC ∴⊥平面11AA B B …………6分(2)解:111224AA B B S AB AB =⨯=⨯= 平行四边形………………8分 取11A B 的中点R ,连结PR , 则11PR AC //,111PR A C 1==2………………10分 又11AC ⊥平面11AA B B ,PR ∴⊥平面11AA B B ………………12分 故点P到平面11AA B B的距离1d =,11111433P AA B B AA B B V S d -∴=⨯⨯=平行四边形…………………14分19. 解:(1)252,252255323825151=++∴=++a a a a a a a a a a ,又5,053=+∴>a a a n , …………………………………………2分又53a a 与的等比中项为2,453=∴a a , 而1,4,),1,0(5353==∴>∴∈a a a a q ,………3分n n n a a q --=⨯=∴==∴5112)21(16,16,21 , ……………………………5分(2)n a b n n -==5log 2, 11-=-∴+n n b b ,4}{1=∴b b n 是以为首项,-1为公差的等差数列. ……………7分(9)2n n n S -∴=, ……………9分 (3)由(2)知(9)9,22n n S n n n S n --=∴= 0,8>≤∴n S n n 时当;当0,9==n S n n 时;当0,9<>nS n n 时,.……………11分31289,18123n S S S S n n∴=++++= 当或时最大.…………………………13分故存在*,k N ∈使得1212n S S S k n+++< 对任意*n N ∈恒成立,k 的最小值为19.…14分20. 解:(1)∵抛物线21:8C y x =的焦点为2(2,0)F , ……………………………… 1分∴双曲线2C 的焦点为1(2,0)F -、2(2,0)F , …………………………… 2分设00(,)A x y 在抛物线21:8C y x =上,且25AF =, 由抛物线的定义得,025x +=,∴03x =, …………………………3分∴2083y =⨯,∴0y =±, ……………………… 4分∴1||7AF ==, …………………………5分又∵点A 在双曲线上,由双曲线定义得,2|75|2a =-=,∴1a =, ……… 6分∴双曲线的方程为:2213y x -=. ……………………………………… 7分(2)s t为定值.下面给出说明. …………………… 8分设圆M 的方程为:222(2)x y r ++=,双曲线的渐近线方程为:y =,∵圆M 与渐近线y =相切,∴圆M 的半径为2r == ………… 9分故圆M:22(2)3x y ++=, ………………………… 10分设1l 的方程为(1)y k x =-,即0kx y k -=,设2l 的方程为1(1)y x k=--,即10x ky +-=,∴点M 到直线1l 的距离为1d =,点N 到直线2l 的距离为2d =11分 ∴直线1l 被圆M截得的弦长s == ……… 12分 直线2l 被圆N截得的弦长t == ………… 13分∴s t ===,故st为定值…………… 14分21. 解:(1)()()()12x x a x a f x x a-+-+'=+由题意,()00f '= 解得1a = ………………………………2分(2)构造函数()[]()25()ln 10,22h x x x x x b x ⎛⎫=+----+∈ ⎪⎝⎭,则()()224545()2121x x x x h x x x --++-'==-++()()()45121x x x +-=+ 令 ()0h x '= 得 5114x x x =-=-=或或 又知[]0,2x ∈∴ 当01x ≤<时,函数()h x 单调递增,当12x <≤函数()h x 单调递减 方程5()2f x x b =-+在区间[]02,上有两个不同的实根,等价于函数()h x 在[]02,上有两个不同的零点,则只需 ()()()0031ln 21022ln 3430h b h b h b =-≤⎧⎪⎪=-+->⎨⎪⎪=-+-≤⎩ 即 01ln 22ln 31b b b ≥⎧⎪⎪<+⎨⎪≥-⎪⎩ ∴ 所求实数b的取值范围是1ln 31ln 22b -≤<+…………………6分 (3)构造函数()2()ln 1g x x x x =+--,则 ()23()1x x g x x -+'=+ 令 ()0g x '= 解得 302x x ==-或 …………8分 当 10x -<< 时 ()0g x '>,()g x 是增函数 当x > 时()0g x '<,()g x 是减函数 ……………………………10分∴ []()max ()00g x g == ∴ ()2ln 10x x x +--≤ 当0x ≠时,有 ()2ln 10x x x +--<取 1x n =,得 2111ln 10n n n⎛⎫⎛⎫+--< ⎪ ⎪⎝⎭⎝⎭ 即 211ln n n n n ++<.。
2017届广东省揭阳一中高三上学期第二次段考文科数学试题及答案
揭阳一中高三文科数学阶段考试2一、选择题:本大题共10小题,每小题5分,满分50分.1.复数z =i1+i在复平面上对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限2.已知全集U ={1,2,3,4,5,6},集合M ={2,3,5},N ={4,5},则∁U (M ∪N )等于( )A .{1,3,5}B .{2,4,6}C .{1,5}D .{1,6}3.设x R ∈,则“12x >”是“2210x x +->”的 ( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 4.点)1,2(-P 为圆25)3(22=+-y x 的弦的中点,则该弦所在直线的方程是( ) A x+y+1=0 B x+y -1=0 C x -y -1=0 D x -y+1=0 5.要得到函数cos(21)y x =+的图象,只要将函数cos 2y x =的图象( )A .向左平移1个单位B .向右平移1个单位C .向左平移12个单位 D .向右平移12个单位 6.如图是一个组合几何体的三视图,则该几何体的体积是 . A 36128π+ B 3616π+ C 72128π+ D 7216π+7.设变量,x y 满足约束条件⎪⎩⎪⎨⎧≤-≥+-≥-+01042022x y x y x ,则目标函数32z x y =-的最小值为( )A .5-B .4-C .2-D .38.若曲线2y x ax b =++在点(0,)b 处的切线方程是10x y -+=,则 ( ) A 1,1a b == B 1,1a b =-= C 1,1a b ==- D 1,1a b =-=-9.设=)(x f R x x x ∈+,3,当02πθ≤≤时,0)1()sin (>-+m f m f θ恒成立,则实数m 的取值范围是( )A .(0,1)B .)0,(-∞C .)21,(-∞ D .)1,(-∞10已知M 是△ABC 内的一点,且32=⋅AC AB ,︒=∠30BAC ,若MBC ∆,MCA ∆和△MAB 的面积分别yx ,,21,则y x 41+的最小值是 ( ) A 9 B 18 C 16 D 20二、填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分11.已知平面向量a =(1,2),b =(-2,m ),且a ∥b ,则m=12..动点P 到点(2,0)F 的距离与它到直线20x +=的距离相等,则P 的轨迹方程为13.已知等差数列{}n a 的前n 项和为55,5,15n S a S ==,则数列11n n a a +⎧⎫⎨⎬⎩⎭的前100项和为选做题:14、将参数方程12cos ,2sin ,x y θθ=+⎧⎨=⎩(θ为参数,],0[πθ∈)化成普通方程为 ______ .15、如图,圆O 是ABC ∆的外接圆,过点C 的切线交AB 的延长线于点D,3CD AB BC ===,则AC 的长为 .三、解答题:本大题共6小题,满分80分,解答须写出文字说明、证明过程和演算步骤.16. (本题满分12分)已知全体实数集R ,集合{(2)(3)0}.A x x x =+-<{0}B x x a =->集合 (1)若1a =时,求()R C A B ; (2)设A B ⊆,求实数a 的取值范围.17.(本小题满分12分)已知函数2()=sin (2+)+sin(2)+2cos 133f x x x x ππ--,x R ∈.(Ⅰ)求函数()f x 的最小正周期; (Ⅱ)求函数()f x 在区间[,]44ππ-上的最大值和最小值.18. (本小题满分14分)如图,四边形ABCD 为矩形,DA ⊥平面ABE ,2AE EB BC ===,BF ⊥平面ACE 于点F ,且点F 在CE 上. (Ⅰ)求证:DE BE ⊥;(Ⅱ)求四棱锥E ABCD -的体积;(Ⅲ)设点M 在线段AB 上,且AM MB =, 试在线段CE 上确定一点N ,使得//MN 平面DAE .19.(本小题满分14分)已知ABC ∆中,点A 、B的坐标分别为(B ,点C 在x 轴上方。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
揭阳市2017届高中三年级(第一学期)学业水平考试数学(文科)本试卷共4页,满分150分.考试用时120分钟.注意事项:1. 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分. 答题前,考生务必将自己的姓名、准考证号填写在答题卡上.2.回答第Ⅰ卷时,选出每个小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮搽干净后,再选涂其他答案标号,写在本试卷上无效.3. 回答第Ⅱ卷时,将答案写在答题卡上,答在本试题上无效.4. 考试结束,将本试题和答题卡一并交回.第Ⅰ卷一、选择题:共12小题,每小题5分,共60分.在每个小题给出的四个选项中,只有一项是符合题目要求的.(1)设集合{}Z k k x x M ∈+==,12,{}Z k k x x N ∈+==,2,则(A )N M =(B )N M ⊂(C )M N ⊂(D )φ=⋂N M(2)复数z 满足(1+i)z =i +2,则z 的虚部为(A )32 (B )12 (C )12- (D )12i - (3)设,a b R ∈,则“()20a b a -<”是“a b <”的(A )充分不必要条件 (B )必要不充分条件 (C )充分必要条件 (D )既不充分也不必要条件(4)已知等差数列{}n a 的前n 项和为n S ,且322315S S -=,则数列{}n a 的公差为(A )3 (B )4(C )5 (D )6(5)已知3cos 5α=,3(,2)2παπ∈,则cos()4πα-=(A )10 (B )10-(C )10 (D )10- (6)若空间四条直线a 、b 、c 、d ,两个平面α、β,满足b a ⊥,d c ⊥,α⊥a ,α⊥c ,则(A )α//b(B )b c ⊥(C )d b //(D )b 与d 是异面直线(7)对于任意的非零实数m ,直线2y x m =+与双曲线()0,012222>>=-b a by a x 有且只有一个交点,则双曲线的离心率为(A (B (C ) 2 (DM M M F F F E E E D D D (8)已知曲线ax x x f 2ln )(+=在点(1,(1))f 处的切线的倾斜角为34π,则a 的值为(A )1 (B )-4 (C )21-(D )-1 (9)阅读如图1所示的程序框图,运行相应程序,输出的结果是(A )242 (B )274(C )275 (D )338 图1(10) 函数],[|,|sin ππ-∈+=x x x y 的大致图象是(A ) (B ) (C ) (D ) (11)在ABC ∆中,有正弦定理:sin sin sin a b cA B C===定值,这个定值就是ABC ∆的外接圆的直径.如图2所示,DEF ∆中,已知DE DF =,点M 在直线EF 上从左到右运动(点M 不与E 、F 重合),对于M 的每一个位置,记DEM ∆的外接圆面积与DMF ∆的外接圆面积的比值为λ,那么(A )λ先变小再变大(B )仅当M 为线段EF 的中点时,λ取得最大值 (C )λ先变大再变小 (D )λ是一个定值图2(12)已知,a b R ∈、且2222290ab a b ++-=,若M 为22a b +的最小值,则约束条件0,.y x y M x y M ⎧≤≤⎪⎪-≥-⎨⎪+≤⎪⎩所确定的平面区域内整点(横坐标纵坐标均为整数的点)的个数为 (A )9(B )13(C )16 (D )18第Ⅱ卷本卷包括必考题和选考题两部分.第(13)题~第(21)题为必考题,每个试题考生都必须做答.第(22)题~第(23)题为选考题,考生根据要求做答.二、填空题:本大题共4小题,每小题5分,共20分,请把正确的答案填写在答题卡相应的横线上.(13)已知向量)1,1(-=a ,)2,(n b = ,若53a b ⋅= ,则n = .(14)偶函数()f x 的图象关于直线3x =对称,(4)4f =,则(2)f -= .(15)鲁班锁是中国传统的智力玩具,起源于古代汉族建筑中首创的榫卯结构,这种三维的拼插器具内部的凹凸部分(即榫卯结构) 啮合,十分巧妙,外观看是严丝合缝的十字立方体,其上下、左右、前后完全对称.从外表上看,六根等长的正四棱柱体分成三组, 图3 经90榫卯起来,如图3,若正四棱柱体的高为6,底面正方形的边长为1,现将该鲁班锁放进 一个球形容器内,则该球形容器的表面积的最小值为 .(容器壁的厚度忽略不计) (16)直线:42l x y +=与圆22:1C x y +=交于A 、B 两点,O 为坐标原点,若直线OA 、OB 的倾斜角分别为α、β,则cos cos αβ+= .三、解答题:解答应写出文字说明,证明过程或演算步骤.(17)(小题满分12分)已知递增数列{}n a 的前n 项和为n S ,且满足22n n S a n =+. (I )求n a ;(II )设12n n n b a +=⋅,求数列{}n b 的前n 项和n T .(18)(本小题满分12分)如图4,在四棱锥ABCD P -中,AD O ∈,AD ∥BC ,AB ⊥AD ,AO=AB=BC=1,3=PC . (I )证明:平面POC ⊥平面P AD ;(II )若P-ABD 与C-PBD 的体积分别为1V 、2V ,求证122V V =. 图4(19)(本小题满分12分)某次数学测验后,数学老师统计了本班学生对选做题的选做情况,得到如下表数据:(单位:人)(I )请完成题中的22⨯列联表;并根据表中的数据判断,是否有超过97.5%的把握认为选 做“坐标系与参数方程”或“不等式选讲”与性别有关?(II )经过多次测试后,甲同学发现自己解答一道“坐标系与参数方程”所用的时间为区间 [5,7]内一个随机值(单位:分钟),解答一道“不等式选讲”所用的时间为区间[6,8]内一个随机值(单位:分钟),试求甲在考试中选做“坐标系与参数方程”比选做“不等式选讲”所用时间更长的概率.附表及公式:()()()()()22n ad bc K a b c d a c b d -=++++(20)(本小题满分12分)已知圆C过点)0,43(A ,且与直线43:-=x l 相切, (I )求圆心C 的轨迹方程;(II ) O 为原点,圆心C 的轨迹上两点M 、N (不同于点O )满足0=⋅,已知13OP OM =,13OQ ON =,证明直线PQ 过定点,并求出该定点坐标和△APQ 面积的最小值.(21)(本小题满分12分)已知函数()(2)=-+x f x x e a .(a R ∈) (I )试确定函数()f x 的零点个数;(II )设12,x x 是函数()f x 的两个零点,证明:122x x +<. 参考公式:为常数)t e ex t xt ()'(---=请考生在第(22)、(23)题中任选一题作答,如果多做,则按所做的第一个题目计分. (22)(本小题满分10分)选修4-4:坐标系与参数方程已知直线l 的参数方程为⎩⎨⎧+=+-=ααsin 1cos 1t y t x (t 为参数).以O 为极点,x 轴的非负半轴为极轴建立极坐标系,曲线C 的极坐标方程为2cos +=θρρ.(I )写出直线l 经过的定点的直角坐标,并求曲线C 的普通方程; (II )若4πα=,求直线l 的极坐标方程,以及直线l 与曲线C 的交点的极坐标.(23)(本小题满分10分)选修4-5:不等式选讲设函数|2||1|)(--+=x m x x f . (I )若1m =,求函数)(x f 的值域;(II )若1m =-,求不等式x x f 3)(>的解集.B ,y 1)x数学(文科)参考答案(12)由2222290ab a b ++-=结合222ab a b ≤+得22223()93a b a b +≥⇒+≥(当且仅当a b =时等号成立)故3M =,在x 轴上整点有7个,在直线x=1上有5个,在x=2上有3个, 在x=3上有1个,共16个. (16)设1122(,),(,)A x y B x y ,由三角函数的定义得:12cos cos x x αβ+=+由2242,1.x y x y +=⎧⎨+=⎩消去y 得:2174120x x --=,则12417x x +=,即4cos cos 17αβ+=. 三、解答题:(17)解:(Ⅰ)当1n =时,21121S a =+,解得11a =;--------------------------------------------1分当2n ≥时,由22n n S a n =+,得21121n n S a n --=+-,两式相减,得()221121n n n n S S a a ---=-+,即()22110n n a a ---=,即11(1)(1)0n n n n a a a a --+---=∵数列{}n a 为递增数列,∴110n n a a -+-≠,∴11n n a a --=,------------------------------------------------------------------------------------------4分 ∴ 数列{}n a 是首项为1、公差为1的等差数列,故n a n =;---------------------------------6分 (Ⅱ)n n n b 2)1(+=,()n n n T 2123222 1⋅++⋅⋅⋅⋅⋅⋅+⋅+⋅=,n T = ()2312232212n n n n +⋅+⋅++⋅++⋅ ,-------------------------------------------8分两式相减,得-()()132212224+⋅+-+⋅⋅⋅+++=n n n n T()()1141241212n n n -+-=+-+⋅-12n n +=-⋅,------------------------------------------------------------------------11分 ,12+⋅=n n n T *n N ∈.-------------------------------------------------------12分(18)解:(Ⅰ)在四边形OABC 中,∵AO //BC ,AO =BC ,AB ⊥AD ,∴四边形OABC 是正方形,得OC ⊥AD ,-----------------------2分在△POC 中,∵222PC OC PO =+,∴OC ⊥PO ,-------4分又O AD PO = ,∴OC ⊥平面P AD ,又⊂OC 平面POC ,∴平面POC ⊥平面P AD ;-------------6分(Ⅱ)由(Ⅰ)知,四边形ABCO 为正方形,∴OC =AB =1, OC ⊥OD -----------8分∴1OD =,从而2AD =, -----------------------------------------------------9分 设点P 到平面ABCD 的距离为h ,∵平行线BC 与AD 之间的距离为1,∴2121121313121==⋅⋅==⋅⋅=BC AD BC AD S S h S h S V V BCD ABD BCD ABD △△△△-------------------------------------------11分即122V V =.---------------------------------------------------------------------------------------------12分其它解法请参照给分. (19)解:(1)22⨯3分由表中数据得()2250221288505.556 5.024*********K ⨯⨯-⨯==≈>⨯⨯⨯,查表可知,有超过97.5%的把握认为选做“坐标系与参数方程”或“不等式选讲”与性别有关;-----------------------------------------------------------------------------------------------------------------------6分 (2)设甲解答一道“坐标系与参数方程”需要x 分钟,解答一道“不等式选讲”需要y 分钟,-------------------------------------------------------------7分记“甲在考试中选做…坐标系与参数方程‟比选做…不等式选讲‟所用时间更长”为事件A , 则总的基本事件构成区域()57,68x x y y ⎧≤≤⎫⎧⎨⎨⎬≤≤⎩⎩⎭,--------------------------------------------------9分而满足事件A 的基本事件构成区域为(){}8675,≤≤≤≤>y x y x y x ,, , ----------10分即图中阴影部分,由几何概型知()11112228P A ⨯⨯==⨯,即甲在考试中选做“坐标系与参数方程”比选做 “不等式选讲”所用时间更长的概率为18.……………12分(20)解:(Ⅰ)法一:由已知得圆心C 的轨迹是以A 为焦点,l 为准线的抛物线,由432=p 得x px y 322==,得圆心C 的轨迹方程为x y 32=;-------------------------3分 【法二:设圆半径为R ,圆心C (x , y ),则|AC |=R =|)43(|--x ,即22)43(y x +-=|)43(|--x ,化简得x y 32=即圆心C 的轨迹方程为x y 32=------------------------------------------------------------------3分】 (Ⅱ)证明:依题意知OM 的斜率k 存在,且0≠k ,设OM 的方程为kx y =, ------------4分∵OM ⊥ON ,则ON 的方程为x k y 1-=, 由⎩⎨⎧==xy kx y 32得x x k 322=,得23kx M=,------------------------------------------------------6分 同理得23k x N =,由已知得21k x P =,2k x N =,∴)1,1(2k k P ,),(2k k Q -,----------------------------8分∴111222--=---=k k kk k k k PQ ,直线PQ 的方程为=+k y )(122k x k k ---, 即0)1()1(2=-+-y k x k ,∴直线PQ 过定点(1,0),---------------------------------10分设B (1,0),则|1|4121||||21k k y y AB S Q P APQ +⨯⨯=-⋅=∆41281|)||1(|81=⨯≥+=k k ,∴△APQ 面积的最小值为41.---------------------------------------------------------------------12分【证法二:设()()1122,,,M x y N x y ,MN 的方程为x ty m =+由23x ty m y x=+⎧⎨=⎩ 得2330y ty m --=,---------------------------------------------------------------------4分 则29120t m ∆=+>,且12123,3y y t y y m +=-=----------------------------------------------------5分 ∵0OM ON ⋅=,∴12120x x y y +=-----------------------------------------------------------------------6分 即221212109y y y y +=,解得129y y =-,所以39m -=-,解得3m =--------------------------- 7分 ∴MN 的方程为3x ty =+,则直线MN 过定点E ()3,0---------------------------------------------8分 设PQ 与x 轴相交于点F 11,33OP OM OQ ON ==,//PQ MN ∴31||||||||==OM OP OE OF ,可得1OF =,则()1,0F ,故PQ 过定点()1,0F -------------------------10分121111122434APQ P Q S AF y y y y ∴=-=⋅⋅⋅-=≥∴△APQ 面积的最小值为14.-------------------------------------12分】(21)解:(I )由0)(=x g 得(2)=-x a x e ,令()(2)=-xg x x e ,函数()f x 的零点个数即直线a y =与曲线()(2)=-x g x x e的交点个数,∵'()(2)(1)=-+-=-xxxg x e x e x e ,-------------2分 由'()0g x >得1x <,∴函数()g x 在(,1)-∞单调递增, 由'()0g x <得1x >,∴函数()g x 在(1,)+∞上单调递减,∴当1=x 时,函数()g x 有最大值,max ()(1)==g x g e ,----------------------------------------3分 又当2<x 时,()g x >0,(2)0=g ,当2>x 时()0<g x ,∴当>a e 时,函数()f x 没有零点;----------------------------------------------------------------4分当=a e 或0≤a 时,函数()f x 有一个零点;------------------------------------------------------5分 当0<<a e 时,函数()f x 有两个零点.------------------------------------------------------------6分 (II )证明:函数()f x 的零点即直线a y =与曲线()(2)=-x g x x e 的交点横坐标,不妨设12<x x ,由(I )知121,1<>x x ,得122<-x , ∵函数()(2)=-x g x x e 在(,1)-∞上单调递增,∴函数a x g x f +-=)()(在(,1)-∞单调递减,要证122x x +<,只需证212x x -<, ------------------------------------------------------------7分 ∴只需证)2()(21x f x f ->,又0)(1=x f ,即要证0)2(2<-x f ,---------------------8分 ∵由)(2x g a =得222222222(2)(2)---=-+=---x x x f x x ea x e x e ,(21>x )--------9分 令2()(2)-=---x x h x xe x e ,则2'()(1)()-=--x x h x x e e ,------------------------------10分当1>x 时,xx e e ->2,'()0<h x ,即函数()h x 在(1,)+∞上单调递减,∴()(1)0<=h x h , ∴当21>x 时,2(2)0-<f x ,即122x x +<.---------------------12分 【证法二:由(Ⅰ)知,0>a ,不妨设211x x <<,设-=)()(x f x F )1()2(>-x x f ,则x x xe e x x F -+-=2)2()(,-----------------------------8分))(1()('2x x e e x x F --=-,易知x x e e y -=-2是减函数,当x >1时,02=-<--e e e ex x,又1-x <0, 得0)('>x F , 所以)(x F 在),1(∞+递增,0)1()(=>F x F ,即)(x f >)2(x f -.---------------------------10分 由12>x 得)(2x f >)2(2x f -,又)(0)(12x f x f ==,所以)()2(12x f x f <-, 由()(2)=-x g x x e 在(,1)-∞上单调递增,得a x g x f +-=)()(在(,1)-∞单调递减,又122<-x ,∴122x x >-,即221<+x x ,得证. ---------------------------------------12分】 (22)解:(Ⅰ)直线l 经过定点)1,1(-,----------------------------------------------------------------2分 由2cos +=θρρ得22)2cos (+=θρρ,得曲线C 的普通方程为222)2(+=+x y x ,化简得442+=x y ;---5分(Ⅱ)若4πα=,得⎪⎪⎩⎪⎪⎨⎧+=+-=t y tx 221221,的普通方程为2+=x y , --------------------------------6分 则直线l 的极坐标方程为2cos sin +=θρθρ,------------------------------------------------8分 联立曲线C :2cos +=θρρ.得1sin =θ,取2πθ=,得2=ρ,所以直线l 与曲线C 的交点为)2,2(π. -----------10分(23)解:(Ⅰ)当1m =时,|2||1|)(--+=x x x f ------------------------------------------------1分∵3|)2()1(|||2||1||=--+≤--+x x x x , ------------------------------------------------3分 3|2||1|3≤--+≤-∴x x ,函数)(x f 的值域为]3,3[-;-------------------------------5分(Ⅱ)当m =-1时,不等式x x f 3)(>即x x x 3|2||1|>-++, ---------------------------------6分①当1-<x 时,得x x x 321>+---,解得51<x ,1-<∴x ;------------------------7分②当21<≤-x 时,得x x x 321>+-+,解得1<x ,11<≤-∴x ;------------------8分 ③当2≥x 时,得x x x 321>-++,解得1-<x ,所以无解;--------------------------- 9分 综上所述,原不等式的解集为)1,(-∞. --------------------------------------------------------10分。
