IPhO第届国际物理奥林匹克竞赛理论试题与解答
国际物理林匹克竞赛试题25th_IPhO_1994
THE EXAMINATIONXXV INTERNATIONAL PHYSICS OLYMPIADBEIJING, PERPLE’S REPUBLIC CHINATHEORETICAL COMPETITIONJuly 13, 1994Time available: 5 hoursREAD THIS FIRST!INSTRUCTIONS:1. Use only the ball pen provided.2. Your graphs should be drawn on the answer sheets attached to the problem.3. Your solutions should be written on the sheets of paper attached to the problems.4. Write at the top of the first page of each problem:●The total number of pages in your solution to the problem●Your name and code numberTheoretical Problem 1RELATIVISTIC PARTICLEIn the theory of special relativity the relation between energy E and momentum P or a free particle with rest mass m 0 is242022mc c m c p E =+=When such a particle is subject to a conservative force, the total energy of the particle, which is the sum of42022c m c p + and the potential energy, is conserved. Ifthe energy of the particle is very high, the rest energy of the particle can be ignored (such a particle is called an ultra relativistic particle).1) consider the one dimensional motion of a very high energy particle (in which rest energy can be neglected) subject to an attractive central force of constant magnitude f . Suppose the particle is located at the centre of force with initial momentum p 0 at time t =0. Describe the motion of the particle by separately plotting, for at least one period of the motion: x against time t , and momentum p against space coordinate x . Specify the coordinates of the “turning points ” in terms of given parameters p 0 and f . Indicate, with arrows, the direction of the progress of the mothon in the (p , x ) diagram. There may be short intervals of time during which the particle is not ultrarelativistic. However, these should be neglected.Use Answer Sheet 1.2) A meson is a particle made up of two quarks. The rest mass M of the meson is equal to the total energy of the two-quark system divided by c 2.Consider a one--dimensional model for a meson at rest, in which the two quarks are assumed to move along the x -axis and attract each other with a force of constant magnitude f It is assumed they can pass through each other freely. For analysis of the high energy motion of the quarks the rest mass of the quarks can be neglected. At time t=0 the two quarks are both at x =0. Show separately the motion of the two quarks graphically by a (x , t ) diagram and a (p , x ) diagram, specify the coordinates of the “turning points ” in terms of M and f , indicate the direction of the process in your (p , x ) diagram, and determine the maximum distance between the two quarks. Use Answer Sheet 2.3) The reference frame used in part 2 will be referred to as frame S , the Lab frame, referred to as S , moves in the negative x -direction with a constant velocity v =0.6c . the coordinates in the two reference frames are so chosen that the pointx =0 in S coincides with the point 0='x in S '' at time 0='=t t . Plot the motion of the two quarks graphically in a (x ', t ') diagram. Specify the coordinates of the turning points in terms of M , f and c , and determine the maximum distance between the two quarks observed in Lab frame S '. Use Answer Sheet 3.The coordinates of particle observed in reference frames S and S '' are related by the Lorentz transformation⎪⎩⎪⎨⎧+='+=')()(c x t t ct x x βγβγwhere c v /=β,21/1βγ-= and v is the velocity of frame S moving relative to the frame S ''.4) For a meson with rest energy Mc 2=140 MeV and velocity 0.60c relative to theLab frame S '', determine its energy E ' in the Lab Frame S ''.ANSWER SHEET 1 ANSWER SHEET 2 1)2)OOtOxptx 1, x 2Ox 1p 1 Ox 2p 2Quark1Quark2The maximum distance betweenthe two quarks is d =ANSWER SHEET 3 3)Theoretical Problem 1—Solution1) 1a. Taking the force center as the origin of the space coordinate x and the zero potential point, the potential energy of the particle is||)(x f x U =(1)The total energy is||42022x f c m c p W ++=.1b. Neglecting the rest energy, we get||||x f c p W +=,(2)Since W is conserved throughout the motion, so we havec p x f c p W 0||||=+=,(3)Let the x axis be in the direction of the initial momentum of the particle,cp fx pc c p fx pc c p fx pc cp fx pc 0000=--=-=+-=+⎪⎪⎭⎪⎪⎬⎫<<><<>>>.0,0;0,0;0,0;0,0p x p x p x p x (4)The maximum distance of the particle from the origin, let it be L , corresponds to p =0. It isf c p L /0=.1c. From Eq. 3 and Newton ’s law⎩⎨⎧<>-==;0,;0,x f x f F dt dp(5)we can get the speed of the particle asc dtdp f c dt dx ==, (6)tx 1′, x 2′OThe maximum distance between the two quarks observed in S ′frame is d ′=when when when wheni.e. the particle with very high energy always moves with the speed of light except that it is in the region extremely close to the points L x ±=. The time for the particle to move from origin to the point L x =, let it be denoted by τ, isf p c L //0==τ.So the particle moves to and for between L x = and L x -= with speed c and periodf p /440=τ. The relation between x and t is⎪⎪⎭⎪⎪⎬⎫≤≤-=≤≤-=≤≤-=≤≤=,43,4,32,2,2,20,τττττττt L ct x t ct L x t ct L x t ct x(7)The required answer is thus as given in Fig. 1 and Fig. 2.Fig. 12) The total energy of the two-quark system can be expressed as||||||21212x x f c p c p Mc -++=,(8)where 1x ,2x are the position coordinates and 1p , 2p are the momenta of quark 1 and quark 2 respectively. For the rest meson, the total momentum of the two quarks is zero and the two quarks move symmetrically in opposite directions, we have021=+=p p p , 21p p -=, 21x x -=.(9)Let p 0 denote the momentum of the quark 1 when it is at x =0, then we havec p Mc 022=or2/0Mc p =(10)From Eq. 8, 9 and 10, the half of the total energy can be expressed in terms of 1p and1x of quark 1:||||110x f c p c p +=,(11)just as though it is a one particle problem as in part 1 (Eq. 3) with initial momentumL= p 0/fc/f2/0Mc p =. From the answer in part 1 we get the (x , t ) diagram and (p , x ) diagram of the motion of quark 1 as shown in Figs. 3 and 4. For quark 2 the situation is similar except that the signs are reversed for both x and p ; its (x , t ) and (p , x ) diagrams are shown in Figs. 3 and 4.The maximum distance between the two quarks as seen from Fig. 3 isf Mc f c p L d //2220===. (12)Fig. 3Fig. 4a Quark1 Fig. 4bQuark23) The reference frame S moves with a constant velocity V =0.6c relative to the Lab frame S '' in the x ' axis direction, and the origins of the two frames are coincident at the beginning (0='=t t ). The Lorentz transformation between these two frames is given by:),/(),(c x t t ct x x βγβγ+='+='(13)where c V /=β, and 21/1βγ-=. With c V 6.0=, we have 5/3=β, and4/5=γ. Since the Lorenta transformation is linear, a straight line in the (x , t ) diagram2L=Mc 2/2fx 1: solid linetransforms into a straight line the (x ', t ') diagram, thus we need only to calculate the coordinates of the turning points in the frame S '.For quark 1, the coordinates of the turning points in the frames S and S ' are as follows:Frame SFrame S ' 1x 1t)(111ct x x βγ+=' )/(111e x t t βγ+=' 114345ct x +=c x t /434511+= 0 0 0L τL L 2)1(=+βγ ττβγ2)1(=+τ2L L 232=γβτγτ252=L - τ3 L L =-)13(βγττβγ3)3(=-0 τ4L L 34=γβτγτ54=where f Mc f c p L 2//20==, f Mc f p 2//0==τ.For quark 2, we have Frame SFrame S ' 2x 2t)(222ct x x βγ+=' )/(222c x t t βγ+=' 224345ct x +=c x t /434522+= 0 0 0L - τL L 21)1(-=--βγττβγ21)1(=-τ2 L L 232=γβτγτ252=L τ3 L L 27)13(=+βγττβγ29)3(=+τ4L L 34=γβτγτ54=With the above results, the (x ', t ') diagrams of the two quarks are shown in Fig. 5.The equations of the straight lines OA and OB are:t c t x '='')(1; ττβγ2)1(0=+≤'≤t ; (14a) t c t x '-='')(2;ττβγ21)1(0=-≤'≤t(14b)The distance between the two quarks attains its maximum d ' when τ21='t , thus wehave maximum distancefMc L c d 2)1(2)1(22=-=-='βγτβγ. (15)Fig. 54) It is given the meson moves with velocity V =0.6 crelative to the Lab frame, its energy measured in the Lab frame is1751408.01122=⨯=-='βMc E MeV . Grading SchemePart 1 2 points, distributed as follows:0.4 point for the shape of x (t ) in Fig. 1; 0.3 point for 4 equal intervals in Fig. 1; (0.3 for correct derivation of the formula only)0.1 each for the coordinates of the turning points A and C , 0.4 point in total; 0.4 point for the shape of p (x ) in fig. 2; (0.2 for correct derivation only)0.1 each for specification of 0p , f c p L /0=, 0p -, L - and arrows, 0.5 pointin total.(0.05 each for correct calculations of coordinate of turning points only).Part 2 4 points, distributed as follows:0.6 each for the shape of )(1t x and )(2t x , 1.2 points in total;0.1 each for the coordinates of the turning points A, B, D and E in Fig. 3, 0.8 pointin total;0.3 each for the shape of )(11x p and )(22x p , 0.6 point in total;0.1 each for 2/0Mc p =, f Mc L 2/2=, 0p -, L - and arrows in Fig. 4a andFig. 4b, 1 point in total; 0.4 point for f Mc d /2=Part 3 3 point, distributed as follows:0.8 each for the shape of )(1t x '' and )(2t x '', 1.6 points in total; 0.1 each for the coordinates of the turning points A, B, D and E in Fig. 5, 0.8 pointin total; (0.05 each for correct calculations of coordinate of turning points only).0.6 point for f Mc d 2/2='.Part 4 1 point (0.5 point for the calculation formula; 0.5 point for the numerical valueand units)Theoretical Problem 2SUPERCONDUCTING MAGNETSuper conducting magnets are widely used in laboratories. The most common form of super conducting magnets is a solenoid made of super conducting wire. The wonderful thing about a superconducting magnet is that it produces high magnetic fields without any energy dissipation due to Joule heating, since the electrical resistance of the superconducting wire becomes zero when the magnet is immersed in liquid helium at a temperature of 4.2 K. Usually, the magnet is provided with a specially designed superconducting switch, as shown in Fig. 1. The resistance r of the switch can be controlled: either r =0 in the superconducting state, or n r r = in the normal state. When the persistent mode, with a current circulating through the magnet and superconducting switch indefinitely. The persistent mode allows a steady magnetic field to be maintained for long periods with the external source cut off.The details of the superconducting switch are not given in Fig. 1. It is usually a small length of superconducting wire wrapped with a heater wire and suitably thermally insulated from the liquid helium bath. On being heated, the temperature of the superconducting wire increases and it reverts to the resistive normal state. The typical value of n r is a few ohms. Here we assume it to be 5Ω. The inductance of a superconducting magnet depends on its size; assume it be 10 H for the magnet in Fig. 1. The total current I can be changed by adjusting the resistance R . This problem will be graded by the plots only!The arrows denote the positive direction of I , I 1 and I 2.Fig. 11) If the total current I and the resistance r of the superconducting switch are controlledto vary with time in the way shown in Figs, 2a and 2b respectively, and assuming the currents I 1 and I 2 flowing through the magnet and the switch respectively are equal at the beginning (Fig. 2c and Fig. 2d), how do they vary with time from t 1 to t 4? Plot your answer in Fig. 2c and Fig. 2d2) Suppose the power switch K is turned on at time t =0 when r =0, I 1=0 and R =7.5Ω, and the total current I is 0.5A. With K kept closed, the resistance r of the superconducting switch is varied in he way shown in Fig. 3b. Plot the corresponding time dependences of I , I 1 and I 2in Figs. 3a, 3c and 3d respectively.3) Only small currents, less than 0.5A, are allowed to flow through theFig.2a2b 2c 2dFig. 3a3b 3c 3dsuperconducting switch when it is in the normal state, with larger currents the switch will be burnt out. Suppose the superconducting magnet is operated in a persistent mode, i. e. I =0, and I 1=i 1(e. g. 20A), I 2=-i 1, as shown in Fig. 4, from t =0 to t =3min. If the experiment is to be stopped by reducting the current through the magnet to zero, how would you do it? This has to be done in several operation steps. Plot the corresponding changes of I , r , I 1 and I 2in Fig. 44) Suppose the magnet is operated in a persistent mode with a persistent current of 20A (t =0 to t =3min. See Fig. 5). How would you change it to a persistent mode with acurrent of 30a? plot your answer in Fig. 5.Fig. 4a4b 4c 4dFig. 5a5b 5cTheoretical Problem 2—Solution 1) For t =t 1 to t 3Since 0=r , the voltage across the magnet dt LdI V M /1==0, therefore,011121)(I t I I ==; 01221I I I I I -=-=.For t =t 3 to t 4Since I 2=0 at t =t 3, and I is kept at 021I after3t t =, 02==n M r I V , therefore, 1I and 2I will not change.0121I I =; 02=IThese results are shown in Fig. 6.5dFig. 6a6b 6c 6d2) For 0=t to 1=t min: Since 0=r , 0/1==dt LdI V M0)0(11==I I5.012=-=I I I A.At 1=t min, r suddenly jumps from O to n r , I will drop from R E / to)/(n r R E + instantaneously, because 1I can not change abruptly due to the inductance of the magnet coil. For R E /=0.5A, Ω=5.7R and Ω=5n R . I will drop to 0.3A. For 1=t min to 2 min:I , 1I and 2I gradually approach their steady values:5.0==REI A, 5.01==I I A 02=I .The time constantnn Rr r R L )(+=τ. When 10=L H, Ω=5.7R and Ω=5n r , 3=τsec. For 2=t min to 3 min:Since 0=r , 1I and 2I will not change, that is5.01=I A and 02=IFig. 7a7b3) The operation steps are: First stepTurn on power switch K , and increase the total current I to 20 A, i. e. equal to 1I .Since the superconducting switch is in the state 0=r , so that L V M = 0/1=dt dI , that is, 1I can not change and 2I increases by 20A, in other words, 2I changes from 20- A to zero. Second stepSwitch r from 0 to n r . Third stepGradually reduce I to zero while keeping 5.02<I A: since n M r V I /2= anddt dI L V m /1=, when 10=L H, Ω=5n r , the requirement 5.02<I A corresponds to 25.0/1<dt dI A/sec, that is, a drop of <15A in 1 min. In Fig. 8 dt dI /～0.1A/sec and dt dI /1 is around this value too, so the requirement has been fulfilled. Final stepSwitch r to zero when 0=M V and turn off the power switch K . These resultsare shown in Fig. 8.7c 7dFig. 8a8b 8c4) First step and second step are the same as that in part 3, resulting in 02=I .Third step Increase I by 10 A to 30 A with a rate subject to the requirement5.02<I A. Fourth step Switch r to zero when 0=M V .Fifth step Reduce I to zero, 301=I A will not change because M V is zero.12I I I -= will change to 30- A. The current flowing through the magnet is thus closed by the superconducting switch. Final step Turn off the power switch K . The magnet is operating in the persistent mode.These results are shown in Fig. 9.Grading SchemePart 1,2 points:0.5 point for each of 1I , 2I from 1t t = to 3t and 1I , 2I from 3t t = to 4t .Part 2,3 points:0.3 point for each of 1I , 2I from 0=t to 1 min, I , 1I , 2I at 1=t min,8dFig. 9a9b 9c 9dand 0I , 1I , 2I from 1=t to 2 min;0.2 point for each of I , 1I , and 2I from 2=t to 3 min. Part 3, 2 points: 0.25 point for each section in Fig. 8 from 3=t to 9 min, 8 sections in total. Part 4,3 points:0.25 point for each section in Fig. 9 from 3=t to 12 min, 12 sections in total.Theoretical Problem 3COLLISION OF DISCS WITH SURFACE FRICTIONA homogeneous disc A of mass m and radius R A moves translationally on a smoothhorizontal x -y plane in the x direction with a velocity V (see the figure on the next page). The center of the disk is at a distance b from the x-axis. It collides with a stationary homogeneous disc B whose center is initially located at the origin of the coordinate system. The disc B has the same mass and the same thickness as A, but its radius is R B . It is assumed that the velocities of the discs at their point of contact, in the direction perpendicular to the line joining their centers, are equal after the collision. It is also assumed that the magnitudes of the relative velocities of the discs along the line joining their centers are the same before and after the collision.1) For such a collision determine the X and Y components of the velocities of the twodiscs after the collision, i. e. AXV ', AY V ', BX V ' and BY V ' in terms of m , A R , B R , V and b .2) Determine the kinetic energies A E ' for disc A and B E ' for disc B after the collision in terms of m , A R , B R , V and b .Theoretical Problem 3—Solution1) When disc A collides with disc B, let n be the unit vector along the normal to the surfaces at the point of contact and t be the tangential unit vector as shown in the figure. Let ϕ be the angle between n and the x axis. Then we haveϕsin )(B A R R b +=The momentum components of A and B along n and t before collision are:0,cos ==Bn An mV mV mV ϕ,0,sin ==Bt At mV mV mV ϕ.Denote the corresponding momentum components of A and B after collision byAnV m ', Bn V m ', At V m ', and Bt V m '. Let A ω and B ω be the angular velocities of A and B about the axes through their centers after collision, and A I and B I be their corresponding moments of intertia. Then,221A A mR I =,221B B mR I =The conservation of momentum givesBn AnV m V m mV '+'=ϕcos , (1) tn AtV m V m mV '+'=ϕsin ,(2)The conservation of angular momentum about the axis through O givesB B A A B A AtI I R R V m mVb ωω+++'=)( (3)The impulse of the friction force exerted on B during collision will cause amomentum change of AtV m ' along t and produces an angular momentum B B I ω simultaneously. They are related by.B B b BtI R V m ω=' (4)During the collision at the point of contact A and B acquires the same tangential velocities, so we haveB B Bt A A AtR V R V ωω-'=-' (5)It is given that the magnitudes of the relative velocities along the normal directionof the two discs before and after collision are equal, i. e.An BnV V V '-'=ϕcos . (6)From Eqs. 1 and 6 we get0='AnV , ϕcos V V Bn='. From Eqs. 2 to 5, we get ϕsin 65V V At=', ϕsin 61V V Bt=',A A R V 3sin ϕω=,BB R V 3sin ϕω=.The x and y components of the velocities after collision are:,)(65sin cos 22B A At An Ax R R Vb V V V +='+'='ϕϕ (7)222)(6)(5cos sin B A B A At An AyR R b R R Vb V V V +-+='+'-='ϕϕ, (8)⎥⎦⎤⎢⎣⎡+-='+'='22)(651sin cos B A Bt Bn Bx R R b V V V ϕϕ, (9)222)(6)(5cos sin B A B A Bt Bn By R R b R R Vb V V V +-+-='+'-='ϕϕ,(10)2) After the collision, the kinetic energy of disc A is222222)(8321)(21B A A A Ay Ax A R R b mV I V V m E +=+'+'='ω(11)while the kinetic energy of disc B is⎥⎦⎤⎢⎣⎡+-=+'+'='222222)(121112121)(21B A B B By Bx BR R b mV I V V m E ω (12)Grading Scheme1. After the collision, the velocity components of discs A and B are shown in Eq. 7, 8, 9 and 10 of the solution respectively. The total points of this part is 8. 0. If the result in which all four velocity components are correct has not been obtained, the point is marked according to the following rules.0.8 point for each correct velocity component;0.8 point for the correct description of that the magnitudes of the relative velocities of the discs along the line joining their centers are the same before and after the collision.0.8 point for the correct description of the conservation for angular momentum;0.8 point for the correct description of the equal tangential velocity at the touching point;0.8 point for the correct description of the relation between the impulse and the moment of the impulse.2. After the collision, the kinetic energies of disc A and disc B are shown in Eqs. 11 and 12 of the solution respectively.1.0 point for the correct kinetic energies of disc A;1.0 point for the correct kinetic energies of disc B;The total points of this part is 2.0XXV INTERNATIONAL PHYSICS OLYMPIADBEIJING, PEOPLE’S REPUBLIC OF CHINAPRACTICAL COMPETITIONJuly 15, 1994Time available: 2.5 hoursREAD THIS FIRST!INSTRUCTIONS:1. Use only the ball pen provided.2. Your graphs should be drawn on the answer sheets attached to the problem.3. Write your solution on the marked side of the paper only.4. The draft papers are provided for doing numerical calculations and draft drawings.5. Write at the top of every page:●The number of the problem●The number of the page of your report in each problem●The total number of pages in your report to the problem●Your name and code numberEXPERIMENTAL PROBLEM 1Determination of light reflectivity of a transparent dielectric surface.Experimental Apparatus1. He-Ne Laser(～1.5mW).The light from this laser is not linearly polarized.2. Two polarizers (P1, P2) with degree scale disk (Fig. 1), one (P1) has been mounted in front of the laser output window as a polarizer, and another one can be fixed in a proper place of the drawing board by push-pins when it is necessary.3. Two light intensity detectors (D1, D2) which consisted of a photocell and a microammeter (Fig. 2).4. Glass beam splitter(B).5. Transparent dielectric plate, whose reflectivity and refractive index are to be determined.6. Sample table mounted on a semicircular degree scale plate with a coaxial swivel arm(Fig. 3).7. Several push-.pins for fixing the sample table on the drawing board and as its rotation axis.8. Slit aperture and viewing screen for adjusting the laser beam in the horizontal direction and for alignment of optical elements.9. Lute for adhere of optical elements in a fixed place.10. Wooden drawing board.11. Plotting papersExperiment Requirement1. Determine the reflectivity of the p-component as a function of the incident angle(the electric field component, parallel to the plane of incidence is called the p-component).(a) Specify the transmission axis of the polarizer (A) by the position of the markedline on the degree scale disk in the p-componet measurement(the transmission axis is the direction of vibration of the electric field vector of the transmitted light).(b) Choose any one of the light intensity detector and set its micro-ammeter at therange of "×5". Verify the linear relation ship between the light intensity and the micro-ammeter reading. Draw the optical schematic diagram. Show your measured data and calculated results(including the calculation formula)in the farm of a table. Plot the linear relationship curve.(c) Determine the reflectivity of the p -component as a function of the incident angle. Draw the optical schematic diagram. Show your measured data and calculated reflectivity(including the calculation formula)in the form of a table. Plot the reflectivity as a function of the incident angle.2. Determine the refractive index of the sample as accurate as possible. Explanation and Suggestion1. Laser radiation avoid direct eye exposure.2. Since the output power of the laser beam may fluctuate from time to time, the fluctuation of light output has to be monitored during the performance of the experiment and a correction of the experimental results has to be made.3. The laser should be lighting all the time, even when you finish your experiment and leave the examination hall, the laser should be keeping in work.4. The reflected light is totally plane polarized at an incident angle B θ while tg B θn = (refractive index).Fig. 1 polarizers with degree scale diskFig. 2 Light intensity detector(1) Insert the plug of photocell into the “INPUT” socket of microammeter (2) Switching on the microammeter.(3) Blocd off the light entrance hole in front of the photocell and adjust the scale reading of micro ammeter to “0”.(4) Set the “Multiple” knob to a proper range.Fig.3 Sample table mounted on a semicircular degree scale plateExperimental Problem 1——Solution1. (a) Determine the transmission axis of the polarizer and the Brewster angle B θ ofthe sample by using the fact that the rerlectivity of the p -component 0=p R at the Brewster angle.Change the orientation of the transmission axis of 1P , specified by the position of the marked line on the degree scale disk (ψ) and the incident angle (i θ) successively until the related intensity 0=r I .Now the incident light consists of p -component only and the incident angle is B θ, thecorresponding values 1ψ and B θ are shown below:︒±︒=5.05.1401ψ or 322.3°±0.1°The Brewster angle B θ is 56.3°±0.1° 1. (b) Verification of the linear relationship between the light intensity and themicroammenter reading.The intensity the transmitted light passing through two polarized 1P and 2Pobeys Malus ’ lawθθ20cos )(I I =where 0I is the intensity of the light polarized by 1p and incident, I is the intensity of the transmitted light, and θ is the angle between the transmission axes of1P and 2p . Thus we can obtain light with various intensities for the verification by using two polarizers. The experimental arrangement is shown in the figure.The light intensity detector 1D serves to monitor the intensity fluctuation of theincident beam (the ratio of 1I to 2I remain unchanged), and 2D measures 2I . Let)(1θi and )(2θi be the readings of 1D and 2D respectively, and )(2θψ be the reading of the marked line position. 02=i when 90=θ°, the corresponding 2ψ is 2ψ(90°), and the value of θ corresponding to 2ψ is|90)90(|22︒±︒-=ψψθData and results;︒=︒4)90(2ψFrom the above data we can obtain the values of )(/)(2θθI I from the formula)0()0()()()(21120i i i i I I ⋅=θθθ and compare them with θ2cos for examining the linear relationship. The results obtained are:1. (c) Reflectivity measurementThe experimental arrangement shown below is used to determine the ratio of 0Ito 1I which is proportional to the ratio of the reading )(20i of 2D to the corresponding reading )(10i of 1D .Then used the experimental arrangement shown below to measure the relativityp R of the sample at various incident angle )(θ while the incident light consists of p -component only. Let )(1θi and )(2θi be the readings of 1D and 2Drespectively.Then the reflectivity is2010120)()()()(i i i i I I R p ⋅==θθθθ Data and results:Ai A i μμψ3.1358.195.14010201=⨯=︒=。
奥林匹克物理竞赛试题及答案
奥林匹克物理竞赛试题及答案国际奥林匹克物理竞赛是国际中学生的物理大赛，高中同学可以用来提升物理解题能力。
下面店铺给大家带来奥林匹克物理竞赛试题，希望对你有帮助。
奥林匹克物理竞赛试题国际物理奥林匹克竞赛简介竞赛设立由参赛成员国组成的国际物理奥林匹克委员会。
竞赛章程规定：目的是为增进中学物理教学的国际交流，通过竞赛促进开展物理学科的课外活动，以加强不同国家青年之间的友好关系和人民间的相互了解合作。
同时帮助参赛者发展物理方面的创造力，把从学校学到的知识用于解决实际问题的能力。
国际物理奥林匹克竞赛每年举办一次。
由各会员国轮流主办，并由各代表团团长和一名主办国指定的主席组成国际委员会。
国际委员会的任务是公平合理地评卷，监督章程规定的执行情况，决定竞赛结果。
每一会员国可选派5名高中学生或技术学校学生参加竞赛。
参加者的年龄到竞赛开始的那一天不能超过20岁。
参赛代表队要有2名团长，2名团长是国际委员会的成员，条件是能胜任解答赛题，能参加竞赛试卷的讨论和评分工作，并能通晓一种国际物理奥林匹克的工作语言。
国际物理奥林匹克的工作语言是英文、法文、德文和俄文。
代表团到达主办国时，团长要将参加学生及团长的情况告诉主办国家组织人员。
竞赛于每年6月底举行。
竞赛分两天进行。
第一天进行3道理论计算题竞赛，另一天的竞赛内容是1—2道实验题。
中间有一天的休息。
参赛者可使用计算尺、不带程序编制的计算器和对数表、物理常数表和制图工具，但不能使用数学和物理公式一览表。
竞赛题由参加国提供题目，主办国命题。
在竞赛前，赛题要保密。
竞赛题内容包括中学物理的4个部分(力学、热力学和分子物理学、光学及原子和核物理学、电磁学) ，解题要求用标准的中等数学而不要用高等数学。
主办国提出评卷标准并指定评卷人。
每题满分为10分。
各代表团团长同时对自己团员竞赛卷的复制品进行评定，最后协商决定成绩。
评奖标准是以参赛者前三名的平均分数计为100%，参赛者达90% 以上者为一等奖，78—90%者为二等奖，65—78%者为三等奖，同时发给证书。
国际物理奥林匹克竞赛试题.doc
国际物理奥林匹克竞赛试题理论试题题1A 某蹦迪运动员系在一根长弹性绳子的一端，绳的另一端固定在一座高桥上，他自静止高桥向下面的河流下落，末与水面相触，他的质量为m，绳子的自然长度为L，绳子的力常数（使绳子伸长lm所需的力）为k，重力场强度为g。
求出下面各量的表达式。
（a）运动员在第一次达到瞬时静止前所落下的距离y。
（b）他在下落过程中所达到的最大速率v。
（c）他在第一次达到瞬时静止前的下落过程所经历的时间t。
设运动员可以视为系于绳子一端的质点，与m相比绳子的质量可忽略不计，当绳子在伸长时服从胡克定律，在整个下落过程中空气的阻力可忽略不计。
B 一热机工作于两个相同材料的物体之间，两物体的温度分别为T A和T B（T A＞T B），每个物体的质量均为m，比热恒定，均为s。
设两个物体的压强保持不变，且不发生相变。
（a）假定热机能从系统获得理论上允许的最大机械能，求出两物体A和B最终达到的温度T?的表达式，给出解题全部过程。
（b）由此得出允许获得的最大功的表达式。
（c）假定热机工作于两箱水之间，每箱水的体积为2.50m3，一箱水的温度为350K，另一箱水的温度为300K。
计算可获得的最大机械能。
已知水的比热容= 4.19×103kg-1K-1，水的密度=1.00 x 103kgm.-3C 假定地球形成时同位素238U和235U已经存在，但不存在它们的衰变产物。
238U和235U的衰变被用来确定地球的年龄T。
（a）同位素238U以4.50×109年为半衰期衰变，衰变过程中其余放射性衰变产物的半衰期比这都短得多，作为一级近似，可忽略这些衰变产物的存在，衰变过程终止于铅的同位素206Ph。
用238U的半衰期、现在238U的数目238N表示出由放射衰变产生的206Pb原子的数目206n。
（运算中以109年为单位为宜）（b）类似地，235U在通过一系列较短半衰期产物后，以0.710×109年为半衰期衰变，终止于稳定的同位素207Pb。
物理奥赛初赛试题及答案
物理奥赛初赛试题及答案一、选择题（每题5分，共20分）1. 光在真空中的传播速度是：A. 3×10^8 m/sB. 3×10^5 m/sC. 3×10^6 m/sD. 3×10^7 m/s答案：A2. 根据牛顿第二定律，力和加速度的关系是：A. F = maB. F = ma^2C. F = m/aD. F = a/m答案：A3. 以下哪个选项是正确的能量守恒定律表述？A. 能量可以被创造B. 能量可以被消灭C. 能量既不能被创造也不能被消灭D. 能量可以在不同形式之间转换答案：C4. 根据库仑定律，两个点电荷之间的力与它们之间的距离的关系是：A. 与距离成正比B. 与距离成反比C. 与距离的平方成正比D. 与距离的平方成反比答案：D二、填空题（每题5分，共20分）5. 一个物体在水平面上以初速度v0开始滑行，摩擦系数为μ，滑行距离为s，则物体滑行时间t为______。
答案：t = v0 / (μg)6. 一个质量为m的物体从高度h自由落下，忽略空气阻力，其落地时的速度v为______。
答案：v = √(2gh)7. 一个电路中，电阻R、电流I和电压V之间的关系是______。
答案：V = IR8. 根据欧姆定律，电阻R、电流I和电压V之间的关系是______。
答案：I = V / R三、计算题（每题10分，共40分）9. 一辆汽车以恒定加速度a从静止开始加速，经过时间t后，汽车的速度v和位移s分别为多少？答案：v = ats = 1/2 * a * t^210. 一个质量为m的物体从高度h自由落下，求物体落地时的动能。
答案：动能 = 1/2 * m * v^2 = 1/2 * m * (2gh) = mgh11. 一个电阻R与一个电容C串联后接在电压为V的直流电源上，求电路达到稳态时的电流I。
答案：I = V / (R + 1/(C * ω))12. 一个质量为m的物体在弹簧的弹力作用下做简谐振动，弹簧的劲度系数为k，求物体的最大速度。
奥林匹克物理竞赛题
选择题：
一个物体在自由落体过程中，其动能与势能之和如何变化？
A. 逐渐增加
B. 逐渐减少
C. 保持不变（正确答案）
D. 无法确定
在一个完全弹性碰撞中，两个物体的总动能会如何变化？
A. 增加
B. 减少
C. 保持不变（正确答案）
D. 可能增加也可能减少
当一束光从空气射入水中时，其速度会如何变化？
A. 增加
B. 减少（正确答案）
C. 保持不变
D. 变为零
在一个电路中，如果电阻增加，那么电流会如何变化？
A. 增加
B. 减少（正确答案）
C. 保持不变
D. 变为零
一个物体在真空中自由下落，其加速度会如何？
A. 逐渐增大
B. 逐渐减小
C. 保持不变（正确答案）
D. 变为零
当一个物体受到与其运动方向相反的恒力作用时，其速度会如何变化？
A. 逐渐增大
B. 逐渐减小（正确答案）
C. 保持不变
D. 变为零后反向加速
在一个闭合电路中，如果电源电压增加，那么电路中的电流会如何变化？
A. 增加（正确答案）
B. 减少
C. 保持不变
D. 无法确定
当一束光线从玻璃射入空气时，其临界角是多大？
A. 0度
B. 45度
C. 90度（正确答案）
D. 取决于玻璃和空气的折射率
在一个简谐振动中，物体的动能和势能之和如何变化？
A. 逐渐增加
B. 逐渐减少
C. 保持不变（正确答案）
D. 周期性变化。
历届奥林匹克物理竞赛试题及解答
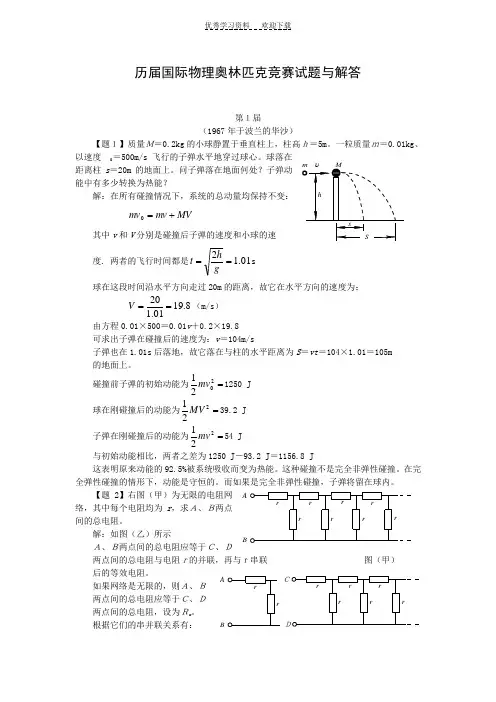
历届国际物理奥林匹克竞赛试题与解答第１届（1967年于波兰的华沙）【题１】质量Ｍ＝0.2kg 的小球静置于垂直柱上，柱高ｈ＝5m 。
一粒质量ｍ＝0.01kg 、以速度0＝500m/s 飞行的子弹水平地穿过球心。
球落在距离柱s ＝20m 的地面上。
问子弹落在地面何处？子弹动能中有多少转换为热能？解：在所有碰撞情况下，系统的总动量均保持不变：MV mv mv +=0其中v 和V 分别是碰撞后子弹的速度和小球的速 度. 两者的飞行时间都是01.12==ght s 球在这段时间沿水平方向走过20m 的距离，故它在水平方向的速度为：8.1901.120==V （m/s ） 由方程0.01×500＝0.01v ＋0.2×19.8 可求出子弹在碰撞后的速度为：v ＝104m/s子弹也在1.01s 后落地，故它落在与柱的水平距离为S ＝vt ＝104×1.01＝105m 的地面上。
碰撞前子弹的初始动能为=2021mv 1250 J 球在刚碰撞后的动能为=221MV 39.2 J 子弹在刚碰撞后的动能为=221mv 54 J与初始动能相比，两者之差为1250 J －93.2 J ＝1156.8 J这表明原来动能的92.5%被系统吸收而变为热能。
这种碰撞不是完全非弹性碰撞。
在完全弹性碰撞的情形下，动能是守恒的。
而如果是完全非弹性碰撞，子弹将留在球内。
【题2】右图（甲）为无限的电阻网络，其中每个电阻均为r ，求Ａ、Ｂ两点间的总电阻。
解：如图（乙）所示Ａ、Ｂ两点间的总电阻应等于Ｃ、Ｄ两点间的总电阻与电阻ｒ的并联，再与ｒ串联 图（甲） 后的等效电阻。
如果网络是无限的，则Ａ、Ｂ两点间的总电阻应等于Ｃ、Ｄ 两点间的总电阻，设为Ｒx 。
根据它们的串并联关系有：m M h SsυABr r r r r r r rA B r r r r r r r r ＣＤrR rR r R x xx ++= 图（乙） 解上式可得： r R x 251+=【题3】给定两个同样的球，其一放在水平面上，另一个以细线悬挂。
物理竞赛初赛试题及答案
物理竞赛初赛试题及答案一、选择题（每题4分，共40分）1. 光在真空中的传播速度是（）。
A. 299,792,458 m/sB. 299,792,458 km/hC. 299,792,458 m/hD. 299,792,458 km/s答案：A2. 牛顿第二定律的表达式是（）。
A. F = maB. F = mvC. F = m/aD. F = ma^2答案：A3. 根据热力学第一定律，系统内能的增加量等于（）。
A. 系统吸收的热量B. 系统对外做的功C. 系统吸收的热量减去对外做的功D. 系统吸收的热量加上对外做的功答案：D4. 一个物体在水平面上受到一个恒定的力，使其做匀加速直线运动。
若力的大小为10N，物体的质量为2kg，那么物体的加速度是（）。
A. 5 m/s^2B. 10 m/s^2C. 20 m/s^2D. 4 m/s^2答案：A5. 电磁波的波速在真空中是（）。
A. 299,792,458 m/sB. 300,000,000 m/sC. 3.00 x 10^8 m/sD. 3.00 x 10^5 km/s答案：C6. 一个电阻为10Ω的电阻器，通过它的电流为2A，那么电阻两端的电压是（）。
A. 20VB. 10VC. 5VD. 4V答案：A7. 根据欧姆定律，电流I与电压V和电阻R之间的关系是（）。
A. I = V/RB. I = VRC. I = V + RD. I = V - R答案：A8. 一个物体从静止开始自由下落，忽略空气阻力，其下落的加速度是（）。
A. 9.8 m/s^2B. 10 m/s^2C. 9.7 m/s^2D. 10.1 m/s^2答案：A9. 根据能量守恒定律，一个物体的动能和势能之和在没有外力作用下是（）。
A. 增加B. 减少C. 保持不变D. 无法确定答案：C10. 一个物体在水平面上受到一个恒定的力，使其做匀速直线运动。
若力的大小为10N，物体的质量为2kg，那么物体的加速度是（）。
历届IPho试题-历届IPho试题-IPhO-37ThCovermand
第37届国际奥林匹克物理竞赛
理论考试
（2006年7月10日，星期一，新加坡）
考试须知:
1.本场考试时间为5小时。
共有3题，每题10分。
2.只能使用考场所提供的笔。
3.只能使用考场所提供的纸张的正面。
4.不同的题目不要在同一张演算纸(Writing Sheets)上解答。
5.请在答卷纸(Answer Script)上答题。
另外还提供演算纸(Writing Sheets)。
根据
题中给出的数据，数值答案请保留正确的有效位数。
不要忘记写物理单位。
6.在演算纸上，写下解题所必需的步骤、内容，并标明希望考官批改的部分。
书
写时，希望用尽可能少的文字，只需提供公式、数值、符号和图表等。
7.请务必在所使用的每张答卷纸和演算纸上指定的方框内，填上国家号和学生
号；在所使用的每张演算纸上，填上题号、演算纸页码号和每题所使用的演算纸总数，以便考官批改。
此外，你可将题号和小题号写在空白纸张的顶部。
如果你不希望某张演算纸上的草稿被批改，请在不要的纸上画一个大叉，且不要把它算在演算纸的总页数内，亦不要编写页码。
8.考试结束时，请将所有答卷纸和演算纸按顺序整理，即每题答卷纸在前，希望
批改的演算纸随后，不希望批改的演算纸其次，未使用的纸张和印刷的考题放在最后。
将所有纸张按题号顺序放置，用所提供的夹子把它们夹好，留在桌面上。
不得把所提供的任何纸张携带出考场。
历届国际物理奥林匹克竞赛试题与解答
历届国际物理奥林匹克竞赛试题与解答第8届（1975年于德意志民主共和国的居斯特罗）【题1】一根杆以恒定的角速度ω绕竖直轴旋转，杆与轴的夹角为（900－α）。
质量为m 的质点可以沿杆滑动，摩擦系数为μ 。
求转动过程中，质点保持在同一高度的条件（如图8.1）。
解：我们发现，采用所谓“滑动摩擦角”概念是有用的。
如果滑动摩擦系数等于某一角度的正切值，就称这个角ε为“滑动摩擦角”（如解图8.1所示），即tan ε＝μ我们必须求出把物体压向平台的合力。
如果合力与平面法线之间的夹角在滑动摩擦角之内，则摩擦力大到足以阻止运动。
极限情形是合力与摩擦角的一臂重合。
对于本题，当我们寻找质点在旋转杆上向上滑动的极限情况时，合力应位于（α＋ε）角的双臂内（如解图8.2所示）。
图8.1ε解图8.1 解图8.2把质点压在杆上的力是重力mg 与m ω2r ＝m ω2L cos α的合力。
故质点在向上滑动的极限情形下，角（α＋ε）的正切为gL mg L m αωαωεαcos cos )tan(22==+ 同理，质点向下滑动的极限情形可用角（α＋ε）的正切得到。
于是，如果)tan(cos )tan(2εααωεα+≤≤g L －则质点在旋转杆上处于平衡。
从边界条件可以看出，存在着一个较高位置（L f ）和一个较低位置（L a ），质点在这两位置之间的任何地方将处于随遇解图8.3平衡状态。
在这两边界之外，质点无法平衡，质点将向上或向下滑动。
随遇平衡位置L f －L a 可由边界条件导出：)tan tan 1(cos tan 22232εααωε⋅-=-g L L a f 解图8.3对不同的α角，画出质点在杆上哪些部分处于随遇平衡，（取ω＝10 s -1，μ＝0.268，ε＝150）。
虚线表示无摩擦时质点非稳定平衡位置。
【题2】求出厚透镜对两个不同波长有同一焦距的条件，并就不同类型的透镜讨论可行性。
解答：我们必须知道厚透镜的性质。
历届国际物理奥林匹克竞赛试题与解答
历届国际物理奥林匹克竞赛试题与解答第６届（1972年于罗马尼亚的布加勒斯特）【题１】给定三个圆柱，它们的长度、外径和质量均相同。
第一个是实心圆柱；第二个是空心圆筒，壁有一定厚度；第三个是同样壁厚的圆筒，但两端用薄片封闭，里面充满一种密度与筒壁相同的液体。
如将它们放在倾角α为的斜面上，如图6.1所示，求出并比较这些圆柱的线加速度。
研究光滑滚动与又滚又滑两种情况。
圆柱与斜面的摩擦系数为μ，液体与筒壁之间的摩擦可以忽略。
解：沿斜面方向作用在圆柱上的力是：作用于质心重力的分量mg sin 和作用于接触点的摩擦力S ，如图6.1所示。
产生的加速度a ：ma ＝mg sin －S 纯滚动时的角加速度为： R a ＝β 转动的运动方程为： I Ra RS = 以上方程组的解为： 21sin mR I g a +=α221sin mR I mR Img S +⋅=α （１）当S 达到最大可能值μmg cos 时，也就到了纯滚动的极限情形，这时：221sin cos mR I mR I mg mg h h +=ααμ即维持纯滚动的极限条件为)1(tan 2ImR h +=μα （２） 下面我们来研究三个圆柱体的纯滚动情形。
（Ⅰ）实心圆柱的转动惯量为221mR I =从（１）式和（２）式分别得到 αsin 32g a =， tan a h ＝３μ ααmg sin S R角加速度为：β＝Ra （Ⅱ）设空心圆筒壁的密度是实心圆柱密度的n 倍。
因已知圆柱的质量是相等的，故可以算出圆筒空腔的半径r ：)(222r R L n L R -=ρπρπ 即nn R r 122-= 转动惯量为：nn mR r LR n R LR n I 125.05.05.022222-=⋅-⋅=ρπρπ 由（１）式和（２）式分别算出： αsin 142g n n a -=， μα1214tan --=n n h 角加速度为：β＝Ra （Ⅲ）对充满液体的圆筒，因液体与筒壁之间无摩擦力，故液体不转动。
历届奥林匹克物理竞赛试题及解答
历届国际物理奥林匹克竞赛试题与解答第１届（1967 年于波兰的华沙）【题１】质量Ｍ＝0.2kg 的小球静置于垂直柱上，柱高ｈ＝5m。
一粒质量ｍ＝0.01kg 、以速度距离柱0＝500m/s 飞行的子弹水平地穿过球心。
球落在s＝20m 的地面上。
问子弹落在地面何处？子弹动m M能中有多少转换为热能？解：在所有碰撞情况下，系统的总动量均保持不变：hmv0mv MVs 其中v 和V 分别是碰撞后子弹的速度和小球的速S2h g 1.01s度. 两者的飞行时间都是t球在这段时间沿水平方向走过20m的距离，故它在水平方向的速度为：201.01V 19.8 （m/s）由方程0.01 ×500＝0.01 v＋0.2 ×19.8可求出子弹在碰撞后的速度为：v＝104m/s子弹也在 1.01s 后落地，故它落在与柱的水平距离为的地面上。
S＝vt ＝104×1.01 ＝105m1 22碰撞前子弹的初始动能为mv 1250 J1MV 2球在刚碰撞后的动能为39.2 J21mv2子弹在刚碰撞后的动能为54 J2与初始动能相比，两者之差为1250 J －93.2 J ＝1156.8 J这表明原来动能的92.5%被系统吸收而变为热能。
这种碰撞不是完全非弹性碰撞。
在完全弹性碰撞的情形下，动能是守恒的。
而如果是完全非弹性碰撞，子弹将留在球内。
【题2】右图（甲）为无限的电阻网 Arr r rr ，求Ａ、Ｂ两点络，其中每个电阻均为间的总电阻。
解：如图（乙）所示rr rrBＡ、Ｂ两点间的总电阻应等于Ｃ、Ｄｒ的并联，再与ｒ串联两点间的总电阻与电阻后的等效电阻。
如果网络是无限的，则两点间的总电阻应等于两点间的总电阻，设为图（甲）ＣA Ａ、ＢＣ、ＤＲx。
rr rrrr rrＤ根据它们的串并联关系有： BrR x R x R xr图（乙）r1 5R xr解上式可得：2 【题 3】给定两个同样的球，其一放在水平面上，另一个以细线悬挂。
国际物理林匹克竞赛试题ipho-Problems-of-2nd-and-9th-IPhO
Problems of the 2nd and 9th International Physics Olympiads (Budapest, Hungary, 1968 and 1976)Péter VankóInstitute of Physics, Budapest University of Technical Engineering, Budapest,HungaryAbstractAfter a short introduction the problems of the 2nd and the 9th International Physics Olympiad, organized in Budapest, Hungary, 1968 and 1976, and their solutions are presented.IntroductionFollowing the initiative of Dr. Waldemar Gorzkowski [1] I present the problems and solutions of the 2nd and the 9th International Physics Olympiad, organized by Hungary. I have used Prof. R ezső Kunfalvi’s problem collection [2], its Hungarian version [3] and in the case of the 9th Olympiad the original Hungarian problem sheet given to the students (my own copy). Besides the digitalization of the text, the equations and the figures it has been made only small corrections where it was needed (type mistakes, small grammatical changes). I omitted old units, where both old and SI units were given, and converted them into SI units, where it was necessary.If we compare the problem sheets of the early Olympiads with the last ones, we can realize at once the difference in length. It is not so easy to judge the difficulty of the problems, but the solutions are surely much shorter.The problems of the 2nd Olympiad followed the more than hundred years tradition of physics competitions in Hungary. The tasks of the most important Hungarian theoretical physics competition (Eötvös Competition), for example, are always very short. Sometimes the solution is only a few lines, too, but to find the idea for this solution is rather difficult.Of the 9th Olympiad I have personal memories; I was the youngest member of the Hungarian team. The problems of this Olympiad were collected and partly invented by Miklós Vermes, a legendary and famous Hungarian secondary school physics teacher. In the first problem only the detailed investigation of the stability was unusual, in the second problem one could forget to subtract the work of the atmospheric pressure, but the fully “open” third problem was really unexpected for us.The experimental problem was difficult in the same way: in contrast to the Olympiads of today we got no instructions how to measure. (In the last years the only similarly open experimental problem was the investigation of “The magnetic puck” in Leicester, 2000, a really nice problem by Cyril Isenberg.) The challenge was not to perform many-many measurements in a short time, but to find out what to measure and how to do it.Of course, the evaluating of such open problems is very difficult, especially for several hundred students. But in the 9th Olympiad, for example, only ten countries participated and the same person could read, compare, grade and mark all of the solutions.2nd IPhO (Budapest, 1968)Theoretical problemsProblem 1On an inclined plane of 30° a block, mass m 2 = 4 kg, is joined by a light cord to a solid cylinder, mass m 1 = 8 kg, radius r = 5 cm (Fig. 1). Find the acceleration if the bodies are released. The coefficient of friction between the block and the inclined plane μ = 0.2. Friction at the bearing and rolling friction are negligible.SolutionIf the cord is stressed the cylinder and the block are moving with the same acceleration a . Let F be the tension in the cord, S the frictional force between the cylinder and the inclined plane (Fig. 2). The angular acceleration of the cylinder is a /r . The net force causing the acceleration of the block:F g m g m a m +-=αμαcos sin 222, and the net force causing the acceleration of the cylinder:F S g m a m --=αsin 11.The equation of motion for the rotation of the cylinder:I ra r S ⋅=.(I is the moment of inertia of the cylinder, S ⋅r is the torque of the frictional force.) Solving the system of equations we get:()221221cos sin rIm m m m m g a ++-+⋅=αμα,(1)Figure 1Figure 2αm 1g()2212212cos sin rI m m m m m g r I S ++-+⋅⋅=αμα,(2)2212212sin cos rIm m r I r I m g m F ++-⎪⎭⎫ ⎝⎛+⋅=ααμ.(3)The moment of inertia of a solid cylinder is 221r m I =. Using the given numericalvalues:()2s m 3.25==+-+⋅=g m m m m m g a 3317.05.1cos sin 21221αμα,()N 13.01=+-+⋅=2122115.1cos sin 2m m m m m g m S αμα,()N 0.192=+-⋅=21125.1sin 5.0cos 5.1m m m g m F ααμ.Discussion (See Fig. 3.)The condition for the system to start moving is a > 0. Inserting a = 0 into (1) we obtain the limit for angle α1:0667.03tan 2121==+⋅=μμαm m m , ︒=81.31α.For the cylinder separately 01=α, and for the block separately ︒==-31.11tan 11μα. If the cord is not stretched the bodies move separately. We obtain the limit by inserting F = 0 into (3):6.031tan 212==⎪⎪⎭⎫⎝⎛+⋅=μμαI r m , ︒=96.302α.The condition for the cylinder toslip is that the value of S (calculated from (2) taking the same coefficient of friction) exceeds the value of αμcos 1g m . This gives the same value for α3 as we had for α2. The acceleration of the centers of the cylinder and the block is the same: ()αμαcos sin -g , the frictional force at the bottom of the cylinder isαμcos 1g m , the peripheral acceleration of the cylinder is αμcos 21g Ir m ⋅⋅.Problem 2There are 300 cm 3 toluene of C 0︒ temperature in a glass and 110 cm 3 toluene of C 100︒ temperature in another glass. (The sum of the volumes is 410 cm 3.) Find the final volume after the two liquids are mixed. The coefficient of volume expansion oftoluene ()1C 001.0-︒=β. Neglect the loss of heat. SolutionIf the volume at temperature t 1 is V 1, then the volume at temperature C 0︒ is ()11101t V V β+=. In the same way if the volume at t 2 temperature is V 2, at C 0︒ we have ()22201t V V β+=. Furthermore if the density of the liquid at C 0︒ is d , then the masses are d V m 101= and d V m 202=, respectively. After mixing the liquids the temperature is212211m m t m t m t ++=.The volumes at this temperature are ()t V β+110 and ()t V β+120. The sum of the volumes after mixing:()()()()()212201102202011010221120102122112120102010201020101111V V t V t V t V V t V V d t m dt m V V m m t m t m d m m V V t V V V V t V t V +=+++==+++=⎪⎭⎫⎝⎛+++==++⋅+⋅++==+++=+ ++βββββββββThe sum of the volumes is constant. In our case it is 410 cm 3. The result is valid for any number of quantities of toluene, as the mixing can be done successively adding always one more glass of liquid to the mixture.Problem 3Parallel light rays are falling on the plane surface of a semi-cylinder made of glass, at an angle of 45︒, in such a plane which is perpendicular to the axis of theβ r, ag α0︒30︒60︒ 90︒F, S (N)α1α2=α31020FSβ raFigure 3semi-cylinder (Fig. 4). (Index of refraction is 2.) Where are the rays emerging out of the cylindrical surface?SolutionLet us use angle ϕ to describe the position of the rays in the glass (Fig. 5). According to the law of refraction 2sin 45sin =︒β, 5.0sin =β, ︒=30β. The refracted angle is 30︒ for all of the incoming rays. We have to investigate what happens if ϕ changes from 0︒ to 180︒. It is easy to see that ϕ can not be less than 60︒ (︒=∠60AOB ). The critical angle is given by 221sin ==n crit β; hence ︒=45crit β. In the case of total internal reflection ︒=∠45ACO , hence ︒=︒-︒-︒=754560180ϕ. If ϕ is more than 75︒ the rays can emerge the cylinder. Increasing the angle we reach the critical angle again if ︒=∠45OED . Thus the rays are leaving the glass cylinder if: ︒<<︒16575ϕ,CE, arc of the emerging rays, subtends a central angle of 90︒.Experimental problemThree closed boxes (black boxes) with two plug sockets on each are present for investigation. The participants have to find out, without opening the boxes, what kind of elements are in them and measure their characteristic properties. AC and DC meters (their internal resistance and accuracy are given) and AC (5O Hz) and DC sources are put at the participants’ disposal .SolutionNo voltage is observed at any of the plug sockets therefore none of the boxes contains a source. Measuring the resistances using first AC then DC, one of the boxes gives the same result. Conclusion: the box contains a simple resistor. Its resistance is determined by measurement. One of the boxes has a very great resistance for DC but conducts AC well. Itcontains a capacitor, the value can be computed as CX C ω1=.Figure 4Figure 5The third box conducts both AC and DC, its resistance for AC is greater. It contains a resistor and an inductor connected in series. The values of the resistance and the inductance can be computed from the measurements.9th IPhO (Budapest, 1976)Theoretical problemsProblem 1A hollow sphere of radius R = 0.5 m rotates about a vertical axis through its centre with an angular velocity of ω = 5 s -1. Inside the sphere a small block is moving together with the sphere at the height of R /2 (Fig. 6). (g = 10 m/s 2.)a) What should be at least the coefficient of friction to fulfill this condition? b) Find the minimal coefficient of friction also for the case of ω = 8 s -1. c) Investigate the problem of stability in both cases,α) for a small change of the position of the block,β) for a small change of the angular velocity of the sphere.Solutiona) The block moves along a horizontal circle of radius αsin R . The net force acting on the block is pointed to the centre of this circle (Fig. 7). The vector sum of the normal force exerted by the wall N , the frictional force S and the weight mg is equal to the resultant: αωsin 2R m .The connections between the horizontal and vertical components:αααωcos sin sin 2S N R m -=,ααsin cos S N mg +=.The solution of the system of equations:⎪⎪⎭⎫⎝⎛-=g R mg S αωαcos 1sin 2,⎪⎪⎭⎫ ⎝⎛+=g R mg N αωα22sin cos .Figure 6Figure 7The block does not slip down if0.2259==+-⋅=≥2333sin cos cos 1sin 222gR gR NSa αωααωαμ.In this case there must be at least this friction to prevent slipping, i.e. sliding down.b) If on the other hand1cos 2>gR αω some friction is necessary to prevent the block to slip upwards. αωsin 2R m must be equal to the resultant of forces S , N and mg . Condition for the minimal coefficient of friction is (Fig. 8):=+-⋅=≥gR g R NSb αωααωαμ222sin cos 1cos sin0.1792==2933.c) We have to investigate μa and μb as functions of α and ω in the cases a) and b) (see Fig. 9/a and 9/b ):In case a): if the block slips upwards, it comes back; if it slips down it does not return. If ω increases, the block remains in equilibrium, if ω decreases it slips downwards.In case b): if the block slips upwards it stays there; if the block slips downwards it returns. If ω increases the block climbs upwards -, if ω decreases the block remains in equilibrium.Problem 2The walls of a cylinder of base 1 dm 2, the piston and the inner dividing wall are perfect heat insulators (Fig. 10). The valve in the dividing wall opens if theFigure 9/aFigure 9/bFigure 8pressure on the right side is greater than on the left side. Initially there is 12 g helium in the left side and 2 g helium in the right side. The lengths of both sides are 11.2 dm each and the temperature is C 0︒. Outside we have a pressure of 100 kPa. The specific heat at constant volume is c v = 3.15 J/gK, at constant pressure it is c p = 5.25 J/gK. The piston is pushed slowly towards the dividing wall. When the valve opens we stop then continue pushing slowly until the wall is reached. Find the work doneon the piston by us.SolutionThe volume of 4 g helium at C 0︒ temperature and a pressure of 100 kPa is 22.4 dm 3 (molar volume). It follows that initially the pressure on the left hand side is 600 kPa, on the right hand side 100 kPa. Therefore the valve is closed.An adiabatic compression happens until the pressure in the right side reaches 600 kPa (κ = 5/3).5356002.11100V ⋅=⋅,hence the volume on the right side (when the valve opens):V = 3.82 dm 3.From the ideal gas equation the temperature is on the right side at this pointK 5521==nRpVT .During this phase the whole work performed increases the internal energy of the gas:W 1 = (3.15 J/gK) ⋅ (2 g) ⋅ (552 K – 273 K) = 1760 J.Next the valve opens, the piston is arrested. The temperature after the mixing has been completed:K 313145522273122=⋅+⋅=T .During this phase there is no change in the energy, no work done on the piston.An adiabatic compression follows from 11.2 + 3.82 = 15.02 dm 3 to 11.2 dm 3:323322.1102.15313⋅=⋅T ,henceT 3 = 381 K.The whole work done increases the energy of the gas:W 3 = (3.15 J/gK) ⋅ (14 g) ⋅ (381 K – 313 K) = 3000 J. The total work done:W total = W 1 + W 3 = 4760 J.The work done by the outside atmospheric pressure should be subtracted:11.2 dm 11.2 dm 1 dm Figure 10W atm = 100 kPa ⋅ 11.2 dm 3 = 1120 J.The work done on the piston by us:W = W total – W atm = 3640 J . Problem 3Somewhere in a glass sphere there is an air bubble. Describe methods how to determine the diameter of the bubble without damaging the sphere.SolutionWe can not rely on any value about the density of the glass. It is quite uncertain. The index of refraction can be determined using a light beam which does not touch the bubble. Another method consists of immersing the sphere into a liquid of same refraction index: its surface becomes invisible.A great number of methods can be found.We can start by determining the axis, the line which joins the centers of the sphere and the bubble. The easiest way is to use the “tumbler -over ” method. If the sphere is placed on a horizontal plane the axis takes up a vertical position. The image of the bubble, seen from both directions along the axis, is a circle.If the sphere is immersed in a liquid of same indexof refraction the spherical bubble is practically inside aparallel plate (Fig. 11). Its boundaries can be determinedeither by a micrometer or using parallel light beams.Along the axis we have a lens system consisting , oftwo thick negative lenses. The diameter of the bubble canbe determined by several measurements and complicated calculations.If the index of refraction of the glass is known we can fit a plano-concave lens of same index of refraction to the sphere at the end of the axis (Fig. 12). As ABCD forms a parallel plate the diameter of the bubble can be measured using parallel light beams.Focusing a light beam on point A of the surface of the sphere (Fig. 13) we get a diverging beam from point A inside the sphere. The rays strike the surface at the other side and illuminate a cap. Measuring the spherical cap we get angle ϕ. Angle ψ can be obtained in a similar way at point B. FromFigure11 Figure12 Figure13d R r +=ϕsin and d R r -=ψsinwe haveϕψϕψsin sin sin sin 2+⋅=R r , ϕψϕψsin sin sin sin +-⋅=R d . The diameter of the bubble can be determined also by the help of X-rays. X-rays are not refracted by glass. They will cast shadows indicating the structure of the body, in our case the position and diameter of the bubble.We can also determine the moment of inertia with respect to the axis and thus the diameter of the bubble.Experimental problemThe whole text given to the students:At the workplace there are beyond other devices a test tube with 12 V electrical heating, a liquid with known specific heat (c 0 = 2.1 J/g ︒C) and an X material with unknown thermal properties. The X material is insoluble in the liquid.Examine the thermal properties of the X crystal material between room temperature and 70 ︒C. Determine the thermal data of the X material. Tabulate and plot the measured data.(You can use only the devices and materials prepared on the table. The damaged devices and the used up materials are not replaceable.)SolutionHeating first the liquid then the liquid and the crystalline substance together two time-temperature graphs can be plotted. From the graphs specific heat, melting point and heat of fusion can be easily obtained.Literature[1]W. Gorzkowski: Problems of the 1st International Physics OlympiadPhysics Competitions 5, no2 pp6-17, 2003[2]R. Kunfalvi: Collection of Competition Tasks from the Ist through XVth International Physics Olympiads 1967-1984Roland Eötvös Physical Society in cooperation with UNESCO, Budapest, 1985[3]A Nemzetközi Fizikai Diákolimpiák feladatai I.-XV.Eötvös Loránd Fizikai Társulat, Középiskolai Matematikai Lapok, 1985[文档可能无法思考全面，请浏览后下载，另外祝您生活愉快，工作顺利，万事如意!]。
历届国际物理奥林匹克竞赛试题与解答
历届国际物理奥林匹克竞赛试题与解答第3届（1969年于捷克斯洛伐克的布尔诺）【题1】右图的力学系统由三辆车组成，质量分别为m A ＝0.3kg ，m B ＝0.2kg ，m C ＝1.5kg 。
（a ）沿水平方向作用于C 车的力F 很大。
使A 、B 两车相对C 车保持静止。
求力F 及绳子的张力。
（b ）C 车静止，求A 、B 两车的加速度及绳子的张力。
（忽略阻力和摩擦力，忽略滑轮和车轮的转动惯量）解：（a ）A 、B 两车相对C 车保持静止，A 车在竖直方向没有加速度，因此它对绳的拉力为m A g 。
这个力使B 车得到加速度g m m a BAB =。
又三车系统以相同的加速度运动，则： g m m m m m F BAC B A )(++= 由给定的数值得：a B ＝a C ＝a A ＝1.5g ＝14.7m/s 2绳中的张力为：T ＝m A g ＝2.94N 水平推力为：F ＝29.4N（b ）如果C 车静止，则力m A g 使质量m A ＋m B 加速，加速度为：BA A AB m m gm a +=＝0.6g ＝5.88N绳中的张力为：T /＝m A g －m A ×0.6g ＝1.176N【题2】在质量为m 1的铜量热器中装有质量为m 2的水，共同的温度为t 12；一块质量为m 3、温度为t 3的冰投入量热器中（如右图所示）。
试求出在各种可能情形下的最终温度。
计算中t 3取负值。
铜的比热c 1＝0.1kcal/kg·0C ，水的比热c 2＝1kcal/kg·0C ，冰的比热c 3＝0.5kcal/kg·0C ，冰的熔解热L ＝80kcal/kg 。
解：可能存在三种不同的终态：（a ）只有冰；（b ）冰水共存；（c ）只有水。
（a ）冰温度升高，但没有熔化，达到某一（负）温度t a ； 放出的热量和吸收的热量相等：c 3 m 3（t a －t 3）＝（c 1 m 1＋c 2 m 2）（t 12－t a ）＋m 2L得出最终的温度为3332112333122211)(c m c m c m Lm t c m t c m c m t a +++++=（1）情况（a ）的条件是t a ＜０（注：指00C ），如果上式的分子为负值，我们得到下列条件： （c 1 m 1＋c 2 m 2）t 12＜―c 3 m 3t 3―m 2L （2）（c ）现在让我们讨论冰块全部熔化的情况。
2023ipho实验题
2023ipho实验题英文回答：The 2023 International Physics Olympiad (IPhO) is an annual competition that brings together talented high school students from around the world to test their knowledge and skills in physics. As a participant in the IPhO, I had the opportunity to tackle a series of challenging experimental problems.One of the experimental problems I encountered involved measuring the speed of sound in different materials. We were provided with various materials, such as metal rods, glass tubes, and plastic pipes, and were tasked with determining the speed of sound in each material using a specific experimental setup. By measuring the time it took for a sound wave to travel through each material and comparing it to the known distance, we were able to calculate the speed of sound.Another interesting experiment I conducted during the IPhO was related to optics. We were given a set of lenses and mirrors and were asked to design an optical system that could produce a specific image. This required a deep understanding of the principles of optics and the abilityto manipulate light rays using different optical components. It was a challenging task, but it allowed me to apply my theoretical knowledge to a practical problem.中文回答：2023年国际物理奥林匹克竞赛（IPhO）是一项年度比赛，汇集了来自世界各地的优秀高中学生，以测试他们在物理学方面的知识和技能。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
moves on the plane without slipping. The free fall acceleration is .
Part B (3 points)
= ,
(A.10)
since it does not slide over the plane.
Solving (A.8)-(A.10) results in velocities at the lowest point of the puck trajectory written as
=2
the equations of motion. It is written for the puck as follows
= sin ,
(A.1)
where is the horizontal projection of the puck acceleration.
For the cylinder the equation of motion with the
Consider the forces acting on the puck and the cylinder and
depicted in the figure on the right. The puck is subject to the
gravity force and the reaction force from the cylinder . The
bubble is found as
= + ,
(B.1)
where the molar heat capacity at arbitrary process is as follows
1
= = + .
(B.2)
Here stands for the molar heat capacity of the gas at constant volume, designates its pressure, is the
(A.3)
Then the equation of rotational motion around the center of mass of the cylinder takes the form
= ,
(A.4)
where the inertia moment of the hollow cylinder is given by
capacitor of capacitance 2 carries the electric charge 0 , a capacitor of
capacitance is uncharged, and there are no electric currents in both coils of
2
surface, caused by surface tension of the interface between liquid and gas, so that ∆ = .
Part C (3 points)
Initially, a switch is unshorted in the circuit shown in the figure on the right, a
bubble. Assume that the thermal equilibrium inside the bubble is reached much faster than the period of
oscillations.
Hint: Laplace showed that there is pressure difference between inside and outside of a curved
total amount of moles of gas in the bubble, and denote the volume and temperature of the gas,
respectively.
Evaluate the derivative standing on the right hand side of (B.2). According to the Laplace formula,
= +
(A.14)
and the acceleration
2
rel = rel
.
(A.15)
At the lowest point of the puck trajectory the acceleration of the cylinder axis is equal to zero,
=
,
(A.12)
(2+ )
(2+ )
ቤተ መጻሕፍቲ ባይዱ
.
(A.13)
In the reference frame sliding progressively along with the cylinder axis, the puck moves in a circle
of radius and, at the lowest point of its trajectory, have the velocity
formula for the frequency of the small radial oscillations of the bubble and evaluate it under the
assumption that the heat capacity of the soap film is much greater than the heat capacity of the gas in the
the gas pressure inside the bubble is defined by
4
= ,
(B.3)
thus, the equation of any equilibrium process with the gas in the bubble is a polytrope of the form
the plane as shown in the figure on the left. Find the interaction force
between the puck and the cylinder at the moment when the puck passes
the lowest point of its trajectory. Assume that the friction between the
(A.7) after integrating that
= 2.
(A.8)
It is obvious that the conservation law for the system is written as
2
2
2
= 2 + 2 + 2 ,
(A.9)
where the angular velocity of the cylinder is found to be
inductance and 2, respectively. The capacitor starts to discharge and at the
moment when the current in the coils reaches its maximum value, the switch is
acceleration is found as
= sin − .
(A.2)
Since the cylinder moves along the plane without sliding its
angular acceleration is obtained as
= /
therefore, the puck acceleration in the laboratory reference frame is also given by (A.15).
2
− = .
then the interaction force between the puck and the cylinder is finally found as
cylinder is subject to the gravity force , the reaction force from
the plane 1 , the friction force and the pressure force from the
puck ′ = −. The idea is to write the horizontal projections of
g
= 1.10 3 . 1) Find formula for the molar heat capacity of the gas in the bubble for such a process when
cm
the gas is heated so slowly that the bubble remains in a mechanical equilibrium and evaluate it; 2) Find
= 3 1 + 3 .
(A.16)
(A.17)
Theoretical competition. Tuesday, 15 July 2014
2/4
Part B