第18届国际物理奥林匹克竞赛试题及解答(英文)
奥林匹克物理竞赛试题及答案
奥林匹克物理竞赛试题及答案比赛设立了由参赛成员国组成的国际物理奥林匹克委员会。
竞赛章程规定，目的是促进中学物理教学的国际交流，通过竞赛促进物理课外活动，加强不同国家青少年之间的友好关系和人与人之间的相互了解与合作。
同时，它有助于参赛者开发他们在物理方面的创造力，并将他们在学校学到的知识应用到解决实际问题的能力中。
国际物理奥林匹克竞赛每年举行一次。
它由会员国轮流主办，由各代表团团长和东道国指定的一名主席组成。
国际委员会的任务是公正合理地评价论文，监督章程的实施，决定竞赛结果。
每个成员国可派出五名高中生或技校学生参加比赛。
参赛者在比赛当天之前不得超过20岁。
参赛队伍要有两个团长，两个团长都是国际委员会成员，前提是能胜任解决竞赛问题，能参与竞赛试卷的讨论和评分，熟悉国际物理奥林匹克的工作语言。
国际体育奥林匹克的工作语言是英语、法语、德语和俄语。
当代表团到达东道国时，代表团团长应向东道国的组织者说明学生和团长的情况。
竞赛于每年6月底举行。
竞赛分两天进行。
第一天进行3道理论计算题竞赛，另一天的竞赛内容是1—2道实验题。
中间有一天的休息。
参赛者可使用计算尺、不带程序编制的计算器和对数表、物理常数表和制图工具，但不能使用数学和物理公式一览表。
比赛题目由参赛国提供，主办国命题。
比赛前，问题要保密。
竞赛内容包括中学物理四个部分(力学、热力学与分子物理、光学与原子核物理、电磁学)，要求使用标准的中学数学而不是高等数学解题。
东道国提出评估标准并指定审查人员。
每道题满分10分。
同时，各代表团团长将对其成员的竞赛论文复印件进行评审，并最终协商决定结果。
评奖标准是以参赛者前三名的平均分数计为100%，参赛者达90% 以上者为一等奖，78—90%者为二等奖，65—78%者为三等奖，同时发给证书。
50—65%者给予表扬，不满50%者发给参赛证明。
竞赛只计个人名次，不计团体总分。
最后竞赛结果由国际委员会决定宣布。
国际物理奥林匹克竞赛流程赛期一般为9天。
第届国际物理奥林匹克竞赛试题与解答(一)
第届国际物理奥林匹克竞赛试题与解答(一)第50届国际物理奥林匹克竞赛是2021年7月17日至7月24日在立陶宛首都维尔纽斯举办的一场国际性的高中物理竞赛。
比赛采用英语作为交流语言，共有来自78个国家和地区的340名高中生参加。
本次比赛的试题难度较大，接下来将展示文本及其解答。
试题一：水球侦探有一个可预知的机器人，它能在20秒中将一个水球从一个瓶子上落下并射入一个篮子内。
现在，在较短的时间内，你需要发现该机器人和瓶子的相对位置，因为您希望以类似的方式射击水球。
您可以使用网球球拍（无障碍物的情况下）将水球从篮子向上弹起，并发现您需要瓶子的相对位置的任何信息；您还可以在所需的任何时间内以水平或垂直方向挡板的形式放置障碍物；在一次试验中，您可以在网球球拍打水球的起始位置上放几个记号来记录启动点。
您可以使用水球、网球球拍、篮子、木板和绳索等物品，还可以在最多五米范围内的工作桌上使用软件和硬件，但不能直接使用摄像机或激光仪来获取机器人方位信息和 distances.1 并且您需要在3次尝试中从一个新的启动点开始，每次都在20秒内打入水球。
问题1: 说明确定机器人的位置最少需要多少次尝试? 您将如何确定第一次尝试的起点和方向？如何优化您的尝试策略？解答1：最小值为3次尝试。
机器人与起始位置之间的最小距离为y，射中目标的距离为 x 在不知道任何具体数据的情况下，我们可以进行如下操作。
第一次尝试可以进行在中心处的最高点，平移到一个$y+\sqrt{2}x$的位置，这种位置需要花费一定的时间来判断，但如果我们成功射入目标，我们就可以找到100％精确的$y_0$值，后续垂直位移的知识问题。
而对于水平位置的了解，我们可以首先考虑将水球从一个中心点射出，使其成为一个匀加速运动，然后用一块水平板从左到右或从右到左预定一个固定距离，进一步将初始位置确定为距板最近的位置，然后调整初始角度。
这个角度可以通过打二角中心的两个球与板的交点来确定。
国际物理林匹克竞赛试题b_a (48)
In this problem we deal with a simplified model of accelerometers designed to activate the safety air bags of automobiles during a collision. We would like to build an electromechanical system in such a way that when the acceleration exceeds a certain limit, one of the electrical parameters of the system such as the voltage at a certain point of the circuit will exceed a threshold and the air bag will be activated as a result.Note: Ignore gravity in this problem.1 Consider a capacitor with parallel plates as in Figure 1. The area of each plate in the capacitoris A and the distance between the two plates is d . The distance between the two plates is much smaller than the dimensions of the plates. One of these plates is in contact with a wall through a spring with a spring constant k , and the other plate is fixed. When the distancebetween the plates is d the spring is neither compressed nor stretched, in other words no force is exerted on the spring in this state. Assume that the permittivity of the air between the plates is that of free vacuum 0ε. The capacitance corresponding to this distance between the plates of the capacitor is d A C 00ε=. We put charges Q + and Q − on the plates and let the system achieve mechanical equilibrium.Figure 11.1Calculate the electrical force, E F , exerted by the plates on each other. 0.81.2Let x be the displacement of the plate connected to the spring. Find x .0.61.3In this state, what is the electrical potential difference V between the plates of thecapacitor in terms of Q , A , d , k ?0.41.5 What is the total energy, U , stored in the system in terms of Q ,A ,d and k ? 0.6Figure 2, shows a mass M which is attached to a conducting plate with negligible mass and also to two springs having identical spring constants k . The conducting plate can move back and forth in the space between two fixed conducting plates. All these plates are similar and have the same area A . Thus these three plates constitute two capacitors. As shown in Figure 2, the fixed plates are connected to the given potentials Vand V −, and the middle plate is connectedthrough a two-state switch to the ground. The wire connected to the movable plate does not disturb the motion of the plate and the three plates will always remain parallel. When the whole complex is not being accelerated, the distance from each fixed plate to the movable plate is d which is much smaller than the dimensions of the plates. The thickness of the movable plate can be ignored.Figure 2The switch can be in either one of the two states α and β. Assume that the capacitor complex is being accelerated along with the automobile, and the acceleration is constant. Assume that during this constant acceleration the spring does not oscillate and all components of this complex capacitor are in their equilibrium positions, i.e. they do not move with respect to each other, and hence with respect to the automobile.Due to the acceleration, the movable plate will be displaced a certain amount x from the middle of the two fixed plates.2Consider the case where the switch is in state α i.e. the movable plate is connected to the ground through a wire, then2.1 Find the charge on each capacitor as a function of x. 0.42.2 Find the net electrical force on the movable plate,EF, as a function of x. 0.42.3 Assume xd>> and terms of order 2x can be ignored compared to terms of order2d. Simplify the answer to the previous part.0.22.4 Write the total force on the movable plate (the sum of the electrical and the spring forces) as xkeff− and give the form ofeffk. 0.72.5 Express the constant acceleration a as a function of x. 0.43 Now assume that the switch is in state β i.e. the movable plate is connected to the groundthrough a capacitor, the capacitance of which is S C (there is no initial charge on the capacitors). If the movable plate is displaced by an amount x from its central position, 3.1 Find S V the electrical potential difference across the capacitor S C as a function ofx. 1.53.2 Again assume that x d >> and ignore terms of order 2x compared to terms oforder 2d . Simplify your answer to the previous part.0.24 We would like to adjust the parameters in the problem such that the air bag will not beactivated in normal braking but opens fast enough during a collision to prevent the driver’s head from colliding with the windshield or the steering wheel. As you have seen in Part 2, the force exerted on the movable plate by the springs and the electrical charges can be represented as that of a spring with an effective spring constant eff k . The whole capacitor complex is similar to a mass and spring system of mass M and spring constant eff k under the influence of a constant acceleration a , which in this problem is the acceleration of the automobile.Note : In this part of the problem, the assumption that the mass and spring are in equilibrium undera constant acceleration and hence are fixed relative to the automobile, no longer holds.Ignore friction and consider the following numerical values for the parameters of the problem:cm 0.1=d , 22m 105.2−×=A , N/m 102.43×=k ,22120/Nm C 1085.8−×=ε,V 12=V , kg 15.0=M .4.1Using this data, find the ratio of the electrical force you calculated in section 2.3 tothe force of the springs and show that one can ignore the electrical forces compared to the spring forces.0.6Although we did not calculate the electrical forces for the case when the switch is in the state β, it can be shown that in this situation, quite similarly, the electrical forces are as small and can be ignored.4.2If the automobile while traveling with a constant velocity, suddenly brakes with aconstant acceleration a , what is the maximum displacement of the movable plate? Give your answer in parameter.0.6Assume that the switch is in state β and the system has been designed such that when the electrical voltage across the capacitor reaches V 15.0=S V , the air bag is activated. We would like the air bag not to be activated during normal braking when the automobile’s acceleration is less than the acceleration of gravity 28.9s m g =, but be activated otherwise.4.3How much should S C be for this purpose?0.6We would like to find out if the air bag will be activated fast enough to prevent the driver’s head from hitting the windshield or the steering wheel. Assume that as a result of collision, the automobile experiences a deceleration equal to g but the driver’s head keeps moving at a constant speed.4.4 By estimating the distance between the driver’s head and the steering wheel, findthe time1t it takes before the driver’s head hits the steering wheel.0.84.5 Find the time2t before the air bag is activated and compare it to1t. Is the air bag activated in time? Assume that airbag opens instantaneously.0.9。
第18届全国中学生物理竞赛预复赛试题及答案
2001年第十八届全国中学生物理竞赛预、复赛试题及答案目录第十八届全国中学生物理竞赛预赛试题 (1)第十八届全国中学生物理竞赛预赛试题参考解答、评分标准 (4)第十八届全国中学生物理竞赛复赛试题 (12)第十八届全国中学生物理竞赛复赛试题参考解答 (15)第十八届全国中学生物理竞赛预赛试题全卷共七题，总分为140分一、（15分）如图预18－l 所示，杆OA 长为R ，可绕过O 点的水平轴在竖直平面内转动，其端点A 系着一跨过定滑轮B 、C 的不可伸长的轻绳，绳的另一端系一物块M ，滑轮的半径可忽略，B 在O 的正上方，OB 之间的距离为H 。
某一时刻，当绳的BA段与OB 之间的夹角为α时，杆的角速度为ω，求此时物块M 的速率M v 。
二、（15分）两块竖直放置的平行金属大平板A 、B ，相距d ，两极间的电压为U 。
一带正电的质点从两板间的M 点开始以竖直向上的初速度0v 运动，当它到达电场中某点N 点时，速度变为水平方向，大小仍为0v ，如图预18－2所示．求M 、N 两点问的电势差．（忽略带电质点对金属板上电荷均匀分布的影响）三、（18分）一束平行光沿薄平凸透镜的主光轴入射，经透镜折射后，会聚于透镜48cm f = 处，透镜的折射率 1.5n =。
若将此透镜的凸面镀银，物置于平面前12cm 处，求最后所成象的位置。
四、（1 8分）在用铀 235作燃料的核反应堆中，铀 235核吸收一个动能约为0.025eV 的热中子（慢中子）后，可发生裂变反应，放出能量和2～3个快中子，而快中子不利于铀235的裂变．为了能使裂变反应继续下去，需要将反应中放出的快中子减速。
有一种减速的方法是使用石墨（碳12）作减速剂．设中子与碳原子的碰撞是对心弹性碰撞，问一个动能为0 1.75MeV E =的快中子需要与静止的碳原子碰撞多少次，才能减速成为0.025eV 的热中子？2001-09-09五、（25分）如图预18－5所示，一质量为M 、长为L 带薄挡板P 的木板，静止在水平的地面上，设木板与地面间的静摩擦系数与滑动摩擦系数相等，皆为μ．质量为m 的人从木板的一端由静止开始相对于地面匀加速地向前走向另一端，到达另一端时便骤然抓住挡板P 而停在木板上．已知人与木板间的静摩擦系数足够大，人在木板上不滑动．问：在什么条件下，最后可使木板向前方移动的距离达到最大？其值等于多少？六、（ 24分）物理小组的同学在寒冷的冬天做了一个这样的实验：他们把一个实心的大铝球加热到某温度t ，然后把它放在结冰的湖面上（冰层足够厚），铝球便逐渐陷入冰内．当铝球不再下陷时，测出球的最低点陷入冰中的深度h ．将铝球加热到不同的温度，重复上述实验8次，最终得到如下数据：已知铝的密度约为水的密度的3倍，设实验时的环境温度及湖面冰的温度均为 0℃．已知此情况下，冰的熔解热53.3410J/kg λ=⨯．1．试采用以上某些数据估算铝的比热c ．2．对未被你采用的实验数据，试说明不采用的原因，并作出解释．七、（ 25分）如图预18－7所示，在半径为a 的圆柱空间中（图中圆为其横截面）充满磁感应强度大小为B 的均匀磁场，其方向平行于轴线远离读者．在圆柱空间中垂直轴线平面内固定放置一绝缘材料制成的边长为 1.6L a =的刚性等边三角形框架DEF ∆，其中心O 位于圆柱的轴线上．DE 边上S 点（14DS L =）处有一发射带电粒子的源，发射粒子的方向皆在图预18-7中截面内且垂直于DE 边向下．发射粒子的电量皆为q （＞0），质量皆为m ，但速度v 有各种不同的数值．若这些粒子与三角形框架的碰撞均为完全弹性碰撞，并要求每一次碰撞时速度方向垂直于被碰的边．试问：1．带电粒子速度v的大小取哪些数值时可使S点发出的粒子最终又回到S点？2. 这些粒子中，回到S点所用的最短时间是多少？第十八届全国中学生物理竞赛预赛试题参考解答、评分标准一、参考解答杆的端点A 点绕O 点作圆周运动，其速度A v 的方向与杆OA 垂直，在所考察时其大小为 A v R ω= （1）对速度A v 作如图预解18-1所示的正交分解，沿绳BA 的分量就是物块M 是速率M v ，则cos M A v v ϕ= （2） 由正弦定理知sin sin OAB H Rα∠=（3） 由图看出 2OAB πϕ∠=+ （4）由以上各式得sin M v H ωα= （5）评分标准：本题15分其中（1）式3分；（2）式5分；（5）式7分。
第18届全国中学生物理竞赛复赛答案.docx
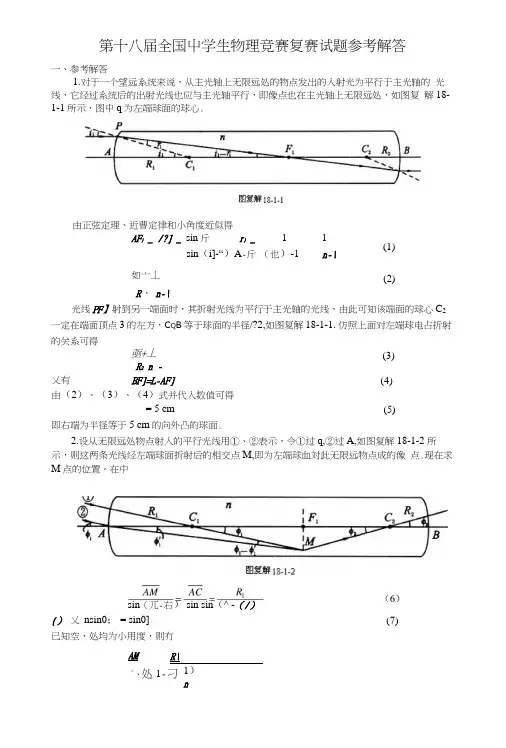
由正弦定理、近曹定律和小角度近似得AF } _ /?] _ sin 斤 r } _1 1sin （i]-“）A -斤 （也）-1n-\如亠丄(1) (2)R 、 n-\光线PF 】射到另一端面时，其折射光线为平行于主光轴的光线，由此可知该端面的球心C 2 一定在端面顶点3的左方，C Q B 等于球面的半径/?2,如图复解18-1-1. 仿照上面对左端球电占折射的关系可得亟+丄 R 2 n -(3) 乂有 BF]=L-AF]由（2）、（3）、（4）式并代入数值可得= 5 cm即右端为半径等于5 cm 的向外凸的球面.2.设从无限远处物点射入的平行光线用①、②表示，令①过q,②过A,如图复解18-1-2 所示，则这两条光线经左端球面折射后的相交点M,即为左端球血対此无限远物点成的像 点.现在求M 点的位置。
在中(4) (5)sin （兀-右） sin sin （^ -（/）{） 乂 nsin0； = sin0]已知空，处均为小用度，则冇R\1）nAM°、处1-刁 第十八届全国屮学生物理竞赛复赛试题参考解答一、参考解答1. 对于一个望远系统来说，从主光轴上无限远处的物点发出的入射光为平行于主光轴的 光线，它经过系统后的出射光线也应与主光轴平行，即像点也在主光轴上无限远处，如图复 解18-1-1所示，图中q 为左端球面的球心.(7)与(2)式比较可知，AM « AF X ,即M位于过片垂直于主光轴的平而上.上而已知，玻璃棒为天文望远系统，则凡是过M点的傍轴光线从棒的右端面射出时都将是相互平行的光线.容易看出，从M 射出C?的光线将沿原方向射出，这也就是过M点的任意光线(包括光线①、②)从玻璃棒射出的平行光线的方向。
此方向与主光轴的夹角即为血，由图复18-1-2 nJ'得01 _ G片=A§_R1(9)~C^~BF\-R2III (2)、(3)式可得~BF{-R2 _ R2(10)二、参考解答1.已知在海平面处，大气压强p(0) = 101.3xl03 Pa .如图复解18-2-1,在z = 5000 m处, 大气压强为”(5000) = 53xlO3 Pa o(1)图复解18-2-1此处水沸腾时的饱和蒸气压"w应等于此值.由图复解18-2-2可知，对应的温度即沸点为t} =82 °C (2)达到此温度吋锅内水开始沸腾，温度不再升高，故在5000m高山上，若不加盖压力锅，锅内温度最高可达82°C.2.由图复解18-2-2可知，在Z = 120°C时，水的饱和蒸气压p w(120°) = 198xl03 Pa ,而在海平面处，大气压强；7(O) = lOlxlO3 Pa.可见压力阀的附加压强为p s = p w(120°)-p(0)= 198x1(P - 101.3x1()3= 96.7x103 Pa (3)在5000m高山上，大气压强与压力阀的附加压强之和为p'=+ “(5000) =96.7X103+53X103= 149.7x 1(? Pa (4)若在25时阀被顶起，贝眦时的几应等于P'，即Pw = P f⑸由图复解18-2-2可知4= 112 °C (6)此时锅内水开始沸腾，温度不再升高，故按正确方法使用此压力锅，在5000m高山上锅内水的温度最高可达112°C.P/103Paf [P r-^0)]/lO3Pa0 10 20 30 40 50 60 70 80 90 100 110 120 130El复解18223.在未按正确方法使用压力锅时，锅内有空气，设加压力阀时，内部水蒸汽已饱和.由图复解18-2-2可知，在/ = 27°C时，题中已给出水的饱和蒸气压仏(27。
海口第18届全国中学生物理竞赛决赛试题及答案
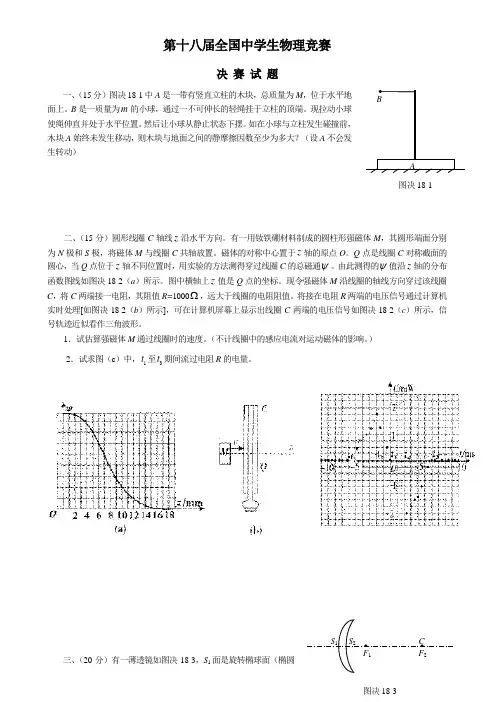
第十八届全国中学生物理竞赛决 赛 试 题一、（15分）图决18-1中A 是一带有竖直立柱的木块，总质量为M ，位于水平地面上。
B 是一质量为m 的小球，通过一不可伸长的轻绳挂于立柱的顶端。
现拉动小球使绳伸直并处于水平位置。
然后让小球从静止状态下摆。
如在小球与立柱发生碰撞前，木块A 始终未发生移动，则木块与地面之间的静摩擦因数至少为多大？（设A 不会发生转动）二、（15分）圆形线圈C 轴线z 沿水平方向。
有一用钕铁硼材料制成的圆柱形强磁体M ，其圆形端面分别为N 极和S 极，将磁体M 与线圈C 共轴放置。
磁体的对称中心置于z 轴的原点O 。
Q 点是线圈C 对称截面的圆心，当Q 点位于z 轴不同位置时，用实验的方法测得穿过线圈C 的总磁通ψ。
由此测得的ψ值沿z 轴的分布函数图线如图决18-2（a ）所示。
图中横轴上z 值是Q 点的坐标。
现令强磁体M 沿线圈的轴线方向穿过该线圈C ，将C 两端接一电阻，其阻值R=1000Ω，远大于线圈的电阻阻值。
将接在电阻R 两端的电压信号通过计算机实时处理[如图决18-2（b ）所示]，可在计算机屏幕上显示出线圈C 两端的电压信号如图决18-2（c ）所示，信号轨迹近似看作三角波形。
1．试估算强磁体M 通过线圈时的速度。
（不计线圈中的感应电流对运动磁体的影响。
） 2．试求图（c ）中，1t 至3t 期间流过电阻R 的电量。
三、（20分）有一薄透镜如图决18-3，S 面是旋转椭球面（椭圆图决18-1绕长轴旋转而成的曲面），其焦点为F 1和F 2；S 2面是球面，其球心C 与F 2重合。
已知此透镜放在空气中时能使从无穷远处位于椭球长轴的物点射来的全部入射光线（不限于傍轴光线）会聚于一个像点上，椭圆的偏心率为e 。
（1）求此透镜材料的折射率n （要论证）；（2）如果将此透镜置于折射率为n '的介质中，并能达到上述的同样的要求，椭圆应满足什么条件？四、（20分）空间有半径为R 长度L 很短的圆柱形的磁场区域，圆柱的轴线为z 轴，磁场中任一点的磁感应强度的方向沿以z 轴为对称轴的圆的切线，大小与该点离z 轴的距离r 成正比，B=K r ，K 为常数，如图决18-4中“· ”与 “×”所示。
第十八届全国高中生物理竞赛复赛试题及答案
第十八届全国中学生物理竞赛复赛试卷、参考答案全卷共六题，总分140分。
一、〔22分〕有一放在空气中的玻璃棒，折射率ｎ＝1.5，中心轴线长Ｌ＝45cm，一端是半径为Ｒ1＝10ｃｍ的凸球面．1．要使玻璃棒的作用相当于一架理想的天文望远镜〔使主光轴上无限远处物成像于主光轴上无限远处的望远系统〕，取中心轴线为主光轴，玻璃棒另一端应磨成什么样的球面？2．对于这个玻璃棒，由无限远物点射来的平行入射光束与玻璃棒的主光轴成小角度φ１时，从棒射出的平行光束与主光轴成小角度φ２，求φ２／φ１〔此比值等于此玻璃棒望远系统的视角放大率〕．解：1．对于一个望远系统来说，从主光轴上无限远处的物点发出的入射光为平行于光轴的光线，它经过系统后的出射光线也应与主光轴平行，即像点也在主光轴上无限远处，如图18－2－6所示，图中Ｃ1为左端球面的球心．图18－2－6由正弦定理、折射定律和小角度近似得〔－Ｒ１〕／Ｒ１＝ｓｉｎｒ１／ｓｉｎ〔ｉ１－ｒ１〕≈ｒ１／〔ｉ１－ｒ１〕＝1／〔〔ｉ１／ｒ１〕－1〕≈1／〔ｎ－1〕，①即〔／Ｒ１〕－1＝1／〔ｎ－1〕．②光线ＰＦ１射到另一端面时，其折射光线为平行于主光轴的光线，由此可知该端面的球心Ｃ２一定在端面顶点Ｂ的左方，Ｃ２Ｂ等于球面的半径Ｒ２，如图18－2－6所示．仿照上面对左端球面上折射的关系可得〔／Ｒ２〕－1＝1／〔ｎ－1〕，③又有＝Ｌ－，④由②、③、④式并代入数值可得Ｒ２＝5ｃｍ．那么右端为半径等于5ｃｍ的向外凸的球面．图18－2－72．设从无限远处物点射入的平行光线用①、②表示，令①过Ｃ１，②过Ａ，如图18－2－7所示，那么这两条光线经左端球面折射后的相交点Ｍ，即为左端球面对此无限远物点成的像点．现在求Ｍ点的位置，在△ＡＣ１Ｍ中，有／ｓｉｎ〔π－φ１〕＝／ｓｉｎφ１＝Ｒ１／ｓｉｎ〔φ１－φ１′〕，又ｎｓｉｎφ１′＝ｓｉｎφ１，φ１、φ１′均为小角度，那么有／φ１＝Ｒ１／φ１〔1－〔1／ｎ〕〕．与②式比拟可知，≈，即Ｍ位于过Ｆ１垂直于主光轴的平面上．上面，玻璃棒为天文望远系统，那么但凡过Ｍ点的傍轴光线从棒的右端面射出时都将是相互平行的光线．容易看出，从Ｍ射出Ｃ２的光线将沿原方向射出，这也就是过Ｍ点的任意光线〔包括光线①、②〕从玻璃棒射出的平行光线的方向，此方向与主光轴的夹角即为φ２，由图18－2－7可得2／φ１＝／＝〔－Ｒ１〕／〔－Ｒ２〕，由②、③式可得〔－Ｒ１〕／〔－Ｒ２〕＝Ｒ１／Ｒ２，那么φ２／φ１＝Ｒ１／Ｒ２＝2．二、〔22分〕正确使用压力锅的方法是：将已盖好密封锅盖的压力锅〔如图复18-2-1〕加热，当锅水沸腾时再加盖压力阀Ｓ，此时可以认为锅只有水的饱和蒸气，空气已全部排除．然后继续加热，直到压力阀被锅的水蒸气顶起时，锅即已到达预期温度〔即设计时希望到达的温度〕．现有一压力锅，在海平面处加热能到达的预期温度为120℃，某人在海拔5000ｍ的高山上使用此压力锅，锅有足量的水．1．假设不加盖压力阀，锅水的温度最高可达多少？2．假设按正确方法使用压力锅，锅水的温度最高可达多少？3．假设未按正确方法使用压力锅，即盖好密封锅盖一段时间后，在点火前就加上压力阀，此时水温为27℃，那么加热到压力阀刚被顶起时，锅水的温度是多少？假设继续加热，锅水的温度最高可达多少？假设空气不溶于水．：水的饱和蒸气压ｐＷ〔ｔ〕与温度ｔ的关系图线如图18-2-2所示．大气压强ｐ〔ｚ〕与高度ｚ的关系的简化图线如图18-2-3所示．当ｔ＝27℃时，ｐＷ〔27°〕＝3.6×10３Ｐａ；ｚ＝0处，ｐ〔0〕＝1.013×10５Ｐａ．解：1．由图18－2－8知在海平面处，大气压强ｐ〔0〕＝101．3×10３Ｐａ．在ｚ＝5000ｍ时，大气压强为ｐ〔5000〕＝53×10３Ｐａ．图18－2－8图18－2－9此处水沸腾时的饱和蒸气压ｐＷ应等于此值．由图18－2－9可知，对应的温度即沸点为ｔ２＝82℃．到达此温度时，锅水开场沸腾，温度不再升高，故在5000ｍ高山上，假设不加盖压力锅，锅温度最高可达82℃．2．由图18－2－9可知，在ｔ＝120℃时，水的饱和蒸气压ｐＷ〔120°〕＝198×10３Ｐａ，而在海平面处，大气压强ｐ〔0〕＝101×10３Ｐａ．可见压力阀的附加压强为ｐＳ＝ｐＷ〔120°〕－ｐ〔0〕＝〔198×10３－101．3×10３〕Ｐａ＝96．7×10３Ｐａ．在5000ｍ高山上，大气压强与压力阀的附加压强之和为ｐ′＝ｐＳ＋ｐ〔5000〕＝〔96．7×10３＋53×10３〕Ｐａ＝149．7×103Ｐａ．假设在ｔ＝ｔ２时阀被顶起，那么此时的ｐＷ应等于ｐ′，即ｐＷ＝ｐ′，由图18－2－9可知ｔ２＝112℃．此时锅水开场沸腾，温度不再升高，故按正确方法使用此压力锅，在5000ｍ高山上锅水的温度最高可达112℃．3．在未按正确方法使用压力锅时，锅有空气，设加压力阀时，部水蒸汽已饱和．由图18－2－9可知，在ｔ＝27℃时，题中已给出水的饱和蒸气压ｐＷ〔27°〕＝3．6×10３Ｐａ，这时锅空气的压强〔用ｐａ表示〕为ｐａ〔27°〕＝ｐ〔5000〕－ｐＷ〔27°〕＝〔53×10３－3．6×10３〕Ｐａ＝49．4×10３Ｐａ．当温度升高时，锅空气的压强也随之升高，设在温度为ｔ〔℃〕时，锅空气压强为ｐａ〔ｔ〕，那么有ｐａ〔ｔ〕／〔273＋ｔ〕＝ｐａ〔27℃〕／〔273＋27〕，ｐａ〔ｔ〕＝〔164．7ｔ＋45．0×10３〕Ｐａ．假设在ｔ＝ｔ′时压力阀刚好开场被顶起，那么有ｐＷ〔ｔ′〕＋ｐａ〔ｔ′〕＝ｐ′，由此得ｐＷ〔ｔ′〕＝ｐ′－ｐａ〔ｔ′〕＝〔105×10３－164．7ｔ′〕Ｐａ，画出函数ｐ′－ｐａ〔ｔ′〕的图线，取ｔ＝0℃，有ｐ′－ｐａ〔0℃〕＝105×10３Ｐａ，取ｔ＝100℃，有ｐ′－ｐａ〔100℃〕＝88．6×10３Ｐａ．由此二点便可在图18－2－9上画出此直线，此直线与图18－2－9中的ｐＷ〔ｔ〕－ｔ曲线的交点为Ａ，Ａ即为所求的满足上式的点，由图可看出与Ａ点对应的温度为ｔ′＝97℃．即在压力阀刚开场被顶起时，锅水的温度是97℃，假设继续加热，压力阀被顶起后，锅空气随水蒸汽一起被排出，最终空气排净，锅水温仍可达112℃．碰撞后二者的速度ｖＡ和ｖＢ在一条直线上，碰撞过程中局部动能有可能被某一氢原子吸收，从而该原子由基态跃迁到激发态，然后，此原子向低能级态跃迁，并发出光子．如欲碰后发出一个光子，试论证：速度ｖ０至少需要多大〔以ｍ／ｓ表示〕？电子电量ｅ＝1．602×10－19Ｃ，质子质量为ｍｐ＝1．673×10－27ｋｇ，电子质量为ｍｅ＝0．911×10－31ｋｇ，氢原子的基态能量为Ｅ１＝－13．58ｅＶ．解：为使氢原子从基态跃迁到激发态，需要能量最小的激发态是ｎ＝2的第一激发态．氢原子的能量与其主量子数的平方成反比．即Ｅｎ＝ｋ１／ｎ２，①又知基态〔ｎ＝1〕的能量为－13．58ｅＶ，即Ｅ１＝ｋ１／1２＝－13．58ｅＶ，所以ｋ＝－13．58ｅＶ．ｎ＝2的第一激发态的能量为Ｅ２＝ｋ１／2２＝－13．58×〔1／4〕＝－3．39ｅＶ．②为使基态的氢原子激发到第一激发态所需能量为Ｅ＝Ｅ２－Ｅ１＝〔－3．39＋13．58〕ｅＶ＝10．19ｅＶ．③这就是氢原子从第一激发态跃迁到基态时发出的光子的能量，即ｈν＝Ｅ＝10．19ｅＶ＝10．19×1．602×10－19Ｊ＝1．632×10－18Ｊ．④式中ν为光子的频率，从开场碰到发射出光子，根据动量和能量守恒定律有ｍｖ０＝ｍｖＡ＋ｍｖＢ＋光子的动量，⑤〔1／2〕ｍｖ０２＝〔1／2〕ｍ〔ｖＡ２＋ｖＢ２〕＋ｈν，⑥光子的动量ｐν＝ｈν／ｃ．由⑥式可推得ｍｖ０＞2ｈν／ｖ０，因为ｖ０<<ｃ，所以ｍｖ０>>ｈν／ｃ，故⑤式中光子的动量与ｍｖ０相比拟可忽略不计．⑤式变为ｍｖ０＝ｍｖＡ＋ｍｖＢ＝ｍ〔ｖＡ＋ｖＢ〕，⑦符合⑥、⑦两式的ｖ0的最小值可推求如下：由⑥式与⑦式可推得〔1／2〕ｍｖ０２＝〔1／2〕ｍ〔ｖＡ＋ｖＢ〕２－ｍｖＡｖＢ＋ｈν＝〔1／2〕ｍｖ０２－ｍｖＡ〔ｖ０－ｖＡ〕＋ｈν，ｍｖＡ２－ｍｖＡｖ０＋ｈν＝0，经配方得ｍ〔ｖＡ－〔1／2〕ｖ０〕２－〔1／4〕ｍｖ０２＋ｈν＝0，〔1／4〕ｍｖ０２＝ｈν＋ｍ〔ｖＡ－〔1／2〕ｖ０〕２，⑧由⑧式可看出，当ｖＡ＝〔1／2〕ｖ０时，ｖ０到达最小值ｖ０ｍｉｎ，此时ｖＡ＝ｖＢ，ｖ０ｍｉｎ＝2，代入有关数值，得ｖ０ｍｉｎ＝6．25×10４ｍ／ｓ．答：Ｂ原子的速度至少应为6．25×10４ｍ／ｓ．四、〔22分〕如图18-4所示，均匀磁场的方向垂直纸面向里，磁感应强度Ｂ随时间ｔ变化，Ｂ＝Ｂ０－ｋｔ〔ｋ为大于零的常数〕．现有两个完全一样的均匀金属圆环相互交叠并固定在图中所示位置，环面处于图中纸面．圆环的半径为Ｒ，电阻为ｒ，相交点的电接触良好，两个环的接触点Ａ与Ｃ间的劣弧对圆心Ｏ的角为60°，求ｔ＝ｔ０时，每个环所受的均匀磁场的作用力，不考虑感应电流之间的作用．解：1．求网络各支路的电流．因磁感应强度大小随时间减少，考虑到电路的对称性，可设两环各支路的感应电流Ｉ１、Ｉ２的方向如图18－2－10所示，对左环电路ＡＤＣＦＡ，有图18－2－10Ｅ＝Ｉ１ｒＣＦＡ＋Ｉ２ｒＡＤＣ，因ｒＣＦＡ＝5ｒ／6，ｒＡＤＣ＝ｒ／6，Ｅ＝ｋπＲ２，故ｋπＲ２＝Ｉ１〔5ｒ／6〕＋Ｉ２〔ｒ／6〕．①因回路ＡＤＣＥＡ所围的面积为2〔〔2π－3〕／12〕Ｒ２，故对该回路有ｋ［2〔〔2π－3〕／12〕Ｒ２］＝2Ｉ２〔ｒ／6〕，解得Ｉ２＝〔〔2π－3〕Ｒ２／2ｒ〕ｋ，代入①式，得Ｉ１＝〔〔10π＋3〕Ｒ２／10ｒ〕ｋ．2．求每个圆环所受的力．图18－2－11先求左环所受的力，如图18－2－11所示，将圆环分割成很多小圆弧，由左手定那么可知，每段圆弧所受的力的方向均为径向，根据对称性分析，因圆弧ＰＭＡ与圆弧ＣＮＱ中的电流方向相反，所以在磁场中受的安培力相互抵消，而弧ＰＱ与弧ＡＣ的电流相对ｘ轴上下是对称的，因而每段载流导体所受的安培力在ｙ方向的合力为零，以载流导体弧ＰＱ上的线段Δｌ′为例，安培力ΔＦ为径向，其ｘ分量的大小表示为｜ΔＦｘ｜＝Ｉ１ＢΔｌ′ｃｏｓα，因Δｌ′ｃｏｓα＝Δｌ，故｜ΔＦｘ｜＝Ｉ１ＢΔｌ，｜Ｆｘ｜＝ΣＩ１ＢΔｌ＝Ｉ１Ｂ＝Ｉ１ＢＲ．由于导体弧ＰＱ在ｙ方向的合力为零，所以在ｔ０时刻所受安培力的合力Ｆ１仅有ｘ分量，即Ｆ１＝｜Ｆｘ｜＝Ｉ１ＢＲ＝〔〔10π＋3〕Ｒ２／10ｒ〕ｋＢＲ＝〔〔10π＋3〕Ｒ２／10ｒ〕ｋ〔Ｂ０－ｋｔ０〕Ｒ，方向向左．同理，载流导体弧ＡＣ在ｔ０时刻所受的安培力为Ｆ２＝Ｉ２ＢＲ＝〔〔2π－3〕Ｒ２／2ｒ〕ｋＢＲ＝〔〔2π－3〕Ｒ２／2ｒ〕ｋ〔Ｂ０－ｋｔ０〕Ｒ，方向向右．左环所受的合力大小为Ｆ＝Ｆ１－Ｆ２＝〔9／5ｒ〕ｋ〔Ｂ０－ｋｔ０〕Ｒ３．方向向左．25分〕如图18-5所示，一薄壁导体球壳〔以下简称为球壳〕的球心在Ｏ点．球壳通过一细导线与端电压Ｕ＝90Ｖ的电池的正极相连，电池负极接地．在球壳外Ａ点有一电量为ｑ１＝10×10－9Ｃ的点电荷，Ｂ点有一电量为ｑ２＝16×10－9Ｃ的点电荷．点Ｏ、Ａ之间的距离ｄ１＝20ｃｍ，点Ｏ、Ｂ之间的距离ｄ２＝40ｃｍ．现设想球壳的半径从ａ＝10ｃｍ开场缓慢地增大到50ｃｍ，问：在此过程中的不同阶段，流向球壳的电量各是多少？静电力常量ｋ＝9×10９Ｎ·ｍ２/Ｃ２．假设点电荷能穿过球壳壁进入导体球壳而不与导体壁接触．解：分以下几个阶段讨论：1．由于球壳外空间点电荷ｑ１、ｑ２的存在，球壳外壁的电荷分布不均匀，用σ表示面电荷密度．设球壳半径ａ＝10ｃｍ时球壳外壁带的电量为Ｑ１，因为电荷ｑ１、ｑ２与球壳外壁的电量Ｑ１在球壳产生的合场强为零，球壳为电势等于Ｕ的等势区，在导体外表上的面元ΔＳ所带的电量为σΔＳ，它在球壳的球心Ｏ处产生的电势为ΔＵ１＝ｋσΔＳ／ａ，球壳外壁所有电荷在球心Ｏ产生的电势Ｕ１为Ｕ１＝ΣΔＵ１＝ｋΣσΔＳ／α＝ｋＱ１／ａ．点电荷ｑ１、ｑ２在球壳的球心Ｏ处产生的电势分别为ｋｑ１／ｄ１与ｋｑ２／ｄ２，因球心Ｏ处的电势等于球壳的电势，按电势叠加原理，即有〔ｋｑ１／ｄ１〕＋〔ｋｑ２／ｄ２〕＋〔ｋＱ１／ａ〕＝Ｕ，代入数值后可解得球壳外壁的电量Ｑ１为Ｑ１＝〔ａＵ／ｋ〕－ａ〔〔ｑ１／ｄ１〕＋〔ｑ２／ｄ２〕〕＝－8×10－９Ｃ．因球壳壁无电荷，所以球壳的电量ＱⅠ等于球壳外壁的电量Ｑ１，即ＱⅠ＝Ｑ１＝－8×10－9Ｃ．2．当球壳半径趋于ｄ１时〔点电荷仍在球壳外〕，设球壳外壁的电量变为Ｑ２，球壳外的电荷ｑ１、ｑ２与球壳外壁的电量Ｑ２在壳产生的合场强仍为零，因球壳仍无电荷，球壳仍保持电势值为Ｕ的等势区，那么有〔ｋｑ１／ｄ１〕＋〔ｋｑ２／ｄ２〕＋〔ｋＱ２／ｄ１〕＝Ｕ，解得球壳外壁的电量Ｑ２＝〔ｄ１Ｕ／ｋ〕－〔ｄ１〔ｑ１／ｄ１＋ｑ２／ｄ２〕〕＝－16×10－9Ｃ．因为此时球壳壁的电量仍为零，所以球壳的电量就等于球壳外壁的电量，即ＱⅡ＝Ｑ２＝－16×10－9Ｃ，在ａ＝10ｃｍ到趋于ｄ１的过程中，流向球壳的电量为ΔＱⅠ＝ＱⅡ－Ｑ１＝－8×10－9Ｃ．3．当点电荷ｑ１穿过球壳，刚进入球壳〔导体半径仍为ｄ１〕，点电荷ｑ１在球壳壁感应出电量－ｑ１，因球壳的静电屏蔽，球壳电荷ｑ１与球壳壁电荷－ｑ１在球壳外产生的合电场为零，说明球壳外电场仅由球壳外电荷ｑ２与球壳外壁的电荷Ｑ３所决定．由于球壳的静电屏蔽，球壳外电荷ｑ２与球壳外壁的电荷Ｑ３在球壳产生的合电场为零，说明对电荷ｑ２与Ｑ３产生的合电场而言，球壳空间是电势值为Ｕ的等势区．ｑ２与Ｑ３在球心Ｏ处产生的电势等于球壳的电势，即〔ｋｑ２／ｄ２〕＋〔ｋＱ３／ｄ１〕＝Ｕ，解得球壳外壁电量Ｑ３＝〔ｄ１Ｕ／ｋ〕－〔ｄ１ｑ２／ｄ２〕＝－6×10－9Ｃ，球壳外壁和壁带的总电量应为ＱⅢ＝Ｑ３＋〔－ｑ１〕＝－16×10－9Ｃ，在这过程中，流向球壳的电量为ΔＱⅡ＝ＱⅢ－ＱⅡ＝0．这个结果说明：电荷ｑ１由球壳外极近处的位置进入壳，只是将它在球壳外壁感应的电荷转至球壳壁，整个球壳与没有电荷交换．4．当球壳半径趋于ｄ２时〔点电荷ｑ２仍在球壳外〕，令Ｑ４表示此时球壳外壁的电量，类似前面第3阶段中的分析，可得〔ｋｑ２／ｄ２〕＋〔ｋＱ４／ｄ２〕＝Ｕ，由此得Ｑ４＝〔ｄ２Ｕ／ｋ〕－〔ｄ２〔ｑ２／ｄ２〕〕＝－12×10－9Ｃ，球壳的电量ＱⅣ等于球壳外壁电量的和，即ＱⅣ＝Ｑ４＋〔－ｑ１〕＝－22×10－9Ｃ，流向球壳的电量为ΔＱⅢ＝ＱⅣ－ＱⅢ＝－6×10－9Ｃ．5．当点电荷ｑ２穿过球壳，刚进入球壳时〔球壳半径仍为ｄ２〕，球壳壁的感应电荷变为－〔ｑ１＋ｑ２〕，由于球壳的静电屏蔽，类似前面的分析可知，球壳外电场仅由球壳外壁的电量Ｑ５决定，即ｋＱ５／ｄ２＝Ｕ，可得Ｑ５＝ｄ２Ｕ／ｋ＝4×10－9Ｃ，球壳的总电量是ＱⅤ＝Ｑ５－〔ｑ１＋ｑ２〕＝－22×10－9Ｃ，〔15〕在这个过程中，流向球壳的电量是ΔＱⅣ＝ＱⅤ－ＱⅣ＝0．〔16〕6．当球壳的半径由ｄ２增至ａ１＝50ｃｍ时，令Ｑ６表示此时球壳外壁的电量，有ｋ〔Ｑ６／ａ１〕＝Ｕ，〔17〕可得Ｑ６＝ａ１〔Ｕ／ｋ〕＝5×10－9Ｃ，球壳的总电量为ＱⅥ＝Ｑ６－〔ｑ１＋ｑ２〕＝－21×10－9Ｃ，流向球壳的电量为ΔＱⅤ＝ＱⅥ－ＱⅤ＝1×10－9Ｃ．六、〔27分〕一玩具“火箭〞由上下两局部和一短而硬〔即劲度系数很大〕的轻质弹簧构成．上局部Ｇ１的质量为ｍ１，下局部Ｇ２的质量为ｍ２，弹簧夹在Ｇ１与Ｇ２之间，与二者接触而不固连．让Ｇ１、Ｇ２压紧弹簧，并将它们锁定，此时弹簧的弹性势能为的定值Ｅ０．通过遥控可解除锁定，让弹簧恢复至原长并释放其弹性势能，设这一释放过程的时间极短．第一种方案是让玩具位于一枯井的井口处并处于静止状态时解除锁定，从而使上局部Ｇ１升空．第二种方案是让玩具在井口处从静止开场自由下落，撞击井底〔井足够深〕后以原速率反弹，反弹后当玩具垂直向上运动到离井口深度为某值ｈ的时刻解除锁定．1．在第一种方案中，玩具的上局部Ｇ１升空到达的最大高度〔从井口算起〕为多少？其能量是从何种形式的能量转化而来的？2．在第二种方案中，玩具的上局部Ｇ１升空可能到达的最大高度〔亦从井口算起〕为多少？并定量讨论其能量可能是从何种形式的能量转化而来的．解：1．在弹簧刚伸长至原长的时刻，设Ｇ１的速度的大小为ｖ，方向向上，Ｇ２的速度大小为ｖ１，方向向下，那么有ｍ１ｖ１－ｍ２ｖ２＝0，①〔1／2〕ｍ１ｖ１２＋〔1／2〕ｍ２ｖ２２＝Ｅ０，②解①、②两式，得ｖ１＝，③ｖ２＝．④设Ｇ１升空到达的最高点到井口的距离为Ｈ１，那么Ｈ１＝ｖ１2／2ｇ＝〔〔ｍ２／ｍ１ｇ〔ｍ１＋ｍ２〕〕Ｅ０，⑤Ｇ１上升到最高点的重力势能为Ｅｐ1＝ｍ１ｇＨ１＝〔ｍ２／〔ｍ１＋ｍ２〕〕Ｅ０．⑥它来自弹簧的弹性势能，且仅为弹性势能的一局部．2．在玩具自井底反弹向上运动至离井口的深度为ｈ时，玩具向上的速度为ｕ＝．⑦设解除锁定后，弹簧刚伸长至原长时，Ｇ１的速度大小为ｖ１′，方向向上，Ｇ２的速度大小为ｖ，方向向下，那么有ｍ１ｖ１′－ｍ２ｖ２′＝〔ｍ1＋ｍ2〕ｕ，⑧〔1／2〕ｍ１ｖ１′＋〔1／2〕ｍ２ｖ２′＝〔1／2〕〔ｍ１＋ｍ２〕ｕ2＋Ｅ０，⑨消去⑧、⑨两式中的ｖ２′，得ｖ１′的方程式为ｍ１〔1＋〔ｍ１／ｍ２〕〕ｖ１′－2ｍ１〔1＋〔ｍ１／ｍ２〕〕ｕｖ１′＋ｍ１〔1＋ｍ１／ｍ２〕ｕ2－2Ｅ０＝0，由此可求得弹簧刚伸长至原长时，Ｇ１和Ｇ２的速度分别为ｖ１′＝ｕ＋，ｖ２′＝－ｕ＋，设Ｇ１从解除锁定处向上运动到达的最大高度为Ｈ２′，那么有Ｈ２′＝ｖ１′／2ｇ＝〔1／2ｇ〕〔ｕ＋〕2＝ｈ＋〔ｍ2Ｅ０／ｍ１ｇ〔ｍ１＋ｍ２〕〕＋2，从井口算起，Ｇ1上升的最大高度为Ｈ２＝Ｈ２′－ｈ＝〔ｍ２Ｅ０／ｍ１ｇ〔ｍ１＋ｍ２〕〕＋2．讨论：可以看出，在第二方案中，Ｇ１上升的最大高度Ｈ２大于第一方案中的最大高度Ｈ１，超出的高度与解除锁定处到井口的深度ｈ有关．到达Ｈ２时，其重力势能为Ｅｐ2＝ｍ１ｇＨ２＝〔ｍ２Ｅ０／〔ｍ１＋ｍ２〕〕＋2，〔ｉ〕假设Ｅｐ2＜Ｅ0，即2＜ｍ１Ｅ０／〔ｍ１＋ｍ２〕，这要求ｈ＜Ｅ０ｍ１／4ｍ２ｇ〔ｍ１＋ｍ２〕．这时，Ｇ１升至最高处的重力势能来自压紧的弹性势能，但仅是弹性势能的一局部．在这一条件下上升的最大高度为Ｈ２＜Ｅ０／ｍ１ｇ．〔ｉｉ〕假设Ｅｐ2＝Ｅ０，2＝ｍ１Ｅ０／〔ｍ１＋ｍ２〕，这要求ｈ＝Ｅ０ｍ１／4ｍ２ｇ〔ｍ１＋ｍ２〕．此时Ｇ１升至最高处的重力势能来自压紧的弹簧的弹性势能，且等于全部弹性势能．在这一条件下，Ｇ１上升的高度为Ｈ２＝Ｅ０／ｍ１ｇ．〔ｉｉｉ〕假设Ｅｐ2＞Ｅ０，2＞ｍ１Ｅ０／〔ｍ１＋ｍ２〕，这要求ｈ＞Ｅ０ｍ１／4ｍ２ｇ〔ｍ１＋ｍ２〕．此时Ｇ１升至最高处的重力势能大于压紧的弹簧的弹性势能，超出局部的能量只能来自Ｇ２的机械能．在这个条件下，Ｇ１上升的最大高度为Ｈ２＞Ｅ０／ｍ１ｇ．。
第20届国际物理奥林匹克竞赛试题及解答(英文)
Problems of the 20th International Physics Olympiad 1(Warsaw, 1989)Waldemar GorzkowskiInstitute of Physics, Polish Academy of Sciences, Warsaw, Poland 2AbstractThe article contains problems given at the 20th International Physics Olympiad (1989) and their solutions. The 20th IPhO was the third IPhO organized in Warsaw, Poland.LogoThe emblem of the XX InternationalPhysics Olympiad contains a picture that is ahistorical record of the first hypernuclear eventobserved and interpreted in Warsaw by M.Danysz and J. Pniewski3. The collision of ahigh-energy particle with a heavy nucleus wasregistered in nuclear emulsion. Tracks of thesecondary particles emitted in the event, seen inthe picture (upper star), consist of tracks due tofast pions (“thin tracks”) and to much slowerfragments of the target nucleus (“black tracks”).The “black track” connecting the upper star (greater) with the lower star (smaller) in the figure is due to a hypernuclear fragment, in this case due to a part of the primary nucleus containing an unstable hyperon Λinstead of a nucleon. Hyperfragments (hypernuclei) are a new kind of matter in which the nuclei contain not only protons and neutrons but also some other heavy particles.In the event observed above the hyperon Λ, bound with nucleon, decays like a free particle through a week (slow) process only. This fact strongly suggested the existence of a new quantum number that could explain suppression of the decay, even in presence of nucleons. Indeed, this was one of the observations that, 30 months later, led to the concept of strangeness.1This article has been sent for publication in Physics Competitions in October 20032e-mail: gorzk@.pl3M. Danysz and J. Pniewski, Bull. Acad. Polon. Sci., 3(1) 42 (1952) and Phil. Mag., 44, 348 (1953). Later the same physicists, Danysz and Pniewski, discovered the first case of a nucleus with two hyperons (double hyperfragment).IntroductionTheoretical problems (including solutions and marking schemes) were prepared especially for the 20th IPhO by Waldemar Gorzkowski. The experimental problem (including the solution and marking scheme) was prepared especially for this Olympiad by Andrzej Kotlicki. The problems were refereed independently (and many times) by at least two persons after any change was made in the text to avoid unexpected difficulties at the competition. This work was done by:First Problem:Andrzej Szadkowski, Andrzej Szymacha, Włodzimierz UngierSecond Problem:Andrzej Szadkowski, Andrzej Szymacha, Włodzimierz Ungier, Stanisław WoronowiczThird Problem:Andrzej Rajca, Andrzej Szymacha, Włodzimierz UngierExperimental Problem:Krzysztof Korona, Anna Lipniacka, Jerzy Łusakowski, Bruno SikoraSeveral English versions of the texts of the problems were given to the English-speaking students. As far as I know it happened for the first time (at present it is typical). The original English version was accepted (as a version for the students) by the leaders of the Australian delegation only. The other English-speaking delegations translated the English originals into English used in their countries. The net result was that there were at least four English versions. Of course, physics contained in them was exactly the same, while wording and spelling were somewhat different (the difference, however, were not too great).This article is based on the materials quoted at the end of the article and on personal notes of the author.THEORETICAL PROBLEMSProblem 1Consider two liquids A and B insoluble in each other. The pressures p i (i = A orB) of their saturated vapors obey, to a good approximation, the formula:i i o i Tp p βα+=)/ln(; i = A or B,where p o denotes the normal atmospheric pressure, T – the absolute temperature of the vapor, and i α and i β (i = A or B) – certain constants depending on the liquid. (The symbol ln denotes the natural logarithm, i.e. logarithm with base e =2.7182818…)The values of the ratio p i /p 0 for the liquids A and B at the temperature 40︒C and 90︒C are given in Tab. 1.1.Table 1.1The errors of these values are negligible.A. Determine the boiling temperatures of the liquids A and B under the pressure p 0.B. The liquids A and B were poured into a vessel in which the layersshown in Fig. 1.1 were formed. The surface of the liquid B has been coveredwith a thin layer of a non-volatile liquid C, which is insoluble in the liquids A and B and vice versa, thereby preventing any free evaporation from the uppersurface of the liquid B, The ratio of molecular masses of the liquids A and B (in the gaseous phase) is:.8/==BA μμγp 0 p 0Fig. 1.1Fig. 1.2The masses of the liquids A and B were initially the same, each equal to m = 100g. The heights of the layers of the liquids in the vessel and the densities of the liquids are small enough to make the assumption that the pressure in anypoint in the vessel is practically equal to the normal atmospheric pressure p0.The system of liquids in the vessel is slowly, but continuously and uniformly, heated. It was established that the temperature t of the liquids changed with timeτ as shown schematically in the Fig. 1.2.Determine the temperatures t1 and t2 corresponding to the horizontal parts of the diagram and the masses of the liquids A and B at the time τ1. Thetemperatures should be rounded to the nearest degree (in ︒C) and the masses of the liquids should be determined to one-tenth of gram.REMARK: Assume that the vapors of the liquids, to a good approximation,(1)obey the Dalton law stating that the pressure of a mixture of gases isequal to the sum of the partial pressures of the gases forming the mixture and(2)can be treated as perfect gases up to the pressures corresponding tothe saturated vapors.SolutionPART AThe liquid boils when the pressure of its saturated vapor is equal to the external pressure. Thus, in order to find the boiling temperature of the liquid i (i - A or B), one should determine such a temperature T bi(or t bi) for which p i/p0 = 1.Hence,Thus, the boiling temperature of the liquid A is equal toT= 3748.49K/10.711 ≈349.95 K.bAIn the Celsius scale the boiling temperature of the liquid A ist(349.95 – 273.15)︒C = 76.80︒C ≈77︒C.=bAFor the liquid B, in the same way, we obtain:α-5121.64 K,≈Bβ13.735,≈BT372-89 K,≈bBt99.74°C ≈100°C.≈bBPART BAs the liquids are in thermal contact with each other, their temperatures increase in time in the same way.At the beginning of the heating, what corresponds to the left sloped part of the diagram, no evaporation can occur. The free evaporation from the uppersurface of the liquid B cannot occur - it is impossible due to the layer of the non-volatile liquid C. The evaporation from the inside of the system is considered below.Table 1.2t67︒ C (with required accuracy).Therefore, ≈1Now we calculate the pressures of the saturated vapors of the liquids A and B at t67°C, i.e. the pressures of the saturated vapors of the liquids A the temperature ≈1and B in each bubble formed on the surface separating the liquids. From the equations (1) and (2), we get:≈A p 0.7340p ,≈B p 0.2670p ,)001.1(00p p p p B A ≈=+.Marking Scheme１．physical condition for boiling 1 point2．boiling temperature of the liquid A (numerical value) 1 point ３．boiling temperature of the liquid B (numerical value) 1 point ４．analysis of the phenomena at the temperaturet 3 points1５．numerical value oft11 point６．numerical value of the mass ratio of the saturated vapors in the bubble 1 pointτ 1 point ７．masses of the liquids at the time1８．determination of the temperaturet 1 point2REMARK: As the sum of the logarithms is not equal to the logarithm of the sum, the formula given in the text of the problem should not be applied to the mixture of the saturated vapors in the bubbles formed on the surface separating the liquids. However, the numerical data have been chosen in such a way that even such incorrect solution of the problem gives the correct value of the temperaturet(within required1accuracy). The purpose of that was to allow the pupils to solve the part B of the problem even if they determined the temperaturet in a wrong way. Of course, one1cannot receive any points for an incorrect determination of the temperaturet even if1its numerical value is correct.Typical mistakes in the pupils' solutionsNobody has received the maximum possible number of points for this problem, although several solutions came close. Only two participants tried to analyze proportion of pressures of the vapors during the upward movement of the bubble trough the liquid B. Part of the students confused Celsius degrees with Kelvins. Many participants did not take into account the boiling on the surface separating the liquids A and B, although this effect was the essence of theproblem. Part of the students, who did notice this effect, assumed a priori that the liquid with lower boiling temperature "must" be the first to evaporate. In general, this need not be true: if γwere, for example, 1/8 instead 8, then liquid A ratherthan B would remain in the vessel. As regards the boiling temperatures,practically nobody had any essential difficulties.Problem 2Three non-collinear points P 1, P 2 and P 3, with known masses m 1, m 2 andm 3, interact with one another through their mutual gravitational forces only; they are isolated in free space and do not interact with any other bodies. Let σ denote the axis going through the center-of-mass of the three masses, and perpendicular to the triangle P 1P 2P 3. What conditions should the angular velocities ω of the system (around the axis σ) and the distances:P 1P 2 = a 12, P 2P 3 = a 23, P 1P 3 = a 13,fulfill to allow the shape and size of the triangle P 1P 2P 3 unchanged during the motion of the system, i.e. under what conditions does the system rotate around the axis σ as a rigid body?SolutionAs the system is isolated, its total energy, i.e. the sum of the kinetic and potential energies, is conserved. The total potential energy of the points P 1, P 2 and P 3 with the masses 1m , 2m and 3m in the inertial system (i.e. when there are no inertial forces) is equal to the sum of the gravitational potential energies of all the pairs of points (P 1,P 2), (P 2,P 3) and (P 1,P 3). It depends only on the distances 12a , 23a and 23a which are constant in time. Thus, the total potential energy of the system is constant. As a consequence the kinetic energy of the system is constant too. The moment of inertia of the system with respect to the axis σ depends only on the distances from the points P 1, P 2 and P 3 to the axis σ which, for fixed 12a , 23a and 23a do not depend on time. This means that the moment of inertia I is constant. Therefore, the angular velocity of the system must also be constant:=ωconst. (1)This is the first condition we had to find. The other conditions will be determined by using three methods described below. However, prior to performingGM a =32ω (9)where321m m m M ++= (10)denotes the total mass of the system.In the same way, for the points P 2 and P 3, one gets the relations:a) the point P 2:1223a a =; GM a =32ωb) the point P 3:2313a a =; GM a =32ωSummarizing, the system can rotate as a rigid body if all the distances between the masses are equal:a a a a ===132312, (11)the angular velocity ω is constant and the relation (9) holds.SECOND METHODAt the beginning we find the moment of inertia I of the system with respect to the axis σ. Using the relation (2), we can write:222)(02323313121212323222221212332211r r r r r r r r r r r r m m m m m m m m m m m m +++++=++=Of course,22i i r =r i = 1, 2, 3and,011312313=-a a hence,The method described here does not differ essentially from the first method. In fact they are slight modifications of each other. However, it is interesting to notice how application of a proper mathematical language, e.g. the vector product, simplifies the calculations.The relation (9) can be called a “generalized Kepler’s law” as, in fact, it is very similar to the Kepler’s law but with respect to the many -body system. As far as I know this generalized Kepler’s law was presented for the first time right at the 20th IPhO.Marking scheme1. the proof that =ωconst 1 point2. the conditions at the equilibrium (conditions for the forcesand their moments or extremum of the total potential energy) 3 points3. the proof of the relation a a ij = 4 points4. the proof of the relation GM a =32ω 2 pointsRemarks and typical mistakes in the pupils' solutionsNo type of error was observed as predominant in the pupils' solutions.Practically all the mistakes can be put down to the students' scant experience in calculations and general lack of skill. Several students misunderstood the text of the problem and attempted to prove that the three masses should be equal. Of course, this was impossible. Moreover, it was pointless, since the masses were given. Almost all the participants tried to solve the problem by analyzingequilibrium of forces and/or their moments. Only one student tried to solve the problem by looking for a minimum of the total potential energy (unfortunately, his solution was not fully correct). Several participants solved the problem using a convenient reference system: one mass in the origin and one mass on the x -axis. One of them received a special prize.Problem 3The problem concerns investigation of transforming the electronmicroscope with magnetic guiding of the electron beam (which is accelerated with the potential difference U = 511 kV) into a proton microscope (in which the proton beam is accelerated with the potential difference –U ). For this purpose, solve the following two problems:A. An electron after leaving a device, which accelerated it with thepotential difference U , falls into a region with an inhomogeneous field Bgenerated with a system of stationary coils L 1, L 2, … , L n . The known currents in the coils are i 1, i 2, … , i n , respectively.What should the currents i 1’, i 2’, … , i n ’ in the coils L 1, L 2, … , L n be, inorder to guide the proton (initially accelerated with the potential difference –U ) along the same trajectory (and in the same direction) as that of the electron?HINT: The problem can be solved by finding a condition under which theequation describing the trajectory is the same in both cases. It may be helpful to use the relation:p dt d p = dt d 21p 2 = dtd 21p 2.B. How many times would the resolving power of the above microscopeincrease or decrease if the electron beam were replaced with the proton beam? Assume that the resolving power of the microscope (i.e. the smallest distance between two point objects whose circular images can be just separated) depends only on the wave properties of the particles.Assume that the velocities of the electrons and protons before theiracceleration are zero, and that there is no interaction between own magneticmoment of either electrons or protons and the magnetic field. Assume also that the electromagnetic radiation emitted by the moving particles can be neglected.NOTE: Very often physicists use 1 electron-volt (1 eV), and its derivativessuch as 1 keV or 1 MeV, as a unit of energy. 1 electron-volt is the energy gained by the electron that passed the potential difference equal to 1 V.Perform the calculations assuming the following data:Rest energy of electron: E e = m e c 2 = 511 keVRest energy of proton: E p = m p c 2 = 938 MeVSolutionPART AAt the beginning one should notice that the kinetic energy of the electron accelerated with the potential difference U = 511 kV equals to its rest energy 0E . Therefore, at least in the case of the electron, the laws of the classical physics cannot be applied. It is necessary to use relativistic laws.The relativistic equation of motion of a particle with the charge e in the magnetic field B has the following form:L dtd F p =It means that the value of the particle momentum (and the value of the velocity) is constant during the motion:==γv m p 0 const; v = const.The same result can be obtained without any formulae in the following way:The Lorentz force L F is perpendicular to the velocity v (and to theis the same in both cases.where c denotes the velocity of light.It is worthwhile to notice that our protons are 'almost classical', because their kinetic energy )(e k E E = is small compared to the proton rest energy p E . Thus, one can expect that the momentum of the proton can be determined, with a good accuracy, from the classical considerations. We have:.212121'22p e e p e e p e e p e p eE E c E E c E E E c E E E E E c E p =≈+=⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛+=In accordance with our expectations, we have obtained the same result as above.that λis inversely proportional to the momentum of the particle. Therefore, after replacing the electron beam with the proton beam the resolving power will be changed by the factor p/p' ≈1/35. It means that our proton microscope would allow observation of the objects about 35 times smaller than the electron microscope.Marking scheme1. the relativistic equation of motion 1 point2. independence of p and v of the time 1 point3. identity of e B/p in both cases 2 points4. scaling of the fields and the currents with the same factor 1 point5. determination of the momenta (relativistically) 1 point6. the ratio of the momenta (numerically) 1 point7. proportionality of the resolving power toλ 1 point8. inverse proportionality of λto p 1 point9. scaling of the resolving power 1 pointRemarks and typical mistakes in the pupils' solutionsSome of the participants tried to solve the problem by using laws of classicalmechanics only. Of course, this approach was entirely wrong. Some studentstried to find the required condition by equating "accelerations" of particles inboth cases. They understood the "acceleration" of the particle as a ratio of theforce acting on the particle to the "relativistic" mass of the particle. Thisapproach is incorrect. First, in relativistic physics the relationship between force and acceleration is more complicated. It deals with not one "relativistic" mass, but with two "relativistic" masses: transverse and longitudinal. Secondly, identity of trajectories need not require equality of accelerations.The actual condition, i.e. the identity of e B/p in both cases, can be obtained from the following two requirements:1° in any given point of the trajectory the curvature should be the same in both cases;2° in the vicinity of any given point the plane containing a small arc of the trajectory should be oriented in space in both cases in the same way.Most of the students followed the approach described just above. Unfortunately, many forgot about the second requirement (they neglected the vector character of the quantity e B/p).EXPERIMENTAL PROBLEM 4The following equipment is provided:1. Two piezoelectric discs of thickness 10 mm with evaporated electrodes (Fig. 4.1) fixed in holders on the jaws of the calipers;Fig. 4.12. The calibrated sine wave oscillator with a photograph of the control panel, explaining the functions of the switches and regulators;3. A double channel oscilloscope with a photograph of the control panel, explaining the functions of the switches and regulators;4. Two closed plastic bags containing liquids;5. A beaker with glycerin (for wetting the discs surfaces to allow better mechanical coupling);6. Cables and a three way connector;7. A stand for support the bags with the liquids;8. Support and calipers.A piezoelectric material changes its linear dimensions under the influence of an electric field and vice-versa, the distortion of a piezoelectric material induces an electrical field. Therefore, it is possible to excite the mechanical vibrations in a piezoelectric material by applying an alternating electric field, and also to induce an alternating electric field by mechanical vibrations.A. Knowing that the velocity of longitudinal ultrasonic waves in the material of the disc is about 3104 m/s, estimate roughly the resonant frequency of the mechanical vibrations parallel to the disc axis. Assume that the disc holders do no4 The Organizing Committee planned to give another experimental problem: a problem on high T c superconductivity. Unfortunately, the samples of superconductors, prepared that time by a factory, were of very poor quality. Moreover, they were provided after a long delay. Because of that the organizers decided to use this problem, which was also prepared, but considered as a second choice.10 mm Electrodesrestrict the vibrations. (Note that other types of resonant vibrations with lower or higher frequencies may occur in the discs.)Using your estimation, determine experimentally the frequency for which the piezoelectric discs work best as a transmitter-receiver set for ultrasound in the liquid. Wetting surfaces of the discs before putting them against the bags improves penetration of the liquid in the bag by ultrasound.B.Determine the velocity of ultrasound for both liquids without opening the bags and estimate the error.C. Determine the ratio of the ultrasound velocities for both liquids and its error.Complete carefully the synopsis sheet. Your report should, apart from the synopsis sheet, contain the descriptions of:-method of resonant frequency estimation;-methods of measurements;-methods of estimating errors of the measured quantities and of final results.Remember to define all the used quantities and to explain the symbols.5In the real Synopsis Sheet the students had more space for filling.Solution (draft)6A. As the holders do not affect vibrations of the disc we may expectantinodes on the flat surfaces of the discs (Fig. 4.2; geometric proportions not conserved). One of the frequencies is expected forfv l 221==λ,where v denotes the velocity of longitudinal ultrasonic wave (its value is given in the text of the problem), f - the frequency and l - the thickness of the disc. Thus:lv f 2=.Numerically 5102⋅=f Hz = 200 kHz.6 This draft solution is based on the camera-ready text of the more detailed solution prepared by Dr. Andrzej Kotlicki and published in the proceedings [3]l = λ/2Fig. 4.2One should stress out that different modes of vibrations can be excited in the disc with height comparable to its diameter. We confine our considerations to the modes related to longitudinal waves moving along the axis of the disc as the sound waves in liquids are longitudinal. We neglect coupling between different modes and require antinodes exactly at the flat parts of the disc. We assume also that the piezoelectric effect does not affect velocity of ultrasound. For these reasons the frequency just determined should be treated as only a rough approximation. However, it indicates that one should look for the resonance in vicinity of 200 kHz.The experimental set-up is shown in Fig. 4.3. The oscillator (generator) is connected to one of the discs that works as a transmitter and to one channel of the oscilloscope. The second disc is connected to the second channel of the oscilloscope and works as a receiver. Both discs are placed against one of the bags with liquid (Fig. 4.4). The distance d can be varied.Fig. 4.3Fig. 4.4One searches for the resonance by slowly changing the frequency of theoscillator in the range 100 – 1000 kHz and watching the signal on theoscilloscope. In this way the students could find a strong resonance at frequency 220≈f kHz. Other resonance peaks could be found at about 110 kHz and 670 kHz. They should have been neglected as they are substantially weaker. (They correspond to some other modes of vibrations.) Accuracy of these measurements was 10 kHz (due to the width of the resonance and the accuracy of the scale on the generator).B. The ultrasonic waves pass through the liquid and generate anelectric signal in the receiver. Using the same set-up (Fig. 4.3 and 4.4) we can measure dependence of the phase shift between the signals at Y 1 and Y 2 vs.distance between the piezoelectric discs d at the constant frequency found in point A . This phase shift is 0/2ϕπϕ+=∆l v df , where l v denotes velocity of ultrasound in the liquid. 0ϕ denotes a constant phase shift occurring whenultrasound passes trough the bag walls (possibly zero). The graph representing dependence )(ϕ∆d should be a straight line. Its slope allows to determine l v and its error. In general, the measurements of ϕ∆ are difficult for manyreflections in the bag, which perturb the signal. One of the best ways is tomeasure d only for πϕn =∆ (n - integer) as such points can be found rather easy. Many technical details concerning measurements can be found in [3] (pp. 37 and 38).The liquids given to the students were water and glycerin. In the standardsolution the author of the problem received the following values:v water = 310)10.050.1(⋅± m/s; v glycerin = 310)10.096.1(⋅± m/s.The ratio of these values was 1531.1 ..0The ultrasonic waves are partly reflected or scattered by the walls of the bag. This effect somewhat affects measurements of the phase shift. To minimize its role one can measure the phase shift (for a given distance) or distance (at the same phase shift) several times, each time changing the shape of the bag. Asregards errors in determination of velocities it is worth to mention that the most important factor affecting them was the error in determination of the frequency.This error, however, practically does not affect the ratio of velocities.Marking SchemeFrequency estimation1.Formula 1 point2.Result (with units) 1 point3.Method of experimental determining the resonance frequency 1 point4.Result (if within 5% of standard value) 2 points5.Error 1 pointMeasurements of velocities1.Explanation of the method 2 points2.Proper number of measurements in each series 3 points3.Result for velocity in the first liquid (if within 5% of standard value) 2 points4.Error of the above 1 point5.Result for velocity in the second liquid (if within 5% of standard value) 2 points6.Error of the above 1 pointRatio of velocities1.Result (if within 3% of standard value) 2 points2.Error of the above 1 pointTypical mistakesThe results of this problem were very good (more than a half of competitors obtained more than 15 points). Nevertheless, many studentsencountered some difficulties in estimation of the frequency. Some of themassumed presence of nodes at the flat surfaces of the discs (this assumption is not adequate to the situation, but accidentally gives proper formula). In part B some students tried to find distances between nodes and antinodes for ultrasonicstanding wave in the liquid. This approach gave false results as the pattern ofstanding waves in the bag is very complicated and changes when the shape of the bag is changed.AcknowledgementI would like to thank very warmly to Prof. Jan Mostowski and Dr. Andrzej Wysmołek for reading the text of this article and for valuable critical remarks. I express special thanks to Dr. Andrzej Kotlicki for critical reviewing the experimental part of the article and for a number of very important improvements.Literature[1] Waldemar Gorzkowski and Andrzej Kotlicki, XX Międzynarodowa Olimpiada Fizyczna - cz. I, Fizyka w Szkole nr1/90, pp. 34 - 39[2] Waldemar Gorzkowski,XX Międzynarodowa Olimpiada Fizyc zna - cz. II, Fizyka w Szkole nr2/3-90, pp. 23 - 32[3] XX International Physics Olympiad - Proceedings of the XX International Physics Olympiad, Warsaw (Poland), July 16 - 24, 1989, ed. by W. Gorzkowski, World Scientific Publishing Company, Singapore 1990 [ISBN 981-02-0084-6]。
第28届国际物理奥林匹克竞赛试题及解答(英文)
28th International Physics OlympiadSudbury, CanadaTHEORETICAL COMPETITIONThursday, July 17th, 1997Time Available: 5 hoursRead This First:1. Use only the pen provided.2. Use only the front side of the answer sheets and paper.3. In your answers please use as little text as possible; express yourself primarily inequations, numbers and figures. Summarize your results on the answer sheet.4. Please indicate on the first page the total number of pages you used.5. At the end of the exam please put your answer sheets, pages and graphs in order.This set of problems consists of 11 pages.Examination prepared at: University of British ColumbiaDepartment of Physics and AstronomyCommittee Chair: Chris WalthamHosted by: Laurentian UniversityTheory Question No.1Scaling(a) A small mass hangs on the end of a massless ideal spring and oscillates up and downat its natural frequency f. If the spring is cut in half and the mass reattached at the end,what is the new frequency? (1.5 mark s)′f(b) The radius of a hydrogen atom in its ground state is a0= 0.0529 nm (the “Bohr radius”). What is the radius of a “muonic-hydrogen” atom in which the electron is′areplaced by an identically charged muon, with mass 207 times that of the electron?Assume the proton mass is much larger than that of the muon and electron. (2 marks)(c) The mean temperature of the earth is T = 287 K. What would the new mean temperature ′T be if the mean distance between the earth and the sun was reduced by1%?(2 marks)(d) On a given day, the air is dry and has a density ρ= 1.2500 kg/m3. The next day the humidity has increased and the air is 2% by mass water vapour. The pressure and temperature are the same as the day before. What is the air density′ρnow? (2 marks)Mean molecular weight of dry air: 28.8 (g/mol)Molecular weight of water: 18 (g/mol)Assume ideal-gas behaviour.(e) A type of helicopter can hover if the mechanical power output of its engine is P. If another helicopter is made which is an exact ½-scale replica (in all linear dimensions) ofthe first, what mechanical power′P is required for it to hover? (2.5 marks)Theory Question 1: Answer Sheet STUDENT CODE: (a) Frequency : ′f(b) R adius : ′a(c) Temperature ′T:(d) Density ′ρ:(e) Power : ′PTheory Question No.2Nuclear Masses and StabilityAll energies in this question are expressed in MeV - millions of electron volts. One MeV = 1.6 × 10-13 J, but it is not necessary to know this to solve the problem.The mass M of an atomic nucleus with Z protons and N neutrons (i.e. the mass number A = N + Z ) is the sum of masses of the free constituent nucleons (protons and neutrons) minus the binding energy B/c 2.M c Zm c Nm c B p n 222=+−The graph shown below plots the maximum value of B/A for a given value of A , vs. A. The greater the value of B/A , in general, the more stable is the nucleus.Binding Energy per Nucleon(a) Above a certain mass number A α , nuclei have binding energies which are always small enough to allow the emission of alpha-particles (A=4). Use a linear approximation to this curve above A = 100 to estimate A α . (3 marks )For this model, assume the following:• Both initial and final nuclei are represented on this curve.• The total binding energy of the alpha-particle is given by B 4 = 25.0 MeV (this cannot be read off the graph!).(b) The binding energy of an atomic nucleus with Z protons and N neutrons (A=N+Z ) is given by a semi-empirical formula:B a A a A a Z A a N Z A v s c a =−−−−−−232132()δThe value of δ is given by:+ a p A -3/4 for odd-N/odd-Z nuclei0 for even-N/odd-Z or odd-N/even-Z nuclei- a p A -3/4 for even-N/even-Z nucleiThe values of the coefficients are:a v = 15.8 MeV; a s = 16.8 MeV; a c = 0.72 MeV; a a = 23.5 MeV; a p = 33.5 MeV.(i) Derive an expression for the proton number Z max of the nucleus with the largest binding energy for a given mass number A . Ignore the δ-term for this part only. (2 marks )(ii) What is the value of Z for the A = 200 nucleus with the largest B/A ? Include the effect of the δ-term. (2 marks )(iii) Consider the three nuclei with A = 128 listed in the table on the answer sheet. Determine which ones are energetically stable and which ones have sufficient energy to decay by the processes listed below. Determine Z max as defined in part (i) and fill out the table on your answer sheet.In filling out the table, please:•Mark processes which are energetically allowed thus: √•Mark processes which are NOT energetically allowed thus: 0•Consider only transitions between these three nuclei.Decay processes:(1) β -- decay; emission from the nucleus of an electron(2) β+- decay; emission from the nucleus of a positron(3)β-β- - decay; emission from the nucleus of two electrons simultaneously(4) Electron capture; capture of an atomic electron by the nucleus.The rest mass energy of an electron (and positron) is m e c2 = 0.51 MeV; that of a proton is m p c2 = 938.27 MeV; that of a neutron is m n c2 = 939.57 MeV.(3 marks)Question 2: Answer Sheet STUDENT CODE:(a) Numerical value for :Aα(b) (i) Expression for Z max:(b) (ii) Numerical value of Z :(b) (iii)Nucleus/Process β−- decay β+- decay Electron-capture ββ−−- decay128I53128Xe54128Cs55A XNotation :ZX = Chemical SymbolTheory Question No.3Solar-Powered AircraftWe wish to design an aircraft which will stay aloft using solar power alone. The mostefficient type of layout is one with a wing whose top surface is completely covered insolar cells. The cells supply electrical power with which the motor drives the propeller. Consider a wing of rectangular plan-form with span l, chord (width) c; the wing area isS = cl, and the wing aspect ratio A = l / c. We can get an approximate idea of the wing’sperformance by considering a slice of air of height x and length l being deflected downward at a small angle ε with only a very small change in speed. Control surfacescan be used to select an optimal value of ε for flight. This simple model correspondsclosely to reality if x = π l /4, and we can assume this to be the case. The total mass of ther v relative to the surrounding air. In aircraft is M and it flies horizontally with velocitythe following calculations consider only the air flow around the wing.Top view of aircraft (in its own frame of reference):incident airclSide view of wing (in a frame of reference moving with the aircraft):xr vincident air wing section air leaving wing vertical(up)Ignore the modification of the airflow due to the propeller.(a) Consider the change in momentum of the air moving past the wing, with no change in speed while it does so. Derive expressions for the vertical lift force L and the horizontal drag force D 1 on the wing in terms of wing dimensions , v, ε, and the air density ρ.Assume the direction of air flow is always parallel to the plane of the side-view diagram. (3 marks )(b) T here is an additional horizontal drag force D 2 caused by the friction of air flowing over the surface of the wing. The air slows slightly, with a change of speed ∆v (<< 1% of v ) given by:∆v v f A=The value of f is independent of ε.Find an expression (in terms of M , f , A , S , ρ and g - the acceleration due to gravity) for the flight speed v 0 corresponding to a minimum power being needed to maintain thisaircraft in flight at constant altitude and velocity. Neglect terms of order (ε 2 f ) or higher. (3 marks )You may find the following small angle approximation useful:122−≈cos sin εε(c) On the answer sheet, sketch a graph of power P versus flight speed v . Show the separate contributions to the power needed from the two sources of drag. Find anexpression (in terms of M , f , A , S , ρ and g ) for the minimum power, P min . (2 marks )(d) If the solar cells can supply sufficient energy so that the electric motors and propellers generate mechanical power of I = 10 watts per square metre of wing area, calculate the maximum wing loading Mg/S (N/m2) for this power and flight speed v0 (m/s). Assume ρ = 1.25 kg/m3, f = 0.004, A = 10. (2 marks)Question 3: Answer Sheet STUDENT CODE: (a) Expression for L :(a) Expression for D1 :(b) Expression for D2 :(b) Expression for v0 :(c)P v P minv 0(c) Expression for P min : (d) M aximum value of Mg/S : (d) Numerical value of v 0 :。
第十八届全国高中生物理竞赛复赛精彩试题及问题详解
第十八届全国中学生物理竞赛复赛试卷、参考答案全卷共六题，总分140分。
一、（22分）有一放在空气中的玻璃棒，折射率ｎ＝ 1.5 ，中心轴线长Ｌ＝ 45cm，一端是半径为Ｒ1＝ 10ｃｍ的凸球面．1．要使玻璃棒的作用相当于一架理想的天文望远镜（使主光轴上无限远处物成像于主光轴上无限远处的望远系统），取中心轴线为主光轴，玻璃棒另一端应磨成什么样的球面？2．对于这个玻璃棒，由无限远物点射来的平行入射光束与玻璃棒的主光轴成小角度φ１时，从棒射出的平行光束与主光轴成小角度φ２，求φ２／φ１（此比值等于此玻璃棒望远系统的视角放大率）．解：1．对于一个望远系统来说，从主光轴上无限远处的物点发出的入射光为平行于光轴的光线，它经过系统后的出射光线也应与主光轴平行，即像点也在主光轴上无限远处，如图18－2－6所示，图中Ｃ1为左端球面的球心．图18－2－6－Ｒ１）／Ｒ１＝ｓｉｎｒ１／ｓｉｎ（ｉ１－ｒ１）≈ｒ１／（ｉ１－ｒ１＝1／（（ｉ１／ｒ１）－1）≈1／（ｎ－1），①即（／Ｒ１）－1＝1／（ｎ－1）．②１射到另一端面时，其折射光线为平行于主光轴的光线，由此可知该端面的球心Ｃ２一定在端面顶点Ｂ的左方，Ｃ２Ｂ等于球面的半径Ｒ２，如图18－2－6所示．／Ｒ２）－1＝1／（ｎ－1），③又有＝Ｌ－，④由②、③、④式并代入数值可得２＝5ｃｍ．5ｃｍ的向外凸的球面．图18－2－72．设从无限远处物点射入的平行光线用①、②表示，令①过Ｃ１，②过Ａ，如图18－2－7所示，则这两条光线经左端球面折射后的相交点Ｍ，即为左端球面对此无限远物点成的像点．现在求Ｍ点的位置，在△ＡＣ１Ｍ中，有／ｓｉｎ（π－φ１）＝／ｓｉｎφ１＝Ｒ１／ｓｉｎ（φ１－φ１′），又ｎｓｉｎφ１′＝ｓｉｎφ１，已知φ１、φ１′均为小角度，则有／φ１＝Ｒ１／φ１（1－（1／ｎ））．≈，即Ｍ位于过Ｆ１垂直于主光轴的平面上．上面已知，玻璃棒为天文望远系统，则凡是过Ｍ点的傍轴光线从棒的右端面射出时都将是相互平行的光线．容易看出，从Ｍ射出Ｃ２的光线将沿原方向射出，这也就是过Ｍ点的任意光线（包括光线①、②）从玻璃棒射出的平行光线的方向，此方向与主光轴的夹角即为φ２，由图18－2－7可得2／φ１＝／＝（－Ｒ１）／（－Ｒ２），－Ｒ１）／（－Ｒ２）＝Ｒ１／Ｒ２，２／φ１＝Ｒ１／Ｒ２＝2．二、（22分）正确使用压力锅的方法是：将已盖好密封锅盖的压力锅（如图复18-2-1）加热，当锅内水沸腾时再加盖压力阀Ｓ，此时可以认为锅内只有水的饱和蒸气，空气已全部排除．然后继续加热，直到压力阀被锅内的水蒸气顶起时，锅内即已达到预期温度（即设计时希望达到的温度）．现有一压力锅，在海平面处加热能达到的预期温度为120℃，某人在海拔5000ｍ的高山上使用此压力锅，锅内有足量的水．1．若不加盖压力阀，锅内水的温度最高可达多少？2．若按正确方法使用压力锅，锅内水的温度最高可达多少？3．若未按正确方法使用压力锅，即盖好密封锅盖一段时间后，在点火前就加上压力阀，此时水温为27℃，那么加热到压力阀刚被顶起时，锅内水的温度是多少？若继续加热，锅内水的温度最高可达多少？假设空气不溶于水．已知：水的饱和蒸气压ｐＷ（ｔ）与温度ｔ的关系图线如图18-2-2所示．大气压强ｐ（ｚ）与高度ｚ的关系的简化图线如图18-2-3所示．当ｔ＝ 27℃时，ｐＷ（27°）＝3.6×10３Ｐａ；ｚ＝ 0处，ｐ（0）＝ 1.013×10５Ｐａ．解：1．由图18－2－8知在海平面处，大气压强ｐ（0）＝101．3×10３Ｐａ．在ｚ＝5000ｍ时，大气压强为5000）＝53×10３Ｐａ．图18－2－8图18－2－918－2－9可知，对应的温度即沸点为２＝82℃．度时，锅内水开始沸腾，温度不再升高，故在5000ｍ高山上，若不加盖压力锅，锅内温度最高可达82℃．2．由图18－2－9可知，在ｔ＝120℃时，水的饱和蒸气压ｐＷ（120°）＝198×10３Ｐａ，而在海平面处，大气压强ｐ（0）＝101×10３Ｐａ．可见压力阀的附加压强为Ｓ＝ｐＷ（120°）－ｐ（0）198×10３－101．3×10３）Ｐａ96．7×10３Ｐａ．5000ｍ高山上，大气压强与压力阀的附加压强之和为Ｓ＋ｐ（5000＝（96．7×10３＋53×10３＝149．7×103Ｐａ．若在ｔ＝ｔ２时阀被顶起，则此时的ｐＷ应等于ｐ′，即Ｗ＝ｐ′，18－2－9可知ｔ２＝112℃．5000ｍ高山上锅内水的温度最高可达112℃．3．在未按正确方法使用压力锅时，锅内有空气，设加压力阀时，内部水蒸汽已饱和．由图18－2－9可知，在ｔ＝27℃时，题中已给出水的饱和蒸气压ｐＷ（27°）＝3．6×10３Ｐａ，这时锅内空气的压强（用ｐａ表示）为ａ（27°）＝ｐ（5000）－ｐＷ（27＝（53×10３－3．6×10３＝49．4×10３Ｐａ．ａ（ｔ），则有ａ（ｔ）／（273＋ｔ）＝ｐａ（27℃）／（273＋27），３）Ｐａ．ａ（ｔ）＝（164．7ｔ＋45．0×10若在ｔ＝ｔ′时压力阀刚好开始被顶起，则有Ｗ（ｔ′）＋ｐａ（ｔ′）＝ｐ′，由此得３－164．7ｔ′）Ｐａ，Ｗ（ｔ′）＝ｐ′－ｐａ（ｔ′）＝（105×10画出函数ｐ′－ｐａ（ｔ′）的图线，取ｔ＝0℃，有ｐ′－ｐａ（0℃）＝105×10３Ｐａ，取ｔ＝100℃，有ｐ′－ｐａ（100℃）＝88．6×10３Ｐａ．18－2－9上画出此直线，此直线与图18－2－9中的ｐＷ（ｔ）－ｔ曲线的交点为Ａ，Ａ即为所求的满足上式的点，由图可看出与Ａ点对应的温度为97℃．即在压力阀刚开始被顶起时，锅内水的温度是97℃，若继续加热，压力阀被顶起后，锅内空气随水蒸汽一起被排出，最终空气排净，锅内水温仍可达112℃．碰撞后二者的速度ｖＡ和ｖＢ在一条直线上，碰撞过程中部分动能有可能被某一氢原子吸收，从而该原子由基态跃迁到激发态，然后，此原子向低能级态跃迁，并发出光子．如欲碰后发出一个光子，试论证：速度ｖ０至少需要多大（以ｍ／ｓ表示）？已知电子电量ｅ＝ 1．602×10－19Ｃ，质子质量为ｍｐ＝ 1．673×10－27ｋｇ，电子质量为ｍｅ＝ 0．911×10－31ｋｇ，氢原子的基态能量为Ｅ１＝－13．58ｅＶ．解：为使氢原子从基态跃迁到激发态，需要能量最小的激发态是ｎ＝2的第一激发态．已知氢原子的能量与其主量子数的平方成反比．即２，①ｎ＝ｋ１／ｎ又知基态（ｎ＝1）的能量为－13．58ｅＶ，即１＝ｋ１／1２＝－13．58ｅＶ， 所以 ｋ＝－13．58ｅＶ． ｎ＝2的第一激发态的能量为２＝ｋ１／2２＝－13．58×（1／4）＝－3．39ｅＶ． ② 为使基态的氢原子激发到第一激发态所需能量为 内＝Ｅ２－Ｅ１＝（－3．39＋13．58）ｅＶ＝10．19ｅＶ． ③ 这就是氢原子从第一激发态跃迁到基态时发出的光子的能量，即内＝10．19ｅＶ＝10．19×1．602×10－19＝1．632×10－18Ｊ． ④式中ν为光子的频率，从开始碰到发射出光子，根据动量和能量守恒定律有 ０＝ｍｖＡ＋ｍｖＢ＋光子的动量， ⑤1／2）ｍｖ０２＝（1／2）ｍ（ｖＡ２＋ｖＢ２）＋ｈν， ⑥ ０＞2ｈν／ｖ０，因为ｖ０<<ｃ，所以ｍｖ０>>ｈν／ｃ，故⑤式中光子的动量与ｍｖ０相比较可忽略不计．⑤式变为 ０＝ｍｖＡ＋ｍｖＢ＝ｍ（ｖＡ＋ｖＢ）， ⑦ 0的最小值可推求如下：由⑥式及⑦式可推得1／2）ｍｖ０２＝（1／2）ｍ（ｖＡ＋ｖＢ）２－ｍｖＡｖＢ＝（1／2）ｍｖ０２－ｍｖＡ（ｖ０－ｖＡ）＋ｈν，Ａ２－ｍｖＡｖ０＋ｈν＝0， 经配方得Ａ－（1／2）ｖ０）２－（1／4）ｍｖ０２＋ｈν＝0，1／4）ｍｖ０２＝ｈν＋ｍ（ｖＡ－（1／2）ｖ０）２， ⑧由⑧式可看出，当ｖＡ＝（1／2）ｖ０时，ｖ０达到最小值ｖ０ｍｉｎ，此时 Ａ＝ｖＢ，０ｍｉｎ＝2，代入有关数值，得ｖ０ｍｉｎ＝6．25×10４ｍ／ｓ．6．25×10４ｍ／ｓ． 四、（22分）如图18-4所示，均匀磁场的方向垂直纸面向里，磁感应强度Ｂ随时间ｔ变化，Ｂ＝Ｂ０－ｋｔ（ｋ为大于零的常数）．现有两个完全相同的均匀金属圆环相互交叠并固定在图中所示位置，环面处于图中纸面内．圆环的半径为Ｒ，电阻为ｒ，相交点的电接触良好，两个环的接触点Ａ与Ｃ间的劣弧对圆心Ｏ的张角为60°，求ｔ＝ｔ０时，每个环所受的均匀磁场的作用力，不考虑感应电流之间的作用．解：1．求网络各支路的电流．因磁感应强度大小随时间减少，考虑到电路的对称性，可设两环各支路的感应电流Ｉ１、Ｉ２的方向如图18－2－10所示，对左环电路ＡＤＣＦＡ，有图18－2－10Ｅ＝Ｉ１ｒＣＦＡ＋Ｉ２ｒＡＤＣ，因ｒＣＦＡ＝5ｒ／6，ｒＡＤＣ＝ｒ／6，Ｅ＝ｋπＲ２，故ｋπＲ２＝Ｉ１（5ｒ／6）＋Ｉ２（ｒ／6）．①因回路ＡＤＣＥＡ所围的面积为2（（2π－3）／12）Ｒ２，故对该回路有2（（2π－3）／12）Ｒ２］＝2Ｉ２（ｒ／6），解得Ｉ２＝（（2π－3）Ｒ２／2ｒ）ｋ，代入①式，得Ｉ１＝（（10π＋3）Ｒ２／10ｒ）ｋ．2．求每个圆环所受的力．图18－2－1118－2－11所示，将圆环分割成很多小圆弧，由左手定则可知，每段圆弧所受的力的方向均为径向，根据对称性分析，因圆弧ＰＭＡ与圆弧ＣＮＱ中的电流方向相反，所以在磁场中受的安培力相互抵消，而弧ＰＱ与弧ＡＣ的电流相对ｘ轴上下是对称的，因而每段载流导体所受的安培力在ｙ方向的合力为零，以载流导体弧ＰＱ上的线段Δｌ′为例，安培力ΔＦ为径向，其ｘ分量的大小表示为ｘ｜＝Ｉ１ＢΔｌ′ｃｏｓα，因Δｌ′ｃｏｓα＝Δｌ，故｜ΔＦｘ｜＝Ｉ１ＢΔｌ，ｘ｜＝ΣＩ１ＢΔｌ＝Ｉ１Ｂ＝Ｉ１ＢＲ．由于导体弧ＰＱ在ｙ方向的合力为零，所以在ｔ０时刻所受安培力的合力Ｆ１仅有ｘ分量，即２／10１＝｜Ｆｘ｜＝Ｉ１ＢＲ＝（（10π＋3）Ｒ＝（（10π＋3）Ｒ２／10ｒ）ｋ（Ｂ０－ｋｔ０）Ｒ，方向向左．０时刻所受的安培力为２／2２＝Ｉ２ＢＲ＝（（2π－3）Ｒ＝（（2π－3）Ｒ２／2ｒ）ｋ（Ｂ０－ｋｔ０）Ｒ，方向向右．左环所受的合力大小为３．１－Ｆ２＝（9／5ｒ）ｋ（Ｂ０－ｋｔ０）Ｒ方向向左．25分）如图18-5所示，一薄壁导体球壳（以下简称为球壳）的球心在Ｏ点．球壳通过一细导线与端电压Ｕ＝ 90Ｖ的电池的正极相连，电池负极接地．在球壳外Ａ点有一电量为ｑ１＝ 10×10－9Ｃ的点电荷，Ｂ点有一电量为ｑ２＝ 16×10－9Ｃ的点电荷．点Ｏ、Ａ之间的距离ｄ１＝ 20ｃｍ，点Ｏ、Ｂ之间的距离ｄ２＝ 40ｃｍ．现设想球壳的半径从ａ＝ 10ｃｍ开始缓慢地增大到50ｃｍ，问：在此过程中的不同阶段，大地流向球壳的电量各是多少？已知静电力常量ｋ＝ 9×10９Ｎ·ｍ２/Ｃ２．假设点电荷能穿过球壳壁进入导体球壳内而不与导体壁接触．解：分以下几个阶段讨论：1．由于球壳外空间点电荷ｑ１、ｑ２的存在，球壳外壁的电荷分布不均匀，用σ表示面电荷密度．设球壳半径ａ＝10ｃｍ时球壳外壁带的电量为Ｑ１，因为电荷ｑ１、ｑ２与球壳外壁的电量Ｑ１在球壳内产生的合场强为零，球壳内为电势等于Ｕ的等势区，在导体表面上的面元ΔＳ所带的电量为σΔＳ，它在球壳的球心Ｏ处产生的电势为ΔＵ１＝ｋσΔＳ／ａ，球壳外壁所有电荷在球心Ｏ产生的电势Ｕ１为１＝ΣΔＵ１＝ｋΣσΔＳ／α＝ｋＱ１／ａ．１、ｑ２在球壳的球心Ｏ处产生的电势分别为ｋｑ１／ｄ１与ｋｑ２／ｄ２，因球心Ｏ处的电势等于球壳的电势，按电势叠加原理，即有１／ｄ１）＋（ｋｑ２／ｄ２）＋（ｋＱ１／ａ）＝Ｕ，代入数值后可解得球壳外壁的电量Ｑ１为－９Ｃ．１＝（ａＵ／ｋ）－ａ（（ｑ１／ｄ１）＋（ｑ２／ｄ２））＝－8×10因球壳内壁无电荷，所以球壳的电量ＱⅠ等于球壳外壁的电量Ｑ１，即－9Ｃ．Ⅰ＝Ｑ１＝－8×102．当球壳半径趋于ｄ１时（点电荷仍在球壳外），设球壳外壁的电量变为Ｑ２，球壳外的电荷ｑ１、ｑ２与球壳外壁的电量Ｑ２在壳内产生的合场强仍为零，因球壳内仍无电荷，球壳内仍保持电势值为Ｕ的等势区，则有１／ｄ１）＋（ｋｑ２／ｄ２）＋（ｋＱ２／ｄ１）＝Ｕ，解得球壳外壁的电量Ｑ２＝（ｄ１Ｕ／ｋ）－（ｄ１（ｑ１／ｄ１＋ｑ２／ｄ２））＝－16×10－9Ｃ．因为此时球壳内壁的电量仍为零，所以球壳的电量就等于球壳外壁的电量，即－9Ｃ，Ⅱ＝Ｑ２＝－16×10在ａ＝10ｃｍ到趋于ｄ１的过程中，大地流向球壳的电量为－9Ｃ．Ⅰ＝ＱⅡ－Ｑ１＝－8×103．当点电荷ｑ１穿过球壳，刚进入球壳内（导体半径仍为ｄ１），点电荷ｑ１在球壳内壁感应出电量－ｑ１，因球壳的静电屏蔽，球壳内电荷ｑ１与球壳内壁电荷－ｑ１在球壳外产生的合电场为零，表明球壳外电场仅由球壳外电荷ｑ２与球壳外壁的电荷Ｑ３所决定．由于球壳的静电屏蔽，球壳外电荷ｑ２与球壳外壁的电荷Ｑ３在球壳内产生的合电场为零，表明对电荷ｑ２与Ｑ３产生的合电场而言，球壳内空间是电势值为Ｕ的等势区．ｑ２与Ｑ３在球心Ｏ处产生的电势等于球壳的电势，即２／ｄ２）＋（ｋＱ３／ｄ１）＝Ｕ，解得球壳外壁电量－9Ｃ，３＝（ｄ１Ｕ／ｋ）－（ｄ１ｑ２／ｄ２）＝－6×10球壳外壁和内壁带的总电量应为－9Ｃ，Ⅲ＝Ｑ３＋（－ｑ１）＝－16×10在这过程中，大地流向球壳的电量为Ⅱ＝ＱⅢ－ＱⅡ＝0．ｑ１由球壳外极近处的位置进入壳内，只是将它在球壳外壁感应的电荷转至球壳内壁，整个球壳与大地没有电荷交换．4．当球壳半径趋于ｄ２时（点电荷ｑ２仍在球壳外），令Ｑ４表示此时球壳外壁的电量，类似前面第3阶段中的分析，可得２／ｄ２）＋（ｋＱ４／ｄ２）＝Ｕ，由此得－9Ｃ，４＝（ｄ２Ｕ／ｋ）－（ｄ２（ｑ２／ｄ２））＝－12×10球壳的电量ＱⅣ等于球壳内外壁电量的和，即－9Ｃ，Ⅳ＝Ｑ４＋（－ｑ１）＝－22×10大地流向球壳的电量为－9Ｃ．Ⅲ＝ＱⅣ－ＱⅢ＝－6×105．当点电荷ｑ２穿过球壳，刚进入球壳内时（球壳半径仍为ｄ２），球壳内壁的感应电荷变为－（ｑ１＋ｑ２），由于球壳的静电屏蔽，类似前面的分析可知，球壳外电场仅由球壳外壁的电量Ｑ５决定，即 ５／ｄ２＝Ｕ，可得 Ｑ５＝ｄ２Ｕ／ｋ＝4×10－9Ｃ， 球壳的总电量是Ⅴ＝Ｑ５－（ｑ１＋ｑ２）＝－22×10－9（15 在这个过程中，大地流向球壳的电量是 Ⅳ＝ＱⅤ－ＱⅣ＝0 （16 6．当球壳的半径由ｄ２增至ａ１＝50ｃｍ时，令Ｑ６表示此时球壳外壁的电量，有６／ａ１（17可得 Ｑ６＝ａ１（Ｕ／ｋ）＝5×10－9Ｃ， 球壳的总电量为Ⅵ＝Ｑ６－（ｑ１＋ｑ２）＝－21×10－9Ｃ， 大地流向球壳的电量为Ⅴ＝ＱⅥ－ＱⅤ＝1×10－9Ｃ． 六、（27分）一玩具“火箭”由上下两部分和一短而硬（即劲度系数很大）的轻质弹簧构成．上部分Ｇ１的质量为ｍ１，下部分Ｇ２的质量为ｍ２，弹簧夹在Ｇ１与Ｇ２之间，与二者接触而不固连．让Ｇ１、Ｇ２压紧弹簧，并将它们锁定，此时弹簧的弹性势能为已知的定值Ｅ０．通过遥控可解除锁定，让弹簧恢复至原长并释放其弹性势能，设这一释放过程的时间极短．第一种方案是让玩具位于一枯井的井口处并处于静止状态时解除锁定，从而使上部分Ｇ１升空．第二种方案是让玩具在井口处从静止开始自由下落，撞击井底（井足够深）后以原速率反弹，反弹后当玩具垂直向上运动到离井口深度为某值ｈ的时刻解除锁定．1．在第一种方案中，玩具的上部分Ｇ１升空到达的最大高度（从井口算起）为多少？其能量是从何种形式的能量转化而来的？2．在第二种方案中，玩具的上部分Ｇ１升空可能达到的最大高度（亦从井口算起）为多少？并定量讨论其能量可能是从何种形式的能量转化而来的．解： 1．在弹簧刚伸长至原长的时刻，设Ｇ１的速度的大小为ｖ，方向向上，Ｇ２的速度大小为ｖ１，方向向下，则有 １ｖ１－ｍ２ｖ２＝0， ①1／2）ｍ１ｖ１２＋（1／2）ｍ２ｖ２２＝Ｅ０， ② 解①、②两式，得１＝， ③２＝． ④１升空到达的最高点到井口的距离为Ｈ１，则１＝ｖ１2／2ｇ＝（（ｍ２／ｍ１ｇ（ｍ１＋ｍ２））Ｅ０， ⑤ Ｇ１上升到最高点的重力势能为 ｐ1＝ｍ１ｇＨ１＝（ｍ２／（ｍ１＋ｍ２））Ｅ０． ⑥2．在玩具自井底反弹向上运动至离井口的深度为ｈ时，玩具向上的速度为．⑦１的速度大小为ｖ１′，方向向上，Ｇ２的速度大小为ｖ，方向向下，则有１ｖ１′－ｍ２ｖ２′＝（ｍ1＋ｍ2）ｕ，⑧1／2）ｍ１ｖ１′＋（1／2）ｍ２ｖ２′＝（1／2）（ｍ１＋ｍ２）ｕ2＋Ｅ０，⑨消去⑧、⑨两式中的ｖ２′，得ｖ１′的方程式为１（1＋（ｍ１／ｍ２））ｖ１′－2ｍ１（1＋（ｍ１／ｍ２））ｕｖ１′＋ｍ１（1＋ｍ１／ｍ２）ｕ2－2Ｅ０＝0，由此可求得弹簧刚伸长至原长时，Ｇ１和Ｇ２的速度分别为１′＝ｕ＋，２′＝－ｕ＋，１从解除锁定处向上运动到达的最大高度为Ｈ２′，则有2＝ｈ＋（ｍ2Ｅ０／ｍ１ｇ（ｍ１＋ｍ２））＋2，1上升的最大高度为２＝Ｈ２′－ｈ＝（ｍ２Ｅ０／ｍ１ｇ（ｍ１＋ｍ２））＋2．可以看出，在第二方案中，Ｇ１上升的最大高度Ｈ２大于第一方案中的最大高度Ｈ１，超出的高度与解除锁定处到井口的深度ｈ有关．到达Ｈ２时，其重力势能为ｐ2＝ｍ１ｇＨ２＝（ｍ２Ｅ０／（ｍ１＋ｍ２））＋2，ｐ2＜Ｅ0，即2＜ｍ１Ｅ０／（ｍ１＋ｍ２），这要求ｈ＜Ｅ０ｍ１／4ｍ２ｇ（ｍ１＋ｍ２）．１升至最高处的重力势能来自压紧的弹性势能，但仅是弹性势能的一部分．在这一条件下上升的最大高度为２＜Ｅ０／ｍ１ｇ．ｐ2＝Ｅ０，2＝ｍ１Ｅ０／（ｍ１＋ｍ２），这要求ｈ＝Ｅ０ｍ１／4ｍ２ｇ（ｍ１＋ｍ２）．１升至最高处的重力势能来自压紧的弹簧的弹性势能，且等于全部弹性势能．在这一条件下，Ｇ１上升的高度为２＝Ｅ０／ｍ１ｇ．ｐ2＞Ｅ０，2＞ｍ１Ｅ０／（ｍ１＋ｍ２），这要求ｈ＞Ｅ０ｍ１／4ｍ２ｇ（ｍ１＋ｍ２）．１升至最高处的重力势能大于压紧的弹簧的弹性势能，超出部分的能量只能来自Ｇ２的机械能．在这个条件下，Ｇ１上升的最大高度为２＞Ｅ０／ｍ１ｇ．。
2018年全国中学生奥林匹克物理竞赛--含答案
2018年全国中学生奥林匹克物理竞赛河南省预赛试卷考试时间：2018年5月27日（星期日）上午8：30～10：30注意事项：1、首先填写密封线内的市、县、学校、姓名和考号；2、用蓝色或黑色水笔、钢笔、圆珠笔直接在试卷上作答；3、答卷过程中可以使用普通型计算器；本试卷共8页，三大题，16小题，总分100分。
一、选择题（本题8小题。
每小题4分，共32分。
在每小题给出的四个选顶中，第1～4题只有一项符合题目要求．第5～8题有多项符合题目要求。
全部选对的锝4分．选对但不全的得2分，有选错的得0分，请将选出的答案序号填在下面的表格中。
1．在国际单位制（简称SI）中，力学和电学的基本单位有：m（米）、kg（千克）、s（秒）、A（安培）．则导出单位V (伏特) 用上述基本单位可表示为A．m2·kg·s-4·A-1B．m2·kg·s-3·A-1C．m2·kg·s-2·A-1D．m2·kg·s-1·A-l2．物理概念和规律的应用都有一定的前提条件，对此，下列说法中正确的是A．牛顿第二定律适用于宏观物体和微观粒子B．只要合外力的功为零，机械能就守恒C．磁感线总是闭合的D．电场线总是开放的3．一油滴静止在极板水平放置的足够大的平行板电容器中，给电容器再充上一些电荷△Q，油滴开始向上运动，经t秒后，电容器突然放电失去一部分电荷△Q'，又经过t秒，油滴回到原位置，假如在运动过程中油滴的电量一定．则A．在两个t秒内，油滴的平均速度相同B．油滴在前后两个t秒内的加速度大小之比为l ∶3C．油滴在前后两个t秒内离出发点的最大距离之比为1∶3D．△Q'∶△Q=1∶3'4、如图所示，质量均为m的两物体A、B用轻绳连接并跨过两光滑的定滑轮处于静止状态，两定滑轮间距为L；现在两定滑轮连线中点处再挂一质量也为m的物体C，从静止释放C 后，若轻绳足够长，则A ．AB ．C 的速度先增大后减小C．B 的速度一直增大 D ．A 上升的最大高度是L /85．如图所示的a 、b 分别表示一列横波上相距3 m 的两个质点A 、B 的振动图像。
历届国际物理奥林匹克竞赛试题与解答
历届国际物理奥林匹克竞赛试题与解答历届国际物理奥林匹克竞赛试题与解答第１届（1967年于波兰的华沙）质量Ｍ＝0.2kg的小球静置于垂直柱上，柱高ｈ＝5m。
一粒质量ｍ＝0.01kg、以速度0＝500m/s飞行的子弹水平地穿过球心。
球落在距离柱s＝20m的地面上。
问子弹落在地面何处？子弹动能中有多少转换为热能？解：在所有碰撞情况下，系统的总动量均保持不变：mv0 mv MV其中v和V分别是碰撞后子弹的速度和小球的速度. 两者的飞行时间都是t2h1.01s g球在这段时间沿水平方向走过20m的距离，故它在水平方向的速度为：V2019.8（m/s）1.01由方程0.01×500＝0.01v＋0.2×19.8 可求出子弹在碰撞后的速度为：v＝104m/s子弹也在1.01s后落地，故它落在与柱的水平距离为S＝vt ＝104×1.01＝105m 的地面上。
碰撞前子弹的初始动能为球在刚碰撞后的动能为12mv0 1250 J 21MV2 39.2 J 212子弹在刚碰撞后的动能为mv 54 J2与初始动能相比，两者之差为1250 J－93.2 J＝1156.8 J这表明原来动能的92.5%被系统吸收而变为热能。
这种碰撞不是完全非弹性碰撞。
在完全弹性碰撞的情形下，动能是守恒的。
而如果是完全非弹性碰撞，子弹将留在球内。
右图（甲）为无限的电阻网A络，其中每个电阻均为r，求Ａ、Ｂ两点rrrr间的总电阻。
解：如图（乙）所示BＡ、Ｂ两点间的总电阻应等于Ｃ、Ｄ两点间的总电阻与电阻ｒ的并联，再与ｒ串联图（甲）后的等效电阻。
AＣ如果网络是无限的，则Ａ、Ｂ两点间的总电阻应等于Ｃ、Ｄrrrr两点间的总电阻，设为Ｒx。
BＤ根据它们的串并联关系有：Rx rrRx图（乙）Rx r1 r 2解上式可得：Rx给定两个同样的球，其一放在水平面上，另一个以细线悬挂。
供给两球相同的热量，问两球温度是否趋于相同？说明你的理由（忽略各种热量损失）解答：如右图所示，球体受热，体积增大。
(生物科技行业)第18届全国中学生物理竞赛预赛试题参考解答
第十八届全国中学生物理竞赛预赛试题参考解答、评分标准一、参考解答杆的端点A 点绕O 点作圆周运动，其速度A v 的方向与杆OA 垂直，在所考察时其大小为 A v R ω= （1）对速度A v 作如图预解18-1所示的正交分解，沿绳BA 的分量就是物块M 是速率M v ，则cos M A v v ϕ= （2）由正弦定理知sin sin OAB H Rα∠= （3） 由图看出 2OAB πϕ∠=+ （4） 由以上各式得sin M v H ωα= （5）评分标准：本题15分其中（1）式3分；（2）式5分；（5）式7分。
二、参考解答带电质点在竖直方向做匀减速运动，加速度的大小为g ；在水平方向因受电场力作用而做匀加速直线运动，设加速度为a 。
若质点从M 到N 经历的时间为t ，则有0x v at v == （1） 00y v v gt =-= （2） 由以上两式得a g = （3）0v t g= （4） M 、N 两点间的水平距离220122v x at g== （5） 于是M 、N 两点间的电势差202MN Uv U U x d dg== （6）评分标准：本题15分（1）、（2）式各3分；（3）、（4）式各2分；（5）式3分；（6）式2分。
三、参考解答1．先求凸球面的曲率半径R 。
平行于主光轴的光线与平面垂直，不发生折射，它在球面上发生折射，交主光轴于F 点，如图预解18-3-1所示。
C 点为球面的球心，CO R =，由正弦定理，可得sin sin()R f r R r i +=- （1） 由折射定律知sin 1sin i r n= （2） 当i 、r 很小时，sin r r ≈，sin()r i r i -≈-，sin i i ≈，由以上两式得11111f r n R r i n n +===+--- （3） 所以(1)R n f =- （4）2. 凸面镀银后将成为半径为R 的凹面镜，如图预解18-3-2所示令P 表示物所在位置，P 点经平面折射成像P '，根据折射定律可推出P O nPO '= （5）由于这是一个薄透镜，P '与凹面镜的距离可认为等于P O '，设反射后成像于P ''，则由球面镜成像公式可得112RP O P O +=''' （6） 由此可解得36cm P O ''=，可知P ''位于平面的左方，对平面折射来说，P ''是一个虚物，经平面折射后，成实像于P '''点。
口第18届全国中学生物理竞赛决赛试题及答案
第十八届全国中学生物理竞赛决 赛 试 题一、（15分）图决18-1中A 是一带有竖直立柱的木块，总质量为M ，位于水平地面上。
B 是一质量为m 的小球，通过一不可伸长的轻绳挂于立柱的顶端。
现拉动小球使绳伸直并处于水平位置。
然后让小球从静止状态下摆。
如在小球与立柱发生碰撞前，木块A 始终未发生移动，则木块与地面之间的静摩擦因数至少为多大？（设A 不会发生转动）二、（15分）圆形线圈C 轴线z 沿水平方向。
有一用钕铁硼材料制成的圆柱形强磁体M ，其圆形端面分别为N 极和S 极，将磁体M 与线圈C 共轴放置。
磁体的对称中心置于z 轴的原点O 。
Q 点是线圈C 对称截面的圆心，当Q 点位于z 轴不同位置时，用实验的方法测得穿过线圈C 的总磁通ψ。
由此测得的ψ值沿z 轴的分布函数图线如图决18-2（a ）所示。
图中横轴上z 值是Q 点的坐标。
现令强磁体M 沿线圈的轴线方向穿过该线圈C ，将C 两端接一电阻，其阻值R=1000Ω，远大于线圈的电阻阻值。
将接在电阻R 两端的电压信号通过计算机实时处理[如图决18-2（b ）所示]，可在计算机屏幕上显示出线圈C 两端的电压信号如图决18-2（c ）所示，信号轨迹近似看作三角波形。
1．试估算强磁体M 通过线圈时的速度。
（不计线圈中的感应电流对运动磁体的影响。
） 2．试求图（c ）中，1t 至3t 期间流过电阻R 的电量。
三、（20分）有一薄透镜如图决18-3，S B图决18-1 A S 2F 1F 2CS 1绕长轴旋转而成的曲面），其焦点为F 1和F 2；S 2面是球面，其球心C 与F 2重合。
已知此透镜放在空气中时能使从无穷远处位于椭球长轴的物点射来的全部入射光线（不限于傍轴光线）会聚于一个像点上，椭圆的偏心率为e 。
（1）求此透镜材料的折射率n （要论证）；（2）如果将此透镜置于折射率为n '的介质中，并能达到上述的同样的要求，椭圆应满足什么条件？四、（20分）空间有半径为R 长度L 很短的圆柱形的磁场区域，圆柱的轴线为z 轴，磁场中任一点的磁感应强度的方向沿以z 轴为对称轴的圆的切线，大小与该点离z 轴的距离r 成正比，B=K r ，K 为常数，如图决18-4中“· ”与 “×”所示。
历届国际物理奥林匹克竞赛试题与解答
历届国际物理奥林匹克竞赛试题与解答第3届（1969年于捷克斯洛伐克的布尔诺）【题1】右图的力学系统由三辆车组成，质量分别为m A ＝0.3kg ，m B ＝0.2kg ，m C ＝1.5kg 。
（a ）沿水平方向作用于C 车的力F 很大。
使A 、B 两车相对C 车保持静止。
求力F 及绳子的张力。
（b ）C 车静止，求A 、B 两车的加速度及绳子的张力。
（忽略阻力和摩擦力，忽略滑轮和车轮的转动惯量）解：（a ）A 、B 两车相对C 车保持静止，A 车在竖直方向没有加速度，因此它对绳的拉力为m A g 。
这个力使B 车得到加速度g m m a BAB =。
又三车系统以相同的加速度运动，则： g m m m m m F BAC B A )(++= 由给定的数值得：a B ＝a C ＝a A ＝1.5g ＝14.7m/s 2绳中的张力为：T ＝m A g ＝2.94N 水平推力为：F ＝29.4N（b ）如果C 车静止，则力m A g 使质量m A ＋m B 加速，加速度为：BA A AB m m gm a +=＝0.6g ＝5.88N绳中的张力为：T /＝m A g －m A ×0.6g ＝1.176N【题2】在质量为m 1的铜量热器中装有质量为m 2的水，共同的温度为t 12；一块质量为m 3、温度为t 3的冰投入量热器中（如右图所示）。
试求出在各种可能情形下的最终温度。
计算中t 3取负值。
铜的比热c 1＝0.1kcal/kg·0C ，水的比热c 2＝1kcal/kg·0C ，冰的比热c 3＝0.5kcal/kg·0C ，冰的熔解热L ＝80kcal/kg 。
解：可能存在三种不同的终态：（a ）只有冰；（b ）冰水共存；（c ）只有水。
（a ）冰温度升高，但没有熔化，达到某一（负）温度t a ； 放出的热量和吸收的热量相等：c 3 m 3（t a －t 3）＝（c 1 m 1＋c 2 m 2）（t 12－t a ）＋m 2L得出最终的温度为3332112333122211)(c m c m c m Lm t c m t c m c m t a +++++=（1）情况（a ）的条件是t a ＜０（注：指00C ），如果上式的分子为负值，我们得到下列条件： （c 1 m 1＋c 2 m 2）t 12＜―c 3 m 3t 3―m 2L （2）（c ）现在让我们讨论冰块全部熔化的情况。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
Hints and Data The atmosphere is to be dealt with as an ideal gas. Influences of the water vapour on the specific heat capacity and the atmospheric density are to be neglected; the same applies to the temperature dependence of the specific latent heat of vaporisation. The temperatures are to be determined to an accuracy of 1 K, the height of the cloud ceiling to an accuracy of 10 m and the precipitation level to an accuracy of 1 mm. Specific heat capacity of the atmosphere in the pertaining temperature range: cp = 1005 J ⋅ kg-1 ⋅ K-1 Atmospheric density for p0 and T0 at station M0: ρ0 = 1.189 kg ⋅ m-3 Specific latent heat of vaporisation of the water within the volume of the cloud: Lv = 2500 kJ ⋅ kg-1
Leibniz-Institute for Science Education (IPN) at the University of Kiel, Germany
Abstract The 18th International Physics Olympiad took place in 1987 in the German Democratic Republic (GDR). This article contains the competition problems, their solutions and also a (rough) grading scheme.
stream in 3 hours, assuming a homogeneous rainfall between points M1 网/
京翰教育中心/
5. What temperature T3 is measured in the back of the mountain range at station M3? Discuss the state of the atmosphere at station M3 in comparison with that at station M0.
The experimental problem (“refracting indices”) was much more easier than the theoretical problems. There were lots of different possibilities of solution and most of the pupils
cp = χ = 1.4 and g = 9.81 m ⋅ s-2 cv
Solution of problem 1:
1. Temperature T1 where the cloud ceiling forms
T1
=
T0
⋅ ⎛⎜ ⎝
p1 p0
⎞1−
1 χ
⎟ ⎠
=
279 K
(1)
2. Height h1 of the cloud ceiling:
1. Determine temperature T1 at M1 where the cloud ceiling forms. 2. What is the height h1 (at M1) above station M0 of the cloud ceiling assuming a linear
京翰教育中心/
managed to come up with partial or complete solutions. Over the half of all teams got more points in the experimental part than in the theoretical part of the competition. The problems and their solutions are based on the original German and English versions of the competition problems. Only minor changes have been made. Despite the fact that nowadays almost all printed figures are generated with the aid of special computer programmes, the original hand-made figures are published here.
Introduction The 18th international Physics olympics in 1987 was the second International Physics Olympiad hosted by the German Democratic Republic (GDR) . The organisation was lead by the ministry for education and the problems were formulated by a group of professors of different universities. However, the main part of the work was done by the physics department of the university of Jena. The company Carl-Zeiss and a special scientific school in Jena were involved also.
p0 − p1 = ρ0 + ρ1 ⋅ g ⋅ h1 , with ρ1 = ρ0 ⋅ p1 ⋅ T0 .
2
p0 T1
h1 =1410 m
(2)
3. Temperature T2 at the ridge of the mountain. The temperature difference when the air is ascending from the cloud ceiling to the mountain ridge is caused by two processes:
In the competition three theoretical and one experimental problem had to be solved. The theoretical part was quite difficult. Only the first of the three problems (“ascending moist air”) had a medium level of difficulty. The points given in the markings were equal distributed. Therefore, there were lots of good but also lots of unsatisfying solutions. The other two theoretical problems were rather difficult. About half of the pupils even did not find an adequate start in solving these problems. The third problem (“infinite LC-grid") revealed quite a few complete solutions. The high level of difficulty can probably be explained with the fact that many pupils nearly had no experience with the subject. Concerning the second problem (“electrons in a magnetic field”) only a few pupils worked on the last part 3 (see below).
1 Contact: Leibniz-Institute for Science Education (IPN) at the University of Kiel
Olshausenstrasse 62, 24098 Kiel, Germany
ipho@ipn.uni-kiel.de
1
高中物理辅导网/
高中物理辅导网/
京翰教育中心/
Problems of the 18th International Physics Olympiad (Jena, 1987)
Gunnar Friege & Gunter Lind1
decrease of atmospheric density? 3. What temperature T2 is measured at the ridge of the mountain range? 4. Determine the height of the water column (precipitation level) precipitated by the air