LU分解法求线性方程组算法流程图
MATLAB报告用LU分解法求解线性方程组
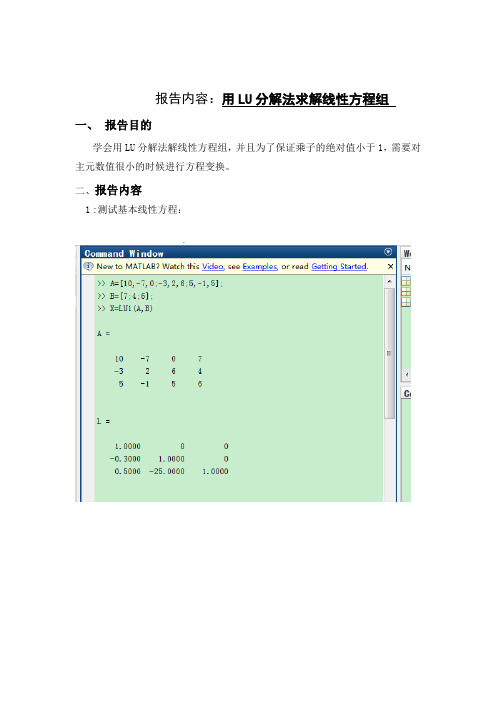
报告内容:用LU分解法求解线性方程组一、报告目的学会用LU分解法解线性方程组,并且为了保证乘子的绝对值小于1,需要对主元数值很小的时候进行方程变换。
二、报告内容1 :测试基本线性方程:可见程序运行结果正确。
2 :测试主元有接近于0的线性方程:可见程序运行结果正确。
3:测试矩阵维度大于5情况:可见程序运行结果正确。
三、源程序function X=LU1(A,B)B=B';A=[A';B]',n=length(B');X=zeros(n,1);y=zeros(n,1);U=zeros(n);L=eye(n);for k=1:nU(1,k)=A(1,k);L(k,1)=A(k,1)/U(1,1);endfor i=2:nfor k=i:nlu=0;lu1=0;for j=1:i-1lu=lu+L(i,j)*U(j,k);lu1=lu1+L(k,j)*U(j,i);endU(i,k)=A(i,k)-lu;L(k,i)=(A(k,i)-lu1)/U(i,i);endendLUfor i=1:nly=0;for j=1:ily=ly+L(i,j)*y(j);endy(i)=B(i)-ly;endfor i=n:-1:1ly1=0;for j=i+1:nly1=ly1+U(i,j)*X(j);endX(i)=(y(i)-ly1)/U(i,i);end四、报告分析与心得MATLAB编程和C编程一样需要仔细的逻辑和十分的细心,自己还有很多需要学习的地方。
LU和QR分解法解线性方程组

LU 和QR 法解线性方程组一、 问题描述求解方程组⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡20116126384102785124⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡4321x x x x ==⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----3772, 要求:1、编写用三角(LU )分解法求解线性方程组;2、编写用正交三角(QR )分解法求解线性方程组。
二、问题分析求解线性方程组Ax=b ,其实质就是把它的系数矩阵A 通过各种变换成一个下三角或上三角矩阵,从而简化方程组的求解。
因此,在求解线性方程组的过程中,把系数矩阵A 变换成上三角或下三角矩阵显得尤为重要,然而矩阵A 的变换通常有两种分解方法:LU 分解法和QR 分解法。
1、LU 分解法:将A 分解为一个下三角矩阵L 和一个上三角矩阵U ,即:A=LU,其中 L=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡10010012121n n l l l , U=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡nn n n u u u u u u 0000022211211 2、QR 分解法:将A 分解为一个正交矩阵Q 和一个上三角矩阵R,即:A=QR三、实验原理1、LU 分解法解Ax=b 的问题就等价于要求解两个三角形方程组: ⑴ Ly=b,求y; ⑵ Ux=y,求x.设A 为非奇异矩阵,且有分解式A=LU , L 为单位下三角阵,U 为上三角阵。
L,U 的元素可以有n 步直接计算定出。
用直接三角分解法解Ax=b (要求A 的所有顺序主子式都不为零)的计算公式:① ),,2,1(n i a u li li ==,11/u a l il il = ,i=2,3,…,n. 计算U 的第r 行,L 的第r 列元素(i=2,3,…,n): ② ∑-=-=11r k ki rkri ri u la u , i=r,r+1,…,n;③ rr r k kr ikir ir u u la l /)(11∑-=-= , i=r+1,…,n,且r ≠n.求解Ly=b ,Ux=y 的计算公式;④:,3,2,,1111n i y l b y b y i k k ik i i =-==∑-=⑤.1,,2,1,/)(,/1--=-==∑+=n n i u x uy x u y x ii ni k k iki i nn n n2、QR 分解法四、实验步骤1、LU 分解法1>将矩阵A 保存进计算机中,再定义2个空矩阵L ,U 以便保存求出的三角矩阵的值。
fortranlu分解法

Fortran LU分解法是一种用于解线性方程组的算法,它可以将一个方阵分解为一个下三角矩阵和一个上三角矩阵的乘积。
这种分解方法可以用于高斯消元法、最小二乘法和特征值计算等多种应用中。
在Fortran中,LU分解可以通过调用预先定义好的子程序实现。
下面是一个示例程序,演示如何使用Fortran LU分解法解一个线性方程组:program LUdecompositionimplicit noneinteger, parameter :: n = 3real, dimension(n,n) :: A, L, Ureal, dimension(n) :: b, xinteger :: i, j, k! Input matrix A and vector bA = reshape([2.0, 1.0, 1.0, 6.0, 2.0, 1.0, -2.0, -1.0, 3.0], shape(A))b = [1.0, 2.0, 3.0]! LU decomposition of Acall lu(n, A, L, U)! Solve Ax=b using forward and backward substitutiondo i = 1, nx(i) = b(i) / L(i,i)end dodo i = n, 1, -1do j = i+1, nx(i) = x(i) - U(i,j) * x(j)end dox(i) = x(i) / U(i,i)end do! Output solution xprint *, "Solution: ", xend program LUdecomposition在上面的程序中,我们首先定义了一个3x3的矩阵A和一个3x1的向量b。
然后,我们调用预先定义的子程序lu对矩阵A进行LU分解,得到下三角矩阵L和上三角矩阵U。
接下来,我们使用前向和后向代入法解方程组Ax=b,得到解向量x。
数值分析_lec4_解线性方程组_LU分解法_1013

第二章(二):LU分解法
2.2.1 LU分解法
矩阵A的LU分解:
A LU
1
若L为单位下三角矩阵:
1 l21 L ln1
1 lnn 1
Doolittle分解
* ** * P2 P 1Qk }(Qk A) U k 1 Qk A Lk -1U k 1
2.2.2* 选主元的LU分解法
一般的,我们有Pn-1Qn 1 Pk 1Qk 1 P2Q2 PQ 1 1 A U , 这里Qk (k 1, 2, , n 1)
为初等置换阵或单位阵,于是有:
2.2.1 LU分解法
(L为单位下三角矩阵,U为上三角矩阵) Doolittle分解算法:
a11 a21 an1
a12 a22 an 2
a1n 1 a2 n l21 1 ann ln1 ln 2
a1 j u1 j ( j 1, 2, , n)
u11 l21 ln1
u12 a22 an 2
u1n 1 a2 n l21 1 ann ln1 ln 2
, n)
u11 u12 u22 1
u1n u2 n unn
* P2 P 1 A QkU k 1 U k 1
2.2.2* 选主元的LU分解法
在执行第k 步之前, 交换第k行与第ik 行, 上式两侧左乘以初等置换矩阵Qk Qk Pk 1
1 1 L* k -1 P 1 P 2 * P2 P 1 A QkU k 1 U k 1
求解线性方程组的LU分解法

由于求解三解方程较易,所以,考虑将系数矩阵A分解成两个三角矩阵的乘积,
即:A=LU的形式
其中,L为下三解矩阵,U为上三解矩阵,则线性方程组:
Ax=b
可改写为LUx=b
令Ux=y
得Ly=b
然后,用前代方法求Ly=b得列矩阵y,再用回代方法求Ux=b,得到的列矩阵x即为所求的线性方程组的解.
free(yAnsList);
}
/*The matrix’s LUPation Method
This version is implemnted by EmilMatthew 05/8/19
You can use these code freely , but I'm not assure them could totally fit your needs.
/*memory apply*/
matrix_L=(Type**)malloc(sizeof(Type*)*len);
matrix_U=(Type**)malloc(sizeof(Type*)*len);
for(i=0;i<len;i++)
{
matrix_L[i]=(Type*)malloc(sizeof(Type)*len);
}
/*Check the input data*/
showArrListFloat(bList,0,len);
show2DArrFloat(matrixArr,len,len);
#if DEBUG
printf("\n*******start of test program******\n");
printf("now is runnig,please wait...\n");
线性方程组数值解法LU分解法

i1
1 ) y 1 b 1 ; y i b i l ij y j )( i 2 ,..., n ); j1
n
2 ) x n y n / a nm ; x i ( y i u ij x j ) / u ii ( i n 1 ,..., 2 ,1 ); ji1
a(1) i1
a(1) 11
则 (1)行(-li1) (i)行 i 2,3,...,n,其矩阵形式为
1 l2 1 .l.3.1 ln1
1
aa((121111))
01
...
......
...
0 0 ...... 1a(n11)
L1
a(1) ... ... a(1) a(1)
12
a(1) 22
3.2.2 Doolittle分解
此 分 解 在 于 如 何 算 出 L,U 的 各 元 素 , 以 n 3为 例
a11 a12 a13 1
a
21
a22
a
2
3
l
2
1
1
u11 u12 u13
u 22
u
2
3
Байду номын сангаас
a31 a32 a33 l31 l32 1
u 33
k 1时 : a1 j u1 j u1 j a1 j ( j 1, 2, 3)
Doolittle分解
计算 l k 1 k ,..., l nk 由于 i k ,于是由
u1k
a ik
[ li1 ...,
l
ik
1
,1
,
0
...
0
]
u kk 0
LU和QR分解法解线性方程组

LU和QR分解法解线性方程组LU 和QR 法解线性方程组一、 问题描述求解方程组⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡20116126384102785124⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡4321x x x x ==⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----3772,要求:1、编写用三角(LU )分解法求解线性方程组;2、编写用正交三角(QR )分解法求解线性方程组。
二、问题分析求解线性方程组Ax=b ,其实质就是把它的系数矩阵A 通过各种变换成一个下三角或上三角矩阵,从而简化方程组的求解。
因此,在求解线性方程组的过程中,把系数矩阵A 变换成上三角或下三角矩阵显得尤为重要,然而矩阵A矩阵其余的元素,每次都要三次循环,求下一个元素需要上一个结果。
3>先由公式④ ,Ly=b:,3,2,,1111n i y l b y b y i k kiki i =-==∑-= 求出y ,因为L 为下三角矩阵,所以由第一行开始求y.4>再由公式⑤,Ux=y.1,,2,1,/)(,/1--=-==∑+=n n i u x u y x u y x ii ni k k ik i i nn n n求出x, 因为U 为上三角矩阵,所以由最后一行开始求x. 2、QR 分解法四、程序流程图1、LU 分解法开始输入系数矩阵A,常数项b及ndet←1K=1,n-1,1调选列主元子程序i=k+1,n,1aik←aik/akk(即求乘数mik)j=k+1,n,1aik←aij-aik *akjjbi←bi←aik*bkidet←akkdetkbn←bn/am(即求出xn)i=n-1,1,-1s←0j=i+1,n,1s←s+aij*bjjbi←(bi-s)/aij输出b及det结束idet←amndet回代过程消元过程由主程序转来d ←akk,p ←k i=k+1,n,1|aik|>|d|d ←aik,p ←ii d=0P=k j=k,n,1t ←apj,apj ←akj,akj ←t jt ←bp,bp ←bk,bk ←tdet ←det 返回主程序返回主程序输出失败标志,|A|=0det ←0结束选列主元≤=≠=2、QR 分解法开始输入数据A,b矩阵A的转置Householder变换转置矩阵相乘输出上三角阵R=H3*H2*H1*A输入正交阵Q=-(H3*H2*H1)T解上三角阵输出结果结束五、实验结果1、LU分解法2、QR分解法六、实验总结为了求解线性方程组,我们通常需要一定的解法。
三角矩阵的lu分解

三角矩阵的lu分解在线性代数中, LU分解(LU Decomposition)是矩阵分解的一种,可以将一个矩阵分解为一个单位下三角矩阵和一个上三角矩阵的乘积(有时是它们和一个置换矩阵的乘积)。
LU分解主要应用在数值分析中,用来解线性方程、求反矩阵或计算行列式。
什么是LU分解如果有一个矩阵A,将A表示成下三角矩阵L和上三角矩阵U的乘积,称为A的LU分解。
更进一步,我们希望下三角矩阵的对角元素都为1:一旦完成了LU分解,解线性方程组就会容易得多。
LU分解的步骤对于满秩矩阵A来说,通过左乘一个消元矩阵,可以得到一个上三角矩阵U。
可以看到,L实际上就是消元矩阵的逆。
容易知道二阶矩阵的逆:现在假设A是一个3×3矩阵,在不考虑行交换的情况下,通过消元得到上三角矩阵的过程是:LU 分解的前提并非所有矩阵都能进行LU分解,能够LU分解的矩阵需要满足以下三个条件:矩阵是方阵(LU分解主要是针对方阵);矩阵是可逆的,也就是该矩阵是满秩矩阵,每一行都是独立向量;消元过程中没有0主元出现,也就是消元过程中不能出现行交换的初等变换。
LU分解的意义LU分解的意义在于求解大型方程组。
一个方程组可以简化为Ax = b的形式,其中A是n阶方阵,x是未知数组成的向量,b是n×1矩阵,例如:以往求解的方式有两种,一是高斯消元法,二是对A求逆,使得x = A-1b。
第二种方式远比消元法复杂,先看一下消元法的计算量。
假设A是n阶满秩方阵,如果不写成增广矩阵,即不考虑 b,那么第一次消元达到的效果是:其中方块是A原来的元素,0是达到的效果,三角是经过消元运算后改变的元素。
以第二行为例,为了使第一个元素为0,需要让第一行乘以某个数(第一行n个元素,共进行了n次乘法运算),再将第一行和第二行相加或相减(第二行n个数与第一行的n个数相加,共进行了n次加法运算)。
如果把一组乘法和加法看成一次运算,那么第二行的消元共进行了n次运算;共有n-1行需要类似运算,所以第一次消元共进行了n(n - 1) ≈ n2次运算。
