集合训练题
高中数学 集合专项训练含答案

高中数学 集合专项训练含答案一、单选题1.设集合(){}0.5log 10A x x =->,{}24x B x =<,则( ) A .A =B B .A B ⊇ C .A B B = D .A B B ⋃=2.已知集合{0A x x =≤或}1≥x ,{}39x B x =<,则A B =( ) A .{}12x x ≤<B .{0x x ≤或}12x ≤<C .{}2x x <D .{}02x x ≤<3.设S 是整数集Z 的非空子集,如果任意的,a b S ∈,有ab S ∈,则称S 关于数的乘法是封闭的.若T 、V 是Z 的两个没有公共元素的非空子集,T V ⋃=Z .若任意的,,a b c T ∈,有abc T ∈,同时,任意的,,x y z V ∈,有xyz V ∈,则下列结论恒成立的是( ) A .T 、V 中至少有一个关于乘法是封闭的B .T 、V 中至多有一个关于乘法是封闭的C .T 、V 中有且只有一个关于乘法是封闭的D .T 、V 中每一个关于乘法都是封闭的4.已知集合(){}2log 21M x y x ==-,103x N x x ⎧⎫+=≤⎨⎬-⎩⎭,则M N =( )A .1,2⎛⎫+∞ ⎪⎝⎭B .[)1,-+∞C .1,32⎛⎫ ⎪⎝⎭D .1,32⎛⎤ ⎥⎝⎦ 5.已知集合{1,1},{0,1}A B =-=,设集合{,,}C z z x y x A y B ==+∈∈∣,则下列结论中正确的是( )A .A C ⋂=∅B .AC A ⋃= C .B C B =D .A B C =6.已知集合{}1,0,1,2A =-,{}03B x x =≤≤,则A B =( )A .{}1B .{}2C .{}1,2D .{}0,1,2 7.已知集合{1,3}A =,{(3)()0}B xx x a =--=∣,若A B A ⋃=,则=a ( ) A .1 B .1-或1 C .1或3 D .38.设集合{A x y =,(){}ln 2B y y x ==-,(){}2,C x y y x ==,则下列集合不为空集的是( )A .A CB .BC ⋂ C .B A ⋂RD .A B C ⋂⋂ 9.已知集合{}2320A x x x =-+>,{}1,B m =,若A B ⋂≠∅,则实数m 的取值范围是( )A .()1,2B .()(),12,-∞+∞C .[]1,2D .()2,+∞10.若集合(){}ln 10A x x =-≤,{}2B x x =≥,则()R AB =( ) A .(2,2)- B .(1,2)C .[)1,2D .(1,2]11.()Z M 表示集合M 中整数元素的个数,设{}1|8A x x =-<<,{}|527B x x =-<<,则()Z A B =( )A .5B .4C .3D .212.已知集合{}10,1,2,A B x y x ⎧⎫===⎨⎬⎩⎭∣,则A B ⋃=( ) A .{}0,1,2 B .{}1,2 C .()0,∞+ D .[)0,∞+13.已知集合{}{}220,1A x x x B x x =+-<=<-,则()U A B =( )A .{}11x x -<<B .{}11x x -≤<C .{}21x x -<<-D .{}12x x -≤<14.已知集合{}2230A x x x =--≤,{}22B x x =-≤<,则A B ⋃=( ) A .{}12x x -≤< B .{}12x x -≤≤ C .{}22x x -<< D .{}23x x -≤≤15.设集合{}*5,,5m M x x C m N m ==∈≤,则M 的子集个数为( ) A .8 B .16 C .32 D .64二、填空题16.设集合{1,2,}A a =,{2,3}B =.若B A ⊆,则=a _______.17.已知全集{1,2,3,4,5,6,7}U =,集合{}1,3,5,7A =,则U A ____________. 18.已知集合{}2,1,2A =-,{}1,B a a =+,且B A ⊆,则实数a 的值是___________. 19.已知集合A 与B 的关系如下图,则图中所示的阴影部分用集合表示为________.(要求用集合A 与B 的符号关系表示)20.已知集合{}2A x x =<,{}2,0,1,2B =-,则A B =_______.21.若将抛掷一枚硬币所出现的结果“正面(朝上)”与“反面(朝上)”,分别记为H 、T ,相应的抛掷两枚硬币的样本空间为{},,,HH HT TH TT Ω=,则与事件“一个正面(朝上)一个反面(朝上)”对应的样本空间的子集为______.22.已知集合{}0,1,2A =,则集合{}3,B b b a a A ==∈=______.(用列举法表示)23.已知集合{}2280P x x x =-->,{}Q x x a =≥,若P Q Q ⋂=,则实数a 的取值范围是___________.24.判断下列命题的真假:(1)集合{}1,2,3是集合{}1,2,3的真子集;( )(2){}1是集合{}1,2,3的元素;( )(3)2是集合{}1,2,3的子集;( )(4)满足{}{}00,1,2,3A 的集合A 的个数是322-个.( )25.以下各组对象不能组成集合的是______(用题号填空).①中国古代四大发明 ②地球上的小河流③方程210x -=的实数解 ④周长为10cm 的三角形⑤接近于0的数三、解答题26.设集合{|34}{|211}A x x B x m x m =-≤≤=-<<+,(1)当 1m =时,求A B ;(2)若,B A ⊆求实数m 的取值范围.27.在①A B A ⋃=,②A B ⋂≠∅,③B A ⊆R 这三个条件中任选一个,补充在下面问题(3)中,若问题中的实数m 存在,求m 的取值范围;若不存在,说明理由.已知一元二次不等式2320ax x -+>的解集为{1A x x =<或}x b >,关于x 的不等式()20ax am b x bm -++<的解集为B (其中m ∈R ).(1)求a ,b 的值;(2)求集合B ;(3)是否存在实数m ,使得_______.(注:如果选择多个条件分别解答,按第一个解答计分).28.设:24p x <<,q :实数x 满足()()()300x a x a a +-<>.(1)若1a =,且p ,q 都为真命题,求x 的取值范围;(2)若p 是q 的充分不必要条件,求实数a 的取值范围.29.设全集U =R ,已知集合2{|2350}A x x x =+-≤,{(8)0}B xx x =->∣. (1)求()R ,A B A B ⋂⋃;(2)求()R ,A B A B ⋂⋃.30.把区间[)1,+∞看成全集,写出它的下列子集的补集:()1,A =+∞;{}1B =;{}15C x x =≤<;[)3,D =+∞.【参考答案】一、单选题1.D【解析】【分析】化简集合,A B ,再判断各选项的对错.【详解】因为0.5{|log (1)0}{|12}A x x x x =->=<<,{}24={|2}x B x x x =<<, 所以A B ⊆且A B ≠,所以A 错,B 错,{|12}A B x x A =<<=,C 错,{|2}A B x x B =<=,D 对,故选:D.2.B【解析】【分析】解出不等式39x <,然后根据集合的交集运算可得答案.【详解】 因为{0A x x =≤或}1≥x ,{}39x B x =< {}2x x =<,所以A B ={0x x ≤或}12x ≤<, 故选:B3.A【解析】【分析】本题从正面解比较困难,可运用排除法进行作答.考虑把整数集Z 拆分成两个互不相交的非空子集T 、V 的并集,如T 为奇数集,V 为偶数集,或T 为负整数集,V 为非负整数集进行分析排除即可.【详解】若T 为奇数集,V 为偶数集,满足题意,此时T 与V 关于乘法都是封闭的,排除B 、C ; 若T 为负整数集,V 为非负整数集,也满足题意,此时只有V 关于乘法是封闭的,排除D ;从而可得T 、V 中至少有一个关于乘法是封闭的,A 正确.故选:A .4.C【解析】【分析】根据对数型函数定义域解法求出集合M ,根据分式不等式解法求出集合N ,再根据集合交集概念即可求得结果.【详解】由题意知(){}21log 21,2M x y x ∞⎛⎫==-=+ ⎪⎝⎭,[)101,33x N x x ⎧⎫+=≤=-⎨⎬-⎩⎭, 所以1,32M N ⎛⎫⋂= ⎪⎝⎭. 故选:C .5.C【解析】【分析】由题意得{1,0,1,2}C =-,再由交集和并集运算求解即可.【详解】由题意可知,{1,0,1,2}C =-,{1,1}A C ⋂=-,{}1,0,1,2A C C ⋃=-=,{0,1},{1,0,1}B C B A B C ⋂==⋃=-≠.故选:C6.D【解析】【分析】依题意需要找到集合A 和集合B 中的公共元素,即是集合A 中在03x ≤≤范围内的元素.【详解】由题意知,对于集合B :03x ≤≤,∴在集合A 中只有0、1、2满足条件,{}012A B ∴=,,故选:D .7.C【解析】由A B A ⋃=得到B A ⊆,直接求解即可.【详解】因为A B A ⋃=,所以B A ⊆.由题可知,1a =或3.故选:C.8.C【解析】【分析】先化简集合A ,B ,C ,再利用集合的类型和运算求解.【详解】解:因为集合{{}2A x y x x ===≥,(){}ln 2B y y x R ==-=,且(){}2,C x y y x ==为点集, 所以A C ⋂=∅,B C =∅,{}|2=<A x x R ,{}|2⋂=<B A x x R ,A B C =∅,故选:C9.B【解析】【分析】根据一元二次不等式的解法求出集合A ,结合交集的概念和运算与空集的概念即可得出结果.【详解】由题可知,{}()(){}{}232012012A x x x x x x x x x =-+>=-->=或. 因为A B ⋂≠∅,所以m A ∈,即1m <或2m >,所以实数m 的取值范围是()(),12,-∞+∞.故选:B10.B【解析】【分析】分别解出集合A 和B ,再根据集合补集和交集计算方法计算即可.【详解】 (){}{}(]ln 10|0111,2A x x x x =-≤=<-≤=, {}(][)2,22,B xx ∞∞=≥=--⋃+,()2,2B =-R , ∴()R A B =(1,2).故选:B.11.B【分析】先求得A B ,再根据()Z M 的定义求解.【详解】解:因为{}1|8A x x =-<<,{}57|527|22⎧⎫=-<<=-<<⎨⎬⎩⎭B x x x x , 所以7|12⎧⎫=-<<⎨⎬⎩⎭A B x x , 所以()4=Z A B ,故选:B12.D【解析】【分析】先解出集合B ,再求A B .【详解】{}0B x y x x⎧===>⎨⎩∣∣. 因为{}0,1,2A =,所以A B ⋃=[)0,+∞.故选:D13.B【解析】【分析】先化简集合A ,在求集合A 与集合B 补集的交集【详解】220x x +-<()()210x x ⇒+-<21x ⇒-<<所以{}|21A x x =-<<{}|1B x x =<-{}U |1B x x ⇒=≥- 所以(){}U |11AB x x =-≤< 故选:B14.D【解析】【分析】 先解一元二次不等式求出集合A ,再按集合的并集运算即可.【详解】 由题意得{}13A x x =-≤≤,因为{}22B x x =-≤<,所以{}23A B x x ⋃=-≤≤. 故选:D.15.A【解析】根据组合数的求解,先求得集合M 中的元素个数,再求其子集个数即可.【详解】因为*5,,5m x C m N m =∈≤,由14555C C ==,235510C C ==,551C =,故集合M 有3个元素,故其子集个数为328=个.故选:A.二、填空题16.3【解析】【分析】由题意可知集合B 是集合A 的子集,进而求出答案.【详解】由B A ⊆知集合B 是集合A 的子集,所以33A a ∈⇒=,故答案为:3.17.{}2,4,6【解析】【分析】由补集的定义即可求解.【详解】解:因为全集{1,2,3,4,5,6,7}U =,集合{}1,3,5,7A =,所以{}2,4,6U A =.故答案为:{}2,4,618.1【解析】【分析】由子集定义分类讨论即可.【详解】因为B A ⊆,所以a A ∈1A ∈,当2a =-1无意义,不满足题意;当1a =12=,满足题意;当2a =11=,不满足题意.综上,实数a 的值1.故答案为:1 19.()A B A B ⋃【解析】【分析】由集合的交并补运算求解即可.【详解】设全集为A B ,则阴影部分表示集合A 与B 交集的补集,即()A B A B ⋃ 故答案为:()A B A B ⋃20.{}0,1【解析】【分析】先求出集合A ,然后根据交集的定义求得答案.【详解】 由题意,{}22A x x =-<<,所以{}0,1A B =.故答案为:{}0,1.21.∅,{}HT ,{}TH ,{},HT TH【解析】【分析】先写出与事件“一个正面(朝上)一个反面(朝上)”对应的样本空间,再写出其全部子集即可.【详解】与事件“一个正面(朝上)一个反面(朝上)”对应的样本空间为{},HT TH ,此空间的子集为∅,{}HT ,{}TH ,{},HT TH故答案为:∅,{}HT ,{}TH ,{},HT TH22.{0,3,6}【解析】【分析】根据给定条件直接计算作答.【详解】因{}0,1,2A =,而{}3,B b b a a A ==∈,所以{0,3,6}B =.故答案为:{0,3,6}23.()4,+∞【解析】【分析】求出集合P ,根据P Q Q ⋂=,得Q P ⊆,列出不等式即可得解.【详解】 解:{}{22804P x x x x x =-->=>或}2x <-, 因为P Q Q ⋂=,所以Q P ⊆,所以4a >.故答案为:()4,+∞.24. 假 假 假 真【解析】【分析】(1)利用真子集的定义即可判断.(2)由集合与集合的关系即可判断真假.(3)由元素与集合的关系即可判断真假.(4)由真子集的定义即可找到满足条件集合A 的个数.【详解】(1)因为{}1,2,3的真子集有{}{}{}{}{}{},1,2,3,1,2,1,3,2,3∅,所以{}1,2,3不是{}1,2,3真子集,命题为假命题.(2){}1是集合,因此不是{}1,2,3的元素,命题为假命题.(3)因为2是元素,因此不是{}1,2,3的子集,命题为假命题.(4)若{}0A ,所以集合A 中至少含有两个元素且其中一个必须为0,又因为{}0,1,2,3A ,所以集合A 可以从1,2,3中再选取一个元素、或者两个元素,所以满足条件的集合A 把∅和{}0,1,2,3去掉,所以满足条件集合A 的个数为322-个,命题为真命题. 故答案为:假;假;假;真25.②⑤【解析】【分析】利用集合元素的基本特征判断.【详解】①中国古代四大发明是造纸术,指南针,火药和印刷术,是确定的,能构成集合; ②地球上的小河流,不确定,不能构成集合;③方程210x -=的实数解是1或-1,是确定的,能构成集合;④周长为10cm 的三角形,是确定的,能构成集合;⑤接近于0的数,不确定,不能构成集合.故答案为:②⑤三、解答题26.(1){}12A B x x ⋂=<<(2)1m ≥-【解析】【分析】(1)直接写出集合B ,再计算A B 即可;(2)分B =∅和B ≠∅列出不等式求解即可.(1)当 1m =时,{}12B x x =<<,{}12A B x x =<<;(2)若B =∅,211m m -≥+,解得2m ≥,符合题意;若B ≠∅,由B A ⊆得21121314m m m m -<+⎧⎪-≥-⎨⎪+≤⎩,解得12m -≤<, 综上:1m ≥-.27.(1)1、2;(2)当2m <时,(),2B m =;当2m =时,B =∅;当2m >时,()2,B m =;(3)若选①:2m ≥;若选②:1m <或2m >;若选③:12m ≤≤.【解析】【分析】(1)由题可知x =1是方程2320ax x -+=的解,由此即可求出a ,从而求出b ;(2)根据a 、b 的值即可分类讨论求解不等式,从而得到B ;(3)若选①,则B ⊆A ,分类讨论m 的范围即可;若选②,则根据题意分类讨论即可;若选③,则先求出A R ,分类讨论即可.(1)由一元二次不等式2320ax x -+>的解集为{1A x x =<或}x b >,得0a >,且方程2320ax x -+=的两根为1、b , ∴0,31,21,a b a b a ⎧⎪>⎪⎪=+⎨⎪⎪=⨯⎪⎩ 解得1,2.a b =⎧⎨=⎩ (2)由(1)可知()20ax am b x bm -++<即为()2220x m x m -++<,即()()20x m x --<.m <2时,2m x <<;m =2时,不等式无解;m >2时,2x m <<.综上,当2m <时,(),2B m =;当2m =时,B =∅;当2m >时,()2,B m =.(3)由(1)知{1A x x =<或}2x >,若选①:A B A ⋃=,则B A ⊆,当2m <时,(),2B m =,不满足;当2m =时,B =∅,满足;当2m >时,()2,B m =,满足;∴选①,则实数m 的取值范围是2m ≥;若选②:A B ⋂≠∅,当2m <时,(),2B m =,则1m <;当2m =时,B =∅,不满足;当2m >时,()2,B m =,满足;∴选②,则实数m 的取值范围是1m <或2m >;若选③:B A ⊆R ,A R []1,2=,当2m <时,(),2B m =,则m ≥1,∴12m ≤<;当2m =时,B =∅,满足;当2m >时,()2,B m =,不满足.∴选③,则实数m 的取值范围是12m ≤≤.28.(1)23x << (2)43a ≥ 【解析】【分析】(1)求出命题q 为真时x 的取值后可求两者均为真命题时x 的取值范围.(2)根据条件关系可得两个范围之间的包含关系,从而可求实数a 的取值范围.(1)1a =,q :实数x 满足()()()300x a x a a +-<>即为()()130x x +-<,因为q 为真命题,故13x ,故当p ,q 都为真命题时,23x <<.(2)因为p 是q 的充分不必要条件,故(2,4)为{}|()(3)0x x a x a +-<的真子集,而{}()|()(3)0,3x x a x a a a +-<=- 故2340a a a -≤⎧⎪≥⎨⎪>⎩(等号不同时取),故43a ≥. 29.(1)()[](]()R 0,5,,58,A B A B ⋂=⋃=-∞⋃+∞(2)[)()(]R 7,0,5,8A B A B ⋂=-⋃= 【解析】【分析】(1)解不等式求得集合,A B ,由此求得()R ,A B A B ⋂⋃.(2)结合(1)来求得()R ,A B A B ⋂⋃.(1) ()()2235750x x x x +-=+-≤,解得75x -≤≤,所以[]7,5A =-,()()R ,75,A =-∞-⋃+∞.()80x x ->,解得0x <或8x >,所以()(),08,B =-∞⋃+∞,[]R 0,8B =, 所以()[](]()R 0,5,,58,A B A B ⋂=⋃=-∞⋃+∞.(2)由(1)得[)()(]R 7,0,5,8A B A B ⋂=-⋃=. 30.{}U 1A =,()U 1,B =+∞,[)U 5,C =+∞,[)U 1,3D =【解析】【分析】根据补集的定义计算可得;【详解】解:因为[)1,U =+∞,所以{}U 1A =,()U 1,B =+∞,[)U 5,C =+∞,[)U 1,3D =。
集合训练题
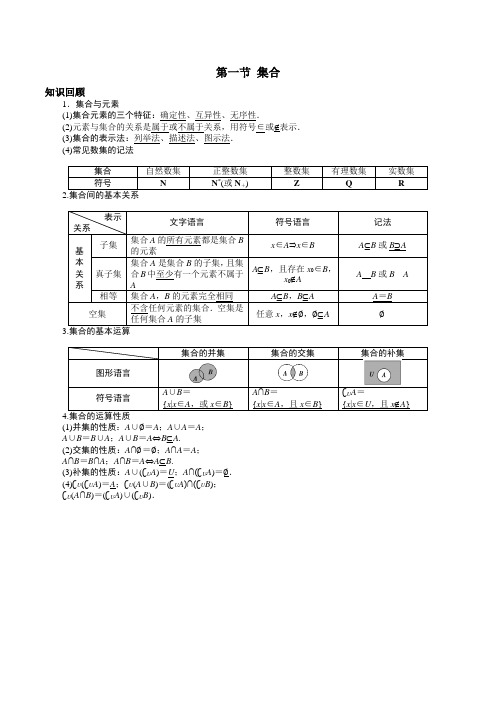
第一节集合知识回顾1.集合与元素(1)集合元素的三个特征:确定性、互异性、无序性.(2)元素与集合的关系是属于或不属于关系,用符号∈或∉表示.(3)集合的表示法:列举法、描述法、图示法.(4)常见数集的记法A B或B A集合的并集集合的交集集合的补集A∪B=A∩B=∁A=(1)并集的性质:A∪∅=A;A∪A=A;A∪B=B∪A;A∪B=A⇔B⊆A.(2)交集的性质:A∩∅=∅;A∩A=A;A∩B=B∩A;A∩B=A⇔A⊆B.(3)补集的性质:A∪(∁U A)=U;A∩(∁U A)=∅.(4)∁U(∁U A)=A;∁U(A∪B)=(∁U A)∩(∁U B);∁U(A∩B)=(∁U A)∪(∁U B).课前检测1.已知数集A ={0,1,x +2},那么x 的取值集合为 ( )A .{x |x ≠-2}B .{x |x ≠-1}C .{x |x ≠-2且x ≠-1}D .x ∈R2.下列判断正确的命题个数为( )①a ∈{a };②{a }∈{a ,b };③{a ,b }⊆{b ,a };④∅⊆{0}.A .1个B .2个C .3个D .4个 3.集合A ={1,2,3}的非空真子集的个数为( )A .3个B .6个C .7个D .8个4.已知{1,2}⊆A ⊆{1,2,3,4,5},则集合A 的个数为 ____________ .5.设全集U =R ,A ={x |1≤x ≤3},B ={x |2<x <4},则A ∩B = ____________;A ∪B =____________;A ∪∁U B =____________.课中讲解考点一. 集合的基本概念例1. 若a ,b ∈R ,集合{1,a +b ,a }={0,ba,b },求b -a 的值.变式1.设集合A ={1,a ,b },B ={a ,a 2,ab },且A =B ,求实数a ,b .例2.若集合A ={x ∈R|ax 2-3x +2=0}中只有一个元素,则a =( ) A.92 B.98 C .0D .0或98变式2.已知集合A ={x ∈N|1<x <log 2k },若集合A 中至少有3个元素,则k 的取值范围为( ) A .(8,+∞) B .[8,+∞) C .(16,+∞)D .[16,+∞)考点二. 集合间的关系例1.设P ={y |y =-x 2+1,x ∈R},Q ={y |y =2x ,x ∈R},则( ) A .P ⊆Q B .Q ⊆P C .∁R P ⊆QD .Q ⊆∁R P变式1.已知集合A ={x |-2≤x ≤5},B ={x |m +1≤x ≤2m -1},若B ⊆A ,则实数m 的取值范围为________.例2 设集合M ={x |x =5-4a +a 2,a ∈R },N ={y |y =4b 2+4b +2,b ∈R },则M 与N 之间有什么关系?变式2 设集合P ={m |-1<m <0},Q ={m |mx 2+4mx -4<0对任意实数x 恒成立,且m ∈R },则集合P 与Q 之间的关系为________.变式3.已知集合A ={x |x 2+4x =0},B ={x |x 2+ax +a =0},是否存在这样的实数a ,使得B ⊆A ?若存在这样的实数a ,求出a 的取值范围;若不存在,说明理由.考点三 集合的运算例1.【2020年高考全国Ⅰ卷理数】设集合A ={x |x 2–4≤0},B ={x |2x +a ≤0},且A ∩B ={x |–2≤x ≤1},则a =() A .–4 B .–2 C .2D .4变式1.【2020年高考全国Ⅰ卷理数】已知集合U ={−2,−1,0,1,2,3},A ={−1,0,1},B ={1,2},则()UA B =A .{−2,3}B .{−2,2,3}C .{−2,−1,0,3}D .{−2,−1,0,2,3}例2.【2020年高考全国Ⅰ卷理数】已知集合{(,)|,,}A x y x y y x =∈≥*N ,{(,)|8}B x y x y =+=,则A B 中元素的个数为 A .2 B .3 C .4D .6变式2.(2020·全国新课标Ⅰ理科试卷)已知集合{(,)|,,}A x y x y y x =∈≥*N ,{(,)|8}B x y x y =+=,则A B中元素的个数为( ) A .2B .3C .4D .6例3.(多选)已知集合A ={x |-1<x ≤3},集合B ={x ||x |≤2},则下列关系式正确的是( ) A .A ∩B =∅B .A ∪B ={x |-2≤x ≤3}C .A ∪∁R B ={x |x ≤-1或x >2}D .A ∩∁R B ={x |2<x ≤3}变式3.(多选)已知集合A ={x |x 2-3x +2≤0},B ={x |2<2x ≤8},则下列判断不正确的是( ) A .A ∪B =B B .(∁R B )∪A =R C .A ∩B ={x |1<x ≤2} D .(∁R B )∪(∁R A )=R考点四.集合的新定义问题例1.如图所示的Venn 图中,A ,B 是两个非空集合,定义集合A ⊗B 为阴影部分表示的集合.若x ,y ∈R ,A ={x |y =2x -x 2},B ={y |y =3x ,x >0},则A ⊗B 为( )A .{x |0<x <2}B .{x |1<x ≤2}C .{x |0≤x ≤1或x ≥2}D .{x |0≤x ≤1或x >2} 变式1.给定集合A ,若对于任意a ,b ∈A ,有a +b ∈A ,且a -b ∈A ,则称集合A 为闭集合,给出如下三个结论:①集合A ={-4,-2,0,2,4}为闭集合; ②集合A ={n |n =3k ,k ∈Z}为闭集合;③若集合A 1,A 2为闭集合,则A 1∪A 2为闭集合. 其中正确结论的序号是________.例2.定义集合的商集运算为A B =⎩⎨⎧⎭⎬⎫x ⎪⎪x =m n ,m ∈A ,n ∈B ,已知集合A ={2,4,6},B =⎩⎨⎧⎭⎬⎫x ⎪⎪x =k 2-1,k ∈A ,则集合BA∪B 中的元素个数为( )A .6B .7C .8D .9变式2.设P 和Q 是两个集合,定义集合P -Q ={x |x ∈P ,且x ∉Q },如果P ={x |log 2x <1},Q ={x ||x -2|<1},那么P -Q =( )A .{x |0<x <1}B .{x |0<x ≤1}C .{x |1≤x <2}D .{x |2≤x <3}课后习题一 单选1.(2020·河北衡水中学高三月考)已知集合{}2|20A x x x =-≤,{}|1381xB x =<<,{}|2,C x x n n N ==∈,则()A B C ⋃⋂=( )A .{}2B .{}0,2C .{}0,2,4D .{}2,42.(2020·山东济宁·高三其他模拟)已知集合{}|21x A x =>,{}2|560B x x x =+-<,则AB =( )A .()1,0-B .()0,6C .()0,1D .()6,1-3.(2020·阳江市第一中学高三其他模拟)已知全集为实数集R ,集合{}36A x x =-<<,{}29140B x x x =-+<,则()U A B ⋂=( )A .()2,6B .()2,7C .(]3,2-D .()3,2-4.(2020·云南高三其他模拟(理))设集合{}2*20,A x x x x N =--<∈,集合{B x y ==,则集合A B 等于( )A .1B .[)1,2C .{}1D .{}1x x ≥5.【2020年新高考全国Ⅰ卷】设集合A ={x |1≤x ≤3},B ={x |2<x <4},则A ∪B =A .{x |2<x ≤3}B .{x |2≤x ≤3}C .{x |1≤x <4}D .{x |1<x <4}6.【2020年高考浙江】已知集合P ={|14}x x <<,Q={|23}x x <<,则P ∩Q =A .{|12}x x <≤B .{|23}x x <<C .{|34}x x ≤<D .{|14}x x <<7. 已知集合A ={x ∈N |x 2-2x -3≤0},B ={1,3},定义集合A ,B 之间的运算“*”:A *B ={x |x =x 1+x 2,x 1∈A ,x 2∈B },则A *B 中的所有元素数字之和为( ) A .15 B .16 C .20 D .218.已知全集U ={x ∈Z|0<x <8},集合M ={2,3,5},N ={x |x 2-8x +12=0},则集合{1,4,7}为( )A .M ∩(∁U N )B .∁U (M ∩N )C .∁U (M ∪N )D .(∁U M )∩N9.已知集合M =⎩⎨⎧⎭⎬⎫x | x 216+y 29=1,N =⎩⎨⎧⎭⎬⎫y |x 4+y 3=1,则M ∩N =( ) A .∅ B .{(4,0),(3,0)} C .[-3,3]D .[-4,4]10.在实数集R 上定义运算*:x *y =x ·(1-y ).若关于x 的不等式x *(x -a )>0的解集是集合{x |-1≤x ≤1}的子集,则实数a 的取值范围是( )A .[0,2]B .[-2,-1)∪(-1,0]C .[0,1)∪(1,2]D .[-2,0]11.非空数集A 满足:(1)0∉A ;(2)若∀x ∈A ,有1x∈A ,则称A 是“互倒集”.给出以下数集:①{x ∈R|x 2+ax +1=0}; ②{x |x 2-4x +1<0};③⎩⎨⎧⎭⎬⎫y ⎪⎪y =ln xx ,x ∈⎣⎡⎭⎫1e ,1∪1,e];④⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫y ⎪⎪⎪⎪y =⎩⎨⎧ 2x +25,x ∈[0,1,x +1x ,x ∈[1,2]. 其中“互倒集”的个数是( ) A .4 B .3 C .2 D .1二.多选12. (多选)设P 是一个数集,且至少含有两个数,若对任意a ,b ∈P ,都有a +b ,a -b ,ab ,ab ∈P (除数b ≠0),则称P 是一个数域,例如有理数集Q 是数域,下列命题中正确的是( ) A .数域必含有0,1两个数 B .整数集是数域C .若有理数集Q ⊆M ,则数集M 必为数域D .数域必为无限集13.(多选)设S 为复数集C 的非空子集.若对任意x ,y ∈S ,都有x +y ,x -y ,xy ∈S ,则称S 为封闭集.下列命题中是真命题的有( )A .集合S ={a +b i|a ,b 为整数,i 为虚数单位}为封闭集B .若S 为封闭集,则一定有0∈SC .封闭集一定是无限集D .若S 为封闭集,则满足S ⊆T ⊆C 的任意集合T 也是封闭集 三.填空14. 对于集合M ,定义函数f M (x )=⎩⎪⎨⎪⎧-1,x ∈M ,1,x ∉M .对于两个集合A ,B ,定义集合A △B ={x |f A (x )·f B (x )=-1}.已知A ={2,4,6,8,10},B ={1,2,4,8,12},则用列举法写出集合A △B 的结果为________.15.当两个集合有公共元素,且互不为对方的子集时,我们称这两个集合“相交”.对于集合M ={x |ax 2-1=0,a >0},N =⎩⎨⎧⎭⎬⎫-12,12,1,若M 与N “相交”,则a =________.四.解答题16.已知集合A ={x |3≤3x ≤27},B ={x |log 2x >1}.(1)分别求A ∩B ,(∁R B )∪A ;(2)已知集合C ={x |1<x <a },若C ⊆A ,求实数a 的取值范围.参考答案1.已知数集A ={0,1,x +2},那么x 的取值集合为 ( )A .{x |x ≠-2}B .{x |x ≠-1}C .{x |x ≠-2且x ≠-1}D .x ∈R答案:C解析:因为集合的元素满足互异性,所以x +2≠0且x +2≠1,得x ≠-2且x ≠-1,故选C . 2.下列判断正确的命题个数为( ) ①a ∈{a };②{a }∈{a ,b };③{a ,b }⊆{b ,a };④∅⊆{0}. A .1个 B .2个 C .3个D .4个答案:C解析:①元素与集合的关系的表示方法,正确; ②两个集合之间的关系,不正确; ③正确; ④∅是任何集合的子集,正确,故选C .3.集合A ={1,2,3}的非空真子集的个数为( ) A .3个 B .6个 C .7个D .8个 答案:B解析:若一个集合的元素个数为n ,则其子集个数为2n , 真子集的个数为2n -1,非空子集的个数为2n -1, 则非空真子集的个数为2n -2,故选B.4.已知{1,2}⊆A ⊆{1,2,3,4,5},则集合A 的个数为 ____________ . 答案:8解析:问题可转化为求集合{3,4,5}的子集个数,即集合A 的个数为8.5.设全集U =R ,A ={x |1≤x ≤3},B ={x |2<x <4},则A ∩B = ____________;A ∪B =____________;A ∪∁U B =____________.答案:{x |2<x ≤3} {x |1≤x <4} {x |x ≤3或x ≥4}解析:在数轴上分别表示出集合A ,B ,∁U B ,即得∁U B ={x |x ≤2或x ≥4}. 课中讲解考点一. 集合的基本概念例1. 若a ,b ∈R ,集合{1,a +b ,a }={0,ba,b },求b -a 的值.解题导引 解决该类问题的基本方法为:利用集合中元素的特点,列出方程组求解,但解出后应注意检验,看所得结果是否符合元素的互异性.解 由{1,a +b ,a }={0,ba ,b }可知a ≠0,则只能a +b =0,则有以下对应法则:⎩⎪⎨⎪⎧a +b =0,ba =a ,b =1① 或⎩⎪⎨⎪⎧a +b =0,b =a ,b a =1.②由①得⎩⎪⎨⎪⎧a =-1,b =1,符合题意;②无解.∴b -a =2.变式1.设集合A ={1,a ,b },B ={a ,a 2,ab },且A =B ,求实数a ,b . 解 由元素的互异性知,a ≠1,b ≠1,a ≠0,又由A =B ,得⎩⎪⎨⎪⎧ a 2=1,ab =b ,或⎩⎪⎨⎪⎧a 2=b ,ab =1,解得a =-1,b =0. 例2.若集合A ={x ∈R|ax 2-3x +2=0}中只有一个元素,则a =( )A.92B.98 C .0D .0或98解析:选D 当a =0时,显然成立;当a ≠0时,Δ=(-3)2-8a =0,即a =98.变式2.已知集合A ={x ∈N|1<x <log 2k },若集合A 中至少有3个元素,则k 的取值范围为( ) A .(8,+∞) B .[8,+∞) C .(16,+∞)D .[16,+∞)解析:选C 因为集合A 中至少有3个元素,所以log 2k >4,所以k >24=16,故选C. 考点二. 集合间的关系例1.设P ={y |y =-x 2+1,x ∈R},Q ={y |y =2x ,x ∈R},则( ) A .P ⊆Q B .Q ⊆P C .∁R P ⊆QD .Q ⊆∁R P变式1.已知集合A ={x |-2≤x ≤5},B ={x |m +1≤x ≤2m -1},若B ⊆A ,则实数m 的取值范围为________. [解析] 例1.因为P ={y |y =-x 2+1,x ∈R}={y |y ≤1},Q ={y |y =2x ,x ∈R}={y |y >0},所以∁R P ={y |y >1},所以∁R P ⊆Q ,故选C.变式1.∵B ⊆A ,∴①若B =∅,则2m -1<m +1,此时m <2. ②若B ≠∅,则⎩⎪⎨⎪⎧2m -1≥m +1,m +1≥-2,2m -1≤5,解得2≤m ≤3.由①②可得,符合题意的实数m 的取值范围为(-∞,3]. [答案] (1)C (2)(-∞,3]例2 设集合M ={x |x =5-4a +a 2,a ∈R },N ={y |y =4b 2+4b +2,b ∈R },则M 与N 之间有什么关系? 解题导引 一般地,对于较为复杂的两个或两个以上的集合,要判断它们之间的关系,应先确定集合中元素的形式是数还是点或其他,属性如何.然后将所给集合化简整理,弄清每个集合中的元素个数或范围,再判断它们之间的关系.解 集合M ={x |x =5-4a +a 2,a ∈R }={x |x =(a -2)2+1,a ∈R }={x |x ≥1}, N ={y |y =4b 2+4b +2,b ∈R }={y |y =(2b +1)2+1,b ∈R }={y |y ≥1}.∴M =N .变式2 设集合P ={m |-1<m <0},Q ={m |mx 2+4mx -4<0对任意实数x 恒成立,且m ∈R },则集合P 与Q 之间的关系为________. 答案 P ⊆Q解析 P ={m |-1<m <0},Q :⎩⎪⎨⎪⎧m <0,Δ=16m 2+16m <0,或m =0.∴-1<m ≤0.∴Q ={m |-1<m ≤0}.∴P ⊆Q变式3.已知集合A ={x |x 2+4x =0},B ={x |x 2+ax +a =0},是否存在这样的实数a ,使得B ⊆A ?若存在这样的实数a ,求出a 的取值范围;若不存在,说明理由.【思路点拨】判断集合与集合的关系,基本方法是归纳为判断元素与集合的关系.对于用描述法表示的集合,要紧紧抓住代表元素及它的属性,可将元素列举出来直接观察或通过元素特征,求同存异,定性分析.解:A ={0,-4}.若B ⊆A ,则B =∅,{0},{-4},{0,-4}.当B =∅时,则x 2+ax +a =0无解,所以a 2-4a <0,解得0<a <4; 当B ={0}时,则x 2+ax +a =0有两个相等的根0,所以a =0;当B ={-4}时,则x 2+ax +a =0有两个相等的根-4,所以a 2-4a =0且14-4a +a =0,无解; 当B ={0.-4}时,则x 2+ax +a =0有两个根0和-4,无解.综上,存在实数 a 满足 0≤a <4,使得B ⊆A .【点评】在解决两个数集关系问题时,避免出错的一个有效手段是合理运用数轴帮助分析与求解,另外,在解含有参数的不等式(或方程)时,要对参数进行讨论.分类时要遵循“不重不漏”的分类原则,然后对于每一类情况都要给出问题的解答.分类讨论的一般步骤:①确定标准;②恰当分类;③逐类讨论;④归纳结论.空集是任意集合的子集,解题时不能忽视! 考点三 集合的运算例1.【2020年高考全国Ⅰ卷理数】设集合A ={x |x 2–4≤0},B ={x |2x +a ≤0},且A ∩B ={x |–2≤x ≤1},则a =() A .–4 B .–2 C .2 D .4【答案】B 【解析】 【分析】由题意首先求得集合A ,B ,然后结合交集的结果得到关于a 的方程,求解方程即可确定实数a 的值. 【详解】求解二次不等式240x -≤可得{}2|2A x x -=≤≤, 求解一次不等式20x a +≤可得|2a B x x ⎧⎫=≤-⎨⎬⎩⎭. 由于{}|21A B x x ⋂=-≤≤,故12a-=, 解得2a =-.故选B .【点睛】本题主要考查交集的运算,不等式的解法等知识,意在考查学生的转化能力和计算求解能力. 变式1.【2020年高考全国Ⅰ卷理数】已知集合U ={−2,−1,0,1,2,3},A ={−1,0,1},B ={1,2},则()UA B =A .{−2,3}B .{−2,2,3}C .{−2,−1,0,3}D .{−2,−1,0,2,3}【答案】A 【解析】 【分析】首先进行并集运算,然后计算补集即可. 【详解】由题意可得{}1,0,1,2A B ⋃=-,则(){}U2,3A B =-.故选A【点睛】本题主要考查并集、补集的定义与应用,属于基础题.例2.【2020年高考全国Ⅰ卷理数】已知集合{(,)|,,}A x y x y y x =∈≥*N ,{(,)|8}B x y x y =+=,则A B 中元素的个数为 A .2 B .3 C .4D .6【答案】C 【解析】 【分析】采用列举法列举出A B 中元素的即可.【详解】由题意,AB 中的元素满足8y xx y ≥⎧⎨+=⎩,且*,x y ∈N ,由82x y x +=≥,得4x ≤,所以满足8x y +=的有(1,7),(2,6),(3,5),(4,4), 故AB 中元素的个数为4.故选C .【点晴】本题主要考查集合的交集运算,考查学生对交集定义的理解,是一道容易题..变式2.(2020·全国新课标Ⅰ理科试卷)已知集合{(,)|,,}A x y x y y x =∈≥*N ,{(,)|8}B x y x y =+=,则A B 中元素的个数为( )A .2B .3C .4D .6【答案】C【详解】由题意,A B 中的元素满足8y x x y ≥⎧⎨+=⎩,且*,x y N ∈,由82x y x +=≥,得4x ≤,所以满足8x y +=的有(1,7),(2,6),(3,5),(4,4),故A B 中元素的个数为4.故选:C.【点晴】本题主要考查集合的交集运算,考查学生对交集定义的理解,是一道容易题.例3.(多选)已知集合A ={x |-1<x ≤3},集合B ={x ||x |≤2},则下列关系式正确的是( )A .A ∩B =∅B .A ∪B ={x |-2≤x ≤3}C .A ∪∁R B ={x |x ≤-1或x >2}D .A ∩∁R B ={x |2<x ≤3}答案 BD解析 ∵A ={x |-1<x ≤3},B ={x ||x |≤2}={x |-2≤x ≤2},∴A ∩B ={x |-1<x ≤3}∩{x |-2≤x ≤2}={x |-1<x ≤2},A 不正确;A ∪B ={x |-1<x ≤3}∪{x |-2≤x ≤2}={x |-2≤x ≤3},B 正确;∵∁R B ={x |x <-2或x >2},∴A ∪∁R B ={x |-1<x ≤3}∪{x |x <-2或x >2}={x |x <-2或x >-1},C 不正确;A ∩∁RB ={x |-1<x ≤3}∩{x |x <-2或x >2}={x |2<x ≤3},D 正确.变式3.(多选)已知集合A ={x |x 2-3x +2≤0},B ={x |2<2x ≤8},则下列判断不正确的是() A .A ∪B =B B .(∁R B )∪A =RC .A ∩B ={x |1<x ≤2}D .(∁R B )∪(∁R A )=R答案 ABD解析 因为x 2-3x +2≤0,所以1≤x ≤2,所以A ={x |1≤x ≤2};因为2<2x ≤8,所以1<x ≤3,所以B ={x |1<x ≤3}.所以A ∪B ={x |1≤x ≤3},A ∩B ={x |1<x ≤2}.(∁R B )∪A ={x |x ≤2或x >3},(∁R B )∪(∁R A )={x |x ≤1或x >2}.考点四.集合的新定义问题例1.如图所示的Venn 图中,A ,B 是两个非空集合,定义集合A ⊗B 为阴影部分表示的集合.若x ,y ∈R ,A ={x |y =2x -x 2},B ={y |y =3x ,x >0},则A ⊗B 为( )A .{x |0<x <2}B .{x |1<x ≤2}C .{x |0≤x ≤1或x ≥2}D .{x |0≤x ≤1或x >2}变式1.给定集合A ,若对于任意a ,b ∈A ,有a +b ∈A ,且a -b ∈A ,则称集合A 为闭集合,给出如下三个结论:①集合A ={-4,-2,0,2,4}为闭集合;②集合A ={n |n =3k ,k ∈Z}为闭集合;③若集合A 1,A 2为闭集合,则A 1∪A 2为闭集合.其中正确结论的序号是________.[解析] 例1.因为A ={x |0≤x ≤2},B ={y |y >1},A ∪B ={x |x ≥0},A ∩B ={x |1<x ≤2},所以A ⊗B =∁A ∪B (A ∩B )={x |0≤x ≤1或x >2}.(2)①中,-4+(-2)=-6∉A ,所以①不正确;②中,设n 1,n 2∈A ,n 1=3k 1,n 2=3k 2,k 1,k 2∈Z ,则n 1+n 2∈A ,n 1-n 2∈A ,所以②正确;③中,令A 1={n |n =3k ,k ∈Z},A 2={n |n =2k ,k ∈Z},则A 1,A 2为闭集合,但3k +2k ∉(A 1∪A 2),故A 1∪A 2不是闭集合,所以③不正确.[答案] (1)D (2)②例2.定义集合的商集运算为A B =⎩⎨⎧⎭⎬⎫x ⎪⎪x =m n ,m ∈A ,n ∈B ,已知集合A ={2,4,6},B =⎩⎨⎧⎭⎬⎫x ⎪⎪x =k 2-1,k ∈A ,则集合B A∪B 中的元素个数为( ) A .6B .7C .8D .9解析:选B 由题意知,B ={0,1,2},B A =⎩⎨⎧⎭⎬⎫0,12,14,16,1,13, 则B A ∪B =⎩⎨⎧⎭⎬⎫0,12,14,16,1,13,2, 共有7个元素,故选B.变式2.设P 和Q 是两个集合,定义集合P -Q ={x |x ∈P ,且x ∉Q },如果P ={x |log 2x <1},Q ={x ||x -2|<1},那么P -Q =( )A .{x |0<x <1}B .{x |0<x ≤1}C .{x |1≤x <2}D .{x |2≤x <3} 解析:选B 由log 2x <1,得0<x <2,所以P ={x |0<x <2}.由|x -2|<1,得1<x <3,所以Q ={x |1<x <3}.由题意,得P -Q ={x |0<x ≤1}.课后习题一 单选1.(2020·河北衡水中学高三月考)已知集合{}2|20A x x x =-≤,{}|1381x B x =<<,{}|2,C x x n n N ==∈,则()A B C ⋃⋂=( )A .{}2B .{}0,2C .{}0,2,4D .{}2,4 【答案】B【详解】∵集合{}2|20A x x x =-≤∴{}02A x x =≤≤∵集合{}|1381x B x =<<∴{}04A x x =<< ∴{}04A B x x ⋃=≤<∵集合{}|2,C x x n n N ==∈∴{}()0,2A B C ⋃⋂=故选B.2.(2020·山东济宁·高三其他模拟)已知集合{}|21x A x =>,{}2|560B x x x =+-<,则A B =( )A .()1,0-B .()0,6C .()0,1D .()6,1-【答案】C 【详解】{}{}{}0|21|22=|0x x A x x x x =>=>>, {}{}{}2|560|(6)(10|61B x x x x x x x x =+-<=+-<=-<<),∴A B =()0,1.故选:C.3.(2020·阳江市第一中学高三其他模拟)已知全集为实数集R ,集合{}36A x x =-<<,{}29140B x x x =-+<,则()U A B ⋂=( )A .()2,6B .()2,7C .(]3,2-D .()3,2- 【答案】C 【详解】{}{}2914027B x x x x x =-+<=<<, {2U B x x ∴=≤或}7x ≥,{}(]()323,2U A B x x ∴⋂=-<≤=-.故选:C.4.(2020·云南高三其他模拟(理))设集合{}2*20,A x x x x N=--<∈,集合{B x y ==,则集合A B 等于( ) A .1B .[)1,2C .{}1D .{}1x x ≥ 【答案】C 【详解】由题得{}{}{}2**20,12,1A x x x x x x x =--<∈=-<<∈=N N , {{}{}{}222log 0log log 11B x y x x x x x x ===≥=≥=≥,{}1A B ∴⋂=.故选: C. 5.【2020年新高考全国Ⅰ卷】设集合A ={x |1≤x ≤3},B ={x |2<x <4},则A ∪B =A .{x |2<x ≤3}B .{x |2≤x ≤3}C .{x |1≤x <4}D .{x |1<x <4} 【答案】C【解析】【分析】根据集合并集概念求解.【详解】[1,3](2,4)[1,4)AB ==. 故选C【点睛】本题考查集合并集,考查基本分析求解能力,属基础题.6.【2020年高考浙江】已知集合P ={|14}x x <<,Q={|23}x x <<,则PQ = A .{|12}x x <≤B .{|23}x x <<C .{|34}x x ≤<D .{|14}x x << 【答案】B【解析】【分析】根据集合交集定义求解【详解】(1,4)(2,3)(2,3)P Q ==.故选B.【点睛】本题考查交集概念,考查基本分析求解能力,属基础题.7. 已知集合A ={x ∈N |x 2-2x -3≤0},B ={1,3},定义集合A ,B 之间的运算“*”:A *B ={x |x =x 1+x 2,x 1∈A ,x 2∈B },则A *B 中的所有元素数字之和为( )A .15B .16C .20D .21答案 D解析 由x 2-2x -3≤0,得(x +1)(x -3)≤0,得A ={0,1,2,3}.因为A *B ={x |x =x 1+x 2,x 1∈A ,x 2∈B },所以A *B 中的元素有:0+1=1,0+3=3,1+1=2,1+3=4,2+1=3(舍去),2+3=5,3+1=4(舍去),3+3=6,所以A *B ={1,2,3,4,5,6},所以A *B 中的所有元素数字之和为21.8.已知全集U ={x ∈Z|0<x <8},集合M ={2,3,5},N ={x |x 2-8x +12=0},则集合{1,4,7}为( )A .M ∩(∁U N )B .∁U (M ∩N )C .∁U (M ∪N )D .(∁U M )∩N解析:选C 由已知得U ={1,2,3,4,5,6,7},N ={2,6},M ∩(∁U N )={2,3,5}∩{1,3,4,5,7}={3,5},M ∩N ={2},∁U (M ∩N )={1,3,4,5,6,7},M ∪N ={2,3,5,6},∁U (M ∪N )={1,4,7},(∁U M )∩N ={1,4,6,7}∩{2,6}={6},故选C.9.已知集合M =⎩⎨⎧⎭⎬⎫x | x 216+y 29=1,N =⎩⎨⎧⎭⎬⎫y |x 4+y 3=1,则M ∩N =( ) A .∅B .{(4,0),(3,0)}C .[-3,3]D .[-4,4]解析:选D 由题意可得M ={x |-4≤x ≤4},N ={y |y ∈R},所以M ∩N =[-4,4].故选D.10.在实数集R 上定义运算*:x *y =x ·(1-y ).若关于x 的不等式x *(x -a )>0的解集是集合{x |-1≤x ≤1}的子集,则实数a 的取值范围是( )A .[0,2]B .[-2,-1)∪(-1,0]C .[0,1)∪(1,2]D .[-2,0]解析:选D 依题意可得x (1-x +a )>0.因为其解集为{x |-1≤x ≤1}的子集,所以当a ≠-1时,0<1+a ≤1或-1≤1+a <0,即-1<a ≤0或-2≤a <-1.当a =-1时,x (1-x +a )>0的解集为空集,符合题意.所以-2≤a ≤0.11.非空数集A 满足:(1)0∉A ;(2)若∀x ∈A ,有1x∈A ,则称A 是“互倒集”.给出以下数集: ①{x ∈R|x 2+ax +1=0};②{x |x 2-4x +1<0};③⎩⎨⎧⎭⎬⎫y ⎪⎪y =ln x x ,x ∈⎣⎡⎭⎫1e ,1∪1,e];④⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫y ⎪⎪⎪⎪ y =⎩⎨⎧ 2x +25,x ∈[0,1,x +1x ,x ∈[1,2]. 其中“互倒集”的个数是( )A .4B .3C .2D .1解析:选C 对于①,当-2<a <2时为空集,所以①不是“互倒集”;对于②,{x |x 2-4x +1<0}={x |2-3<x <2+3},所以12+3<1x <12-3,即2-3<1x <2+3,所以②是“互倒集”;对于③,y ′=1-ln x x 2≥0,故函数y =ln x x是增函数,当x ∈⎣⎡⎭⎫1e ,1时,y ∈[-e,0),当x ∈(1,e]时,y ∈⎝⎛⎦⎤0,1e ,所以③不是“互倒集”;对于④,y ∈⎣⎡⎭⎫25,125∪⎣⎡⎦⎤2,52=⎣⎡⎦⎤25,52且1y ∈⎣⎡⎦⎤25,52,所以④是“互倒集”.故选C.二.多选12. (多选)设P 是一个数集,且至少含有两个数,若对任意a ,b ∈P ,都有a +b ,a -b ,ab ,a b∈P (除数b ≠0),则称P 是一个数域,例如有理数集Q 是数域,下列命题中正确的是( )A .数域必含有0,1两个数B .整数集是数域C .若有理数集Q ⊆M ,则数集M 必为数域D .数域必为无限集答案 AD解析 当a =b 时,a -b =0,a b=1∈P ,故可知A 正确. 当a =1,b =2时,12∉Z 不满足条件,故可知B 不正确. 当M 比Q 多一个元素i 时,则会出现1+i ∉M ,所以它也不是一个数域,故可知C 不正确.根据数域的性质易得数域有无限多个元素,必为无限集,故可知D 正确.13.(多选)设S 为复数集C 的非空子集.若对任意x ,y ∈S ,都有x +y ,x -y ,xy ∈S ,则称S 为封闭集.下列命题中是真命题的有( )A .集合S ={a +b i|a ,b 为整数,i 为虚数单位}为封闭集B .若S 为封闭集,则一定有0∈SC .封闭集一定是无限集D .若S 为封闭集,则满足S ⊆T ⊆C 的任意集合T 也是封闭集答案 AB解析 两个复数的和、差、积仍是复数,且运算后的实部、虚部仍为整数,所以集合S ={a +b i|a ,b 为整数,i 为虚数单位}为封闭集,A 正确.当S 为封闭集时,因为x -y ∈S ,取x =y ,得0∈S ,B 正确.对于集合S ={0},显然满足所有条件,但S 是有限集,C 错误.取S ={0},T ={0,1},满足S ⊆T ⊆C ,但由于0-1=-1不属于T ,故T 不是封闭集,D 错误.三.填空14. 对于集合M ,定义函数f M (x )=⎩⎪⎨⎪⎧-1,x ∈M ,1,x ∉M .对于两个集合A ,B ,定义集合A △B ={x |f A (x )·f B (x )=-1}.已知A ={2,4,6,8,10},B ={1,2,4,8,12},则用列举法写出集合A △B 的结果为________.答案 {1,6,10,12}解析 要使f A (x )·f B (x )=-1,必有x ∈{x |x ∈A 且x ∉B }∪{x |x ∈B 且x ∉A }={1,6,10,12},所以A △B ={1,6,10,12}.15.当两个集合有公共元素,且互不为对方的子集时,我们称这两个集合“相交”.对于集合M ={x |ax 2-1=0,a >0},N =⎩⎨⎧⎭⎬⎫-12,12,1,若M 与N “相交”,则a =________. 答案 1解析 M =⎩⎨⎧⎭⎬⎫-1a ,1a ,由1a =12,得a =4,由1a=1,得a =1. 当a =4时,M =⎩⎨⎧⎭⎬⎫-12,12,此时M ⊆N ,不合题意; 当a =1时,M ={-1,1},满足题意.四.解答题16.已知集合A ={x |3≤3x ≤27},B ={x |log 2x >1}.(1)分别求A ∩B ,(∁R B )∪A ;(2)已知集合C ={x |1<x <a },若C ⊆A ,求实数a 的取值范围.解:(1)∵3≤3x ≤27,即31≤3x ≤33,∴1≤x ≤3,∴A ={x |1≤x ≤3}.∵log 2x >1,即log 2x >log 22,∴x >2,∴B ={x |x >2}.∴A ∩B ={x |2<x ≤3}.∴∁R B ={x |x ≤2},∴(∁R B )∪A ={x |x ≤3}.(2)由(1)知A ={x |1≤x ≤3},C ⊆A .当C 为空集时,满足C ⊆A ,a ≤1;当C 为非空集合时,可得1<a ≤3.综上所述,实数a的取值范围是(-∞,3].。
集合经典试题及答案

第一章 第一节 集合达标训练 技能过关[课堂训练]1.(2012·江西)若集合A ={-1,1},B ={0,2},则集合{z |z =x +y ,x ∈A ,y ∈B }中的元素的个数为A .5B .4C .3D .2解析 由题意得-1与0和2的和分别为-1,1;1与0和2的和分别为1和3,则集合{z |z =x +y ,x ∈A ,y ∈B }中的元素共有-1,1,3三个.故选C.答案 C2.(2012·辽宁)已知全集U ={0,1,2,3,4,5,6,7,8,9},集合A ={0,1,3,5,8},集合B ={2,4,5,6,8},则(∁U A )∩(∁U B )等于A .{5,8}B .{7,9}C .{0,1,3}D .{2,4,6}解析 由题意得:∁U A ={2,4,6,7,9},∁U B ={0,1,3,7,9}.故(∁U A )∩(∁U B )={7,9},选B. 答案 B3.(2013·济南模拟)已知U ={y |y =log 2x ,x >1},P =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫y ⎪⎪⎪ y =1x ,x >2,则∁U P 等于A.⎣⎢⎡⎭⎪⎫12,+∞ .⎝ ⎛⎭⎪⎫0,12 C .(0,+∞) D .(-∞,0]∪⎣⎢⎡⎭⎪⎫12,+∞解析 化简得U ={y |y =log 2x ,x >1}=(0,+∞),P =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫y ⎪⎪⎪ y =1x ,x >2=⎝⎛⎭⎪⎫0,12,所以∁U P =⎣⎢⎡⎭⎪⎫12,+∞.故选A. 答案 A4.如图所示的Venn 图中,A ,B 是非空集合,定义集合A #B 为阴影部分表示的集合.x ,y ∈R ,A ={x |y =2x -x 2},B ={y |y =3x ,x >0},则A #B 为A.{x |0<x <2}B .{x |1<x ≤2}C .{x |0≤x ≤1或x ≥2}D .{x |0≤x ≤1或x >2}解析 ∵A ={x |0≤x ≤2},B ={y |y >1}, ∴A #B ={x |0≤x ≤1或x >2}. 答案 D[课下作业][时间45分钟,满分80分]一、选择题(每题6分,共30分)1.(2012·广东)设集合U ={1,2,3,4,5,6},M ={1,2,4},则∁U M 等于 A .U B .{1,3,5} C .{3,5,6}D .{2,4,6} 解析 据集合在全集中补集的定义可知∁U M ={3,5,6},故选C. 答案 C2.若集合M ={y |y =3x },集合S ={x |y =lg(x -1)},则下列各式正确的是 A .M ∪S =M B .M ∪S =S C .M =SD .M ∩S =∅解析 ∵M ={y |y =3x }={y |y >0},S ={x |y =lg(x -1)}={x |x >1},∴M ∪S =M . 答案 A3.(2012·北京)已知集合A ={x ∈R|3x +2>0},B ={x ∈R|(x +1)(x -3)>0},则A ∩B 等于 A .(-∞,-1) B .⎩⎨⎧⎭⎬⎫-1,-23 C.⎝ ⎛⎭⎪⎫-23,3 D .(3,+∞)解析 因为A =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ∈R ⎪⎪⎪x >-23,B ={x |x <-1,或x >3},画出数轴如图所示,易得:A ∩B={x |x >3}.答案 D4.(预测题)设全集U=R,A={x|x(x-2)<0},B={x|y=ln(1-x)},则A∩(∁U B)是A.(-2,1) B.(1,2)C.(-2,1] D.[1,2)解析由x(x-2)<0得0<x<2,∴A={x|0<x<2},由1-x>0得x<1,∴B={x|x<1},∴∁U B={x|x≥1},∴A∩(∁U B)={x|1≤x<2}.答案 D5.设集合A={x||x-a|<1,x∈R},B={x|1<x<5,x∈R}.若A∩B=∅,则实数a的取值范围是A.{a|0≤a≤6} B.{a|a≤2或a≥4}C.{a|a≤0或a≥6} D.{a|2≤a≤4}解析由|x-a|<1得a-1<x<a+1,又A∩B=∅,所以a+1≤1或a-1≥5,解得a≤0或a≥6.答案 C二、填空题(每题6分,共12分)6.(2012·天津)已知集合A={x∈R||x+2|<3},集合B={x∈R|(x-m)(x-2)<0},且A∩B=(-1,n),则m=________,n=________.解析化简集合A=(-5,1),集合B=(m,2)或B=(2,m)(舍).又A∩B=(-1,n),故m=-1,n=1.答案-1 17.已知集合A={x|x≤a},B={x|1≤x≤2},且A∪(∁R B)=R,则实数a的取值范围是________.解析∵∁R B=(-∞,1)∪(2,+∞),且A∪(∁R B)=R,∴结合数轴,得a≥2.答案[2,+∞)三、解答题(12分+12分+14分,共38分)8.设集合A={x2,2x-1,-4},B={x-5,1-x,9},若A∩B={9},求A∪B.解析由9∈A,可得x2=9,或2x-1=9,解得x =±3,或x =5.当x =3时,A ={9,5,-4},b ={-2,-2,9},B 中元素重复,故舍去;当x =-3时,A ={9,-7,-4},B ={-8,4,9},A ∩B ={9}满足题意,故A ∪B ={-8,-7,-4,4,9};当x =5时,A ={25,9,-4},B ={0,-4,9},此时A ∩B ={-4,9}与A ∩B ={9}矛盾,故舍去.综上所述,A ∪B ={-8,-7,-4,4,9}.9.(易错题)已知集合A ={x |a -1<x <2a +1},B ={x |0<x <1},若A ∩B =∅,求实数a 的取值范围.解析 ∵A ∩B =∅,(1)当A =∅时,有2a +1≤a -1⇒a ≤-2; (2)当A ≠∅时,有2a +1>a -1⇒a >-2.又∵A ∩B =∅,则有2a +1≤0或a -1≥1⇒a ≤-12或a ≥2,∴-2<a ≤-12或a ≥2,由以上可知a ≤-12或a ≥2.10.已知集合A ={x |x 2-2x -3≤0,x ∈R},B ={x |x 2-2mx +m 2-4≤0,x ∈R}. (1)若A ∩B =[1,3],求实数m 的值; (2)若A ⊆∁R B ,求实数m 的取值范围.解析 A ={x |-1≤x ≤3},B ={x |m -2≤x ≤m +2}. (1)∵A ∩B =[1,3],∴⎩⎪⎨⎪⎧m -2=1m +2≥3,得m =3.(2)∁R B ={x |x <m -2或x >m +2}. ∵A ⊆∁R B ,∴m -2>3或m +2<-1. ∴m >5或m <-3.。
数学集合练习题及答案

一、选择题(每题4分,共40分)1、下列四组对象,能构成集合的是 ( ) A 某班所有高个子的学生 B 著名的艺术家 C 一切很大的书 D 倒数等于它自身的实数2、集合{a ,b ,c }的真子集共有 个 ( ) A 7 B 8 C 9 D 103、若{1,2}⊆A ⊆{1,2,3,4,5}则满足条件的集合A 的个数是 ( ) A. 6 B. 7 C. 8 D. 94、若U={1,2,3,4},M={1,2},N={2,3},则C U (M ∪N )= ( ) A . {1,2,3} B. {2} C. {1,3,4} D. {4}5、方程组 11x y x y +=-=- 的解集是 ( )A .{x=0,y=1} B. {0,1} C. {(0,1)} D. {(x,y)|x=0或y=1} 6、以下六个关系式:{}00∈,{}0⊇∅,Q ∉3.0, N ∈0, {}{},,a b b a ⊂ ,{}2|20,x xx Z -=∈是空集中,错误的个数是 ( )A 4B 3C 2D 17、点的集合M ={(x,y)|xy≥0}是指 ( ) A.第一象限内的点集 B.第三象限内的点集C. 第一、第三象限内的点集D. 不在第二、第四象限内的点集8、设集合A=}{12x x <<,B=}{x x a <,若A ⊆B ,则a 的取值范围是 ( ) A }{2a a ≥ B }{1a a ≤ C }{1a a ≥ D }{2a a ≤9、 满足条件M }{1=}{1,2,3的集合M 的个数是 ( ) A 1 B 2 C 3 D 410、集合{}|2,P x x k k Z ==∈,{}|21,Q x x k k Z ==+∈,{}|41,R x x k k Z ==+∈,且,a P b Q ∈∈,则有 ( )A a b P +∈B a b Q +∈C a b R +∈D a b +不属于P 、Q 、R 中的任意一个 二、填空题11、若}4,3,2,2{-=A ,},|{2A t t x x B ∈==,用列举法表示B 12、集合A={x| x 2+x-6=0}, B={x| ax+1=0}, 若B ⊂A ,则a=__________13、设全集U={}22,3,23a a +-,A={}2,b ,C U A={}5,则a = ,b = 。
集合专题训练(含答案)

集合专题训练(含答案)1.对集合中有关概念的考查在2020年校运动会中,集合A表示参加比赛的运动员,集合B表示参加比赛的男运动员,集合C表示参加比赛的女运动员。
那么下列关系正确的是()A。
A是B的子集B。
B是C的子集C。
A与B的交集等于CD。
B与C的并集等于A解析:根据题意,A包含了所有参加比赛的运动员,B只包含了男运动员,C只包含了女运动员。
因此,B是A的子集。
选项A正确。
点评:此题考查了集合的子集概念和集合运算,需要注意从元素的角度理解集合的含义。
2.对集合性质及运算的考查已知全集U={2,3,4,5,6,7},集合M={3,4,5,7},集合N={2,4,5,6},那么下列哪个选项是正确的?A。
M与N的交集为{4,6},N等于全集UB。
M与N的并集为{2,3,4,5,6,7},N等于全集UC。
(C并N)与M的并集等于全集UD。
(C并M)与N的交集等于N解析:根据题意,M与N的交集为{4,5},N不等于全集U;M与N的并集为{2,3,4,5,6,7},N不等于全集U;(C并N)与M的并集包含了全集U中的所有元素,因此选项C正确;(C并M)与N的交集为{4},不等于N。
因此选项D错误。
点评:此题考查了集合的并、交、补运算以及集合间的关系应用。
可以使用文氏图来帮助理解。
3.对与不等式有关集合问题的考查已知集合M={x|x+3<x-1},集合N={x|-3<x<1},那么集合{ x | x-1<x }等于哪个选项?A。
M并NB。
M交NC。
实数集RD。
(M交N)的补集解析:将集合M中的不等式化简得到-3<x,将集合N中的不等式化简得到-3<x<1,因此集合M交N等于{x|-3<x<1}。
而{x|x-1<x}等价于{x|x<1},因此选项C正确。
点评:此题考查了解不等式的知识内容,同时也考查了集合的运算。
需要注意参数的取值范围以及数形结合思想的应用。
集合的表示方法专题训练

集合的表示方法专题训练(建议用时:45分钟)[学业达标]一、选择题1.把集合{x|x2-3x+2=0}用列举法表示为()A.{x=1,x=2} B.{x|x=1,x=2}C.{x2-3x+2=0} D.{1,2}2.设集合A={1,2,4},集合B={x|x=a+b,a∈A,b∈A},则集合B中的元素个数为()A.4 B.5 C.6 D.73.下列各组两个集合M和N表示同一集合的是()A.M={π},N={3.141 59} B.M={2,3},N={(2,3)}C.M={(x,y)|x+y=1},N={y|x+y=1}D.M={x|x2+1=0},N=∅4.设集合A={-2,0,1,3},集合B={x|-x∈A,1-x∉A},则集合B中元素的个数为()A.1 B.2 C.3 D.45.已知P={x|2<x<k,x∈N},若集合P中恰有3个元素,则()A.5<k<6 B.5≤k<6 C.5<k≤6 D.5≤k≤6 二、填空题6.已知集合A={-1,-2,0,1,2},B={x|x=y2,y∈A},则用列举法表示B 应为________.7.已知集合A={x|x2+2x+a=0},若1∈A,则A=________.8.若2∉{x|x-a<0},则实数a的取值集合是________.三、解答题9.用适当的方法表示下列集合:(1)方程x2+y2-4x+6y+13=0的解集;(2)1 000以内被3除余2的正整数组成的集合;(3)二次函数y=x2-10图象上的所有点组成的集合.10.若-3∈{a-3,2a-1,a2+1},求实数a的值.[能力提升]1.集合A={1,2,3,4,5},B={1,2,3},C={z|z=xy,x∈A且y∈B},则集合C 中的元素个数为()A.3 B.4 C.11 D.122.已知集合A ={2,0,1,4},B ={k |k ∈R ,k 2-2∈A ,k -2∉A },则集合B 中所有的元素之和为( )A .2B .-2C .0 D. 23.集合{1,4,9,16,25},用描述法表示为________.4.设集合B =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ∈N ⎪⎪⎪ 62+x ∈N , (1)试判断元素1和2与集合B 的关系;(2)用列举法表示集合B .集合的表示方法专题训练答案(建议用时:45分钟)[学业达标]一、选择题1.把集合{x|x2-3x+2=0}用列举法表示为()A.{x=1,x=2} B.{x|x=1,x=2}C.{x2-3x+2=0} D.{1,2}【解析】解方程x2-3x+2=0可得x=1或2,所以集合{x|x2-3x+2=0}用列举法可表示为{1,2}.【答案】 D2.设集合A={1,2,4},集合B={x|x=a+b,a∈A,b∈A},则集合B中的元素个数为()A.4 B.5 C.6 D.7【解析】由题意,B={2,3,4,5,6,8},共有6个元素,故选C.【答案】 C3.下列各组两个集合M和N表示同一集合的是()A.M={π},N={3.141 59} B.M={2,3},N={(2,3)}C.M={(x,y)|x+y=1},N={y|x+y=1}D.M={x|x2+1=0},N=∅【解析】对于A,∵π≠3.141 59,∴{π}≠{3.141 59}.对于B,前者包含2个元素,而后者只含一个元素,是个点.对于C,前者是直线x+y=1上点的集合,而后者是函数y=-x+1的值域.对于D,∵x2+1=0无解,∴{x|x2+1=0}=∅,故选D.【答案】 D4.设集合A={-2,0,1,3},集合B={x|-x∈A,1-x∉A},则集合B中元素的个数为()A.1 B.2 C.3 D.4【解析】若x∈B,则-x∈A,∴x的可能取值为:2,0,-1,-3,当2∈B时,则1-2=-1∉A,∴2∈B;当0∈B时,则1-0∈A,∴0∉B;当-1∈B时,则1-(-1)=2∉A,∴-1∈B;当-3∈B时,则1-(-3)=4∉A,∴-3∈B.综上,B={-3,-1,2},所以集合B含有的元素个数为3,故选C.【答案】 C5.已知P={x|2<x<k,x∈N},若集合P中恰有3个元素,则()A.5<k<6 B.5≤k<6 C.5<k≤6 D.5≤k≤6 【解析】因为P中恰有3个元素,所以P={3,4,5},可得5<k≤6,故选C.【答案】 C二、填空题6.已知集合A={-1,-2,0,1,2},B={x|x=y2,y∈A},则用列举法表示B 应为________.【解析】(-1)2=12=1,(-2)2=22=4,02=0,所以B={0,1,4}.【答案】{0,1,4}7.已知集合A={x|x2+2x+a=0},若1∈A,则A=________.【解析】把x=1代入方程x2+2x+a=0可得a=-3,解方程x2+2x-3=0可得A={-3,1}.【答案】{-3,1}8.若2∉{x|x-a<0},则实数a的取值集合是________.【解析】由题意,{x|x-a<0}={x|x<a},∵2∉{x|x-a<0},∴a≤2,∴实数a的取值集合是{a|a≤2}.【答案】{a|a≤2}三、解答题9.用适当的方法表示下列集合:(1)方程x2+y2-4x+6y+13=0的解集;(2)1 000以内被3除余2的正整数组成的集合;(3)二次函数y=x2-10图象上的所有点组成的集合.【解】(1)方程x2+y2-4x+6y+13=0可化为(x-2)2+(y+3)2=0,解得x =2,y=-3,所以方程的解集为{(x,y)|x=2,y=-3}.(2)集合的代表元素是数,用描述法可表示为{x|x=3k+2,k∈N且x<1 000}.(3)“二次函数y=x2-10图象上的所有点”用描述法表示为{(x,y)|y=x2-10}.10.若-3∈{a-3,2a-1,a2+1},求实数a的值.【解】∵-3∈{a-3,2a-1,a2+1},又a2+1≥1,∴-3=a-3,或-3=2a-1,解得a=0,或a=-1,当a=0时,{a-3,2a-1,a2+1}={-3,-1,1},满足集合三要素;当a=-1时,{a-3,2a-1,a2+1}={-4,-3,2},满足集合三要素;∴a=0或-1.[能力提升]1.集合A={1,2,3,4,5},B={1,2,3},C={z|z=xy,x∈A且y∈B},则集合C 中的元素个数为()A .3B .4C .11D .12【解析】 C ={1,2,3,4,5,6,8,9,10,12,15},故选C.【答案】 C2.已知集合A ={2,0,1,4},B ={k |k ∈R ,k 2-2∈A ,k -2∉A },则集合B 中所有的元素之和为( )A .2B .-2C .0 D. 2【解析】 若k 2-2=2,得k =2或k =-2,当k =2时,k -2=0不满足条件,当k =-2时,k -2=-4,满足条件;若k 2-2=0,得k =±2,显然满足条件;若k 2-2=1,得k =±3,显然满足条件;若k 2-2=4,得k =±6,显然满足条件.所以集合B 中的元素为-2,±2,±3,±6,所以集合B 中的元素之和为-2,则选B.【答案】 B3.集合{1,4,9,16,25},用描述法表示为________.【解析】 1=12,4=22,9=32,16=42,25=52,故用描述法表示为{x |x =n 2,n ∈Z 且1≤n ≤5}.【答案】 {x |x =n 2,n ∈Z 且1≤n ≤5}4.设集合B =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ∈N ⎪⎪⎪ 62+x ∈N , (1)试判断元素1和2与集合B 的关系;(2)用列举法表示集合B .【解】 (1)当x =1时,62+1=2∈N ;当x =2时,62+2=32∉N ,所以1∈B,2∉B .(2)令x =0,1,4代入62+x∈N 检验,可得B ={0,1,4}.。
职高数学《集合》练习题

(一)集合及表示方法1、“①难解的题目;②方程012=+x ;③平面直角坐标系内第四象限的一些点;④很多多项式”中,能组成集合的是 ( )。
A .②B .① ③C .② ④D .① ② ④2.下列选项中元素的全体可以组成集合的是 ( ) A.学校篮球水平较高的学生 B.校园中长的高大的树木C.2007年所有的欧盟国家D.中国经济发达的城市3、下列命题正确的个数为…………………( )。
(1)很小两实数可以构成集合;(2)}1|{2-=x y y 与}1|),{(2-=x y y x 是同一集合(3)5.0,21,46,23,1-这些数组成的集合有5个数;(4)集合},,0|),{(R y x xy y x ∈≤是指第二、四象限内的点集;A .0个B .1个C .2个D .3个4.集合{(x ,y)|y =2x -1}表示 ( )A .方程y =2x -1B .点(x ,y)C .平面直角坐标系中的所有点组成的集合D .函数y =2x -1图象上的所有点组成的集合 5.已知集合}{,,S a b c=中的三个元素是ABC ∆的三边长,那么ABC ∆一定不是 ( )A.锐角三角形B.直角三角形C.钝角三角形D.等腰三角形6.设集合M ={x ∈R|x≤33},a =26,则( )A .a ∉MB .a ∈MC .{a}∈MD .{a|a =26}∈M 7.方程组⎩⎨⎧x +y =1x -y =9的解集是( )A .(-5,4)B .(5,-4)C .{(-5,4)}D .{(5,-4)}8.方程组20{=+=-y x y x 的解构成的集合是( )A .)}1,1{(B .}1,1{C .(1,1)D .}1{ 9.下列集合中,不同于另外三个集合的是( )A .{0}B .{y|y 2=0} C .{x|x =0} D .{x =0}10.由实数x ,-x ,x 2,-3x 3所组成的集合里面元素最多有________个.11.用适当的符号填空:(1)∅ }01{2=-x x ; (2){1,2,3} N ;(3){1} }{2x x x =; (4)0 }2{2x x x =. 12.含有三个实数的集合既可表示成}1,,{ab a ,又可表示成}0,,{2b a a +,则=+20042003b a .13、⑴用列举法表示下列集合:①},,20,20|),{(Z y x y x y x ∈<≤<≤ =② _;__________},,,|{},2,1,0{=≠∈+===b a M b a b a x x P M14. 用描述法表示下列集合:①所有正偶数组成的集合 ②被9除余2的数组成的集合15.用适当的方法表示以下集合:(1)大于10而小于20的合数所组成的集合 ;(2)方程组2219x y x y +=⎧⎨-=⎩的解集 。
集合基础题训练

1、设集合A = {1, 2, 3},B = {x | x是A中的元素且x > 1},则集合B的元素个数为?A. 0B. 1C. 2D. 3(答案:C)2、若集合M = {x | x2 - x - 6 = 0},N = {x | ax - 1 = 0},且N是M的子集,则a的值为?A. 0或1/2B. 0或-1/2C. 0或1/3D. 0或-1/3(答案:D)3、设全集U = {1, 2, 3, 4, 5},集合A = {1, 2, 3},B = {3, 4},则A∩B的补集为?A. {1, 2}B. {1, 2, 5}C. {4, 5}D. {3, 4, 5}(答案:B)4、若集合A = {x | x = 2k, k ∈Z},B = {x | x = 3m, m ∈Z},则A∩B的元素特征是?A. 既是2的倍数又是3的倍数B. 仅是2的倍数C. 仅是3的倍数D. 既不是2的倍数也不是3的倍数(答案:A)5、设集合A = {x | -2 ≤x ≤5},B = {x | x > 3},则A∪B的元素范围是?A. -2 ≤x ≤5B. x > 3C. x ≥-2D. 以上都不对(答案:C)6、若集合A = {x | x是质数且小于10},则A中元素的个数为?A. 2B. 3C. 4D. 5(答案:C)7、设集合A = {x | x是等腰三角形},B = {x | x是等边三角形},则B与A的关系是?A. B = AB. B ⊆ AC. A ⊆ BD. B与A无关系(答案:B)8、若集合M = {x | x是平行四边形},N = {x | x是矩形},则N与M的关系是?A. N = MB. N ⊆ MC. M ⊆ ND. N与M是同一集合的不同表示(答案:B)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三、课后练习
1.下列八个关系式:①{0}=φ ②φ=0 ③φ {φ} ④φ∈{φ}⑤{0}⊇φ ⑥0∉φ ⑦φ≠{0} ⑧φ≠{φ} 其中正确的个数 ( C )
(A )4 (B )5 (C )6 (D )7
2.设A 、B 是全集U 的两个子集,且A ⊆B ,则下列式子成立的是 (C )
(A )C U A ⊆C U B (B )C U A C U B=U (C )A C U B=φ (D )C U A B=φ
3.已知M=},13|{},,13|{},,3|{Z n n x x P Z n n x x N Z n n x x ∈-==∈+==∈=,且P c N b M a ∈∈∈,,,
设c b a d +-=,则∈d ( B )
(A )M (B )N (C )P (D )P M
4.设集合},214|{},,412|{Z k k x x N Z k k x x M ∈+==∈+=
=,则 (A ) (A )N M ⊆ (B )M N ⊆ (C )N M = (D )Φ=N M
5.集合A,B 的并集A ∪B={a 1,a 2,a 3},当且仅当A≠B 时,(A,B)与(B,A)视为不同的对,则这样的(A,B)对的个数有_________________.
6.解:A=φ时,有1种可能;A 为一元集时,B 必须含有其余2元,共有6种可能;A 为二元集时,B 必须含有另一元.共有12种可能;A 为三元集时,B 可为其任一子集.共8种可能.故共有1+6+12+8=27个.
7.若非空集合A={x|2a+1≤x≤3a -5},B={x|3≤x≤22},则能使A ⊆A∩B 成立的a 的取值范围是_______________.
7.解:由A 非空知2a+1≤3a-5,故a ≥6. 由A ⊂A ⋂B 知A ⊂B. 即3≤2a+1且3a-5≤22, 解之,得1≤a ≤9. 于是知6≤a ≤9
8.若A={x|0≤x 2+ax+5≤4}为单元素集合,则实数a 的值为___________________.
8.解:由24122125)(5a a x ax x -++=++.若4524
1<-a ,则A 有无数个元,≠
⊂
若45241>-a ,则A 为空集,只有当4524
1=-a 即2±=a 时,A 为单元素集}1{-或}1{.所以2±=a
9.设A={n|100≤n≤600,n ∈N},则集合A 中被7除余2且不能被57整除的数的个数为______________.
9.解:被7除余2的数可写为7k+2. 由100≤7k+2≤600.知14≤k ≤85. 又若某个k
使7k+2能被57整除,则可设7k+2=57n. 即72725672578--+-+===n n n n n k . 即n-2应为7的倍数. 设n=7m+2代入,得k=57m+16. ∴14≤57m+16≤85. m=0,1.于是所求的个数为85-(14-1)-2=70
10.记集合}6,5,4,3,2,1,0{=T ,⎭
⎬⎫⎩⎨⎧=∈+++=4,3,2,1,77774433221i T a a a a a M i ,将M 中的元
素按从大到小顺序排列,则第2005个数是 . 396
2401
11. 321,,S S S 为非空集合,对于1,2,3的任意一个排列k j i ,,,若j i S y S x ∈∈,,则k S y x ∈-
(1) 证明:三个集合中至少有两个相等。
(2) 三个集合中是否可能有两个集无公共元素?
证明:(1)若j i S y S x ∈∈,,则 i k S x y x y S x y ∈-=--∈-)(,
所以每个集合中均有非负元素。
当三个集合中的元素都为零时,命题显然成立。
否则,设321,,S S S 中的最小正元素为a ,不妨设1S a ∈,设b 为32,S S 中最小的非负元素,不妨设,2S b ∈则b -a ∈3S 。
若b >0,则0≤b -a <b ,与b 的取法矛盾。
所以b =0。
任取,1S x ∈因0∈2S ,故x -0=x ∈3S 。
所以⊆1S 3S ,同理3S 1S ⊆。
所以1S =3S 。
(3) 可能。
例如1S =2S ={奇数},3S ={偶数}显然满足条件,1S 和2S 与3S 都无
公共元素。
