Matlab图形绘制经典案例
实验二MATLAB绘制图形

grid on %在所画出的图形坐标中加入栅格
绘制图形如下
50
10
1
0.8
40
10
0.6
0.4
30
10
0.2
0
1020
-0.2
-0.4
1010
-0.6
-0.8
0
10
-1
-2
0
2
-2
0
2
10
10
10
10
10
10
如果在图中不加栅格
程序如下:
clear x=logspace(-1,2);%在10^(-1)到10^2之间产生50个 对数等分的行向量 subplot(121); loglog(x,10*exp(x),'-p') subplot(122); semilogx(x,cos(10.^x))
(2)plot(x,y): 基本格式,x和y可为向量或矩阵. 1. 如果x,y是同维向量,以x元素为横坐标,以y元素 为纵坐标绘图. 2. 如果x是向量,y是有一维与x元素数量相等的矩阵, 则以x为共同横坐标, y元素为纵坐标绘图,曲线数目 为y的另一维数. 3. 如果x,y是同维矩阵,则按列以x,y对应列元素为 横、纵坐标绘图,曲线数目等于矩阵列数.
y=2*exp(-0.5*x).*cos(4*pi*x);
2
plot(x,y)
1.5
1
0.5
0
-0.5
-1
-1.5
-2
0
1
2
3
4
5
6
7
例4 绘制曲线
t=(0:0.1:2*pi);
x=t.*sin(3*t);
y=t.*sin(t).*sin(t);
(打印)实验四 MATLAB 高级图形绘制
实验四MATLAB 高级图形绘制一、实验目的及要求:1.熟悉各种绘图函数的使用;2.掌握图形的修饰方法和标注方法;3.了解MATLAB 中图形窗口的操作。
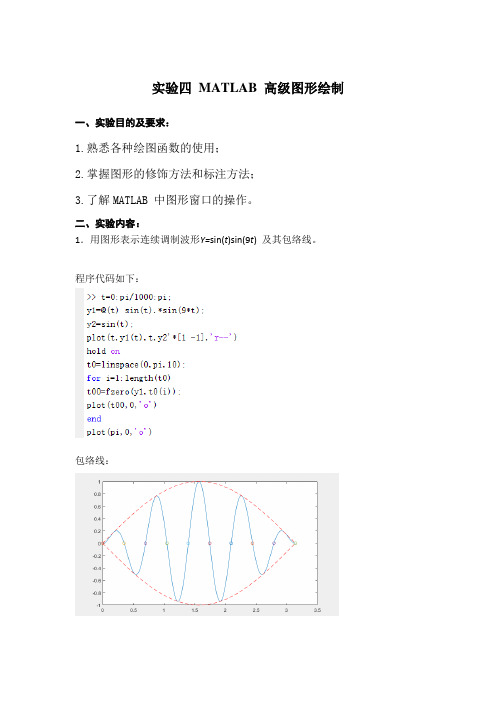
二、实验内容:1.用图形表示连续调制波形Y=sin(t)sin(9t)及其包络线。
程序代码如下:包络线:2.x=[-2π,2π],y1=sinx、y2=cosx、y3=sin2x、y4=cos 2x①用MATLAB语言分四个区域分别绘制的曲线,并且对图形标题及横纵坐标轴进行标注。
程序:结果:②另建一个窗口,不分区,用不同颜色、线型绘出四条曲线,并标注图例注解。
程序:结果:③绘制三维曲线:⎪⎩⎪⎨⎧=≤≤==)cos()sin()200()cos()sin(t t t z t t y t x π程序:结果:3.绘制极坐标曲线ρ=asin(b+nθ),并分析参数a、b、n对曲线形状的影响。
(1)a=1;b=1;n=1(2)a=10;b=1;n=1(3)a=10;b=10;n=1 (4)a=10;b=10;n=10参数a、b、n对曲线形状的影响:由上面绘制的图形可知:a决定图形的大小,当a为整数时,图形半径大小就是a;b决定图形的旋转角度,图形的形状及大小不变;n决定图形的扇叶数,当n 为奇数时,扇叶数为n,当n为偶数时,扇叶数为2n。
三、结论本次实验用到了曲线绘图、三位曲线绘图的知识,与老师上课的内容一致,让我学的matlab绘图的知识得到了巩固,我还学会了如何使用title、subplot、plot、axis等函数。
在做实验的过程复习了hold on指令是覆盖函数继续绘图的意思。
应用MATLAB图形函数和绘图实例

应用MATLAB图形函数和绘图实例例1.输入MATLAB程序如下:x = 0 : 0.2 : 12;y1 = Bessel ( 1, x );y2 = Bessel ( 2, x );y3 = Bessel ( 3, x );figure ( 1 )subplot ( 2, 2, 1 )h = plot ( x, y1, x, y2, x, y3 );set ( h, ‘LineWidth’, 2, {‘ LineStyle’}, {‘--’ ; ‘ : ’, ‘ -. ’}) set ( h, {‘ Color’ }, { ‘ R’; ‘ G ’; ‘ B ’})axis ( [ 0 12 –0.5 1] )grid onxlabel ( ‘ Time ’ )ylabel ( ‘ Amplitude ’ )legend ( h, ‘ First’, ‘ Second ’, ‘ Third ’ )title ( ‘ Bessel Functions’)[ y, ix ] = min ( y1 );text ( x ( ix ), y, ‘First Min \ rightarrow’, …‘ HorizontalAlignment’, ‘right’)Print – depsc -tiff –r200 myplot应用图形编辑模式 如图所示。
同学们自己练习各项功能。
例2. 输入MATLAB 程序如下:t = 0 : pi/100 : 2*pi; y = sin ( t ); plot ( t, y ) grid on继续输入程序如下: y2 = sin ( t – 0.25 ); y3 = sin ( t – 0.5 ); plot ( t, y, t, y2, t, y3 )按此按钮开始图形编辑模式按这些钮开始增加字符箭头和线 改变一个轴的3D 视角可以对线的类型进行定义:t = 0 : pi/100 : 2*pi;y = sin ( t );y2 = sin ( t – 0.25 );y3 = sin ( t – 0.5 );plot ( t, y, ‘ - ’, t, y2, ‘ -- ’, t, y3, ‘ : ’ )练习,对红的颜色进行编辑。
matlab--函数图形绘制实验报告1

实验报告课程名称: 数学实验学院名称: 数学与统计学院班级:姓名:学号:2012-2013 学年第学期数学与统计学院制(二)参数方程作图例2: 画出星形线{ 及旋轮线{ 的图形解: 输入以下命令:%星形线作图t=linspace(0,2*pi,5000);x=2*(cos(t)).^3;y=2*(sin(t)).^3;plot(x,y),grid;结果:%旋轮线作图t=linspace(0,4*pi,5000); x=2*(t-sin(t));y=2*(1-cos(t));plot(x,y),axis equal; axis(0,8*pi,0,5);grid;结果:(三)极坐标方程图形例3:画出四叶玫瑰线的图形。
知其极坐标方程: ρ=acos(2 )。
解: 取a=5做图。
在命令窗口输入下命令theta=linspace(0,2*pi);r=2*cos(2*theta);polar(theta,r)结果:(四)空间曲面(线)的绘制例4: 绘制双曲抛物面z= 。
解:将其化为参数方程:{ , 编写m文件运行以下命令r=linspace(-4,4,30);s=r;[u,v]=meshgrid(r,s);x=u;y=v;z=(u.^2-v.^2)./4;surf(x,y,z);bix on;结果:(五)空间曲线在坐标平面上的投影曲面和投影柱面例5: 画出螺旋线{ , 在xOz面上的正投影曲线的图形。
解:化为参数方程{ , 运行下列程序t=linspace(-2*pi,2*pi);x=10*cos(t);z=2*t;h=plot(x,z);grid;xlabel('x');ylabel('z');set(h,'linewidth',2);结果:(一)实验分析:(二)在本次实验中我们初步了解了matlab。
(三)学会了一些简单绘图。
(四)在编制中我们要很明确“点乘的重要性”。
案例28使用matlab绘制专业图形——绘制曲线和曲面图

案例28使用MATLAB 绘制专业图形绘制曲线和曲面图案例主要信息提示 ● 案例内容:使用MATLAB 进行专业作图。
● 关键词:MATLAB ,作图,二维作图,三维作图 ● 建议课时:2课时● 适合专业:理工科各专业●光盘中的数字资源:二维曲线绘图M 文件graph_line.m三维曲面绘图M 文件graph_surface.m一、 实验内容实验内容1.绘制曲线图在1个绘图窗口的4个不同子窗口中分别绘制以下曲线: ①在子窗口1中绘制两条二维曲线,分别为:0.510.2cos(4)x y e x π-=和0.522cos()x y e x π-=并显示网格线。
②在子窗口2中绘制两条二维曲线,分别为:0.512x y e -=和2cos(2)y x π=并添加标题、x/y 轴名称、图形说明和图例。
③在子窗口3中绘制一条极坐标曲线,如下:sin()cos()r t t =④在子窗口4中绘制一条极三维螺旋线。
全部4个子窗口绘制效果如图28-1所示。
图28-1曲线绘制效果图实验内容2.绘制曲面图在1个绘图窗口的4个不同子窗口中分别绘制以下曲面:①在子窗口1和子窗口2中以不同着色方式绘制两个球面。
②在子窗口3和子窗口4中以不同视角绘制两个直径相等的圆管相交的图形。
全部4个子窗口绘制效果如图28-2所示。
图28-1曲面绘制效果图二、预备知识2.1 MATLAB绘图功能简介MA TLAB软件提供了丰富的图形表达功能,包括常用的二维图形和三维图形。
其中,各种二维图形近30种,三维图形20多种。
应用MA TLAB除了能作一般的曲线、散点图、条形图等,还能绘制流线图、三维矢量图等工程实用图形。
下面我们介绍一些基本的二维和三维绘图函数。
2.2 二维图形的绘制二维图形是将平面坐标上的数据点连接起来的平面图形。
可以采用不同的坐标系,如直角坐标、对数坐标、极坐标等。
二维图形的绘制是其他绘图操作的基础。
2.2.1绘制二维曲线的plot函数在MATLAB中,plot函数是最简单、最基本而且应用最为广泛的线性绘图函数,利用它可以在二维平面上生成线段、曲线和参数方程曲线等的函数图形。
MATLAB绘图及例子总结

MATLAB 绘图及例⼦总结MATLAB 绘图及例⼦总结⼆维图例 1结果:例 2结果:X1=[1,2,4,6,7,8,10,11,12,14,16,17,18,20];Y1=[1,2,4,6,7,8,10,10,8,7,6,4,2,1];figure(1)plot(X1,Y1,'o','MarkerSize',15)X2=1:20;Y2=log(X2);figure(2)plot(X2,Y2,'o','MarkerSize',15)X1=(0:12)*pi/6;Y1=cos(3*X1);X2=(0:360)*pi/180;Y2=cos(3*X2);figure(1)subplot(2,2,1);plot(X1,Y1,'o','MarkerSize',3); % 设置标准尺⼨为3xlim([0 2*pi]) % 补充知识点xlim% x 轴上下限设定xlim([a,b]);% y 轴上下限设定ylim([a,b])subplot(2,2,2);plot(X1,Y1,'LineWidth',2); % 设置线宽度为2xlim([0 2*pi])subplot(2,2,3);plot(X2,Y2,'o','MarkerSize',3);xlim([0 2*pi])subplot(2,2,4);plot(X2,Y2,'LineWidth',2);xlim([0 2*pi])例 3结果:例 4x=-pi/2:0.01:pi/2;y=x+sin(x)+exp(x);plot(x,y,'-ro'); % 颜⾊红⾊grid on % ⽹格title('y 的函数图像');xlabel('x');ylabel('y');legend('y=x+sinx+e^(x)');A=magic(20);A(9:20,:)=[];figure(1);结果:例 5结果:figure(1);plot(A);for i=1:5for j=1:6B(i,j)=i+j;endendx=0.2:0.2:1;figure(2)subplot(2,2,1);plot(B,x,'LineWidth',1.5);subplot(2,2,2);plot(x,B,'LineWidth',1.5);C=reshape(1:30,5,6); % 变换成特定维数5×6的矩阵subplot(2,2,3);plot(B,C,'LineWidth',1.5);subplot(2,2,4);plot(C,B,'LineWidth',1.5);x=-pi:pi/10:pi;y=tan(sin(x))-sin(tan(x));plot(x,y,'--rs','LineWidth',2,'MarkerEdgeColor','k','MarkerFaceColor','g','MarkerSize',10);% MarkerFaceColor :点符号填充颜⾊% MarkerEdgeColor :点边框颜⾊例 6结果:例 7结果:clear allx=-pi:pi/10:pi;y=[sin(x);sin(x+3);sin(x+5)];z=[cos(x);cos(x+3);cos(x+5)];figure;plot(x,y,'r:*',x,z,'g-.v');% r 是红⾊,:是点线,*是星号标记% g 是绿⾊,-.是点画线,v 是倒三⾓形% 绘制双坐标轴figureangl=0:0.01*pi:2*pi;ampl=sin(0:0.01*pi:2*pi);z=ampl.*(cos(angl)+sqrt(-1)*sin(angl));[AX,H1,H2]=plotyy(0:200,abs(z),0:200,angle(z)*180/pi);% angle ⽤来求复数矩阵相位⾓的弧度值,其取值为-pi 到pi ,z 是⼀个复数,abs(z)是复数的模set(get(AX(1),'Ylabel'),'String','amplitude') % amplitude 振幅set(get(AX(2),'Ylabel'),'String','phase') % phase 阶段% get 返回某些对象属性的当前值set(H1,'LineWidth',3);set(H2,'LineStyle',':','LineWidth',3)例 8结果1:结果2:% x 轴对数坐标x=10.^(0.1:0.1:4);y=1./(x+1000);figuresubplot(1,2,1);semilogx(x,y,'+','MarkerSize',5,'LineWidth',2);title('y=(x+1000)^{-1}')subplot(1,2,2);plot(x,y,'+','MarkerSize',5,'LineWidth',2);title('y=(x+1000)^{-1}')% y 轴对数坐标同理% x 轴和y 轴均为对数坐标a=0.1:0.1:5;x=log10(a);y=10.^a;figuresubplot(1,2,1)loglog(x,y,'+','MarkerSize',5,'LineWidth',2)title('lgy=10^x')subplot(1,2,2)plot(x,y,'+','MarkerSize',5,'LineWidth',2)title('lgy=10^x')例 9结果:例 10结果:y=[75.995,91.972,105.711,123.203,131.669...150.697,179.323,203.212,226.505,249.633,281.422];figure;bar(y);x=-2:2;Y=[6,8,7,4,5;4,8,1,12,0;4,6,21,1,3];subplot(1,2,1),bar(x',Y','stacked')xlabel('x'),ylabel('\Sigma y'),colormap(cool)legend('因素 1','因素 2','因素 3')subplot(1,2,2),barh(x',Y','grouped') % barh 创建⽔平直⽅图xlabel('y'),ylabel('x')例 11结果:例 12结果:例 13x=[1,5,0.5,3.5,2];explode=[0,1,0,0,0];pie(x,explode) % 饼图colormap jetfigurepie3(x,explode)colormap hsvx=-4:0.1:4;y=randn(5000,1);hist(y,x) % 直⽅图clearfigure;结果:三维图例 1结果:例 2结果:figure;x=[1,5,6,7,9,5,1,3,12,20];y=[20,15,6,3,1,5,3,0,1,5];subplot(121);scatter(x,y); % 散点图subplot(122);scatter(x,y,[],[1,0,0],'fill');theta=0:0.01*pi:2*pi;x=sin(theta);y=cos(theta);z=cos(4*theta);figureplot3(x,y,z,'LineWidth',2);hold on;theta=0:0.02*pi:2*pi;x=sin(theta);y=cos(theta);z=cos(4*theta);plot3(x,y,z,'rd','MarkerSize',10,'LineWidth',2)X=-10:0.1:10;Y=-10:0.1:10;[X,Y]=meshgrid(X,Y);Z=-X.^2-Y.^2+200;mesh(X,Y,Z)例 3结果:例 4···[X,Y,Z]=peaks(30); %peaks 函数是⼀个典型的多元函数,本质上是⼀个⼆元⾼斯分布的概率密度函数subplot(1,2,1);surfl(X,Y,Z),colormap(copper),title('Default Lighting'),shading interpsubplot(1,2,2);surfl(X,Y,Z,[-90,30],[.55,.6,2,10]),shading interp···结果:figuresurf(X,Y,Z,'FaceColor','red','EdgeColor','none');camlight left; % 左侧加⼀个发光物体lighting phong % 光照模式,使图表⾯光滑细腻,⾊彩丰富view(-15,65) % 视⾓的⾓度例 5结果:例 6结果:% 等⾼线图[X,Y,Z]=peaks(30);figuresubplot(2,2,1);contour(X,Y,Z);axis square subplot(2,2,2);contour(X,Y,Z,10);axis squaresubplot(2,2,3);contour(X,Y,Z,-10:1:10);axis square subplot(2,2,4);contour(X,Y,Z,':');axis square[X,Y,Z]=peaks(30);R=sqrt(X.^2+Y.^2);subplot(1,2,1);surf(X,Y,Z,Z);axis tightsubplot(1,2,2);surf(X,Y,Z,R);axis tight。
利用Matlab绘制各类特殊图形的实例代码

利⽤Matlab绘制各类特殊图形的实例代码Matlab绘图介绍强⼤的绘图功能是Matlab的特点之⼀,Matlab提供了⼀系列的绘图函数,⽤户不需要过多的考虑绘图的细节,只需要给出⼀些基本参数就能得到所需图形,这类函数称为⾼层绘图函数。
此外,Matlab还提供了直接对图形句柄进⾏操作的低层绘图操作。
这类操作将图形的每个图形元素(如坐标轴、曲线、⽂字等)看做⼀个独⽴的对象,系统给每个对象分配⼀个句柄,可以通过句柄对该图形元素进⾏操作,⽽不影响其他部分。
Matlab绘制特殊图形1. 绘制极坐标图说明:使⽤polarplot函数绘制极坐标图,每组数据表⽰⼀条闭合曲线,共有20条曲线构成20条封闭同⼼曲线。
t = linspace(0,2*pi,500);y = 1+0.3*sin(20*t)+0.1*sin(30*t)+0.1*sin(40*t);polarplot(t,y,t,1.1*y,t,1.2*y,t,1.3*y,t,1.4*y,t,1.5*y,t,1.6*y,t,1.7*y,t,1.8*y,t,1.9*y,...t,2.0*y,t,2.1*y,t,2.2*y,t,2.3*y,t,2.4*y,t,2.5*y,t,2.6*y,t,2.7*y,t,2.8*y,t,2.9*y,'linewidth',1.5);2. 单条曲线绘制分段函数(反⽐例函数y=1/x)说明:反⽐例函数在x接近于0时,趋近于奇异(1/0 趋近于⽆穷⼤),使⽤nan⾮数对图形进⾏镂空,可以实现⼀条曲线绘制y=1/x的整个定义域。
x = linspace(-3,3,500);f = @(x) 1./x;y = f(x);for ii = 1:length(x)if abs(x(ii))<0.03x(ii) = nan;y(ii) = nan;endendplot(x,y)legend('y=1/x')3. 正⽅体内绘制随机分布的颜⾊⽚图说明:使⽤plot3绘制正⽅体12条边,使⽤fill3函数绘制颜⾊⽚,颜⾊⽚位置和填充颜⾊随机⽣成。
第三章 matlab图形绘制

指定
grid 图形中加网格
例3.在同一坐标系下画出sinx和cosx的图形,并适当加 标注.
x=linspace(0,2*pi,30);y=[sin(x);cos(x)]; plot(x,y);grid;xlabel (‘x’);ylabel (‘y’); title(‘sine and cosine curves’); text(3*pi/4,sin(3*pi/4),’\leftarrowsinx’); text(2.55*pi/2,cos(3*pi/2),’cos\rightarrow’)
结果见下图.
4.多幅图形
subplot(m,n,p)可以在同一个图形窗口中画出多个图 形,用法见下例.
x=linspace(0,2*pi,30);y=sin(x);z=cos(x);u=2*sin(x).* cos(x);v=sin(x)./cos(x); subplot(2,2,1),plot(x,y),title(‘sin(x)’) subplot(2,2,2),plot(x,z),title(‘cos(x)’) subplot(2,2,3),plot(x,u),title(‘2sin(x)cos(x)’) subplot(2,2,4),plot(x,v),title(‘sin(x)/cos(x)’)
plot(x1,y1,x2,y2, …) 在此格式中,每对x,y必须符合 plot(x,y)中的要求,不同对之间没有影响,命令对每 一对x,y绘制曲线.
例1.做出y=sinx在[0,2π]上的图形,结果见下图.
x=linspace(0,2*pi,30); sin(x);plot(x,y)
例2.在同一坐标系下做出两条曲线y=sinx和y=cosx 在[0,2π]上的图形.结果见下图.
