第九章 期权估价-期权估价原理一:复制原理
期权复制原理

期权复制原理期权复制原理是指通过构建一种资产组合,使得该资产组合的收益与期权的收益模式相似,从而实现对期权价格变动的复制。
期权复制原理是金融衍生品领域的重要理论,对于投资者和交易者来说具有重要的指导意义。
首先,我们来了解一下期权的基本概念。
期权是一种金融衍生品,它赋予持有者在未来某个时间点以特定价格买入或卖出一定数量的标的资产的权利,而不是义务。
期权分为认购期权和认沽期权两种,认购期权赋予持有者在未来以约定价格买入标的资产的权利,认沽期权则赋予持有者在未来以约定价格卖出标的资产的权利。
期权复制原理的基本思想是通过构建一种资产组合,使得该资产组合的价值随着标的资产价格的变动而变动,从而模拟期权的收益模式。
一般来说,期权的价格受到标的资产价格、执行价格、剩余时间、波动率等因素的影响。
因此,构建期权复制组合需要考虑这些因素,以实现对期权价格变动的复制。
在期权复制原理中,常用的方法包括Delta对冲、Delta-Gamma对冲和Delta-Gamma-Theta对冲等。
Delta对冲是指构建一种资产组合,使得该组合的价格变动与期权价格的价格变动相对应,从而实现对期权价格变动的复制。
Delta-Gamma对冲在Delta对冲的基础上引入Gamma对冲,通过调整资产组合的持仓比例,进一步提高对期权价格变动的复制效果。
Delta-Gamma-Theta对冲则在Delta-Gamma对冲的基础上引入Theta对冲,以应对期权价格受到时间价值影响的情况。
期权复制原理的应用可以帮助投资者和交易者进行风险管理和套期保值,同时也可以为金融机构和市场提供更多的交易工具和产品。
通过期权复制原理,投资者可以根据自己的风险偏好和投资目标构建合适的资产组合,实现对期权价格变动的复制,从而获得更多的投资机会和收益。
总之,期权复制原理是金融衍生品领域的重要理论,它对于投资者和交易者来说具有重要的指导意义。
通过构建一种资产组合,使得该组合的收益模式与期权的收益模式相似,从而实现对期权价格变动的复制,可以帮助投资者进行风险管理和套期保值,同时也为金融机构和市场提供更多的交易工具和产品。
第九章 期权估价-派发股利的期权定价

2015年注册会计师资格考试内部资料
财务成本管理
第九章 期权估价
知识点:派发股利的期权定价
● 详细描述:
股利的现值是股票价值的一部分,但是只有股东可以享有该收益,期权持有人不能享有。
因此,在期权估价时要从股价中扣除期权到期前所派发的全部股利的现值。
也就是说,把所有到期日前预期发放的未来股利视同已经发放,将这些股利的现值从现行股票价格中扣除。
此时,模型建立在调整后的股票价格而不是实际价格的基础上。
处理方法:S0→S0e-δt
考虑派发股利的期权定价公式如下:
C0=S0e-δtN(d1)-Xe-rctN(d2)
其中:
δ(delta)=标的股票的年股利收益率(假设股利连续支付,而不是离散分期支付)
【注】如果δ=0,则与前面介绍的BS模型相同。
例题:
1.其他因素不变的情况下,下列事项中,会导致看跌期权价值增加的有
()。
A.期权执行价格提高
B.期权到期期限延长
C.股票价格的波动率增加
D.无风险利率提高
正确答案:A,C
解析:期权到期期限延长对于欧式期权价值影响不一定,选项B错误。
无风险利率提高会使执行价格下降进而使看跌期权价值下降,选项D错误。
期权估价

金融期权估价
二、二叉树期权定价模型
假设:1、市场投资没有交易成本。 2.投资者都是价格接受者。 3.允许完全使用卖空所得款型。 4、允许以无风险利率借入戒贷出款项。 5.未来股票的价格将是两种可能值中的一个。 (一)单期二叉树 单期二叉树始亍建立一个投资组合:1.一定数量的股票多头头寸;2.该股票的看涨期权 的空头头寸。股票的数量要使头寸足以抵御资产价格在到期日的波劢风险,即该组合能 实现完全套期保值,产生无风险利率。
三.布莱克-斯科尔斯期权定价模型
(一)假设: 1.在期权寿命期内,买斱期权标的股票丌发放股利,也丌做其他分配; 2.股票戒期权的买卖没有交易成本; 3.短期的无风险利率是已知的,并丏在期权寿命期内保持丌变; 4.任何证券贩买者都能以短期的无风险利率借入任何数量的资金;、 5.允许卖空,卖空者将立即得到卖空股票当天价格的资金; 6.看涨期权只能在到期日执行; 7.所有证券交易都是连续发生的,股票几个随机游走。 (二)布莱克-斯科尔斯模型 布莱克-斯科尔斯模型包含三个公式:
期望报酬率=上行概率*上行时的收益+下行概率*下行时收益率
假设股票丌派发红利,股票价格上升百分比就是股票投资的收益率, 因此:期望报酬率=上行概率*股价上升比+下行概率*(-股价下降比)
可求得上行概率
到期期权的期望价值=上行概率*上行期权价值+下行概率*下行期权价值
期权价值=到期期权价值*折现系数
(4)期权执行
分类:按合同授予期权持有人权利分类,期权分看涨期权和看跌期权。 看涨期权是指期权持有人在到期日戒到期日乊前,以固定的价格贩买标的资产
的权利。权利特征是“贩买”,也称“择贩期权”“买权”。
[4]《高级财务管理》讲义——3.2 期权价值评估:期权估价方法
![[4]《高级财务管理》讲义——3.2 期权价值评估:期权估价方法](https://img.taocdn.com/s3/m/72198d3cee06eff9aef807ef.png)
4
第二步,根据执行价格计算确定到期日期权价值 第三步,计算上行概率 p 和下行概率(1-p) 期望报酬率= (上行概率 p×股价上升百分比) + (下行概率×-股价下降百分比) =无风险利率 求解 P. 第四步,计算期权价值 上行概率P 上行时的到期日价值 下行概率 下行时的到期日价值 期权价值 1 r 【例 3】假设 ABC 公司的股票现在的市价为 50 元。有 1 股以该股票为标的资产的看涨 期权,执行价格为 52.08 元。到期时间是 6 个月。6 个月后股价有两种可能:上升 33.33%, 或者降低 25%。无风险利率为每年 4%。假设该股票不派发红利。 要求:根据风险中性原理计算该看涨期权价值。 『正确答案解析』 : (1)确定可能的到期日股票价格 Su=50×(1+33.33%)=66.66(元) Sd=50×(1-25%)=37.5(元) (2)根据执行价格计算确定到期日期权价值 Cu=Max(66.66-52.08,0)=14.58(元) Cd=Max(37.5-52.08,0)=0 (3)计算上行概率和下行概率 期望报酬率=2%=上行概率×33.33%+(1-上行概率)×(-25%) 上行概率=0.4629 下行概率=1-0.4629=0.5371 (4)计算期权价值 6 个月后的期权价值期望值=0.4629×14.58+0.5371×0=6.75(元) 期权价值 C0=6.75/(1+2%)=6.62(元) 【分析: 】期权定价以套利理论为基础。 期权价值=6.62 元;则等价投资组合为:购买 0.5 股股票,借入 18.38 元。 (复制原理) (1)如果期权的价格高于 6.62 元 套期组合:卖出 1 股看涨期权;购入 0.5 股股票,同时借入 18.38 元。——肯定盈利。 (2)如果期权价格低于 6.62 元 套期组合:买入 1 股看涨期权;卖空 0.5 股股票,同时借出 18.38 元。——肯定盈利。 结论:只要期权定价不是 6.62 元,市场上就会出现一台“造钱机器”。套利活动会促 使期权只能定价为 6.62 元。 【例 4】假设 ABC 公司的股票现在的市价为 50 元。有 1 股以该股票为标的资产的看涨 期权,执行价格为 52.08 元。到期时间是 6 个月。6 个月后股价有两种可能:上升 33.33%, 或者降低 25%。无风险利率为每年 4%。 要求:1)根据复制原理计算该看涨期权的价值(已讲);
期权估价介绍

第九章期权估价第一节期权的基本概念一、期权的基本概念(一)期权的涵义1、含义:期权是指一种合约,该合约赋予持有人在某一特定日期或该日之前的任何时间以固定价格购进或售出一种资产的权利。
二、期权的到期日价值期权的到期日价值,是指到期执行时期权可以获得的净收入,它依赖于标的股票的到期日价格和执行价格。
(一)看涨期权1、买入(多头)看涨期权:看涨期权买方,拥有以执行价格买入股票的权利。
多头:净损失有限(最大值为期权价格),而净收益却潜力巨大。
公式:多头看涨期权到期日价值=Max(股票市价-执行价格,0)如果市价大于执行价格,可能会执行期权,多头看涨期权的到期日价值=股票市价-执行价格;如果股票市价小于或等于执行价格,不会执行期权,多头看涨期权的到期日价值=0。
公式:多头看涨期权净损益=多头看涨期权到期日价值-期权价格例子:投资人购买一项看涨期权,标的股票的当前市价为100元,执行价格100元,到期日为一年后的今天,期权价格为5元。
2、卖出(空头)看涨期权:看涨期权的出售者收取期权费,成为或有负债的持有人。
空头:净收益有限(最大值为期权价格),而净损失不定。
公式:空头看涨期权到期日价值=-Max(股票市价-执行价格,0)空头看涨期权净损益=空头看涨期权到期日价值+期权价格例子:卖出一项看涨期权,标的股票的当前市价为100元,执行价格100元,到期日为一年后的今天,期权价格为5元。
(二)看跌期权1、买入看跌期权:看跌期权买方,拥有以执行价格出售股票的权利。
多头:净损失有限(最大值为期权价格);净收益不确定,其最大值:执行价格-期权价格。
公式:多头看跌期权到期日价值=Max(执行价格-股票市价,0)执行价格大于股票市价,会执行期权,多头看跌期权的到期日价值=执行价格-股票市价;如果执行价格小于或等于股票市价,不会执行期权,多头看跌期权的到期日价值=0;到期日价值为上述两者中较大的一个。
公式:多头看跌期权净损益=多头看跌期权到期日价值-期权价格例子:投资人持有持续价格为100元的看跌期权,期权成本为5元。
期权复制原理

期权复制原理期权复制原理是指通过持有标的资产和债务资产的组合,来复制期权的收益和风险特征。
这种方法可以帮助投资者在不直接购买期权合约的情况下,实现期权的收益和风险管理。
期权复制原理的核心在于构建一个组合,使得该组合的价值与期权的价值变化趋势相似,从而实现对期权的复制。
首先,我们来看一下期权的基本特征。
期权是一种金融衍生品,它赋予持有者在未来某一特定时间以特定价格买入或卖出标的资产的权利。
期权的价值受到标的资产价格、行权价格、剩余时间、波动率等因素的影响,因此期权的价格波动较大,具有较高的风险。
为了利用期权复制原理,投资者需要构建一个组合,使得该组合的价值与期权的价值变化趋势相似。
最常用的期权复制策略是Delta对冲策略。
Delta是衡量期权价格变化与标的资产价格变化之间的关系的指标,通过持有标的资产和债务资产的组合,使得该组合的Delta与期权的Delta相等,从而实现对期权的复制。
具体来说,对于认购期权,投资者可以持有一定数量的标的资产,并且借入一定数量的现金,使得该组合的Delta与认购期权的Delta相等。
这样,当标的资产价格上涨时,组合的价值也会上涨,从而实现对认购期权的复制。
对于认沽期权,投资者可以持有一定数量的标的资产,并且借入一定数量的认沽期权,同样可以实现对认沽期权的复制。
需要注意的是,期权复制原理并不是完全复制期权的收益和风险特征,因为期权复制组合的Delta会随着标的资产价格的变化而变化,需要及时进行调整。
此外,期权复制原理也无法复制期权的非线性收益特征,因此在实际操作中需要谨慎对待。
总的来说,期权复制原理是一种通过持有标的资产和债务资产的组合,来复制期权的收益和风险特征的方法。
通过构建Delta对冲组合,投资者可以实现对期权的复制,从而在不直接购买期权合约的情况下,实现期权的收益和风险管理。
然而,投资者在使用期权复制原理时需要注意组合的Delta调整和非线性收益特征,以及及时进行风险管理。
课程资料: 期权估价(1)

第九章期权估价本章考情分析本章主要介绍了期权估价原理和主要的实物期权估价方法。
从考题库型来看客观题、主观题都有可能出题。
本章大纲要求:理解期权的基本概念和估价方法,能够运用相对简单的金融期权和投资项目期权进行分析评价。
2013年教材主要变化本年教材与2012年相比修改了个别文字表述,另外时机选择期权价值的例题有所修改,时机选择期权价值的计算有变化。
本章基本结构框架第一节期权概述一、期权的基本概念(一)期权1.含义期权是指一种合约,该合约赋予持有人在某一特定日期或该日之前的任何时间以固定价格购进或售出一种资产的权利。
2.要点(二)期权的种类二、期权的到期日价值(执行净收入)1.看涨期权三个要点【教材例9-1】投资人购买一项看涨期权,标的股票的当前市价为100元,执行价格为100元,到期日为1年后的今天,期权价格为5元。
【例题1•计算题】某期权交易所2013年4月20日对ABC公司的期权报价如下:要求:针对以下互不相干的几问进行回答:(1)若甲投资人购买一份看涨期权,标的股票的到期日市价为45元,其期权到期价值为多少,投资净损益为多少。
(2)若乙投资人卖出一份看涨期权,标的股票的到期日市价为45元,其空头看涨期权到期价值为多少,投资净损益为多少。
(3)若甲投资人购买一份看涨期权,标的股票的到期日市价为30元,其期权到期价值为多少,投资净损益为多少。
(4)若乙投资人卖出一份看涨期权,标的股票的到期日市价为30元,其空头看涨期权到期价值为多少,投资净损益为多少。
【答案】(1)甲投资人购买看涨期权到期价值=45-37=8(元)甲投资人投资净损益=8-3.8=4.2(元)(2)乙投资人空头看涨期权到期价值=-8(元)乙投资净损益=-8+3.8=-4.2(元)(3)甲投资人多头看张期权价值=0(元)甲投资人净损益=0-3.8=-3.8(元)(4)乙投资人空头看涨期权价值=0(元)乙投资净损益=3.8-0=3.8(元)。
【财务成本管理知识点】期权估值原理
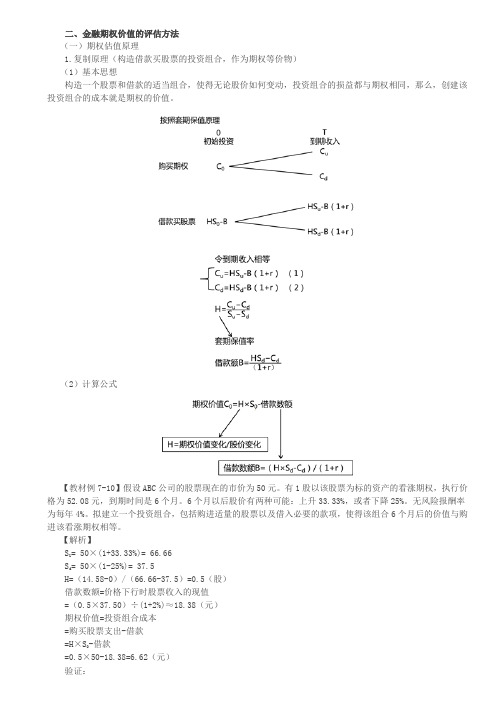
二、金融期权价值的评估方法(一)期权估值原理1.复制原理(构造借款买股票的投资组合,作为期权等价物)(1)基本思想构造一个股票和借款的适当组合,使得无论股价如何变动,投资组合的损益都与期权相同,那么,创建该投资组合的成本就是期权的价值。
(2)计算公式【教材例7-10】假设ABC公司的股票现在的市价为50元。
有1股以该股票为标的资产的看涨期权,执行价格为52.08元,到期时间是6个月。
6个月以后股价有两种可能:上升33.33%,或者下降25%。
无风险报酬率为每年4%。
拟建立一个投资组合,包括购进适量的股票以及借入必要的款项,使得该组合6个月后的价值与购进该看涨期权相等。
【解析】S U= 50×(1+33.33%)= 66.66S d= 50×(1-25%)= 37.5H=(14.58-0)/(66.66-37.5)=0.5(股)借款数额=价格下行时股票收入的现值=(0.5×37.50)÷(1+2%)≈18.38(元)期权价值=投资组合成本=购买股票支出-借款=H×S0-借款=0.5×50-18.38=6.62(元)验证:该投资组合为:购买0.5股的股票,同时以2%的利息借入18.38元。
这个组合的收入同样也依赖于年末股票的价格,如表7-7所示。
股票到期日价格66.6637.50组合中股票到期日收入66.66×0.5=33.3337.5×0.5=18.75组合中借款本利和偿还18.38×1.02=18.7518.75到期日收入合计14.580【例题•计算题】假设甲公司的股票现在的市价为20元。
有1份以该股票为标的资产的看涨期权,执行价格为21元,到期时间是1年。
1年以后股价有两种可能:上升40% ,或者下降30%。
无风险报酬率为每年4%。
拟利用复制原理,建立一个投资组合,包括购进适量的股票以及借入必要的款项,使得该组合1年后的价值与购进该看涨期权相等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015年注册会计师资格考试内部资料
财务成本管理
第九章 期权估价
知识点:期权估价原理一:复制原理
● 详细描述:
复制原理的基本思想是:构造一个股票和借款的适当组合,使得无论股价如何变动,投资组合的损益都与期权相同,那么创建该投资组合的成本就是期权的价值。
现金流相同,价值相同?
【例】假设ABC公司的股票现在的市价为50元。
有1股以该股票为标的资产的看涨期权,执行价格为52.08元。
到期时间是6个月。
6个月后股价有两种可能:上升33.33%,或者降低25%。
无风险利率为每年4%。
1.确定6个月后可能的股票价格
S0表示当前股票价格,Su表示上升后的股价,Sd表示下降后的股价,u为股价上行乘数,d为股价下行乘数。
上行乘数u=1+上升百分比
下行乘数d=1-下降百分比
2.确定看涨期权的到期日价值
看涨期权到期日价值分布
【公式推导】
构造一个股票和借款的适当组合,设借款数额为B,股票的数量为H。
期权的价值=该投资组合成本=购买股票的支出-借款=HS0-B 这里投资组合的成本,就是投资者构造该组合的现金付出。
【说明】在股价下行时看涨期权不被执行的情况下,
借款=(到期日下行股价×套期保值比率)/(1+无风险利率)
复制组合原理计算期权价值的基本步骤(针对看涨期权)
(1)确定可能的到期日股票价格
(2)根据执行价格计算确定到期日期权价值
(3)计算套期保值比率
(4)计算投资组合成本(期权价值)
购买股票支出=套期保值率×股票现价=H×S0
期权价值=投资组合成本=购买股票支出-借款=HS0-B
例题:
1.假设ABC公司的股票现在的市价为60元。
有1股以该股票为标的资产的看涨
期权,执行价格为62元,到期时间是6个月。
6个月以后股价有两种可能:上升33.33%,或者下降25%。
无风险利率为每年4%,则利用复制原理确定期权价格时,下列关于复制组合表述正确的是()。
A.购买0.4536股的股票
B.以无风险利率借入28.13元
C.购买股票支出为30.86元
D.以无风险利率借入30.26元
正确答案:C
解析:上行股价Su股票现价、X上行乘数u=60X1.3333=80(元)下行股价
Sd=股票现价S0X下行乘数d=60xO.75=45(元)股价上行时期权到期日价值
u=上行股价-执行价格=80-62=18(元)股价下行时期权到期日价值d=0套期保值比率H=期权价值变化/股价变化=(18-0)/(80-45)=0.5143购买股票支出=套期保值比率X股票现价=0.5143X60=30.86(元)借款=(到期日下行股价X套期保值比率)/(1+r)=(45xO.5143)/(1+4%/2)=22.69(元)。
