第3章 SM模型化
第三章系统的教学模型

3 系统的数学模型3.1 概述3.1.1 数学模型在进行控制系统分析和设计时,通常首先需要建立系统的数学模型。
所谓系统的数学模型,是用数学方程式来描述机械系统、电气系统、,, 以及生物系统、社会系统的动态特性,是一组能精确,或者至少是相当好地表示系统动态特性的微分方程式、差分方程式或其它数学方程表示式。
数学模型可以有多种形式,采取何种形式来建立数学模型取决于具体的系统及条件,如,一个单输入单输出简单系统的响应分析,可能采用传递函数形式比较简单方便,而如要进行最优控制,则采用状态空间表达式可能更为有利。
对于同一系统的描述,数学模型也可能具有不同的复杂程度。
如以一个液压控制阀为例,如果是考虑它在一个复杂系统中的动作,可以用一个二阶微分方程式(基于牛顿第二运动定理)来做为其数学模型,而如果是为了设计这个控制阀并预测其性能,则需要考虑阀的泄漏,尺寸精度影响等更多因素,所建立的数学模型可能是一个6-7 阶的微分方程组。
另一方面,严格地说,任何实际中的电、机械系统、液压系统、气动系统等其变量间的关系都不是绝对性线的,有些甚至是严重非线性的。
然而,由于至今非线性系统的求解依然存在着数学难关,比较常用的做法是用一个“等效”的或“近似”的线性系统代替实际上的非线性系统来分析和求解。
这意味着,我们既要掌握在建立数学模型时的线性化方法,又要了解所取的“线性”数学模型有效的范围和条件。
3.1.2 数学模型表示形式控制系统的数学模型通常采用以下几种表示形式:1.传递函数模型一个连续的SISO 系统,一般可用一个常定系数线性常微分方程来描述若系统的输入为u(t),输出的y(t),其微分方程可表示为:a n 叩…3^ 5)dt ndt nde对该式进行Lap lace 变换,可得系统的传递函数模型丫(s)二 b m S m b m 」sm —b oU(s) a n S n- a n j S n A^ …宀a 。
离散时间动态系统一般以差分方程描述,对一个离散 SISO 系统,设采样周期为T ,系统输入为u(i),输出为y(i),可描述为:g n y(i n) g n 4y(i n -1)g °y(i)=f m u(i m) f m 」u(i m -1)f o u(i)对该方程进行Z 变换,可得离散SISO 系统的传递函数模型m -1 m 4 Z n 4n洱 • go对于多输入多输出系统,系统的传递函数模型为传递函数矩阵。
现代精算风险理论 第3章 聚合风险模型

E[etX ] exp( et 1)
P(N
k)
r
k k
1 pr
(1
p)k
,
E[etX
]
1
p (1
p)et
r
E[ X
]
r (1 p
p)
,Var[ X
]
r (1 p2
p)
,
例 3.3. l(泊松分布,参数的不确定性) 设某个汽车驾驶员
3.1 引 言
本章我们要引入聚合风险模型.同第2章那样,我们要 计算在某个时间段内理赔总额的分布函数,但是现在 要把风险组合理解为在随机时间点上产生的理赔全体. 记
其中N 表示理赔次数, X i 表示第i个理赔额. 此外,按习惯约定当N = 0 时S = 0.
这样的模型称为聚合风险模型!
• 在聚合模型中我们要求理赔次数和理赔额之间 相互独立,即(N与X1, X2,… Xn)
例3.4.3(应用:稀疏向量算法) 如果理赔额X 是
非负整值随机变量,可以用一种有效的方式来计
算复合泊松分布F.
设
4
,
Pr X
1, 2,3
1,1,1. 424
S 1N1 2N2 3N3
采用卷积来计算S 的分布。
1
4
1 4
1, 2
4 1 2
2, 3
故S是一个复合泊松随机变量.
(1)m个独立复合泊松保单组合的总和仍然服从复合泊松 分布. (2)对同一个复合泊松保单观测m年且假设逐年的结果相 互独立,则m年结果的总和也仍然服从复合泊松分布.
当每一个Si 有非随机的理赔额xi 时,我们有Si xi Ni ,
第三章新安江模型

R P E (WM W0)
表明,在蓄满产流模式下,总径流量是降水量、雨期蒸 散发量和流域初始土壤含水量的函数。
3.水源划分
按蓄满产流模型计算出的总径流量 R中包括了各 种径流成分,由于各种水源的汇流规律和汇流速度不 相同,相应采用的计算方法也不同。因此,须进行水 源划分。
(1)二水源
二水源的水源划分结构是根据霍尔顿的产流概念,
(2)三水源 对S’积分
S0
AU 0
(1
f F
)dS '
AU 0
(1
S' MS
)EX
dS '
S0
MS [1 (1 EX 1
AU MS
)EX 1 ]
SM MS EX 1
AU
MS
1 (1
S0 SM
1
)1 EX
(2)三水源
产流面积FR为: FR R PE
对地面径流RS积分
Q AU
RS
(2)三水源
由于饱和坡面流的产流面积是不断变化的,所以在
产流面积上自由水蓄水容量分布是不均匀的。三水源
水源划分结构是采用类似于流域蓄水容量面积分配曲
线的流域自由水蓄水容量面积分配曲线来考虑流域内
自由水蓄水容量分布不均匀的问题。所谓流域自由水
蓄水容量面积分配曲线是指:部分产流面积随自由水
蓄水容量而变化的累计频率曲线。流域自由水蓄水容
EL=C×(EP-EU),ED=0 若 WL>C×LM 且 WL<C×(EP-EU) 则
EL=WL,ED=C ×(EP-EU)-WL
2.产流计算(蓄满)
蓄满产流是指:降水在满足田间持水量以前不产流, 所有的降水都被土壤所吸收;降水在满足田间持水量 以后,所有的降水(扣除同期蒸发量)都产流。 其概念就是设想流域具有一定的蓄水能力,当这种蓄 水能力满足以后,全部降水变为径流,产流表现为蓄 量控制的特点。湿润地区产流的蓄量控制特点,解决 了产流计算在这些地区处理雨强和入渗动态过程的问 题;
庞皓计量经济学第三章多元线性回归模型学习辅导
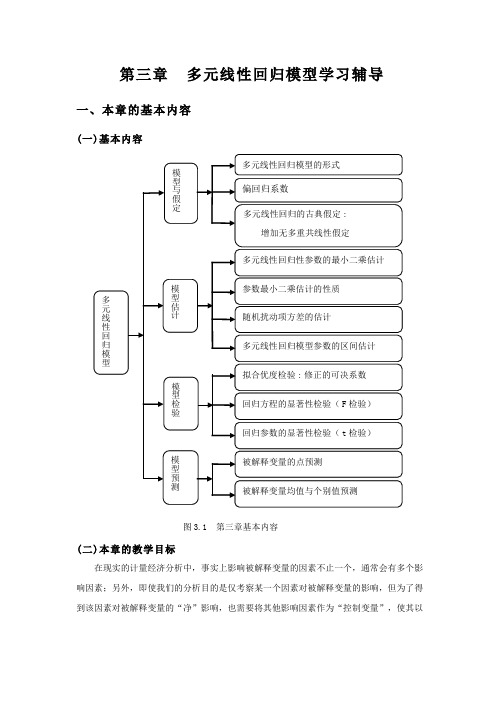
第三章 多元线性回归模型学习辅导一、本章的基本内容(一)基本内容图3.1 第三章基本内容(二)本章的教学目标在现实的计量经济分析中,事实上影响被解释变量的因素不止一个,通常会有多个影响因素;另外,即使我们的分析目的是仅考察某一个因素对被解释变量的影响,但为了得到该因素对被解释变量的“净”影响,也需要将其他影响因素作为“控制变量”,使其以显性形式出现在模型中,以提高模型估计精度。
因此,在对现实经济问题进行计量经济分析时,通常需要建立包含两个及两个以上解释变量的计量模型,此类模型称为多元回归模型。
多元回归模型是在简单回归模型理论基础上的扩展,其建模的理论基础、基本思路、模型估计等与一元回归模型基本一致,只是因解释变量增多,从而带来一些新的内容,比如模型整体显著性检验(F 检验)、修正的可决系数(2R )以及解释变量之间多重共线性等问题。
本章的教学目标是:深刻理解建立多元回归模型的目的;掌握多元线性回归模型估计、检验的理论与方法;熟练掌握多元线性回归EViews 输出结果的解释。
二、重点与难点分析1.对多元线性回归模型参数意义的理解多元线性回归模型的参数与简单线性回归模型的参数有重要区别。
在多元线性回归模型中,解释变量对应的参数是偏回归系数,表达的是控制其他解释变量不变的条件下,该解释变量的单位变动对被解释变量平均值的“净”影响。
为了更深刻理解偏回归系数,可以两个解释变量的多元线性回归模型为例加以说明1。
例如,被解释变量Y 与解释变量2X 和3X 都有关,如果分别建立模型:多元线性回归: 12233i i i i Y X X u b b b =+++简单线性回归 : 1221i i i Y a a X u =++由于Y 与3X 有关,可以作回归:1332i i i Y b b X u =++,若用OLS 估计其参数,并计算残差213333ˆˆˆi i i i i e Y b b X y b x =--=-,这里的2i e 表示除去3i X 影响后的i Y 。
通信原理第3章图

第3章 模拟调制系统
3.1 信号的频谱搬移概述 3.2 线性调制原理 3.3 线性调制的抗噪声性能 3.4 非线性调制 3.5 模拟调制系统的性能比较 3.6 频分复用与多级调制
第3章 模拟调制系统
由于搬移是线性的,因此幅度调制通常又称为线 性调制 线性调制的一般模型 m(t) s m(t)
2 nc (t ) ns2 (t )
1 2
x (1 x) 1 , x 1 2
1 2
Anc (t ) n (t ) n (t )
2 c 2 s
nc (t ) n (t ) n (t )
2 c 2 s
m(t )
第3章 模拟调制系统
• 在小信噪比情况下,包络检波器会把有用信号 扰乱成噪声,这种现象通常称为“门限效应”: 指当包络检波器的输入信噪比降低到一个特定 的数值后,检波器输出信噪比出现急剧恶化的 一种现象 • 该特定的输入信噪比被称为“门限”
• SFM(t) 带通限幅器 鉴频器 低通滤波器 m(t)
调频信号的解调方框图
第3章 模拟调制系统
3.6 频分复用(FDM)
• 频分复用(Frequency Division Multiplex) 是调制技术的典型应用,它通过对多路调 制信号进行不同载频的调制,使得多路信 号的频谱在同一个传输信道的频率特性中 互不重叠,从而完成在一个信道中同时传 输多路信号的目的。
第3章 模拟调制系统
3.4非线性调制(角度调制)的原理
一、非线性调制(角度调制)的原理 • DSB、AM、SSB和VSB都是幅度调制,即把欲传 送的信号调制到载波的幅值上。而我们知道一个 正弦型信号由幅度、频率和相位(初相)三要素 构成,既然幅度可以作为调制信号的载体,那么 其它两个要素(参量)是否也可以承载调制信号 呢? • 这就是我们将要介绍的频率调制和相位调制,统 称为角度调制,这种调制是已调信号频谱与基带 信号频谱之间存在着非线性变换关系,所以称为 非线性调制
第三讲 Sm-Nd法

4.60 Ga 参考等时线
提示: 1)检验陨石Sm-Nd等 时线年龄; 2)确定未经历过地球 地壳幔分异事件(原始 地幔)的物质储库 (CHUR)的现今SmNd同位素组成; 3)建立Nd同位素示踪 研究参数的基准点。
Sm-Nd isochron diagram for whole-rock samples of six different chondrites. SS = St Severin; MU = Murchison; GU = Guarena; PR = Peace River; ALL = Allende. JUV = new analysis of the Juvinas achondrite. The large apparent errors are due to very expanded axis scales. After Jacobsen and Wasserburg (1980).
Sm-Nd同位素体系的主要应用领域
通过对陨石系统研究,建立壳幔演化关系模型; 建立全球地壳生长模型、判别岩石圈演化过程 中的区域初生地壳加入与壳幔物质再循环机制、 对岩浆物质来源等重要地质问题进行示踪研究; 在中低级变质和高级变质条件下,对原岩形成 和变质事件进行定年研究等。
陨石Sm-Nd同位素研究的意义
almandine
GROSSULAR on DIOPSIDE
GROSSULAR
albite
monazite
apatite
hornblen
augite
olivine diopside
范例:石榴石高Sm/Nd比值与定年
扬子克拉通陆核崆岭太古宙基底岩系中约19.5亿年热改造事件的识别 (Ling WL, et al., 2001)
第三讲 Sm-Nd法

REE离子半径与质量数的关系图
自然界中不存在
Rare Earth Elements
LREE趋向于在长石 feldspars、黑云母biotite 中富集; HREE则趋向于在角闪石amphibole、辉石 pyroxene和石榴石garnet中富集;
太阳系的 Sm/Nd比值为 0.31;
Composite acid-basic SmNd isochron diagram for a suite of Archean rocks from Kambalda, Western Australia. Open symbols were omitted from the regression. After McCulloch and Compston (1981).
第三讲
Sm-Nd同位素体系
火星陨石
内容提要
REE及Sm-Nd元素地球化学特征
Sm-Nd同位素定年原理
Nd与Nd同位素模式年龄
Nd同位素地球化学示踪研究原理
地壳生长模型
其它研究范例
3.1 稀土元素地球化学 Geochemistry of Rare Earth Elements
提示:太古宙岩石 多采用基性岩(如斜 长角闪岩)与TTG片 麻岩组合的方法进 行等时线定年。 WHY??
崆岭高级变质区太古宙基底岩系Sm-Nd全岩等时线年龄:斜 长角闪岩、TTG片麻岩、斜长角闪岩+TTG片麻岩。 (凌文黎等,科学通报,1999。)
变质事件定年 Dating a metamorphic event
现 在组 成
147Sm衰变新
初 始组 成
形成的143Nd
143 Nd Nd Nd 14 4Nd 普通样品 143Nd/144Nd变化范围约为:0.1%, 约10个单位
通信原理第三章 模拟调制系统

当载波为cosωct时
1 1 ) S ( t ) = m ( t ) cos t m ( t ) sin t LSB c c 2 2
1 1 ) S ( t ) = m ( t ) cos t m ( t ) sin t U SB c c 2 2 当载波为sinωct时
w
w
w
w
1 1 ) S ( t ) = m ( t ) sin t m ( t ) cos t L SB c c 2 2 1 1 ) S ( t ) = m ( t ) sin t m ( t ) cos t U SB c c 2 2
w) , h(t) = H(w) = jsgn(
1
t
3)、Hilbert变换的性质: (1)、信号和它的希尔波特变换具有相同的能量谱密度或相 同的功率谱密度。 推论: (2)、信号和它的希尔波特变换的能量(或功率)相同。 (3)、信号和它的希尔波特变换具有相同的自相关函数。 (4)、信号和它的希尔波特变换互为正交。 4)、Hilterb变换的用途: 在单边带调制中,用来实现相位选择,以产生单边带信号
1 S ( w ) = A w w w w [ M ( w w ) M ( w w )] A M c c c c 2
c(t) 载波 调制 信号 已调 信号 m(t)
-f
H
C(f)
-f c 0 fc
f
M(f)
f
-fL 0 f
L
fH
sm(t)
第三章 模拟调制系统
引言 3.1 幅度调制 标准调幅(AM) 双边带调幅(DSB) 单边带调幅(SSB) 残留边带调幅(VSB) 3.2 角度调制原理 3.3 抗噪声性能 各种幅度调制系统的噪声性能 非线性调制系统的抗噪性能 模拟系统比较
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课程名称系统工程计划学时 2授课章节第三章系统模型和模型化(1)教学目的和要求:在本讲中,使学生了解系统模型和模型化的概念,建模的基本步骤和方法。
教学基本内容:1.系统模型的概念2.系统模型的分类3.系统模型化的基本步骤4.系统模型化的基本方法教学重点和难点:系统模型化的概念系统模型化的基本方法授课方式、方法和手段:多媒体教学为主,结合板书,同时加以作业和答疑作业与思考题:1.系统模型的概念2.系统模型化的基本步骤1第三章系统模型与模型化第一节系统模型与模型化概述一、系统模型的定义系统模型是一个系统某一方面本质属性的描述,它以某种确定的形式提供关于该系统的知识。
模型的特征:(1)是现实世界部分的抽象或模仿;(2)反映了系统本质或特征的主要因素构成;(3)集中体现了主要因素之间的关系。
模型化就是为了描述系统的构成和行为,对实体系统的各种因素进行适当筛选后,用一定方式(数学、图像等)表达系统实体的方法。
二、模型化的本质、作用及地位(见下图)1.本质:利用模型与原型之间某方面的相似关系,在研究过程中用模型来代替原型,通过对于模型的研究得到关于原型的一些信息。
2.作用:①模型本身是人们对客体系统一定程度研究结果的表达。
这种表达是简洁的、形式化的。
②模型提供了脱离具体内容的逻辑演绎和计算的基础,这会导致对科学规律、理论、原理的发现。
③利用模型可以进行“思想”试验。
3.地位:模型的本质决定了它的作用的局限性。
它不能代替以客观系统内容的研究,只有在和对客体系统相配合时,模型的作用才能充分发挥。
三、系统模型的分类23四、构造模型的一般原则1.建立方框图2.考虑信息相关性3.考虑准确性4.考虑结集性五、建模的基本步骤①明确建模的目的和要求。
以便使模型满足实际要求,不致产生太大偏差;②对系统进行一般语言描述。
因为系统的语言描述是进一步确定模型结构的基础;③弄清系统中的主要因素(变量)及其相互关系(结构关系和函数关系)。
以便使模型准确表示现实系统;④确定模型的结构。
这一步决定了模型定量方面的内容;⑤估计模型的参数。
用数量来表示系统中的因果关系;⑥实验研究。
对模型进行实验研究,进行真实性检验,以检验模型与实际系统的符合性;⑦必要修改。
根据实验结果,对模型作必要的修改。
六、模型化的基本方法1.分析方法;2.实验方法;3.综合法;4.老手法;5.辩证法;七、模型的简化①减少变量,减去次要变量;②改变变量性质;③合并变量(集结);④改变函数关系;⑤改变约束条件;课程名称系统工程计划学时 2授课章节第三章系统模型与模型化(2)教学目的和要求:在本讲中,使学生了解系统模型化的基础。
教学基本内容:1.系统结构的集合表达2.系统结构的有向图表达3.系统结构的矩阵表达4.可达阵的求解教学重点和难点:系统结构三种表达方式的转换以及可达阵的求解方法授课方式、方法和手段:多媒体教学为主,结合板书,同时加以作业和答疑作业与思考题:1.说明系统结构表达的三种方式,并指出它们的不同之处。
2.简述结构模型的特点4第二节系统结构模型化技术一、结构模型的定义任何系统都是由两个以上有机联系、相互作用的要素所组成的,是具有特定功能与结构的整体。
结构即组成系统诸要素之间相互关联的方式,包括现代企业在内的大规模复杂系统具有要素及其层次众多、结构复杂和社会性突出等特点。
在研究和解决这类系统问题时,往往要通过建立系统的结构模型,进行系统的结构分析,以求得对问题全面和本质的认识。
结构模型是定性表示系统构成要素以及它们之间存在着的本质上相互依赖、相互制约和关联情况的模型。
结构模型化即建立系统结构模型的过程。
结构分析是一个实现系统结构模型化并加以解释的过程。
其具体内容包括:对系统目的——功能的认识;系统构成要素的选取;对要素间的联系及其层次关系的分析;系统整体结构的确定及其解释。
系统结构模型化是结构分析的基本内容。
结构分析是系统分析的重要内容,是系统优化分析、设计与管理的基础。
系统的结构模型反映的是系统中各组成部分(可能是实物,也可能是一个抽象因素)之间的关系,更多地反映了系统中功能之间的关系。
系统是由单元组成的,各单元之间又存在着大量的相互作用关系。
研究一个系统,需要了解这些关系,特别是先要了解各单元之间关系的存在与否。
这就是说,先要了解系统结构,建立系统的结构模型。
二、系统结构的基本表达方式要素及其关系形成结构集合、有向图、矩阵等三种相互对应的方式表达系统的某种结构。
1.系统结构的集合表达设系统由n(n≥2)个要素(S1,S2,…,Sn)所组成,其集合为S,则有:S={S1,S2,…,S n}。
二元关系:是根据系统的性质和研究的目的所约定的一种需要讨论的,存在于系统中的两个要素(S i,S j)之间的关系R ij(记为R)。
关系:有影响关系、因果关系、包含关系、隶属关系以及各种可以比较56 的关系(如大小、先后、轻重、优劣等)。
S i 与S j 间有某种二元关系R ,即S iRS j ;S i 与S j 间无某种二元关系R ,即S i R S j ;S i 与S j 间无某种二元关系R ,即S i R ~S j ;传递性:若S iR S j 、SjR S k ,则有S iR S k (Si 、S j 、S k )为系统的任意构成要素。
间接联系,可记作t R (t 为传递次数),如将SiR S k 记作S i 2R S k 强连接:若S iR S j ,又有S jR S i ,相互关联二元关系集合R b},....2,1,,),{(n j i RS S S S S S S R j i j i j i b =∈=、、2.系统结构的有向图表达有向图(D )是由节点和连接各节点的有向弧(箭线)组成的,可用来表达系统的结构。
具体方法:用节点表示系统的各构成要素,用有向弧表示要素之间的二元关系。
从节点(S i)到(S j)的最少有向弧数称为D 中节点间的通路长度(路长),也即要素S i 与S j 间二元关系的传递次数。
呈强连接关系的要素节点间具有双向回路。
例:给出的系统要素及其二元关系的有向图如图所示。
其中S3到S 5、S 3到S 6和S 7到S1的路长均为2。
另外S 4和S6间具有强连接关系,S4和S 6相互到达,在其间形成双向回路。
12345673.系统结构的矩阵表达7 (1)邻接矩阵:是表示系统要素间基本二元关系或直接联系情况的方阵。
在一般情况下,如果系统S 有n 个单元,则邻接矩阵为:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡ann an an n a a a n a a a ...21............2 (22)211...1211A=S1S2SnS1S2Sn ......a i j =例:生产领域加工分工程度技术进步流通效率A BC ⎪⎪⎪⎭⎫⎝⎛001101110A B CA B C邻接矩阵在一般情况下,如果系统S 有n 个单元,则邻接矩阵 ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡ann an an n a a a n a a a ...21............2...22211...1211A=S1S2SnS1S2Sn ......其中各个元素为a i j =0,当S i 对S j 无影响时 1,S iR S j0,S i R S j1,当S i 对S j 有影响时8 邻接矩阵的元素只能是0或1,所以它属于布尔矩阵。
布尔矩阵的运算(逻辑和运算U 、逻辑乘运算 )基础是布尔代数中的基本运算。
布尔矩阵 000= 110=000= 010=C B A = C 是n n ⨯阶布尔矩阵],max[ij ij ij ij ij b a b a c ∆∆==C B A = ],min[ij ij ij ij ij b a b a c ∆∆==D AB = )},min()...,min(),,max{min(2211nj in j i j i ij b a b a b a d ∆=邻接矩阵A 具有的性质如下:a.邻接矩阵和系统结构模型图是一一对应的。
有了图,邻接矩阵就唯一确定了,反之亦然。
b. A 转置后得到矩阵T A 是结构模型图所有箭头反过来之后的图所对应的邻接矩阵。
c.在A 中如有一列元素全为0,(第i 列),则S i 是系统的输入,如果有一行元素全为0(第k 行),则S k 是系统的输出。
d.从S i 出发,经过k 段路到达S j ,则S i 与S j 间有长度为k 的通路存在,计算k A 得出n n ⨯阶方阵中各元素表示的便是相应各单元间有无长度为k 的通路存在。
(2)可达阵所谓可达阵,就是表示系统要素之间任意次传递性二元关系或有向图上两个节点之间通过任意长路径可以达到的方阵。
从某一单元S i 出发能达到哪一些单元,则可以把A 连乘 n A A A A R ...32=。
有时为了方便起见,认为单元S i 到它本身也是可以达到的,这样应再加9 一单位阵n A A A A I R ...32=22)]([)]([)(A A I A I A A I I A I ==R A A A I A I n n ==⇒ ...)(2当1)()(+=r r I A I A 时,则长度为r 的通路存在。
若n n ij m M ⨯=)(,且在无回路条件下的最大路长或传递次数为r ,则可达矩阵的定义式为r I A M )(+=其中I 为与A 同阶次的单位矩阵(主对角线元素全为“1”)最大传递次数(路长)r 根据下式确定:n r r r I A I A I A I A I A I A I A )(...)()()(......)()()(1132+==+=+≠+≠≠+≠+≠++-(3)缩减阵根据强连接要素的可替换性,将具有强连接关系的一组要素看作一个要素,删掉其余要素及其在的行和列。
(4)骨架矩阵对于给定系统,A 的可达矩阵M 是唯一的,但实现某一可达矩阵M 的邻接矩阵有多个。
把实现某一可达矩阵M 具有最小二元关系个数(“1”元素最少)的邻接矩阵叫做R 的最小实现二元关系矩阵或称之为骨架矩阵。
记A ′。
课程名称系统工程计划学时 4授课章节第三章系统模型与模型化(3)教学目的和要求:在本讲中,使学生掌握建立递阶结构模型的方法。
教学基本内容:1.系统结构模型的区域划分2.系统结构模型的级位划分3.系统结构模型的提取骨架阵4.有向图的绘制教学重点和难点:建立递阶结构模型的四个基本步骤授课方式、方法和手段:多媒体教学为主,结合板书,同时加以作业和答疑作业与思考题:根据可达阵求解递阶结构模型1011一、建立递阶结构模型的规范方法:建立反映系统问题要素间层次关系的递阶结构模型,在可达矩阵M 的基础上进行,要经过区域划分、级位划分、骨架矩阵提取和多级递阶有向图绘制等四个阶段。
