高三数学课件:含参不等式恒成立
合集下载
含参数的不等式的恒成立

例 12.已知 f x x2 2x a 当 x 1, , f x 的值域是0, ,试求实数 a 的值.
x
思考与运用
1.设 a 0 , 3x2 a 2x b 0 在 a,b 上恒成立,则 b a 的最大值为
2.设集合 A= x x2 2x 3 0 ,集合 B= x x2 2ax 1 0, a 0 .若 A B 中恰含有一个整数,则实
min
注意不等式能成立问题(即不等式有解问题)与恒成立问题的区别.从集合观点看,含参不等式 f x k
f
x k 在区间 D 上恒成立 D x
f
x k
f
x max
k
D x
f
x k
f
x min
k
,而含
参不等式 f x k f x k 在区间 D 上能成立 至少存在一个实数 x 使不等式 f x k
0 时,
f
(x)
0在x [, ]
上恒成立
f f
0, 0.
f
(x)
0在x
[,
]
上恒成立
b 2a
或
b 2a
或
b 2a
,
f ( ) 0 0
f ( ) 0.
例 2.已知不等式 mx2 4mx 4 0 对任意实数 x 恒成立.则 m 取值范围是
取值范围的基本步骤:
(1)将参数与变量分离,即化为 g f x (或 g f x )恒成立的形式;
高考数学复习优质课件:含参不等式恒成立问题新人教版.pptx

x 2a (极大值点),x 2a (极小值点);
3
3
由于x [1,2], 对极大值点进行分类,
(i)当
2a 3
1,即0 a
3 2
时, f min(来自x)f (1)
2 2a 0, 得0 a 1;
(ii)当1
2a 3
2,即
3 2
a
6时,fmin ( x)
f(
2a ) 3
4a 2a 1 0, 得a 3 3 2 , 故a不存在;
求实数t的取值范围.
课堂小结
通过今天这堂复习课,我们再次领略 了解决恒成立问题的多种常见求解方法 ,事实上,这些方法都不是孤立的,在 具体的解题实践中,往往需要综合考虑 ,灵活运用,才能使问题得以顺利解决 .但是,不管哪一种解法,都渗透了数 学最本质的思想,通过化归到函数求其 最值来处理.
思考:(2010年绍兴市一模数学试卷 理第17题改编) 在区间[t, t 1]上满足不等式 | x3 3 x 1 | 1恒成立,
含参不等式恒成立问题
的求解策 略
例题1、已知不等式 x2 2ax 1 0对x [1,2]恒成立, 其中a 0.求实数a的取值范围.
思路1、通过化归最值,直接 求函数f ( x) x2 2ax 1 的最小值,即 fmin ( x) 0即可.
思路2、通过分离变量,转化 为a x2 1 1 ( x 1 ). 2x 2 x
思路3、通过数形结合,转化 到x2 1 2ax.
y
O
x
归纳
化归最值 分离变量 数形结合
实质
通过构造 函数,化归 到函数的 性质(最值) 或图像解决
例题1、已知不等式 x2 2ax 1 0对x [1,2]恒成立, 其中a 0.求实数a的取值范围.
含参不等式恒成立问题的解法PPT完美课件

则a要大于右边式子在(1,4)的最大值
令t=2/x, t的范围则为(1/2,2) 则 2/x-2/x^2 = 2t-t^2/2 = -1/2(t-2)^2 + 2
这便是两次函数求最值 当t=2时 2t-2t^2 的最大值 为 2(但取不到) 所以a的范围是 [2, 正无穷﹚
含参不等式恒成立问题的解法PPT完美 课件
恒成立 恒成立
又 令1+2t=m(m > 1),则
f(m)=
m 1(m21)2
m242mm5(m4m5)2
4 2 52
521(当且仅当m=
5 时等号成立)
∴ a ≥ [f (x)] max=
5 2*
1
即a
≥
5 1 2
含参不等式恒成立问题的解法PPT完美 课件
含参不等式恒成立问题的解法PPT完美 课件
b
含参不等式恒成立问题的解法PPT完美 课件
含参不等式恒成立问题的解法PPT完美 课件
(2) 0<b≤1时,对x ∈(0,1],|f(x)|≤1 恒成立
(
bx-
1 x
)max ≤a ≤(bx+
)1xmin
此时
(
bx-
1 x
)max=b-1
(x=1时取得)
而
bx +
1 x
在(0,1]上递减
故
(
bx+
•
10保尔身上的人格特征或完美的精神 操守: 自我献 身的精 神、坚 定不移 的信念 、顽强 坚韧的 意志
•
11把记叙、描写、抒情和议论有机地 融合为 一体, 充满诗 情画意 。如描 写百草 园的景 致,绘 声绘色 ,令人 神往。
•
令t=2/x, t的范围则为(1/2,2) 则 2/x-2/x^2 = 2t-t^2/2 = -1/2(t-2)^2 + 2
这便是两次函数求最值 当t=2时 2t-2t^2 的最大值 为 2(但取不到) 所以a的范围是 [2, 正无穷﹚
含参不等式恒成立问题的解法PPT完美 课件
恒成立 恒成立
又 令1+2t=m(m > 1),则
f(m)=
m 1(m21)2
m242mm5(m4m5)2
4 2 52
521(当且仅当m=
5 时等号成立)
∴ a ≥ [f (x)] max=
5 2*
1
即a
≥
5 1 2
含参不等式恒成立问题的解法PPT完美 课件
含参不等式恒成立问题的解法PPT完美 课件
b
含参不等式恒成立问题的解法PPT完美 课件
含参不等式恒成立问题的解法PPT完美 课件
(2) 0<b≤1时,对x ∈(0,1],|f(x)|≤1 恒成立
(
bx-
1 x
)max ≤a ≤(bx+
)1xmin
此时
(
bx-
1 x
)max=b-1
(x=1时取得)
而
bx +
1 x
在(0,1]上递减
故
(
bx+
•
10保尔身上的人格特征或完美的精神 操守: 自我献 身的精 神、坚 定不移 的信念 、顽强 坚韧的 意志
•
11把记叙、描写、抒情和议论有机地 融合为 一体, 充满诗 情画意 。如描 写百草 园的景 致,绘 声绘色 ,令人 神往。
•
含参数不等式恒成立问题的解题策略课件

问题1:用判别式法需注意什么?
变式一 若
f ( x) ax 2ax 4 ,当 x R 时, f ( x) 0 恒成立,则实数 a 的取值范围 。
2
解: (1)当a 0时,要使f ( x) 0恒成立,
2 则=(-2a) 4a 4 0, 解得0 a 4
三、 思维拓展,直击高考
练习二: 已知 x 1是函数 f ( x) mx3 3(m 1) x2 nx 1的一个极值 点,其中 m, n R, m 0 , (1)求 m 与 n 的关系式;
(2)当 x [1,1] 时,函数 y f ( x) 的图像上任意一点的
一、追根溯源,构建方法
例 1 (必修5 P115A第3题,B组第2题改编)若
f ( x) x 2ax 4 ,当 x R 时,f ( x) 0恒成立,求实数
2
a
的取值范围
归纳总结:
。
1.判别式法 设 f ( x) ax2 bx c(a 0) f ( x) 0在x R 上恒成立 a 0且 0 ; f ( x) 0在x R 上恒成立 a 0且 0 . 2.最值法(转化为求原函数的最值) f ( x) 0 恒成立 f ( x)min 0 ; f ( x) 0 恒成立 f ( x)max 0 .
提高题:
4.(2012年惠州调研)已知函数 f ( x) ax ln x(a R) (1)求 f ( x) 的单调区间;
(2)设 g ( x) x2 2x 2,若对任意 x1 (0, ) ,均存在 x2 [0,1] , 使得 f ( x1 ) g ( x2 ) ,求 a 的取值范围. x3 5.(2012广州调研理)已知函数 f ( x) ln 2ax 1 x 2 2ax (1)若 x 2 为的极值点,求实数 a 的值; (2)若 y f ( x) 在 3, 上为增函数,求实数 a 的取值范围;
《含参不等式专题》课件

几何法
总结词
通过几何意义和图形,将含参不等式问题转化为几何问题。
详细描述
几何法是一种直观的解含参不等式的方法,它通过几何意义和图形,将含参不等式问题转化为几何问题。这种方 法需要了解平面几何、解析几何等基础知识,能够根据不等式的几何意义画出图形,通过观察图形找到不等式的 解。
参数分离法
总结词
将含参不等式中的参数分离出来,转化为容易解决的不等式。
意事项
解题技巧
因式分解法
配方法
对于形如$ax^2 + bx + c > 0$的不等式,如果$a > 0$ ,则可以将不等式化为$(x
+ frac{b}{2a})^2 + frac{4ac - b^2}{4a} > 0$ 的形式,然后进行因式分解
。
对于形如$ax^2 + bx + c > 0$的不等式,如果$a < 0$, 则可以通过配方将其化为$(x + frac{b}{2a})^2 - frac{b^2 - 4ac}{4a^2} < 0$的形式,
在制定计划和决策时,含参不 等式可以用来解决资源分配、 成本预算等问题。
含参不等式在优化资源配置、 提高效率等方面发挥着重要作 用。
在其他学科中的应用
01
含参不等式在其他学科 中也有着重要的应用, 例如物理学、化学、生 物学等。
02
在物理学中,含参不等 式可以用来描述物理现 象和规律,如力学、热 学等。
03
在化学中,含参不等式 可以用来描述化学反应 和平衡状态。
04
在生物学中,含参不等 式可以用来描述生物种 群的增长和变化规律。
04
含参不等式的变式与拓展
含参不等式恒成立问题的解法完美课件
∴ x ∈(0,1]时原式恒成立的充要条件为: 0 <a≤ b+1
又 x=0时,|f(x)|≤1恒成立
∴ x ∈[0,1]时原式恒成立的充要条件为: 0 <a≤ b+1
又 a>0
*故 ( bx+ )min =b+1
*
三、课时小结:
2、二次函数型问题,结合抛物线图像,转化成最值问 题,分类讨论。
例1、对于不等式(1-m)x2+(m-1)x+3>0 ................ (*) (1)当| x | ≤2,(*)式恒成立,求实数m的取值范围 ;(2)当| m | ≤2,(*)式恒成立,求实数x的取值范围 .
*则 g(m)>0恒成立g(-2)=3x2-3x+343;px+1>2x+p恒成立,则实数x的取值范围是: ——————————。
*2、ax2+bx+c>0在R上恒成立的充要条件是:a=b=
*
二、典型例题:例1、对于不等式(1-m)x2+(m-1)x+3>0 ................ (*) (1)当| x | ≤2,(*)式恒成立,求实数m的取值范围 ;(2)当| m | ≤2,(*)式恒成立,求实数x的取值范围 .
x<-1或x>3
小结:1、一次函数型问题,利用一次函数的图像特征求解。
2、二次函数型问题,结合抛物线图像,转化成最值问 题,分类讨论。
*练习1:x<-1或x>3小结:2、二次函数型问题,结合抛物
*
y=kx
②解:原不等式可化为:x2+2>kx
在同一坐标系下作它们的图象如右图:
又 x=0时,|f(x)|≤1恒成立
∴ x ∈[0,1]时原式恒成立的充要条件为: 0 <a≤ b+1
又 a>0
*故 ( bx+ )min =b+1
*
三、课时小结:
2、二次函数型问题,结合抛物线图像,转化成最值问 题,分类讨论。
例1、对于不等式(1-m)x2+(m-1)x+3>0 ................ (*) (1)当| x | ≤2,(*)式恒成立,求实数m的取值范围 ;(2)当| m | ≤2,(*)式恒成立,求实数x的取值范围 .
*则 g(m)>0恒成立g(-2)=3x2-3x+343;px+1>2x+p恒成立,则实数x的取值范围是: ——————————。
*2、ax2+bx+c>0在R上恒成立的充要条件是:a=b=
*
二、典型例题:例1、对于不等式(1-m)x2+(m-1)x+3>0 ................ (*) (1)当| x | ≤2,(*)式恒成立,求实数m的取值范围 ;(2)当| m | ≤2,(*)式恒成立,求实数x的取值范围 .
x<-1或x>3
小结:1、一次函数型问题,利用一次函数的图像特征求解。
2、二次函数型问题,结合抛物线图像,转化成最值问 题,分类讨论。
*练习1:x<-1或x>3小结:2、二次函数型问题,结合抛物
*
y=kx
②解:原不等式可化为:x2+2>kx
在同一坐标系下作它们的图象如右图:
高三数学最新课件-含参数不等式恒成立问题 精品
身体健康!天天开心!
湖南邵东一中 金光辉
向领导、老师们 有朋自远方来, 请领导、老师们 祝领导、老师们: 不亦乐乎? 学习!致敬! 多多指导!
已知不等式
2x 9x m 0
2
在区间[ 2,3]上, 取值范围
求实数m的
?
湖南邵东一中 金光辉
已知不等式
2x 9x m 0
2
在区间
9 2 81 ∵g(x)= -2(x- ) + 4 8 x [2,3]
∴ m≤9
y=m o 2 3
x
湖南邵东一中 金光辉
例:关于x的不等式 2 x2 9 x m 0
在区间[ 2,3]上 恒成立 , 取值范围
解:据题意,
求实数m的
=81-8m≥0
9 81 8m 9 81 8m ] 不等式解集为:[ , 4 4 9 81 8m 3 4 由已知得: 9 81 8m 2 4
2.解题方法:
求根法;最值法;图象法。
f ( x) min a
f ( x)max a
3.数学思想:
分类讨论;等价转化;数形结合。
湖南邵东一中 金光辉
请领导、老师们 多多指教!
湖南邵东一中 金光辉
练习与作业:
1.不等式 2 x 2 9 x m 0 在区间[2,3]上恒成立 求实数m的范围。 2 2.不等式 2 x 9 x m 0 在区间[2,3]上有解,
求实数m的
10 m 0 9 m 0
f (2) 0 f (3) 0
o ∴m≤9
2
3
x
湖南邵东一中 金光辉
例:关于x的不等式 2 x2 9 x m 0
湖南邵东一中 金光辉
向领导、老师们 有朋自远方来, 请领导、老师们 祝领导、老师们: 不亦乐乎? 学习!致敬! 多多指导!
已知不等式
2x 9x m 0
2
在区间[ 2,3]上, 取值范围
求实数m的
?
湖南邵东一中 金光辉
已知不等式
2x 9x m 0
2
在区间
9 2 81 ∵g(x)= -2(x- ) + 4 8 x [2,3]
∴ m≤9
y=m o 2 3
x
湖南邵东一中 金光辉
例:关于x的不等式 2 x2 9 x m 0
在区间[ 2,3]上 恒成立 , 取值范围
解:据题意,
求实数m的
=81-8m≥0
9 81 8m 9 81 8m ] 不等式解集为:[ , 4 4 9 81 8m 3 4 由已知得: 9 81 8m 2 4
2.解题方法:
求根法;最值法;图象法。
f ( x) min a
f ( x)max a
3.数学思想:
分类讨论;等价转化;数形结合。
湖南邵东一中 金光辉
请领导、老师们 多多指教!
湖南邵东一中 金光辉
练习与作业:
1.不等式 2 x 2 9 x m 0 在区间[2,3]上恒成立 求实数m的范围。 2 2.不等式 2 x 9 x m 0 在区间[2,3]上有解,
求实数m的
10 m 0 9 m 0
f (2) 0 f (3) 0
o ∴m≤9
2
3
x
湖南邵东一中 金光辉
例:关于x的不等式 2 x2 9 x m 0
高中数学 含参不等式恒成立问题的求解策略课件
的导数 f (x) 0 恒成立,则实数 a 的
取值范围是 {a|a≥9}
回归课本 提炼方法
变式 1 (2009 重庆理第 5 题)不等 式 x 3 x 1 a2 3a 对任意实数 x 恒成
立,则实数 a 的取值范围为( A )(新课
标选修 4-5 第 20 页第 9 题改编)
A.(, 1] [4, ) B.(, 2] [5, )
由 ex 1 x(x 0) 可得 ex 1 x(x 0) .从而当 a 1 时, 2
f '(x) ex 1 2a(ex 1) ex (ex 1)(ex 2a) ,
故 当 x (0, ln 2a) 时 , f '(x) 0 , 而 f (0) 0 , 于 是 当 x (0, ln 2a) 时, f (x) 0 . 综合得 a 的取值范围为 (, 1] .
范围.
解 : 由 题 意 , f (x) 0 在 区 间 (1,1) 恒 成 立 。
ekx (1 kx) 0 在区间 (1,1) 恒成立。因为 ekx 0 ,即
1 kx 0 在区间 (1,1) 恒成立。
答案:1, 0
方法 1 (1 kx)min 0 , x (1,1)
0,1
方法 2 分离变量 kx 1, x (1,1)
了解高考,把握热点
08 安徽理第20题 文第21题 全国II文第21题理第22题
陕西理文第22题理第21题 辽宁理第22题 全国I理第19题
39 湖南理第21题文第21题 天津理第20题 文第21题
套
有12套
09 重庆理第5题
浙江文第21题理第22题 上海理第11题
辽宁理第21题 江西理第15,17题 湖北文理21题
C.[1, 2]
取值范围是 {a|a≥9}
回归课本 提炼方法
变式 1 (2009 重庆理第 5 题)不等 式 x 3 x 1 a2 3a 对任意实数 x 恒成
立,则实数 a 的取值范围为( A )(新课
标选修 4-5 第 20 页第 9 题改编)
A.(, 1] [4, ) B.(, 2] [5, )
由 ex 1 x(x 0) 可得 ex 1 x(x 0) .从而当 a 1 时, 2
f '(x) ex 1 2a(ex 1) ex (ex 1)(ex 2a) ,
故 当 x (0, ln 2a) 时 , f '(x) 0 , 而 f (0) 0 , 于 是 当 x (0, ln 2a) 时, f (x) 0 . 综合得 a 的取值范围为 (, 1] .
范围.
解 : 由 题 意 , f (x) 0 在 区 间 (1,1) 恒 成 立 。
ekx (1 kx) 0 在区间 (1,1) 恒成立。因为 ekx 0 ,即
1 kx 0 在区间 (1,1) 恒成立。
答案:1, 0
方法 1 (1 kx)min 0 , x (1,1)
0,1
方法 2 分离变量 kx 1, x (1,1)
了解高考,把握热点
08 安徽理第20题 文第21题 全国II文第21题理第22题
陕西理文第22题理第21题 辽宁理第22题 全国I理第19题
39 湖南理第21题文第21题 天津理第20题 文第21题
套
有12套
09 重庆理第5题
浙江文第21题理第22题 上海理第11题
辽宁理第21题 江西理第15,17题 湖北文理21题
C.[1, 2]
人教版高中数学课件 第三册:不等式恒成立问题
例1.若不等式x 2 2 xy a ( x y )对一切 正数x, y恒成立, 则正数a的最小值为( A. 1 B.2 C. 2 1 2
B
).
D. 2 2 1
练习求使 x .
y a x y ( x 0, y 0)
恒成立的a的最小值
2
例2.设f ( x) lg
1 2 4 a
x x
(其中a R),
3 如果当x (,1]时, f ( x)恒有意义, 求a的 取值范围.
a
3 4
练习.设 f ( x) lg 1 2 3 ( n 1) n a
x x x x
, 其中
n a是实数, n是任意给定的自然数且n 2, 如果 f ( x)当x ( ,1]时恒有意义, 求a的取值范围.
2
取值范围是 _______________ .
1 7 x 1 3
2 2 换个角度看问题,换个方面去解释,换个方向去 思考.
1.利用一次函数的单调性
设一次函数f(x)=ax+b (a≠0),当a > 0时f(x)在R上是 增函数;当a < 0时f(x)在R上是减函数.所以关于不等 式恒成立问题,若能将不等式化为关于主元(或参数) 的一次函数,则可用一次函数的单调性求解.
x 1 x
) ( x 0).
2 1
(1)求f ( x)的反函数f
( x);
(2)若x 2时, 不等式 ( x 1) f
1
1
( x) a (a
1 x 1 ( x 1);
x )恒成立,
求实数a的取值范围.
(1) f ( x)
(2) 1 a
第1部分专题1微专题3含参不等式恒成立或存在性问题-高三数学二轮复习课件
5.(2020·北京模拟)已知函数f(x)=
0,x<1,
ln
x,x≥1,
若不等
式f(x)≤|x-k|对任意x∈R恒成立,则实数k的取值范围是
()
A.(-∞,1]
B.[1,+∞)
C.[0,1)
D.(-1,0]
答案 A
解析
当x≥1时,f(x)=ln
x,所以f′(x)=
解得m<-
2.所以实数m的取值范围是
(-∞,- 2).
答案 (-∞,- 2)
对于二次函数f(x)=ax2+bx+c(a≠0,x∈R),有f(x)>0对 x∈R恒成立⇔aΔ><00,; f(x)<0对x∈R恒成立⇔Δa<<00,.
方法二 最值法 将不等式恒成立问题转化为求函数最值问题的常用处理 方法,其一般类型有:f(x)>a恒成立⇔a<f(x)min,f(x)<a恒成立 ⇔a>f(x)max;f(x)>a有解⇔a<f(x)max,f(x)<a有解⇔a>f(x)min.
【例3】 已知f(x)=7x2-28x-a,g(x)=2x3+4x2-40x, 当x∈[-3,3]时,f(x)≤g(x)恒成立,求实数a的取值范围.
解析 设F(x)=f(x)-g(x)=-2x3+3x2+12x-a, 则由题可知F(x)≤0对任意x∈[-3,3]恒成立, 令F′(x)=-6x2+6x+12=0,得x=-1或x=2, 而F(-1)=-7-a,F(2)=20-a,F(-3)=45-a,F(3) =9-a,所以F(x)max=45-a≤0, 所以a≥45,即实数a的取值范围为[45,+∞).
即需抛物线g(x)=x2+2x+a在x∈[1,+∞)上的最小值 g(x)min=g(1)=3+a>0,即a>-3.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
令 又
y t x (t > 0) , 则
y x 2 xy 1 2 x xy y 1 x
a≥
恒成立
令1+2t=m(m > 1),则
1 2t 1 t 2
(t > 0) 恒成立
f(m)=
m 4m 4 1 ( m 1)2 m 2 2m 5 (m 5 ) 2 m 2
②若不等式x2-kx+2>0,对x [-3,3]恒成立,则实数k的
-2 2 <k<2 2 取值范围是 —————————— 。
②解:原不等式可化为:x2+2>kx
11
y
y=x2+2
y=2 2 x
设 y1= x2+2 (x [-3,3]) y2= kx
在同一坐标系下作它们的图
2
y=kx
象如右图:
由图易得: -2
值范围。
4 、已知f(x)= 2x a (xR) 在区间 [-1,1]上是增函数。 x2 2
(1)求实数 a 的值所组成的集合A;
1 (2)设关于x 的方程f(x)= x 的两根为x1、x2,试问:是否存 在实数m,使得不等式 m2 + t m + 1≥| x1 - x2| 对任意a A 及t[-1,1] 恒成立?若存在,求出m的取值范围;若不存在,
四、课后练习:
1、当x (0,1)时,不等式x2< loga(x 值范围是_____________。
+ 1)恒成立,则实数a的取
2、若不等式|x-a|+|x-1|>2 对x R恒成立,则实数a的取值 范围是_____________。
3、若不等式ax2-2x+2>0 对x(1,4)恒成立,求实数a的取
4 5 1 (当且仅当m= 5 时等号成立) 2 2 5 2
∴ a ≥ [f (x)] max=
5 1 2
即a ≥
5 1 2
小结:
4、 通过分离参数,将问题转化为a≥f(x)
(或a≤f(x))恒成立,再运用不等式知识或求
函数最值的方法,使 问题获解。
例4、已知a>0,函数f (x)=ax-bx2, (1)当b>1,证明对任意的x ∈[0,1],|f(x)|≤1充要条件是: b-1≤a≤2 ; b
—————————— 。 y
x2
(x (0,
1 2 ))
y2= logax
在同一坐标系下作它们 的图象如右图: 由图易得:
y=x2 1 4
0
1 2
1
x
1 y=log 16x
1 16 ≤a <1
例2、①若不等式x2
<logax对x
1 (0, 2 )恒成立,则实数a的取
值范围是 ————————————。
ax2+bx+c<0在R上恒成立的充要条件是: a <0 a=b=0 或
C<0 Δ=b -4ac<0 ______________________。
2
a≥[f (x)] max 3、a≥f(x)恒成立的充要条件是:_____________;
a≤[f (x)] min a≤f(x)恒成立的充要条件是:_____________。
b-1≤a≤2
故 x ∈(0,1]时原式恒成立的充要条件为: 又 x=0时,|f(x)|≤1恒成立
b b
∴ x ∈[0,1]时原式恒成立的充要条件为:
b-1≤a≤2
(2) 0<b≤1时,对x ∈(0,1],|f(x)|≤1 恒成立 ( bx- பைடு நூலகம் )max ≤a ≤(bx+
x
)min
1 x
……
(*)
请说明理由。
二、典型例题:
例1、对于不等式(1-m)x2+(m-1)x+3>0
................
(*)
(1)当| x | ≤2,(*)式恒成立,求实数m的取值范围 ;
(2)当| m | ≤2,(*)式恒成立,求实数x的取值范围 .
当1-m>0时,即m<1 ,(*)式在x [-2,2]时恒成立的充
-3 -
2 0 2 3
x
2 <k<2 2
y= - 2
2x
小结: 3、对于f(x)≥g(x)型问题,利用数形结合思想转化为函数 图象的关系再处理。 练习2、 若
x ≤ kx-1 对x [1,+ ) 恒成立,则实数k的取值范
k≥2 围是:_____________。
例3、若不等式x +2 xy ≤a(x+y)对一切正数x、y恒成 立,则实数a的取值范围是 —————————。 解: 分离参数得: a ≥
此时 而 故
x 1 在(0,1]上递减 bx + x 1 ) =b+1 (x=1时取得) ( bx+ min x
( bx- 1 )max=b-1
(x=1时取得)
故 (*)式成立的充要条件为: b-1≤a≤b+1 又 a>0 ∴ x ∈(0,1]时原式恒成立的充要条件为: 0 <a≤ b+1
又 ∴
x=0时,|f(x)|≤1恒成立 x ∈[0,1]时原式恒成立的充要条件为: 0 <a≤ b+1
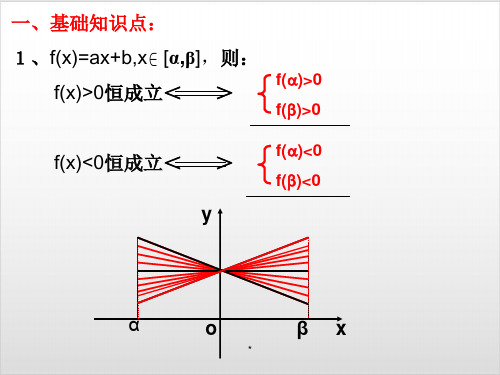
一、基础知识点:
1、f(x)=ax+b,x [α,β],则:
f(x)>0恒成立< >
f()>0 f()>0
f(x)<0恒成立< y
>
f()<0 f()<0
α
o
β
x
2、ax2+bx+c>0在R上恒成立的充要条件是: 或 C>0 Δ=b2-4ac<0 ______________________。 a=b=0 a >0
要条件为: △=(m-1)2-12(I-m)<0 , 解得:
解:(1)当1-m=0即m=1时, (*)式恒成立, 故m=1适合(*) ;
当1-m<0时,即m>1, (*)式在x [-2,2]时恒成立的充
要条件为: (1-m)•(-2)2+(m-1)•(-2)+ 3 >0 解得: 综上可知:
-11<m<1;
g(m)>0恒成立 x R
g(-2)=3x2-3x+3>0 g(2)=-x2+x+3>0
即
1 13 1 13 <x< 2 2
∴ x (
1 13 , 13 ) 1 2 2
小结:
1、一次函数型问题,利用一次函数的图像特征求解。 2、二次函数型问题,结合抛物线图像,转化成最值问 题,分类讨论。
3 1<m< 2
适合条件的m的范围是:
-11<m < 2 。
3
例1、对于不等式(1-m)x2+(m-1)x+3>0
................
(*)
(1)当| x | ≤2,(*)式恒成立,求实数m的取值范围 ;
(2)当| m | ≤2,(*)式恒成立,求实数x的取值范围 .
解(2) : 设g(m)=(-x2+x)m+(x2-x+3) (m [-2,2]) 则
(2)当0<b≤1,讨论:对任意的x ∈[0,1],|f(x)|≤1充要条件。
解:(1) b>1时,对x ∈(0,1],|f(x)|≤1
-1≤ax-bx2≤1
bx2-1≤ ax ≤1+bx2
bx - 1 ≤ a ≤ 1 +bx x x
∵ x ∈(0,1], b>1 ∴ 又 ∴
1≥ 2 bx+ x (x= 1 时取等号 ) b b bx - 1 在(0,1]上递增 x ( bx- 1 )max=b-1 (x=1时取得 ) x
三、课时小结:
1、一次函数型问题,利用一次函数的图像特征求解。 2、二次函数型问题,结合抛物线图像,转化成最值问 题,分类讨论。
3、对于f(x)≥g(x)型问题,利用数形结合思想转化为函数图 象的关系再处理。 4、通过分离参数,将问题转化为a≥f(x)(或a≤f(x))恒
成立,再运用不等式知识或求函数最值的方法,使 问题获解。
练习1:
对于一切 |p| ≤2,p∈R,不等式x2+px+1>2x+p
x<-1或x>3 恒成立,则实数x的取值范围是: ——————————。
例2、①若不等式x2
1 16 ≤a<1 取值范围是 ————————。
的取值范围是
设 y1= ①解:
<logax对x
1 (0, 2 )恒成立,则实数a的
②若不等式x2-kx+2>0,对x [-3,3]恒成立,则实数k
y t x (t > 0) , 则
y x 2 xy 1 2 x xy y 1 x
a≥
恒成立
令1+2t=m(m > 1),则
1 2t 1 t 2
(t > 0) 恒成立
f(m)=
m 4m 4 1 ( m 1)2 m 2 2m 5 (m 5 ) 2 m 2
②若不等式x2-kx+2>0,对x [-3,3]恒成立,则实数k的
-2 2 <k<2 2 取值范围是 —————————— 。
②解:原不等式可化为:x2+2>kx
11
y
y=x2+2
y=2 2 x
设 y1= x2+2 (x [-3,3]) y2= kx
在同一坐标系下作它们的图
2
y=kx
象如右图:
由图易得: -2
值范围。
4 、已知f(x)= 2x a (xR) 在区间 [-1,1]上是增函数。 x2 2
(1)求实数 a 的值所组成的集合A;
1 (2)设关于x 的方程f(x)= x 的两根为x1、x2,试问:是否存 在实数m,使得不等式 m2 + t m + 1≥| x1 - x2| 对任意a A 及t[-1,1] 恒成立?若存在,求出m的取值范围;若不存在,
四、课后练习:
1、当x (0,1)时,不等式x2< loga(x 值范围是_____________。
+ 1)恒成立,则实数a的取
2、若不等式|x-a|+|x-1|>2 对x R恒成立,则实数a的取值 范围是_____________。
3、若不等式ax2-2x+2>0 对x(1,4)恒成立,求实数a的取
4 5 1 (当且仅当m= 5 时等号成立) 2 2 5 2
∴ a ≥ [f (x)] max=
5 1 2
即a ≥
5 1 2
小结:
4、 通过分离参数,将问题转化为a≥f(x)
(或a≤f(x))恒成立,再运用不等式知识或求
函数最值的方法,使 问题获解。
例4、已知a>0,函数f (x)=ax-bx2, (1)当b>1,证明对任意的x ∈[0,1],|f(x)|≤1充要条件是: b-1≤a≤2 ; b
—————————— 。 y
x2
(x (0,
1 2 ))
y2= logax
在同一坐标系下作它们 的图象如右图: 由图易得:
y=x2 1 4
0
1 2
1
x
1 y=log 16x
1 16 ≤a <1
例2、①若不等式x2
<logax对x
1 (0, 2 )恒成立,则实数a的取
值范围是 ————————————。
ax2+bx+c<0在R上恒成立的充要条件是: a <0 a=b=0 或
C<0 Δ=b -4ac<0 ______________________。
2
a≥[f (x)] max 3、a≥f(x)恒成立的充要条件是:_____________;
a≤[f (x)] min a≤f(x)恒成立的充要条件是:_____________。
b-1≤a≤2
故 x ∈(0,1]时原式恒成立的充要条件为: 又 x=0时,|f(x)|≤1恒成立
b b
∴ x ∈[0,1]时原式恒成立的充要条件为:
b-1≤a≤2
(2) 0<b≤1时,对x ∈(0,1],|f(x)|≤1 恒成立 ( bx- பைடு நூலகம் )max ≤a ≤(bx+
x
)min
1 x
……
(*)
请说明理由。
二、典型例题:
例1、对于不等式(1-m)x2+(m-1)x+3>0
................
(*)
(1)当| x | ≤2,(*)式恒成立,求实数m的取值范围 ;
(2)当| m | ≤2,(*)式恒成立,求实数x的取值范围 .
当1-m>0时,即m<1 ,(*)式在x [-2,2]时恒成立的充
-3 -
2 0 2 3
x
2 <k<2 2
y= - 2
2x
小结: 3、对于f(x)≥g(x)型问题,利用数形结合思想转化为函数 图象的关系再处理。 练习2、 若
x ≤ kx-1 对x [1,+ ) 恒成立,则实数k的取值范
k≥2 围是:_____________。
例3、若不等式x +2 xy ≤a(x+y)对一切正数x、y恒成 立,则实数a的取值范围是 —————————。 解: 分离参数得: a ≥
此时 而 故
x 1 在(0,1]上递减 bx + x 1 ) =b+1 (x=1时取得) ( bx+ min x
( bx- 1 )max=b-1
(x=1时取得)
故 (*)式成立的充要条件为: b-1≤a≤b+1 又 a>0 ∴ x ∈(0,1]时原式恒成立的充要条件为: 0 <a≤ b+1
又 ∴
x=0时,|f(x)|≤1恒成立 x ∈[0,1]时原式恒成立的充要条件为: 0 <a≤ b+1
一、基础知识点:
1、f(x)=ax+b,x [α,β],则:
f(x)>0恒成立< >
f()>0 f()>0
f(x)<0恒成立< y
>
f()<0 f()<0
α
o
β
x
2、ax2+bx+c>0在R上恒成立的充要条件是: 或 C>0 Δ=b2-4ac<0 ______________________。 a=b=0 a >0
要条件为: △=(m-1)2-12(I-m)<0 , 解得:
解:(1)当1-m=0即m=1时, (*)式恒成立, 故m=1适合(*) ;
当1-m<0时,即m>1, (*)式在x [-2,2]时恒成立的充
要条件为: (1-m)•(-2)2+(m-1)•(-2)+ 3 >0 解得: 综上可知:
-11<m<1;
g(m)>0恒成立 x R
g(-2)=3x2-3x+3>0 g(2)=-x2+x+3>0
即
1 13 1 13 <x< 2 2
∴ x (
1 13 , 13 ) 1 2 2
小结:
1、一次函数型问题,利用一次函数的图像特征求解。 2、二次函数型问题,结合抛物线图像,转化成最值问 题,分类讨论。
3 1<m< 2
适合条件的m的范围是:
-11<m < 2 。
3
例1、对于不等式(1-m)x2+(m-1)x+3>0
................
(*)
(1)当| x | ≤2,(*)式恒成立,求实数m的取值范围 ;
(2)当| m | ≤2,(*)式恒成立,求实数x的取值范围 .
解(2) : 设g(m)=(-x2+x)m+(x2-x+3) (m [-2,2]) 则
(2)当0<b≤1,讨论:对任意的x ∈[0,1],|f(x)|≤1充要条件。
解:(1) b>1时,对x ∈(0,1],|f(x)|≤1
-1≤ax-bx2≤1
bx2-1≤ ax ≤1+bx2
bx - 1 ≤ a ≤ 1 +bx x x
∵ x ∈(0,1], b>1 ∴ 又 ∴
1≥ 2 bx+ x (x= 1 时取等号 ) b b bx - 1 在(0,1]上递增 x ( bx- 1 )max=b-1 (x=1时取得 ) x
三、课时小结:
1、一次函数型问题,利用一次函数的图像特征求解。 2、二次函数型问题,结合抛物线图像,转化成最值问 题,分类讨论。
3、对于f(x)≥g(x)型问题,利用数形结合思想转化为函数图 象的关系再处理。 4、通过分离参数,将问题转化为a≥f(x)(或a≤f(x))恒
成立,再运用不等式知识或求函数最值的方法,使 问题获解。
练习1:
对于一切 |p| ≤2,p∈R,不等式x2+px+1>2x+p
x<-1或x>3 恒成立,则实数x的取值范围是: ——————————。
例2、①若不等式x2
1 16 ≤a<1 取值范围是 ————————。
的取值范围是
设 y1= ①解:
<logax对x
1 (0, 2 )恒成立,则实数a的
②若不等式x2-kx+2>0,对x [-3,3]恒成立,则实数k
