川大版高数_物理类专用_第三册_
川大版高数_物理类专用题目

则 , , ③
有 ≤ ③≤ .又
即有
习题三
15、⑴解:对增广矩阵进行初等变换.
B=
则 无解
⑵解:对方程组的增广矩阵进行初等变换.
B=
则 无解
⑶解:对方程组的增广矩阵进行初等变换.(课本第119页题目出错,应该为
B=
则 有唯一解。即唯一解为(3,2,1,)。
由方程组 解得:
(4)、解:对方程组的增广矩阵进行初等变换.
AB=BA
充分性: AB=BA
(AB)’=B’A’=-BA
AB为反对称矩阵
综上所述:AB是反对称矩阵的充分必要条件是AB=BA。
26.解:设矩阵X为x=
则 =
Ax=o
=0
即 =0
对任意n 1矩阵都成立
A=0
27.证: : A为正交矩阵
=A
A = = =
又 正交矩阵为可逆矩阵
A =A
:
A = = =A
4.计算下列矩阵乘积
(1) = =
(2) = =
(3). (1,-1,2) =(1*2+(-1)*1+2*4,1*1+(-1)*1+2*2,1*0+(-1)*3+2*1=
(9,4,1)
(4)(x,y,1)
=(x,y,1)
=
(5)
=
=
5.设A= ,B= ,求
= =
= =
= =
= =
= =
6.
(1)A=
B=
则 <6只方程组有无穷多解。
先求它的一个特解,与阶梯形矩阵对应的方程组为
令上式中的 ,解得 。
于是得到特解:
川大版高数 物理类专用 第三册 答案#(精选.)

第一章 行列式1.()()[][][]23154110103631254=520010=8(1)3(1)321(1)(2)(3)2441(1)3214243(1)321012)4n n n n n n n n m n m n n n m n m n n m 1τ=++++=2τ+++++-τ-⋯=-+-+-+⋯+2+1+0===+τ-⋯=+=+τ-⋯=⋯()该数列为奇排列()该排列为偶排列() 当或时,为偶数,排列为偶排列当或时,为奇数,排列为奇排列(其中,,()[][][]12(1)13521)246(2)0123(1)244113521)246(2)424313521)246(2)012)2.(1)(2)(n n n n n n n m n m n n n m n m n n m i i i k n n n -τ⋯-⋯=++++⋯+-===+τ⋯-⋯=+=+τ⋯-⋯=⋯⋯-+-+( 当或时,(为偶数,排列为偶排列当或时,(为奇数,排列为奇排列(其中,,解:已知排列的逆序数为,这个数按从大到小排列时逆序数为()()111112(1)3)2(1)2x x x n x n x n n n n n n x i r i i i n x r i n x n n i i i i i i -+-+---+⋯+2+1+0=----τ⋯=-τ⋯个.设第数之后有个数比小,则倒排后的位置变为,其后个数比小,两者相加为故3 证明:.因为:对换改变排列的奇偶性,即一次变换后,奇排列改变为偶排列,偶排列改变为奇排列∴当n ≥2时,将所有偶排列变为奇排列,将所有奇排列变为偶排列 因为两个数列依然相等,即所有的情况不变。
∴偶排列与奇排列各占一半。
4 (1)13243341a a a a 不是行列式的项 14233142a a a a 是行列式的项 因为它的列排排列逆序列τ=(4321)=3+2+0+0=5为奇数,∴应带负号(2)5142332451a a a a a 不是行列式的项 1352413524a a a a a =1324354152a a a a a 因为它的列排排列逆序列τ(34512)=2+2+2+0+0=6 为偶数∴应带正号。
大学物理(川大物三)答案
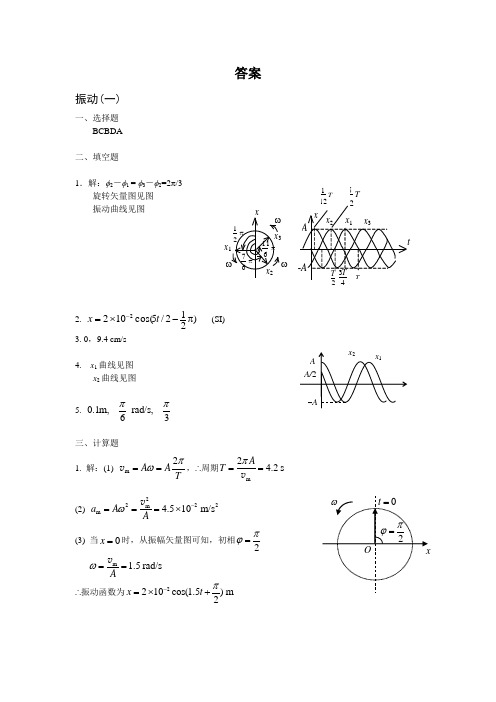
答案振动(一)一、选择题BCBDA二、填空题1.解:φ2-φ1 = φ3-φ2=2π/3旋转矢量图见图 振动曲线见图2. )212/5cos(1022π-⨯=-t x (SI)3. 0,9.4 cm/s4. x 1曲线见图x 2曲线见图5. 0.1m ,rad/s,63ππ三、计算题1. 解:(1) m 2A ATπω==v ,∴周期m2 4.2s A T π==v(2) 2222m m 4.510m/s a A Aω-===⨯v(3) 当0x =时,从振幅矢量图可知,初相2πϕ=m 1.5r a d /sAω==v ∴振动函数为2210cos(1.5)m 2x t π-=⨯+TT1T 5ω x12T 1212. 解:弹簧劲度系数 260 2.010N /m 0.3F k x===⨯ 静止时弹簧伸长量为 0249.80.196m 2.010m g x k⨯===⨯(1) 设向下为正方向,则 0ϕ= (若设向上为正方向,则 ϕπ=);0.1mA =7.07r a d /sω== 振动函数为 0.1cos(7.07)m x t =(2) 物体在平衡位置上方5cm (即0.05m ),此时弹簧的净伸长为 00.050.1960.050.146m l x =-=-=弹簧对物体的拉力 2000.14629.2N F kl ==⨯=(3) 5cm 是振幅之半,物体从平衡位置到振幅之半所需最短时间是112T ,2T πω=∴10.074s 126t T πω===3.解:(1) 容器中每滴入一油滴的前后,水平方向动量值不变,而且在容器回到O 点滴入下一油滴前, 水平方向动量的大小与刚滴入上一油滴后的瞬间后的相同。
依此,设容器第一次过O 点油滴滴入前的速度为v ,刚滴入第个油滴后的速度为v ′,则有 v v '+=)(nm M M ① 3分系统机械能守恒 2202121v M kl = ② 2分22)(2121v '+=nm M kx③ 2分由①、②、③、解出0)/(l nm M M x +=2分(2) 时间间隔( t n +1-t n )应等于第n 滴油滴入容器后振动系统周期T n 的一半.k nm M T t t t n n n n /)(211+==-=∆+π 3分4.解:由旋转矢量图和 |v A | = |v B | 可知 T /2 = 4秒, ∴ T = 8 s , ν = (1/8) s -1, ω = 2πν = (π /4) s -1 3分 (1) 以AB 的中点为坐标原点,x 轴指向右方.t = 0时, 5-=x cm φcos A =t = 2 s时, 5=x cm φφωsin )2cos(A A -=+= 由上二式解得 tg φ = 1因为在A 点质点的速度大于零,所以φ = -3π/4或5π/4(如图) 2分 25c o s/==φx A cm 1分∴ 振动方程 )434c o s (10252π-π⨯=-t x (SI) 1分 (2)速率 )434s i n (41025d d 2π-π⨯π-==-t t x v (SI) 2分 当t = 0 时,质点在A 点221093.3)43sin(10425d d --⨯=π-⨯π-==tx v m/s 1分5*.解:令θ 为杆和竖直线之间的夹角.运动方程为:θθθθc o s s i n s i n 21/d d 222kL MgL t J --= 3分θ 很小时,sin θ ≈θ ,cos θ ≈1所以:0/d d )21(222=++tJ kL MgL θθ 2分上式中231ML J =是杆绕其一端的转动惯量,所以0/d d 31)21(22=++tML Lk Mg θθ可知杆作角谐振动,并得到 )2/()2(3ML kL Mg +=ω2分)2(322/2kL Mg ML T +π=π=ω 1分振动(二)一、选择题ADDBB二、填空题 1.T /8,3T /8 2.222/2T mA π3.动能曲线见图 势能曲线见图 机械能曲线见图4.0.02 5.0三、计算题1.解:设小球的质量为m ,则弹簧的劲度系数 0/l mg k =.选平衡位置为原点,向下为正方向.小球在x 处时,根据牛顿第二定律得T220d /d )(t x m x l k mg =+- 将 0/l mg k = 代入整理后得0//d d 022=+l gx t x∴ 此振动为简谐振动,其角频率为. 3分 π===1.958.28/0l g ω 2分设振动表达式为 )c o s (φω+=t A x由题意: t = 0时,x 0 = A=2102-⨯m ,v 0 = 0,解得 φ = 0 1分∴ )1.9c o s (1022t x π⨯=- 2分2.解一:(1) 取平衡位置为原点,向下为x 正方向.设物体在平衡位置时弹簧的伸长量为∆l ,则有l k mg ∆=, 加拉力F 后弹簧又伸长x 0,则0)(0=+-+∆x l k mg F解得F = kx 02分 由题意,t = 0时v0 = 0;x = x 0 则 02020)/(x x A =+=ωv 2分又由题给物体振动周期4832=T s, 可得角频率 Tπ=2ω, 2ωm k =∴ 444.0)/4(22=π==A T m kA F N 1分 (2) 平衡位置以下1 cm 处: )()/2(2222x A T -π=v 2分 221007.121-⨯==vm E K J 2分2222)/4(2121x T m kxE p π=== 4.44³10-4J 1分解二:(1) 从静止释放,显然拉长量等于振幅A (5 cm ),kA F = 2分2224νωπ==m m k ,ν = 1.5 Hz 2分 ∴ F = 0.444 N 1分(2) 总能量 221011.12121-⨯===FA kAE J 2分当x = 1 cm 时,x = A /5,E p 占总能量的1/25,E K 占24/25. 2分∴ 21007.1)25/24(-⨯==E E K J , 41044.425/-⨯==E E p J 1分3.解:(1) 选地心为x 坐标原点,向上为x 轴正方向.质量为m 的物体在地球内部距地心为x 处受到的地心引力为232/)3/4(/x m x G x G M m F ρπ-=-=3/4x Gm ρπ-= 3分由牛顿第二定律得 xm x Gm =π-3/4ρ, 03/4=π+x G xρ 1分 令 3/420ρωG π=, 则 020=+x x ω. 显然物体作简谐振动. 2分(2) 2/10)/3(4/32/2ρρωG G T π=ππ=π=已知 G = 6.67³10-11 N ²m 2²kg -2,ρ = 5.5³103 kg/m 3代入上式 T = 5.07³103 s 2分 物体从地面落到地心的时间 t = T /4 = 1.27³103 s 2分4.解:选平板位于正最大位移处时开始计时,平板的振动方程为 t A x π=4c o s (SI)t A xπ4c o s π162-= (SI) 1分 (1) 对物体有 x m N mg =- ① 1分 t A mg xm mg N ππ+=-=4cos 162 (SI) ②物对板的压力为 t A mg N F ππ--=-=4cos 162 (SI)t ππ--=4c o s 28.16.192 ③ 2分 (2) 物体脱离平板时必须N = 0,由②式得 1分 04c o s 162=ππ+t A mg (SI) Aq t 2164cos π-=π 1分若能脱离必须 14cos ≤πt (SI) 即221021.6)16/(-⨯=π≥g A m 2分5.解:依合振动的振幅及初相公式可得 φ∆++=c o s 2212221A A A A A 22210)4143cos(65265-⨯π-π⨯⨯⨯++=m21081.7-⨯= m 2分)4/c o s (6)4/3c o s (5)4/s i n (6)4/3s i n (5a r c t g π+ππ+π=φ = 84.8°=1.48 rad 2分则所求的合成振动方程为 )48.110cos(1081.72+⨯=-t x (SI) 1分波动(一)一、选择题CBDCD 二、填空题1.φλ+π-/2Lλk L ± ( k = 1,2,3,…) λ)12(21+±k L ( k = 0, 1,2,…)2.1cos x y A t u ωϕ⎡+⎤⎛⎫=++ ⎪⎢⎥⎝⎭⎣⎦3. ]4/)/(cos[11π+-=u L t A y ω;uL L )(21+ω4. ]2)2(2cos[π-+-π=ux t uA y λ]2)2(2c o s [π+-π=t uA y P λ5.0.2cos m 22p y t ππ⎛⎫=-⎪⎝⎭三、计算题1. 解:反射波在x 点引起的振动相位为 π+π--+π-=+21)55(4x t t φωπ-π+π+=10214x t 3分反射波表达式为)10214cos(01.0π-π+π+=x t y (SI) 2分或 )214c o s (01.0π+π+=x t y (SI)2.解: λxu t A y -π=2c o s = -0.01 m 1分1.0,2d d ===t x ty v 0)2s i n (2=-ππ-=λλxut uA 2分22d d ty a =)2c o s ()2(2λλxut uA -ππ-= = 6.17³103m/s 22分3.解:用旋转矢量解此题,如图可得A为代表P 点振动的旋转矢量. 210)cos sin 3(21-⨯-=t t y P ωω210)]cos()21cos(3(21-⨯π++π-=t t ωω)3/4c o s (1012π+⨯=-t ω (SI). 3分波的表达式为:]2/234c o s [1012λλω-π-π+⨯=-x t y )312c o s (1012π+π-⨯=-λωxt (SI) 2分4.解:从y -x 波形图中可知 40m,A λ==由振幅矢量图可知 ,2P Q πϕϕπ=-=)由20m/s u =可得 2s,rad/s T uλωπ==∴=0.2cos()m20.2cos()mP Q y t y t ππππ∴=-=+5.解:(1) 由y -x 曲线可知160m λ=。
四川版高等数学第三册课后习题(八)答案word版本

解:令 A=(取到1只正品),B=(取到1只废品)
P(有 一 只 正 品 的 条 件 下 ,另 一 只 是 废 品) P(B | A) P( AB) P( A)
C
1 M
C1
m m
C
2 M
1
Cm2
C
2 M
C
1 M
C1
m m
CM2 - Cm2
(M m) m M ( M 1) m(m 1)
个发生的概率。
解: P( A, B,C至 少 一 个 发 生) 1 P(ABC )
1 P(A B C) P(A B C) P( A) P(B) P(C ) P( AC ) 13 1
48 0.625
16. 设有M只晶体管,其中有m只废品,从中任取2只,求所取 晶体管有1只正品的条件下,另1只是废品的概率。
解:号码盘所有可能的组合为10×10×10种,其中只有一种可
以开锁,
P
1 103
0.1%
7. 有50件产品,其中4件不合格,从中随机抽取3件,求至少一 件不合格的概率。
解: P(至少一件不合格)1 - P(所有都合格)
1
C436 C530
22.5%
8. 一个纸盒中混放着60只外形类似的电阻,其中甲乙两厂生产
13. 设 P( A) P(B) 0.4 ,P( AB) 0.28 ,求:
解:
P( A | B) P( AB) P(B AB) 0.4 0.28 0.3
P(B)
P(B)
0.4
P( A | B ) P( AB ) P( A AB) 0.4 0.28 0.2
川大版高数-物理类专用-第三册-标准答案

川大版高数-物理类专用-第三册-答案————————————————————————————————作者:————————————————————————————————日期:第一章 行列式1.()()[][][]23154110103631254=520010=8(1)3(1)321(1)(2)(3)2441(1)3214243(1)321012)4n n n n n n n n m n m n n n m n m n n m 1τ=++++=2τ+++++-τ-⋯=-+-+-+⋯+2+1+0===+τ-⋯=+=+τ-⋯=⋯()该数列为奇排列()该排列为偶排列() 当或时,为偶数,排列为偶排列当或时,为奇数,排列为奇排列(其中,,()[][][]12(1)13521)246(2)0123(1)244113521)246(2)424313521)246(2)012)2.(1)(2)(n n n n n n n m n m n n n m n m n n m i i i k n n n -τ⋯-⋯=++++⋯+-===+τ⋯-⋯=+=+τ⋯-⋯=⋯⋯-+-+( 当或时,(为偶数,排列为偶排列当或时,(为奇数,排列为奇排列(其中,,解:已知排列的逆序数为,这个数按从大到小排列时逆序数为()()111112(1)3)2(1)2x x x n x n x n n n n n n x i r i i i n x r i n x n n i i i i i i -+-+---+⋯+2+1+0=----τ⋯=-τ⋯个.设第数之后有个数比小,则倒排后的位置变为,其后个数比小,两者相加为故3 证明:.因为:对换改变排列的奇偶性,即一次变换后,奇排列改变为偶排列,偶排列改变为奇排列∴当n ≥2时,将所有偶排列变为奇排列,将所有奇排列变为偶排列 因为两个数列依然相等,即所有的情况不变。
∴偶排列与奇排列各占一半。
4 (1)13243341a a a a 不是行列式的项 14233142a a a a 是行列式的项 因为它的列排排列逆序列τ=(4321)=3+2+0+0=5为奇数,∴应带负号(2)5142332451a a a a a 不是行列式的项 1352413524a a a a a =1324354152a a a a a 因为它的列排排列逆序列τ(34512)=2+2+2+0+0=6 为偶数∴应带正号。
川大版高数_物理类专用_第三册_答案

第一章 行列式1.()()[][][]23154110103631254=520010=8(1)3(1)321(1)(2)(3)2441(1)3214243(1)321012)4n n n n n n n n m n m n n n m n m n n m 1τ=++++=2τ+++++-τ-⋯=-+-+-+⋯+2+1+0===+τ-⋯=+=+τ-⋯=⋯()该数列为奇排列()该排列为偶排列() 当或时,为偶数,排列为偶排列当或时,为奇数,排列为奇排列(其中,,()[][][]12(1)13521)246(2)0123(1)244113521)246(2)424313521)246(2)012)2.(1)(2)(n n n n n n n m n m n n n m n m n n m i i i k n n n -τ⋯-⋯=++++⋯+-===+τ⋯-⋯=+=+τ⋯-⋯=⋯⋯-+-+( 当或时,(为偶数,排列为偶排列当或时,(为奇数,排列为奇排列(其中,,解:已知排列的逆序数为,这个数按从大到小排列时逆序数为()()111112(1)3)2(1)2x x x n x n x n n n n n n x i r i i i n x r i n x n n i i i i i i -+-+---+⋯+2+1+0=----τ⋯=-τ⋯个.设第数之后有个数比小,则倒排后的位置变为,其后个数比小,两者相加为故3 证明:.因为:对换改变排列的奇偶性,即一次变换后,奇排列改变为偶排列,偶排列改变为奇排列∴当n ≥2时,将所有偶排列变为奇排列,将所有奇排列变为偶排列 因为两个数列依然相等,即所有的情况不变。
∴偶排列与奇排列各占一半。
4 (1)13243341a a a a 不是行列式的项 14233142a a a a 是行列式的项 因为它的列排排列逆序列τ=(4321)=3+2+0+0=5为奇数,∴应带负号(2)5142332451a a a a a 不是行列式的项 1352413524a a a a a =1324354152a a a a a 因为它的列排排列逆序列τ(34512)=2+2+2+0+0=6 为偶数∴应带正号。
川大版高数第三册规范标准答案

=
=
= A
28.解:==时源自依次用V左乘和用U右乘 消去
得从而得证
29.解:(1)判断X可逆即:
因A、C可逆,
则 即
则X可逆。
(2)设 则
由
=
=E
30.证明:
31.解:(1)
原式=
(2)
(3)
第3章线性方程组
1.证:假设 线性相关,
则 不会为0,使得
整理得:
又由 ,故
由于
故由克莱默法则知:
故结论正确。
,其中 . 为任意的实数
AB=BA
充分性: AB=BA
(AB)’=B’A’=-BA
AB为反对称矩阵
综上所述:AB是反对称矩阵的充分必要条件是AB=BA。
26.解:设矩阵X为x=
则 =
Ax=o
=0
即 =0
对任意n 1矩阵都成立
A=0
27.证: : A为正交矩阵
=A
A = = =
又 正交矩阵为可逆矩阵
A =A
:
A = = =A
则
这样得到了 的另一种表出式,即表出不唯一
综上,假设成立条件下得到的结论与“ 可用 唯一表出”矛盾
故假设不成立, 线性无关
7、将A表示为 ,B表示为
若 线性无关,则必有
同理可证A
P117 T8
解:(1)
由此r=3
解:(2)
由此r=2
解:(3)
由此r=3
解:(4)
由此r=2
解:(5)
由此r=3
解:(6)
6.证:假设 线性相关,
由题意知,必存在一组使得
7.证:设
由于
6、证明:假设 线性相关,则 , 线性相关(部分相关则全体相关)
《高等数学》(四川大学)答 案第一册第二册第三册第四册

我在大学本科学习的高数,遗憾的是物理考研不考高数,所以本人对所学的高数书很有感情,总渴望能有个习题集啊,作为物理系学生数学的一个总结,更自信的面对理工科的高数!我们学得比他们还要好,对么??
各位大侠,帮帮忙啊
头秃了了啊!
回楼主(chengbo67) 的帖子我也要一份!!!!!!!!!!!!!!!!!11
回楼主(chengbo67) 的帖子考试急用发一份吧跪求啊哇哇哇****************发一下吧
考试急用发一份吧跪求啊哇哇哇*****************发一下吧
我也要一份!
v好啊,哈萨克哈萨克好
这么好的帖子怎么没人顶?全是精华啊
真的是很好的资料。
考试急用。
哇哇。
发一下吧****************谢谢啦
求发一下啊****************
虚的,还是等我做好了发
谁有?
求好人发资料****************
川大第四版1234册答案发一份吧白了少年头啊****************
请帮忙发一份川大版高等数学(物理专业)第二册、第三册答案。
谢谢!
我也急需,那位朋友有请给我发一份。
****************
我也急需,那位朋友有请给我发一份。
****************
考试急用发一份吧跪求啊
急需第三册和第四册的的哪个好心的大侠帮忙发一分啊****************谢谢啦
考研屋:提供各大机构考研、公务员、四六级辅导视频课程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
川大版高数_物理类专用_第三册
1. 引言
川大版高数是中国四川大学推出的一套高等数学教材,分为多册。
本文档将介绍川大版高数的物理类专用第三册内容。
2. 内容概述
物理类专用第三册是川大版高数系列的一部分,主要介绍了与物理相关的高等数学知识。
本册主要包括以下几个方面的内容:
1.微分方程
2.矢量分析
3.置换与反射
4.复变函数
5.特殊函数
6.微分方程的初值问题
7.应用题
下面将对以上每个部分进行详细介绍。
3. 微分方程
微分方程是物理学中常用的数学工具之一,用于描述自然
界中的变化过程。
本册中的微分方程部分主要介绍了一阶和二阶微分方程的求解方法,包括常系数线性齐次微分方程、非齐次微分方程、欧拉方程等,同时还涉及到一些常见的应用问题。
4. 矢量分析
矢量分析是研究矢量场的数学方法,广泛应用于物理学中。
本册中的矢量分析部分主要涵盖了矢量的基本概念,如数量积、矢量积等,同时还介绍了曲线、曲面的参数化表示,以及与曲线、曲面相关的重要公式和定理。
5. 置换与反射
在物理学中,置换和反射是常见的几何变换。
本册中的置
换与反射部分主要介绍了置换和反射的基本概念,如置换的定义、置换的合成以及反射的性质等。
6. 复变函数
复变函数是研究复数域上的函数的数学分支,其在物理学
中也有广泛的应用。
本册中的复变函数部分主要介绍了复数的基本概念、复变函数的导数和积分,以及一些与复变函数相关的定理和公式。
7. 特殊函数
特殊函数是用于解决特殊类型问题的一类数学函数。
本册
中的特殊函数部分主要介绍了常见的特殊函数,如贝塞尔函数、勒让德多项式、连带勒让德函数等,以及这些特殊函数的性质和应用。
8. 微分方程的初值问题
微分方程的初值问题是指在已知微分方程的一个解的初始
条件下,求解满足该条件的解。
本册中的微分方程的初值问题部分主要介绍了一阶微分方程和二阶线性齐次微分方程的初值问题的求解方法。
9. 应用题
应用题是通过将数学方法应用于实际问题而得出的题目。
本册中的应用题部分主要涵盖了物理学中常见的应用问题,如运动学、力学、热学等问题,并结合微分方程、矢量分析和特殊函数等知识进行求解。
10. 结语
川大版高数的物理类专用第三册是一本涵盖了与物理相关
的高等数学知识的教材。
通过学习这本教材,读者可以掌握微分方程、矢量分析、置换与反射、复变函数、特殊函数等知识,并能应用于解决物理学领域的问题。
希望本文档能对读者了解该教材的内容有所帮助。
