界面内聚力模型及有限元法
有限元法介绍

通俗地说,有限元法就是一种计算机模拟技术,使人们能够在计算机上用软件模拟一个工程问题的发生过程而无需把东西真的做出来。
这项技术带来的好处就是,在图纸设计阶段就能够让人们在计算机上观察到设计出的产品将来在使用中可能会出现什么问题,不用把样机做出来在实验中检验会出现什么问题,可以有效降低产品开发的成本,缩短产品设计的周期。
有限元法也叫有限单元法(finite element m ethod, FEM),是随着电子计算机的发展而迅速发展起来的一种弹性力学问题的数值求解方法。
五十年代初,它首先应用于连续体力学领域—飞机结构静、动态特性分析中,用以求得结构的变形、应力、固有频率以及振型。
由于这种方法的有效性,有限单元法的应用已从线性问题扩展到非线性问题,分析的对象从弹性材料扩展到塑性、粘弹性、粘塑性和复合材料,从连续体扩展到非连续体。
有限元法最初的思想是把一个大的结构划分为有限个称为单元的小区域,在每一个小区域里,假定结构的变形和应力都是简单的,小区域内的变形和应力都容易通过计算机求解出来,进而可以获得整个结构的变形和应力。
事实上,当划分的区域足够小,每个区域内的变形和应力总是趋于简单,计算的结果也就越接近真实情况。
理论上可以证明,当单元数目足够多时,有限单元解将收敛于问题的精确解,但是计算量相应增大。
为此,实际工作中总是要在计算量和计算精度之间找到一个平衡点。
有限元法中的相邻的小区域通过边界上的结点联接起来,可以用一个简单的插值函数描述每个小区域内的变形和应力,求解过程只需要计算出结点处的应力或者变形,非结点处的应力或者变形是通过函数插值获得的,换句话说,有限元法并不求解区域内任意一点的变形或者应力。
大多数有限元程序都是以结点位移作为基本变量,求出结点位移后再计算单元内的应力,这种方法称为位移法。
有限元法本质上是一种微分方程的数值求解方法,认识到这一点以后,从70年代开始,有限元法的应用领域逐渐从固体力学领域扩展到其它需要求解微分方程的领域,如流体力学、传热学、电磁学、声学等。
单搭接结构胶接头连接效率的影响因素分析

单搭接结构胶接头连接效率的影响因素分析陈涛;曾俊伟;段利斌;李卓【摘要】对单搭接结构胶接头进行拉伸试验,同时建立其有限元模型进行仿真,对单搭接结构胶接头连接效率的影响因素、接头两端刚度的差异对接头连接效率的影响进行分析.结果表明:对于钢材与铝材之间的结构胶连接,随着母材材料屈服强度的增大,接头连接效率不断提高,但当母材屈服强度增加到一定值后,接头连接效率反而呈现下降的趋势;与钢材相比,接头连接效率对铝材屈服强度更为敏感.接头连接效率也随接头几何尺寸(母材厚度、接头搭接长度和搭接宽度)的增加而提高.而对于两端刚度不同的结构胶连接,接头连接效率随着其两端刚度差异的加大而降低,因此为提高接头的连接效率,应尽量选用屈服极限相近的母材.【期刊名称】《汽车工程》【年(卷),期】2016(038)008【总页数】8页(P1030-1036,1024)【关键词】结构胶接头;单搭接;连接效率;刚度差异【作者】陈涛;曾俊伟;段利斌;李卓【作者单位】湖南大学,汽车车身先进设计制造国家重点实验室,长沙410082;汽车噪声振动和安全技术国家重点实验室,重庆400039;湖南大学,汽车车身先进设计制造国家重点实验室,长沙410082;湖南大学,汽车车身先进设计制造国家重点实验室,长沙410082;湖南大学,汽车车身先进设计制造国家重点实验室,长沙410082【正文语种】中文随着汽车轻量化技术的发展,车身所用材料呈现出多样化的趋势,由于异种材料之间的物理、化学和力学性能方面存在较大差异,因此多材料轻量化车身对连接技术提出了新的挑战,从而使异种材料之间的连接技术成为研究的热点。
由于异种材料采用传统连接技术连接时具有很明显的缺点,如传统点焊连接由于技术瓶颈和成本的原因,无法广泛应用于异种材料的连接;而铆接和螺栓连接则在连接处有显著的应力集中[1-2]。
结构胶连接作为一种新型连接技术,具有良好的异种材料连接性能,且有利于车身轻量化、提高车辆的碰撞性能和增加车身结构的刚度、强度和耐久性,同时结构胶连接技术也解决了传统连接技术可能产生的应力集中和疲劳强度差等问题[3]。
基于内聚力模型(CZM)的单筋拉拔数值分析方法研究

基于内聚力模型(CZM)的单筋拉拔数值分析方法研究景剑;强峰;施凯【摘要】目前化学植筋粘结性能数值模拟中界面单元均以双弹簧单元为主,但是模拟结果与相应的试验结果有较大偏差.为了提高数值模拟的精确度,本文基于双线性内聚力模型(Cohesive Zone Model)进行了单筋拉拔试验的有限元模拟,采用双线性应力-张开位移模型定义内聚力单元本构关系,进行了参数分析,得到了内聚力参数对计算结果的影响规律,并对一些试验的荷载-位移曲线进行参数拟合以确定合理参数,从而验证了该植筋模拟方法的有效性.【期刊名称】《低温建筑技术》【年(卷),期】2018(040)007【总页数】5页(P57-60,64)【关键词】化学植筋;单筋拉拔试验;内聚力模型;参数分析【作者】景剑;强峰;施凯【作者单位】江苏省建筑工程质量检测中心有限公司,南京210008;河海大学土木与交通学院,南京210098;江苏省建筑工程质量检测中心有限公司,南京210008【正文语种】中文【中图分类】TU5020 引言化学植筋是目前加固改造领域应用相当广泛的后锚固连接技术,现有植筋承载力和力学性能的相关研究大多限于单筋拉拔试验研究,由于拉拔试验试件制作及试验装置比较简单,试验结果便于分析,长期以来一直作为研究化学植筋性能的有效方法,但是由于试验中存在诸多不确定性因素,如果通过大量的拉拔试验研究化学植筋性能,不仅耗费过多的试验材料,而且需要很长的试验周期,给研究带来诸多不便。
近些年来,应用有限元分析方法进行化学植筋锚固性能研究已成为一种方便有效的数值模拟方法。
在早期的植筋锚固系统研究中,国内外同行已发表了一些有关粘结锚固的研究成果。
Cook等人[1]通过单筋拉拔试验总结出了在混凝土构件中,植筋的破坏模式,研究了单个钢筋锚固的破坏过程和机理,给出了单筋的粘结锚固建议;郭晓飞[2]提出了采用双弹簧单元模拟混凝土与植筋胶界面单元和钢筋与植筋胶界面单元,并考虑了植筋胶的厚度,采用四边形滑移单元对植筋胶进行模拟。
ABAQUS中Cohesive单元建模方法讲解

复合材料模型建模与分析1。
Cohesive单元建模方法1。
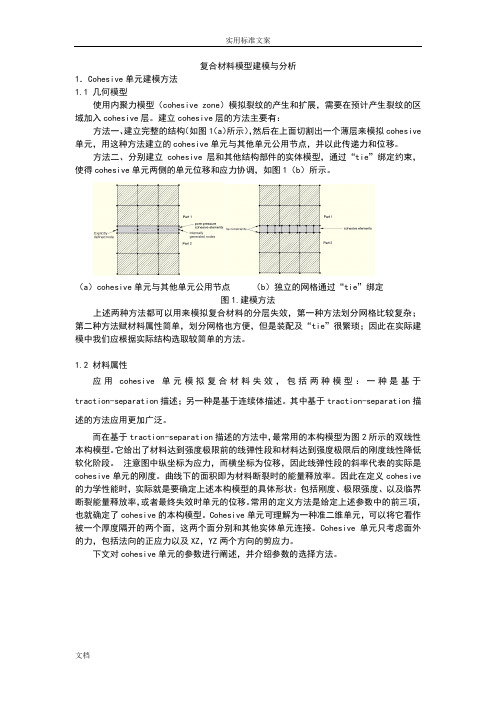
1 几何模型使用内聚力模型(cohesive zone)模拟裂纹的产生和扩展,需要在预计产生裂纹的区域加入cohesive层。
建立cohesive层的方法主要有:方法一、建立完整的结构(如图1(a)所示),然后在上面切割出一个薄层来模拟cohesive 单元,用这种方法建立的cohesive单元与其他单元公用节点,并以此传递力和位移.方法二、分别建立cohesive层和其他结构部件的实体模型,通过“tie”绑定约束,使得cohesive单元两侧的单元位移和应力协调,如图1(b)所示。
(a)cohesive单元与其他单元公用节点(b)独立的网格通过“tie”绑定图1。
建模方法上述两种方法都可以用来模拟复合材料的分层失效,第一种方法划分网格比较复杂;第二种方法赋材料属性简单,划分网格也方便,但是装配及“tie”很繁琐;因此在实际建模中我们应根据实际结构选取较简单的方法。
1.2 材料属性应用cohesive单元模拟复合材料失效,包括两种模型:一种是基于traction-separation描述;另一种是基于连续体描述。
其中基于traction—separation描述的方法应用更加广泛.而在基于traction-separation描述的方法中,最常用的本构模型为图2所示的双线性本构模型。
它给出了材料达到强度极限前的线弹性段和材料达到强度极限后的刚度线性降低软化阶段. 注意图中纵坐标为应力,而横坐标为位移,因此线弹性段的斜率代表的实际是cohesive 单元的刚度.曲线下的面积即为材料断裂时的能量释放率.因此在定义cohesive的力学性能时,实际就是要确定上述本构模型的具体形状:包括刚度、极限强度、以及临界断裂能量释放率,或者最终失效时单元的位移。
常用的定义方法是给定上述参数中的前三项,也就确定了cohesive的本构模型。
Cohesive单元可理解为一种准二维单元,可以将它看作被一个厚度隔开的两个面,这两个面分别和其他实体单元连接。
有限元法概述

(2)MSC/NASTRAN。 MSC/NASTRAN是在原NAST RAN基础上进行大量改进后的系统软件,主要包括MS C.Patran并行框架式有限元前后处理及分析系统、 MS C.GS-Mesher快速有限元网格、 MSC.MARC非线性有 限元软件等。其中MSC.MARC具有较强的结构分析能
.
5.在产品制造或工程施工前预先发现潜在的问题; 6. 模拟各种试验方案,减少试验时间和经费; 7. 进行机械事故分析,查找事故原因。
轴承强度分析
.
汽车碰撞实验
.
刹车制动时地盘的应力分析
.
钢板精轧机热轧制分析
.
三维椭圆封头开孔补强
.
水轮机叶轮的受力分析模拟
.
人体股骨端受力分析
.
半导体芯片温度场的数值仿真
知量时称为混合法。 位移法易于实现计算自动化,所以,在有限单元法
中位移法应用范围最广。
.
2、有限元法的发展
有限单元法基本思想的提出,可以追溯到Courantl在1 943年的工作,他第一次尝试应用定义在三角形区域上的 分片连续函数和最小位能原理相结合,来求解St·Venant 扭转问题。相继一些应用数学家、物理学家和工程师由于 各种原因都涉足过有限单元的概念。
.
4、有限元的特点
(1) 概念清楚,容易理解。可以在不同的专业背景和水平 上建立起对该方法的理解。从使用的观点来讲,每个人的 理论基础不同,理解的深度也可以不同,既可以通过直观的 物理意义来学习,也可以从严格的力学概念和数学概念推 导。
Cohesive经典讲解
复合材料模型建模与分析1.Cohesive单元建模方法1.1 几何模型使用内聚力模型(cohesive zone)模拟裂纹的产生和扩展,需要在预计产生裂纹的区域加入cohesive层。
建立cohesive层的方法主要有:方法一、建立完整的结构(如图1(a)所示),然后在上面切割出一个薄层来模拟cohesive 单元,用这种方法建立的cohesive单元与其他单元公用节点,并以此传递力和位移。
方法二、分别建立cohesive层和其他结构部件的实体模型,通过“tie”绑定约束,使得cohesive单元两侧的单元位移和应力协调,如图1(b)所示。
(a)cohesive单元与其他单元公用节点(b)独立的网格通过“tie”绑定图1.建模方法上述两种方法都可以用来模拟复合材料的分层失效,第一种方法划分网格比较复杂;第二种方法赋材料属性简单,划分网格也方便,但是装配及“tie”很繁琐;因此在实际建模中我们应根据实际结构选取较简单的方法。
1.2 材料属性应用cohesive单元模拟复合材料失效,包括两种模型:一种是基于traction-separation描述;另一种是基于连续体描述。
其中基于traction-separation描述的方法应用更加广泛。
而在基于traction-separation描述的方法中,最常用的本构模型为图2所示的双线性本构模型。
它给出了材料达到强度极限前的线弹性段和材料达到强度极限后的刚度线性降低软化阶段。
注意图中纵坐标为应力,而横坐标为位移,因此线弹性段的斜率代表的实际是cohesive单元的刚度。
曲线下的面积即为材料断裂时的能量释放率。
因此在定义cohesive 的力学性能时,实际就是要确定上述本构模型的具体形状:包括刚度、极限强度、以及临界断裂能量释放率,或者最终失效时单元的位移。
常用的定义方法是给定上述参数中的前三项,也就确定了cohesive的本构模型。
Cohesive单元可理解为一种准二维单元,可以将它看作被一个厚度隔开的两个面,这两个面分别和其他实体单元连接。
沥青混凝土的细观开裂模拟方法研究

本研究的目的是建立一个更有效、更精确的细观沥青混凝土模型研究其开裂 问题。本文采用两种数值建模方法分析沥青混凝土的开裂问题。第一种是随机骨 料分布及嵌入粘结单元有限元模型。本方法将沥青混凝土分为四个重要组成部分: 骨料、沥青砂浆、界面过渡区和初始缺陷。根据由 Full 和 Thompson 开发的级配 曲线,将骨料颗粒模拟成大小不同的随机分布多边形。采用了一些有效的方法来 提高骨料投递的成功率。对于初始缺陷,本研究仅考虑空隙。在沥青砂浆的初始 网格内,沿骨料与沥青砂浆的界面插入零厚粘性单元,模拟混凝土的开裂过程。 修正了以往的开裂初始准则和牵引分离规律,并用以描述粘结构件的破坏行为。 基于 python 语言,开发了骨料投递、内聚力单元插入和修正的构造本构模型的 用户自定义程序,并将其嵌入到商业有限元软件包 abaqus 中。通过与试验结果 的比较,验证了所提出的细观模型的有效性和准确性,并研究了细观结构对沥青 混凝土的宏观性能的影响。第二种方法采用基于 Voronoi 多边形的细观刚体弹簧 法进行数值建模,在第一种方法的基础上,采用随机骨料投递技术随机投放圆形 骨料,然后根据骨料形心点生成 Voronoi 网格,过 Voronoi 单元网格边界的几何 形状寻找骨料之间的相互作用关系,骨料间的粘结材料被浓缩为骨料间的界面弹 簧,其刚度由粘结材料的厚度定义。通过二维和三维数值单轴压缩实验进行验证 其有效性。 关键词:细观沥青混凝土;随机骨料投递算法;粘结单元嵌入算法;Voronoi 多 边形;细观刚体弹簧法
i
ABSTRACT
The purpose of this study is to establish a more effective and accurate mesoscopic asphalt mixture model to study its cracking problem.In this paper, two numerical modeling methods are used to analyze the cracking of asphalt mixture.The first is the random aggregate distribution and the embedded bond element finite element model.This method divides asphalt mixture into four important components: aggregate, asphalt mortar, interface transition zone and initial defect.Aggregate particles were simulated as randomly distributed polygons of different sizes according to the grading curves developed by Full and Thompson.Some effective methods are adopted to improve the success rate of aggregate delivery. For the initial defects, only the void was considered in this study. In the initial grid of asphalt mortar, zero-thickness viscous unit is inserted along the interface between aggregate and asphalt mortar to simulate the cracking process of concrete.The former cracking initial criterion and traction separation rule are modified to describe the failure behavior of bonded components. Based on the python language, a user-defined program for aggregate delivery, cohesive force unit insertion and modification of constitutive model construction was developed and embedded in abaqus, a commercial finite element software package. Compared with the experimental results, the validity and accuracy of the proposed meso-structure model are verified, and the effect of meso-structure on the macro performance of asphalt mixture is studied. The second method based on Voronoi polygon of the mesoscopic numerical model based on the rigid spring method and random on the circular aggregate by random aggregate delivering technology, then Voronoi grids were generated according to the aggregate centroid and a Voronoi unit grid boundary geometry for the interaction relationship between aggregate and bond between aggregate material is concentrated to aggregate the interface between the spring, defined by the thickness of the bonding material, The validity of the method is verified by two-dimensional and three-dimensional numerical uniaxial compression experiments.
有限元课件ppt

将所有单元的刚度矩阵依照一定的方式组合起来,形成整体的刚度 矩阵。
载荷向量与束缚条件
载荷向量
表示作用在结构上的外力,包括集中力和散布力。
束缚条件
表示结构在某些结点上的位移受到限制,常见的束缚有固定束缚、 弹性束缚等。
载荷向量和束缚条件的引入
在建立整体刚度矩阵后,需要将载荷向量和束缚条件引入到整体刚 度矩阵中,形成完全的线性方程组。
并行计算
采取并行计算技术,提高计算效率。
算法改进
优化算法,提高计算精度和效率。
06 有限元分析软件 介绍
ANSYS
01
功能特点
ANSYS是一款功能强大的有限元分析软件,广泛应用于结构、流体、
电磁等多种工程领域。它提供了丰富的建模工具和求解器,能够处理复
杂的工程问题。
02
优点
ANSYS具有友好的用户界面和强大的前后处理功能,使得建模和网格
有限元法的应用领域
结构分析
有限元法在结构分析中应用最 为广泛,可以用于分析各种类 型的结构,如桥梁、建筑、机
械零件等。
热传导
有限元法可以用于求解温度场 的问题,如热传导、热对流和 热辐射等问题。
流体动力学
有限元法在流体动力学领域也 有广泛应用,可以用于求解流 体流动和流体传热等问题。
其他领域
除了上述领域外,有限元法还 广泛应用于电磁场、声场、化
学反应等领域。
02 有限元的数学基 础
线性代数基础
向量与矩阵
01
介绍向量的基本概念、向量的运算、矩阵的表示和运算规则等
。
线性方程组
02
论述线性方程组的解法,包括高斯消元法、LU分解等。
特征值与特征向量
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
界面内聚力模型
指数内聚力模型法向与切向的单向断裂能计算式分别
为
n
n
n
exp
n
n
1
r
n
n
1 q r 1
q
rq r 1
n
n
t
n
n
q
1
q
exp
2 t
2 t
在单向开裂过程中,总断裂能值等于该向的断裂能计 算值,通过考察单向开裂条件下的应力值或断裂能的值, 都可以判断内聚力模型的计算结果与状态。
界面内聚力模型及内聚力 有限元法
xxx xxxx.xx.xx
界面内聚力模型
随着复合材料结构种类的多样性发展,传统断裂力学 已不能满足韧性开裂以及复合材料界面开裂等研究需求。 基于弹塑性断裂力学的内聚力模型(cohesive zone model, CZM) 已被应用于计算复合材料界面损伤和断裂过程。
断裂能的控制方程
27 4
T0
0
1
2
n 0
2
1
4 3
n 0
1 2
n 0
2
1 2
t 0
2
1
4 3
t 0
1 2
n 0
2
为法向与切向刚度之间的一个比例系数,T0 为纯法
向时的最大内聚力,0 为最大张开量。
界面内聚力模型
由
T
可得
Tn
27 4 T0
界面内聚力模型
指数内聚力模型在开裂过程中的断裂能控制方程为:
n
n
exp
n
n
1
r
n
n
1 q r 1
q
rq r 1
n
n
exp
t2
t2
n 、t 分别为界面上的法向与切向位移值,n 为纯法 向开裂状态下界面完全开裂时的界面断裂能, n、 t 为 法向与切向界面开裂特征位移,即应力最大值点对应的
内聚力区
=f ( )
内聚力区域中定义的“虚 拟裂纹”描述了一对虚拟面 之间的动态应力场。
图1 裂纹尖端的内聚力区
界面内聚力模型
内聚力模型的重要特征是张力-位移曲线的形状和内 聚力参数。
目前,应用较为广泛的内聚力准则,如图2所示。
t
t
a)指数型
b)双线性
t
t型
c)多项式型
d)梯形型
图2 不同形式的内聚力准则 a)指数 b)双线性 c)多项式 d)梯形区
指数内聚力模型
指数内聚力模型被广泛的应用于计算复合材料界面开 裂、脆性材料中的动态裂纹扩展、韧性基体上薄膜涂层 之间的开裂裂纹萌生等过程。
指数内聚力模型具有连续性的张力位移关系,同时其 断裂能的值也为连续变化。
与双线性以及梯形法则相比,指数法则的张力位移关 系是非线性连续变化的,更符合实际界面开裂的状态。
2t
2 t
1 q r 1
1
exp
2t
t2
r
n
n
2
Tt
- n n
2
n t
t
t
q
r q r 1
n
n
exp
n
n
exp
2t
2 t
max max分别为内聚力界面上法向与切向强度,则指数 内聚力模型中的参数之间的关系为:
n e max n
t
e 2
max
t
界面内聚力模型
复合开裂时应力耦合关系分析
界面内聚力模型
复合开裂条件下,在 q 1 时,不论两向同时开裂速 度的差异,两向的张力位移关系完全耦合。计算开裂过 程的总断裂能以及法向与切向的单向断裂能,其随着开 裂位移变化如图5所示。
实际材料或结构开裂过程中,在复合开裂条件下,若 有一向出现开裂失效,则整个裂纹面完全开裂,该处不 能再承载任何方向载荷。在内聚力模型中即为各向应力 的完全耦合关系。
相比较于其他类型的内聚力模型张力位移关系,指数 内聚力模型为具有耦合关系的内聚力法则,参数q,r对 于耦合关系产生作用。
在指数内聚力模型计算时,界面开裂过程中,断裂能 值连续变化,其同样能够表征着界面开裂的状态。
界面内聚力模型
双线性张力位移法则 双线性张力位移法则是一种简单有效的内聚力法则,
被广泛应用于有限元软件中已实现内聚力模型计算。 控制方程为
max
0 n
max
f n
f n
0 n
(
0)
n
(
0)
n
max
0 t
max
tf tf
tf
(
0)
t
(
0)
t
界面内聚力模型
其中 为法向的应力值, max
为切向的应力值, max 、 max
n 0
2
1
2
n 0
n 0
2
n 0
2
n 0
1
Tr
27 4
T0
t 0
2
1
t 0
n 0
2
与双线性及梯形张力位移关系不同,多项式张力位移
关系为连续性的方程,首先提出断裂能的控制方程,对
其进行偏导求得张力位移关系的控制方程。
界面内聚力模型
界值 nc
,tc 。计算公
f n
tc
1 2
max
t
f
双线性内聚力模型简单有效,能较好的在有限元等方法 中计算而一般不会出现计算困难。
界面内聚力模型
梯形张力位移法则(逐段线性张力位移法则)
控制方程为
f
max 1 max
max( f -2
- )
1 1 2 2 f
f
0
临界的断裂能值为: c
1 2
m
( ax
f
2
1)
梯形张力位移关系中,其模型 的参数除了最大应力值以及临界 断裂能之外,还必须给出 1 2 的值。
max
c
1
2 f
图4 梯形张力位移
界面内聚力模型
多项式张力位移法则
多项式张力位移法则的内聚力模型由Needleman于 1992年提出,采用了高次多项式的函数。
内聚力实际上是物质原子或分子之间的相互作用力。 在内聚力区域内,应力是开裂位移的函数,即张力-开 裂位移(Traction-separation)关系,也称为内聚力准则。
界面内聚力模型
内聚力区域代表了待扩展 的裂尖前沿的区域,其中内 聚力区域中裂尖的概念是一 种数值定义,而非实际材料 裂纹尖端 中的裂尖范畴。
分别为法向及切向的最大
n
max
t
0 t
tf
应力值,对应的裂纹界面
0 n
f n
张开位移值分别为
0 n
0 t
。
a)法向张力位移关系 b)切向张力位移关系
图线斜率为内聚力刚度。 图3 双线性张力位移关系
界面内聚力模型
在达到其最大值后应力开始减小至零时裂纹开裂完成,
其对应的位移值为最终开裂位移值
f n
。各项的断裂能临
位移值。+
参数
q,r 分别为:
q
t n
r
* n
n
t 为纯切向开裂状态下界面完全开裂时的界面断裂能。
*n 为在法向应力为零时,切向完全开裂时的法向位移值。
界面内聚力模型
界面上的各向应力为: T
将断裂能控制方程对于各向位移值进行偏导得到各向
应力与位移的关系式为:
Tn
-
n n
exp
n
n
n
n
exp
