锐角三角函数应用题训练(全)
人教版初3数学9年级下册 第28章(锐角三角函数)应用题综合训练(含解析)

初中三角函数应用题综合一.解直角三角形的应用(共10小题)1.如图,小明同学用仪器测量一棵大树AB的高度,在C处测得∠ADM=30°,在E处测得∠AFM =60°,CE=10米,仪器高度CD=1.5米,求这棵树AB的高度.(结果精确到0.1,参考数据:≈1.41,≈1.73,≈2.24)2.如图,小明家A和地铁口B两地恰好处在东西方向上,且相距3km,学校C在他家A正北方向的4km处,公园D与地铁口B和学校C的距离分别5km和km.(1)若∠BDA=10°,求∠ADC的大小;(2)计算公园D与小明家A的距离.3.如图,A、B两地间有一座山,汽车原来从A地到B地需要经折线ACB绕山行驶.为加快城乡对接,建立全域美丽乡村,某地区对A、B两地间的公路进行改建,在这座山打一条隧道,使汽车可以直接沿AB行驶.已知AC=80千米,∠A=30°,∠B=45°.求:(1)开通隧道前,汽车从A地到B地需要行驶多少千米;(2)开通隧道后汽车从A地到B地大约少行驶多少千米?(结果精确到0.1千米)(参考数据:≈1.41,≈1.73)4.如图,数学兴趣小组利用硬纸板自制的Rt△DEF来测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条边DE=1m,EF=0.6m,测得边DF离地面的高度AC=0.8m,CD=6m,求树高AB.5.如图是小朋友玩的“滚铁环”游戏的示意图,⊙O向前滚动时,铁棒DE保持与OE垂直.⊙O与地面接触点为A,若⊙O的半径为25cm,∠AOE=53°.(1)求点E离地面AC的距离BE的长;(2)设人站立点C与点A的距离AC=53cm,DC⊥AC,求铁棒DE的长.(参考数据:sin53°≈0.8,cos53°≈0.6)6.某中学数学活动小组设计了如图检测公路上行驶的校车速度的实验:先在公路旁边选取一点C,再在笔直的车道l上确定点D,使CD与l垂直,测得CD的长等于30米,在l上点D的同侧取点A,B,使∠CAD=30°,∠CBD=45°.(1)求AB的长(精确到0.1米,参考数据:≈1.73,≈1.41);(2)已知本路段对校车限速为40千米/小时,若测得校车从A到B用时2秒,这辆校车是否超速?说明理由.7.为了测量旗杆AB的高度,小颖画了如下的示意图,其中CD,EF是两个长度为2m的标杆.(1)如果现在测得∠DEC=30°,EG=4m,求旗杆AB的高度;(参考数据:≈1.41,≈1.73)(2)如果CE的长为x,EG的长为y,请用含x,y的代数式表示旗杆AB的高度.二.解直角三角形的应用−坡度坡角问题(共7小题)8.如图所示,斜坡的坡比i=h:l=1:,则斜坡的坡度是( )A.30°B.60°C.1:D.:19.如图,要测量山高CD,可以把山坡“化整为零”地划分为AB和BC两段,每一段上的山坡近似是“直”的.若量得坡长AB=600m,BC=800m,测得坡角∠BAD=30°,∠CBE=45°,则山高CD为( )A.(300+800)m B.700mC.(300+400)m D.(400+300)m10.如图,河坝横断面迎水坡AB的坡比为1:,坝高BC为4m,则AC的长度为( )A.8m B.4m C.8m D.m11.如图所示,某拦水大坝的横断面为梯形ABCD,AE,DF为梯形的高,其中迎水坡AB的坡角α=45°,坡长AB=10米,背水坡CD的坡度i=1:,则背水坡的坡长CD为( )米.A.20B.20C.10D.2012.为了学生的安全,某校决定把一段如图所示的步梯路段进行改造.已知四边形ABCD为矩形,DE =10m,其坡度为i1=1:,将步梯DE改造为斜坡AF,其坡度为i2=1:4,求斜坡AF的长度是 米.(结果精确到0.01m,参考数据:≈1.732,≈4.123)13.某校有一露天舞台,纵断面如图所示,AC垂直于地面,AB表示楼梯,AE为舞台面,楼梯的坡角∠ABC=45°,坡长AB=2m,为保障安全,学校决定对该楼梯进行改造,降低坡度,拟修新楼梯AD,使∠ADC=30°.(1)求舞台的高AC(结果保留根号);(2)求DB的长度(结果保留根号).14.某居民楼MN后有一个坡度为i=1:2.4的小山坡,小区物业准备在小山坡上加装一广告牌PQ (如图所示),已知QA=5.2米,水平地面上居民楼MN距坡底A点的距离AN=1.2米.当太阳光线与水平线成53°角时,测得广告牌PQ落在居民楼上的影子EN长为3米,求广告牌PQ的高.(参考数据:sin53°≈,cos53°≈,tan53°≈)三.解直角三角形的应用−仰角俯角问题(共8小题)15.若从楼顶A点测得点C的俯角为31°,测得点D的俯角为42°,则∠ADC的度数为( )A.31°B.42°C.48°D.59°16.如图,某建筑物的顶部有一块宣传牌CD,小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°,已知斜坡AB的坡角为30°,AB=10米,AE=15米,则宣传牌CD的高度是( )A.B.C.D.17.某通信公司准备逐步在歌乐山上建设5G基站.如图,某处斜坡CB的坡度(或坡比)为i=1:2.4,通讯塔AB垂直于水平地面,在C处测得塔顶A的仰角为45°,在D处测得塔顶A的仰角为53°,斜坡路段CD长26米,则通讯塔AB的高度为( )(参考数据:,,)A.米B.米C.56米D.66米18.某中学九年级数学兴趣小组想测量建筑物AB的高度.他们在C处仰望建筑物顶端,测得仰角为48°,再往建筑物的方向前进6米到达D处,测得仰角为64°,则建筑物的高度为 米.(测角器的高度忽略不计,结果精确到0.1米)(参考数据:sin48°≈,tan48°≈,sin64°≈,tan64°≈2)19.如图,某校数学兴趣小组要测量楼房DC的高度.在点A处测得楼顶D的仰角为30°,再往楼房的方向前进30m至B处,测得楼顶D的仰角为45°,则楼房DC的高度为 m.20.如图,小马同学在数学综合实践活动中,利用所学的数学知识对山坡一棵树的高度进行测量,先测得小马同学离底部C的距离BC为10m,此时测得对树的顶端D的仰角为55°,已知山坡与水平线的夹角为20°,小马同学的观测点A距地面1.6m,求树木CD的高度(精确到0.1m).(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43,sin20°≈0.34,cos20°≈0.94,tan20°≈0.36).21.如图,某中学数学活动小组在学习了“利用三角函数测高”后,选定测量小河对岸一幢建筑物BC 的高度,他们先在斜坡上的D处,测得建筑物顶端B的仰角为30°.且D离地面的高度DE=5m.坡底EA=30m,然后在A处测得建筑物顶端B的仰角是60°,点E,A,C在同一水平线上,求建筑物BC的高.(结果用含有根号的式子表示)22.如图,某人在D处测得山顶C的仰角为37°,向前走100米来到山脚A处,测得山坡AC的坡度为i=1:0.5,求山的高度(不计测角仪的高度,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75).参考答案与试题解析一.解直角三角形的应用(共10小题)1.如图,小明同学用仪器测量一棵大树AB的高度,在C处测得∠ADM=30°,在E处测得∠AFM =60°,CE=10米,仪器高度CD=1.5米,求这棵树AB的高度.(结果精确到0.1,参考数据:≈1.41,≈1.73,≈2.24)【解答】解:由题意知,四边形CDBM、CDEF、EFMB是矩形,∴BM=CD=1.5米,CE=DF=10米.在Rt△ADM中,∵tan∠ADM=,∴DM==AM.在Rt△AFM中,∵tan∠AFM=,∴FM==AM.∵DF=DM﹣FM,∴AM﹣AM=10.∴AM=10.AM=5.∴AB=AM+MB=5+1.5≈5×1.73+1.5=8.65+1.5=10.15=10.2(米).答:这棵树AB的高度为10.2米.2.如图,小明家A和地铁口B两地恰好处在东西方向上,且相距3km,学校C在他家A正北方向的4km处,公园D与地铁口B和学校C的距离分别5km和km.(1)若∠BDA=10°,求∠ADC的大小;(2)计算公园D与小明家A的距离.【解答】解:(1)由题意得:BD=5km,CD=5km,∠BAC=90°,AB=3km,CA=4km,∴BC===5(km),∴BC=BD,∵BC2+BD2=52+52=50,CD2=(5)2=50,∴BC2+BD2=CD2,∴△BCD是等腰直角三角形,∴∠CBD=90°,∴∠BDC=45°,∴∠ADC=∠BDC﹣∠BDA=45°﹣10°=35°;(2)过D作DE⊥AB,交AB的延长线于E,如图所示:则∠DEB=90°,∴∠BDE+∠DBE=90°,由(1)得:∠CBD=90°,∴∠DBE+∠CBA=90°,∴∠BDE=∠CBA,在△BDE和△CBA中,,∴△BDE≌△CBA(AAS),∴DE=BA=3km,BE=CA=4km,∴AE=BE+AB=7(km),∴AD===(km).∴公园D与小明家A的距离为km.3.如图,A、B两地间有一座山,汽车原来从A地到B地需要经折线ACB绕山行驶.为加快城乡对接,建立全域美丽乡村,某地区对A、B两地间的公路进行改建,在这座山打一条隧道,使汽车可以直接沿AB行驶.已知AC=80千米,∠A=30°,∠B=45°.求:(1)开通隧道前,汽车从A地到B地需要行驶多少千米;(2)开通隧道后汽车从A地到B地大约少行驶多少千米?(结果精确到0.1千米)(参考数据:≈1.41,≈1.73)【解答】解:(1)如图,过点C作AB的垂线CD,垂足为D,∵AB⊥CD,sin30°=,AC=80千米,∴CD=AC•sin30°=80×=40(千米),BC===40(千米),∴AC+BC=80+40≈1.41×40+80=136.4(千米).∴开通隧道前,汽车从地到地大约要走136.4千米.(2)∵cos30°=,AC=80千米,∴AD=AC•cos30°=80×=40(千米),∵tan45°=,CD=40(千米),∴BD===40(千米),∴AB=BD+AD=40+40≈40+40×1.73=109.2(千米).∴汽车从A地到B地比原来少走的路程为:AC+BC﹣AB=136.4﹣109.2=27.2(千米).∴开通隧道后,汽车从A地到B地大约可以少走27.2千米.4.如图,数学兴趣小组利用硬纸板自制的Rt△DEF来测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条边DE=1m,EF=0.6m,测得边DF离地面的高度AC=0.8m,CD=6m,求树高AB.【解答】解:方法一:在Rt△EDF中,DE=1m,EF=0.6m,∴tan∠EDF===,在Rt△BCD中,CD=6m,∵tan∠BDC=tan∠EDF,∴=,∴BC=3.6m,∵AC=0.8m,∴AB=AC+BC=3.6+0.8=4.4(m),答:树高AB为4.4m;方法二:由题意得:∠BCD=∠DEF=90°,∠CDB=∠EDF,∴△DCB∽△DEF,∴,∵DE=1m,EF=0.6m,CD=6m,∴=,解得:BC=3.6,∵AC=0.8m,∴AB=AC+BC=3.6+0.8=4.4(m),答:树高AB为4.4m.5.如图是小朋友玩的“滚铁环”游戏的示意图,⊙O向前滚动时,铁棒DE保持与OE垂直.⊙O与地面接触点为A,若⊙O的半径为25cm,∠AOE=53°.(1)求点E离地面AC的距离BE的长;(2)设人站立点C与点A的距离AC=53cm,DC⊥AC,求铁棒DE的长.(参考数据:sin53°≈0.8,cos53°≈0.6)【解答】解:过E作与AC平行的直线,与OA、FC分别相交于H、N.(1)在Rt△OHE中,∠OHE=90°,OE=25cm,∠AOE=53°,∴HO=OE×cos53°=15cm,EH=20cm,EB=HA=25﹣15=10(cm),所以铁环钩离地面的高度为10cm;(2)∵铁环钩与铁环相切,∴∠EOH+∠OEH=∠OEH+∠DEN=90°,∠DEN=∠EOH,∴DE==,在Rt△DEN中,∠DNE=90°,EN=BC=AC﹣AB=53﹣20=33(cm),DE===55(cm),∴铁环钩的长度DE为55cm.6.某中学数学活动小组设计了如图检测公路上行驶的校车速度的实验:先在公路旁边选取一点C,再在笔直的车道l上确定点D,使CD与l垂直,测得CD的长等于30米,在l上点D的同侧取点A,B,使∠CAD=30°,∠CBD=45°.(1)求AB的长(精确到0.1米,参考数据:≈1.73,≈1.41);(2)已知本路段对校车限速为40千米/小时,若测得校车从A到B用时2秒,这辆校车是否超速?说明理由.【解答】解:(1)由题意得:在Rt△ADC中,AD==≈51.9(米),在Rt△BDC中,BD===30(米),∴AB=AD﹣BD≈51.9﹣30=21.9(米),答:AB的长为21.9米;(2)不超速,理由:∵汽车从A到B用时2秒,∴速度为21.9÷2=10.95(米/秒),∵10.95×3600=39420(米/时),∴该车速度为39.42千米/小时,∵39.42千米/小时<40千米/小时,∴这辆校车在AB路段不超速.7.为了测量旗杆AB的高度,小颖画了如下的示意图,其中CD,EF是两个长度为2m的标杆.(1)如果现在测得∠DEC=30°,EG=4m,求旗杆AB的高度;(参考数据:≈1.41,≈1.73)(2)如果CE的长为x,EG的长为y,请用含x,y的代数式表示旗杆AB的高度.【解答】解:(1)由题意得:∠ABC=∠DCE=∠FEG=90°,在Rt△DCE中,CE===2m,∵∠DEC=∠AEB,∴△DEC∽△AEB,∴=,∴=,∵∠FGE=∠AGB,∴△FGE∽△AGB,∴=,∴=,∴=,∴EB=(8+12)m,∴=,∴AB=8+4≈14.92m,答:旗杆AB的高度为14.92米;(2)由(1)得:△DEC∽△AEB,∴=,∴=,由(1)得:△FGE∽△AGB,∴=,∴=,∴=,∴EB=,∴=,∴AB=,答:旗杆AB的高度为m.二.解直角三角形的应用−坡度坡角问题(共7小题)8.如图所示,斜坡的坡比i=h:l=1:,则斜坡的坡度是( )A.30°B.60°C.1:D.:1【解答】解:∵斜坡的坡比i=h:l=1:,∴斜坡的坡度为1:,故选:C.9.如图,要测量山高CD,可以把山坡“化整为零”地划分为AB和BC两段,每一段上的山坡近似是“直”的.若量得坡长AB=600m,BC=800m,测得坡角∠BAD=30°,∠CBE=45°,则山高CD为( )A.(300+800)m B.700mC.(300+400)m D.(400+300)m【解答】解:由题意可知,四边形BFDE为矩形,∴DE=BF,在Rt△BAF中,∠BAF=30°,AB=600m,则BF=AB=300(m),∴DE=300m,在Rt△CBE中,∠CBE=45°,BC=800m,∴CE=BC=400(m),∴CD=CE+DE=(300+400)m,故选:C.10.如图,河坝横断面迎水坡AB的坡比为1:,坝高BC为4m,则AC的长度为( )A.8m B.4m C.8m D.m【解答】解:∵迎水坡AB的坡比为1:=,BC=4m,∴AC=BC=4(m),故选:B.11.如图所示,某拦水大坝的横断面为梯形ABCD,AE,DF为梯形的高,其中迎水坡AB的坡角α=45°,坡长AB=10米,背水坡CD的坡度i=1:,则背水坡的坡长CD为( )米.A.20B.20C.10D.20【解答】解:由题意得:四边形AEFD是矩形,∴DF=AE,∵迎水坡AB的坡角α=45°,坡长AB=10米,∴DF=AE=10×sin45°=10(米),∵背水坡CD的坡度i=1:,∴tan C=i===,∴∠C=30°,∴CD=2DF=2AE=20(米),故选:A.12.为了学生的安全,某校决定把一段如图所示的步梯路段进行改造.已知四边形ABCD为矩形,DE =10m,其坡度为i1=1:,将步梯DE改造为斜坡AF,其坡度为i2=1:4,求斜坡AF的长度是 20.62 米.(结果精确到0.01m,参考数据:≈1.732,≈4.123)【解答】解:∵DE的坡度为i1=1:,∴tan∠DEC==,∴∠DEC=30°,∴DC=DE=5(m),∵四边形ABCD为矩形,∴AB=CD=5m,∵斜坡AF的坡度为i2=1:4,AB=5m,∴BF=4AB=20(m),在Rt△ABF中,AF==≈20.62(m),∴斜坡AF的长度约为20.62米,故答案为:20.62.13.某校有一露天舞台,纵断面如图所示,AC垂直于地面,AB表示楼梯,AE为舞台面,楼梯的坡角∠ABC=45°,坡长AB=2m,为保障安全,学校决定对该楼梯进行改造,降低坡度,拟修新楼梯AD,使∠ADC=30°.(1)求舞台的高AC(结果保留根号);(2)求DB的长度(结果保留根号).【解答】解:(1)在Rt△ABC中,AB=2m,∠ABC=45°,∴AC=BC=AB•sin45°=2×=(m),答:舞台的高AC为m;(2)在Rt△ADC中,∠ADC=30°,则CD===,∴BD=CD﹣BC=(﹣)m,答:DB的长度为(﹣)m.14.某居民楼MN后有一个坡度为i=1:2.4的小山坡,小区物业准备在小山坡上加装一广告牌PQ (如图所示),已知QA=5.2米,水平地面上居民楼MN距坡底A点的距离AN=1.2米.当太阳光线与水平线成53°角时,测得广告牌PQ落在居民楼上的影子EN长为3米,求广告牌PQ的高.(参考数据:sin53°≈,cos53°≈,tan53°≈)【解答】解:过点E作EF⊥PQ于点F,延长PQ交BA于点G,则QG⊥BA,∴设QG=x米,∵山坡的坡度为i=1:2.4,∴AG=2.4x米,由勾股定理得:x2+(2.4x)2=5.22,解得:x=2,则QG=2米,AG=2.4x=4.8米,∴EF=NG=4.8+1.2=6(m),在Rt△PEF中,∠PEF=53°,EF=6m,则PF=EF•tan∠PEF=6×tan53°≈6×=8(m),∵FQ=EN﹣QG=3﹣2=1(m),∴PQ=8+1=9(m).答:信号塔PQ的高约为9m.三.解直角三角形的应用−仰角俯角问题(共8小题)15.若从楼顶A点测得点C的俯角为31°,测得点D的俯角为42°,则∠ADC的度数为( )A.31°B.42°C.48°D.59°【解答】解:由题意得:∠ADB=42°,∠BDC=90°,∴∠ADC=∠BDC﹣∠ADB=90°﹣42°=48°,故选:C.16.如图,某建筑物的顶部有一块宣传牌CD,小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°,已知斜坡AB的坡角为30°,AB=10米,AE=15米,则宣传牌CD的高度是( )A.B.C.D.【解答】解:过B作BF⊥AE,交EA的延长线于F,作BG⊥DE于G.在Rt△ABF中,∠BAF=30°,AB=10米,∴BF=AB=5(米),AF=BF=5(米).∴BG=AF+AE=(5+15)(米),在Rt△BGC中,∠CBG=45°,∴△BGC是等腰直角三角形,∴CG=BG=(5+15)(米),在Rt△ADE中,∠DAE=60°,AE=15米,∴DE=AE=15(米),∴CD=CG+GE﹣DE=5+15+5﹣15=(20﹣10)(米),即宣传牌CD的高度是(20﹣10)米,故选:A.17.某通信公司准备逐步在歌乐山上建设5G基站.如图,某处斜坡CB的坡度(或坡比)为i=1:2.4,通讯塔AB垂直于水平地面,在C处测得塔顶A的仰角为45°,在D处测得塔顶A的仰角为53°,斜坡路段CD长26米,则通讯塔AB的高度为( )(参考数据:,,)A.米B.米C.56米D.66米【解答】如图,延长AB与水平线交于F,过D作DM⊥CF,M为垂足,过D作DE⊥AF,E为垂足,连接AC,AD,∵斜坡CB的坡度为i=1:2.4,∴==,设DM=5k米,则CM=12k米,在Rt△CDM中,CD=26米,由勾股定理得,CM2+DM2=CD2,即(5k)2+(12k)2=262,解得k=2,∴DM=10(米),CM=24(米),∵斜坡CB的坡度为i=1:2.4,设DE=12a米,则BE=5a米,∵∠ACF=45°,∴AF=CF=CM+MF=(24+12a)米,∴AE=AF﹣EF=24+12a﹣10=(14+12a)米,在Rt△ADE中,DE=12a米,AE=(14+12a)米,∵tan∠ADE==tan53°≈,∴=,解得a=,∴DE=12a=42(米),AE=14+12a=56(米),BE=5a=(米),∴AB=AE﹣BE=56﹣=(米),答:基站塔AB的高为米.故选:B.18.某中学九年级数学兴趣小组想测量建筑物AB的高度.他们在C处仰望建筑物顶端,测得仰角为48°,再往建筑物的方向前进6米到达D处,测得仰角为64°,则建筑物的高度为 14.7 米.(测角器的高度忽略不计,结果精确到0.1米)(参考数据:sin48°≈,tan48°≈,sin64°≈,tan64°≈2)【解答】解:根据题意,得∠ADB=64°,∠ACB=48°在Rt△ADB中,tan64°=,则BD=≈AB,在Rt△ACB中,tan48°=,则CB=≈AB,∴CD=BC﹣BD,即6=AB﹣AB,解得:AB=≈14.7(米),∴建筑物的高度约为14.7米,故答案为:14.7.19.如图,某校数学兴趣小组要测量楼房DC的高度.在点A处测得楼顶D的仰角为30°,再往楼房的方向前进30m至B处,测得楼顶D的仰角为45°,则楼房DC的高度为 (15+15) m.【解答】解:设BC的长为x米.在Rt△CBD中,∠D=90°,∠CBD=45°,∴CD=BC=x米,在Rt△CAD中,∠ACD=90°,∠DAC=30°,∴tan∠CAD===,解得:x=15+15,答:楼房DC的高度为(15+15)米,故答案为:(15+15).20.如图,小马同学在数学综合实践活动中,利用所学的数学知识对山坡一棵树的高度进行测量,先测得小马同学离底部C的距离BC为10m,此时测得对树的顶端D的仰角为55°,已知山坡与水平线的夹角为20°,小马同学的观测点A距地面1.6m,求树木CD的高度(精确到0.1m).(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43,sin20°≈0.34,cos20°≈0.94,tan20°≈0.36).【解答】解:延长DC交BF于F,过A作AH⊥DC于H,则HF=AB=1.6m,AH=BF,在Rt△ACF中,∵∠CBF=20°,BC=10m,∴CF=BC•sin20°≈10×0.34=3.4(m),BF=BC•cos20°≈10×0.94=9.4(m),∴AH=BF=9.4m,在Rt△ADH中,∵∠DAH=55°,∴DH=AH•tan55°≈9.4×1.43≈13.4(m),∴DC=DH+HF﹣CF=13.4+1.6﹣3.4=11.6(m),答:树木CD的高度约为11.6m.21.如图,某中学数学活动小组在学习了“利用三角函数测高”后,选定测量小河对岸一幢建筑物BC 的高度,他们先在斜坡上的D处,测得建筑物顶端B的仰角为30°.且D离地面的高度DE=5m.坡底EA=30m,然后在A处测得建筑物顶端B的仰角是60°,点E,A,C在同一水平线上,求建筑物BC的高.(结果用含有根号的式子表示)【解答】解:过点D作DH⊥BC于点H,如图所示:则四边形DHCE是矩形,DH=EC,DE=HC=5,设建筑物BC的高度为xm,则BH=(x﹣5)m,在Rt△DHB中,∠BDH=30°,∴DH=(x﹣5),AC=EC﹣EA=(x﹣5)﹣30,在Rt△ACB中,∠BAC=60°,tan∠BAC=,∴=解得:x=,答:建筑物BC的高为m.四.解直角三角形的应用−仰角俯角问题(共1小题)22.如图,某人在D处测得山顶C的仰角为37°,向前走100米来到山脚A处,测得山坡AC的坡度为i=1:0.5,求山的高度(不计测角仪的高度,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75).【解答】解:设山高BC=x,则AB=x,由tan37°==0.75,得:=0.75,解得x=120,经检验,x=120是原方程的根.答:山的高度是120米.。
河北省中考系统复习:第19讲锐角三角函数(8年真题训练)

第19讲 锐角三角函数命题点 解直角三角形1.(·承德模拟)如图,在Rt △ABC 中,∠C =90°,BC =8,tanB =12,点D 在BC 上,且BD =AD ,求AC 的长和cos∠ADC 的值.解:∵在Rt △ABC 中,BC =8,tanB =AC BC =12,∴AC =BC ·tanB =4.设AD =x ,则BD =x ,CD =8-x ,在Rt △ADC 中,(8-x)2+42=x 2,解得x =5. ∴AD =5,CD =8-5=3,∴cos ∠ADC =DC AD =35.2.(·河北模拟)如图,AD 是△ABC 的中线,tanB =13,cosC =22,AC = 2.求:(1)BC 的长;(2)sin ∠ADC 的值.解:(1)过点A 作AE ⊥BC 于点E. ∵cosC =22,∴∠C =45°. 在Rt △ACE 中,CE =AC ·cosC =1, ∴AE =CE =1.在Rt △ABE 中,tanB =13,即AE BE =13,∴BE =3AE =3.∴BC =BE +CE =4.(2)∵AD 是△ABC 的中线,∴CD =12BC =2.∴DE =CD -CE =1.∵AE ⊥BC ,DE =AE ,∴∠ADC =45°. ∴sin ∠ADC =22.重难点1 解直角三角形(·河北模拟)已知,在△ABC 中,∠ACB =90°,tanB =43,AB =5,D 在AB 上.(1)求BC 的长;(2)如图1,若∠CDB =∠B ,求sin ∠DCB 的值;(3)如图2,过点B 作BE ⊥CD 所在的直线,垂足为E ,BE 的延长线交直线AC 于点F. ①当tan ∠BCD =2时,求S △CBF ; ②当AF =54时,求线段AD 的长.【思路点拨】 (1)由正切的定义可知△ABC 是一个勾3,股4,弦5的直角三角形;(2)可通过过点D 作DE ⊥BC ,利用tanB 找到DE ,BE 的数量关系,再解直角△DCE ,求得sin ∠DCB 的值;(3)因为∠BCD =∠CFB :①利用tan ∠CFB 的值,求CF ,进而求S △CBF ;②可通过过点A 作BC 的平行线交CD 延长线于点G ,先求AG ,再利用相似求AD 的长. 【自主解答】 解:(1)在△ABC 中,∠ACB =90°,tanB =43,∴tanB =AC BC =43,∴AC =43BC.∵AC 2+BC 2=AB 2,∴(43BC)2+BC 2=52,∴BC =3.(2)过点D 作DE ⊥BC ,则tanB =43=DEBE ,∴BE =34DE ,∴CE =BC -BE =3-34DE.∵∠CDB =∠B ,∴CD =CB =3.∵CD 2=CE 2+DE 2,∴32=DE 2+(3-34DE)2,解得DE =7225.∴sin ∠DCB =DE DC =2425.(3)①∵∠BCD +∠FCE =90°,∠CFB +∠FCE =90°, ∴∠BCD =∠CFB.∴tan ∠BCD =tan ∠CFB =2.∵tan ∠CFB =BC CF =2,BC =3,∴CF =32.∴S △CBF =94.②当点F 在线段AC 上时,如图3,过点A 作AG ∥BC 交CD 延长线于点G , ∵tan ∠ACG =tan ∠CBF =AG AC =CF BC =1112,AC =4,∴AG =113.∵AG ∥BC ,∴AG BC =ADBD .∴119=AD 5-AD ,AD =114.图3 图4当点F 在线段CA 的延长线上,如图4,过点A 作AG ∥BC 交CD 延长线于点G. ∵tan ∠ACG =tan ∠CBF =AG AC =CF BC =74,AC =4,∴AG =7.∵AG ∥BC ,∴AG BC =AD BD .∴73=AD 5-AD .∴AD =72.方法指导1.解直角三角形,需知除直角以外的两个条件(一边和一角或两边),可求得其余的边或角.2.在求解时,一般选取既含未知边(角)又含有已知边(或角)的直角三角形,通过锐角三角函数的定义或勾股定理,建构已知或未知之间的桥梁;从而实现求解.3.若所求的线段(或角)不能直接求解,可以通过作出点到直线的距离或三角形高线,进而转化成直角三角形求解. 4.解直角三角形和相似三角形的性质,是几何求解中的重要工具.K,【变式训练1】 如图是由一个角为60°且边长为1的菱形组成的网格,每个菱形的顶点称为格点,点A ,B ,C 都在格点上,则tan ∠BAC =233.【变式训练2】(·上海)如图,已知在△ABC 中,AB =BC =5,tan ∠ABC =34.(1)求边AC 的长;(2)设边BC 的垂直平分线与边AB 的交点为D ,求ADDB的值.解:(1)过点A 作AE ⊥BC ,在Rt △ABE 中, tan ∠ABC =AE BE =34,AB =5,∴AE =3,BE =4.∴CE =BC -BE =5-4=1.在Rt △AEC 中,根据勾股定理,得AC =32+12=10.(2)如图,∵DF 垂直平分BC ,∴BD =CD ,BF =CF =52.∵tan ∠DBF =DF BF =34,∴DF =158.在Rt △BFD 中,根据勾股定理,得BD =(52)2+(158)2=258, ∴AD =5-258=158,则AD DB =35. 重难点2 解直角三角形的应用(1)如图1,为了游客的安全,某景点将原坡角为60°的斜坡AB 改为坡度为1∶3的斜坡AC ,已知AB =100米,BC 在同一水平线上,求改造后斜坡的坡脚向前移动距离BC 的长;(2)(·郴州)小亮在某桥附近试飞无人机,如图2,为了测量无人机飞行的高度AD ,小亮通过操控器指令无人机测得桥头B ,C 的俯角分别为∠EAB =60°,∠EAC =30°,且D ,B ,C 在同一水平线上.已知桥BC =30米,求无人机飞行的高度AD ;(精确到0.01米,参考数据:2≈1.414,3≈1.732)(3)(·湘西)如图3,某市郊外景区内一条笔直的公路l 经过A ,B 两个景点,景区管委会又开发了风景优美的景点C.经测量,C 位于A 的北偏东60°的方向上,C 位于B 的北偏东30°的方向上,且AB =10 km.①求景点B 与C 的距离;②为了方便游客到景点C 游玩,景区管委会准备由景点C 向公路l 修一条距离最短的公路,不考虑其他因素,求出这条最短公路的长.(结果保留根号)【思路点拨】这三个问题均可以通过过点A 作直线BC 的垂线,垂足为D ,再利用解直角三角形ABD 和直角三角形ACD 来解决.【自主解答】解:(1)过点A 作AD ⊥BC 于点D ,在Rt △ABD 中,∠ABD =60°,∴BD =AB ·cos ∠ABD =100×cos60°=50(米),AD =AB ·sin ∠ABD =503米. ∵AC 的坡度为1∶3, ∴AD ∶CD =1∶ 3.∴CD =150,BC =CD -BD =150-50=100(米).∴改造后斜坡的坡脚向前移动距离BC 的长是100 m. (2)由题意,得∠EAC =30°,∠EAB =60°,∵AE ∥BC ,∴∠EAC =∠ACB =30°,∠EAB =∠ABD =60°. ∵∠ABD =∠ACB +∠BAC ,∴∠BAC =∠ACB =30°. ∴AB =BC =30.在Rt △ABD 中,∴AD =AB ·sin ∠ABD =153≈25.98(米). (3)①由题意,得∠CAB =30°,∠ABC =90°+30°=120°, ∴∠C =180°-∠CAB -∠ABC =30°.∴∠CAB =∠C =30°. ∴BC =AB =10 km ,即景点B ,C 的距离为10 km.②过点C 作CD ⊥AB 于点D ,∵BC =10 km ,C 位于B 的北偏东30°的方向上,∴∠CBD =60°,在Rt △CBD 中,CD =32BC =5 3 km. 【变式训练3】(·常州)京杭大运河是世界文化遗产.综合实践活动小组为了测出某段运河的河宽(岸沿是平行的),如图,在岸边分别选定了点A ,B 和点C ,D ,先用卷尺量得AB =160 m ,CD =40 m ,再用测角仪测得∠CAB =30°,∠DBA =60°,求该段运河的河宽(即CH 的长).解:过点D作DE⊥AB于点E,可得四边形CHED为矩形,∴HE=CD=40 m.设CH=DE=x m,在Rt△BDE中,∠DBA=60°,∴BE=33x.在Rt△ACH中,∠BAC=30°,∴AH=3x.由AH+HE+EB=AB=160 m,得3x+40+33x=160,解得x=303,即CH=30 3 m.答:该段运河的河宽为30 3 m.方法指导1.对于解直角三角形的实际应用题,要灵活运用转化思想,通常是根据以下方法和步骤解决:(1)有图的要先将题干中的已知量在图中表示出来,找到与已知量和未知量相关联的三角形,画出平面几何图形,弄清已知条件中各量之间的关系;(2)若三角形是直角三角形,根据边角关系进行计算;若三角形不是直角三角形,可通过添加辅助线构造直角三角形来解决,其中作某边上的高是常用的辅助线.总的来说,解直角三角形的实际应用问题,关键是要根据实际情况建立数学模型,正确画出图形或作出辅助线并找准直角三角形.,模型建立)本题的三个题均可以抽象出如下图形:另外实际问题还可以抽象的几何图形为:1.(·孝感)如图,在Rt△ABC中,∠C=90°,AB=10,AC=8,则sinA等于(A)A.35B.45C.34D.432.(·保定模拟)在△ABC中,∠A,∠B均为锐角,且(tanB-3)(2sinA-3)=0,则△ABC一定是(D) A.等腰三角形B.等边三角形C.直角三角形D.有一个角是60°的三角形3.(·唐山丰南区模拟)在△ABC 中,AB =AC =13,BC =24,则tanB 等于(B)A.513B.512C.1213 D.1254.(·贵阳)如图,A ,B ,C 是小正方形的顶点,且每个小正方形的边长为1,则tan ∠BAC 的值为(B)A.12B .1C.33D. 35.(·河北模拟)如图,△ABC 在边长为1个单位长度的方格纸中,它的顶点在小正方形的顶点位置.如果△ABC 的面积为10,且sinA =55,那么点C 的位置可以在(D) A .点C 1处B .点C 2处C .点C 3处D .点C 4处6.如图是一辆小汽车与墙平行停放的平面示意图,汽车靠墙一侧OB 与墙MN 平行且距离为0.8米,一辆小汽车车门宽AO 为1.2米,当车门打开角度∠AOB 为40°时,车门是否会碰到墙?否;(填“是”或“否”)请简述你的理由点A 到OB 的距离小于OB 与墙MN 平行的距离.(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)7.【分类讨论思想】(·无锡)已知在△ABC 中,AB =10,AC =27,∠B =30°,则△ABC 的面积等于153或10 3.8.(·贵阳)如图1,在Rt △ABC 中,以下是小亮探究a sinA 与bsinB之间关系的方法:∵sinA =a c ,sinB =b c ,∴c =a sinA ,c =b sinB .∴a sinA =bsinB ,根据你掌握的三角函数知识.在图2的锐角△ABC中,探究a sinA ,b sinB ,csinC之间的关系,并写出探究过程.解:a sinA =b sinB =c sinC.理由:过点A 作AD ⊥BC ,过点B 作BE ⊥AC , 在Rt △ABD 中,sinB =ADc ,即AD =c ·sinB ,在Rt △ADC 中,sinC =ADb ,即AD =b ·sinC ,∴c ·sinB =b ·sinC ,即b sinB =csinC .同理可得a sinA =csinC ,则a sinA =b sinB =c sinC.9.(·衡阳)一名徒步爱好者来衡阳旅行,他从宾馆C 出发,沿北偏东30°的方向行走2 000米到达石鼓书院A 处,参观后又从A 处沿正南方向行走一段距离,到达位于宾馆南偏东45°方向的雁峰公园B 处,如图所示.(1)求这名徒步爱好者从石鼓书院走到雁峰公园的途中与宾馆之间的最短距离;(2)若这名徒步爱好者以100米/分的速度从雁峰公园返回宾馆,那么他在15分钟内能否到达宾馆?解:(1)过点C 作CP ⊥AB 于点P ,由题意,得∠A =30°,AP =2 000米, 则CP =12AC =1 000米.(2)∵在Rt △PBC 中,PC =1 000,∠PBC =∠BCP =45°, ∴BC =2PC =1 0002米.∵这名徒步爱好者以100米/分的速度从雁峰公园返回宾馆, ∴他到达宾馆需要的时间为1 0002100=102<15. ∴他在15分钟内能到达宾馆.10.如图,在四边形ABCD 中,AB =8,BC =1,∠DAB =30°,∠ABC =60°,则四边形ABCD 的面积为53,AD 的长是23.提示:延长AD ,BC 相交于点E ,可得△ABE 为直角三角形.11.(·眉山)如图,在边长为1的小正方形网格中,点A ,B ,C ,D 都在这些小正方形的顶点上,AB ,CD 相交于点O ,则tan ∠AOD =2.提示:连接BE ,构造Rt △BOF ,根据△AOC ∽△BOK 可得OK 与CK 的数量关系,求出OF 与BF 的数量关系即可.12.如图,已知,在△ABC 中,AB =AC =25,sinB =255,D 为边BC 的中点,E 为边BC 的延长线上一点,且CE=BC.连接AE ,F 为线段AE 的中点.求:(1)线段DE 的长; (2)∠CAE 的正切值.解:(1)连接AD.∵AB =AC ,D 为BC 的中点, ∴AD ⊥BC , 即∠ADB =90°.∵AB =AC =25,sinB =255,∴AD AB =255.∴AD =4. 由勾股定理,得BD =2,∴DC =BD =2,BC =4. ∵CE =BC ,∴CE =4. ∴DE =DC +CE =2+4=6.(2)过点C 作CM ⊥AE 于点M, 则∠CMA =∠CME =90°. 在Rt △ADE 中,由勾股定理,得 AE =AD 2+DE 2=213.∵CM 2=AC 2-AM 2=CE 2-EM 2, ∴(25)2-AM 2=42-(213-AM)2, 解得AM =141313.∴CM =AC 2-AM 2=81313.∴tan ∠CAE =CM AM =47.13.(·河北模拟)阅读下面的材料:嘉嘉在数学课外小组活动中遇到这样一个问题:如果α,β都为锐角,且tan α=12,tan β=13,求α+β的度数.淇淇是这样解决问题的:如图1,把α,β放在正方形网格中,使得∠ABD =α,∠CBE =β,且BA ,BC 在直线BD 的两侧,连接AC ,可证得△ABC 是等腰直角三角形,因此可求得α+β=∠ABC =45°.请参考小敏思考问题的方法解决问题:如果α,β都为锐角,当tan α=4,tan β=35时,在图2的正方形网格中,利用已作出的锐角α,画出∠MON=α-β,由此可得α-β=45°.解:如图.。
锐角三角函数应用题训练全

锐角三角函数应用题训练(全)锐角三角函数应用题训练1.如图,某数学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C 的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上)。
请你根据他们测量数据计算这棵树CD的高度(结果精确到0.1m)。
(参考数据:2≈1.414,3≈1.732)2.如图,一艘核潜艇在海面DF下600米A点处测得俯角为30°正前方的海底C 点处有黑匣子,继续在同一深度直线航行1464米到B点处测得正前方C点处的俯角为45°.求海底C点处距离海面DF的深度(结果精确到个位,参考数据:2≈1.414,3≈1.732,5≈2.236).3.如图,在电线杆CD上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆6米的B处安置高为1.5米的测角仪AB,在A处测得电线杆上C处的仰角为30°,求拉线CE的长(结果保留小数点后一位,参考数据:2 1.41,3 1.73≈≈).4.如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A点测得建筑物CD的顶点C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.(1)求两建筑物底部之间水平距离BD的长度;(2)求建筑物CD的高度(结果保留根号).EA CDB5.钓鱼岛自古以来就是我国的神圣领土,为维护国家主权和海洋权利,我国海监和渔政部门对钓鱼岛 海域实现了常态化巡航管理.如图,某日在我国钓鱼岛附近海域有两艘自西向东航行的海监船A 、B ,B 船在A 船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A 的东北方向,B 的北偏东15°方向有一我国渔政执法船C ,求此时船C 与船B 的距离是多少.(结果保留根号)6.一测量爱好者,在海边测量位于正东方向的小岛高度AC ,如图所示,他先在点B 测得山顶点A 的仰角为30°,然后向正东方向前行62米,到达D 点,在测得山顶点A 的仰角为60°(B 、C 、D 三点在同一水平面上,且测量仪的高度忽略不计).求小岛高度AC (结果精确的1米,参考数值:2 1.4≈,3 1.7≈)7.如图,我省在修建泛亚铁路时遇到一座山,要从A 地向B 地修一条隧道(A ,B 在同一水平面上),为了测量A ,B 两地之间的距离,某工程师乘坐热气球从M 地出发垂直上升150 米到达C 处,在C 处观察A 地的俯角为60°,然后保持同一高度向前平移200米到达D 处,在D 处观察B 地的俯角为45°,则A 、B 两地之间的距离为多少米?(参考数据:3 1.73;结果保留整数)60°N 45°D C8.甲、乙两条轮船同时从港口A出发,甲轮船以每小时30海里的速度沿着北偏东60°的方向航行,乙轮船以每小时15海里的速度沿着正东方向行进,1小时后,甲船接到命令要与乙船会合,于是甲船改变了行进的速度,沿着东南方向航行,结果在小岛C处与乙船相遇.假设乙船的速度和航向保持不变,求:(1)港口A与小岛C之间的距离;(2)甲轮船后来的速度.9.如图,游客从某旅游景区的景点A处下山至C处有两种路径,一中是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客同时从A处下山,甲沿AC匀速步行,速度为45m/min.乙开始从A乘缆车到B,在B处停留5min后,再从B匀速步行到C,两人同时到达.已知缆车匀速直线运动的速度为180m/min,山路AC长为2430m,经测量,∠CAB=45°,∠CBA=105°.(参考数据: 1.4,1.7)(1)求索道AB的长;(2)为乙的步行速度.10.某中学九年级数学兴趣小组为测量校内旗杆高度,如图,在C点测得旗杆顶端A的仰角为30°,向前走了6米到达D点,在D点测得旗杆顶端A的仰角为60°(测角器的高度不计).(1)AD 米;(2)求旗杆AB的高度(结果保留1位小数,3 1.73≈).11.某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘刚在南海巡航的渔政船前往救援.当飞机到达距离海面3000米的高空C处,测得A处渔政船的俯角为60°,测得B处发生险情渔船的俯角为30°,请问:此时渔政船和渔船相距多远?(结果保留根号)12.如图,小明在M处用高1米(DM=1米)的测角仪测得旗杆AB的顶端B的仰角为30°,再向旗杆方向前进10米到F处,又测得旗杆顶端B的仰角为60°,请求出旗杆AB的高度(取≈1.73,结果保留整数)13.如图,有小岛A和小岛B,轮船以45km/h的速度由C向东航行,在C处测得A的方位角为北偏东60°,测得B的方位角为南偏东45°,轮船航行2小时后到达小岛B处,在B处测得小岛A在小岛B的正北方向.求小岛A与小岛B之间的距离(结果保留整数,参考数据:≈1.41,≈2.45)14.一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里每小时的速度前往救援,求海警船到大事故船C处所需的大约时间.(温馨提示:sin53°≈0.8,cos53°≈0.6)15.根据道路管理规定,在羲皇大道秦州至麦积段上行驶的车辆,限速60千米/时.已知测速站点M距羲皇大道l(直线)的距离MN为30米(如图所示).现有一辆汽车由秦州向麦积方向匀速行驶,测得此车从A点行驶到B点所用时间为6秒,∠AMN=60°,∠BMN=45°.(1)计算AB的长度.(2)通过计算判断此车是否超速.16.如图,在东西方向的海岸线l上有一长为1千米的码头MN,在码头西端M的正西方向30 千米处有一观察站O.某时刻测得一艘匀速直线航行的轮船位于O 的北偏西30°方向,且与O相距千米的A处;经过40分钟,又测得该轮船位于O的正北方向,且与O相距20千米的B处.(1)求该轮船航行的速度;(2)如果该轮船不改变航向继续航行,那么轮船能否正好行至码头MN靠岸?请说明理由.17.如图,我国的一艘海监船在钓鱼岛A 附近沿正东方向航行,船在B 点时测得钓鱼岛A 在船的北偏东60°方向,船以50海里/时的速度继续航行2小时后到达C 点,此时钓鱼岛A 在船的北偏东30°方向.请问船继续航行多少海里与钓鱼岛A 的距离最近?18.如图,A ,B 两地之间有一座山,汽车原来从A 地到B 地须经C 地沿折线A –C -B 行驶,全长68 km .现开通隧道后,汽车直接沿直线AB 行驶.已知∠A =30°,∠B =45°,则隧道开通后,汽车从A 地到B 地比原来少走多少千米?(结果精确到0.1 km )(参考数据:4.12≈,7.13≈)19.水利部门为加强防汛工作,决定对某水库大坝进行加固,大坝的横截面是梯形ABCD ,如图所示,已知迎水坡面AB 的长为16米,∠B =60°,背水坡面CD 的长为163米,加固后大坝的横截面为梯形ABED ,CE 的长为8米.(1)已知需加固的大坝长为150米,求需要填土石方多少立方米?(2)求加固后的大坝背水坡面DE 的坡度.20.如图,一段河坝的横截面为梯形ABCD ,试根据图中数据,求出坝底宽AD.(i =CE ∶ED ,单位:m )ABC30° 45°本卷由【在线组卷网 】自动生成,请仔细校对后使用,答案仅供参考。
锐角三角函数应用题专题

1、(09年湖北仙桃)如图所示,小华同学在距离某建筑物6米的点A 处测得广告牌B 点、C 点的仰角分别为52°和35°,则广告牌的高度BC 为_____________米(精确到0.1米).(sin35°≈0.57,cos35°≈0.82,tan35°≈0.70;sin52°≈0.79,cos52°≈0.62,tan52°≈1.28)2、(09年湖南怀化)如图,小明从A 地沿北偏东 30方向走1003m 到B 地,再从B 地向正南方向走200m 到C 地,此时小明离A 地 m .3、(09年山东潍坊)如图,小明要测量河内小岛B 到河边公路l 的距离,在A 点测得30BAD ∠=°,在C 点测得60BCD ∠=°,又测得50AC =米,则小岛B 到公路l 的距离为( )米. A .25B .253C .10033D .25253+4、(09年山东济南)九年级三班小亮同学学习了“测量物体高度”一节课后,他为了测得右图所放风筝的高度,进行了如下操作: (1)在放风筝的点A 处安置测倾器,测得风筝C 的仰角60CBD =︒∠;(2)根据手中剩余线的长度出风筝线BC 的长度为70米; (3)量出测倾器的高度 1.5AB =米.根据测量数据,计算出风筝的高度CE 约为 米.(精确到0.1米,3 1.73≈)5、(09年广东深圳、山东东营)如图,斜坡AC 的坡度(坡比)为1:3,AC =10米.坡顶有一旗杆BC ,旗杆顶端B 点与A 点有一条彩带AB 相连,AB =14米.试求旗杆BC 的高度.6、(09年广东湛江)如图,某军港有一雷达站P ,军舰M 停泊在雷达站P 的南偏东60°方向36海里处,另一艘军舰N 位于军舰M 的正西方向,与雷达站P 相距182海里.求: (1)军舰N 在雷达站P 的什么方向?(2)两军舰M N 、的距离.(结果保留根号)第6题图NMP北 A BC D 6米52° 35°(第1题图)ADB EC60°(第4题图)第2题图BC AD l第3题图ABC D第5题图7、(09年湖南常德)如图,某人在D 处测得山顶C 的仰角为30o ,向前走200米来到山脚A 处,测得山坡AC 的坡度为i=1∶0.5,求山的高度(不计测角仪的高度,3 1.73≈,结果保留整数).8、(09年湖南娄底)在学习实践科学发展观的活动中,某单位在如图8所示的办公楼迎街的墙面上垂挂一长为30米的宣传条幅AE ,张明同学站在离办公楼的地面C 处测得条幅顶端A 的仰角为50°,测得条幅底端E 的仰角为30°. 问张明同学是在离该单位办公楼水平距离多远的地方进行测量?(精确到整数米)(参考数据:sin50°≈0.77,cos50°≈0.64, tan50°≈1.20,sin30°=0.50,cos30°≈0.87,tan30°≈0.58)9、(09湖南湘西)如图,在离水面高度为5米的岸上有人用绳子拉船靠岸,开始时绳子与水面的夹角为30°,此人以每秒0.5米收绳.问:(1) 未开始收绳子的时候,图中绳子BC 的长度是多少米? (2) 收绳8秒后船向岸边移动了多少米?(结果保留根号)11、(09年湖北黄石)如图9,山顶建有一座铁塔,塔高CD=30m ,某人在点A 处测得塔底C 的仰角为20°,塔顶D 的仰角为23°,求此人距CD 的水平距离AB 。
专题01 锐角三角函数和特殊角的三角函数(六大类型)(题型专练)(解析版)

专题01 锐角三角函数和特殊角的三角函数(六大类型)【题型1锐角三角函数的概念】【题型2 锐角三角函数的增减性】【题型3特殊角三角函数值】【题型4 同角三角函数的关系】【题型5 互余两角三角函数的关系】【题型6 三角函数的计算】【题型1锐角三角函数的概念】1.(2022秋•道县期末)在Rt△ABC中,∠C=90°,AC=5,BC=12,则tan A 的值为( )A.B.C.D.【答案】B【解答】解:在Rt△ABC中,∠C=90°,AC=5,BC=12,∴tan A=.故选:B.2.(2023•南岗区校级开学)在Rt△ABC中,∠C=90°,AB=2BC,则tan B 等于( )A.B.C.D.【答案】D【解答】解:∵∠C=90°,AB=2BC,∴AC===BC,∴tan B===.故选:D.3.(2022秋•路北区校级期末)在Rt△ABC中,∠C=90°,AB=10,AC=8,则cos B的值等于( )A.B.C.D.【答案】A【解答】解:∵∠C=90°,AB=10,AC=8,∴BC==6,∴cos B===.故选:A.4.(2023•新华区校级模拟)在Rt△ABC中,∠C=90°,若c为斜边,a、b 为直角边,且a=5,b=12,则sin A的值为( )A.B.C.D.【答案】B【解答】解:在Rt△ABC中,c===13,sin A=.故选:B.5.(2023•陈仓区模拟)如图,在Rt△ABC中,∠A=90°,AB=8,BC=10,则sin B的值是( )A.B.C.D.【答案】C【解答】解:∵在Rt△ABC中,∠A=90°,AB=8,BC=10,∴AC=,∴sin B===,故选:C .6.(2023•虹口区一模)如图,在Rt △ABC 中,∠C =90°,AC =1,BC =2,那么cos A 的值为( )A .B .2C .D .【答案】C【解答】解:在Rt △ABC 中,∠C =90°,AC =1,BC =2,由勾股定理,得AB ==.由锐角的余弦,得cos A ===.故选:C .7.(2023•金山区一模)在Rt △ABC 中,∠ACB =90°,AC =4,BC =3,则∠B 的正切值等于( )A .B .C .D .【答案】A【解答】解:∵∠ACB =90°,AC =4,BC =3,∴tan B ==.故选:A .8.(2023•长宁区一模)在△ABC 中,∠C =90°,已知AC =3,AB =5,那么∠A 的余弦值为( )A .B .C .D .【答案】C【解答】解:在Rt △ABC 中,AC =3,AB =5,故选:C.【题型2 锐角三角函数的增减性】9.(2023•未央区校级三模)若tan A=2,则∠A的度数估计在( )A.在0°和30°之间B.在30°和45°之间C.在45°和60°之间D.在60°和90°之间【答案】D【解答】解:∵tan45°=1,tan60°=,而tan A=2,∴tan A>tan60°,∴60°<∠A<90°.故选:D.10.(2022秋•惠山区校级期中)已知∠A为锐角,且tan A=3,则∠A的取值范围是( )A.0°<∠A<30°B.30°<∠A<45°C.45°<∠A<60°D.60°<∠A<90°【答案】D【解答】解:tan30°=,tan45°=1,tan60°=,∵tan A=3,∴3,又∵一个锐角的正切值随锐角度数的增大而增大,∴60°<∠A<90°,故选:D.11.(2021秋•淮北月考)已知角α为△ABC的内角,且cosα=,则α的取值范围是( )A.0°<α<30°B.30°<α<45°C.45°<α<60°D.60°<α<90°【答案】C【解答】解:∵cos60°=,cos45°=,∴cos60°<cosα<cos45°,∴45°<α<60°,故选:C.【题型3特殊角三角函数值】12.(2022秋•嵊州市期末)已知tan A=,∠A是锐角,则∠A的度数为( )A.30°B.45°C.60°D.90°【答案】A【解答】解:∵,且∠A是锐角,∴∠A=30°,故选:A.13.(2023•河西区模拟)计算2cos30°的结果为( )A.B.1C.D.【答案】C【解答】解:∵cos30°=,∴2cos30°=2×=.故选:C.14.(2023•肃州区三模)sin60°的相反数( )A.B.C.D.【答案】C【解答】解:∵sin60°=,∴sin60°的相反数是﹣.故选:C.15.(2023•高州市一模)在Rt△ABC中,∠C=90°,若cos A=,则∠A的大小是( )A.30°B.45°C.60°D.75°【答案】C【解答】解:∵在Rt△ABC中,∠C=90°,∴∠A为锐角,∵cos A=,∴∠A=60°,故选:C.16.(2023•南开区二模)下列三角函数中,结果为的是( )A.cos30°B.tan30°C.sin60°D.cos60°【答案】D【解答】解:A.cos30°=,不符合题意;B.tan30°=,不符合题意;C.sin60°=,不符合题意;D.cos60°=sin30°=,符合题意.故选:D.17.(2023•河西区一模)cos60°的值等于( )A.B.C.D.【答案】D【解答】解:cos60°=,故选:D.18.(2023•东莞市校级一模)已知∠A为锐角且tan A=,则∠A=( )A.30°B.45°C.60°D.不能确定【答案】C【解答】解:∵∠A为锐角,tan A=,∴∠A=60°.故选:C.19.(2023•迎泽区校级二模)在Rt△ABC中,∠C=90°,BC=1,AC=,那么∠B的度数是( )A.15°B.45°C.30°D.60°【答案】D【解答】解:在Rt△ABC中,∠C=90°,∵tan B===,∴∠B=60°,故选:D.【题型4 同角三角函数的关系】20.(2023•泉港区模拟)已知∠A是锐角△ABC的内角,,则cos A的值是( )A.B.C.D.【答案】C【解答】解:由勾股定理可得sin2A+cos2A=1,∵,∴()2+cos2A=1,∴cos2A=,∴cos A=或cos A=﹣(舍去),故选:C.21.(2022秋•日照期末)若α为锐角,且sinα=,则tanα为( )A.B.C.D.【答案】D【解答】解:由α为锐角,且sinα=,得cosα===,tanα===,故选:D.22.(2022秋•桐柏县期末)已知在Rt△ABC中,∠C=90°.若sin A=,则cos A等于( )A.B.C.D.1【答案】A【解答】解:∵sin2A+cos2A=1,sin A=,∴+cos2A=1,∵∠A为锐角,∴cos A=.故选:A.23.(2022秋•滦州市期中)在Rt△ABC中,∠C=90°,,则cos A=( )A.B.C.D.【答案】C【解答】解:在Rt△ABC中,∠C=90°,=,可设BC=4k,则AB=5k,由勾股定理得,AC==3k,∴cos A==,故选:C.24.(2023•钟楼区校级模拟)在Rt△ABC中,∠C=90°,tan A=,则cos A 等于( )A.B.C.D.【答案】D【解答】解:如图:设BC=5x,∵tan A=,∴AC=12x,AB==13x,∴cos A===.故选:D.25.(2023秋•二道区校级月考)在Rt△ABC中,∠C=90°,若cos A=,则sin A的值为 .【答案】.【解答】解:∵sin2A+cos2A=1,又∵,∴,∴sin A=或(舍去),故答案为:.【题型5 互余两角三角函数的关系】26.(2023秋•肇源县校级月考)已知在Rt△ABC中,∠C=90°,sin A=,则tan B的值为( )A.B.C.D.【答案】D【解答】解:在Rt△ABC中,∵∠C=90°,,∴,设BC=12x,则AB=13x,,∴,故选:D.27.(2023•二道区校级模拟)在Rt△ABC中,AC≠BC,∠C=90°,则下列式子成立的是( )A.sin A=sin B B.sin A=cos B C.tan A=tan B D.cos A=tan B 【答案】B【解答】解:A、sin A=,sin B=,sin A≠sin B,故不符合题意;B、sin A=,cos B=,sin A=cos B,故B符合题意;C、tan A=,tan B=,tan A≠tan B,故不符合题意;D、cos A=,tan B=,则cos A≠tan B,故不符合题意;故选:B.28.(2023秋•东阿县校级月考)在Rt△ABC中,∠C=90°,sin A=,则cos B 的值为( )A.B.C.D.【答案】B【解答】解:∵cos B=,sin A==,∴cos B=.故选:B.29.(2022秋•双牌县期末)已知在Rt△ABC中,∠C=90°,sin A=,则tan B 的值为( )A.B.C.D.【答案】D【解答】解:在Rt△ABC中,∠C=90°,sin A=,∴sin A==,∴设BC=4a,AB=5a,∴AC===3a,∴tan B==,故选:D.30.(2023•新邵县校级一模)已知△ABC中,∠A=90°,tan B=,则sin C= .【答案】.【解答】解:如图.∵∠A=90°,tan B=,∴设AC=x,则AB=2x.∴BC==.∴sin C=.故答案为:.31.(2023•未央区校级二模)在Rt△ABC中,∠C=90°,sin A=,则tan B 的值为 .【答案】.【解答】解:在Rt△ABC中,∠C=90°,sin A=,∴sin A==,∴设BC=3a,AB=5a,∴AC===4a,∴tan B===.故答案为:.【题型6 三角函数的计算】32.(2023春•江岸区校级月考)计算:.【答案】1.【解答】解:==2﹣1=1.33.(2022秋•蜀山区校级期末)计算:sin245°+tan60°•cos30°.【答案】2.【解答】解:原式=()2+×=+=2.34.(2023春•朝阳区校级期末)计算:.【答案】见试题解答内容【解答】解:=2×﹣+1﹣×=﹣+1﹣=.35.(2022秋•武功县期末)计算:sin45°+2cos30°﹣tan60°.【答案】见试题解答内容【解答】解:原式=+2×﹣=+﹣=.36.(2022秋•南通期末)计算:tan45°﹣2sin30°+4cos230°.【答案】3.【解答】解:原式==1﹣1+3=3.37.(2022秋•辛集市期末)计算:sin60°•tan30°+.【答案】1.【解答】解:原式==+=1.。
锐角三角函数练习题及答案
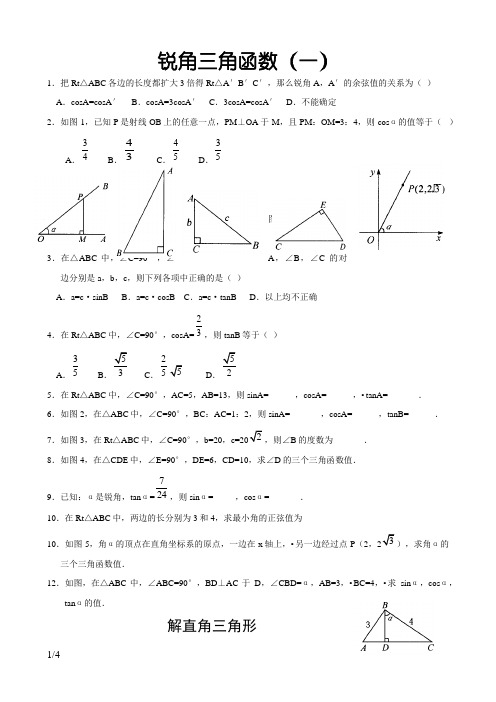
锐角三角函数(一)1.把Rt△ABC各边的长度都扩大3倍得Rt△A′B′C′,那么锐角A,A′的余弦值的关系为()A.cosA=cosA′ B.cosA=3cosA′ C.3cosA=cosA′ D.不能确定2.如图1,已知P是射线OB上的任意一点,PM⊥OA于M,且PM:OM=3:4,则cosα的值等于()A.34 B.43 C.45 D .35图 1 图 2 图3 图4图53.在△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c,则下列各项中正确的是()A.a=c·sinB B.a=c·cosB C.a=c·tanB D.以上均不正确4.在Rt△ABC中,∠C=90°,cosA=23,则tanB等于()A.35 B.53 C.255 D.525.在Rt△ABC中,∠C=90°,AC=5,AB=13,则sinA=______,cosA=______,•tanA=_______.6.如图2,在△ABC中,∠C=90°,BC:AC=1:2,则sinA=_______,cosA=______,tanB=______.7.如图3,在Rt△ABC中,∠C=90°,b=20,c=202,则∠B的度数为_______.8.如图4,在△CDE中,∠E=90°,DE=6,CD=10,求∠D的三个三角函数值.9.已知:α是锐角,tanα=724,则sinα=_____,cosα=_______.10.在Rt△ABC中,两边的长分别为3和4,求最小角的正弦值为10.如图5,角α的顶点在直角坐标系的原点,一边在x轴上,•另一边经过点P(2,23),求角α的三个三角函数值.12.如图,在△ABC中,∠ABC=90°,BD⊥AC于D,∠CBD=α,AB=3,•BC=4,•求sinα,cosα,tanα的值.解直角三角形一、填空题1. 已知cosA=23,且∠B=900-∠A ,则sinB=__________.2. 在Rt △ABC 中,∠C 为直角,cot(900-A)=1.524,则tan(900-B)=_________.3. ∠A 为锐角,已知sinA=135,那么cos (900-A)=___________.4. 已知sinA=21(∠A 为锐角),则∠A=_________,cosA_______,tanA=__________.5. 用不等号连结右面的式子:cos400_______cos200,sin370_______sin420.6. 若cot α=0.3027,cot β=0.3206,则锐角α、β的大小关系是______________. 7. 计算: 2sin450-3tan600=____________. 8. 计算: (sin300+tan450)·cos600=______________.9. 计算: tan450·sin450-4sin300·cos450+6cot600=__________.10. 计算: tan 2300+2sin600-tan450·sin900-tan600+cos 2300=____________. 二、选择题:1. 在Rt △ABC 中,∠C 为直角,AC=4,BC=3,则sinA=( )A . 43;B . 34;C .53;D . 54.2. 在Rt △ABC 中,∠C 为直角,sinA=22,则cosB 的值是( )A .21;B .23;C .1;D .223. 在Rt △ABC 中,∠C 为直角,∠A=300,则sinA+sinB=( )A .1;B .231+;C .221+;D .414. 当锐角A>450时,sinA 的值( )A .小于22; B .大于22; C .小于23; D .大于235. 若∠A 是锐角,且sinA=43,则( )A .00<∠A<300; B .300<∠A<450;C .450<∠A<600;D . 600<∠A<9006. 当∠A 为锐角,且tanA 的值大于33时, ∠A( )A .小于300; B .大于300; C .小于600; D .大于6007. 如图,在Rt △ABC 中,∠C 为直角,CD ⊥AB 于D ,已知AC=3,AB=5,则tan ∠BCD 等于( )A .43;B .34;C .53;D .548. Rt △ABC 中,∠C 为直角,AC=5,BC=12,那么下列∠A 的四个三角函数中正确的是( )A . sinA=135; B .cosA=1312; C . tanA=1213;D . cotA=1259. 已知α为锐角,且21<cos α<22,则α的取值范围是( )A .00<α<300;B .600<α<900;C .450<α<600;D .300<α<450.三、解答题1、 在△ABC 中,∠C 为直角,已知AB=23,BC=3,求∠B 和AC .2、在△ABC 中,∠C 为直角,直角边a=3cm ,b=4cm ,求sinA+sinB+sinC 的值.3、在△ABC 中,∠C 为直角,∠A 、∠B 、∠C 所对的边分别是a 、b 、c ,已知b=3, c=14. 求∠A 的四个三角函数.4、在△ABC 中,∠C 为直角,不查表解下列问题: (1)已知a=5,∠B=600.求b ; (2)已知a=52,b=56,求∠A .5、在△ABC 中,∠C 为直角, ∠A 、∠B 、∠C 所对的边分别是a 、b 、c ,已知a=25,b=215,求c 、∠A 、∠B .6、在Rt △ABC 中,∠C =90°,由下列条件解直角三角形: (1) 已知a =156, b =56,求c; (2) 已知a =20, c =220,求∠B ; (3) 已知c =30, ∠A =60°,求a ;(4) 已知b =15, ∠A =30°,求a .7、已知:如图,在ΔABC 中,∠ACB =90°,CD ⊥AB ,垂足为D ,若∠B =30°,CD =6,求AB 的长.8、已知:如图,在山脚的C 处测得山顶A 的仰角为︒45,沿着坡度为︒30︒=∠30DCB ,400=CD 米),测得A 的仰角为︒60,求山的高度DCAB9、会堂里竖直挂一条幅AB,如图5,小刚从与B成水平的C点观察,视角∠C=30°,当他沿CB方向前进2米到达到D时,视角∠ADB=45°,求条幅AB的长度。
锐角三角函数同步练习(应用题)

第28章锐角三角函数练习题 姓名:________1.(2009年郴州市)如图,数学活动小组来到校园内的一盏路灯下测量路灯的高度,测角仪AB α为30,点B 到电灯杆底端N 的距离BN 为10米,求路灯的高度MN 是多少米?(取23=1. 732,结果保留两位小数)2.(2009成都)某中学九年级学生在学习“直角三角形的边角关系”一章时,开展测量物体高度的实践活动,他们要测量学校一幢教学楼的高度.如图,他们先在点C 测得教学楼AB 的顶点A 的仰角为30°,然后向教学楼前进60米到达点D ,又测得点A 的仰角为45°.请你根据这些数据,求出这幢教学楼的高度.(计算过程和结果均不取近似值)3.(2009年黄石市)三楚第一山——东方山是黄石地区的佛教圣地,也是国家AAA 级游览景区.它的主峰海拔约为600米,主峰AB 上建有一座电信信号发射架BC ,现在山脚P 处测得峰顶的仰角为α,发射架顶端的仰角为β,其中35tan tan 58αβ==,,求发射架高BC .4.(2009年云南省)如图,小芸在自家楼房的窗户A 处,测量楼前的一棵树CD 的高. 现测得树顶C 处的俯角为45°,树底D 处的俯角为60°,楼底到大树的距离BD 为20米.请5.(2009年济宁市)坐落在山东省汶上县宝相寺内的太子灵踪塔始建于北宋(公元1112年),为砖彻八角形十三层楼阁式建筑.数学活动小组开展课外实践活动,在一个阳光明媚的上午,他们去测量太子灵踪塔的高度,携带的测量工具有:测角仪.皮尺.小镜子.(1)小华利用测角仪和皮尺测量塔高. 图1为小华测量塔高的示意图.她先在塔前的平地上选择一点A ,用测角仪测出看塔顶()M 的仰角35α=,在A 点和塔之间选择一点B ,测出看塔顶()M 的仰角45β=,然后用皮尺量出A .B 两点的距离为18.6m,自身的高度为1.6m.请你利用上述数据帮助小华计算出塔的高度(tan 350.7≈,结果保留整数).CB AP600米山顶 发射架 45° AB C D 60°(2)如果你是活动小组的一员,正准备测量塔高,而此时塔影NP 的长为a m (如图2),你能否利用这一数据设计一个测量方案?如果能,请回答下列问题:①在你设计的测量方案中,选用的测量工具是: ;②要计算出塔的高,你还需要测量哪些数据? . 6.(2009年山东青岛市)在一次数学活动课上,老师带领同学们去测量一座古塔CD 的高度.他们首先从A 处安置测倾器,测得塔顶C 的仰角21CFE ∠=°,然后往塔的方向前进50米到达B 处,此时测得仰角37CGE ∠=°CD 的高度. (参考数据:3sin 375°≈,3tan 374°≈,9sin 2125°≈,3tan 218°≈)7.(2009年铁岭市)某旅游区有一个景观奇异的望天洞,D 点是洞的入口,游人从入口进洞游览后,可经山洞到达山顶的出口凉亭A 处观看旅游区风景,最后坐缆车沿索道AB 返回山脚下的B 处.在同一平面内,若测得斜坡BD 的长为100米,坡角10DBC ∠=°,在B 处测得A 的仰角40ABC ∠=°,在D 处测得A 的仰角85ADF ∠=°,过D 点作地面BE 的垂线,垂足为C .(1)求ADB ∠的度数;(2)求索道AB 的长.(结果保留根号)8.(2009年福州)如,在边长为1的小正方形组成的网格中,ABC △的三个顶点均在格点上,请按要求完成下列各题:(1)用签字笔...画AD ∥BC (D 为格点),连接CD ; (2)线段CD 的长为 ;(3)请你在ACD △的三个内角中任选一个锐角..,若你所选的 锐角是 ,则它所对应的正弦函数值是 . (4) 若E 为BC 中点,则tan ∠CAE 的值是 .9.(2009年日照)如图,斜坡AC 的坡度(坡比)为1:3,AC =10米.坡顶有一旗杆BC ,旗杆顶端B 点与A 点有一条彩带AB 相连,AB =14米.试求旗杆BC 的高度.10.(2009贺州)如图,︒=∠25MON ,矩形ABCD 的对角线ON AC ⊥,边BC 在OM 上,当AC=3时,AD11.(2009年天津市)在一次课外实践活动中,同学们要测量某公园人工湖两侧A B ,两个凉亭之间的距离.现测得30AC =m ,70BC =m ,120CAB ∠=°,请计算A B ,两个凉亭之间的距离. A CD EFBCG E DB A F ACD AO25°CBM NDC A12. ( 2009年嘉兴市)如图,已知一次函数b kx y +=的图象经过)1,2(--A ,)3,1(B 两点,并且交x 轴于点C ,交y 轴于点D ,(1)求该一次函数的解析式; (2)求OCD ∠tan 的值;(3)求证:︒=∠135AOB .13. (2009年泸州)如图11,在△ABC 中,AB=BC ,以AB为直径的⊙O 与AC 交于点D ,过D 作DF⊥BC, 交AB 的延长线于E ,垂足为F .(1)求证:直线DE 是⊙O 的切线;(2)当AB=5,AC=8时,求cosE的值. 14.(2009呼和浩特)要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角α一般满足5075α°≤≤°.如图,现有一个长6m 的梯子,梯子底端与墙角的距离为3m .(1)求梯子顶端B 距离墙角C(2)计算此时梯子与地面所成角α,并判断人能否安全使用这个梯子. (3 1.732≈,2 1.414≈)15.(2009年郴州市)如图,数学活动小组来到校园内的一盏路灯下测量路灯的高度,测角仪AB α为30,点B 到电灯杆底端N 的距离BN 为10米,求路灯的高度MN 是多少米?(取2316.(2009年常德市)如图,某人在D 处测得山顶C 的仰角为30o,向前走200米来到山脚A 处,测得山坡AC 度(不计测角仪的高度,3 1.73≈,结果保留整数).17.(2009年包头)如图,线段AB DC 、分别表示甲.乙两建筑物的高,AB BC DC BC ⊥,⊥,从B 点测得D 点的仰角α为60°从A 点测得D 点的仰角β为30°,已知甲建筑物高36AB =米.(1)求乙建筑物的高DC ; (2)求甲.乙两建筑物之间的距离BC(参考数据:2 1.4143 1.732≈,≈)18.(2009眉山)海船以5海里/小时的速度向正东方向行驶,在A 处看见灯塔B 在海船的北偏东60°方向,2小时后船行驶到C 处,发现此时灯塔B 在海船的北偏西45方向,求此时灯塔B 到C 处的距离.19.(2009年台州市)如图,有一段斜坡BC 长为10米,坡角12CBD ︒∠=,为方便残疾人的轮椅车通行,现准备把坡角降为5°. (1)求坡高CD ; (2)求斜坡新起点A 与原起点B 的20.(2009年赤峰市)公园里有一块形如四边形ABCD 的草地,测得BC=CD=10米,B D CA O1 1yx图11 BC A 墙地面 C BA5°D乙C B A甲EC∠B=∠C=120°,∠A=45°.请你求出这块草地的面积.21.(2009年娄底)在学习实践科学发展观的活动中,某单位在如图8所示的办公楼迎街的墙面上垂挂一长为30米的宣传条幅AE ,张明同学站在离办公楼的地面C 处测得条幅顶端A 的仰角为50°,测得条幅底端E 的仰角为30°. 问张明同学是在离该单位办公楼水平距离多远的地方进行测量?(精确到整数米)22. (2009年金华市) 如图1是工人将货物搬运上货车常用的方法,把一块木板斜靠在货车车厢的尾部,形成一个斜坡,货物通过斜坡进行搬运.根据经验,木板与地面的夹角为20°(即图2中∠ACB =20°)时最为合适,已知货车车厢底部到地面的距离ABADCD24.(2009重庆綦江)如图,在矩形ABCD 中,E 是BC 边上的点,AE=BC ,DF ⊥AE ,垂足为F ,连接DE . (1)求证:ABE △DFA ≌△; (2)如果10AD AB =,=6,求sin EDF ∠的值.第28章锐角三角函数练习题参考答案1. 解:在直角三角形MPA 中,30α∠=°,10AP 米310tan 30105.7733MP米因为 1.5AB 米所以 1.5 5.87.27MN米2.解:如图,由已知可得∠ACB=30°,∠ADB=45° ∴在Rt △ABD 中,BD=AB 又在Rt △ABC 中,∵ tan30°=BCAB ∴33=BC AB ,即BC=3AB ∵BC=CD+BD ,∴3AB=CD+AB 即(3-1)AB=60A BCD图1 图2DABCEF∴AB=1360-=30(3+1)米∴教学楼高度为30(3+1)米. 3. 解:在Rt PAB △中,∵tan AB PA α=, ∴6001000m 3tan 5AB PA α===.在Rt PAC △中, ∵tan ACPAβ=, ∴5tan 1000625m 8AC PA β===. ∴62560025m BC =-=. 答:发射架高为25m .4. 解:过点A 作AE ∥BD 交DC 的延长线于点E , 则∠AEC =∠BDC =90°.∵45EAC ∠=,20AE BD ==, ∴20EC =.∵tan tan ABADB EAD BD∠=∠=, ∴20tan 60203AB =⋅=2032014.6CD ED EC AB EC =-=-=≈(米).答:树高约为14.6米.5. 解:(1)设CD 的延长线交MN 于E 点,MN 长为xm ,则( 1.6)ME x m =-. ∵045β=,∴ 1.6DE ME x ==-.∴ 1.618.617CE x x =-+=+. ∵0tan tan 35ME CE α==,∴ 1.60.717x x -=+,解得45x m =. ∴太子灵踪塔()MN 的高度为45m .(2) ①测角仪.皮尺; ② 站在P 点看塔顶的仰角.自身的高度. 6. 解:由题意知CD AD ⊥,EF AD ∥,45°AB ED60°C∴90CEF ∠=°,设CE x =, 在Rt CEF △中,tan CE CFE EF ∠=,则8tan tan 213CE x EF x CFE ===∠°; 在Rt CEG △中,tan CECGE GE ∠=, 则4tan tan 373CE x GE x CGE ===∠°;∵EF FG EG =+, ∴845033x x =+. 37.5x =,∴37.5 1.539CD CE ED =+=+=(米). 答:古塔的高度约是39米.7. (1)解:∵DC CE ⊥,∴90BCD ∠=°. 又∵10DBC ∠=°, ∴80BDC ∠=°, ∵85ADF ∠=°,∴360809085105ADB ∠=---=°°°°°. (2)过点D 作DG AB ⊥于点G .在Rt GDB △中,401030GBD ∠=-=°°°, ∴903060BDG ∠=-=︒°° 又∵100BD =, ∴111005022GD BD ==⨯=. 3cos301005032GB BD ==⨯=°. A CDEFBG在Rt ADG △中,1056045GDA ∠=-=︒°° ∴50GD GA ==,∴50503AB AG GB =+=+(米) 答:索道长50503+米. 8. (1)如图 (2)5;(3)∠CAD ,55(或∠ADC ,552); (4)21. 9. 延长BC 交AD 于E 点,则CE ⊥AD . 在Rt △AEC 中,AC =10,由坡比为1: 3可知:∠CAE =30°, ∴ CE =AC·sin30°=10×21=5, AE =AC·cos30°=10×23=53 . 在Rt △ABE 中,BE =22AE AB -=()223514-=11.∵ BE =BC +CE ,∴ BC =BE -CE =11-5=6(米). 答:旗杆的高度为6米. 10. 解:延长AC 交 ON 于点E , ∵AC ⊥ON , ∠OEC=90°,∵四边形ABCD 是矩形, ∴∠ABC=90°,A D=BC , 又∵∠OCE=∠ACB , ∴∠BAC=∠O=25°, 在Rt △ABC 中,AC=3, ∴BC=AC· ∴ADABCED A25°CBMDECAD11. 如图,过C 点作CD 垂直于AB 交BA 的延长线于点D .在Rt CDA △中,3018018012060AC CAD CAB =∠=-∠=︒-︒=︒,°.∴•=AC CD 31560sin 30sin =︒•=∠CAD ,︒•=∠•=60cos 30cos CAD AC AD =15.又在Rt CDB△中,22270BC BD BC CD ==,-,()227015365BD ∴=-=.651550AB BD AD ∴=-=-=,答:A B ,两个凉亭之间的距离为50m.12. (1)由⎩⎨⎧+=+-=-b k b k 321,解得⎪⎩⎪⎨⎧==3534b k ,所以3534+=x y (2)5(0)4C -,,5(0)3D ,. 在Rt △OCD 中,35=OD ,45=OC , ∴OCD ∠tan 34==OC OD .(3)取点A 关于原点的对称点(21)E ,, 则问题转化为求证︒=∠45BOE . 由勾股定理可得,5=OE ,5=BE ,10=OB ,∵222BE OE OB +=, ∴△EOB 是等腰直角三角形. ∴︒=∠45BOE . ∴135AOB ∠=°.BD CAO 1 1yE13.14. 解:(1)在Rt ACB △中, (2)在Rt ACB △中,31cos 62AC AB α=== ∴可以安全使用.15.. 解:在直角三角形MPA 中,30α∠=°,10AP 米310tan 30105.7733MP米因为 1.5AB 米所以 1.5 5.87.27MN米16. 设山高BC =x ,则AB =12x , 由tan 3012002BC x BDx==+,得1)400x=,解得1)16211x ==≈米17.解:(1)过点A 作AE CD ⊥于点E ,根据题意,得6030DBC DAE αβ∠=∠=∠=∠=°,°,36AE BC EC AB ===,米,设DE x =,则36DC DE EC x =+=+, 在Rt AED △中,tan tan 30DEDAE AE∠==°, AE BC AE ∴=∴==,,在Rt DCB △中,tan tan 60DC DBC BC ∠===°,3361854x x x DC ∴=+=∴=,,(米). (2)BC AE ==,18x =,1818 1.73231.18BC ∴==⨯≈(米).18. 解:如图,过B 点作BD⊥AC 于DD乙CBA 甲 E∴∠DAB =90°-60°=30°,∠DCB=90°-45°=45° 设BD =x,在Rt△ABD 中,AD =x ⋅tan30°=33x 在Rt△BDC 中,BD =DC =x BC =2x又AD =5×2=10 ∴3103x x +=得5(31)x =- ∴25(31)5(62)BC =⋅-=-(海里)答:灯塔B 距C 处5(62)-海里19. 解:(1)在BCD Rt ∆中,︒=12sin BC CD 1.221.010=⨯≈(米). (2)在BCD Rt ∆中,︒=12cos BC BD8.998.010=⨯≈(米); 在ACD Rt ∆中,︒=5tan CD AD 2.123.330.09≈≈(米), 23.339.813.5313.5AB AD BD =-≈-=≈(米). 20解:连接BD ,过C 作CE BD ⊥于E ,10120BC DC ABC BCD ==∠=∠=,°, 123090ABD ∴∠=∠=∴∠=°,°.553CE BE ∴=∴=,.452103A AB BD BE ∠=∴===°,..21. 解:方法一:过D 点作DF ⊥AB 于F 点 在Rt △DEF 中,设EF =x ,则DF =3x在Rt △ADF 中,tan 50°=303xx+30+x=3∴DF =3x≈48答:张明同学站在离办公楼约48米处进行测量的 方法二:过点D 作DF ⊥AB 于F 点在Rt △DEF 中,EF =FD·tan 30°在Rt △AFD 中,AF =FD·tan 30°∵AE +EF =AF∴30+FDtan 30°=FD·tan 50°∴FD ≈48答:张明同学站在离办公楼约48米处进行测量的22. 解:由题意可知:AB ⊥BC∴在Rt △ABC 中, sin ∠ACB =AB AC ∴AC = ABsin ∠ACB = = ∴CD = AC +AD23. (1)证明:在矩形ABCD 中,ABE DFA ∴△≌△.(2)解:由(1)知ABE DFA △≌△ 在直角ADF △中,在直角DFE △中,10sin 210EF EDF DE ∴∠===。
锐角三角函数解答题大全100题(A)

锐角三角函数解答题大全100题一、解答题1.如图,某消防队在一居民楼前进行演习,消防员利用云梯成功救出点B处的求救者后,又发现点B正上方点C处还有一名求救者.在消防车上点A处测得点B和点C的仰角分别是45°和65°,点A距地面2.5米,点B距地面10.5米.为救出点C处的求救者,云梯需要继续上升的高度BC约为多少米?(结果保留整数.参考数据:≈1.4)2.如图,Rt△ABC中,∠ABC=90°,以AB为直径作⊙O,点D为⊙O上一点,且CD=CB、连接DO并延长交CB的延长线于点E.(1)判断直线CD与⊙O的位置关系,并说明理由;(2)若BE=4,DE=8,求AC的长.3.已知BC是⊙O的直径,点D是BC延长线上一点,AB=AD,AE是⊙O的弦,∠AEC=30°.(1)求证:直线AD是⊙O的切线;(2)若AE⊥BC,垂足为M,⊙O的半径为4,求AE的长.4.由我国完全自主设计、自主建造的首艘国产航母于2018年5月成功完成第一次海上试验任务.如图,航母由西向东航行,到达A 处时,测得小岛C 位于它的北偏东70︒方向,且与航母相距80海里,再航行一段时间后到达B 处,测得小岛C 位于它的北偏东37︒方向.如果航母继续航行至小岛C 的正南方向的D 处,求还需航行的距离BD 的长. (参考数据:sin700.94︒≈,cos700.34︒≈,tan70 2.75︒≈,sin370.6︒≈,370.80cos ︒≈,tan370.75︒≈)5.如图,为了测量出楼房AC 的高度,从距离楼底C 处D (点D 与楼底C 在同一水平面上)出发,沿斜面坡度为i=1DB 前进30米到达点B ,在点B 处测得楼顶A 的仰角为53°,求楼房AC 的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈43,计算结果用根号表示,不取近似值).6.“高低杠”是女子体操特有的一个竞技项目,其比赛器材由高、低两根平行杠及若干支架组成,运动员可根据自己的身高和习惯在规定范围内调节高、低两杠间的距离.某兴趣小组根据高低杠器材的一种截面图编制了如下数学问题,请你解答.如图所示,底座上A ,B 两点间的距离为90cm .低杠上点C 到直线AB 的距离CE 的长为155cm ,高杠上点D 到直线AB 的距离DF 的长为234cm ,已知低杠的支架AC 与直线AB 的夹角∠CAE 为82.4°,高杠的支架BD 与直线AB 的夹角∠DBF 为80.3°.求高、低杠间的水平距离CH 的长.(结果精确到1cm ,参考数据sin82.4°≈0.991,cos82.4°≈0.132,tan82.4°≈7.500,sin80.3°≈0.983,cos80.3°≈0.168,tan80.3°≈5.850)7.小婷在放学路上,看到隧道上方有一块宣传“中国﹣南亚博览会”的竖直标语牌CD .她在A 点测得标语牌顶端D 处的仰角为42°,测得隧道底端B 处的俯角为30°(B ,C ,D 在同一条直线上),AB=10m ,隧道高6.5m (即BC=65m ),求标语牌CD 的长(结果保留小数点后一位).(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90≈1.73)8.如图,大楼底右侧有一障碍物,在障碍物的旁边有一幢小楼DE ,在小楼的顶端D 处测得障碍物边缘点C 的俯角为30°,测得大楼顶端A 的仰角为45°(点B ,C ,E 在同一水平直线上).已知AB =80m ,DE =10m ,求障碍物B ,C 两点间的距离.(结果保留根号)9.如图是某市一座人行天桥的示意图,天桥离地面的高BC 是10米,坡面AC 的倾斜角45CAB ∠=︒,在距A 点10米处有一建筑物HQ .为了方便行人推车过天桥,市政府部门决定降低坡度,使新坡面DC 的倾斜角30BDC ∠=︒,若新坡面下D 处与建筑物之间需留下至少3米宽的人行道,问该建筑物是否需要拆除(计算最后结果保留一位小数).1.414≈ 1.732≈)10.如图,BC 是路边坡角为30°,长为10米的一道斜坡,在坡顶灯杆CD 的顶端D 处有一探射灯,射出的边缘光线DA 和DB 与水平路面AB 所成的夹角∠DAN 和∠DBN 分别是37°和60°(图中的点A 、B 、C 、D 、M 、N 均在同一平面内,CM ∥AN ). (1)求灯杆CD 的高度;(2)求AB 的长度(结果精确到0.1米).(.sin37°≈060,cos37°≈0.80,tan37°≈0.75)11.某数学活动小组实地测量湛河两岸互相平行的一段东西走向的河的宽度,在河的北岸边点A 处,测得河的南岸边点B 处在其南偏东45°方向,然后向北走20米到达点C 处,测得点B 在点C 的南偏东33°方向,求出这段河的宽度.(结果精确到1米,参考数据:sin33°=0.54,cos33°≈0.84,tan33°=0.65≈1.41)12.如图,某大楼的顶部树有一块广告牌CD ,小李在山坡的坡脚A 处测得广告牌底部D 的仰角为60°.沿坡面AB 向上走到B 处测得广告牌顶部C 的仰角为45°,已知山坡AB 的坡度i=1AB=10米,AE=15米.(i=1是指坡面的铅直高度BH 与水平宽度AH的比)(1)求点B距水平面AE的高度BH;(2)求广告牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:3 1.414, 1.732)13.如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向的B处,求此时轮船所在的B处与灯塔P的距离.≈2.449,结果保留整数)14.如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30º,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°. 若坡角∠FAE=30°,求大树的高度. (结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,≈1.73)15.如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4).(1)请在图中,画出△ABC向左平移6个单位长度后得到的△A1B1C1;(2)以点O为位似中心,将△ABC缩小为原来的12,得到△A2B2C2,请在图中y轴右侧,画出△A2B2C2,并求出∠A2C2B2的正弦值.16.如图,A,B两座城市相距100千米,现计划要在两座城市之间修筑一条高等级公路(即线段AB)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
锐角三角函数应用题训练
1.如图,某数学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上)。
请你根据他们测量数据计算这棵树CD的高
度(结果精确到0.1m)。
(参考数据:2≈1.414,3≈1.732)
2.如图,一艘核潜艇在海面DF下600米A点处测得俯角为30°正前方的海底C
点处有黑匣子,继续在同一深度直线航行1464米到B点处测得正前方C点处的俯角为45°.求海底C点处距离海面DF的深度(结果精确到个位,参考数据:
≈2.236).
3.如图,在电线杆CD上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆6米的B处安置高为1.5米的测角仪AB,在A处测得电线杆上C处的仰角为30°,求拉线CE的长(结果保留小数点后一位,参考数据:
≈).
1.41, 1.73
4.如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A 点测得建筑物CD的顶点C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.
(1)求两建筑物底部之间水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号).
5.钓鱼岛自古以来就是我国的神圣领土,为维护国家主权和海洋权利,我国海监和渔政部门对钓鱼岛 海域实现了常态化巡航管理.如图,某日在我国钓鱼岛附近海域有两艘自西向东航行的海监船A 、B ,
B 船在A 船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A 的东北方向,B 的北偏东15°方向有一我国渔政执法船
C ,求此时船C 与船B 的距离是多少.(结果保留根号)
6.一测量爱好者,在海边测量位于正东方向的小岛高度AC ,如图所示,他先在点B 测得山顶点A 的仰角为30°,然后向正东方向前行62米,到达D 点,在测得山顶点
A 的仰角为60°(
B 、
C 、D
三点在同一水平面上,且测量仪的高度忽略不计).求小岛高度AC
(结果精确的1 1.4≈ 1.7≈)
7.如图,我省在修建泛亚铁路时遇到一座山,要从A 地向B 地修一条隧道(A ,B 在同一水平面上),为了测量A ,B 两地之间的距离,某工程师乘坐热气球从M 地出发垂直上升150 米到达C 处,在C 处观察A 地的俯角为60°,然后保持同一高度
向前平移200米到达D 处,在D 处观察B
地的俯角为
45
°,则A 、B 两地之间的距离为多少米?( 1.73;结果保留整数)
8.甲、乙两条轮船同时从港口A出发,甲轮船以每小时30海里的速度沿着北偏东60°的方向航行,乙轮船以每小时15海里的速度沿着正东方向行进,1小时后,甲船接到命令要与乙船会合,于是甲船改变了行进的速度,沿着东南方向航行,结果在小岛C处与乙船相遇.假设乙船的速度和航向保持不变,求:
(1)港口A与小岛C之间的距离;
(2)甲轮船后来的速度.
9.如图,游客从某旅游景区的景点A处下山至C处有两种路径,一中是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客同时从A处下山,甲沿AC匀速步行,速度为45m/min.乙开始从A乘缆车到B,在B处停留5min后,再从B匀速步行到C,两人同时到达.已知缆车匀速直线运动的速度为180m/min,山路AC长为2430m,经测量,∠CAB=45°,
∠CBA=105°.(参考数据: 1.4,1.7)
(1)求索道AB的长;
(2)为乙的步行速度.
10.某中学九年级数学兴趣小组为测量校内旗杆高度,如图,在C点测得旗杆顶端A的仰角为30°,向前走了6米到达D点,在D点测得旗杆顶端A的仰角为60°(测角器的高度不计).
(1)AD 米;
(2)求旗杆AB的高度(结果保留1 1.73).
11.某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘刚在南海巡航的渔政船前往救援.当飞机到达距离海面3000米的高空C处,测得A处渔政船的俯角为60°,测得B处发生险情渔船的俯角为30°,请问:此时渔政船和渔船相距多远?(结果保留根号)
12.如图,小明在M处用高1米(DM=1米)的测角仪测
得旗杆AB的顶端B的仰角为30°,再向旗杆方向前进10米到F处,又测得旗杆顶端B的仰角为60°,请求出旗杆AB的高度(取≈1.73,结果保留整数)
13.如图,有小岛A和小岛B,轮船以45km/h的速度由C向东航行,在C处测得A 的方位角为北偏东60°,测得B的方位角为南偏东45°,轮船航行2小时后到达小岛B处,在B处测得小岛A在小岛B的正北方向.求小岛A与小岛B之间的距离
(结果保留整数,参考数据:≈1.41,≈2.45)
14.一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里每小时的速度前往救援,求海警船到大事故船C处所需的大约时间.(温馨提示:sin53°≈0.8,cos53°≈0.6)
15.根据道路管理规定,在羲皇大道秦州至麦积段上行驶的车辆,限速60千米/时.已知测速站点M距羲皇大道l(直线)的距离MN为30米(如图所示).现有一辆汽车由秦州向麦积方向匀速行驶,测得此车从A点行驶到B点所用时间为6秒,∠AMN=60°,∠BMN=45°.
(1)计算AB的长度.
(2)通过计算判断此车是否超速.
16.如图,在东西方向的海岸线l上有一长为1千米的码头MN,在码头西端M的正西方向30 千米处有一观察站O.某时刻测得一艘匀速直线航行的轮船位于O的北偏西30°方向,且与O相距千米的A处;经过40分钟,又测得该轮船位于O的正北方向,且与O相距20千米的B处.
(1)求该轮船航行的速度;
(2)如果该轮船不改变航向继续航行,那么轮船能否正好行至码头MN靠岸?请说明理由.
17.如图,我国的一艘海监船在钓鱼岛A 附近沿正东方向航行,船在B 点时测得钓
鱼岛A 在船的北偏东60°方向,船以50海里/时的速度继续航行2小时后到达C 点,此时钓鱼岛A 在船的北偏东30°方向.请问船继续航行多少海里与钓鱼岛A 的距离最近?
18.如图,A ,B 两地之间有一座山,汽车原来从A 地到B 地须经C 地沿折线A –C -B 行驶,全长68 km .现开通隧道后,汽车直接沿直线AB 行驶.已知∠A =30°,∠B =45°,则隧道开通后,汽车从A 地到B 地比原来少走多少千米?(结果精确到0.1 km )(参考数据:4.12≈,7.13≈)
19.水利部门为加强防汛工作,决定对某水库大坝进行加固,大坝的横截面是梯形ABCD ,如图所示,已知迎水坡面AB 的长为16米,∠B =60°,背水坡面CD 的长为
米,加固后大坝的横截面为梯形ABED ,CE 的长为8米.
(1)已知需加固的大坝长为150米,求需要填土石方多少立方米?
(2)求加固后的大坝背水坡面DE 的坡度.
20.如图,一段河坝的横截面为梯形ABCD ,试根据图中数据,求出坝底宽AD.(i =CE ∶ED ,单位:m )
A B
C
30° 45°
学习好资料欢迎下载参考答案
1.这棵树CD的高度为8.7米
2.2600米.
3.5.7米.
4.(1)两建筑物底部之间水平距离BD的长度为60米;(2)建筑物CD的高度为(60﹣203)米.
5.此时船C与船B的距离是
6.53米.
7.A、B两地之间的距离为264米
8.(1)(+15)海里.(2)/小时.9.(1)AB=1260m;(2)乙的步行速度是45m/min. 10.(1)6
AD
(2) 5.2
AB≈米.
11.米.
12.10米
13.小岛A与小岛B之间的距离是100km.
14.
15.(1)AB=(30+303)米;
(2)不会超速.
16.(1)轮船航行的速度为30千米/时;
(2)该轮船不改变航向继续航行,不能行至码头MN靠岸.17.50.
18.14.
. 19.(1)需填土 (立方米);(2)DE的坡度为
4
20.(7.5+m。
