(完整版)平行四边形的性质判定练习题.doc
(完整)平行四边形的判定典型例题及练习
平行四边形一、知识点复习1、平行四边形的判定平行四边形的判定方法①两组对边分别平行的四边形是平行四边形。
②一组对边平行且相等的四边形是平行四边形。
③两组对边分别相等的四边形是平行四边形。
④对角线相互平分的四边形是平行四边形。
2、平行线等分线段和三角形中位线定理（1）平行线等分线段定理:如果一组平行线在一条直线上截得的线段相等，那么在其它直线上截得的线段也相等.（2）平行线等分线段定理的推论:经过三角形一边中点与另一边平行的直线必平分第三边.（3）三角形的中位线:连接三角形两边中点的线段叫做三角形的中位线。
（4）三角形中位线定理：三角形两边中点的连线平行于第三边，并且等于第三边的一半。
3、三角形的重心(1）重心的定义：三角形的三条中线交于一点，这点就是三角形的重心.（2)重心的性质：三角形的三条中线相交于一点，这点和各边中点的距离等于相应各边上中线的三分之一。
二、典型例题讲解模块1:平行四边形的判定题型1：平行四边形的判定例题1：如图所示，在平行四边形ABCD 中,CF AE ,分别是DAB ∠，BCD ∠的平分线,求证：四边形AFCE 是平行四边形.例题2：如图，在等边三角形ABC 中，D 是BC 的中点，以AD 为边向左侧作等边三角形ADE 。
（1）求CAE ∠的度数.（2）取AB 的中点F ,连接CF 、EF 。
试证明四边形CDEF 是平行四边形.例题3：如图，在平行四边形ABCD 中，BD 为对角线，F E ,是BD 上的点，且DF BE =. 求证：四边形AECF 是平行四边形。
变式练习:1。
如图，在ABC ∆中，中线BD ，CE 相交于点O ,F 、G 分别是OB 、OC 的中点,连接DE GD FG EF ,,,，求证：四边形DEFG 是平行四边形。
2。
如图，已知DE AB //,DE AB =，DC AF =，求证：四边形BCEF 是平行四边形.3.如图,四边形ABCD 中,BC AD //，作DC AE //交BC 于E 。
平行四边形性质判定练习题
平行四边形性质判定练习题平行四边形是几何学中常见的一个概念，它具备一些独特的性质和判定条件。
为了更好地理解和应用这些性质，下面将通过一些练习题来帮助你巩固对平行四边形的认识。
练习题一：已知四边形ABCD，AB∥CD。
如果∠BAD = 80°，则∠ADC等于多少度？解析：由于AB∥CD，根据平行线性质可知∠BAD + ∠ADC = 180°。
又∠BAD = 80°，代入得80° + ∠ADC = 180°，解方程得∠ADC = 100°。
练习题二：在平行四边形ABCD中，已知AB = 6 cm，BC = 8 cm，AD = 5 cm，求CD的长度。
解析：由平行四边形的性质可知，对角线相等，即AC = BD。
又ABCD为平行四边形，AB∥CD，所以AD与BC平行，根据平行线性质可知∠ADC = ∠CBD。
根据余弦定理，可以得出∠ADC关于边长AD、CD、AC的关系：AD² + CD² - 2·AD·CD·cos∠ADC = AC²代入已知数据，得5² + CD² - 2·5·CD·cos∠ADC = AC²根据AC = BD，即6² + 8² = 10²，可以求得AC = 10 cm。
再代入已知数据，得25 + CD² - 10·CD·cos∠ADC = 100整理得CD² - 10·CD·cos∠ADC - 75 = 0根据解一元二次方程的方法，求得CD = 15 cm。
练习题三：平行四边形ABCD中，已知AB = 7 cm，将ABCD绕点A逆时针旋转120°得到四边形A'B'C'D'，连接DD'交AC于点E。
(完整版)平行四边形的性质判定练习题
第一部分 平行四边形的性质练习题 例题1、平行四边形得周长为50cm ，两邻边之差为5cm,求各边长。
变题1.平行四边形ABCD 的周长为40cm,两邻边AB 、AC 之比为2：3，则AB=_______,BC=________. 变题2.四边形ABCD 是平行四边形，∠BAC=90°,AB=3,AC=4,求AD 的长。
例题2.平行四边形ABCD 中，∠A-∠B=20°,求平行四边形各内角的度数。
变题3.平行四边形ABCD 中，AE 平分∠DAB, ∠DEA=20°,则∠C=_________,∠B_________. 变题4.如图，在平行四边形ABCD 中，∠BAC=34°, ∠ACB=26°，求∠DAC 与∠D 的度数。
例题3.如图，在平行四边形ABCD 中，CE ⊥AD,CF ⊥BA 交BA 的延长线于F ，∠FBC=30°,CE=3cm,CF=5cm,求平行四边形ABCD 的周长。
变题5.如图，平行四边形ABCD 的周长为50，其中AB=15，∠ABC=60°，求平行四边形面积。
1、如图，四边形ABCD 是平行四边形，AB=6cm,BC=8cm ，∠B=70°,则AD=________,CD=______,∠D=_______,∠A=______,∠C=_______.2、平行四边形ABCD 的周长为40cm,两邻边AB 、AC 之比为2：3，则AB=_______,BC=________.3、平行四边形得周长为50cm ，两邻边之差为5cm,则长边是________ ，短边是__________.4、平行四边形ABCD 中，∠A-∠B=20°, 则∠A=_______ ∠B=________5、.平行四边形ABCD 中，AE 平分∠DAB, ∠DEA=20°,则∠C=____,∠B_____.6、平行四边形 ABCD 中，∠A+∠C=200°.则：∠A= _______，∠B= _________ .7、如图，平行四边形ABCD 的周长为50，其中AB=15，∠ABC=60°，求平行四边形面积。
平行四边形的判定练习题(含答案)
平行四边形的判定练习题(含答案)（1）因为AD∥BC，AB=CD，所以ABCD是平行四边形．（）（2）因为AB∥CD，AD=BC，所以ABCD是平行四边形．（）（3）因为AD∥BC，AD=BC，所以ABCD是平行四边形．（）（4）因为AB∥CD，AD∥BC，所以ABCD是平行四边形．（）（5）因为AB=CD，AD=BC，所以ABCD是平行四边形．（）（6）因为AD=CD，AB=AC，所以ABCD是平行四边形．（）5．已知AD∥BC，要使四边形ABCD为平行四边形，需要增加条件________．6．如图所示，∠1=∠2，∠3=∠4，问四边形ABCD是不是平行四边形．7．如图所示，在四边形ABCD中，AB=CD，BC=AD，E，F 为对角线AC上的点，且AE=CF，求证：BE=DF．8．如图所示，D为△ABC的边AB上一点，DF交AC于点E，且AE=CE，FC∥AB．求证：CD=AF．9．如图所示，已知四边形ABCD是平行四边形，在AB 的延长线上截取BE=•AB，BF=BD，连接CE，DF，相交于点M．求证：CD=CM．10．如图所示，在四边形ABCD中，DC∥AB，以AD，AC为边作□ACED，延长DC•交EB于F，求证：EF=FB．知能点2 三角形的中位□线11．如图所示，已知E为□ABCD中DC边的延长线上的一点，且CE=DC，连接AE，分别交BC，BD于点F，G，连接AC交BD于点O，连接OF，求证：AB=2OF．12．如图所示，在ABCD中，EF∥AB且交BC于点E，交AD于点F，连接AE，BF•交于点M，连接CF，DE交AD．于点N，求证：MN∥AD且MN=1213．如图所示，DE是△ABC的中位线，BC=8，则DE=_______．14．如图所示，在□ABCD中，对角线AC，BD交于点O，OE∥BC交CD•于E，•若OE=3cm，则AD的长为（）． A．3cm B．6cm C．9cm D．12cm 15．如图所示，在四边形ABCD中，E，F，G，H分别是AB，BC，CD，AD的中点，•则四边形EFGH是平行四边形吗？为什么？16．如图所示，在△ABC中，AC=6cm，BC=8cm，AB=10cm，D，E，F分别是AB，BC，CA的中点，求△DEF的面积．规律方法应用17．如图所示，A，B两点被池塘隔开，在A，B外选一点C，连接AC和BC，•并分别找出AC和BC的中点M，N，如果测得MN=20m，那么A，B两点间的距离是多少？18．如图所示，在□ABCD中，AB=2AD，∠A=60°，E，F 分别为AB，CD的中点，EF=1cm，那么对角线BD的长度是多少？你是怎样得到的？19．如图所示，在△ABC中，E为AB的中点，CD平分∠ACB，AD⊥CD于点D．•（BC-AC）．试说明：（1）DE∥BC．（2）DE=12开放探索创新20．如图所示，在△ABC中，∠BAC=90°，AD⊥BC于D，BE平分∠ABC交AD•于E，EF∥BC交AC于F，那么AE与CF相等吗？请验证你的结论．中考真题实战21．（长沙）如下左图所示，在四边形ABCD中，AB∥CD，要使四边形ABCD•为平行四边形，则应添加的条件是________．（添加一个即可）22．（呼和浩特）如上右图所示，已知E，F，G，H是四边形ABCD各边的中点，•则S四边形EFGH ：S四边形ABCD的值是_________．23．（南京）已知如图19-1-55所示，在Y ABCD中，E，F分别是AB，CD的中点.求证：（1） △AFD≌△CEB．（2）四边形AECF是平行四边形．答案:1．C 2．C 3．D4．（1）× （2）× （3）∨ （4）∨ （5）∨ （6）×5．AD=BC或AB∥CD6．解：∵∠1=∠2，∴AD∥BC．又∵∠3=∠4，∴AB∥CD．∴四边形ABCD是平行四边形．7．证明：∵AB=CD，BC=AD，∴四边形ABCD是平行四边形．∴AB∥CD，∴∠BAE=∠DCF．又∵AE=CE，∴△ABE≌△CDF（SAS），∴BE=EF．8．证明：∵FC∥AB，∴∠DAC=∠ACF，∠ADF=∠DFC．又∵AE=CE，∴△ADE≌△CFE（AAS），∴DE=EF．∵AE=CE，∴四边形ADCF为平行四边形．∴CD=AF．9．证明：∵四边形ABCD是平行四边形．∴AB//DC．又∵BE=AB，∴BE//DC，∴四边形BDCE是平行四边形．∵DC∥BF，∴∠CDF=∠F．同理，∠BDM=∠DMC．∵BD=BF，∴∠BDF=∠F．∴∠CDF=∠CMD，∴CD=CM．10．证明：过点B作BG∥AD，交DC的延长线于G，连接EG．∵DC∥AB，∴ABGD是平行四边形，∴BG// AD．在□ACED中，AD//CE，∴CE//BG．∴四边形BCEG为平行四边形，∴EF=FB．11．证明：∵四边形ABCD是平行四边形，∴AB//CD，AD=BC．∵CE=CD，∴AB//CE，∴四边形ABEC为平行四边形．∴BF=FC，∴OF//1AB，即AB=2OF．212．证明：∵四边形ABCD是平行四边形，∴AB∥CD，AD∥BC．又∵EF∥AB，∴EF∥CD．∴四边形ABEF，ECDF均为平行四边形．又∵M，N分别为Y ABEF和Y ECDF对角线的交点．∴M为AE的中点，N为DE的中点，即MN为△AED的中位线．∴MN∥AD且MN=12AD．13．4 14．B15．解：EFGH是平行四边形，连接AC，在△ABC中，∵EF是中位线，∴EF//12AC．同理，GH//12AC．∴EF//GH，∴四边形EFGH为平行四边形．16．解：∵EF，DE，DF是△ABC的中位线，∴EF=12AB，DE=12AC，DF=12BC．又∵AB=10cm，BC=8cm，AC=6cm，∴EF=5cm，DE=3cm，DF=4cm，而32+42=25=52，即DE2+DF2=EF2．∴△EDF为直角三角形．∴S△EDF =12DE·DF=12×3×4=6（cm2）．17．解：∵M，N分别是AC，BC的中点．∴MN是△ABC的中位线，∴MN=12AB．∴AB=2MN=2×20=40（m）．故A，B两点间的距离是40m．18．解：连接DE．∵四边形ABCD是平行四边形，∴AB//CD．∵DF=12CD，AE=12AB，∴DF//AE．∴四边形ADFE是平行四边形．∴EF=AD=1cm．∵AB=2AD，∴AB=2cm．∵AB=2AD，∴AB=2AE，∴AD=AE．∴∠1=∠4．∵∠A=60°，∠1+∠4+∠A=180°，∴∠1=∠A=∠4=60°．∴△ADE是等边三角形，∴DE=AE．∵AE=BE，∴DE=BE，∴∠2=∠3．∵∠1=∠2+∠3，∠1=60°，∴∠2=∠3=30°．∴∠ADB=∠3+∠4=90°．=cm）．19．解：延长AD交BC于F．（1）∵AD⊥CD，∴∠ADC=∠FDC=90°．∵CD平分∠ACB，∴∠ACD=∠FCD．在△ACD与△FCD中，∠ADC=∠FDC，DC=DC，∠ACD=∠FCD．∴△ACD≌△FCD，∴AC=FC，AD=DF．又∵E为AB的中点，∴DE∥BF，即DE∥BC．（2）由（1）知AC=FC，DE=12BF．∴DE=12（BC-FC）=12（BC-AC）．20．解：AE=CF．理由：过E作EG∥CF交BC于G，∴∠3=∠C．∵∠BAC=90°，AD⊥BC，∴∠ABC+∠C=90°，∠ABD+∠BAD=90°．∴∠C=∠BAD，∴∠3=∠BAD．又∵∠1=∠2，BE=BE，∴△ABE≌△GBE（AAS），∴AE=GE．∵EF∥BC，EG∥CF，∴四边形EGCF是平行四边形，∴GE=CF，∴AE=CF．21．答案不唯一，如AB=CD或AD∥BC．22．1223．解：（1）在□ABCD中，AD=CB，AB=CD，∠D=∠B．∵E，F分别为AB，CD的中点，∴DF=12CD，BE=12AB，∴DF=BE，∴△AFD≌△CEB．（2）在□ABCD中，AB=CD，AB∥CD．由（1）得BE=DF，∴AE=CE，∴四边形AECF是平行四边形．。
(完整版)平行四边形性质和判定习题(答案详细)(可编辑修改word版)
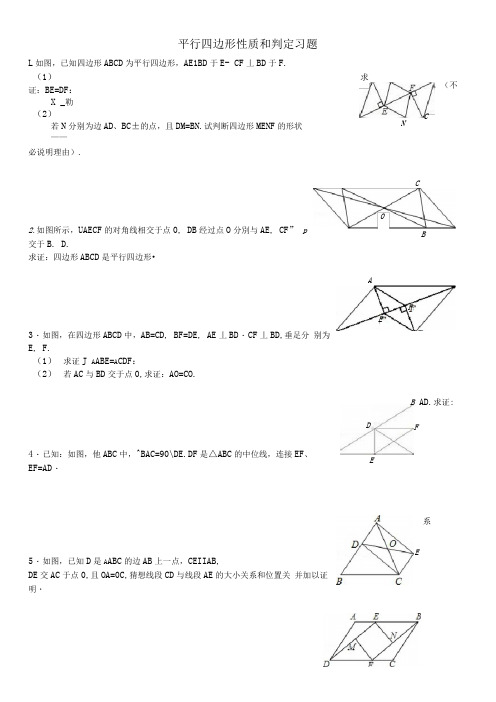
平行四边形性质和判定习题L如图，已知四边形ABCD为平行四边形，AE1BD于E- CF丄BD于F.（1）求证：BE=DF：X _勒（2）若N分别为边AD、BC±的点，且DM=BN.试判断四边形MENF的形状——必说明理由）.2.如图所示，UAECF的对角线相交于点0, DB经过点O分別与AE, CF” p交于B. D.求证：四边形ABCD是平行四边形•3・如图，在四边形ABCD中，AB=CD, BF=DE, AE丄BD・CF丄BD,垂足分别为E, F.（1）求证J A ABE=A CDF：（2）若AC与BD交于点0,求证：AO=CO.4・已知：如图，他ABC中，^BAC=90\DE.DF是△ABC的中位线，连接EF、EF=AD・5・如图，已知D是A ABC的边AB上一点，CEIIAB,DE交AC于点0,且OA=0C,猜想线段CD与线段AE的大小关系和位置关并加以证明・B AD.求证:。
（不CNCBAFED FE系E6・如图，已知，UABCD中，AE=CF, M、N分别是DE、BF的中点.求证：四边形MFNE是平行四边形•7・如图，平行四边形ABCD, E 、F 两点在对角线BD 上，且BE=DF,连接AE. EG CF, FA ・求证：四边形AECF 是平行四边形•& 在UABCD 中，分别以AD 、BC 为边向内作等边△ADE 和等边△BCF,连接BE. DF ・求证：四边形BEDF 是平 行四边形・DBIIAC,且DB 丄AC. E 是AC 的中点，求证：BC=DE ・2如图，在梯形ABCD 中，ADIIBC, AD=24cm. BC=30cm,点P 自点A 向D 以IcmZs 的速度运动，到D 点Q 自点C 向B 以2cm/s 的速度运动，到B点即停止，直线PQ 截梯形为两个四边形•问当P. Q同时10. 已知脣 点即停止. 出发，几秒后其中一个四边形为平行四边形？IL 如图：已知D 、E 、F 分别是A ABC 各边的中点, 求证：AE 仃DF 互相平分.如图所示, 9・ED13.如图，已知四边形ABCD中，点E, F. G, H分别是AB、CD、AC. BD的中点，并且点E、F、G、H有在同一条直线上.求证：EF和GH互相平分・14.如图J oABCD 中，MNIIAC.试说明MQ=NP.15.已知：如图所示「平行四边形ABCD的对角线AC, BD柑交于点6 EF经过点0并且分别和AB. CD相交于点E, F,点G, H分别为OA, 0C的中点.求证：四边形EHFG是平行四边形.-46 如制已知的ABCD中,E、F是对角线BD上的两点，BE=DF,点G、H分别在BA和DC的延长线上，且AG=CH. 连接GE、EH、HF、FG.（1）求证：四边形GEHF是平行四边形；（2）若点G、H分别在线段BA和DC上，尖余条件不变，则（1）中的结论是否成立？（不用说明理由）17.如图，在A ABC中，D是AC的中点，E是线段BC延长线一点，过点A作BE的平行线与线段ED的延长线交于点F,连接AE、CF.（1）求证J AF=CE：（2）如果AC=EF,且ZACB=135\试判断四边形AFCE是什么样的四边形，并证明你的结论・18,如图平行四边形ABCD 中.mBC=6（几 点E 、F 分別在CD.BC 的延长线上，AE||BD ・ EEhBB 垂足为点F, DF=2 （1） 求证：D 是EC 中点； （2） 求FC 的长.19.如图，已知A ABC 是等边三角形，点D 、F 分别在线段BC 、AB 匕 厶EFB=60。
(完整版)平行四边形的性质和判定练习题.doc
初 2017 级寒假培训（八） A 层----平行四边形的性质与判定班级： 姓名：1.定 ：两 互相平行的四 形叫做平行四 形，平行四 形 ABCD 作： □ ABCD几何 言：AB // CD , AD // BC , 四边形 ABCD 是平行四边形AD2.性 ：平行四 形的 平行且相等， 角相等， 角互 ， 角 互相平分；几何 言：∵四 形 ABCD 是平行四 形O∴ AD ∥ BC, _________ （ 平行）； AD=BC ,__________（ 相等）；BCBAC BCD ， _________（ 角相等）； BACABC 180 ⋯（ 角互 ） ；OA OC ，（ 角 互相平分） 。
平行四边形的判定：判定 1.两 分 平行的四 形是平行四 形 判定 2.两 分 相等的四 形是平行四 形 判定 3.两 角分 相等的四 形是平行四 形 判定 4. 角 互相平分的四 形是平行四 形 判定 5. 一 平行且相等的四 形是平行四 形； 几何 言判定 1.AB // CD , AD // BC , 四边形 ABCD 是平行四边形判定 2. AB DC , AD BC ， 四边形 ABCD 是平行四边形判定 3. ABCADC , BADBCD , 四边形 ABCD 是平行四边形 判定 4. AO CO, BO DO , 四边形 ABCD 是平行四边形 判定 5.AB // CD , AB CD ,四边形 ABCD 是平行四边形夯 基 ：1. 如 ，将 □ ABCD 的一 BC 延 至 E ，若∠ A =110°， ∠ 1=________．ADABADB E1 D C BCCE242. 如 ，在 □ ABCD 中， A 120，D ＝°．3. 在平行四 形ABCD 中， AB6cm ， BC 8cm ， 平行四 形ABCD 的周cm ．4. 如 ，在 □ ABCD 中，已知 AD 8CM , AB 6CM , ，DE 平分 ADC 交 BC 于点 E ，则 BE 等于（）A.2CMB.4CMC.6CM D .8CM5．平行四边形中一边的长为10cm，那么它的两条对角线的长度可以是（）A.4cm和 6cmB.20cm和30cmC.6cm和8cmD.8cm和12cm6.在□ABCD中，对角线 AC，BD相交于点 O，若 BD与 AC的和为 18cm，CD： DA=2：3，AOB的周长为 13cm，那么 BC的长为（）A. 6cmB. 9cm C .3cm D .12cm7.如图， ?ABCD 中， AC 、 BD 为对角线， BC=6 ， BC 边上的高为4，则阴影部分的面积为．8. 在下面给出的条件中，能判定四边形ＡＢＣＤ是平行四边形的是（）A. AB BC, AD CDB.AB // CD, AD BCC.AB // CD , B DD. AB, C D9. 一个四边形的三个相邻内角度数依次如下，那么其中是平行四边形的是（）A.88 ,108 ,88B.88 ,104 ,108 C .88 ,92 ,92 D.108 ,72 ,10810.点 A， B，C， D 在同一平面内，从①AB∥CD，② AB=CD，③ BC∥ AD，④ BC=AD 这四个条件中任选两个，能使四边形ABCD是平行四边形的选法有（）种A． 3 B．4 C．5 D． 6 ADB C8.如图，在平行四边形 ABCD 中，若 AB=6 ，AD=10 ，?ABC 的平分线交 AD 于点 E，交 CD 的延长线于点 F，求 DF 的长．9. 已知：如图a，ABCD 的对角线 AC 、 BD 相交于点 O ， EF 过点 O 与 AB 、 CD 分别相交于点 E 、 F ．（1）求证：OE OF , AE CF , BE DF .（2）若上题中的条件都不变，将EF 转动到图 b 的位置，那么结论是否成立？若将EF向两方延长与平行四边形的两对边的延长线分别相交（图 c 和图 d），结论是否成立，说明你的理由．10.已知如图， O 为平行四边形 ABCD的对角线 AC 的中点， EF 经过点 O，且与 AB 交于 E，与 CD 交于 F，求证：四边形 AECF是平行四边形。
(完整版)平行四边形的性质习题(有答案)
平行四边形的性质测试题一、选择题（每题 3 分共 30 分）1．下边的性质中，平行四边形不必定具备的是（）A．对角互补B．邻角互补C．对角相等D．内角和为 360°2．在中，∠ A：∠ B：∠ C：∠ D 的值能够是（）A ．1：2：3：4B ．1：2：1：2C ．1：1：2：2 D．1： 2：2：13．平行四边形的对角线和它的边能够构成全等三角形（）A．3对B．4 对 C ．5对D． 6 对A D 4．以下图，在中，对角线 AC、BD交于点 O，?以下式子中一O 定建立的是（）B CA．AC⊥ BD B ． OA=OC C． AC=BD D ．AO=OD5．以下图，在中， AD=5，AB=3，AE均分∠ BAD交BC A D边于点 E，则线段 BE、 EC的长度分别为（）BE C A ．2和3 B．3和2 C ．4和1 D ．1和46．的两条对角线订交于点 O，已知 AB=8cm，BC=6cm，△AOB的周长是 18cm，那么△ AOD的周长是（）A ．14cmB ．15cmC ．16cmD ．17cm7．平行四边形的一边等于14，它的对角线可能的取值是（）A ．8cm和 16cmB ．10cm和 16cmC ． 12cm和 16cmD ． 20cm和 22cm 8．如图，在中，以下各式不必定正确的选项是（）A．∠ 1+∠ 2=180° B ．∠ 2+∠ 3=180C．∠ 3+∠ 4=180°D．∠ 2+∠4=180°9．如图，在中，∠ ACD=70°，AE⊥ BD于点E，则∠ ABE等于（）A、20°B、25° C 、 30° D 、35°10．如图，在△ MBN中， BM=6，点 A、C、D 分别在 MB、NB、MN上，四边形 ABCD为平行四边形，∠NDC=∠ MDA，那么的周长是（）二、填空题（每题 3 分共 18 分）11．在中，∠ A：∠ B=4：5，则∠ C=______．12．在中， AB：BC=1：2，周长为 18cm，则 AB=______cm，AD=_______cm．13．在中，∠A=30°，则∠ B=______，∠C=______，∠D=________．14．如图，已知：点 O是的对角线的交点， ?AC=?48mm，?BD=18mm，AD=16mm，那么△ OBC的周长等于 _______mm．15．如图，在中，E、F是对角线BD上两点，要使△ ADF≌△ CBE，还需增添一个条件是 ________．16．如图，在中，EF∥ AD，MN∥ AB，那么图中共有_______?个平行四边形．三、解答题17．已知：如图，在中，E、F是对角线AC?上的两点，AE=CF．BE与DF的大小有什么关系，并说明原因。
平行四边形的判定练习题(有答案)
平行四边形的判定练习题(有答案)平行四边形的判定练题1.用边长为2cm，3cm，4cm的两个全等三角形拼成四边形，可以拼成6个四边形，其中3个为平行四边形。
2.在四边形ABCD中，若AB=CD且AD=BC，则四边形ABCD为平行四边形。
3.延长△ABC的中线AD至E，使DE=AD，连接BE，CE，则有AB=CE，AC=BE。
4.若四边形ABCD中，AC，BD相交于点O，要判定它为平行四边形，从角的关系看应满足相邻角之和为180度，从对角线的关系看应满足对角线互相平分。
5.四边形EFGH为平行四边形，且其边长分别为AB，BC，CD，DA的中点E，F，G，H。
6.能识别四边形ABCD是平行四边形的题设是AB∥CD，AD=BC。
7.选法有6种。
8.正确的结论是一组对边平行且一组对角相等的四边形是平行四边形。
9.不能判定四边形ABCD是平行四边形的条件是AB=CD，AD∥BC。
10.添加条件①或②可以使四边形AFCE为平行四边形。
11.正确的说法有3个，即DE∥AF，FD∥CE，EF∥BD。
12.在四边形ABCD中，点E和F分别在BD上，且BF=DE。
证明四边形AECF是平行四边形，可以使用两种方法。
14.在四边形ABCD中，对角线AC和BD相交于点O。
过点O作两条直线分别与AB、BC、CD、AD相交于点G、F、H、E。
证明四边形EGFH是平行四边形。
15.在△ABC中，以BC、AC、AB为边长分别作等边三角形ABD、BCE、ACF，连接DE和EF。
证明四边形ADEF是平行四边形。
16.在四边形ABCD中，AE⊥BD，CF⊥BD，垂足分别为点E和F，点G和H分别为AD和BC的中点。
证明EF和GH互相平分。
17.在△ABC中，P是内部任意一点。
过点P作EF∥AB分别交AC和BC于点E和F，作GH∥BC分别交AB和AC于点G和H，作MN∥AC分别交AB和BC于点M和N。
猜想EF+GH+MN的值是多少，并说明理由。
平行四边形的性质与判定练习题
平行四边形性质与判定练习题苏萍一、选择题1、如图，在△ABC中，BD、CE是△ABC的中线，BD与CE相交于点O，点F、G分别是BO、CO的中点，连接AO．若AO=6cm，BC=8cm，则四边形DEFG的周长是（）A．14cm B．18cm C．24cm D．28cm2、如图，在平行四边形ABCD中，EF∥AD，HN∥AB，则图中的平行四边形的个数共有（）A．12个B．9个C．7个D．5个3、如图，在平行四边形ABCD中，过对角线BD上一点P，作EF∥BC，HG∥AB，若四边形AEPH和四边形CFPG的面积分另为S1和S2，则S1与S2的大小关系为（）A．S1=S2B．S1＞S2C．S1＜S2D．不能确定4、图1、图2、图3分别表示甲、乙、丙三人由A地到B地的路线图（箭头表示行进的方向）．其中E为AB的中点，AJ＞JB．判断三人行进路线长度的大小关系为（）A．甲=乙=丙B．甲＜乙＜丙C．乙＜丙＜甲D．丙＜乙＜甲二、填空题5、如图，点O是AC的中点，将周长为8cm的平行四边形ABCD沿对角线AC方向平移AO长度得到平行四边形OB′C′D′，则四边形OECF的周长为______________6、如图，△ABC是等边三角形，点P是三角形内的任意一点，PD∥AB，PE∥BC，PF∥AC，若△ABC的周长为12，则PD+PE+PF=（）7、如图，在▱ABCD中，对角线AC、BD相交于点O，E、F是对角线AC上的两点，当E、F满足下列哪个条件时，四边形DEBF不一定是平行四边形____________A．AE=CF B．∠AED=∠CFB C．∠ADE=∠CBF D．DE=BF8、如图，平行四边形ABCD，E，F分别是BC，AD上的点，BE=DF，M，N分别是AE，CF的中点，四边形EMFN是平行四边形吗？请说明理由．9、如图1，已知在△ABC中，AB=AC，点P为底边BC上（端点B、C除外）的任意一点，且PE∥AC，PF∥AB．（1）试问线段PE、PF、AB之间有什么数量关系，并说明理由；（2）如图2，将“点P为底边BC上任意一点”改为“点P为底边BC延长线上任意一点”，其它条件不变，上述结论还成立吗？如果不成立，你能得出什么结论？请说明你的理由10、如图所示，在平行四边形ABCD中，E、F分别在AD、BC上，AE=CF，AF与BE交于点G，CE与DF交于点H，猜想EF与GH间的关系？并证明你的猜想。
(完整版)平行四边形的判定练习题(含答案)
平行四边形的判定及中位线知能点1 平行四边形的判定方法1．能够判定四边形ABCD是平行四边形的题设是（）．A．AB∥CD，AD=BC B．∠A=∠B，∠C=∠DC．AB=CD，AD=BC D．AB=AD，CB=CD2．具备下列条件的四边形中，不能确定是平行四边形的为（）．A．相邻的角互补 B．两组对角分别相等C．一组对边平行，另一组对边相等 D．对角线交点是两对角线中点3．如下左图所示，四边形ABCD的对角线AC和BD相交于点O，下列判断正确的是（）．A．若AO=OC，则ABCD是平行四边形;B．若AC=BD，则ABCD是平行四边形;C．若AO=BO，CO=DO，则ABCD是平行四边形;D．若AO=OC，BO=OD，则ABCD是平行四边形4．如上右图所示，对四边形ABCD是平行四边形的下列判断，正确的打“∨”，错误的打“×”．（1）因为AD∥BC，AB=CD，所以ABCD是平行四边形．（）（2）因为AB∥CD，AD=BC，所以ABCD是平行四边形．（）（3）因为AD∥BC，AD=BC，所以ABCD是平行四边形．（）（4）因为AB∥CD，AD∥BC，所以ABCD是平行四边形．（）（5）因为AB=CD，AD=BC，所以ABCD是平行四边形．（）（6）因为AD=CD，AB=AC，所以ABCD是平行四边形．（）5．已知AD∥BC，要使四边形ABCD为平行四边形，需要增加条件________．6．如图所示，∠1=∠2，∠3=∠4，问四边形ABCD是不是平行四边形．7．如图所示，在四边形ABCD中，AB=CD，BC=AD，E，F为对角线AC上的点，且AE=CF，求证：BE=DF．8．如图所示，D为△ABC的边AB上一点，DF交AC于点E，且AE=CE，FC∥AB．求证：CD=AF．9．如图所示，已知四边形ABCD是平行四边形，在AB的延长线上截取BE=•AB，BF=BD，连接CE，DF，相交于点M．求证：CD=CM．10．如图所示，在四边形ABCD中，DC∥AB，以AD，AC为边作□ACED，延长DC•交EB于F，求证：EF=FB．知能点2 三角形的中位□线11．如图所示，已知E为□ABCD中DC边的延长线上的一点，且CE=DC，连接AE，分别交BC，BD于点F，G，连接AC交BD于点O，连接OF，求证：AB=2OF．12．如图所示，在ABCD中，EF∥AB且交BC于点E，交AD于点F，连接AE，BF•交于点M，连接CF，DE交于点N，求证：MN∥AD且MN=12 AD．13．如图所示，DE是△ABC的中位线，BC=8，则DE=_______．14．如图所示，在□ABCD中，对角线AC，BD交于点O，OE∥BC交CD•于E，•若OE=3cm，则AD的长为（）． A．3cm B．6cm C．9cm D．12cm15．如图所示，在四边形ABCD中，E，F，G，H分别是AB，BC，CD，AD的中点，•则四边形EFGH是平行四边形吗？为什么？16．如图所示，在△ABC中，AC=6cm，BC=8cm，AB=10cm，D，E，F分别是AB，BC，CA的中点，求△DEF的面积．规律方法应用17．如图所示，A，B两点被池塘隔开，在A，B外选一点C，连接AC和BC，•并分别找出AC和BC的中点M，N，如果测得MN=20m，那么A，B两点间的距离是多少？18．如图所示，在□ABCD中，AB=2AD，∠A=60°，E，F分别为AB，CD的中点，EF=1cm，那么对角线BD 的长度是多少？你是怎样得到的？19．如图所示，在△AB C中，E为AB的中点，CD平分∠ACB，AD⊥CD于点D．•试说明：（1）DE∥BC．（2）DE=12（BC-AC）．开放探索创新20．如图所示，在△ABC中，∠BAC=90°，AD⊥BC于D，BE平分∠ABC交AD•于E，EF∥BC交AC于F，那么AE与CF相等吗？请验证你的结论．中考真题实战21．（长沙）如下左图所示，在四边形ABCD中，AB∥CD，要使四边形ABCD•为平行四边形，则应添加的条件是________．（添加一个即可）22．（呼和浩特）如上右图所示，已知E，F，G，H是四边形ABCD各边的中点，•则S四边形EFGH：S四边形ABCD的值是_________．23．（南京）已知如图19-1-55所示，在Y ABCD中，E，F分别是AB，CD的中点.求证：（1） △AFD≌△CEB．（2）四边形AECF是平行四边形．答案:1．C 2．C 3．D4．（1）× （2）× （3）∨ （4）∨ （5）∨ （6）× 5．AD=BC或AB∥CD6．解：∵∠1=∠2，∴AD∥BC．又∵∠3=∠4，∴AB∥CD．∴四边形ABCD是平行四边形．7．证明：∵AB=CD，BC=AD，∴四边形ABCD是平行四边形．∴AB∥CD，∴∠BAE=∠DCF．又∵AE=CE，∴△ABE≌△CDF（SAS），∴BE=EF．8．证明：∵FC∥AB，∴∠DAC=∠ACF，∠ADF=∠DFC．又∵AE=CE，∴△ADE≌△CF E（AAS），∴DE=EF．∵AE=CE，∴四边形ADCF为平行四边形．∴CD=AF．9．证明：∵四边形ABCD是平行四边形．∴AB//DC．又∵BE=AB，∴BE//DC，∴四边形BDCE是平行四边形．∵DC∥BF，∴∠CDF=∠F．同理，∠BDM=∠DMC．∵BD=BF，∴∠BDF=∠F．∴∠CDF=∠CMD，∴CD=CM．10．证明：过点B作BG∥AD，交DC的延长线于G，连接EG．∵DC∥AB，∴ABGD是平行四边形，∴BG// AD．在□ACED中，AD//CE，∴CE//BG．∴四边形BCEG为平行四边形，∴EF=FB．11．证明：∵四边形ABCD是平行四边形，∴AB//CD，AD=BC．∵CE=CD，∴AB//CE，∴四边形ABEC为平行四边形．∴BF=FC，∴OF//12AB，即AB=2OF．12．证明：∵四边形ABCD是平行四边形，∴AB∥CD，AD∥BC．又∵EF∥AB，∴EF∥CD．∴四边形ABEF，ECDF均为平行四边形．又∵M，N分别为Y ABEF和Y ECDF对角线的交点．∴M为AE的中点，N为DE的中点，即MN为△AED的中位线．∴MN∥AD且MN=12 AD．13．4 14．B15．解：EFGH是平行四边形，连接AC，在△ABC中，∵EF是中位线，∴EF//12 AC．同理，GH//12 AC．∴EF//GH，∴四边形EFGH为平行四边形． 16．解：∵EF，DE，DF是△ABC的中位线，∴EF=12AB，DE=12AC，DF=12BC．又∵AB=10cm，BC=8cm，AC=6cm，∴EF=5cm，DE=3cm，DF=4cm，而32+42=25=52，即DE2+DF2=EF2．∴△EDF为直角三角形．∴S△EDF=12DE·DF=12×3×4=6（cm2）．17．解：∵M，N分别是AC，BC的中点．∴MN是△ABC的中位线，∴MN=12 AB．∴AB=2MN=2×20=40（m）．故A，B两点间的距离是40m．18．解：连接DE．∵四边形ABCD是平行四边形，∴AB//CD．∵DF=12CD，AE=12AB，∴DF//AE．∴四边形ADFE是平行四边形．∴EF=AD=1cm．∵AB=2AD，∴AB=2cm．∵AB=2AD，∴AB=2AE，∴AD=AE．∴∠1=∠4．∵∠A=60°，∠1+∠4+∠A=180°，∴∠1=∠A=∠4=60°．∴△ADE是等边三角形，∴DE=AE．∵AE=BE，∴DE=BE，∴∠2=∠3．∵∠1=∠2+∠3，∠1=60°，∴∠2=∠3=30°．∴∠ADB=∠3+∠4=90°．222221AB AD-=-3cm）． 19．解：延长AD交BC于F．（1）∵AD⊥CD，∴∠ADC=∠FDC=90°．∵CD平分∠ACB，∴∠ACD=∠FCD．在△ACD与△FCD中，∠ADC=∠FDC，DC=DC，∠ACD=∠FCD．∴△ACD≌△FCD，∴AC=FC，AD=DF．又∵E为AB的中点，∴DE∥BF，即DE∥BC．（2）由（1）知AC=FC，DE=12 BF．∴DE=12（BC-FC）=12（BC-AC）．20．解：AE=CF．理由：过E作EG∥CF交BC于G，∴∠3=∠C．∵∠BAC=90°，AD⊥BC，∴∠ABC+∠C=90°，∠ABD+∠BAD=90°．∴∠C=∠BAD，∴∠3=∠BAD．又∵∠1=∠2，BE=BE，∴△ABE≌△GBE（AAS），∴AE=GE．∵EF∥BC，EG∥CF，∴四边形EGCF是平行四边形，∴GE=CF，∴AE=CF．21．答案不唯一，如AB=CD或AD∥BC．22．1 223．解：（1）在□ABCD中，AD=CB，AB=CD，∠D=∠B．∵E，F分别为AB，CD的中点，∴DF=12CD，BE=12AB，∴DF=BE，∴△AFD≌△CEB．（2）在□ABCD中，AB=CD，AB∥CD．由（1）得BE=DF，∴AE=CE，∴四边形AECF是平行四边形．。
（完整版）平行四边形的性质练习题及答案
（完整版）平⾏四边形的性质练习题及答案平⾏四边形的性质、课中强化（10分钟训练）1?如图3,在平⾏四边形 ABCD 中，下列各式不⼀定正确的是（）A. / 1 + Z 2=180 °B. / 2+ / 3=180 °C. / 3+Z 4=180的周长为（）3. 如图5,」ABCD 中,EF 过对⾓线的交点 O,如果AB=4 cm,AD=3 cm,OF=1 cm,则四边形 BCFE 的周长为 ____________________ .4. 如图6,已知在平⾏四边形 ABCD 中，AB=4 cm , AD=7 cm , / ABC 的平分线交 AD 于点E ,5. 如图7,在平⾏四边形 ABCD 中，点E 、F 在对⾓线6. 如图 8,在 ABCD 中,AE 丄BC 于 E,AF 丄 CD 于 F,BE=2 cm,DF=3 cm, / EAF=60° ,试求 CF 的长.D. /2+ /4=180O , OE 丄AC 交AD 于丘，则⼛DCEA.4 cmB.6 cmC.8 cmD.10 cm交CD 的延长线于点 F ,贝U DF= _____________cm.BD 上，且 BE=DF ，求证:AE=CF.图32?如图4,⼆ABCD 的周长为图5图6图7图8三、课后巩固（30分钟训练）1?⼆ABCD中，/A⽐/ B⼤20。
，则/ C的度数为（）A.60 °B.80 °C.100 °D.120 2?以A、B、C三点为平⾏四边形的三个顶点,作形状不同的平⾏四边形，⼀共可以作（A.0个或3个B.2个C.3个D.4个3?如图9 所⽰，在—ABCD 中,对⾓线AC、BD交于点0,下列式⼦中⼀定成⽴的是（）A.AC 丄BDB.OA=OCC.AC=BDD.AO=OD4?如图10,平⾏四边形ABCD中，对⾓线AC、BD相交于点O ,将⼛AOD平移⾄△ BEC的位置，则图中与OA相等的其他线段有（）A.1条B.2条C.3条D.4条5?如图11,在平⾏四边形ABCD中，EF // AB , GH // AD , EF与GH交于点O,则该图中的平⾏四边形的个数共有（）6?如图12,平⾏四边形ABCD中，AE丄BD , CF丄BD，垂⾜分别为E、F，求证：/ BAE= / DCF.7、如图13所⽰,已知平⾏四边形ABCD中，E、F分别是BC和AD上的点，且BE=DF.求证:△ ABE CDF.A.7个B.8个C.9个D.11 个图12图138?如图14,已知四边形ABCD是平⾏四边形，/ BCD的平分线CF交边AB于F，/ ADC的平分线DG交边AB于G.⑴求证:AF=GB ;（2）请你在已知条件的基础上再添加⼀个条件，使得△EFG是等腰直⾓三⾓形，并说明理由?19.1.2平⾏四边形的判定⼆、课中强化（10分钟训练）1?如图3,在ABCD中，对⾓线AC、BD相交于点O,E、F是对⾓线AC上的两点，当E、F满⾜下列哪个条件时，四边形DEBF不⼀定是平⾏四边形（）A.AE=CFC.Z ADE= / CBFD. / AED= / CFB，使四边形AECF是平⾏四边形.4. 如图6,AD=BC,要使四边形ABCD是平⾏四边形，还需补充的⼀个条件是：__________________5. 如图，在，ABCD中，已知M和N分别是边AB、DC的中点，试说明四边形BMDN也是平⾏四边形.2.如图4,AB 喪DC ,DC=EF=10 ,DE=CF=8，则图中的平⾏四边形有，理由分别是图4 图53.如图5,E、F是平⾏四边形ABCD对⾓线BD上的两点,B.DE=BF图14三、课后巩固（30分钟训练）1?以不在同⼀直线上的三个点为顶点作平⾏四边形最多能作（）是平⾏四边形的是（）4?已知四边形 ABCD 的对⾓线 AC 、BD 相交于点② OA=OC :③ AB=CD ;④/ BAD= / DCB :⑤ AD // BC.（1）从以上5个条件中任意选取 2个条件，能推出四边形 ABCD 是平⾏四边形的有（⽤序号表⽰）： _____________________________ :（2）对由以上5个条件中任意选取 2个条件，不能推出四边形请选取⼀种情形举出反例说明平⾏四边形？6?如图，E 、F 是四边形ABCD 的对⾓线 AC 上的两点，AF=CE , DF=BE , DF // BE. 求证：⑴△AFD ◎△ CEB;（2）四边形ABCD 是平⾏四边形A.4个B.3个C.2个D.1个2?下⾯给出了四边形 ABCD 中/A 、/ B 、/ C 、/ D 的度数之⽐,其中能判定四边形 ABCDA.1 : 2 : 3 : 4B. 2 : 2 : 3 : 3C. 2 : 3 : 3 : 2D. 2 : 3 : 2 : 33?九根⽕柴棒排成如右图形状，图中 ____ 个平⾏四边形 ,你判断的根据是O ,给出下列 5个条件：①AB // CD ;5?若三条线段的长分别为20 cm,14 cm,16 cm,以其中两条为对⾓线 ABCD 是平⾏四边形的,，另17?如图,已知DC // AB，且DC= — AB , E为AB的中点.2(1) 求证:△ AED ◎△ EBC ;(2) 观察图形，在不添加辅助线的情况下，除△EBC⼣⼘，请再写出两个与△ AED的⾯积相等的三⾓形(直接写出结果，不要求证明)： ___________________________8?如图,已知⼆ABCD中DE丄AC,BF丄AC,证明四边形DEBF为平⾏四边形9?如图，已知■ ABCD中,E、F分别是AB、CD的中点?求证:(1) △ AFD ◎△ CEB;(2) 四边形AECF是平⾏四边形?⼆、课中强化(10 分钟训练)1 答案:D2. 解析：因为四边形ABCD 是平⾏四边形，所以OA=OC. ⼜0E丄AC , 所以EA=EC.贝U △ DCE 的周长=CD+DE+CE=CD+DE+EA=CD+AD. 在平⾏四边形ABCD 中，AB=CD ，AD=BC ，且AB+BC+CD+AD=16 cm ，所以CD+AD=8 cm.答案:C3?解析：0E=0F=1,其周长=BE+BC+CF+EF=CD+BC+EF=AD+AB+2DF=8(cm).答案:8 cm4?解析：由平⾏四边形的性质AB // DC,知/ ABE= / F,结合⾓平分线的性质/ ABE= / EBC，得/ EBC= / F,再根据等⾓对等边得到BC=CF=7 ,再由AB=CD=4 , AD=BC=7 得到DF=DE=AD-AE=3.答案:35?答案：证明：四边形ABCD是平⾏四边形，AB // CD , AB=CD./ ABE= / CDF.AB CD,在⼛ABE和⼛CDF中，ABE CDF ,BE DF .△ ABE ◎△ CDF.AE=CF.6. 解：/ EAF=60°AE 丄BC,AF 丄CD, C=120°. B=60°「./ BAE=30° .AB=2BE=4(cm). CD=4(cm). CF=1(cm).三、课后巩固(30 分钟训练)1 答案:C2. 解析：分两种情况,A、B、C三点共线时，可作0个当点A、B、C不在同⼀直线上时，可作3 个. 答案:A3. 解析：平⾏四边形对⾓线互相平分,所以OA=OC. 答案:B4. 解析：由平⾏四边形的对⾓线互相平分知OA=OC；再由平移的性质：经过平移，对应线段平⾏且相等可得OA=BE.答案:B5?解析：本题借助于平⾏四边形的定义，按照从左到右，从⼩到⼤的顺序，可找到下列的平⾏四边形：DEOH，.HOFC,. DEFC, EAGO，OGBF，EABF，■ DAGH，■ HGBC，⼆ABCD.答案:C6?答案：证明：四边形ABCD是平⾏四边形，AB // CD , AB=CD. /-Z ABE= / CDF ?/ AE 丄BD , CF 丄BD ,「./ AEB= / CFD=90 .△ABE ◎△ CDF. /.Z BAE= Z DCF.7、答案:证明：四边形ABCD是平⾏四边形，AB=CD, Z B= Z D.在⼛ABE和⼛CDF中,AB CD,B D, ?/△ ABE 也⼛CDF.BE DF.8?答案：(1)证明：四边形ABCD是平⾏四边形，? AB // CD. AGD= Z CDG.vZ ADG= Z CDG，/?/ ADG= Z AGD. ? AD=AG ?同理,BC=BF.⼜四边形ABCD 是平⾏四边形，? AD=BC,AG=BF. ? AG-GF=BF-GF ,即AF=GB.(2)解:添加条件EF=EG.理由如下：1 1由(1)证明易知Z AGD= Z ADG= Z ADC , Z BFC= Z BCF= Z BCD.2 2/ AD // BC，/?/ ADC+ Z BCD=180 ./Z AGD+ Z BFC=90 ./Z GEF=90 .⼜v EF=EG ,?△ EFG为等腰直⾓三⾓形.⼆、课中强化(10分钟训练)1. 解析：当E、F满⾜AE=CF时，由平⾏四边形的对⾓线相等知OB=OD,OA=OC , 故OE=OF.可知四边形DEBF是平⾏四边形.当E、F满⾜Z ADE= Z CBF 时，因为AD // BC,所以Z DAE= Z BCF.⼜AD=BC，可证出⼛ADE ◎△ CBF，所以DE=BF , Z DEA= Z BFC.故Z DEF= Z BFE.因此DE // BF，可知四边形DEBF是平⾏四边形.类似地可说明D也可以.。
18.1-18.2平行四边形的性质与判定练习题-新版.doc
E D C OF B A 18.1~18.2平行四边形的性质与判定一、选择题1、下面各条件中，能判定四边形是平行四边形的是 （ ）A 、对角线互相垂直B 、对角线互相平分C 、一组对角相等D 、一组对边相等2、已知下列四个命题：①一组对边平行且相等的四边形；②两组对角分别相等的四边形；③对角线相等的四边形；④对角线互相平分的四边形。
其中能判定平行四边形的命题的个数为 （ ）A 、1个B 、2个C 、3个D 、4个A 、6、6、6B 、6、4、3C 、6、4、6D 、3、4、55、以不共线三点为三个顶点作平行四边形，一共可作平行四边形的个数是 （ ）A 、2个B 、3个C 、4个D 、5个6、 四边形ABCD 的四个角∠A ∶∠B ∶∠C ∶∠D 满足下列哪一条件时，四边形ABCD 是平行四边形？（ ）A 、1∶2∶2∶1B 、2∶1∶1∶1C 、1∶2∶3∶4D 、2∶1∶2∶17、四边形ABCD 中，AD ∥BC ，要判定四边形ABCD 是平行四边形，还应满足（ ）A 、∠A ＋∠C ＝180°B 、∠B ＋∠D ＝180°C 、∠A ＋∠B ＝180°D 、∠A ＋∠D ＝180°8、根据下列条件，得不到平行四边形的是（ ）A 、AB ＝CD ，AD ＝BC B 、AB ∥CD ，AB ＝CD C 、AB ＝CD ，AD ∥BC D 、AB ∥CD ，AD ∥BC9、如图，在□ABCD 中，EF 过对角线的交点，若AB ＝4，BC ＝7，OE ＝3，则四边形EFDC 的周长是（ ）A 、14B 、11C 、10D 、179题图 10题图 11题图 12题图10、如图，线段a 、b 、c 的端点分别在直线l 1、l 2上，则下列说法中正确的是（ ）A ．若l 1∥l 2，则a=bB ．若l 1∥l 2，则a=cC ．若a∥b，则a=bD ．若l 1∥l 2，且a∥b，则a=bA 、13cmB 、3cmC 、7cmD 、11.5cm14、平行四边形的对角线长分别是x 和y ，一边长为12，则下列各组数据可能是x 与y 的值的是（ ）A 、8与14B 、10与14C 、18与20D 、10与3615、□ABCD 中,∠A:∠B=13：5，则∠A 和∠B 的度数分别为（ ）A ．80° ，100° B．130°，50° C ．160°，20° D ．60°，120°16、一个平行四边形的两条对角线把它分成的全等三角形的对数是( )A.2B.4C.6D.817、E 、F 分别是□ABCD 的边AB 、DC 中点，DE 、BF 交AC 于M 、N ，则( )A.AM=MEB.AM=DFC.AM=NCD.AM ⊥MD18、在□ABCD 中若∠A ＞∠B ，则∠A 的补角与∠B 的余角之和( )A.小于90°B.等于90°C.大于90°D.不能确定19、从等腰三角形底边上任意一点分别作两腰的平行线与两腰所围成的平行四边形的周长等于三角形( )A B E C F DO A B D C A.周长 B.周长的一半 C.腰长 D.两腰长的和20、已知平行四边形两条邻边的长分别是6厘米和4厘米，它们的夹角是60°，则它的面积是( ) A.123cm 2 B.73cm 2 C.63cm 2 D.43cm 221、下列说法正确的有（ ）①平行四边形的对角线相等；②平行四边形的对边相等；③平行四边形的对角线互相垂直；④平行四边形的对角线互相平分；⑤两组对边分别相等的四边形是平行四边形；A.1∶2B.1∶3C.1∶4D.1∶523、如图，□ABCD 和□EAFC 的顶点D 、E 、F 、B 在一条直线上，则下列关系中一定正确的是( )A.DE ＞BFB.DE=BFC.DE ＜BFD.DE=EF=BF23题图 24题图 25题图 4AC AC1、□ABCD 中，∠B －∠A ＝40°，则∠D ＝________.2、□ABCD 的周长是44cm ，AB 比AD 大2cm ，则AB ＝________cm ，AD ＝________cm.3、平行四边形的两个相邻内角的平分线相交所成的角的度数是________.4、平行四边形的两条邻边的比为2∶1，周长为60cm ，则这个四边形较短的边长为________.5、如右上图，在□ABCD 中，AE ⊥BC 于E ，AF ⊥CD 于F ，∠BAD ＝120°，BE ＝2，FD ＝3，则∠EAF ＝________，□ABCD 的周长为________.6、若平行四边形的两邻边的长分别为16和20，两长边间的距离为8，则两短边间的距离为________．7、□ABCD 中，AB=6cm,BC=8cm ，∠B=70°,则AD=__________,CD=__________, ∠D=__________,∠A=__________,∠C=__________.8、平行四边形周长为50cm ，两邻边之差为5cm,各边长为 . 9、如右图，平行四边形ABCD 的周长为30cm,它的对角线AC 和BD 相交于O,且△AOB 的周长比△BOC 的周长大5cm,则AB=________，BC=________. 10、□ABCD 的对角线AC 和BD 相交于O,则其中全等的三角形有________对.(1)由平行四边形的一个顶点在形内向两边引垂线，二垂线夹角为65°，则这个平行四边形各内角的度数分别为________.(2)在□ABCD 中，∠A 的补角与∠B 的和等于210°，则∠A=________,∠B=________.(3)在□ABCD 中，AB ∶BC=1∶2，∠D=30°，AE ⊥BC 于E ，AE=3cm,则AB=________cm.这个平行四边形的周长是________cm.(4)平行四边形周长是40cm ，二邻边的比为3∶2，则两邻边长分别是________.(5)在□ABCD 中，两邻边AB 、AD 的比是1∶2，M 是大边AD 的中点，则∠BMC 的度数是________.(6)平行四边形的周长为50厘米，那么它两邻边之和是______cm ，每条对角线的长不能超过______cm.(7)□ABCD 中，周长为50厘米，AB=15cm ，∠A=30°，则此平行四边形的面积为______cm 2.(8)□ABCD 的周长为50厘米，对角线交于O 点，△AOB 的周长比△BOC 的周长大5厘米，则AB 、BC 的长分别是______、______.(9)有五条平行的直线，每相邻两条的距离相等，有一条直线和这组平行线相交成30°角，它介于相邻两条A BF CD EA BE CFDA BFOC DE平行线之间的线段长是10厘米，则这一组平行线最外面两条之间的距离是______厘米.(10)已知平行四边形周长为68厘米，被两条对角线分成两个不同的三角形的周长的和等于82厘米，两条对角线的长度比为2∶1，则两条对角线的长分别为______厘米，______厘米.11、等腰△ABC底边上任意一点D，AB=AC=5cm，过D作DE∥AC交AB于E，DF∥AB交AC于F，则四边形AEDF的周长为．12、如图（在下页），已知等边△ABC的边长为8，P是△ABC内一点，PD∥AC，PE∥AD，PF∥BC，点D，E，F分别在AB，BC，AC上，则PD+PE+PF= ．第12题第13题第14题13、如图，在□ABCD中，E，F分别为AB，DC的中点，连接DE，EF，FB，则图中共有个平行四边形．14、如图，在□ABCD中，E，F是对角线AC上的两点且AE=CF，在①BE=DF；②BE∥DF；③AB=DE；④四边形EBFD为平行四边形；⑤S△ADE=S△ABE；⑥AF=CE这些结论中正确的是．15、如图，已知梯形ABCD，AD∥BC，∠B+∠C=90°，EF=10，E，F分别是AD，BC的中点，则BC﹣AD= ．第15题第16题第17题16、如图，六边形ABCDEF的每个内角都是120°，AB∥DE，BC∥EF，CD∥FA，且AB=4，BC=5，CD=6，DE=7，那么，六边形ABCDEF的周长是．17、如图，△ABC中，如果AB=30，BC=24，AC=27，DN∥GM∥AB，EG∥DF∥BC，FM∥EN∥AC，则图中阴影部分的三个三角形周长之和为．18、如右图所示，木工师傅把曲尺的一边紧靠木板边缘，从曲尺的另一边上可以读出木板另一边缘的刻度，然后将曲尺移动到另一处（紧靠木板边缘），如果两次读数相同，说明木板两个边缘平行，其中道理是 .三、解答题与证明题1、在□ABCD中，E、F分别在DC、AB上，且DE＝BF。
平行四边形的性质与判定练习题
平行四边形的性质与判定练习题
平行四边形的性质
平行四边形是指具有以下性质的四边形：
- 两对对边分别相等；
- 两对对边分别平行；
- 两对对角线分别相等。
平行四边形的判定方法
平行四边形可以通过以下方法进行判定：
方法一：边长判定法
若一个四边形的两对对边分别相等，则该四边形为平行四边形。
方法二：角度判断法
若一个四边形的两对对角线所代表的角度相等，则该四边形为
平行四边形。
方法三：结合边长与角度判断法
若一个四边形的两对对边分别平行且两对对角线所代表的角度相等，则该四边形为平行四边形。
练题
1. 判定下列四边形是否为平行四边形：
正方形 ABCD，其中 AB = BC = CD = DA
矩形 EFGH，其中 EF = FG = GH = HE
菱形 IJKL，其中 IJ = JK = KL = LI
梯形 MNOP，其中 MN ∥ OP
平行四边形 QRST，其中 QR ∥ TS
2. 对于练题1中的每个四边形，判断其是否满足平行四边形的判定方法。
3. 写出一个例子，展示一种方法可以判定一个四边形是平行四边形的。
请按照题目要求回答练习题，并在回答中使用适当的数学符号和推理步骤。
y平行四边形性质判定
EDC O FBA AB ECFD 1. 能够判定一个四边形是平行四边形的条件是 ( )A. 一组对角相等B. 两条对角线互相平分C. 两条对角线互相垂直D. 一对邻角的和为180° 2. 在平行四边形ABCD 中,∠B-∠A=20°,则∠D 的度数是 ( )A. 80°B. 90°C. 100°D. 110°3、将一张平行四边形的纸片折一次，使得折痕平分这个平行四边形的面积，则这样的折纸方法共有( ) A ．1种 B ．2种 C ．3种 D ．无数种4.平行四边形的两条对角线及一边的长可依次取（ ）A 、6、6、6 B 、6、4、3 C 、6、4、6 D 、3、4、55.如图所示，在ABCD 中，EF 过对角线的交点，若AB ＝4，BC ＝7，OE ＝3，则四边形EFDC 的周长是（ ）A 、14B 、11C 、10D 、176.在ABCD 中，M 为CD 的中点，如DC =2AD ，则AM 、BM 夹角度数是（ ） A.90° B.95° C.85° D.100°7.如图2，□ABCD 中，BD ＝CD ，∠C ＝700，AE ⊥BD 于点E ，则∠DAE ＝（ ） A 、200B 、250C 、300D 、3508. 平行四边形的一组对角的平分线 ( ) A. 一定相互平行 B. 一点相交 C. 可能平行也可能相 D. 平行或共线 9、一个四边形的三个内角的度数依次如下选项，其中是平行四边形的是（ ） A 、88°，108°，88°B 、88°，104°，108°C 、88°，92°，88°D 、88°，92°，92°10.下列条件中，能判定四边形是平行四边形的条件是( )A.一组对边平行，另一组对边相等B.一组对边平行，一组对角相等C.一组对边平行，一组邻角互补D.一组对边相等，一组邻角相等 11. 已知平行四边形的面积是144,相邻两边上的高分别为8和9,则它的周长是______________. 12.□ABCD 的周长是30，AC 、BD 相交于点O ，△OAB 的周长比△OBC 的周长大3，则AB ＝ 。
(完整版)平行四边形的性质练习题及答案-1
平行四边形的性质一、课中强化(10分钟训练)1.如图3,在平行四边形ABCD中，下列各式不一定正确的是( )A.∠1+∠2=180°B.∠2+∠3=180°C.∠3+∠4=180°D.∠2+∠4=180°图3 图4 图52.如图4,ABCD的周长为16 cm，AC、BD相交于点O，OE⊥AC交AD于E，则△DCE的周长为( )A.4 cmB.6 cmC.8 cmD.10 cm3.如图5，ABCD中,EF过对角线的交点O,如果AB=4 cm,AD=3 cm,OF=1 cm,则四边形BCFE的周长为__________________.4.如图6,已知在平行四边形ABCD中，AB=4 cm，AD=7 cm，∠ABC的平分线交AD于点E，交CD的延长线于点F，则DF=_____________ cm.图6 图75.如图7,在平行四边形ABCD中，点E、F在对角线BD上，且BE=DF，求证:AE=CF.6.如图8,在ABCD中,AE⊥BC于E,AF⊥CD于F,BE=2 cm,DF=3 cm,∠EAF=60°,试求CF的长.图8二、课后巩固(30分钟训练)1.ABCD中,∠A比∠B大20°,则∠C的度数为( )A.60°B.80°C.100°D.120°2.以A、B、C三点为平行四边形的三个顶点,作形状不同的平行四边形,一共可以作( )A.0个或3个B.2个C.3个D.4个3.如图9所示,在ABCD中,对角线AC、BD交于点O,下列式子中一定成立的是( )A.AC⊥BDB.OA=OCC.AC=BDD.AO=OD图9 图10 图11 4.如图10,平行四边形ABCD中，对角线AC、BD相交于点O，将△AOD平移至△BEC的位置，则图中与OA相等的其他线段有( )A.1条B.2条C.3条D.4条5.如图11,在平行四边形ABCD中，EF∥AB，GH∥AD，EF与GH交于点O，则该图中的平行四边形的个数共有( )A.7个B.8个C.9个D.11个6.如图12,平行四边形ABCD中，AE⊥BD，CF⊥BD，垂足分别为E、F，求证:∠BAE=∠DCF.图127、如图13所示,已知平行四边形ABCD中,E、F分别是BC和AD上的点,且BE=DF.求证:△ABE≌△CDF.图138.如图14,已知四边形ABCD是平行四边形，∠BCD的平分线CF交边AB于F，∠ADC的平分线DG交边AB于G.(1)求证:AF=GB；(2)请你在已知条件的基础上再添加一个条件，使得△EFG是等腰直角三角形,并说明理由.图1419.1.2 平行四边形的判定一、课中强化(10分钟训练)1.如图3,在ABCD中，对角线AC、BD相交于点O,E、F是对角线AC上的两点，当E、F满足下列哪个条件时，四边形DEBF不一定是平行四边形( )A.AE=CFB.DE=BFC.∠ADE=∠CBFD.∠AED=∠CFB2.如图4,AB DC，DC=EF=10，DE=CF=8，则图中的平行四边形有_________________，理由分别是_________________、____________________.图4 图5 图6 3.如图5,E、F是平行四边形ABCD对角线BD上的两点，请你添加一个适当的条件:__________，使四边形AECF是平行四边形.4.如图6,AD=BC,要使四边形ABCD是平行四边形,还需补充的一个条件是:______ ________.5.如图,在ABCD中,已知M和N分别是边AB、DC的中点,试说明四边形BMDN 也是平行四边形.二、课后巩固(30分钟训练)1.以不在同一直线上的三个点为顶点作平行四边形最多能作( )A.4个B.3个C.2个D.1个2.下面给出了四边形ABCD中∠A、∠B、∠C、∠D的度数之比，其中能判定四边形ABCD是平行四边形的是( )A.1∶2∶3∶4B.2∶2∶3∶3C.2∶3∶3∶2D.2∶3∶2∶33.九根火柴棒排成如右图形状,图中_____个平行四边形,你判断的根据是________________.4.已知四边形ABCD的对角线AC、BD相交于点O，给出下列5个条件:①AB∥CD；②OA=OC；③AB=CD；④∠BAD=∠DCB；⑤AD∥BC. (1)从以上5个条件中任意选取2个条件，能推出四边形ABCD是平行四边形的有(用序号表示):_____________________________;(2)对由以上5个条件中任意选取2个条件，不能推出四边形ABCD是平行四边形的，请选取一种情形举出反例说明.5.若三条线段的长分别为20 cm,14 cm,16 cm,以其中两条为对角线,另一条为一边,是否可以画平行四边形?6.如图,E 、F 是四边形ABCD 的对角线AC 上的两点，AF=CE ，DF=BE ，DF ∥BE. 求证:(1)△AFD ≌△CEB;(2)四边形ABCD 是平行四边形.7.如图,已知DC ∥AB ，且DC=21AB ，E 为AB 的中点.(1)求证:△AED ≌△EBC ；(2)观察图形，在不添加辅助线的情况下，除△EBC 外，请再写出两个与△AED 的面积相等的三角形(直接写出结果，不要求证明):______________________________.8.如图,已知ABCD中DE⊥AC,BF⊥AC,证明四边形DEBF为平行四边形.9.如图,已知ABCD中,E、F分别是AB、CD的中点.求证:(1)△AFD≌△CEB;(2)四边形AECF是平行四边形.二、课中强化(10分钟训练)1答案:D2.解析：因为四边形ABCD是平行四边形，所以OA=OC.又OE ⊥AC ，所以EA=EC.则△DCE 的周长=CD+DE+CE=CD+DE+EA=CD+AD.在平行四边形ABCD 中，AB=CD ，AD=BC ，且AB+BC+CD+AD=16 cm ，所以CD+AD=8 cm.答案:C3.解析：OE=OF=1,其周长=BE+BC+CF+EF=CD+BC+EF=AD+AB+2DF=8(cm). 答案:8 cm4.解析：由平行四边形的性质AB ∥DC,知∠ABE=∠F ，结合角平分线的性质∠ABE=∠EBC ，得 ∠EBC=∠F ，再根据等角对等边得到BC=CF=7， 再由AB=CD=4，AD=BC=7得到DF=DE=AD-AE=3. 答案:35.答案：证明：∵四边形ABCD 是平行四边形, ∴AB ∥CD ，AB=CD. ∴∠ABE=∠CDF.在△ABE 和△CDF 中，⎪⎩⎪⎨⎧=∠=∠=.,,DF BE CDF ABE CD AB∴△ABE ≌△CDF. ∴AE=CF.6.解：∵∠EAF=60°,AE ⊥BC,AF ⊥CD,∴∠C=120°.∴∠B=60°.∴∠BAE=30°. ∴AB=2BE=4(cm).∴CD=4(cm).∴CF=1(cm). 三、课后巩固(30分钟训练) 1答案:C2.解析：分两种情况,A 、B 、C 三点共线时,可作0个,当点A 、B 、C 不在同一直线上时,可作3个.答案:A3.解析：平行四边形对角线互相平分,所以OA=OC.答案:B4.解析：由平行四边形的对角线互相平分知OA=OC ；再由平移的性质:经过平移，对应线段平行且相等可得OA=BE.答案:B 5.解析：本题借助于平行四边形的定义，按照从左到右，从小到大的顺序，可找到下列的平行四边形:DEOH ，HOFC ，DEFC ，EAGO ，OGBF ，EABF ，DAGH ，HGBC ，ABCD.答案:C 6.答案:证明：∵四边形ABCD 是平行四边形, ∴AB ∥CD，AB=CD.∴∠ABE=∠CDF ∵AE ⊥BD，CF ⊥BD，∴∠AEB=∠CFD=90°.∴△ABE ≌△CDF.∴∠BAE=∠DCF. 7、答案:证明：∵四边形ABCD 是平行四边形, ∴AB=CD,∠B=∠D. 在△ABE 和△CDF 中,⎪⎩⎪⎨⎧=∠=∠=.,,DF BE D B CD AB ∴△ABE ≌△CDF. 8.答案：(1)证明：∵四边形ABCD 是平行四边形，∴AB ∥CD.∴∠AGD=∠CDG . ∵∠ADG=∠CDG ，∴∠ADG=∠AGD.∴AD=AG .同理,BC=BF.又∵四边形ABCD 是平行四边形，∴AD=BC,AG=BF.∴AG-GF=BF-GF ， 即AF=GB.(2)解:添加条件EF=EG .理由如下: 由(1)证明易知∠AGD=∠ADG=21∠ADC ，∠BFC=∠BCF=21∠BCD. ∵AD ∥BC ，∴∠ADC+∠BCD=180°.∴∠AGD+∠BFC=90°.∴∠GEF=90°. 又∵EF=EG ，∴△EFG 为等腰直角三角形.二、课中强化(10分钟训练)1.解析：当E 、F 满足AE=CF 时，由平行四边形的对角线相等知OB=OD,OA=OC ，故OE=OF.可知四边形DEBF 是平行四边形.当E 、F 满足∠ADE=∠CBF 时，因为AD ∥BC ，所以∠DAE=∠BCF. 又AD=BC ，可证出△ADE ≌△CBF ，所以DE=BF ，∠DEA=∠BFC. 故∠DEF=∠BFE.因此DE ∥BF ，可知四边形DEBF 是平行四边形.类似地可说明D 也可以. 答案:B2.解析：因为AB DC ，根据一组对边平行且相等的四边形是平行四边形可判定四边形ABCD 是平行四边形；DC=EF ，DE=CF,根据两组对边分别相等的四边形是平行四边形可判定四边形CDEF 是平行四边形.答案:四边形ABCD ，四边形CDEF 一组对边平行且相等的四边形是平行四边形 两组对边分别相等的四边形是平行四边形3.解析：根据平行四边形的定义和判定方法可填BE=DF ；∠BAE=∠CDF 等. 答案:BE=DF 或∠BAE=∠CDF 等任何一个均可4.解析：根据平行四边形的判定定理,知可填①AD ∥BC,②AB=CD,③∠A+∠B=180°,④∠C+∠D=180°等.答案:不唯一,以上几个均可.5.答案：证明：∵ABCD,∴AB CD.∵M 、N 是中点,∴BM=21AB,DN=21CD.∴BM DN. ∴四边形BMDN 也是平行四边形.三、课后巩固(30分钟训练)1.解析：要求最多能作几个，只要连结起三个顶点后构成三角形，分别以其中一边作为对角线，另两边作为平行四边形的邻边作图，即可得出三种.答案:B2.解析：由两组对角分别相等的四边形是平行四边形易知，要使四边形ABCD 是平行四边形需满足∠A=∠C ，∠B=∠D ，因此∠A 与∠C ，∠B 与∠D 所占的份数分别相等.答案:D3.答案：有3 两组对边分别相等的四边形是平行四边形4.解析：本题是条件开放性试题，要使四边形ABCD 是平行四边形，从边、角、对角线上考虑共有5种判定方法，因此只需将任意两个条件组合加以 评砼卸? 答案:(1)①与②；①与③；①与④；①与⑤；②与⑤；④与⑤(2)③与⑤两个条件不能推出四边形ABCD 是平行四边形.如图，AB=CD 且AD ∥BC ，而四边形ABCD 不是平行四边形.5.解析：由平行四边形对角线互相平分,能否画平行四边形,应以任两条的一半和第三边为三边,看是否能构成三角形即可.20,16或20,14为对角线,另一条为一边可画平行四边形.6.答案:证明：(1)∵DF ∥BE ，∴∠AFD=∠CEB.又∵AF=CE ，DF=BE ，∴△AFD ≌△CEB.(2)由(1)△AFD ≌△CEB 知AD=BC ，∠DAF=∠BCE ，∴AD ∥BC.∴四边形ABCD 是平行四边形.7.答案:证明：(1)∵E 为AB 的中点，∴AE=EB=21AB.∵DC=21AB ，DC ∥AB ， ∴AE DC ，EB DC.∴四边形AECD 和四边形EBCD 都是平行四边形. ∴AD=EC ，ED=BC.又∵AE=BE ，∴△AED ≌△EBC.(2)△ACD ，△ACE ，△CDE(写出其中两个三角形即可)8.答案:证明：在ABCD 中,AD=BC,AD ∥BC,∴∠DAC=∠BCA.又∵∠DEA=∠BFC=90°,∴Rt △ADE ≌Rt △CBF.∴DE=BF.同理,可证DF=BE.∴四边形DEBF 为平行四边形.9.答案:证明：(1)在ABCD 中,AD=CB,AB=CD,∠D=∠B.∵E 、F 分别是AB 、CD 的中点,∴DF=21CD,BE=21AB.∴DF=BE.∴△AFD ≌△CEB. (2)在ABCD 中,AB=CD,AB ∥CD.由(1)得BE=DF,∴AE=CF.∴四边形AECF 是平行四边形.。
平行四边形性质和判定测试
一、选择题1、平行四边形的两邻边分别为3、4，那么其对角线必（）A.大于1B.小于7C.大于1且小于7D.小于7或大于12、在ABCD中，M为CD的中点，如DC=2AD，则AM、BM夹角度数是（）A.90°B.95°C.85°D.100°3、如图，四边形ABCD是平行四边形，∠D=120°，∠CAD=32°.则∠ABC、∠CAB的度数分别为（）A.28°，120°B.120°，28°C.32°，120°D.120°，32°4、在□ABCD中，∠A∶∠B∶∠C∶∠D的值可以是（）A.1∶2∶3∶4B.1∶2∶2∶1C.1∶1∶2∶2D.2∶1∶2∶15、平行四边行的两条对角线把它分成全等三角形的对数是（）A.2B.4C.6D.86、在□ABCD中，∠A、∠B的度数之比为5∶4，则∠C等于（）A.60°B.80°C.100°D.120°7、A、B、C、D在同一平面内，从①AB∥CD；②AB=CD；③BC=AD；④BC∥AD这四个条件中任选两个，能使四边形ABCD是平行四边形的选法有（）A.3种B.4种C.5种D.6种8、能够判别一个四边形是平行四边形的条件是（）A.一组对角相等B.两条对角线互相垂直且相等C.两组对边分别相等D.一组对边平行9、下列条件中不能确定四边形ABCD是平行四边形的是（）A.AB=CD，AD∥BCB.AB=CD，AB∥CDC.AB∥CD，AD∥BCD.AB=CD，AD=BC10．已知在平行四边形ABCD中，AB=6，BC=4，若∠B=45°，则平行四边形ABCD的面积为（）A．8 B．122C．162D．2411．将一张平行四边形纸片折一次，使得折痕平分这个平行四边形的面积，•则这样的折纸方法有（）A．1种B．2种C．3种D．无数种12．在平行四边形ABCD中，∠A的平分线交BC于点E，若CD=10，AD=16，则EC为（）A．10 B．16 C．6 D．13二、填空题1、以不在一条直线上的三点A、B、C为顶点的平行四边形共有个3、ABCD中，若∠A∶∠B=1∶3,那么∠A=________，∠B=________，∠C=________，∠D=________.4、平行四边形的周长等于56 cm，两邻边长的比为3∶1，那么这个平行四边形较长的边长为_______.5.□ABCD的周长为80cm，对角线AC、BD相交于O，若△OAB的周长比△OBC的周长小8cm，则AB＝ cm.6.一个四边形的边长依次为a，b，c，d，且a2+b2+c2+d2＝2ac+2bd，则这个四边形是 .7. 如图，四边形ABCD中，AD=BC，F、E、G分别是AB、CD、AC的中点，若∠DAC=200，∠ACB=600，则∠FEG=.三、解答题1、如图，四边形ABCD是平行四边形，BD⊥AD，求BC，CD及OB的长.2..如图，平行四边形ABCD中，M、N分别为AD、BC的中点，连结AN、DN、BM、CM，且AN、BM交于点P，CM、DN交于点Q.证明：四边形MGNP是平行四边形3、已知如图：在ABCD中，延长AB到E，延长CD到F，使BE=DF，证明：线段AC与EF是否互相平分5.已知E为平行四边形ABCD边的延长线上的一点，且CE=DC,连结AE，分别交BC、BD于F、G，连结AC 交BD于O点,连AF。
(完整版)平行四边形的性质及判定典型例题
平行四边形的性质及判定 （典型例题）1.平行四边形及其性质例1如图，O 是卜二・ABCD 对角线的交点.△ OBC 的周长为59, BD=38 , AC=24，贝卩AD= __ 若厶OBC 与厶OAB 的周长之差为 15，贝y AB=QABCD 的周长= _____ .AC ,可得BC ,再由平行四边形对边相等知 AD=BC ，由平行四 边形的对角线互相平分，可知△ OBC 与厶OAB 的周长之差就为BC 与AB 之差，可得AB ，进而可得」ABCD 的周长.解 EBCD 中0A 二= OB = OD = |E D （平行四边形的对角线互相平分）•••△ OBC 的周长=0B + 0C +EC分析: 根据平行四边形对角线互相平先 所OC =1=19 + 12 + BC=59••• BC=28—ABCD 中，•BC=AD(平行四边形对边相等)•AD=28△ OBC的周长-△ OAB的周长=(OB + OC + BC)-(OB + OA+AB)=BC-AB=15•AB=13•••二ABCD的周长=AB + BC + CD + AD=2(AB + BC)=2(13 + 28)=82说明：本题条件中的△ OBC占厶OAB的周长之差为15”，用符号语言表示出来后，便容易发现其实质，即BC与AB之差是15 .例2判断题(1) 两条对边平行的四边形叫做平行四边形. ()(2) 平行四边形的两角相等.()(3) 平行四边形的两条对角线相等.()(4) 平行四边形的两条对角线互相平分. ()(5) 两条平行线中，一条直线上任一点到另一条直线的垂线段叫做两条平行线的距离.()(6) 平行四边形的邻角互补.()分析：根据平行四边形的定义和性质判断.解：(1) 错两组对边分别平行的四边形叫做平行四边形”是两组对边，而不是两条对边.如图四边形ABCD，两条对边AD // BC .显然四边形ABCD 不是平行四边形．(2) 错平行四边形的性定理1，“平行四边形的对角相等．”对角是指四边形中设有公共边的两个角，也就是相对的两个角．(3) 错平行四边形的性质定理3，“平行四边形的对角线互相平分．”一般地不相等．(矩形的两条对角线相等)．(4) 对根据平行四边形的性质定理 3 可判断是正确的．(5) 错线段图形，而距离是指线段的长度，是正值正确的说法是：两条平行线中，一条直线上任一点到另一条直线的垂线段的长度叫做这两条平行线的距离．(6) 对由定义知道，平行四边形的对边平行，根据平行线的性质可知．平行四边形的邻角互补．例3 .如图1,在二ABCD中，E、F是AC上的两点.且AE=CF .求证：ED // BF .分析：欲址DE // BF，只需/ DEC二/ AFB,转证=/ ABF CDF, 因卜二，ABCD，则有AB丄CD，从而有/ BAC= / CDA .再由AF=CF 得AF=CE .满足了三角形全等的条件.证明：v AE=CFAE+EF二CF+EF••• AF=CE在二ABCD中AB // CD（平行四边形的对边平行）• / BAC= / DCA（两直线平行内错角相等）AB=CD（平行四边形的对边也相等）•••△ ABF刍乂 CDE（SAS）•••/ AFB= / DCE• ED // BF（内错角相等两直线平行）说明：解决平行四边形问题的基本思想是化为三角形问题不处理.例4如图已知在△ ABC中DE // BC // FG，若BD=AF、求证; DE + FG=BC .分析1:要证DE + FG=DC由于它们是平行线，由平行四边形定义和性质.考虑将DE平移列BC上为此，过E（或D）作EH // AB（或DM // AC）,得至U DE=BH、只需证HC=FG ,因AF=BD=EH , / CEH=/ A. / AGF = Z C所以△ AFG幻/ EHC .此方法称为截长法.分析2:过C点作CK // AB交DE的延长线于K，只需证FG=EK , 转证△ AFG CKE .过E作EH // AB交于Hv DE // BC•••四边形DBHE是平行四边形（平行四边形定义）••• DB=EHDE=BH（平行四边形对边也相等）又BD=AF• AF=EHv BC // FGAGF= / C（两直线平行同位角相等）同理 / A= / CEH• △ AFG EHC(AAS)••• FG=HC••• BC二BH+HC二DE二FG.过C作CK // AB交DE的延长线于K.v DE // BC•四边形DBCK是平行四边形（平行四边形定义）•CK=BD DK=BC（平行四边形对边相等）又BD=AF•AF=CKv CK // AB• / A= / ECK（两直线平行内错角相等）v BC // FG•••/ AGF二/ AED（两直线平行同位角相等）又/ CEK二/ AED（对顶角相等）•••/ AGF= / CEK•••△ AFG S' CKE（AAS）FG=EKDE+EK=BC• DE+FG=BC例 5 如图I—ABCD 中，/ ABC=3 /A，点 E 在CD 上,CE=1 , EF丄CD交CB延长线于F，若AD=1，求BF的长.u --- ---------- r分析：根据平行四边形对角相等，邻角互补，可得/ C= / F=45°进而由勾股定理求出CF ,再根据平行四边形对边相等，得BF的长.解：在二ABCD 中，AD // BC•••/ A +/ ABC=180 （两直线平行同旁内角互补）vZ ABC=3 / A•••/ A=45 ,Z ABC=135•••Z C= Z A=45 （平行四边形的对角相等）•EF 丄CD•Z F=45°（直角三角形两锐角互余）•EF=CE=1在RtAOEF中,CF = JCE之》EF金=（勾股定理）v AD=BC=1二BF = CF”EC = Q[例6如图1，‘ ■ ABCD中，对角线AC长为10cm , Z CAB=30 , AB长为6cm，求一ABCD的面积.解：过点C作CH丄AB，交AB的延长线于点H .(图2)vZ CAB=30-■.CH 二丄= 1 X10=52 2••• S—ABCD = AB-CH = 6X5=30(cm2)答：二ABCD的面积为30cm2 .说明：由于二=底＞高，题设中已知AB的长，须求出与底AB 相应的高，由于本题条件的制约，不便于求出过点D的高，故选择过点C 作高.例7如图，E、F分别在’・ABCD的边CD、BC上，且EF //求证：S△ ACE二S △ ABF分析：运用平行四形的性质，利用三角形全等，将其转化为等底同高的三角形.证明：将EF向两边延长分别交AD、AB的延长线于G、H.二ABCD DE // AB•••/ DEG= / BHF（两直线平行同位角相等）/ GDE= / DAB（同上）AD // BC•••/ DAB= / FBH（同上）:丄 GDE= / FBHv DE // BH , DB // EH•四边形BHED是平行四边形V DE二BH（平行四边形对边相等）GDE 刍乂 FBH（ASA）••• S△ GDE=S △ FBH（全等三角形面积相等）.GE=FH（全等三角形对应边相等）.S△ ACE=S △ AFH（等底同高的三角形面积相等）.S △ ADE = S △ ABF说明：平行四边形的面积等于它的底和高的积.即S二二a・ha .a 可以是平行四边形的任何一边，h必须是a边与其对边的距离.即对应的高，为了区别，可以把高记成ha，表明它所对应的底是a.例8如图，在二ABCD中，BE平分/ B交CD于点E, DF 平分/ D交AB于点F,求证BF=DE .分析EF二DE （目标）十BEDP 为口DF"d叫西3 ]1=Z 3 r Z 1=Z 2f t"S亠彩姑皤彩B口ABCD证明：T四边形ABCD是平行四边形二DE // FB，/ ABC= / ADC（平行四边形的对边也平行对角相等）•••/仁/ 3（两直线平行内错角相等）而Z]=^Z ADC,Z2=|ZABC•••/ 2= / 3• DF // BE（同位角相等两条直线平行）•四边形BEDF为平行四边形（平行四边形定义）• BF=DE .（平行四边形的对边相等）说明：此例也可通过△ ADF CBE来证明，但不如上面的方法简捷.例9如图，CD的Rt△ ABC斜边AB上的高，AE平分/ BAC 交CD于E, EF // AB，交BC于点F,求证CE=BF .分析作EG // BC,交AB于G,易得EG=BF .再由基本图, 可得EG=EC ,从而得出结论.过E点作EG // BC交AB于G点.v EF // AB••• EG=BFv CD为Rt△ ABC斜边AB上的高•/ BAC + / B=90°.Z BAC + / ACD = 90°•/ B= Z ACD•Z ACD=Z EGAv AE 平分Z BAC•Z 1= Z 2又AE=AE•△ AGE ACE(AAS)•CE=EG•CE=BF .说明：(1)在上述证法中，“平移”起着把条件集中的作用.(2)本题也可以设法平移AE .(连F点作FG // AE，交AB于G)例10如图，已知I —ABCD的周长为32cm , AB : BC=5 : 3, AE 丄BC 于E, AF 丄DC 于F，/ EAF=2 / C,求AE 和AF 的长.分析：从化简条件开始①由二ABCD的周长及两邻边的比，不难得到平行四边形的边长.口虹CD 的周长=321 fAB=10AB : BC-5 : 3 p |BC=6②/ EAF=2 / C告诉我们什么？AF i FC1 ZFAE^ZC=180°] oAE 1 EAF-2 Z C j討c=6°这样，立即可以看ADF、△ AEB都是有一个锐角为30°的直角三角形.于是有= = = 3再由勾股定理求出解：——ABCD的周长为32cm即AB+BC+CD+DA=32v AB=CD BC=DA（平行四边形的对边相等）/.AB + BC = - X32 = 16 2又AB : BC=5 : 35+3BC= —X3 = 65+3/ EAF+ / AFC+ / C+ / CEA=360 （四边形内角和等于360°v AE 丄BC / AEC=90AF 丄DC / AFC=90•••/ EAF+ / C=180/ EAF=2 / CT AB // CD(平行四边形的对边平行)•••/ ABE二/ C=60 (两直线平行同位角相等)同理/ ADF=60SRiAABE 中，ZBAE = 30* BE = |AB = 5£—■Al = ja =E^ = 5^3 (cm)在RtAADF中，ZDAF = 30° DF= ^AP = |B C=3■f-j d—iAF - 7A D3 -I>F a = M Ccm)说明：化简条件，化简结论，总之，题目中哪一部分最复杂就从化简那一部分开始，这是一种常用的解题策略，我们把这种解题策略称为：从最复杂的地方开始.它虽简单，却很有效.2 .平行四边形的判定例1填空题(1)如图1,四边形ABCD与四边形BEFC都是平行四边形，则四边形AEFD是—，理由是（2）如图2, D、E分别在△ ABC的边AB、AC上，DE=EF , AE=EC , DE // BC贝卩四边形ADCF是__,理由是__ ,四边形BCFD 是—，理由是—分析：判定一个四边形是平行四边形的方法较多，要从已知条件出发，具体问题具体分析：（1）根据平行四边形的性质可得AD平行且等于BC，BC平行且等于EF，从而得AD平行且等于EF，由判定定理4可得.（2）由AE=EC , DE=EF，由判定定理3可得四边形ADCF是平行四边形，从而得AD // CF即BD // CF，再由条件，可得四边形BCFD是平行四边形.解：（1）平行四边形，一组对边平行且相等的四边形是平行四边形（2）平行四边形，对角线互相平分的四边形是平行四边形，平行四边形，两组对边分别平行的四边形是平行四边形.说明：平行四边形的定义（两组对边分别平行的四边形叫做平行 四边形，既是平行四边形的一个性质，又是平行四边形的一个判定 方法.例 2 女口图，四边形 ABCD 中，AB=CD . / ADB 二 /CBD=90 .求 证：四边形ABCD 是平行四边形.分析：判定一个四边形是平行四边形，有三类五个判定方法, 这三类也是按边、角和对角线分类，具体的五个方法如下表：CIID 从对角钱看一（5 ）对角线互相平分 因此必须根据已知条件与图形结构特点，选择判定方法.证法一:v AB=CD . Z ADB= / CBD=90 , BD=DB .••• Rt △ ABD 坐 Rt △ CDB .「（ 1）两组对边分别平存C I ）从边看 —（2）两组对边分别相等_（3）-组对边平行且相尊 （1）从边看 （II ）从角看 （4）两组对角分别相等 的四边形绘平行四边形•••/ ABD= / CDB，/ A= / C.•/ ABD+ / CBD= / CDB+ / ADB即 / ABC= / CDA .•四边形ABCD 是平行四边形（两组对角分别相等的四边形是平行四边形）．证法二：vZ ADB= / CBD=90 , AB=CD、BD=DB .•Rt△ ABD 坐Rt△ CDB .•Z ABD=Z CDB．•AB //CD.（内错角相等两直线平行）•四边形ABCD 是平行四边形（一组对边平行且相等的四边形是平行四边形）．证法三：由证法一知，Rt △ ABD幻Rt △ CDB .••• DA=BC又T AB二CD•四边形ABCD是平行四边形（两组对边分别相等的四边形是平行四边形）说明：证明一个四边形是平行四边形，往往有多种证题思路，我们必须注意分析，通过比较，选择最简捷的证题思路.本题三种证法中，证法二与证法三比较简捷，本题还可用定义来证明.例3如图，‘「ABCD中，E、G、F、H分别是四条边上的点, 且AE=CF , BG=DH，求证：EF与GH互相平分.分析：只须证明EGFH为平行四边形.证明：连结EG 、GF、FH 、HE．T四边形ABCD是平行四边形•••/ A= / C, AD=CB .T BG=DH•AH=CG又AE=CF•△ AEH CFG（SAS）•HE=GF同理可得EG=FH•四边形EGFH 是平行四边形（两组对边分别相等的四边形是平行四边形）•EF 与GH 互相平分（平行四边形的对角线互相平分）．说明：平行四边形的性质，判定的综合运用是解决有关线段和角问题基本方法．例4如图，二ABCD中，AE丄BD于E, CF丄BD于F.求证：四边形AECF是平行四边形.分析：由平行四边形的性质，可得△ ABE CDF••• AE= CF进而可得四边形AECF是平行四边形.证明：口ABCD中，AB屯CD（平行四边形的对边平行，对边相等）•/ ABD= / CDB（两直线平行内错角相等）AE 丄BD、CF 丄BD•AE // CF / AEB= / CFD=90•△ ABE CDF（AAS）•AE=CF•四边形AECF是平行四边形（一组对边平行且相等的四边形是平行四边形）说明：平行四边形的定义，既是平行四边形的一个性质，又是平行四边形的一个判定方法.例5如图，二ABCD中，E、F分别在AD、BC上，且AE=CF , AF、BE相交于G, CE、DF相交于H求证：EF与GH互相平分分析：欲证EF与GH互相平分，只需四边形EGFH为平行四边形，利用已知条件可知四边形AFCE、四边形EBFD都为平行四边形，所以可得AF // EC , BE // DF，从而四边形GEHF为平行四边形.证明：」ABCD中，AD丄BC（平行四边形对边平行且相等）v AE=CF /. DE=BFT四边形AFCE、四边形BFDE是平行四边形（一组对边平行且相等的四边形是平形四边形）二AF // CE , BE // DF（平行四边形对边平行）•••四边形EGFH是平行四边形（两组对边分别平行的四边形是平行四边形）••• GH与EF互相平分（平行四边形的对角线互相平分）说明：平行四边形问题，并不都是以求证某一个四边形为平行四边形的形式出现的.往往更多的是求证线段的相等、角的相等、直线的平行、线段的互相平分等等.要灵活地根据题中已知条件，以及定义、定理等.先判定某一四边形为平行四边形，然后再应用平行四边形的性质加以证明.例6如图，已知—ABCD中，EF在BD上，且BE=DF ,点G、H 在AD、CB上，且有AG=CH , GH与BD交于点0,求证EG丄HF分析：证EF 、GH 互相平分二GEHF 为平行四边形.证明:连 BG 、DH 、GF 、EHT ABCD 为平行四边形.••• AD 垒 BC又 AG=HC• DG 丄 BH•四边形BGDH 为平行四边形（一组对边平行且相等的四边形是平行四边形）• HO = GO , DO=BO （平行四边形的对角线互相平分） 又 BE=DF•OE=OF•四边形GEHF为平行四边形（对角线互相平分的四边形是平行四边形）••• EG丄HF.（平行四边形的对边平行相等）说明：由于条件BE=DF涉及到对角线BD，所以考虑用对角线互相平分来证明例7如图，——ABCD中，AE丄BD于E, CF丄BD于F, G、H分别为AD、BC的中点，求证：EF和GH互相平分.分析：连结EH , HF、FG、GE，只须证明EHFG为平行四边证法一:连结EH , HF、FG、GEv AE丄BD , G是AD中点.-■.GE=C J D =^AD2/ GED二 / GDE同理可得HF =HB =^EC,Z HFE =Z HEFV四边形ABCD是平行四边形••• AD 岂BC,/ GDE= / HBF••• GE=HF，/ GED= / HFB•GE // HF•四边形GEHF为平行四边形（一组对边平行且相等的四边形是平行四边形）•EF和GH互相平分.（平行四边形对角线互相平分）证法二：容易证明厶ABE CDF• BE=DFT四边形ABCD为平行四边形••• AD 些BCT G、H分别为AD、BC的中点•DG 丄BH•四边形BHDG为平行四边形（一组对边平行且相等的四边形是平行四边形）•BD和GH互相平分（平行四边形对角线互相平分）•OG=OH , OB=OD又BE=DF•OE=OF•EF和GH互相平分.例8如图，已知线段a、b与/ a,求作：—ABCD ,使/ ABC二/ a, AB=a , BC=b ,分析：已知两边与夹角，可先确定△ ABC，根据判定定理2(两组对边分别相等的四边形是平行四边形)，再确定点D，从而平行四边形可作出.作法:(1) 作/ EBF二/ a,⑵在BE、BF上分别截取BA=a , BC=b ,⑶分别为A、C为圆心，b, a为半径作弧，两弧交于点D, 二四边形ABCD为所求.*证明：由作法可知AB=CD = aBC=AD=b二四边形ABCD 为平行四边形(两组对边分别相等的四边形为平 行四边形)且/ ABC 二 / a, AB=a , BC=b- ABCD 为所求说明：常见的平行四边形作图有以下几种：(1) 已知两邻边(AB 、BC)和夹角(/ B).(2) 已知一边(BC)和两条对角线(AC , BD).(3) 已知一边(BC)和这条边与两条对角线的夹角 (如/ DBC ,Z ACB).⑷已知一边(CD)和一个内角(/ ABC)以及过这个角的顶点的一条对角线(BD ，且BD > CD)求作平行四边形(如图)完成这些作图的关键点，都在于先作出一个三角形，然后再完成平行四边形的作图，体现了把平行四边形的问题化归为三角形问题的思想方法.。
(完整版)平行四边形练习题及答案(DOC).doc
20.1平行四边形的判定一、选择题1 ．四边形ABCD，从（ 1）AB∥CD；（ 2）AB=CD；（ 3）BC∥AD；（ 4） BC=AD这四个条件中任选两个，其中能使四边形ABCD是平行四边形的选法有（）A ． 3 种B．4种C．5种D．6种2．四边形的四条边长分别是a， b， c，d，其中 a，b 为一组对边边长， c，d?为另一组对边边长且满足a2+b2+c2+d2=2ab+2cd，则这个四边形是（）A ．任意四边形B．平行四边形C．对角线相等的四边形 D ．对角线垂直的四边形3．下列说法正确的是（）A．若一个四边形的一条对角线平分另一条对角线，则这个四边形是平行四边形B．对角线互相平分的四边形一定是平行四边形C．一组对边相等的四边形是平行四边形D．有两个角相等的四边形是平行四边形二、填空题4 ．在□ ABCD中，点 E， F 分别是线段A D， BC上的两动点，点 E 从点 A 向 D 运动，点 F从 C?向 B 运动，点 E 的速度边形．m与点F 的速度n 满足 _______关系时，四边形BFDE为平行四5．如图 1 所示，平行四边形ABCD中， E， F 分别为AD，BC边上的一点，连结EF，若再增加一个条件_______，就可以推出BE=DF．图 1图 26 ．如图 2 所示， AO=OC，BD=16cm，则当 OB=_____cm时，四边形ABCD是平行四边形．三、解答题7．如图所示，四边形 ABCD中，对角线 BD=4，一边长 AB=5，其余各边长用含有未知数 x的代数式表示，且 AD⊥BD于点 D，BD⊥BC 于点 B．问：四边形 ABCD?是平行四边形吗？为什么？四、思考题8．如图所示，在□ABCD中， E，F 是对角线 AC上的两点，且 AF=CE，?则线段 DE?与 BF的长度相等吗？参考答案一、 1． B 点拨：可选择条件（1）（3）或（2）（ 4）或（ 1）（ 2）或（ 3）（4）．故有 4 种选法．2． B 点拨： a2+b 2+c2+d2=2ab+2cd 即（ a-b）2+（ c-d ）2=0，即（ a-b ）2=0 且（ c-d ）2=0．所以 a=b， c=d，即两组对边分别相等，所以四边形为平行四边形．3． B 点拨：熟练掌握平行四边形的判定定理是解答这类题目的关键．二、 4．相等点拨：利用“一组对边平行且相等的四边形是平行四边形”来确定．5 ．AE=CF 点拨：本题答案不惟一，只要增加的条件能使四边形EBFD?是平行四边形即可．6． 8 点拨：根据对角线互相平分的四边形为平行四边形来进行判别．三、 7．解：如图所示，四边形ABCD是平行四边形．理由如下：在 Rt△BCD 中，根据勾股定理，得BC2+BD 2=DC 2，即（ x-5 ）2+42=（ x-3 ）2，解得 x=8．所以 AD=11-8=3， BC=x-5=3， DC=x-3=8-3=5 ，所以 AD=BC， AB=DC．所以四边形ABCD是平行四边形．点拨：本题主要告诉的是线段的长度，故只要说明AD=BC， AB=DC即可，本题也可在Rt△ABD中求 x 的值．四、 8．解：线段DE与BF 的长度相等；连结BD交AC于O点，连结DF， BE，如图所示．在ABCD中， DO=OB， AO=OC，又因为 AF=EC，所以 AF-AO=CE-OC，即 OF=OE，所以四边形 DEBF是平行四边形，所以DE=BF．点拨：本题若用三角形全等，也可以解答，但过程复杂，学了平行四边形性质后，要学会应用．20.2 矩形的判定一、选择题1 ．矩形具有而一般平行四边形不具有的性质是（）A ．对角相等B ．对边相等C ．对角线相等D ．对角线互相垂直2 ．下列叙述中能判定四边形是矩形的个数是（）①对角线互相平分的四边形；②对角线相等的四边形；③对角线相等的平行四边形；④对角线互相平分且相等的四边形．A ． 1B ． 2C ． 3D ． 43．下列命题中，正确的是（）A．有一个角是直角的四边形是矩形 B ．三个角是直角的多边形是矩形C ．两条对角线互相垂直且相等的四边形是矩形D ．有三个角是直角的四边形是矩形二、填空题4．如图 1 所示，矩形 ABCD中的两条对角线相交于点O，∠ AOD=120°， AB=4cm，则矩形的对角线的长为 _____．D E CF OA B图 1 图 25．若四边形 ABCD的对角线 AC， BD相等，且互相平分于点 O，则四边形 ABCD?是_____ 形，若∠ AOB=60°，那么AB：AC=______．6．如图 2 所示，已知矩形ABCD周长为 24cm，对角线交于点O，OE⊥DC 于点 E，于点 F， OF-OE=2cm，则 AB=______， BC=______．三、解答题7．如图所示，□ABCD的四个内角的平分线分别相交于E， F， G，H 两点，试说明四边形EFGH是矩形．四、思考题8．如图所示，△ABC 中， CE， CF分别平分∠ACB和它的邻补角∠ACD．AE⊥CE 于 E，AF⊥CF 于F，直线EF分别交AB， AC于 M， N 两点，则四边形AECF是矩形吗？为什么？参考答案一、 1． C点拨：A与B都是平行四边形的性质，而D是一般矩形与平行四边形都不具有的性质．2 ．B点拨：③是矩形的判定定理；④中对角线互相平分的四边形是平行四边形，对角线相等的平行四边形是矩形，故④能判定矩形，应选B．3． D 点拨：选项 D 是矩形的判定定理．二、 4． 8cm5．矩； 1： 2 点拨：利用对角线互相平分来判定此四边形是平行四边形，再根据对角线相等来判定此平行四边形是矩形．由矩形的对角线相等且互相平分，?可知△ AOB 是等腰三角形，又因为∠ AOB=60°，所以AB=AO=1AC．26 ． 8cm； 4cm三、 7．解：在□ABCD中，因为AD∥BC，所以∠ DAB+∠CBA=180°，又因为∠ HAB= 1∠DAB，∠ HBA=1∠CBA．2 2所以∠ HAB+∠HBA=90°，所以∠ H=90°．所以四边形EFGH是矩形．点拨：由于“两直线平行，同旁内角的平分线互相垂直”，所以很容易求出四边形EFGH 的四个角都是直角，从而求得四边形EFGH是矩形．四、 8．解：四边形AECF是矩形．理由：因为CE平分∠ ACB， ?CF?平分∠ ACD， ?所以∠ ACE=1∠ACB，∠ ACF=1∠ACD．所以∠ ECF=1（∠ ACB+∠ACD）=90°．22 2又因为 AE⊥CE，AF⊥CF， ?所以∠ AEC=∠AFC=90°，所以四边形AECF是矩形．点拨： ?本题是通过证四边形中三个角为直角得出结论．还可以通过证其为平行四边形，再证有一个角为直角得出结论．20.3菱形的判定一、选择题1．下列四边形中不一定为菱形的是（）A ．对角线相等的平行四边形B．每条对角线平分一组对角的四边形C．对角线互相垂直的平行四边形D．用两个全等的等边三角形拼成的四边形2．四个点 A， B， C，D 在同一平面内，从① AB∥CD；② AB=CD；③ AC⊥BD；④ AD=BC；5 个条件中任选三个，能使四边形ABCD是菱形的选法有（）．A ． 1 种B．2种C．3种D．4种3 ．菱形的周长为32cm，一个内角的度数是60°，则两条对角线的长分别是（）A．8cm和 4 3 cm B．4cm和83 cm C．8cm和83 cm D．4cm和43 cm二、填空题4．如图 1 所示，已知□ABCD，AC，BD相交于点O，?添加一个条件使平行四边形为菱形，添加的条件为 ________．（只写出符合要求的一个即可）图 1图 25．如图 2 所示， D， E，F 分别是△ ABC 的边 BC， CA，AB 上的点，且 DE∥AB，DF∥CA，要使四边形 AFDE是菱形，则要增加的条件是 ________．（只写出符合要求的一个即可）6 ．菱形 ABCD的周长为48cm，∠ BAD：∠ ABC=1：?2，?则 BD=?_____，?菱形的面积是______．7．在菱形ABCD中， AB=4， AB 边上的高DE垂直平分边AB，则 BD=_____，AC=_____．三、解答题8．如图所示，在四边形ABCD中， AB∥CD， AB=CD=BC，四边形 ABCD是菱形吗？ ?说明理由．四、思考题9．如图，矩形 ABCD的对角线相交于点 O，PD∥AC，PC∥BD， PD，PC相交于点 P，四边形 PCOD是菱形吗？试说明理由．参考答案一、 1． A点拨：本题用排除法作答．2． D 点拨：根据菱形的判定方法判断，注意不要漏解．3． C点拨：如图所示，若∠ ABC=60°，则△ABC为等边三角形，?所以 AC=AB=1×32=8（ cm）， AO=1AC=4cm．4 2因为 AC⊥BD，在 Rt△AOB中，由勾股定理，得OB= 2 2 2 2AB OA 8 4 =43 （cm ? ），所以 BD=2OB=8 3 cm．二、 4． AB=BC 点拨：还可添加AC⊥BD 或∠ ABD=∠CBD等．5．点 D 在∠ BAC的平分线上（或 AE=AF）26． 12cm； 723 cm点拨：如图所示，过 D 作 DE⊥AB 于 E，因为 AD∥BC， ?所以∠ BAD+∠ABC=180°．又因为∠ BAD：∠A BC=1：2，所以∠ BAD=60°，因为 AB=AD，所以△ ABD 是等边三角形，所以BD=AD=12cm．所以 AE=6cm．在Rt△AED 中，由勾股定理，得 AE 2+ED 2=AD 2， 62+ED 2=12 2，所以 ED 2=108 ，所以 ED=6 3 cm，所以S菱形ABCD=12×63=72 3 （cm2）．7． 4；4 3 点拨：如图所示，因为DE垂直平分 AB，又因为 DA=AB，所以 DA=DB=4．所以△ ABD 是等边三角形，所以∠ BAD=60°，由已知可得AE=2．在 Rt△AED中，2 2 2 2 2 2 2?AE +DE=AD，即 2 +DE=4 ，所以 DE=12，所以 DE=2 3 ，因为1AC·BD=AB·DE，即1AC·4=4×2 3 ，所以AC=4 3 ．2 2三、 8．解：四边形ABCD是菱形，因为四边形ABCD中， AB∥CD，且AB=CD，所以四边形ABCD是平行四边形，又因为AB=BC，所以Y ABCD是菱形．点拨：根据已知条件，不难得出四边形ABCD为平行四边形，又AB=BC，即一组邻边相等，由菱形的定义可以判别该四边形为菱形．四、 9．解：四边形PCOD是菱形．理由如下：因为 PD∥OC，PC∥OD， ?所以四边形P COD是平行四边形．又因为四边形ABCD是矩形，所以OC=OD，所以平行四边形PCOD是菱形．20.4正方形的判定一、选择题1．下列命题正确的是（）A．两条对角线互相平分且相等的四边形是菱形B．两条对角线互相平分且垂直的四边形是矩形C．两条对角线互相垂直，平分且相等的四边形是正方形D．一组邻边相等的平行四边形是正方形2．矩形四条内角平分线能围成一个（）A．平行四边形B．矩形C．菱形 D ．正方形二、填空题3．已知点 D， E，F 分别是△ ABC 的边 AB， BC， CA的中点，连结 DE， EF， ?要使四边形ADEF是正方形，还需要添加条件_______．4．如图 1 所示，直线L 过正方形ABCD的顶点 B，点 A， C 到直线 L?的距离分别是 1 和2，则正方形ABCD的边长是 _______．图 1图2图 35．如图 2 所示，四边形 ABCD是正方形，点 E 在 BC的延长线上， BE=BD且 AB=2cm，则∠E的度数是 ______， BE 的长度为 ____．6．如图 3 所示，正方形 ABCD的边长为 4，E 为 BC上一点， BE=1，F?为 AB?上一点，AF=2， P 为 AC上一动点，则当 PF+PE取最小值时， PF+PE=______．三、解答题7．如图所示，在 Rt△ABC中， CF为∠ ACB的平分线， FD⊥AC 于 D，FE⊥BC于点 E，试说明四边形 CDFE是正方形．BEF四、思考题8．已知如图所示，在正方形 ABCD中， E，F 分别是（1） AF 与 DE相等吗？为什么？（2） AF 与 DE是否垂直？说明你的理由．C D A AB，BC边上的点，且 AE=BF，?请问：参考答案一、 1． C点拨：对角线互相平分的四边形是平行四边形，?对角线互相垂直的平行四边形是菱形，对角线相等的平行四边形是矩形，既是菱形又是矩形的四边形一定是正方形，故选 C．2． D 点拨：由题意画出图形后，利用“一组邻边相等的矩形是正方形”来判定．二、 3．△ ABC是等腰直角三角形且∠ BAC=90°点拨：还可添加△ ABC 是等腰三角形且四边形ADEF是矩形或∠ BAC=90°且四边形ADEF 是菱形等条件．4．5点拨：观察图形易得两直角三角形全等，由全等三角形的性质和勾股定理得正方形的边长为 22 12 = 5．5． 67. 5°； 2 2 cm点拨：因为BD是正方形ABCD的对角线，所以∠ DBC=45°， AD=?AB=2cm．在Rt△BAD中，由勾股定理得 AD 2+AB 2=BD 2，即 22+22=BD 2，所以 BD=2 2 cm，所以 BE=BD=2 2（ cm），又因为BE=BD，所以∠ E=∠EDB= 1（180°- 45°）=67. 5°．26．17 点拨：如图所示，作 F 关于AC的对称点G．连结EG交AC于P，则PF+?PE=PG+PE=GE为最短．过 E 作 EH⊥AD．在Rt△GHE中，HE=4，HG=AG-AH=AF-BE=1，所以 GE= 4212 = 17，?即 PF+PE= 17．三、 7．解：因为∠ FDC=∠FEC=∠BCD=90°，所以四边形CDFE是矩形，因为 CF?平分∠ ACB，FE⊥BC，FD⊥AC，所以FE=FD，所以矩形CDFE是正方形．点拨：本题先说明四边形是矩形，再求出有一组邻边相等，?还可以先说明其为菱形，再求其一个内角为90°．四、 8．解：（ 1）相等．理由：在△ ADE 与△ BAF 中， AD=AB，∠ DAE=∠ABF=90°， AE=BF，所以△ ADE≌△ BAF（ S． A． S．），所以 DE=AF．（ 2） AF 与 DE垂直．理由：如图，设DE与 AF 相交于点O．因为△ ADE≌△ BAF， ?所以∠ AED=∠BFA．又因为∠ BFA+∠EAF=90°，所以∠ AEO+∠EAO=90°，所以∠ EOA=90°，所以DE⊥AF．20.5等腰梯形的判定1 A C 一、选择题．下列结论中，正确的是（．等腰梯形的两个底角相等．一组对边平行的四边形是梯形）BD．两个底角相等的梯形是等腰梯形．两条腰相等的梯形是等腰梯形2．如图所示，等腰梯形ABCD的对角线 AC，BD相交于点O，则图中全等三角形有（）A． 2 对B．3对C．4对D．5对3．课外活动课上， ?老师让同学们制作了一个对角线互相垂直的等腰梯形形状的风筝，其面积为450cm，则两条对角线所用的竹条长度之和至少为（）A ． 30 2 cm B．30cm C．60cm D．60 2 cm二、填空题4．等腰梯形上底，下底和腰分别为 4，?10，?5，?则梯形的高为 _____，?对角线为 ______．5．一个等腰梯形的上底长为5cm，下底长为 12cm，一个底角为 60°，则它的腰长为____cm，周长为 ______cm．6．在四边形 ABCD中， AD∥BC，但 AD≠BC，若使它成为等腰梯形，则需要添加的条件是__________ （填一个正确的条件即可）．三、解答题7．如图所示，AD是∠ BAC的平分线， DE∥AB， DE=AC，AD≠EC．求证： ?四边形 ADCE是等腰梯形．四、思考题8．如图所示，四边形ABCD中，有 AB=DC，∠ B=∠C，且AD<BC，四边形 ABCD是等腰梯形吗？为什么？参考答案一、 1． D点拨：梯形的底角分为上底上的角和下底上的角，?因此在等腰梯形的性质和判别方法中必须强调同一底上的两个内角（?指上底上的两个内角或下底上的两个内角），否则就会出现错误，因此A， B 选项都不正确，而 C 选项中漏掉了限制条件另外一组对边不平行，若平行该四边形就形成了平行四边形了，因此应选D．2． B点拨：因为△ ABC≌△DCB，△ BAD≌△CDA，△ AOB≌△DOC，所以共有 3 对全等的三角形．3． C点拨：设该等腰梯形对角线长为Lcm，因为两条对角线互相垂直，?所以梯形面积为122L =450，解得 L=30，所以所用竹条长度之和至少为2L=2× 30=60（cm）．二、 4． 4：65点拨：如图所示，连结BD，过 A，D 分别作 AE⊥BC，DF⊥BC，垂足分别为E， F．易知△ BAE≌△ CDF，在四边形 AEFD为矩形，所以BE=CF=3， AD=EF=4．在Rt△CDF 中， FC2+DF 2=CD 2，即 32+DF 2=52，所以 DF=4 ，在 Rt △BFD 中， BF2+DF 2=BD 2，即 72+42=BD 2，所以 BD=65 ．5． 7；31点拨：如图所示，过点D作 DE∥AB 交 BC于 E．因为ABED是平行四边形．所以 BE=AD=5（cm）， AB=DE．又因为 AB=CD，所以 DE=?DC，又因为∠ C=60°，所以△ DEC 是等边三角形，所以 DE=DC=EC=7（ cm），所以周长为5+?12+7+7=31（cm）．6． AB=CD（或∠ A=∠D，或∠ B=∠C，或 AC=BD，或∠ A+∠C=180°，或∠B+∠D=180°）三、 7．证明：因为 AB∥ED，所以∠ BAD=∠ADE．又因为 AD是∠ BAC的平分线，所以∠ BAD=∠CAD，所以∠ CAD=∠ADE，所以 OA=OD．又因为AC=DE，所以 AC-OA=DE-OD即 OC=OE， ?所以∠ OCE=∠OEC，又因为∠ AOD=∠COE，所以∠ CAD=∠OCE．所以AD∥CE，而 AD≠CE，故四边形ADCE是梯形．又因为∠ CAD=∠ADE， AD=DA， AC=DE，所以△ DAC≌△ ADE，所以DC=?AE，所以四边形ADCE是等腰梯形．点拨：证明一个四边形是等腰梯形时，应先证其是梯形而后再证两腰相等或同一底上的两个角相等．四、 8．解：四边形ABCD是等腰梯形．理由：延长BA， CD，相交于点 E，如图所示，由∠ B=∠C，可得EB=EC．又AB=DC，所以 EB-AB=EC-DC，即 AE=DE，所以∠ EAD=∠EDA．因为∠ E+∠EAD+∠EDA=180°，∠ E+∠B+∠C=180°，所以∠ EAD=∠B．故 AD∥BC． ?又 AD<BC，所以四边形 ABCD是梯形．又AB=DC，所以四边形 ABCD是等腰梯形．点拨：由题意可知，只要推出 AD∥BC，再由 AD<BC就可知四边形 ABCD为梯形，再由AB=DC，即可求得此四边形是等腰梯形，由∠ B=∠C联想到延长 BA，CD，即可得到等腰三角形，从而使AD∥BC．华东师大版数学八年级（下）第 20 章平行四边形的判定测试（答卷时间： 90 分钟，全卷满分： 100 分）姓名得分 ____________一、认认真真选，沉着应战！（每小题 3 分，共 30 分）1. 正方形具有菱形不一定具有的性质是()（A ）对角线互相垂直（B）对角线互相平分（C）对角线相等（D）对角线平分一组对角2.如图 (1)，EF 过矩形 ABCD 对角线的交点 O，且分别交 AB 、CD 于 E、 F，那么阴影部分的面积是矩形ABCD 的面积的（）（A ）A 1 1 1（ D ）3A5（B ）（ C）104 3D E FFEB C D HB C(1)(2)(3)3．在梯形ABCD 中， AD ∥ BC ，那么 A : B : C : D 可以等于（）（ A ）4：5：6：3（B）6：5：4：3（C）6：4：5：3（D）3：4：5：64．如图 (2) ，平行四边形ABCD 中，DE ⊥ AB 于 E，DF⊥ BC 于 F，若Y ABCD的周长为48，DE ＝ 5， DF＝ 10，则Y ABCD的面积等于 ()（ A ）87.5（B）80（C）75（D）72.55． A 、 B、 C、 D 在同一平面内，从① AB∥CD;② AB=CD;③ BC∥AD;④ BC=AD这四个条件中任选两个，能使四边形ABCD 是平行四边形的选法有（）（ A ）3种（B）4种（C）5种（D）6种6．如图 (3) ，D、E、F分别是VABC各边的中点，AH 是高，如果 ED5cm ，那么 HF的长为（）（ A ） 5cm（B）6cm（C）4cm（D）不能确定7.如图（ 4）：E 是边长为 1 的正方形 ABCD 的对角线 BD 上一点，且 BE ＝ BC， P 为 CE 上任意一点， PQ⊥BC 于点 Q， PR⊥ BE 于点 R，则 PQ＋PR 的值是（）2 13 2（ A ）2 （ B）2 （ C）2 （ D）38．如图（ 5），在梯形ABCD 中， AD ∥ BC ， AB CD ， C 60 ， BD 平分ABC ，如果这个梯形的周长为30，则AB的长（）（ A ）4 （ B ）5 （ C ）6 （ D ）7A DA DERPB C（ 5）B（ 4）Q C9．右图是一个利用四边形的不稳定性制作的菱形晾衣架．A B C 已知其中每个菱形的边长为20cm，墙上悬挂晾衣架的两个铁钉 A 、 B 之间的距离为20 3 cm，则∠1等于()1）（ A ） 90°（Ｂ） 60°（Ｃ） 45°（Ｄ） 30°10．某校数学课外活动探究小组，在老师的引导下进一步研究了完全平方公式．结合实数的性质发现以下规律：对于任意正数a、 b，都有 a+b ≥ 2 ab 成立．某同学在做一个面积为3600cm2，对角线相互垂直的四边形风筝时，运用上述规律，求得用来做对角线用的竹条至少需要准备xcm．则 x 的值是（）(A) 1202(B) 602(C) 120(D) 60二、仔仔填，自信！( 每小 2 分，共20 分)11．一个四形四条次是a、b、c、d，且a2 b 2 c 2 d 2 2ac 2bd，个四形是 _______________ ．12．在四形ABCD中，角AC、BD交于点O，从（1）AB CD ；（2） AB ∥CD ；（3）OA OC；（4）OB OD ；（5） AC ⊥ BD ；（6） AC 平分 BAD 六个条件中，取三个推出四形ABCD 是菱形．如（ 1）（ 2）（ 5）ABCD 是菱形，再写出符合要求的两个：ABCD 是菱形；ABCD 是菱形．13. 如，已知直l 把 Y ABCD 分成两部分，要使两部分的面相等，直l 所在位置需足的条件是____________________. （只需填上一个你合适的条件）lA DB C(第 13 )(第 16 )14.梯形的上底 6cm ，上底的一点引一腰的平行，与下底相交，所构成的三角形周 21cm ，那么梯形的周_________ cm。
平行四边形性质及判定练习题及答案
平行四边形性质及判定练习题及答案1、已知平行四边形ABCD中，AE⊥BC，AF⊥CD，E，F分别是BC，CD的中点，则2、已知平行四边形ABCD中，AB=3cm，BC=5cm，对角线AC，BD相交于点O，则OA的取值范围是多少？3、已知平行四边形ABCD中，AD=2AB，CE平分∠BCD交AD边于点E，且AE=3，求AB的长。
4、下列哪些命题是正确的：（1）两组对边分别相等的四边形是平行四边形；（2）两组对角分别相等的四边形是平行四边形；（3）对角线互相平分的四边形是平行四边形；（4）一组对边平行且相等的四边形是平行四边形。
5、已知平行四边形ABCD中，AB=6，AC=4，E，D，F 分别是AB，BC，CA的中点，求四边形AEDF的周长。
6、已知平行四边形ABCD的对角线AC、BD相交于点O，下列哪个结论不正确：（A）DC∥AB；（B）OA=OC；（C）AD=BC；（D）DB平分∠ADC。
7、已知平行四边形ABCD中，AB=4，AD=2AB，CE平分∠BCD交AD边于点E，且AE=3，求BC的长。
8、已知平行四边形ABCD中，BD为对角线，E、F分别是AD、BD的中点，连接EF，若EF=3，则CD的长为多少？9、已知平行四边形ABCD中，对角线AC、BD相交于点O，点E是BC的中点，OE=3，求AB的长。
10、已知平行四边形ABCD中，AB=8，AD=5，E，F分别是AB，AD的中点，连接EF，求四边形CDEF的周长。
11、已知平行四边形ABCD中，AB=6，BC=8，对角线AC，BD相交于点O，OE=3，求AD的长。
12、已知平行四边形ABCD中，AB=5，BC=7，对角线AC，BD相交于点O，点E是BC的中点，求AE的长。
13、已知平行四边形ABCD中，AB=4，BC=6，BC边上的高AE=2，求DC边上的高AF的长度。
14、在平行四边形ABCD中，AB=2cm，BC=3cm，∠B、∠C的平分线分别交AD于F、E，求EF的长度。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第一部分平行四边形的性质练习题例题 1、平行四边形得周长为50cm，两邻边之差为5cm,求各边长。
变题 1. 平行四边形 ABCD的周长为 40cm,两邻边 AB、AC之比为 2：3，则 AB=_______,BC=________. 变题 2. 四边形 ABCD是平行四边形，∠ BAC=90° ,AB=3,AC=4,求 AD的长。
例题 2. 平行四边形 ABCD中，∠ A- ∠B=20°, 求平行四边形各内角的度数。
变题 3. 平行四边形 ABCD中， AE平分∠ DAB, ∠DEA=20° , 则∠ C=_________,∠B_________.变题 4. 如图，在平行四边形ABCD中，∠ BAC=34°,∠ ACB=26°，求∠ DAC与∠D的度数。
例题 3. 如图，在平行四边形 ABCD中，CE⊥ AD,CF⊥BA交 BA的延长线于 F，∠FBC=30° ,CE=3cm,CF=5cm, 求平行四边形 ABCD的周长。
变题 5. 如图，平行四边形ABCD的周长为 50，其中 AB=15，∠ ABC=60°，求平行四边形面积。
A E D AD FAA DE DA DB C B CBC B C B C1、如图，四边形ABCD是平行四边形， AB=6cm,BC=8cm，∠ B=70°, 则 AD=________,CD=______∠, D=_______,∠A=______,∠ C=_______.2、平行四边形 ABCD的周长为 40cm,两邻边 AB、AC之比为 2：3，则 AB=_______,BC=________.3、平行四边形得周长为50cm，两邻边之差为 5cm,则长边是 ________ ，短边是 __________.4、平行四边形 ABCD中，∠ A-∠B=20° , 则∠ A=_______ ∠B=________5、. 平行四边形 ABCD中， AE平分∠ DAB, ∠ DEA=20°, 则∠C=____,∠B_____.6、平行四边形 ABCD中，∠A+∠C=200° . 则：∠ A= _______，∠B= _________ . AD7、如图，平行四边形 ABCD的周长为 50，其中 AB=15，∠ ABC=60°，求平行四边形面积。
B C8、如图，在ABCD中， DE⊥AB，E 是垂足，如果∠ C=40°，求∠ A 与∠ ADE的度数。
D CA E B9 、如图，在ABCD中，已知对角线 AC和 BD相交于点 O，△ BOC的周长为 24，BC=10，A D 求对角线 AC与 BD的和是多少？OB C10．如图所示，在Y ABCD中， AB=10cm，AB边上的高 DH=4cm， BC=6cm，求 BC边上的高 DF的长．111、如图，ABCD的周长为 60 ㎝，△ AOB的周长比△ BOC大 8 ㎝，求 AB、BC的长。
D COAB第二部分平行四边形的判定练习题1. 如图，已知： E、F 是平行四边形 ABCD对角线 AC 上的两点，并且 AE=CF。
求证：四边形 BFDE 是平行四边形变式一：在□ABCD中， E，F 为 AC上两点， BE//DF．求证：四边形BEDF为平行四边形．变式二：在□ABCD中， E,F 分别是 AC上两点， BE⊥AC于 E， DF⊥AC于 F. 求证 : 四边形 BEDF为平行四边形2.如图，平行四边形 ABCD中， AF＝CH，DE＝BG求证： EG和 HF互相平分。
D H CEGA F B图20.1.3-13. 如图所示，在四边形ABCD中， M是 BC中点， AM、BD互相平分于点 O，那么请说明 AM=DC且 AM∥ADDCOBM C4、如图所示，已知□ABCD中， AE、CF分别是∠ DAB、∠ BCD的平分线，D E C求证：四边形 AFCE是平行四边形。
3 412A F B图 35. 如图，在△ ABC中， BD平分∠ ABC，DE∥BC交 AB于点 E， EF∥AC交 BC于点 F，那么A BE=CF，请你说明理由 . E DB F C6.已知，如图 4，△ ABC是等边三角形，过 AC边上的点 D 作 DG∥BC，交 AB于点 G，在GD和延长线上取点E，使 DE＝DC，连接 AE、BD。
（1）求证：△ AGE≌△ DAB；A（2）过点 E 作 EF∥ DB，交 BC于点 F，连结 AF，求∠ AFE的度数。
G D EB F C图 47.已知如图所示，点 O为平行四边形 ABCD的对角线 BD的中点，直线 EF经过点 O，分别交 BA、DC的延长线于 E、F 两点，求证： AE=CF．8.已知：如图所示，平行四边形 ABCD的对角线 AC、BD?相交于点 O，EF经过点 O并且分别和 AB、CD 相交于点 E、F，又知 G、H分别为 OA、 OC的中点．求证：四边形 EHFG是平行四边形．EDAF B C9.已知：如图，四边形 ABCD是平行四边形，且EA D B A F。
（1）说明CEF是等腰三角形。
（ 2）CEF的哪两边之和等于平行四边形ABCD的周长，为什么？10. 等边三角形 ABC的边长为 a， P 为△ ABC内一点，且 PD∥AB，PE∥BC，PF∥ AC，那么， PD+PE+PF 的值为一个定值 . 这个定值是多少 ?请你说出这个定值的来历.菱形的性质和判定复习一、性质1．下面性质中菱形有而矩形没有的是（）（ A）邻角互补（B）内角和为360°（C）对角线相等（D）对角线互相垂直2. 如图，在菱形ABCD中，∠ BAD=60°， BD=4，则菱形ABCD的周长是 _______．2题3题5题6题3、如图，菱形ABCD的边长是 2cm，E 是 AB的中点，且DE丄 AB，则菱形 ABCD的面积为错误!未找到引用源。
cm2．4．已知菱形两条对角线的长分别为5cm和 8cm，则这个菱形的面积是______cm．5、如图，菱形ABCD的对角线AC、BD 相交于点O，且 AC＝ 8， BD＝6，过点 O 作 OH丄 AB，垂足为H，则点 O 到边AB的距离6、如图，将两张等宽的长方形纸条交叉叠放，重叠部分是一个四边形ABCD，若 AD=6cm，∠ ABC=60°，则四边形ABCD的面积等于cm2．7、如图，已知菱形ABCD，其顶点 A， B 在数轴上对应的数分别为－ 4 和 1，则 BC＝．8、如图，依次连结第一个矩形各边的中点得到一个菱形，再依次连结菱形各边的中点得到第二个矩形，按照此方法继续下去 . 已知第一个矩形的面积为1，则第 n 个矩形的面积为.7题8题9、如图， P 为菱形 ABCD的对角线上一点，PE⊥AB于点E，PF⊥AD于点F，PF=3cm，则P点到AB的距离是_____ cm10、如图，菱形ABCD的两条对角线分别长 6 和 8，点P是对角线AC上的一个动点，点M N分别是边 AB、BC的中点，则PM+PN的最小值是_______．11、如图，四边形ABCD为菱形，已知A（0， 4）， B（﹣ 3， 0）．（ 1）求点 D 的坐标；（ 2）求经过点C的反比例函数解析式．11 题12 题12、如图，已知矩形ABCD的两条对角线相交于O，∠ ACB=30°， AB=2．4（ 3）以 OB、 OC为邻边作菱形 OBEC，求菱形 OBEC的面积．二、判定1．小明和小亮在做一道习题，若四边形ABCD是平行四边形，请补充条件明补充的条件是 AB=BC；小亮补充的条件是AC=BD，你认为下列说法正确的是（A、小明、小亮都正确 B 、小明正确，小亮错误C、小明错误，小亮正确 D 、小明、小亮都错误2．如图，已知四边形ABCD是平行四边形，下列结论不正确的是（）A. 当 AB=BC时，它是菱形；B. 当 AC⊥ BD时，它是菱形；C. 当∠ ABC=90°时，它是矩形；D. 当 AC=BD时，它是菱形3. 用直尺和圆规作一个菱形，如图，能得到四边形ABCD是菱形的依据是（），使得四边形ABCD是菱形。
小）A DOB CA、一组临边相等的四边形是菱形B、四边相等的四边形是菱形C、对角线互相垂直的平行四边形是菱形D、每条对角线平分一组对角的平行四边形是菱形4、如图，在已知平行四边形ABCD中， AE平分∠ BAD，与 BC相交于点 E， EF//AB ，与 AD相交于点 F.求证 : 四边形 ABEF是菱形 .5、如图，在平行四边形ABCD中，∠ DAB＝ 60°， AB＝2AD，点 E 、F 分别是 CD的中点，过点A作 AG∥ BD，交 CB 的延长线于点G．（1）求证：四边形 DEBF是菱形；（2）请判断四边形 AGBD是什么特殊四边形？并加以证明．6、如图，在△ ABC中，∠ ACB=90°， BC的垂直平分线DE交 BC于 D，交 AB于 E， F 在 DE上，且 AF=CE=AE．（1）说明四边形 ACEF是平行四边形；（2）当∠ B 满足什么条件时，四边形 ACEF是菱形，并说明理由．7、如图，矩形ABCD的对角线相交于点O，DE∥ CA， AE∥ BD．（1）求证：四边形 AODE是菱形；（2）若将题设中“矩形 ABCD”这一条件改为“菱形 ABCD”，其余条件不变，则四边形AODE是怎样的四边形？5矩形的性质1．下面的图形中，既是轴对称图形，又是中心对称图形的是()A. 角B. 任意三角形C. 矩形D. 等腰三角形2． 若矩形的一条角平分线分一边为 3cm 和 5cm 两部分，则矩形的周长为（） A ．22B ． 26C ．22 或 26D ．283．已知一矩形的周长是 24cm ，相邻两边之比是 1:2 ，那么这个矩形的面积是（）A ． 24cm 2B ． 32cm 2C ． 48cm 2D ． 128cm 24．由矩形的一个顶点向其所对的对角线引垂线，该垂线分直角为1：3 两部分，则该垂线与另一条对角线的夹角为（ ）A 、 22.5 °B 、 45°C、 30°D、 60°5．如图，在矩形 ABCD 中， DE ⊥ AC,∠ ADE= ∠ CDE,那么∠ BDC 等于 （）A ． 60°B ． 45°C ． 30°D． 22.5 °6．如图，矩形 ABCD 中， E 是 BC 的中点，且∠ AED=90°．当AD=10cm 时， AB 等于（）7．如图，过矩形 ABCD 的对角线 BD 上一点 R 分别作矩形两边的平行线MN 与 PQ ，那P D么图中矩形 AMRP 的面积 S 1A ，与矩形 QCNR 的面积 2的大小关系是()S MND. 不能确定 R12121 2A.S >SB.S=SC. S < S填空题：BC1、矩形 ABCD 的两条对角线相交于O,∠ AOB ＝ 60o ,AB ＝ 8, 则矩形对角线的长＿＿＿ Q2、矩形的两条对角线的夹角为60°，若一条对角线与短边的和为15，则短边的长是，对角线的长是；若较短的边长为 5cm ．则这个矩形的面积是 _____cm 2.3、矩形 ABCD 的对角线相交于 O ，AC=2AB ，则△ COD 为 ________三角形。