方位角课件
合集下载
人教版数学七年级上册4.3.3:方位角课件(共15张PPT)

30°
●
远望一号
●
远望二号
-11-
另一时刻,费俊龙、聂海胜在“神舟六号”
另一时刻,费俊龙、聂海胜在“神舟六号”上测得“远望一号”“远望二号”在他的南偏西70°和南偏西20°的方向,你能在图中画出此时神舟六号所处的位置吗?
上测得“远望一号”“远望二号”在他的南偏 方向的一条射线,仿照这条射线画出
(2)西北方向:___ ②你认为方位角运用时应注意的地方有哪些?
③你还有哪些感想和大家交流?
的方向为 。
方位角别其实就测是表示方得向的角神。 舟六号在北偏东60°和北偏东30°的方
向,你能在下图中画出当时神舟六号所处的位置
吗?
●
●
远望一号
远望二号
-10-
远望一、二号停在太平洋洋面上,某一
时刻,分别测得神舟 六号在北偏东60°和北
偏东30°的方向。
神舟六号
60°
我国当时派出远望一号~四号船队,跟踪检测,其中 (1)南偏东25°(2)北偏西60°
注意:方位角不能以正东、正西为基准,如不能说成“东偏北60°”“西偏南50°”等,但有时如“北偏东45°”时,我们可以说成东北方向。
现请你确定缉私艇的航线,画出示意图,并用语言描述出来。 的方向为 ______.
远望一、二号停在太平洋洋面上,某一时刻,分 【师生反思、课堂小结】
三.教学过程:
《孔子拜师》是关于孔子谦虚求学的故事。在这个故事里,作者描写了孔子去拜见老子,让老子成为他的老师的故事。在孔子去拜师
测得神舟六号在北偏东70°和北偏 的时候,孔子已经是远近闻名的学者了,但是他还孜孜不倦地努力求上进。在设计上这节课时要注意引导学生从孔子的言行中学习其
谦虚的精神。 教学方法:
方位角课件
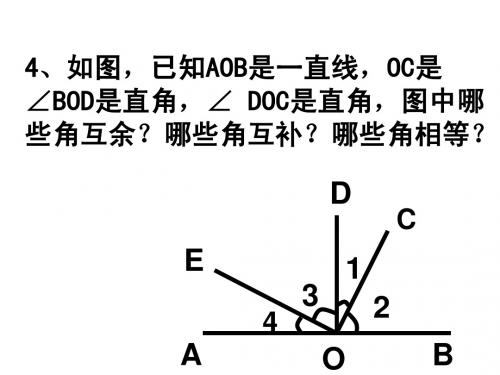
乙地对甲地的方位角 乙地
北
甲地
3.度量向北的射线和蓝色线之间的角度
甲地对乙地的方位角 乙地
ቤተ መጻሕፍቲ ባይዱ
甲地
1. 先找出中心点,然后画出方向指标
甲地对乙地的方位角 乙地
甲地
2. 把中心点和目的地用线连接起來
甲地对乙地的方位角
乙地
南
甲地
3.度量向南的射线和绿色线之间的角度
说出B在A的 北偏东40°
那么A在B的 南偏西40°
● 东
射 线 OC 的 方 向 就 是 ∴ 射 线 OA 的 方 向 就 射 线 OD 的 方 向 就 是 射 线 OB 的 方 向 就 是 南 偏 西 10 ° , 即 货 是 南 偏 东 60 ° , 即 北 偏 西 45 ° , 即 海 北 偏 东 40 ° , 即 客 轮 C 所在的方向。 灯塔 A所在的方向。 岛 D 所在的方向。 轮 B 所在的方向。
北
(3)南偏西25°
射线OA
东
60°
C
B 西
70° O
北偏西70° 射线OB 南偏东60° 射线OC
25°
A 南
例2:如图.货轮O在航行过程中,发现灯塔A 在它南偏东60°的方向上,同时,在它北偏 东40°,南偏西10°,西北(即北偏西45°) 方向上又分别发现了客轮B, 货轮C和海岛D.仿照表示 北 ●B 灯塔方位的方法画出 ● D 45°40° 表示客轮B,货轮C和 海岛D方向的射线. 西 O
4、如图,已知AOB是一直线,OC是 ∠BOD是直角,∠ DOC是直角,图中哪 些角互余?哪些角互补?哪些角相等?
D
C
E
4
3
1
2
O
A
《方位角问题》课件

《方位角问题》ppt课件
目录
• 方位角的基本概念 • 方位角的应用 • 方位角的计算实例 • 方位角问题解析 • 方位角问题的实际应用
01 方位角的基本概念
定义
01
02
03
方位角
指从正北方向顺时针转到 目标方向线的夹角,范围 在0°到360°之间。
真方位角
以真北方向为基准,顺时 针旋转至目标方向线的夹 角。
航海学
船舶导航
在航海学中,方位角是船舶导航 的重要参数之一,通过测量和计 算船只相对于不同地标的方位角 ,可以确定船只的位置和航向。
海上交通控制
海上交通控制中心通过监测船舶的 方位角变化,可以判断船舶的航行 轨迹和航向,确保海上交通的安全 和有序。
海洋调查
海洋调查船利用方位角来定位和测 量海洋参数,如海流、潮汐等。
掌握基本概念
了解和掌握方位角的基本 概念和计算方法是解决方 位角问题的关键。
熟练使用工具
使用量角器、罗盘等工具 进行测量和计算,可以提 高计算的准确性和效率。
实践应用
通过实践应用,如地图阅 读、导航等,可以加深对 方位角概念的理解,并提 高解决实际问题的能力。
05 方位角问题的实际应用
军事应用
1 2 3
航空学
飞机导航
航空飞行中,飞机需要精确的导 航信息来确保安全飞行,方位角 是飞机导航系统中的重要参数之
一。
机场调度
机场调度员通过监测飞机的方位 角变化,可以判断飞机的起降轨 迹和方向,确保机场的正常运行
和飞机的安全起降。
气象观测
气象观测中,方位角也被用来测 量风向、风速等气象参数。
03 方位角的计算实例
科研应用
天文学
目录
• 方位角的基本概念 • 方位角的应用 • 方位角的计算实例 • 方位角问题解析 • 方位角问题的实际应用
01 方位角的基本概念
定义
01
02
03
方位角
指从正北方向顺时针转到 目标方向线的夹角,范围 在0°到360°之间。
真方位角
以真北方向为基准,顺时 针旋转至目标方向线的夹 角。
航海学
船舶导航
在航海学中,方位角是船舶导航 的重要参数之一,通过测量和计 算船只相对于不同地标的方位角 ,可以确定船只的位置和航向。
海上交通控制
海上交通控制中心通过监测船舶的 方位角变化,可以判断船舶的航行 轨迹和航向,确保海上交通的安全 和有序。
海洋调查
海洋调查船利用方位角来定位和测 量海洋参数,如海流、潮汐等。
掌握基本概念
了解和掌握方位角的基本 概念和计算方法是解决方 位角问题的关键。
熟练使用工具
使用量角器、罗盘等工具 进行测量和计算,可以提 高计算的准确性和效率。
实践应用
通过实践应用,如地图阅 读、导航等,可以加深对 方位角概念的理解,并提 高解决实际问题的能力。
05 方位角问题的实际应用
军事应用
1 2 3
航空学
飞机导航
航空飞行中,飞机需要精确的导 航信息来确保安全飞行,方位角 是飞机导航系统中的重要参数之
一。
机场调度
机场调度员通过监测飞机的方位 角变化,可以判断飞机的起降轨 迹和方向,确保机场的正常运行
和飞机的安全起降。
气象观测
气象观测中,方位角也被用来测 量风向、风速等气象参数。
03 方位角的计算实例
科研应用
天文学
直线定向及方位角测量ppt课件

CD BC 1求80已知2 180 右
BA AB 180
DE CD 180 3
3、坐标方位角的计算公式
左角:
已知:аAB
观测的水平角βi
前进方向
β1 аBC
β3
аAB
B
βаBA 2
аCD
D
аCB
A
C
E
求:各直线的坐
标方位角
BC AB 180 1
BC BA 1 360
真方位角A 天文或陀螺仪测定
磁方位角Am
罗盘仪测定
坐标方位角 坐标反算而得
N N磁
A
B P
S磁 S
A=Am+δ
a=A-γ
X
γ
A P
Q
Y
2.分类及关系:
(1)真方位角A=磁方位角Am+磁偏角δ 真方位角A=坐标方位角α+子午线收敛角γ
(2)同一直线正反坐标方位角相差180°,即:
正 反 180 0
CD BC 1求80已知2 180 左
BA AB 180
DE CD 180 3
综合:
求 已知 180 右左
注意: 1、 已知 180, 取减号 已知 180, 取加号
2、 左加右减
3、 求 360, 减360 已知 0, 加360
示例: 已知AB=151 06
δ N N磁 B
S磁 S
X
γ
P
Y
磁偏角(magnetic declination)δ——地面上同一点的真、 磁子午线方向不重合,其夹角称为磁偏角。磁子午线方向 在真子午线方向东侧,称为东偏,δ为正。反之称为西偏, δ为负。
子午线收敛角(mapping angle)γ——当轴子午线方向在真 子午线方向以东,称为东偏,γ为正。反之称为西偏,γ 为负。可见在中央子午线上,真子午线与轴子午线重合, 其他地区不重合,两者的夹角即为γ。
方位角俯角仰角课件

从而
答:这根电线杆与这座楼的距离约为112m.
实际问题
建立几何模型
转化
B
数学问题
A
75° · D
C
1.5m 28.5m
解直角三角形
例3 : 如图,河对岸有一铁塔AB,测角器的高
度为1m,在C处测得塔顶A的仰角为30°,向塔前 进16m到达D,在D处测得塔顶A的仰角为45°, 求铁塔AB的高。 A 分析: 解决此题的关键是什么? 根据题意画出 几何模型
布置作业:
1、为了测量顶部不能到达的建筑物AB的高度,现在地 平面上取一点C,用测量仪器测得A点的仰角为45°,再向 前行走20m取一点D,使点D在BC的延长线上,此时测得 A点的仰角为30°,已知测角仪器的高为1.5m,求建筑物 A AB的高度。
F D
30º E
45º
G B
C
布置作业:
2、如图,在一座山的山顶处用高为1m的测角器望地面 C、D两点,测得俯角分别为60°和45° ,若已知DC长 为20m,求山高。
答: AC = 2400 tan 60
= 4157(m ) .
A B
图4-27
2400m
C
2、A港在B地的正南方10千米处,一艘轮船由A 港开出向西航行,某同学第一次在B处测得该 船在南偏西30°,半小时后又测得该船在南偏 西60°,求该船速度.
例2 如图4-26,在高为28.5m的楼顶平台D处,用仪 器测得一路灯电线杆底部B的俯角为 15 ,仪器高度 AD为1.5m.求这根电线杆与这座楼的距离BC(精确到 1m).
视线 铅 直 线 视线 仰角 俯角 水平线
例1 如图4-25,一艘游船在离开码头A后,以和河岸 成 30°角的方向行驶了500m到达B处,求B处与河岸 的距离.
测量坐标方位角计算课件

误差积累规律
随着测量次数的增加,误 差会逐渐积累,导致最终 结果精度下降。
提高测量精度的措施
01
02
03
04
选择高精度仪器
使用高精度测量仪器,可以降 低仪器本身带来的误差。
提高观测技术水平
通过培训观测者,提高其技术 水平和经验,可以降低观测误
差。
多次测量求平均值
通过多次测量并取平均值,可 以减小随机误差的影响。
观测误差
由于观测者技术水平、 经验等因素导致的误差
。
环境误差
由于大气折射、地球曲 率等因素引起的误差。
计算误差
在数据处理过程中,由 于舍入误差、算法限制
等因素引起的误差。
误差传播规律
01
02
03
线性传播规律
当多个测量值相互关联时 ,任何一个测量值的误差 都会传递到其他测量值中 。
非线性传播规律
某些情况下,测量值的误 差之间存在非线性关系, 误差传递规律较为复杂。
在矿山测量中,除了坐标方位角外,还需要测量矿体的长 度、宽度、高度等信息,以及矿岩的物理性质和采矿工程 的设计和施工。同时,需要考虑矿山的特殊环境和安全要 求,采取相应的测量技术和措施。
04
坐标方位角计算中的存在的误 差,如望远镜、水准器
等部件的精度限制。
实例二
已知点A(x1, y1)和点B(x2, y2)的坐标 ,求两点间的边长d和方位角α。
03
测量中坐标方位角的应用
测量控制网布设
测量控制网是进行各种测量的基础,而坐标方位角是确定测 量控制点位置的重要参数之一。在控制网布设中,需要根据 测量任务和要求,计算出各个控制点的坐标方位角,以确保 测量结果的准确性和可靠性。
《方位角》PPT课件(福建省市级优课)

∴∠1=∠2
同(等)角的余角相等
练习 1、如图1,∠1+∠3=90°,∠1+∠2=9B0°C,
则∠2=
(
) 1
∠3 同角的余角相等
32
D
A O
图1
2、如图2,∠1+∠3=180°,∠2+∠C3=180°,B
2
则∠1=
(
)3 O
∠2 同角的补角相等
1
A
图2
D
例2:如图,A,O,B在同一直线上,射线 OD和射线OE分别平分∠AOC 和 ∠BOC ,则
2
= 90°
所以,∠2 和∠3互为余角,
同理,∠1 和∠3,
∠2 和∠4,
∠1 和∠4也互为余角。
开动脑筋:
A
问:如图这座塔其 中两堵墙围一个角 AOB,但人不能进 C 入围墙,我们如何 去测量这个角的大 小呢?
A
1
2 C
O
B O
B
今天我们学了什么?
两个角的 特殊关系
互为余角
对应图形
1 2
互为补角
21
数量关系 ∠1+ ∠2 = 90 ° ∠1+ ∠2 = 180 °
性质
同角或等角的 同角或等角的
余角相等。
补角相等。
注意: 互余、互补是指两个角的数量关系,与位置无关. 方程思想的运用
作业
课本140页 第11题、第13题 优化设计63-64页 轻松尝试1-7题、知 能演练1、2、3、5、6、8、10
30° + 60° 45° + 45° 10° + 80° 15° + 75°
= 90° = 90° = 90° = 90°
6.3.3 余角和补角(2)——方位角 课件 人教版(2024)数学七年级上册
东北方向
;
;
.
;
6.3.3
余角和补角(2)——方位角
课堂学练
知识点1:方位角的表示
1. 【例】如图,写出下列方位角.
(1)射线 OA 表示的方向是 北偏西30°方向 ;源自(2)射线 OB 表示的方向是
西南方向
;
(3)射线 OC 表示的方向是 南偏东15°方向 .
1
2
3
4
5
6
7
8
9
10
11
B. OB 的方向是北偏西60°
C. OC 的方向是南偏西60°
D. OD 的方向是南偏东60°
1
2
3
4
5
6
7
8
9
10
11
12
13
14
6.3.3
余角和补角(2)——方位角
分层检测
8. 如图,写出下列方位角.
(1)射线 OA 表示的方向是
北偏东60° ;
(2)射线 OB 表示的方向是 东南方向
(3)射线 OD 表示的方向是
A , B , C 处时,经测量得,甲船位于港口的北偏东44°方向,乙船位
于港口的北偏东76°方向,丙船位于港口的北偏西45°方向.
(1)求∠ BOC 的度数;
解:由题意得∠ EOB =76°,
∠ EOC =45°.
∴∠ BOC =∠ EOB +∠ EOC =121°;
1
2
3
4
5
6
7
8
9
10
11
12
是
西北方向
北偏东30°方向 ,射线 OB 表示的方向
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北
●B 45° 40°
O
●
60° C ●10南°
东
●A
16
如图,A地和B地都是海上观测站,从A地发现它
的北偏东600方向上有一艘船,同时从B地发现这
艘船在它的北偏东300方向,试在图中确定这艘
船的位置。
北
解:
C
东
500
300
A
B
则这艘船在点C处
2020/1/16
17
互相谈一谈
这节课你学到了什么?(学习了 哪些内容?掌握了哪些方法,有 什么体会?)
∴ 射 线 OA 的 方 向 就 是 南 偏 东 60°,即灯塔A所在的方向。
●D
∴ 射 线 OB 的 方 向 就 是 北 偏 东
40°,即客轮B所在的方向。 西
∴ 射 线 OC 的 方 向 就 是 南 偏 西
10°,即货轮C所在的方向。
∴射线OD的方向就是北偏西
45°2,020/即1/16海岛D所在的方向。
2020/1/16
18
2020/1/16
19
面八方?
西北方向 G 北偏西45°
北 A
45° 45°
东北方向 E 北偏东45°
西C O
D东
45° 45°
F
西南方向 H
B
东南方向
南偏西45°
南
南偏东45°
西东正正东正北南南南东北西方方方方方向向向向向:::::射射射射射线线线线线OOOOOHGFBDAEC
2020/1/16
4
方位角的定义:
指北或指南方向线与目标方向线所 成的小于90°的角叫做方位角.
60° 60°
45° 30°
2020/1/16
7
说出B在A的
2020/1/16
B
西●
●
B
北
●B
40° 70°
●A
65°
东
●B
南
8
例:点O在点A的_______南__偏__东_ 80°
点A在点O的__北__偏__西___8_0_°_
北
总结:从谁看从谁建系
西
2020/1/16
北
A
东
80°
80° 西
第四章 几何图形初步
4.3 角
4.3.3 余角和补角(2) -----方位角
2020/1/16
1
复习旧知 ☞
你知道表示方向的成语“四面八方” 是指哪几个方向吗?
“四面”—东、南、西、北
“八方”--东、南、西、北和 东北、东南、西北、西南
2020/1/16
3
如果我们在点O的位置,能否识别O点的四
O东
南
南 9
2020/1/16
10
练习2.A看B的方向是北偏东30°,那么B
看A的方向是( )
北
(A)南偏东60° (B)南偏西60°
(C)南偏东30° (D)南偏西30°
北B
东
12
A
东
2020/1/16
11
如图,下列说法中错误的是( D )
A.OD的方向是北偏东30° B.OC的方向是南偏东60° C.OB的方向是西南方向 西 D.OA的方向是北偏西60°
北
A
D
60 60°
东
°
45°
O
30°
C
B
南
2020/1/16
12
归纳
北
观
测
点
甲地
2020/1/16
乙地
被观测点
13
归纳
北
甲地
2020/1/16
ห้องสมุดไป่ตู้
乙地
视线
14
归纳
北
方 位 角
甲地
2020/1/16
乙地
量角器度量时要注意: 量角器的零刻度线与 正北或正南方向线重 合。
. 15
动手画图,深入探究
例2.如图.货轮O在航行过程中,发现灯塔A在它南偏东 60°的方向上,同时,在它北偏东40°,南偏西10°,西北(即 北偏西45°)方向上又分别发现了客轮B,货轮C和海岛D. 仿照表示灯塔方位的方法画出表示客轮B,货轮C和海岛 D方向的射线.
2020/1/16
5
知识考点:①知图表示方向
北 北偏东60°
北偏西70°
C
70° 60°
西
20° 30° O
D
60° 45°
A
东
东南方向或者
南偏西60°
南偏东45°
南
B
2020/1/16
6
(1)射线OA表示北偏_西__6_0_°_____方向;
(2)射线OB表示南偏_西__4_5_°_____方向; (3)射线OC表示南偏_东__3_0_°_____方向; (4)射线OD表示北偏东__6_0__° _____方向;
