一级直线倒立摆matlab程序(最新整理)
基于MATLAB的直线一级倒立摆的PID控制研究

基于MATLAB的直线一级倒立摆的PID控制研究一、内容概述本文旨在研究基于MATLAB的直线一级倒立摆的PID控制策略。
倒立摆系统作为控制理论中的重要实验对象,具有非线性、不稳定性以及快速运动等特点,对于控制系统的设计与实现提出了较高要求。
PID控制作为一种经典的控制方法,在倒立摆系统中具有广泛的应用价值。
本文利用MATLAB软件平台,对直线一级倒立摆的PID控制进行深入研究和探讨。
文章对直线一级倒立摆系统的基本原理进行介绍,包括其物理模型、运动方程以及稳定性分析等方面。
在此基础上,详细阐述了PID 控制器的基本原理、参数整定方法及其在倒立摆系统中的应用。
通过对比不同PID参数下的控制效果,分析了PID控制器在倒立摆系统中的性能特点。
文章重点介绍了基于MATLAB的直线一级倒立摆PID控制系统的设计与实现过程。
利用MATLAB的Simulink仿真工具,搭建了直线一级倒立摆的仿真模型,并设计了PID控制器进行仿真实验。
通过不断调整PID控制器的参数,观察系统的动态响应和稳态性能,得到了较优的控制参数。
文章还讨论了在实际应用中可能遇到的挑战与问题,并提出了相应的解决方案。
针对倒立摆系统的非线性特性,可以采用模糊PID控制或神经网络PID控制等智能控制方法进行改进;针对干扰和噪声的影响,可以采用滤波技术或鲁棒控制策略来提高系统的抗干扰能力。
文章总结了基于MATLAB的直线一级倒立摆PID控制研究的主要成果和贡献,并展望了未来研究方向和应用前景。
通过本文的研究,不仅加深了对倒立摆系统和PID控制方法的理解,也为实际工程应用提供了有益的参考和借鉴。
1. 直线一级倒立摆系统的介绍直线一级倒立摆系统,作为一个复杂且典型的非线性不稳定系统,历来被视为控制理论教学及实验的理想平台。
它不仅能够有效地反映出控制中的多种问题,如非线性、鲁棒性、镇定等,还因其在多个领域中的实际应用价值而备受关注。
直线一级倒立摆系统主要由小车、摆杆等部件构成,它们之间通过自由连接形成一个整体。
一阶倒立摆控制系统设计matlab

一阶倒立摆控制系统设计matlab一、控制系统简介控制系统是指通过对某些物理系统或过程的改变以获取期望输出或行为的一种系统。
其中涉及到了对系统的建模、分析以及控制方法的选择和设计等多方面的问题。
控制系统可以通过标准的数学和物理模型来描述,并可以通过物理或者仿真实验进行验证。
本文将围绕一阶倒立摆控制系统设计和仿真展开。
主要内容包括:1.一阶倒立摆系统简介2.系统建模3.系统分析4.设计控制器5.仿真实验及结果分析一阶倒立摆(controlled inverted pendulum)是一种比较常见的控制系统模型。
它的系统模型简单,有利于系统学习和掌握。
一般而言,一阶倒立摆系统是由一个竖直的支杆和一个质量为$m$的小球组成的。
假设球只能在竖直方向上运动,当球从垂直平衡位置偏离时,支杆会向相反的方向采取动作,使得小球可以回到平衡位置附近。
为了控制一阶倒立摆系统,我们首先需要对其进行建模。
由于系统并不是非常复杂,所以建模过程相对简单。
假设支杆长度为$l$,支杆底端到小球的距离为$h$,支杆与竖直方向的夹角为$\theta$,小球的质量为$m$,地球重力为$g$,该系统的拉格朗日方程可以表示为:$L =\frac{1}{2}m\dot{h}^{2}+\frac{1}{2}ml^{2}\dot{\theta}^{2}-mgh\cos{\theta}-\frac{1}{2}I\dot{\theta}^{2}$$I$表示支杆的惯性矩,它可以通过支杆的质量、长度以及截面积等参数计算得出。
$h$和$\theta$分别表示小球和支杆的位置。
我们可以通过拉格朗日方程可以得出系统的动力学方程:$b$表示摩擦系数,$f_{c}$表示对支杆的控制力。
由于一阶倒立摆会发生不稳定的倾斜运动,即未受到外部控制时会继续倾斜。
我们需要对系统加上控制力,使得系统保持在稳定的位置上。
在进行控制器设计之前,我们需要对系统进行分析,以便更好地了解系统在不同条件下的特性表现。
模糊控制一级倒立摆matlab实现

模糊控制一级倒立摆MATLAB实现课程:现代仿真技术及应用专业:控制理论与控制工程学号:姓名:模糊控制一级倒立摆MATLAB实现摘要:一级倒立摆是一个典型的非线性,强耦合,多变量的不稳定系统,为了控制其平衡性,对一级倒立摆系统建立了数学模型,采用模糊控制法设计了控制器,并用MATLAB/SIMULINK对控制系统进行了仿真实验研究,实验结果表明,模糊控制器具有良好的控制效果。
关键词:一级倒立摆;模糊控制;MATLAB/SIMULINK一引言倒立摆最初研究开始于20世纪50年代,麻省理工学院的控制论专家根据火箭发射器原理设计出一级倒立摆实验设备,而后倒立摆就成了验证控制方法和理论的实验平台,被广泛应用与实验教学中。
一级倒立摆具有结构简单,便于模拟的优点,同时它在控制过程中能够优先的反应控制中的许多关键问题,如系统的非线性、鲁棒性等。
因此对倒立摆的研究一直是控制领域中经久不衰的课题。
二一级倒立摆数学模型的建立在忽略各种摩擦之后,一级倒立摆系统是由小车、质量块和匀质杆组成的系统,通过控制小车位置,以使小车上的倒立摆始终处于反转垂直位置,左右倾斜角在︒±5.0范围内,原理结构图如图1.1所示。
图1.1 一级倒立摆原理结构图对该模型进行受力分析,作如下假设:M 小车质量 1.096Kg m 摆杆质量 0.109Kg b 小车摩擦系数 0.1N/m/sec I 摆杆惯量 0.0034Kg*m*m T 采样频率 0.005sl 摆杆转动轴心到杆质心的长度 0.25m F 夹在小车上的力 x 小车位置φ 摆杆与垂直向上方向的夹角θ 摆杆与垂直向下方向的夹角分析小车水平方向所受的合力:N x b F xM --= 摆杆水平方向的合力:)sin (22θl x dtd m N +=即: θθθθsin cos 2ml ml x m N -+= 把这个等式代入上式中,得到系统的第一个运动方程:F ml ml x b xm M =-+++θθθθsin cos )(2 对摆杆垂直方向上的合力进行分析,得到以下方程:θθθcos 2 ml ml mg P --=- 力矩平衡方程如下:θθθ I Nl Pl =--cos sin合并以上两个方程,得到第二个运动方程:θθθcos sin )(2xml mgl ml I -=++ 线性化后两个运动方程如下:⎪⎩⎪⎨⎧=-++=-+u ml x b x m M x ml mgl ml I φφφ)()(2 对方程组进行拉普拉斯变换,得到摆杆角度和小车位移之间的传递函数:mgls ml I mls X s -+=Φ22)()()( 将实际参数代入后得到实际模型:26705.00102125.002725.0)()(2-=Φs s X s 三 模糊控制器控制 3.1 模糊控制原理模糊逻辑控制简称模糊控制,是以模糊集合论、模糊语言变量和模糊逻辑推理为基础的一种计算机数字智能控制技术。
基于MATLAB-GUI的一级倒立摆控制仿真软件设计

基于MATLAB-GUI的一级倒立摆控制仿真软件设计基于MATLAB/GUI的一级倒立摆控制仿真软件设计摘要:本文介绍了一种基于MATLAB/GUI的一级倒立摆控制仿真软件的设计方法。
倒立摆是一个经典的控制系统问题,通过控制摆杆使其保持垂直状态。
本文使用MATLAB作为仿真平台,并通过GUI界面设计,使得用户可以方便地输入参数、观察系统状态和结果。
通过该仿真软件,可以有效地学习和研究控制系统的设计与应用。
关键词:MATLAB;倒立摆;控制系统;仿真软件;GUI一、引言倒立摆是一种非线性、强耦合且不稳定的控制系统,是控制理论中经典的问题之一。
倒立摆控制系统受到广泛的研究关注,其在机器人、飞行器、自动驾驶等领域有着重要的应用。
为了帮助学习者理解控制系统的原理和特点,设计了一种基于MATLAB/GUI的一级倒立摆控制仿真软件。
二、仿真软件设计1. 系统模型建立使用MATLAB工具箱中的Simulink建立倒立摆的系统模型。
系统包含两个部分:摆杆和电机控制器。
摆杆模型包括质量、长度、角度等参数;电机控制器模型包括电压、电流、转速等参数。
连接两个模块,构建完整的倒立摆控制系统。
2. GUI界面设计使用MATLAB的GUI工具进行界面设计,用户可以通过界面方便地输入参数、选择控制算法和观察系统状态。
界面包括输入参数框、按钮、图表等控件。
3. 控制算法设计通过GUI界面,用户可以选择不同的控制算法,如PID控制、模糊控制、自适应控制等。
根据选择的算法,修改Simulink模型中的控制器参数,并进行仿真分析。
4. 仿真结果可视化在GUI界面中添加图表,可以实时显示倒立摆的角度、位置等参数。
用户可以通过修改参数和算法,观察系统的响应结果并进行分析。
三、应用实例以PID控制算法为例,进行系统仿真。
用户可以通过GUI界面输入摆杆的质量、长度、角度等参数。
选择PID控制算法后,可以调节PID参数的值,观察系统响应和稳定性。
直线一级倒立摆MATLAB仿真报告
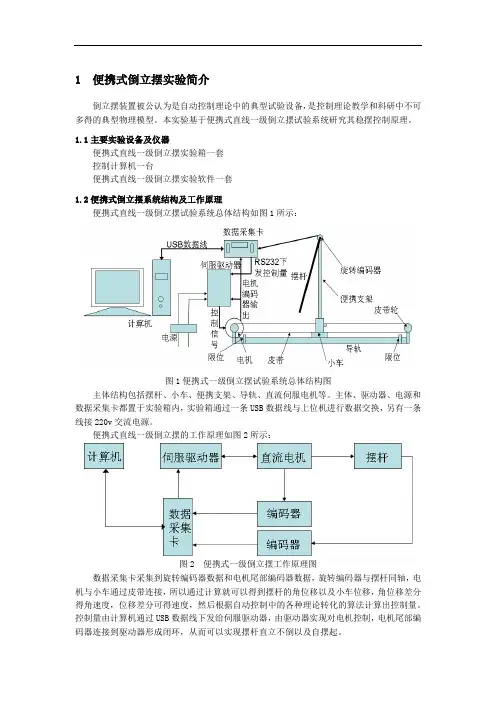
1便携式倒立摆实验简介倒立摆装置被公认为是自动控制理论中的典型试验设备,是控制理论教学和科研中不可多得的典型物理模型。
本实验基于便携式直线一级倒立摆试验系统研究其稳摆控制原理。
1.1主要实验设备及仪器便携式直线一级倒立摆实验箱一套控制计算机一台便携式直线一级倒立摆实验软件一套1.2便携式倒立摆系统结构及工作原理便携式直线一级倒立摆试验系统总体结构如图1所示:图1 便携式一级倒立摆试验系统总体结构图主体结构包括摆杆、小车、便携支架、导轨、直流伺服电机等。
主体、驱动器、电源和数据采集卡都置于实验箱内,实验箱通过一条USB数据线与上位机进行数据交换,另有一条线接220v交流电源。
便携式直线一级倒立摆的工作原理如图2所示:图2 便携式一级倒立摆工作原理图数据采集卡采集到旋转编码器数据和电机尾部编码器数据,旋转编码器与摆杆同轴,电机与小车通过皮带连接,所以通过计算就可以得到摆杆的角位移以及小车位移,角位移差分得角速度,位移差分可得速度,然后根据自动控制中的各种理论转化的算法计算出控制量。
控制量由计算机通过USB数据线下发给伺服驱动器,由驱动器实现对电机控制,电机尾部编码器连接到驱动器形成闭环,从而可以实现摆杆直立不倒以及自摆起。
2便携式倒立摆控制原理方框图便携式倒立摆是具有反馈功能的闭环系统,其控制目标是实现在静态和动态下的稳摆。
当输入量为理想摆角,即∅∅=0时,偏差为0,控制器不工作;当输入量不为理想摆角时,偏差存在,控制器做出决策,驱动电机,使小车摆杆系统发生相应位移,输出的摆角通过角位移传感器作用于输出量,达到减小偏差的目的。
根据控制原理绘制出控制方框图如图3所示:图3 便携式一级倒立摆控制原理方框图3建立小车-摆杆数学模型便携式倒立摆系统主要由小车、摆杆等组成,它们之间自由连接。
小车可以在导轨上自由移动,摆杆可以在铅垂的平面内自由地摆动。
在忽略了空气阻力和各种摩擦之后,可将便携式倒立摆系统抽象成小车和匀质杆组成的刚体系统,在惯性坐标内应用经典力学理论建立系统的动力学方程,采用力学分析方法建立小车-摆杆的数学模型。
单级倒立摆控制系统设计及MATLAB中的仿真汇总

单级倒立摆控制系统设计及simulink仿真摘要:倒立摆系统是一个典型的多变量、非线性、强藕合和快速运动的自然不稳定系统。
因此倒立摆在研究双足机器人直立行走、火箭发射过程的姿态调整和直升机飞行控制领域中有重要的现实意义,相关的科研成果己经应用到航天科技和机器人学等诸多领域。
单级倒立摆系统是一种广泛应用的物理模型。
控制单级倒立摆载体的运动是保证倒立摆稳定性的关键因素。
为了避免常用的物理反馈分析方法和运动轨迹摄像制导控制方法的某些缺点,本文从力学的角度提出对倒立摆的运动进行纯角度制导分析,完成了对倒立摆载体的角度制导运动微分方程的数学建模,设计了该模型的模糊控制系统,并利用 Matlab\simulink软件工具对倒立摆的运动进行了计算机仿真。
实验表明,这种模糊控制配合代数解析方法的运算速度和计算机仿真的效果均较物理反馈制导控制方法有了一定的提高。
该方法可以有效地改善单级倒立摆控制系统的性能。
本论文的主要工作是研究了直线一级倒立摆系统的模糊控制问题,用Matlab和Simulink对一级倒立摆模糊控制系统进行了仿真,验证了设计的可行性。
本文论述了一级倒立摆数学建模方法,推导出他们的微分方程,以及线性化后的状态方程。
讨论了单级倒立摆系统的模糊控制方法和操作步骤。
用Simulink实现了单级倒立摆模糊控制仿真系统,分别给出一级倒立摆系统控制量的响应曲线。
通过仿真说明控制器的有效性和实现性。
关键词:单级倒立摆;仿真;模糊控制;运动;建模;SimulinkDesign of single stage inverted pendulum control systemand Simulink simulationAbstract: inverted pendulum system is unstable system with a typical multi variable, nonlinear, strong coupled and fast motion. So the research on the attitude adjustment of the double foot robot and the attitude adjustment of the rocket launching process and the helicopter flight control field have practical,significance. The related scientific research achievements have been applied to many fields such as aerospace science and robotics. Single inverted pendulum system is a widely used physical model. Controlling the movement of the single inverted pendulum is the key factor to guarantee the stability of the inverted pendulum. In order to avoid some shortcomings of common physical feedback analysis method and motion trajectory camera guidance control method, this paper presents a pure angle guidance analysis on the motionof the inverted pendulum, and designs the fuzzy control system of the model. Experimental results show that the operation speed and computer simulation of this kind of fuzzy control combined with algebraic analysis method are improved by the physical feedback control method. This method can effectively improve the performance of a single stage inverted pendulum control system. In this paper, the main work of this paper is to study the fuzzy control of a linear inverted pendulum system, and the Matlab and Simulink to simulate the fuzzy control system of a single inverted pendulum, verify the feasibility of the design. And a mathematical modeling method of an inverted pendulum is described, their differential equations are derived, and the equation of state is linearized. The fuzzy control method and operation steps of single stage inverted pendulum system are discussed. Using Simulink to realize the fuzzy control simulation system of a single inverted pendulum, the response curve of the control of an inverted pendulum system is given. The effectiveness and the implementation of the controller are illustrated by simulation.Keywords: Inverted pendulum; Simulation; Fuzzy control; Motion; modeling; Simulink 引言倒立摆系统是研究控制理论的一种典型实验装置,具有成本低廉,结构简单,物理参数和结构易于调整的优点,是一个具有高阶次、不稳定、多变量、非线性和强藕合特性的不稳定系统。
用Matlab完成倒立摆系统的分析与综合
现代控制理论用Matlab 完成倒立摆系统的分析与综合2013/5/23 Thursday 学号:**********杨 博用Matlab 完成倒立摆系统的分析与综合一、实验要求1、熟悉非线性系统数学模型的建立过程。
2、非线性数学模型的近似线性化。
3、判断系统的能控性及能观性。
4、学习利用MATLAB 来分析系统的能观性、能控性和稳定性(Lyapunov 第一法)。
5、掌握状态反馈极点配置控制,并能用MATLAB 仿真软件进行控制算法的仿真验证与分析。
二、实验原理底座导轨摆杆XFϕl图1 一级倒立摆系统模型 图2 小车水平方向受力分析图3 摆杆垂直方向的受力分析Pb ẋ N F小车水平方向受力: Mẍ+bẋ+N =F摆杆水平方向受力:2(sin )2d N m x l dtθ=+即: N =mẍ+mlθcos θ−mlθsin θ得第一个运动方程:(M +m )ẍ+bẋ+mlθcos θ−mlθsin θ=F摆杆垂直方向受力:2(cos )2d P mg m l dtθ-=力矩平衡方程:−Pl sin θ−Nl cos θ=Iθ=+θπφ,cos cos φ=-sin sin φθ=-第二个运动方程:(I +ml 2)θ+mgl sin θ=−mlẍcos θ 两个运动方程化简得:{(I +ml 2)ϕ−mgl∅=mlẍ(M +m )ẍ+bẋ−mlϕ=u拉普拉斯变换得:222()()()()22()()()()()I ml s s mgl s mlX s sM m X s s bX s s ml s s U s ⎧+Φ-Φ=⎪⎨⎪++-Φ=⎩三、实验内容1、一级直线倒立摆传递函数的建立 摆杆输出角度和电机作用力的传递函数为:2()2()()()432ml s s qU s b I ml mgl M m bmgls s s sq q q⋅Φ=+++⋅-⋅-⋅ 其中22[()()()]q M m I ml ml =++-2、一级直线倒立摆状态空间方程的建立求解可得ẍ、ϕ,整理后得到系统的状态空间方程为:010002222()00222()()()00010()00222()()()x x I ml b m gl I ml x xI M m Mml I M m Mml I M m Mml umlbmgl M m ml I M m Mml I M m Mml I M m Mml φφφφ⎡⎤⎡⎤⎢⎥⎢⎥⎡⎤⎡⎤-++⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥++++++⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-+⎢⎥⎣⎦⎣⎦⎢⎥⎢⎥⎢⎥⎢⎥++++++⎣⎦⎣⎦1000000100x x x y u φφφ⎡⎤⎢⎥⎡⎤⎡⎤⎡⎤⎢⎥==+⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎢⎥⎣⎦3、MATLAB 仿真要求 ➢ 求出状态空间表达式矩阵。
直线一级倒立摆控制方法设计
直线一级倒立摆控制方法设计倒立摆的数学模型设计倒立摆系统是一个典型的非线性、强耦合、多变量和不稳定系统,作为控制系统的被控对象,许多抽象的控制概念都可以通过倒立摆直观地表现出来。
本设计是以一阶倒立摆为被控对象来进行设计的。
状态空间法:状态空间法可以进行单输入多输出系统设计,因此在这个实验中,我们将尝试同时对摆杆角度和小车位置进行控制。
根据设计要求,给小车加一个阶跃输入信号。
此次用Matlab 求出系统的状态空间方程各矩阵,并仿真系统的开环阶跃响应。
在这里给出一个state.m 文件,执行这个文件,Matlab 将会给出系统状态空间方程的A,B,C 和D 矩阵,并绘出在给定输入为一个0.2m 的阶跃信号时系统的响应曲线。
直线一级倒立摆系统数学建模 在忽略了空气阻力、各种摩擦之后,可将直线一级倒立摆系统抽象成小车和匀质杆组成的系统。
如图所示:系统状态方程为:XAX Bu Y CX Du=+=+假设系统内部各相关参数为:M 小车质量 0.5kg m 摆杆质量 0.2kgb 小车摩擦系数 0.1N/m/sec l 摆杆转动轴心到杆质心的长度 0.3mI 摆杆惯量 0.006kg*m*m T 采样时间 0.005s x 小车位置φ 摆杆与垂直向上方向的夹角θ 摆杆与垂直向下方向的夹角(考虑到摆杆初始位置为竖直向下) 应用牛顿-欧拉方法,可得到系统状态空间方程为:222222201()0()()0()0()()x I ml b m gl x I M m Mml I M m Mml lb mgl M m I M m Mml I M m Mml φφ⎡⎤⎢⎥⎡⎤-+⎢⎥⎢⎥⎢⎥++++⎢⎥=⎢⎢⎥⎢⎢⎥⎢-+⎢⎥⎣⎦⎢++++⎣⎦ 0 0 0 0 0 0m 0 2220()0()x I ml x I M m Mml u ml I M m Mml φφ⎡⎤⎢⎥⎡⎤+⎢⎥⎢⎥⎢⎥++⎢⎥+⎥⎢⎥⎢⎥⎥⎢⎥⎢⎥⎥⎢⎥⎢⎥⎣⎦⎥⎢⎥++⎣⎦1000000100x x x Y u φφφ⎡⎤⎢⎥⎡⎤⎡⎤⎡⎤⎢⎥==+⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦ 以上就是一阶倒车摆系统的状态空间表达式。
一级倒立摆课程设计--倒立摆PID控制及其Matlab仿真
一级倒立摆课程设计--倒立摆PID控制及其Matlab仿真倒立摆PID控制及其Matlab仿真学生姓名:学院:电气信息工程学院专业班级:专业课程:控制系统的MATLAB仿真与设计任课教师:2014 年 6 月 5 日倒立摆PID控制及其Matlab仿真Inverted Pendulum PID Control and ItsMatlab Simulation摘要倒立摆系统是一个典型的快速、多变量、非线性、不稳定系统,对倒立摆的控制研究无论在理论上和方法上都有深远的意义。
本论文以实验室原有的直线一级倒立摆实验装置为平台,重点研究其PID 控制方法,设计出相应的PID控制器,并将控制过程在MATLAB上加以仿真。
本文主要研究内容是:首先概述自动控制的发展和倒立摆系统研究的现状;介绍倒立摆系统硬件组成,对单级倒立摆模型进行建模,并分析其稳定性;研究倒立摆系统的几种控制策略,分别设计了相应的控制器,以MATLAB为基础,做了大量的仿真研究,比较了各种控制方法的效果;借助固高科技MATLAB实时控制软件实验平台;利用设计的控制方法对单级倒立摆系统进行实时控制,通过在线调整参数和突加干扰等,研究其实时性和抗千扰等性能;对本论文进行总结,对下一步研究作一些展望。
关键词:倒立摆;PID控制器;MATLAB仿真设计报告正文1.简述一级倒立摆系统的工作原理;倒立摆是一个数字式的闭环控制系统,其工作原理为:角度、位移信号检测电路获取后,由微分电路获取相应的微分信号。
这些信号经A/D转换器送入计算机,经过计算及内部的控制算法解算后得到相应的控制信号,该信号经过D/A变换、再经功率放大由执行电机带动皮带卷拖动小车在轨道上做往复运动,从而实现小车位移和倒立摆角位移的控制。
2.依据相关物理定理,列写倒立摆系统的运动方程;2lO1小车质量为M ,倒立摆的质量为m ,摆长为2l ,小车的位置为x ,摆的角度为θ,作用在小车水平方向上的力为F ,1O 为摆杆的质心。
基于MATLAB的一阶倒立摆的建模及仿真
基于MATLAB的一阶倒立摆的建模及仿真作者:韦忠海来源:《中国科技博览》2014年第10期[摘要]倒立摆系统是一个典型的快速、多变量、非线性、不稳定系统,建立其数学模型研究其稳定性对于很多工程控制有着重大意义。
采用机理建模法对一阶倒立摆系统进行分析,建立其数学模型,在用Matlab 软件进行仿真验证,仿真时,观察不同的初始条件下倒立摆的运行特性。
[关键词]倒立摆,数学模型,MATLAB软件,仿真Modeling and Simulation of an inverted pendulum based on MATLABWei Zhong-hai(GUANGXI UNIVERSITY College of Electrical Engineering, Nanning, 530004)[Abstract]the inverted pendulum system is a typical fast, multi variable, nonlinear, unstable system, study the stability is of great significance for many engineering control to establish its mathematical model. Analysis on the inverted pendulum system by using mechanism modeling method, the mathematical model was established, using Matlab software simulation,simulation, observe the running characteristics of different initial conditions of the inverted pendulum.[Key words]inverted pendulum, mathematical model, MATLAB software, simulation中图分类号:TH139 文献标识码:A 文章编号:1009-914X(2014)10-0016-031、倒立摆的简介图1(a)为直线单级倒立摆实际设备,为方便分析,将其抽象这小车与摆杆的示意图,如图1(b)所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
非线性作业
一 一级直线倒立摆
如图1所示系统里的各参数变量
M :小车系统的等效质量(1.096kg );:摆杆的质量(0.109kg );1m :摆杆的半长(0.25m )
;2m J :摆杆系统的转动惯量(0.0034kg*m );g :重力加速度(9.8N/Kg );r :小车的水平位置(m );
θ:摆角大小(以竖直向上为0起始位置,逆时针方向为正方向);
:小车对摆杆水平方向作用力(N )
(向左为正方向),’是其反作用力;h F h F :小车对摆杆竖直方向作用力(N )
(向上为正方向),’是其反作用力;v F v F U :电动机经传动机构给小车的力,可理解为控制作用u’(向左为正方向);:摆杆重心的水平位置(m );:摆杆重心的竖直位置(m )。
p x p y 1.1一级倒立摆的数学建模定义系统的状态为[r,r, θ, θ]
经推导整理后可以达到倒立摆系统的牛顿力学模型:
(1)θθθsin cos )(2mgl l r m ml I =-+ (2)
u ml r m M ml -⋅=+-⋅2sin )(cos θ
θθθ 因为摆杆一般在工作在竖直向上的小领域内θ=0,可以在小范围近似处理:
,则数学模型可以整理成:
0,0sin ,1cos 2==≈θθθ (3)θθmgl l r m ml I =-+ )(2 (4)
u r m M ml =++- )(θ系统的状态空间模型为
=+ (5)
⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡θθ r r ⎥⎥⎥⎥⎥⎥⎦
⎤⎢⎢⎢⎢⎢⎢⎣
⎡+++++0)()(0
10
000)(0000102
2
2
2
Mml m M I m M mgl Mml m M I gl m ⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡θθ
r r ⎥⎥⎥⎥⎥⎥⎥⎦
⎤
⎢⎢⎢
⎢⎢⎢⎢⎣⎡+++++222
)(0
)(0Mml m M I ml Mml m M I ml I u (6)
u r r r y ⎥⎦
⎤⎢⎣⎡+⎥⎥⎥⎥⎥
⎦⎤
⎢⎢⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=0000101000θθθ 代人实际系统的参数后状态方程为:
=+ (7)
⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣
⎡θθ r r ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡08285.2700100006293.0000010⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡θθ r r u ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡3566.208832.00 (8)
u r r r y ⎥⎦
⎤⎢⎣⎡+⎥⎥⎥⎥⎥
⎦⎤
⎢⎢⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=0000101000θθθ 1.2滑模变结构在一级倒立摆系统的应用
主要包括切换函数的设计、控制率的设计和系统消除抖振的抑制。
基于线性二次型最优化理论的切换函数设计,定义系统的优化积分指标是:
Q>0,
Qxdt x J T ⎰∞
=0
本文采用指数趋近律:,其中k 和ε为正数。
将其代人S=Cx=0)sgn(S kS S ε--=
中,可以得到:
(9))sgn(S kS CBu CAx x C S
ε--=+== 控制率为:
(10)
))sgn(()(1S kS CAx CB u ε++-=-ε的选取主要是为了抑制系统的摩擦力和近似线性化所带来的误差和参数摄动等因素,从而使得系统具有良好的鲁棒性。
文中k=25, ε=0.8。
取变换矩阵T 。
其中T=,⎥⎥⎥⎥⎥
⎦
⎤
⎢⎢⎢⎢
⎢⎣⎡+-10
00
0100)(010
00012
ml ml I 去Q*11=diag([300 50 350]),Q22=10
关于Riccati 方程的解有MATLAB 的lqr
01112122121111=+-+*
-**Q P A Q PA P A PA T T
函数可以解出
⎢⎢⎢⎣⎡-=6098.3599281.2147165.692P 8204.1491894.1129281.214-⎥⎥
⎥⎦⎤
--4007.3548204.1496098.359 [0000.1000-=C 2717.69-6295.210]9610.35 [r C x S ⋅=0)(r
θ]
T θ 二 程序
%主程序:直线一级倒立摆
clear all close all
global C M0 F
ts=0.02; %采样时间T=30; %仿真时间TimeSet=[0:ts:T];
para=[];
%options 为解微分函数中的调整参数,reltol 和abstol 分别是设置相对误差和绝对误差
options=odeset('RelTol',1e-3,'AbsTol',[1e-3 1e-3 1e-3 1e-3]);%options=[];
x0=[0.5,0.3,0,0]; %初始值
[t,xout]=ode45('daolibai2eq',TimeSet,x0,options,para);%固定格式,子程序调用%返回值x1=xout(:,1);x2=xout(:,2);x3=xout(:,3);x4=xout(:,4);
s=C(1)*x1+C(2)*x2+C(3)*x3+C(4)*x4; %切换函数或切换面%选择控制器if F==1
% for k=1:1:T/ts+1
M0=40;
%u(k)=-M0*sign(s(k));
u=-M0*sign(s);
%end
else if F==2
beta=30;
delta=0;
for k=1:1:T/ts+1
u(k)=-
beta*(abs(x1(k))+abs(x2(k))+abs(x3(k))+abs(x4(k))+delta)*sign(s(k));
end
end
%绘图
figure(1);
plot(t,x1,'r');
xlabel('time(s)');ylabel('Cart Position');
figure(2);
plot(t,x2,'r');
xlabel('time(s)');ylabel('Pendulum Angle');
figure(3);
plot(t,s,'r');
xlabel('time(s)');ylabel('s');
figure(4);
plot(t,u,'r');
xlabel('time(s)');
ylabel('u');
end
%子程序
function dx=DxnamicModel(t,x,flag,para)%自定义动态函数
global C M0 F
%倒立摆经计算后模型
M=1.096;m=0.109;b=0.1;l=0.25;I=0.0034;T=0.005;g=0.98;
k22=-(I+m*l^2)*b/(I*(M+m)+M*m*l^2);
k23=m^2*g*l^2/(I*(M+m)+M*m*l^2);
k42=-m*l*b/(I*(M+m)+M*m*l^2);
k43=m*g*l*(M+m)/(I*(M+m)+M*m*l^2);
b12=(I+m*l^2)/(I*(M+m)+M*m*l^2);
b14=m*l/(I*(M+m)+M*m*l^2);
A=[0,1,0,0;0,k22,k23,0;0,0,0,1;0,k42,k43,0];
b=[0;b12;0;b14];
%Ackermann's formula
n1=-1;n2=-2;n3=-3;
C=[0,0,0,1]*inv([b,A*b,A^2*b,A^3*b])*(A-n1*eye(4))*(A-n2*eye(4))*(A-
n3*eye(4));s=C*x;F=2;if F==1
M0=40;
u=-M0*sign(s);elseif F==2 beta=30; delta=0;
u=-beta*(abs(x(1))+abs(x(2))+abs(x(3))+abs(x(4))+delta)*sign(s);end
%state equation dx=zeros(4,1);f0=0.5;
ft=f0*sin(3*t);dx=A*x+b*(u+ft);
三 仿真结果
time(s)
C a r t P o s i t i o n
图2
time(s)
P e n d u l u m A n g l e
图3
time(s)
s
图4
time(s)
图5。
