人教课标版高中数学必修2第一单元《空间几何体》章末综合检测
人教版高中数学必修2第一章-空间几何体练习题及答案(全)

人教版高中数学必修2第一章-空间几何体练习题及答案(全)第一章空间几何体1.1 空间几何体的结构一、选择题1、下列各组几何体中是多面体的一组是()A 三棱柱四棱台球圆锥B 三棱柱四棱台正方体圆台C 三棱柱四棱台正方体六棱锥D 圆锥圆台球半球2、下列说法正确的是()A 有一个面是多边形,其余各面是三角形的多面体是棱锥B 有两个面互相平行,其余各面均为梯形的多面体是棱台C 有两个面互相平行,其余各面均为平行四边形的多面体是棱柱D 棱柱的两个底面互相平行,侧面均为平行四边形3、下面多面体是五面体的是()A 三棱锥B 三棱柱C 四棱柱D 五棱锥4、下列说法错误的是()A 一个三棱锥可以由一个三棱锥和一个四棱锥拼合而成B 一个圆台可以由两个圆台拼合而成C 一个圆锥可以由两个圆锥拼合而成D 一个四棱台可以由两个四棱台拼合而成5、下面多面体中有12条棱的是()A 四棱柱B 四棱锥C 五棱锥D 五棱柱6、在三棱锥的四个面中,直角三角形最多可有几个()A 1 个B 2 个C 3个D 4个二、填空题7、一个棱柱至少有————————个面,面数最少的棱柱有————————个顶点,有—————————个棱。
8、一个棱柱有10个顶点,所有侧棱长的和为60,则每条侧棱长为————————————9、把等腰三角形绕底边上的高旋转1800,所得的几何体是——————10、水平放置的正方体分别用“前面、后面、上面、下面、左面、右面”表示。
图中是一个正方体的平面展开图,若图中的“似”表示正方体的前面,“锦”表示右面,“程”表示下面。
则“祝”“你”“前”分别表示正方体的—————祝你前程似锦一、选择题1、两条相交直线的平行投影是()A 两条相交直线B 一条直线C 一条折线D 两条相交直线或一条直线2、如图中甲、乙、丙所示,下面是三个几何体的三视图,相应的标号是()①长方体②圆锥③三棱锥④圆柱A ②①③B ①②③C ③②④D ④③②。
数学《必修2》第一章“空间几何体”测试题与答案

数学《必修2》第一章“空间几何体”测试题一、选择题:(本大题共10个小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符号题目要求的)1.利用斜二测画法得到的:①三角形的直观图一定是三角形;②正方形的直观图一定是正方形;③等腰梯形的直观图一定是等腰梯形;④平行四边形的直观图一定是平行四边形。
以上结论正确的是()A.①②B.①④C.③④D. ①②③④2.下列说法正确的是()A.棱柱的侧面可以是三角形B.正方体和长方体都是特殊的四棱柱C.所有的几何体的表面都能展开成平面图形D.棱柱的各条棱都相等3.圆台的母线长为6,两底面半径分别为2、7,则圆台的侧面积为()A.54πB.8πC.4πD.164.给出下列结论:①圆柱的母线是其上底面圆周上任意一点与下底面圆周上任意一点的连线;②圆锥的母线是圆锥顶点与底面圆周上任意一点的连线;③圆台的母线是圆台上、下底面圆周上任意两点的连线。
其中正确的是()A.①②B.②③C.①③D.②。
5.已知底面为正方形的长方体的各顶点都在一个球面上,长方体的高为4,体积为16,则这个球的表面积是()A.16πB.20πC.24πD.32π6.下列说法错误的是()A.棱柱最少有5个面B.棱锥最少有4个面C.棱台的底面有2个D.棱锥的底面边数和侧棱数不一定相同7.下列四个图形不是下图1中几何体的三视图之一的是()图1 A B C D8.下面几何体中,过轴的截面一定是圆面的是( )A.圆柱B.圆锥C.球D.圆台 9.正方体的表面积是96,则正方体的体积是( )A. B.64 C.16 D. 96 10.若某几何体的三视图如图所示,则这个几何体的直观图可以是( )二、填空题:(本大题共5个小题,每小题5分,共25分)11.半径为2的球的体积等于 ,表面积等于12.圆锥的侧面展开图为圆心角为120、半径为1的扇形,则圆锥的侧面积为 13.如下图所示,等腰梯形ABCD ,上底1CD =,腰AD CB ==3AB =,以下底所在直线为x 轴,则由斜二测画法画的直观图''''A B C D 的面积为 14.某几何体的三视图如下图所示, 则其体积为_______.15.某几何体的三视图如下图所示,则该几何体的体积是____________.第13题图14题图第15题图三、解答题:(本大题共6个小题,共75分,解答应写出文字说明,证明过程或演算步骤)16.求下列几何体的体积与表面积。
高中数学必修2第一章《空间几何体》单元检测卷含解析

必修2第一章《空间几何体》单元检测卷本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120分钟.第Ⅰ卷(选择题共60分)一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中只有一个是符合题目要求的)1.以边长为1的正方形的一边所在直线为旋转轴,将该正方形旋转一周所得圆柱的侧面积等于 ( ) A.2πB.πC.2 D.12.如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的表面积为( )A.18+36 5 B.54+18 5C.90 D.813.已知一个底面是菱形、侧面是矩形的四棱柱,侧棱长为5,菱形的对角线的长分别是9和15,则这个棱柱的侧面积是 ( )A.3034 B.6034C.3034+135 D.1354.已知圆柱与圆锥的底面积相等,高也相等,它们的体积分别为V1和V2,则V1:V2= ( )A.1:3 B.1:1C.2:1 D.3:15.若两个球的表面积之比为1:4,则这两个球的体积之比为 ( )A.1:2 B.1:4C.1:8 D.1:166.如图,△O′A′B′是水平放置的△OAB的直观图,则△OAB的面积为 ( )A .6B .3 2C .6 2D .127.某四棱锥的三视图如图所示,该四棱锥最长棱的棱长为 ( )A .1B . 2C . 3D .28.若一圆柱与圆锥的高相等,且轴截面面积也相等,那么圆柱与圆锥的体积之比为 ( ) A .1 B .12 C .32D .349.半径为R 的半圆卷成一个圆锥,则它的体积为 ( ) D .324πR 3B .38πR 3C .525πR 3D .58πR 3 10.《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧度为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放斛的米约有 ( )A .14斛B .22斛C .36斛D .66斛11.已知底面为正三角形,侧面为矩形的三棱柱有一个半径为 3 cm 的内切球,则此棱柱的体积是 ( )A .9 3 cm 3B .54 cm 3C .27 cm 3D .18 3 cm 312.一个由半球和四棱锥组成的几何体,其三视图如图所示.则该几何体的体积为 ( )D .13+23π B .13+23π C .13+26π D .1+26π 第Ⅱ卷(非选择题 共90分)二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上) 13.如图是△AOB 用斜二测画法画出的直观图,则△AOB 的面积是________.14.圆柱的高是8 cm ,表面积是130π cm 2,则它的底面圆的半径等于________cm.15.棱锥的高为16,底面积为512,平行于底面的截面面积为50,则截得的棱台的高为________. 16.如图是一个组合几何体的三视图,则该几何体的体积是________.三、解答题(本大题共6个大题,共70分,解答应写出文字说明,证明过程或演算步骤)17.(本小题满分10分)把一个圆锥截成圆台,已知圆台的上、下底面半径的比是1:4,母线长为10 cm.求圆锥的母线长.18.(本小题满分12分)如图所示,四棱锥V-ABCD的底面为边长等于2 cm的正方形,顶点V与底面正方形中心的连线为棱锥的高,侧棱长VC=4 cm,求这个四棱锥的体积.19.(本小题满分12分)如下图,一个圆锥形的空杯子上面放着一个半球形的冰淇淋,如果冰淇淋融化了,会溢出杯子吗?请用你的计算数据说明理由.20.(本小题满分12分)已知某几何体的侧视图与其正视图相同,相关的尺寸如图所示,求这个几何体的体积.21.(本小题满分12分)据说伟大的阿基米德逝世后,敌军将领马塞拉斯给他建了一块墓碑,在墓碑上刻了一个如图所示的图案,图案中球的直径与圆柱底面的直径和圆柱的高相等,圆锥的顶点为圆柱上底面的圆心,圆锥的底面是圆柱的下底面.试计算出图案中圆锥、球、圆柱的体积比.22.(本小题满分12分)如图所示,有一块扇形铁皮OAB,∠AOB=60°,OA=72 cm,要剪下来一个扇形环ABCD,作圆台形容器的侧面,并且余下的扇形OCD内剪下一块与其相切的圆形使它恰好作圆台形容器的下底面(大底面).试求:(1)AD的长;(2)容器的容积.必修2第一章《空间几何体》单元检测题侧A.【第2题解析】由三视图,知该几何体是一个斜四棱柱,所以该几何体的表面积S =2×3×6+2×3×3+2×3×35=54+185,故选B .【第5题解析】设两个球的半径分别为r 1、r 2,∴S 1=4πr 21,S 2=4πr 22. ∴S 1S 2=r 21r 22=14,∴r 1r 2=12. ∴V 1V 2=43πr 3143πr 32=(r 1r 2)3=18. 故选C . 【第6题解析】△OAB 是直角三角形,OA =6,OB =4,∠AOB =90°,∴S △OAB =12×6×4=12. 故选D.【第7题解析】根据三视图,可知几何体的直观图为如图所示的四棱锥V -ABCD ,其中VB ⊥平面ABCD ,且底面ABCD 是边长为1的正方形,VB =1.所以四棱锥中最长棱为VD . 连接BD ,易知BD =2,在Rt △VBD 中,VD =VB 2+BD 2= 3. 故选C .【第8题解析】设圆柱与圆锥的底半径分别为R , r ,高都是h ,由题设,2R ·h =12×2r ·h ,∴r =2R ,V 柱=πR 2h ,V 锥=13πr 2h =43πR 2h ,∴V 柱V 锥=34,故选D .【第9题解析】依题意,得圆锥的底面周长为πR ,母线长为R ,则底面半径为R 2,高为32R ,所以圆锥的体积为13×π×(R 2)2×32R =324πR 3. 故选A .【第10题解析】设圆锥底面半径为r ,则14×2×3r =8,∴r =163,所以米堆的体积为14×13×3×(163)2×5=3209,故堆放的米约为3209÷1.62≈22,故选B . 【第11题解析】由题意知棱柱的高为2 3 cm ,底面正三角形的内切圆的半径为 3 cm ,∴底面正三角形的边长为6 cm ,正三棱柱的底面面积为9 3 cm 2,∴此三棱柱的体积V =93×23=54(cm 3).故选B . 【第12题解析】根据三视图可知,四棱锥的底面是边长为1的正方形、高是1,半球的半径为22,所以该几何体的体积为13×1×1×1+12×43π(22)3=13+26π. 故选C .【第16题解析】由三视图可知该组合几何体下面是一个圆柱,上面是一个三棱柱,故所求体积为V =12×3×4×6+16π×8=36+128π. 故填36+128π. 【第17题答案】403cm【第17题解析】如图,设圆锥母线长为l ,则l -10l =14,所以l =403cm.【第18题答案】4143cm 3【第18题解析】如图,连接AC 、BD 相交于点O ,连接VO ,∵AB =BC =2 cm , 在正方形ABCD 中, 求得CO = 2 cm , 又在直角三角形VOC 中, 求得VO =14 cm ,∴V V -ABCD =13S ABCD ·VO =13×4×14=4143(cm 3).故这个四棱锥的体积为4143cm 3.【第20题答案】7π4.【第20题解析】由三视图可知,该几何体是大圆柱内挖掉了小圆柱,两个圆柱高均为1,底面是半径为2和32的同心圆,故该几何体的体积为4π×1-π(32)2×1=7π4.【第21题答案】1:2:3.【第21题解析】设圆柱的底面半径为r ,高为h ,则V 圆柱=πr 2h . 由题意知圆锥的底面半径为r ,高为h ,球的半径为r ,∴V 圆锥=13πr 2h ,∴V 球=43πr 3.又h =2r ,∴V 圆锥:V 球:V 圆柱=(13πr 2h ):(43πr 3):(πr 2h )=(23πr 3):(43πr 3):(2πr 3)=1:2:3.。
人教版高一数学必修二第一章空间几何体章末检测题 附答案解析

必修二 第一章 空间几何体章末检测题一、选择题1.右面的三视图所示的几何体是( ).A .六棱台B .六棱锥C .六棱柱D .六边形 (第1题)2.已知两个球的表面积之比为1∶9,则这两个球的半径之比为( ). A .1∶3B .1∶3C .1∶9D .1∶813.一个长方体去掉一个小长方体,所得几何体的正(主)视图与侧(左)视图分别如右图所示,则该几何体的俯视图为( ).4.A ,B 为球面上相异两点,则通过A ,B 两点可作球的大圆(圆心与球心重合的截面圆)有( ).A .一个B .无穷多个C .零个D .一个或无穷多个5.右图是一个几何体的三视图,则此几何体的直观图是( ). ).A B C D6.下图为长方体木块堆成的几何体的三视图,堆成这个几何体的木块共有( ). A .1块 B .2块 C .3块 D .4块正(主)视图侧(左)视图ABCD(第3题)正视图侧视图俯视图(第5题)正视图俯视图侧视图(第6题)7.关于斜二测画法画直观图说法不正确的是().A.在实物图中取坐标系不同,所得的直观图有可能不同B.平行于坐标轴的线段在直观图中仍然平行于坐标轴C.平行于坐标轴的线段长度在直观图中仍然保持不变D.斜二测坐标系取的角可能是135°8.如图,下列几何体各自的三视图中,有且仅有两个视图相同的是().①正方体②圆锥③三棱台④正四棱锥(第8题)A.①②B.①③C.①④D.②④9.一正方体的各顶点都在同一球面上,用过球心的平面去截这个组合体,截面图不能是().A B C D10.如果一个三角形的平行投影仍然是一个三角形,则下列结论正确的是().A.原三角形的内心的平行投影还是投影三角形的内心B.原三角形的重心的平行投影还是投影三角形的重心C.原三角形的垂心的平行投影还是投影三角形的垂心D.原三角形的外心的平行投影还是投影三角形的外心二、填空题11.一圆球形气球,体积是8 cm3,再打入一些空气后,气球仍然保持为球形,体积是27 cm3.则气球半径增加的百分率为.12.底面是菱形的棱柱其侧棱垂直于底面,且侧棱长为5,它的体对角线的长分别是9和15,则这个棱柱的侧面积是.13.右图是一多面体的展开图,每个面内都给了字母,请根据要求回答问题:①如果A 是多面体的下底面,那么上面的面是 ;②如果面F 在前面,从左边看是面B ,那么上面的面是 . 14.一个几何体的三视图如下图所示,则此几何体的体积是 .三、解答题15.圆柱内有一个四棱柱,四棱柱的底面是圆柱底面的内接正方形.已知圆柱表面积为6 ,且底面圆直径与母线长相等,求四棱柱的体积.16.下图是一个几何体的三视图(单位:cm ) (1)画出这个几何体的直观图(不要求写画 法);(2)求这个几何体的表面积及体积.题)侧视图俯视BBA C 正视BA侧视(第16题)17.如图,在四边形ABCD 中,∠DAB =90°,∠ADC =135°,AB =5,CD =22,AD =2,求四边形ABCD 绕直线AD 旋转一周所成几何体的表面积及体积.18.已知正方体、球、底面直径与母线相等的圆柱,它们的表面积相等,试比较它们的体积V 正方体,V 球,V 圆柱的大小.19.如图,一个圆锥形容器的高为a ,内装有一定量的水.如果将容器倒置,这时水所形成的圆锥的高恰为2a,求原来水面的高度.20.如图,四棱柱的底面是菱形,各侧面都是长方形.两个对角面也是长方形,面积分别为Q 1,Q 2.求四棱柱的侧面积.(第20题)(第19题)(第17题)参考答案一、选择题 1.B解析:由正视图和侧视图可知几何体为锥体,由俯视图可知几何体为六棱锥. 2.A解析:由设两个球的半径分别为r ,R ,则 4 r 2∶4πR 2=1∶9. ∴ r 2∶R 2=1∶9, 即r ∶R =1∶3.3.C解析:在根据得到三视图的投影关系,∵正视图中小长方形位于左侧,∴小长方形也位于俯视图的左侧;∵小长方形位于侧视图的右侧,∴小长方形一定位于俯视图的下侧, ∴ 图C 正确.4.D解析:A ,B 不在同一直径的两端点时,过A ,B 两点的大圆只有一个;A ,B 在同一直径的端点时大圆有无数个.5.D解析:由几何体的正视图和侧视图可知,几何体上部分为圆锥体,由三个视图可知几何体下部分为圆柱体,∴ 几何体是由圆锥和圆柱组成的组合体.6.D解析:由三视图可知几何体为右图所示,显然组成几何体的长方体木块有4块.7.C解析:由平行于x 轴和z 轴的线段长度在直观图中仍然保持不变,平行于y 轴的线段长度在直观图中是原来的一半,∴ C 不对.8.D解析:①的三个视图均相同;②的正视图和侧视图相同;③的三个视图均不相同;④的正视图和侧视图相同.∴有且仅有两个视图相同的是②④.9.A(第6题)解析:B 是经过正方体对角面的截面;C 是经过球心且平行于正方体侧面的截面;D 是经过一对平行的侧面的中心,但不是对角面的截面.10.B解析:在平行投影中线段中点在投影后仍为中点,故选B . 二、填空题 11.50%.解析:设最初球的半径为r ,则8=34πr 3;打入空气后的半径为R ,则27=34πR 3. ∴ R 3∶r 3=27∶8.∴ R ∶r =3∶2.∴气球半径增加的百分率为50%. 12.160.解析:依条件得菱形底面对角线的长分别是22515-=200和2259-=56. ∴菱形的边长为4256256220022=⎪⎪⎭⎫⎝⎛+⎪⎪⎭⎫ ⎝⎛= 8. ∴棱柱的侧面积是5×4×8=160. 13.F ,C .解析:将多面体看成长方体, A ,F 为相对侧面.如果A 是多面体的下底面,那么上面的面是F ;如果面F 在前面,从左边看是面B ,则右面看必是D ,于是根据展开图,上面的面应该是C .14.80.解析:由三视图可知,几何体是由棱长为4的正方体和底面边长为4,高为3的四棱锥组成,因此它的体积是V =43+31×42×3=64+16=80.三、解答题15.参考答案:设圆柱底面圆半径为r ,则母线长为2r . ∵圆柱表面积为6π,∴ 6π=2πr 2+4πr 2. ∴ r =1.∵ 四棱柱的底面是圆柱底面的内接正方形, ∴ 正方形边长为2. ∴ 四棱柱的体积V =(2)2×2=2×2=4. 16.(1)略.(2)解:这个几何体是三棱柱.由于底面△ABC 的BC 边上的高为1,BC =2,∴ AB =2. 故所求全面积S =2S △ABC +S BB ′C ′C +2S ABB ′A ′=8+62(cm 2). 几何体的体积V =S △ABC ·BB ′=21×2×1×3=3(cm 3). 17.解:S 表面=S 下底面+S 台侧面+S 锥侧面=π×52+π×(2+5)×5+π×2×22=(60+42)π.V =V 台-V 锥=31π(21r +r 1r 2+22r )h -31πr 2h 1=3148π.18.解:设正方体的边长为a ,球的半径为r ,圆柱的底面直径为2R , 则6a 2=4πr 2=6πR 2=S .∴ a 2=6S ,r 2=π4S,R 2=π6S . ∴(V 正方体)2=(a 3)2=(a 2)3=36⎪⎭⎫⎝⎛S =2163S ,(V 球)2=23π34⎪⎭⎫⎝⎛r =916π2(r 2)3=916π23π4⎪⎭⎫ ⎝⎛S ≈1083S ,(V 圆柱)2=(πR 2×2R )2=4π2(R 2)3=4π23π6⎪⎭⎫⎝⎛S ≈1623S .∴V 正方体<V 圆柱<V 球.19.解:设水形成的“圆台”的上下底面半径分别为r ,R ,高为h ,则R r =aha -. 则依条件得3π·h ·(r 2+rR +R 2)=3π·2a ·22⎪⎭⎫⎝⎛R ,化简得(h -a )3=-87a 3.解得h =a -873a .即h =⎪⎪⎭⎫ ⎝⎛-271a . 20.解:设底面边长为a ,侧棱长为l ,底面的两对角线长分别为c ,d .则⎪⎪⎩⎪⎪⎨⎧③ = 21 + 21② = ① = 22221a d c Q dl Q cl ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛33(第20题)由 ① 得c =l Q 1,由 ② 得d =l Q 2,代入 ③ 得212⎪⎭⎫ ⎝⎛l Q +222⎪⎭⎫⎝⎛l Q =a 2.∴21Q +22Q =4l 2a 2, ∴2la =2221+Q Q . 故S 侧=4al =22221+Q Q .。
高中数学必修二:各章章末检测(含解析)
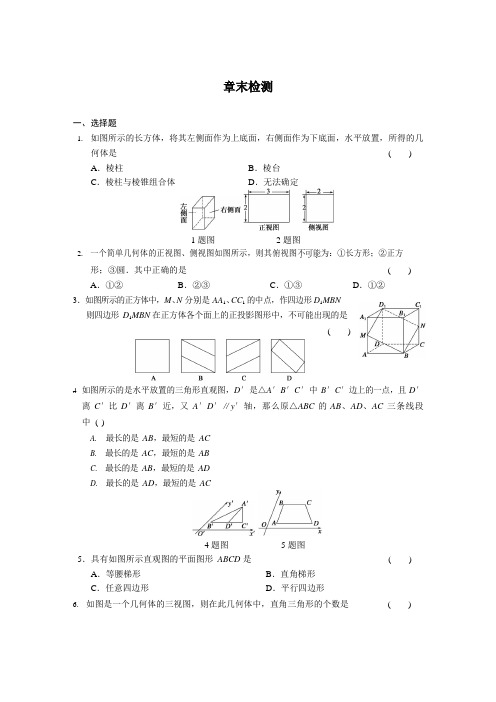
章末检测一、选择题1.如图所示的长方体,将其左侧面作为上底面,右侧面作为下底面,水平放置,所得的几何体是( ) A.棱柱B.棱台C.棱柱与棱锥组合体D.无法确定1 题图2 题图2.一个简单几何体的正视图、侧视图如图所示,则其俯视图不.可.能.为:①长方形;②正方形;③圆.其中正确的是( ) A.①②B.②③C.①③D.①②3.如图所示的正方体中,M、N分别是AA1、CC1的中点,作四边形D1MBN则四边形D1MBN 在正方体各个面上的正投影图形中,不可能出现的是( )4.如图所示的是水平放置的三角形直观图,D′是△A′B′C′中B′C′边上的一点,且D′离C′比D′离B′近,又A′D′∥y′轴,那么原△ABC 的AB、AD、AC 三条线段中( )A.最长的是AB,最短的是ACB.最长的是AC,最短的是ABC.最长的是AB,最短的是ADD.最长的是AD,最短的是AC4 题图5 题图5.具有如图所示直观图的平面图形ABCD 是( ) A.等腰梯形B.直角梯形C.任意四边形D.平行四边形6.如图是一个几何体的三视图,则在此几何体中,直角三角形的个数是( )A .1B .2C .3D .47. 如图,网格纸上小正方形的边长为 1,粗线画出的是某几何体的三视图,则此几何体的体积为()A .6B .9C .12D .188. 平面α截球 O 的球面所得圆的半径为 1,球心 O 到平面α的距离为 2,则此球的体积为() B .4 3πC .4 6πD .6 3π9. 如图所示,则这个几何体的体积等于()A .4B .6C .8D .1210. 将正三棱柱截去三个角(如图 1 所示,A ,B ,C 分别是△GHI 三边的中点)得到几何体如图 2,则该几何体按图 2 所示方向的侧视图为选项图中的()11. 圆锥的表面积是底面积的 3 倍,那么该圆锥的侧面展开图扇形的圆心角为( )A .120°B .150°C .180°D .240°12. 已知三棱锥 S -ABC 的所有顶点都在球 O 的球面上,△ABC 是边长为 1 的正三角形,SC 为球 O 的直径,且 SC =2,则此棱锥的体积为()A. 6πA.26二、填空题B.36 C.23 D.2213.一个几何体的正视图为一个三角形,则这个几何体可能是下列几何体中的(填入所有可能的几何体前的编号).①三棱锥②四棱锥③三棱柱④四棱柱⑤圆锥⑥圆柱14.已知某三棱锥的三视图(单位:cm)如图所示,则该三棱锥的体积等于cm3.15.已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积是.16.一个水平放置的圆柱形储油桶(如图所示),桶内有油部分所在圆弧占底面圆周长的1,则油桶直立时,油的高度与桶的高度的比值是.4三、解答题17.某个几何体的三视图如图所示(单位:m),(1)求该几何体的表面积(结果保留π);(2)求该几何体的体积(结果保留π).18.如图是一个空间几何体的三视图,其中正视图和侧视图都是边长为2 的正三角形,俯视图如图.(1)在给定的直角坐标系中作出这个几何体的直观图(不写作法);(2)求这个几何体的体积.19.如图所示,在四边形ABCD 中,∠DAB=90°,∠ADC=135°,AB=5,CD=2 2,AD=2,求四边形ABCD 绕AD 旋转一周所成几何体的表面积及体积.20.如图所示,有一块扇形铁皮OAB,∠AOB=60°,OA=72 cm,要剪下来一个扇形环ABCD,作圆台形容器的侧面,并且余下的扇形OCD 内剪下一块与其相切的圆形使它恰好作圆台形容器的下底面(大底面).试求:(1)AD 的长;(2)容器的容积.= 答案1.A 2.B 3.D 4.C 5.B 6.D 7.B 8.B 9.A 10.A 11.C 12.A 13.①②③⑤ 14.1 15.24π 16.1- 1 4 2π17.解 由三视图可知:该几何体的下半部分是棱长为 2 m 的正方体,上半部分是半径为 1 m 的半球.(1) 几何体的表面积为 S 1× 24π×12+6×22-π×12=24+π(m 2).(2)几何体的体积为 V =23+1×4×π×13=8+2π(m 3).2 3 318.解 (1)直观图如图.(2) 这个几何体是一个四棱锥. 它的底面边长为 2,高为 3,所以体积 V =1×22× 3=4 3.3 319.解 S 表面=S 圆台底面+S 圆台侧面+S 圆锥侧面=π×52+π×(2+5)×5+π×2×2 2=(4 2+60)π.V =V 圆台-V 圆锥 =1π(r 2+r r +r 2)h -12 ′1 12 2 3πr 1h3 =1π(25+10+4)×4-1π×4×2 3 3 148 π. 320.解 (1)设圆台上、下底面半径分别为 r 、R ,AD =x ,则 OD =72-x ,由题意得2πR =60·π×72 180 72-x =3R即 AD 应取 36 cm.R =12,∴ .x =36 (2)∵2πr =π·OD =π·36,3 3 ∴r =6 cm ,圆台的高 h = x 2-(R -r )2= 362-(12-6)2=6 35. ∴V =1 2+Rr +r 2)=1π·6 35·(122+12×6+62)=504 35π(cm 3).πh (R 3 3=章末检测一、选择题1.下列推理错误的是( ) A.A∈l,A∈α,B∈l,B∈α⇒l⊂αB.A∈α,A∈β,B∈α,B∈β⇒α∩β=ABC.l⊄α,A∈l⇒A∉α D.A∈l,l⊂α⇒A∈α2.长方体ABCD-A1B1C1D1 中,异面直线AB,A1D1 所成的角等于( ) A.30°B.45°C.60°D.90°3.下列命题正确的是( )A.若两条直线和同一个平面所成的角相等,则这两条直线平行B.若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行C.若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行D.若两个平面都垂直于第三个平面,则这两个平面平行4.在空间四边形ABCD 的边AB,BC,CD,DA 上分别取E、F、G、H 四点,如果EF,GH 交于一点P,则( )A.P 一定在直线BD 上B.P 一定在直线AC 上C.P 一定在直线AC 或BD 上D.P 既不在直线AC 上,也不在直线BD 上5.给定下列四个命题:①若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行;②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;③垂直于同一直线的两条直线相互平行;④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直.其中,为真命题的是( )A.①和②B.②和③C.③和④D.② 和④ 6.已知平面α⊥平面β,α∩β=l,点A∈α,A∉l,直线AB∥l,直线AC⊥l,直线m∥α,m∥β,则下列四种位置关系中,不一定成立的是( )A.AB∥m B.AC⊥m C.AB∥βD.AC⊥β7.如图(1)所示,在正方形SG1G2G3 中,E,F 分别是G1G2 及G2G3 的中点,D 是EF 的中点,现在沿SE,SF 及EF 把这个正方形折成一个四面体,使G1,G2,G3 三点重合,重合后的点记为G,如图(2)所示,那么,在四面体S-EFG 中必有( )A.SG⊥△EFG 所在平面B.SD⊥△EFG 所在平面C.GF⊥△SEF 所在平面D.GD⊥△SEF 所在平面8.如图所示,在正方体ABCD—A1B1C1D1 中,若E 是A1C1 的中点,则直线CE 垂直于( )A.AC B.BD C.A1D D.A1D18 题图9 题图9.如图所示,将等腰直角△ABC 沿斜边BC 上的高AD 折成一个二面角,此时∠B′AC=60°,那么这个二面角大小是( ) A.90°B.60°C.45°D.30°10.如图,ABCD-A1B1C1D1 为正方体,下面结论错误的是( )A.BD∥平面CB1D1B.AC1⊥BDC.AC1⊥平面CB1D1D.异面直线AD 与CB1 所成的角为60°10 题图11 题图11.如图所示,在长方体ABCD—A1B1C1D1 中,AB=BC=2,AA1=1,则BC1 与平面BB1D1D所成角的正弦值为( )A. 63B.2 65C. 155D. 10512.已知正四棱柱ABCD-A1B1C1D1 中,AB=2,CC1=2 2,E 为CC1 的中点,则直线AC1与平面BED 的距离为( )A.2二、填空题D.113.设平面α∥平面β,A、C∈α,B、D∈β,直线AB 与CD 交于点S,且点S 位于平面α,β之间,AS=8,BS=6,CS=12,则SD=.14.下列四个命题:①若a∥b,a∥α,则b∥α;②若a∥α,b⊂α,则a∥b;③若a∥α,则B. 3C. 2a 平行于α内所有的直线;④若a∥α,a∥b,b⊄α,则b∥α.其中正确命题的序号是.15.如图所示,在直四棱柱ABCD—A1B1C1D1 中,当底面四边形A1B1C1D1 满足条件时,有A1C⊥B1D1(注:填上你认为正确的一种情况即可,不必考虑所有可能的情况).15 题图16 题图16.如图所示,已知矩形ABCD 中,AB=3,BC=a,若PA⊥平面AC,在BC 边上取点E,使PE⊥DE,则满足条件的E 点有两个时,a 的取值范围是.三、解答题17.如图所示,长方体ABCD-A1B1C1D1 中,M、N 分别为AB、A1D1 的中点,判断MN 与平面A1BC1 的位置关系,为什么?18.ABCD 与ABEF 是两个全等正方形,AM=FN,其中M∈AC,N∈BF.求证:MN∥平面BCE.19.如图,在四棱锥P-ABCD 中,底面ABCD 是矩形,PA⊥底面ABCD,E 是PC 的中点.已知AB=2,AD=2 2,PA=2.求:(1)三角形PCD 的面积;(2)异面直线BC 与AE 所成的角的大小.20.如图所示,ABCD 是正方形,O 是正方形的中心,PO⊥底面ABCD,底面边长为a,E 是PC 的中点.(1)求证:PA∥面BDE;(2)求证:平面PAC⊥平面BDE;(3)若二面角E-BD-C 为30°,求四棱锥P-ABCD 的体积.21.如图,四棱锥P-ABCD 中,底面ABCD 为菱形,PA⊥底面ABCDAC=2 2,PA=2,E 是PC 上的一点,PE=2EC.(1)证明:PC⊥平面BED;(2)设二面角A-PB-C 为90°,求PD 与平面PBC 所成角的大小.答案1.C 2.D 3.C 4.B 5.D 6.D 7.A 8.B 9.A 10.D 11.D 12.D 13.914.④15.B1D1⊥A1C1(答案不唯一)16.a>617.解直线MN∥平面A1BC1,M 为AB 的中点,证明如下:∵MD/∈平面A1BC1,ND/∈平面A1BC1.∴MN⊄平面A1BC1.如图,取A1C1 的中点O1,连接NO1、BO1.∵NO1 綊1D1C1,MB 綊1D1C1,2 2∴NO1 綊MB.∴四边形NO1BM 为平行四边形.∴MN∥BO1.又∵BO1⊂平面A1BC1,∴MN∥平面A1BC1.18.证明如图所示,连接AN,延长交BE 的延长线于P,连接CP.∵BE∥AF,∴FN=AN,NB NP由AC=BF,AM=FN 得MC=NB.∴FN=AM. NB MC∴AM=AN,MC NP∴MN∥PC,又PC⊂平面BCE.AC ∴MN ∥平面 BCE .19. 解 (1)因为 PA ⊥底面 ABCD ,所以 PA ⊥CD .又 AD ⊥CD ,所以 CD ⊥平面 PAD ,从而 CD ⊥PD . 因 为 PD = 22+(2 2)2=2 3,CD =2,所以三角形 PCD 的面积为1×2×2 3=2 3.2(2)如图,取 PB 中点 F ,连接 EF 、AF ,则 EF ∥BC ,从而∠AEF (或其补角)是异面直线BC 与 AE 所成的角.在△AEF 中,由 EF = 2,AF = 2,AE =2 知△AEF 是等腰直角三角形, 所以∠AEF =45°.因此,异面直线 BC 与 AE 所成的角的大小是 45°. 20.(1)证明 连接 OE ,如图所示.∵O 、E 分别为 AC 、PC 的中点,∴OE ∥P A. ∵OE ⊂面 BDE ,PA ⊄面 BDE , ∴PA ∥面 BDE .(2) 证明 ∵PO ⊥面 ABCD ,∴PO ⊥BD .在正方形 ABCD 中,BD ⊥AC , 又∵PO ∩AC =O , ∴BD ⊥面 PAC . 又∵BD ⊂面 BDE , ∴面 PAC ⊥面 BDE .(3) 解 取 OC 中点 F ,连接 EF .∵E 为 PC 中点,∴EF 为△POC 的中位线,∴EF ∥PO . 又∵PO ⊥面 ABCD ,∴EF ⊥面 ABCD . ∵OF ⊥BD ,∴OE ⊥BD .∴∠EOF 为二面角 E -BD -C 的平面角,∴∠EOF =30°.在 Rt △OEF 中,OF =1OC =1 = 2a ,∴EF =OF ·tan 30°= 6a ,2 4 4 12 ∴OP =2EF = 6a .62 3 ∴V P1 6 6-ABCD= ×a × = . 361821.(1)证明 因为底面 ABCD 为菱形, 所以 BD ⊥AC .又 PA ⊥底面 ABCD ,所以 PC ⊥BD . 如图,设 AC ∩BD =F ,连接 EF .因为 AC =2 2,PA =2,PE =2EC ,故 PC =2 3,EC =2 3,FC = 2,3从而PC= 6,FC AC= 6. EC因为PC =AC,∠FCE =∠PCA ,FC EC所以△FCE ∽△PCA ,∠FEC =∠PAC =90°.由此知 PC ⊥EF . 因为 PC 与平面 BED 内两条相交直线 BD ,EF 都垂直, 所以 PC ⊥平面 BED .(2)解 在平面 PAB 内过点 A 作 AG ⊥PB ,G 为垂足. 因为二面角 A -PB -C 为 90°, 所以平面 PAB ⊥平面 PBC . 又平面 PAB ∩平面 PBC =PB , 故 AG ⊥平面 PBC ,AG ⊥BC .因为 BC 与平面 PAB 内两条相交直线 PA ,AG 都垂直, 故 BC ⊥平面 PAB ,于是 BC ⊥AB , 所以底面 ABCD 为正方形,AD =2, PD = PA 2+AD 2=2 2. 设 D 到平面 PBC 的距离为 d .因为 AD ∥BC ,且 AD ⊄平面 PBC ,BC ⊂平面 PBC ,故 AD ∥平面 PBC ,A 、D 两点到平面 PBC 的距离相等,即 d =AG = 2. 设 PD 与平面 PBC 所成的角为α,则 sin α= d =1.PD 2 所以 PD 与平面 PBC 所成的角为 30°.章末检测一、选择题1.若直线过点(1,2),(4,2+ 3),则此直线的倾斜角是()A .30°B .45°C .60°D .90°2.如果直线 ax +2y +2=0 与直线 3x -y -2=0 平行,则系数 a 为 ( )A .-3B .-6C .-3 2 3.若经过点(3,a )、(-2,0)的直线与经过点(3,-4) 1D.2 3 a 的值为( )且斜率为 的直线垂直,则 2A.5 2B.2 5 C .10 D .-104.过点(1,0)且与直线 x -2y -2=0 平行的直线方程是 ( )A .x -2y -1=0B .x -2y +1=0C .2x +y -2=0D .x +2y -1=05.实数 x ,y 满足方程 x +y -4=0,则 x 2+y 2 的最小值为 A .4 B .6 C .8 ()D .126.点 M (1,2)与直线 l :2x -4y +3=0 的位置关系是 () A .M ∈l B .M ∉l C .重合 D .不确定7.直线 mx +ny -1=0 同时过第一、三、四象限的条件是()A .mn >0B .mn <0C .m >0,n <0D .m <0,n <08. 若点 A (-2,-3),B (-3,-2),直线 l 过点 P (1,1)且与线段 AB 相交,则 l 的斜率 k 的取值范围是() A .k ≤3或 k ≥4B .k ≤-4或 k ≥-34 3 C.3≤k ≤4 3 4 D .-4≤k ≤-34 33 49.已知直线 l 1:ax +4y -2=0 与直线 l 2:2x -5y +b =0 互相垂直,垂足为(1,c ),则 a +b +c 的值为 ()A .-4B .20C .0D .2410.过点 P (0,1)且和 A (3,3),B (5,-1)距离相等的直线的方程是() A .y =1B .2x +y -1=0C .y =1 或 2x +y -1=0D .2x +y -1=0 或 2x +y +1=011. 直线 mx +ny +3=0 在 y 轴上的截距为-3,而且它的倾斜角是直线 3x -y =3 3倾斜角的 2 倍,则 ()A .m =- 3,n =1B .m =- 3,n =-3C .m = 3,n =-3D .m = 3,n =10,7 12. 过点A 3 与B (7,0)的直线 l 1 与过点(2,1),(3,k +1)的直线 l 2 和两坐标轴围成的四边 形内接于一个圆,则实数 k 等于 ()A .-3B .3C .-6D .6二、填空题13.若 O (0,0),A (4,-1)两点到直线 ax +a 2y +6=0 的距离相等,则实数 a =.14. 甲船在某港口的东 50 km ,北 30 km 处,乙船在同一港口的东 14 km ,南 18 km 处,那么甲、乙两船的距离是 .15. 已知直线 l 与直线 y =1,x -y -7=0 分别相交于 P 、Q 两点,线段 PQ 的中点坐标为(1, -1),那么直线 l 的斜率为.16. 已知实数 x ,y 满足 y =-2x +8,当 2≤x ≤3 时,则y的最大值为.x三、解答题17. 已知点 M 是直线 l : 3x -y +3=0 与 x 轴的交点,将直线 l 绕点 M 旋转 30°,求所得到的直线 l ′的方程.18. 求直线 l 1:2x +y -4=0 关于直线 l :3x +4y -1=0 对称的直线 l 2 的方程.19. 在△ABC 中,已知 A (5,-2)、B (7,3),且 AC 边的中点 M 在 y 轴上,BC 边的中点 N 在x 轴上,求:(1) 顶点 C 的坐标; (2) 直线 MN 的方程.20. 如图,已知△ABC 中 A (-8,2),AB 边上的中线 CE 所在直线的方程为x +2y -5=0,AC 边上的中线 BD 所在直线的方程为 2x -5y +8=0, 求直线 BC 的方程.21. 光线沿直线 l 1:x -2y +5=0 射入,遇直线 l :3x -2y +7=0 后反射,求反射光线所在的直线方程.22. 某房地产公司要在荒地 ABCDE (如图)上划出一块长方形地面(不改变方位)建一幢公寓,问如何设计才能使公寓占地面积最大?并求出最大面积(精确到 1 m 2).-5=0 答案1.A 2.B 3.D 4.A 5.C 6.B 7.C 8.C 9.A 10.C 11.D 12.B 13.-2 或 4 或 6 14.60 km15.-23 16.217.解 在 3x -y +3=0 中,令 y =0,得 x =- 3,即 M (- 3,0).∵直线 l 的斜率 k = 3,∴其倾斜角θ=60°.若直线 l 绕点 M 逆时针方向旋转 30°,则直线 l ′的倾斜角为 60°+30° =90°,此时斜率不存在,故其方程为 x =- 3.若直线 l 绕点 M 顺时针方向旋转 30°,则直线 l ′的倾斜角为 60°-30°=30°,此时斜率为 tan 30°= 3,故其方程为 y = 3(x + 3),3 3 即 x - 3y + 3=0.综上所述,所求直线方程为 x + 3=0 或 x - 3y + 3=0.18.解 设直线 l 2 上的动点 P (x ,y ),直线 l 1 上的点 Q (x 0,4-2x 0),且 P 、Q 两点关于直线 l :3x +4y -1=0 对称,则有|3x +4y -1| |3x 0+4(4-2x 0)-1|= , 5 5 y -(4-2x 0)=4.x -x 03 消去 x 0,得 2x +11y +16=0 或 2x +y -4=0(舍). ∴直线 l 2 的方程为 2x +11y +16=0.5+x 0,y 0-219.解 (1)设 C (x 0,y 0),则 AC 中点 M 2 2 ,7+x 0 y 0+3,BC 中点 N 2 2 .∵M 在 y 轴上,∴5+x 0=0,x 0=-5.2 ∵N 在 x 轴上,∴y 0+3=0,y 0=-3,即 C (-5,-3).2 (2)∵M 0,-52 ,N (1,0).∴直线 MN x y 的方程为 + 15=1. - 2 即 5x -2y -5=0.x 0-8y 0+2 ,20. 解 设 B (x 0,y 0),则 AB 中点 E 的坐标为 2 2 ,由条件可得:2x 0-5y 0+8=0x 0-8+2·y 0+2 , 2 2205y 0+8=0 得 , x 0+2y 0-14=0x 2 x 0=6 y 0=4,即 B (6,4),同理可求得 C 点的坐标为(5,0).故所求直线 BC 的方程为y -0=x -5,即 4x -y -20=0.4-0 6-521. 解 设直线 x -2y +5=0 上任意一点 P (x ,y )关于直线 l 的对称点为 P ′(x ,y ),则y 0-y=-2,30 0x +x 0,y +y 0x 0-x又 PP ′的中点 Q 2 2 在l 上, ∴3 x +x 0 y +y 0× -2× 2 2 +7=0,y 0-y =-2,x 0-x3 由 3×x +x 0-(y +y )+7=0.2 可得 P 点的坐标为x 0=-5x +12y -42,y 0=12x +5y +28,13 13代入方程 x -2y +5=0 中,化简得 29x -2y +33=0, ∴所求反射光线所在的直线方程为 29x -2y +33=0.22. 解 在线段 AB 上任取一点 P ,分别向 CD 、DE 作垂线划出一块长方形土地,以 BC ,EA的交点为原点,以 BC ,EA 所在的直线为 x 轴,y 轴,建立直角坐标系,则 AB 的方程为 x + y=1,30 20 x ,20-2x设 P 3 ,则长方形的面积20-2xS =(100-x ) 80- 3 (0≤x ≤30).化简得 S =-2x 2+20+6 000(0≤x ≤30).3 3 当 x =5,y 50= 时,S 最大,其最大值为 6 017 m .3章末检测一、选择题1.方程x2+y2+2ax+2by+a2+b2=0 表示的图形是( )A.以(a,b)为圆心的圆B.以(-a,-b)为圆心的圆C.点(a,b)D.点(-a,-b)2.点P(m,3)与圆(x-2)2+(y-1)2=2 的位置关系为( ) A.点在圆外B.点在圆内C.点在圆上D.与m 的值有关3.空间直角坐标系中,点A(-3,4,0)和B(x,-1,6)的距离为86,则x 的值为( )A.2 B.-8C.2 或-8 D.8 或-24.若直线x-y+1=0 与圆(x-a)2+y2=2 有公共点,则实数a 的取值范围是( )A.[-3,-1] B.[-1,3]C.[-3,1] D.(-∞,-3]∪[1,+∞)5.设A、B 是直线3x+4y+2=0 与圆x2+y2+4y=0 的两个交点,则线段AB 的垂直平分线的方程是( ) A.4x-3y-2=0 B.4x-3y-6=0C.3x+4y+6=0 D.3x+4y+8=06.圆x2+y2-4x=0 过点P(1,3)的切线方程为( ) A.x+3y-2=0 B.x+3y-4=0C.x-3y+4=0 D.x-3y+2=07.对任意的实数k,直线y=kx+1 与圆x2+y2=2 的位置关系一定是( )A.相离B.相切C.相交但直线不过圆心D.相交且直线过圆心8.已知圆O:x2+y2=5 和点A(1,2),则过A 且与圆O 相切的直线与两坐标轴围成的三角形的面积为( )A.5 B.10 C.252D.2549.将直线2x-y+λ=0 沿x 轴向左平移1 个单位,所得直线与圆x2+y2+2x-4y=0 相切,则实数λ的值为( )A.-3 或7 B.-2 或8 C.0 或10 D.1 或1110.已知圆C:x2+y2-4x=0,l 是过点P(3,0)的直线,则( ) A.l 与C 相交B.l 与C 相切C.l 与C 相离D.以上三个选项均有可能11.若直线mx+2ny-4=0(m、n∈R,n≠m)始终平分圆x2+y2-4x-2y-4=0 的周长,则mn 的取值范围是( )A.(0,1) B.(0,-1)C.(-∞,1) D.(-∞,-1)12.过点P(-2,4)作圆O:(x-2)2+(y-1)2=25 的切线l,直线m:ax-3y=0 与直线l 平行,则直线l 与m 的距离为( )A.4 B.2 C.85D.125二、填空题13.与直线2x+3y-6=0 关于点(1,-1)对称的直线方程为.14.过点P(-2,0)作直线l 交圆x2+y2=1 于A、B 两点,则|PA|·|PB|=.15.若垂直于直线2x+y=0,且与圆x2+y2=5 相切的切线方程为ax+2y+c=0,则ac 的值为.16.在平面直角坐标系xOy 中,圆C 的方程为x2+y2-8x+15=0,若直线y=kx-2 上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,则k的最大值是.三、解答题17.自点A(-3,3)发出的光线l 射到x 轴上,被x 轴反射,其反射光线所在的直线与圆x2+y2-4x-4y+7=0 相切,求光线l 所在直线的方程.18.已知圆x2+y2+x-6y+m=0 与直线x+2y-3=0 相交于P,Q 两点,O 为原点,若OP⊥OQ,求实数m 的值.19.已知圆x2+y2-6mx-2(m-1)y+10m2-2m-24=0(m∈R).(1)求证:不论m 为何值,圆心在同一直线l 上;(2)与l 平行的直线中,哪些与圆相交、相切、相离;(3)求证:任何一条平行于l 且与圆相交的直线被各圆截得的弦长相等.20.如图,已知圆O:x2+y2=1 和定点A(2,1),由圆O 外一点P(a,b向圆O 引切线PQ,切点为Q,且有|PQ|=|PA|.(1)求a、b 间关系;(2)求|PQ|的最小值;(3)以P 为圆心作圆,使它与圆O 有公共点,试在其中求出半径最小的圆的方程.1+k 2答案章末检测1.D 2.A 3.C 4.C 5.B 6.D 7.C 8.D 9.A 10.A 11.C 12.A 13.2x +3y +8=0 14.3 15.±5 16.4 317. 解 如图所示,已知圆 C :x 2+y 2-4x -4y +7=0 关于 x 轴对称的圆为 C 1:(x -2)2+(y +2)2=1,其圆心 C 1 的坐标为(2,-2),半径为 1,由光的反射定律知,入射光线所在直线方程与圆 C 1 相切.设l 的方程为 y -3=k (x +3),即 kx -y +3+3k =0. 则|5k +5|=1,即 12k 2+25k +12=0.∴k 1=-4,k 2=-3.3 4则 l 的方程为 4x +3y +3=0 或 3x +4y -3=0.18. 解 设P ,Q 两点坐标为(x 1,y 1)和(x 2,y 2),由 OP ⊥OQ 可得 x 1x 2+y 1y 2=0, x 2+y 2+x -6y +m =0, 由x +2y -3=0, 可得 5y 2-20y +12+m =0.①所以 y 1y 2=12+m,y 1+y 2=4.5 又 x 1x 2=(3-2y 1)(3-2y 2)=9-6(y 1+y 2)+4y 1y 2=9-24+4(12+m ),5所以 x 1x 2+y 1y 2=9-24+4(12+m )+12+m =0,5 5 解得 m =3.将 m =3 代入方程①,可得Δ=202-4×5×15=100>0,可知 m =3 满足题意,即 3 为所求 m 的值.19.(1)证明 配方得:(x -3m )2+[y -(m -1)]2=25,设圆心为(x ,y ),x =3m 则 , y =m -1消去 m 得 x -3y -3=0,则圆心恒在直线 l :x -3y -3=0 上.10 22+12( (2) 解 设与 l 平行的直线是 l 1:x -3y +b =0,则圆心到直线 l 1 的距离为 d =|3m -3(m -1)+b | |3+b |∵圆的半径为 r =5,∴当 d <r ,即-5 10-3<b <5 10-3 时,直线与圆相交; 当 d =r ,即 b =±5 10-3 时,直线与圆相切;当 d >r ,即 b <-5 10-3 或 b >5 10-3 时,直线与圆相离.(3) 证明 对于任一条平行于 l 且与圆相交的直线 l 1:x -3y +b =0,由于圆心到直线 l 1 的距离 d |3+b |弦长=2 r 2-d 2且 r 和 d 均为常量.∴任何一条平行于 l 且与圆相交的直线被各圆截得的弦长相等. 20.解 (1)连接 OQ 、OP ,则△OQP 为直角三角形,又|PQ |=|PA |,所以|OP |2=|OQ |2+|PQ |2=1+|PA |2,所以 a 2+b 2=1+(a -2)2+(b -1)2,故 2a +b -3=0.(2)由|PQ |2=|OP |2-1=a 2+b 2-1=a 2+9-12a +4a 2-1=5a 2- 12a +8=5(a -1.2)2+0.8,得|PQ |min =2 5.5 (3)以 P 为圆心的圆与圆 O 有公共点,半径最小时为与圆 O 相切的情形,而这些半径的最小值为圆 O 到直线 l 的距离减去圆 O 的半径,圆心 P 为过原点且与 l 垂直的直线 l ′与 l 的交点 P 0,所以 r = 3 -1=3 5-1,5 又 l ′:x -2y =0,联立 l :2x +y -3=0 得 P 0(6,3).5 5 所以所求圆的方程为(x -6)2+(y -3)2= 3 5-1)2.5 5 510 10= .= ,。
人教版高中数学必修二 第一章空间几何体章末检测A 附答案解析
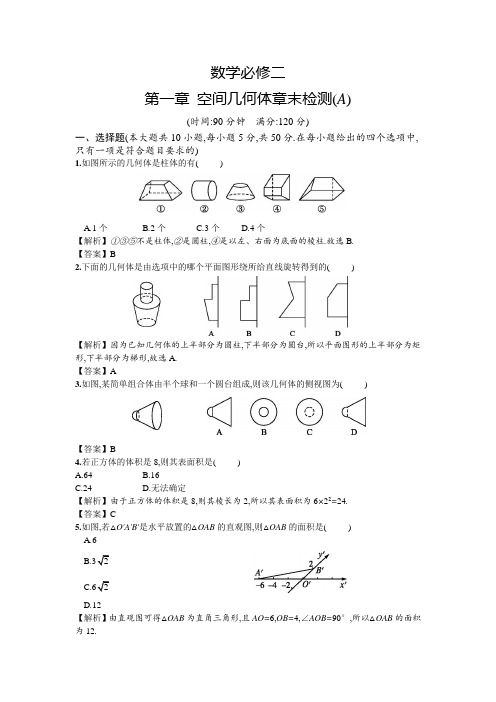
数学必修二第一章空间几何体章末检测(A)(时间:90分钟满分:120分)一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.如图所示的几何体是柱体的有()A.1个B.2个C.3个D.4个【解析】①③⑤不是柱体,②是圆柱,④是以左、右面为底面的棱柱.故选B.【答案】B2.下面的几何体是由选项中的哪个平面图形绕所给直线旋转得到的()【解析】因为已知几何体的上半部分为圆柱,下半部分为圆台,所以平面图形的上半部分为矩形,下半部分为梯形,故选A.【答案】A3.如图,某简单组合体由半个球和一个圆台组成,则该几何体的侧视图为( )【答案】B4.若正方体的体积是8,则其表面积是()A.64B.16C.24D.无法确定【解析】由于正方体的体积是8,则其棱长为2,所以其表面积为6×22=24.【答案】C5.如图,若△O'A'B'是水平放置的△OAB的直观图,则△OAB的面积是()A.6B.C.D.12【解析】由直观图可得△OAB为直角三角形,且AO=6,OB=4,∠AOB=90°,所以△OAB的面积为12.【答案】D6.若三个球的半径之比为1∶2∶3,则最大球的表面积是其余两个球的表面积之和的( ) A.1倍 B.2倍C.95倍 D.74倍 【解析】设最小球的半径为r ,则另两个球的半径分别为2r ,3r ,所以各球的表面积分别为4πr 2,16πr 2,36πr 2.故2223694165r r r πππ=+. 【答案】C7.已知圆台的一个底面周长是另一个底面周长的3倍,母线长为3,圆台的侧面积为84π,则圆台较小底面的半径为( ) A.7 B.6 C.5 D.3【解析】设圆台较小底面的半径为r ,由题意知另一底面的半径R=3r.所以S 侧=π(r+R )l=π(r+3r )×3=84π,解得r=7. 【答案】A8.若一个几何体的三视图如图所示,则这个几何体的体积为( )A .2B .103C .43D .83【解析】由三视图可知该几何体是由一个四棱柱与一个四棱锥组合而成的.其中,四棱柱的高为2,底面是边长为1的正方形;四棱锥的高为1,底面是边长为2的正方形.易知四棱柱的体积为1×1×2=2,四棱锥的体积为13×2×2×1=43,故该几何体的体积为410233+=.【答案】B9.如果用表示1个立方体,用表示2个立方体叠加,用表示3个立方体叠加,那么图中由立方体摆成的几何体,从正前方观察可画出的平面图形是( )【解析】画出该几何体的正视图的形状为,其上层有2个立方体,下层中间有3个立方体,左侧有1个立方体,右侧有2个立方体,故B 项满足条件. 【答案】B10.如图,在三棱台ABC-A 1B 1C 1中,A 1B 1∶AB=1∶2,则三棱锥B-A 1B 1C 1与三棱锥A 1-ABC 的体积之比为( )A .1∶2B .1∶3C .D .1∶4【解析】三棱锥B-A 1B 1C 1与三棱锥A 1-ABC 的高相等,故其体积之比等于△A 1B 1C 1与△ABC 的面积之比.而△A 1B 1C 1与△ABC 的面积之比等于A 1B 1与AB 之比的平方,即1∶4.故三棱锥B-A 1B 1C 1与三棱锥A 1-ABC 的体积之比为1∶4. 【答案】D二、填空题(本大题共5小题,每小题5分,共25分.把答案填在题中的横线上)11.若圆柱的高是8 cm,表面积是130π cm 2,则它的底面半径等于 cm . 【解析】设圆柱的底面半径为r cm,所以S 圆柱表=2π×r×8+2πr 2=130π.解得r=5(负值舍去),即圆柱的底面半径为5 cm . 【答案】512.若某几何体的正视图如图所示,则该几何体的俯视图可能是下面给出的 .(只填序号)【解析】由该几何体的正视图可知,该组合体的上面是球体,下面可能是圆柱也可能是四棱柱,所以其俯视图有可能是①③,不可能是②④. 【答案】①③13.已知一个平面图形的斜二测画法的直观图是一个边长为a 的正方形,则原平面图形的面积为 .【解析】如图,由直观图还原出原图,在原图中找出对应线段的长度进而求出面积.所以2S a =⋅=.【答案】214.某几何体的三视图如图所示(单位:cm),则该几何体的表面积是 cm 2,体积是 cm 3. 【解析】由三视图知该组合体是一个长方体上面放置了一个小正方体,故S 表=6×22+2×42+4×2×4-2×22=80(cm 2),V=23+4×4×2=40(cm 3). 【答案】80 4015.用一张圆弧长为12π,半径为10的扇形胶片制作一个圆锥体模型,这个圆锥体的体积等于 . 【解析】如图,设圆锥的底面半径为r ,母线长为l ,高为h ,则l=10,2πr=12π,r=6,h=8.所以圆锥的体积V=13πr 2h=96π.【答案】96π三、解答题(本大题共5小题,共45分.解答时应写出文字说明、证明过程或演算步骤)16.(8分)把一个圆锥截成圆台,已知圆台的上、下底面半径之比是1∶4,母线长为10 cm .求圆锥的母线长. 【解析】设圆锥的母线长为l ,圆台上、下底面半径分别为r ,R.∵10l r l R -=,∴1014l l -=, ∴l=403(cm).故圆锥的母线长为403cm ..17.(8分)如图,在底面半径为2,母线长为4,求圆柱的表面积.【解析】设圆锥的底面半径为R ,圆柱的底面半径为r ,表面积为S ,则R=OC=2,AC=4,=如图,易知△AEB ∽△AOC ,∴AE EBAO OC =,2r =, ∴r=1.S 底=2πr 2=2π,S 侧=2πr ·h=.∴S=S 底+S 侧=2π+π=(2+π.18.(9分)如图,正方体ABCD-A'B'C'D'的棱长为a ,连接A'C',A'D ,A'B ,BD ,BC',C'D ,得到一个三棱锥.求:(1)三棱锥A'-BC'D 的表面积与正方体的表面积的比值; (2)三棱锥A'-BC'D 的体积.【解析】(1)因为ABCD-A'B'C'D'是正方体,所以a ,所以三棱锥A'-BC'D 的表面积为4×12a=2.而正方体的表面积为6a 2,故三棱锥A'-BC'D 的表面积与正方体的表面积的比值为2263a =. (2)三棱锥A'-ABD ,C'-BCD ,D-A'D'C',B-A'B'C'是完全一样的. 故V 三棱锥A'-BC'D =V 正方体-4V 三棱锥A'-ABD=a 3-4×1132⨯a 2×a=33a .19.(10分)已知几何体的三视图如图所示(单位:cm). (1)画出这个几何体的直观图(不要求写画法); (2)求这个几何体的表面积及体积.【解析】(1)这个几何体的直观图如图所示.(2)连接B 1C 1,A 1D 1,则这个几何体可看成是正方体AC 1和三棱柱B 1C 1Q-A 1D 1P 的组合体(图略).由PA 1=PD 1,A 1D 1=AD=2, 可得PA 1⊥PD 1.故所求几何体的表面积S=5×22+2×2+2×12×)2=22+(cm 2),所求几何体的体积V=23+12×)2×2=10(cm 3).20.(10分)如图,四边形ABCD 是直角梯形,求图中阴影部分绕AB 旋转一周所成几何体的表面积和体积.【解析】由题意知所求几何体的表面积等于圆台下底面面积、圆台的侧面积与半球面面积的和.又S 半球面=12×4π×22=8π(cm 2),S 圆台侧=π×(2+5)35π(cm 2),S 圆台下底=π×52=25π(cm 2), 所以所求几何体的表面积为 8π+35π+25π=68π(cm 2). 又V 圆台=3π×(22+2×5+52)×4=52π(cm 3),V半球=1423π⨯×23=163π(cm3).所以所求几何体的体积为V圆台-V半球=161405233πππ-=(cm3).。
空间几何体(必修2第一章)综合检测题

9.两个平行于圆锥底面的平面将圆锥的高分成相等的三段,那么圆锥被分成的三部分 的体积的比是( A.1∶8∶27 ) B.1∶1∶1 C.1∶7∶19 D.1∶2∶3
正方体
10.把表面积相等的球与正方体的体积依次记为 V 球与 V 棱长为 a,则有( ) B.d>a,V 球<V 正方体 D.d<a,V 球<V正四棱台的斜高与上、 下底面边长之比为 5∶2∶8, 体积为 14cm3, 求棱台的高.
20.(本小题满分 14 分)已知一个圆锥的底面半径为 R,高为 H,在圆锥内部有一个高为 x 的内接圆柱. (1)画出圆锥及其内接圆柱的轴截面; (2)求圆柱的侧面积; (3)x 为何值时,圆柱的侧面积最大?
21.(本小题满分 15 分)如图,BD 是正方形 ABCD 的对角线, BD 的圆心是 A,半径为 AB,正方形 ABCD 以 AB 为轴旋转,求图中Ⅰ、Ⅱ、Ⅲ三部分旋转所 得旋转体的体积之比.
22.(本题满分 15 分)已知三棱台 ABC-A1B1C1 中,S△ABC=25,S△A1B1C1=9,高 h=6. (1)求三棱锥 A1-ABC 的体积 VA1-ABC. (2)求三棱锥 B-A1B1C1 的体积 VB-A1B1C1. (3)求三棱锥 A1-BCC1 的体积 VA1-BCC1.
1 3.圆锥的高扩大到原来的 2 倍,底面半径缩短到原来的 ,则圆锥的体积( 2 A.缩小到原来的一半 C.不变 B.扩大到原来的 2 倍 1 D.缩小到原来的 6
4.两个完全相同的长方体的长、宽、高分别为 5 cm、4 cm、3 cm,把它们重叠在一起 组成一个新长方体,在这些新长方体中,最长的对角线的长度是( A. 77 cm B.7 2 cm C.5 5 cm )
高中数学 第一章 空间几何体章末综合测评1(含解析)新人教A版必修2(2021年最新整理)

2017-2018学年高中数学第一章空间几何体章末综合测评1(含解析)新人教A版必修2编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2017-2018学年高中数学第一章空间几何体章末综合测评1(含解析)新人教A版必修2)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2017-2018学年高中数学第一章空间几何体章末综合测评1(含解析)新人教A版必修2的全部内容。
第一章空间几何体[自我校对]①棱锥②圆锥③正视图④侧视图⑤俯视图⑥S表=S侧+S底,V=Sh⑦S表=S侧+S底,V=错误!Sh⑧S表=4πR2,V=错误!πR3(教师用书独具)空间几何体的结构特征(1)(2)圆柱、圆锥和圆台都是旋转体,其轴截面其实为旋转的平面图形及其关于旋转轴对称的图形的组合,它反应了这三类几何体基本量之间的关系,因此轴截面是解决这三类几何体问题的关键.(3)球是比较特殊的旋转体,球的对称性是解题的突破口.(4)对于简单组合体的性质的研究多采用分割法,将其分解为几个规则的几何体再进行研究.根据下列对几何体结构特征的描述,说出几何体的名称.(1)由六个面围成,其中一个面是凸五边形,其余各面是有公共顶点的三角形;(2)一个等腰梯形绕着两底边中点的连线所在的直线旋转180°形成的封闭曲面所围成的图形;(3)一个直角梯形绕较长的底边所在的直线旋转一周形成的曲面所围成的几何体.【精彩点拨】根据所给的几何体结构特征的描述,结合所学几何体的结构特征做出判断.【规范解答】(1)如图①,因为该几何体的五个面是有公共顶点的三角形,所以是棱锥,又其底面是凸五边形,所以是五棱锥.(2)如图②,等腰梯形两底边中点的连线将梯形平分为两个直角梯形,每个直角梯形旋转180°形成半个圆台,故该几何体为圆台.(3)如图③,过直角梯形ABCD的顶点A作AO⊥CD于点O,将直角梯形分为一个直角三角形AOD和一个矩形AOCB,绕CD旋转一周形成一个组合体,该组合体由一个圆锥和一个圆柱组成.[再练一题]1.斜四棱柱的侧面是矩形的面最多有( )A.0个B.1个C.2个D.3个【解析】如图所示,在斜四棱柱AC′中,若AA′不垂直于AB,则DD′也不垂直于DC,所以四边形ABB′A′和四边形DCC′D′就不是矩形,但面AA′D′D和面BB′C′C可以为矩形.故选C。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《空间几何体》章末综合检测一、选择题:(本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的).1.[2018湖北宜昌七校教学协作体高一(下)期末考试]下列结论正确的是( )A.各个面都是三角形的几何体是三棱锥B.上、下底面为相似的正多边形的棱台一定是正棱台C.顶点在底面上的射影到底面各顶点的距离相等的三棱锥是正三棱锥D.圆锥的顶点与底面圆周上的任意一点的连线都是母线2.如图,已知平面111A B C 与平面ABC 平行,则能推断出这个几何体是三棱台的是( )A.11112,3,3,4A B AB B C BC ====B.11111131,2,,3,2,32A B AB B C BC AC AC ====== C.11111131,2,,3,2,42A B AB B C BC AC AC ====== D.111111,,AB A B BC B C CA C A ===3.[2018陕西西安铁一中高一月考]已知一个正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积是( )81A.4B.16C.927D.4ππππ4.[2017重庆万州纯阳中学高二(上)月考]如图所示的正方形ABCD 用斜二测画法得到的直观图是一个平行四边形,平行四边形中有一条边的边长为4,则此正方形的面积是( )A.16B.64C.1664D.或无法确定5.[2018河北唐山一中高一月考]一个空间几何体的三视图如图所示,则该几何体的体积为( )40A.380B.3C.40D.80 6.[2018湖南岳阳一中高一月考]祖暅原理:“幂势既同,则积不容异”.“幂”是截面积,“势”是几何体的高,意思是两个同高的几何体,如在等高处截面的面积相等,则体积相等.已知某不规则几何体与如图所示的三视图所对应的几何体满足“幂势同”,则该不规则几何体的体积为( )A.42 4B.83C.8D.82ππππ----7.[2018湖北宜昌一中高一期末考试]某几何体的三视图如图所示,则该几何体的表面积为()A.182B.20C.202D.16ππππ++++8.[2017河北衡水中学高三(下)三调]已知一个棱长为2的正方体,被一个平面截去一部分后所得几何体的三视图如图所示,则该几何体的体积是()14A.317B.320C.3D.89.[2018天津新华中学高一月考]已知四棱锥S ABCD -的所有顶点在同一球上,底面ABCD 是正方形且球心O 在此平面内,当四棱锥体积取得最大值时,其表面积等于16163+,则球O 的体积等于()42A.3162B.3322C.3642D.3ππππ10.一个封闭的正三棱柱容器,高为3,内装水若干(如图甲,底面处于水平状态),将容器放倒(如图乙,一个侧面处于水平状态),这时水面与各棱交点 11,,F ,E F E 分别为所在棱的中点,则图甲中水面的高度为( )3.27.4.29.4A B C D11.[2018山西平遥中学高一月考]已知体积为43π的球O 放置在棱长为4的正方体1111ABCD A B C D -上,且与上表面1111A B C D 相切,切点为该表面的中心,则四棱锥O ABCD -的外接球的半径为( )10A.333B.10C.223D.612.[2018江西南昌六校联考]今有底面为矩形的屋脊状楔体,两侧面为全等的等腰梯形,下底面宽3cm ,长4cm ,上棱长1cm ,高1cm (如图),若该几何体所有顶点都在一个球的表面上,则该球的表面积为( )2222A.50cm B.26cm C.49cm D.50cm πππππ或二、填空题:(本题共4小题,每小题5分,共20分).13.[2017江西临川一中期末考试]某几何体的三视图如图所示,且该几何体的体积是3,则正视图中的x 的值是_____.14.[2018河北保定一中检测]已知一块正方形薄铁片的边长为4cm ,以它的一个顶点为圆心,一边长为半径画弧,沿弧剪下一个扇形(如图),若用这块扇形铁片围成一个无底的圆锥,则这个无底的圆锥的容积为_____3cm .15.[2018山西忻州一中高一月考]如图,网格纸上小正方形的边长为1,粗线画出的是某多面体的三视图,则该几何体的各个面的面积的最大值为_____.16.有两个相同的直三棱柱,高为()20a a>,底面三角形的三边长分别为3,4,5a a a .用它们拼成一个三棱柱或四棱柱,在所有可能的情形中,表面积最小的是一个四棱柱,则实数a 的取值范围是_____.参考答案1.答案:D解析:如图所示,由两个结构相同的三棱锥叠放在一起构成的几何体,各面都是三角形,但它不是棱锥,故A 错误;底面相似但侧棱长不相等,这样的棱台不是正棱台,故B 错误;当三棱锥的侧棱长相等时,顶点在底面上的射影到底面各顶点的距离相等,此时三棱锥不一定是正三棱锥,故C 错误;由圆锥母线的定义,知D 正确.2.答案:C解析;根据棱台是由棱锥截成的,对于A,1111A B B C AB BC≠,故A 不正确;对于B ,1111B C AC BC AC ≠故B 不正确;对于C ,111111=A B B C AC AB BC AC=,故C 正确;对于D ,满足这个条件的不是三棱台,故选C.3.答案:A解析:由已知条件,可知球心在正四棱锥的高所在的直线上,设球的半径为r ,球心为O ,正四棱锥底面中心为E ,则OE 垂直于棱锥的底面,4OE r =-或4r -,所以()22242r r -+=或()22242r r -+=,解得9=4r ,所以球的表面积28144S r ππ==.故选A. 4.答案:C 解析:由题意,可知在直观图(图略)中,若边长为4的边与x '轴平行,则原正方形的边长为4,此时正方形的面积为16;若边长为4的边与y '轴平行,则原正方形的边长为8,此时正方形的面积为64.【名师点睛】()1原图中与x 轴平行的线段在直观图中长度不变,与y 轴平行的线段在直观图中长度减半;()2注意分类讨论思想的应用.5.答案:A解析:由三视图,可知该几何体为如图所示的四棱锥(即S ABCD -),其中=4SA ABCD SA ⊥平面,,底面ABCD 为直角梯形,AD=4=1=4BC AB ,,,∴该几何体的体积11440V=44=323+⨯⨯⨯.故选A. 6.答案:C解析:由祖暅原理,可知该不规则几何体的体积与已知三视图所对应的几何体体积相等,图中所对应的几何体是一个正方体去掉一个半圆柱,从而其体积为8π-,故选C.7.答案:B解析:由三视图,可知这个几何体是一个棱长为2的正方体割去了两个半径为1、高为1的14圆柱,其表面积相当于正方体五个面的面积与两个14圆柱的侧面积的和,即该几何体的表面积1S=452211=204ππ⨯+⨯⨯⨯⨯+,故选B. 8.答案:B解析:由三视图,知该几何体的直观图是如图所示的多面体111B C D BCDFE -, 该多面体可补全为棱长为2的正方体,其中,E F 分别为AB AD ,的中点,多面体111AEF-A B D 为棱台,棱台高为2,上、下底面均为等腰直角三角形.则该几何体的体积是111717222222832233⎛⎫⨯⨯-⨯⨯++⨯=-= ⎪ ⎪⎝⎭,故选B.9.答案:D解析:由题意,知当此四棱锥体积取得最大值时,四棱锥为正四棱锥.如图,设球O 的半径为R ,则2AC R =,SO R =,∴该四棱锥的底面边长为2AB R =, 则有()222122421616322R R R R ⎛⎫+⨯+=+ ⎪ ⎪⎝⎭,解得22R = ∴球O 的体积是34233R ππ=,故选D.10.答案:D解析:因为11E F F E ,,,分别为所在棱的中点,所以棱柱1111EFCB E FC B -的体积393344ABC ABC EFCB S S S ∆∆⨯=⨯=梯形.设甲中水面的高度为h ,则94ABC ABC S h S ∆∆⨯=,解得94h =,故选D. 11.答案:B解析:由题可知球O 的半径为1.如图所示,四棱锥O ABCD -的高415h =+=,设四棱锥O ABCD -的外接球球心为E ,半径为r ,底面ABCD 的中心为F , 连接AE AF OF ,,,显然E 在OF 上,则5EA EO r EF r ===-,.在RT AFE ∆中,222222,(22)(5)EA AFEF r r =+=+-即,解得3310r =,故选B. 12.答案:D解析:设球心到上棱的距离为t .当球心在几何体内时,01t <<, 则()22222212512t R t R ⎧⎛⎫+=⎪ ⎪⎪⎝⎭⎨⎛⎫⎪+-= ⎪⎪⎝⎭⎩,解得72t =,舍去;当球心在几何体底面下方时,1t >, 同理可得72t =,2252R =,符合题意,所以该球的表面积()22450S R cm ππ==, 故选D.13.答案:3解析:根据三视图可判断题中几何体为四棱锥,其直观图如图所示.所以该几何体的体积1122=332V x +=⨯⨯⨯,解得3x =.14.答案:153π 解析:由已知,可得这个无底的圆锥的母线长为4,设底面半径为r ,则12244r ππ=⨯⨯,所以1r =,故这个无底的圆锥的高224115h =-=,所以其体积()2311511533V cm ππ=⨯⨯=. 15. 答案:23解析:构造棱长为2的正方体,由三视图,可知该几何体为如图所示的三棱锥P ABC -,其中点A 为相应棱的中点.因为11212ABC PAB S S ∆∆==⨯⨯=,(2322234PBC S ∆==,221122526222PAC PC S PC AC ∆⎛⎫=⨯-=-= ⎪⎝⎭因为361>>,所以该几何体的各个面的面积的最大值为2316.答案:15(0, 解析:由题意,知这两个直三棱柱拼成一个三棱柱或四棱柱,有如下四种情况:①边长为5a 的边重合在一起,拼成一个四棱柱,表面积为22428a +; ②边长为4a 的边重合在一起,拼成一个三棱柱或四棱柱,表面积为22432a +, ③边长为3a 的边重合 在一起,拼成一个三棱柱或四棱柱,表面积为22436a +;④竖直放在一起,拼成一个三棱柱,表面积为21248a +.因为表面积最小的是一个四棱柱,所以2224281248a a +<+,即21220a <,解得0a <<.。
