初联难度几何题100道
初中几何100题--高难度版

E B
A
C
D O
M
第三十四题:
如图,四边形 ABCD 中, BC CD , BCA 21 , CAD 39 , CDA 78 ,求 BAC 的度数.
C
B
A
D
第三十五题:
如图,四边形 ABCD 中, AD CD , BAC 10 , ABD 50 , ACD 20 ,求 CBD 的度数.
C
E MA D
B
N
第三十二题:
如图, ABC 中, BD AC 于 D , E 为 BD 上一点,且 ABD 38 , CBD 68 , BCE 14 , DCE 8 ,求 DAE 的度数.
B
E
A
D
C
第三十三题:
CD 为⊙ O 的直径, A 、 B 为半圆上两点, DE 为过点 D 的切线, AB 交 DE 于 E ,连接 OE ,交 CB 于 M ,交 AC 于 N . 求证: ON OM
A
O
B
C
第九题:
已知:正方形 ABCD 中, OAD ODA 15 ,求证: OBC 为正三角形.
A
D
O
B
C
第十题:
已知:正方形 ABCD 中, E 、 F 为 AD 、 DC 的中点,连接 BE 、 AF ,相交于点 P ,连 接 PC . 求证: PC BC .
A
E
D
P
F
C P
Q A
B R
第十八题:
如图,已知 AD 是⊙ O 的直径,D 是 BC 中点,AB 、AC 交⊙ O 于点 E 、F ,EM 、FM 是⊙ O 的切线, EM 、 FM 相交于点 M ,连接 DM . 求证: DM BC .
初中难度几何100题

第一题:已知:ABC ∆外接于⊙O ,︒=∠60BAC ,BC AE ⊥,AB CF ⊥,AE 、CF 相交于点H ,点D 为弧BC 的中点,连接HD 、AD 。
求证:AHD ∆为等腰三角形第二题:如图,F为正方形ABCD边CD上一点,连接AC、AF,延长AF交AC的平行线DE于点E,连接CE,且AC=AE。
CE求证:CFE第三题:已知:ABC ∆中,AC AB =,︒=∠20BAC ,︒=∠30BDC 。
求证:BC AD =B第四题:已知:ABC ∆中,D 为AC 边的中点,C A ∠=∠3,︒=∠45ADB 。
求证:BC AB ⊥AC第五题:如图,四边形ABCD 的两条对角线AC 、BD 交于点E ,︒=∠50BAC ,︒=∠60ABD ,︒=∠20CBD ,︒=∠30CAD ,︒=∠40ADB 。
求ACD ∠。
BD第六题:已知,︒=∠30ABC ,︒=∠60ADC ,DC AD =。
求证:222BD BC AB =+DB第七题:如图,PC切⊙O于C,AC为圆的直径,PEF为⊙O的割线,AE、AF与直线PO相交于B、D。
求证:四边形ABCD为平行四边形第八题:已知:在ABC ∆中,AC AB =,︒=∠80A ,︒=∠10OBC ,︒=∠20OCA 。
求证:OB AB =CB第九题:已知:正方形ABCD 中,︒=∠=∠15ODA OAD ,求证:OBC ∆为正三角形。
第十题:已知:正方形ABCD中,E、F为AD、DC的中点,连接BE、AF,相交于点P,连接PC。
PC求证:BC第十一题:如图,ACB ∆与ADE ∆都是等腰直角三角形,︒=∠=∠90ACB ADE ,︒=∠45CDF ,DF 交BE 于F ,求证:︒=∠90CFDEB第十二题:已知:ABC ∆中,CAB CBA ∠=∠2,CBA ∠的角平分线BD 与CAB ∠的角平分线AD 相交于点D ,且AD BC =。
求证:︒=∠60ACBA第十三题:已知:在ABC ∆中,BC AC =,︒=∠100C ,AD 平分CAB ∠。
初联难度几何题100道
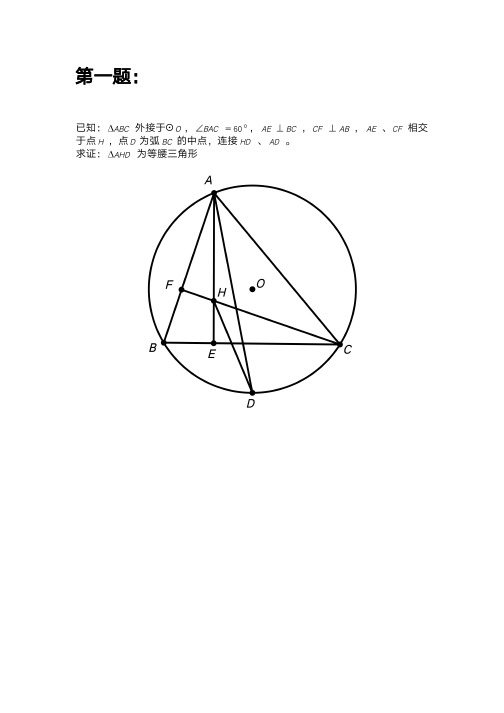
第一题:已知:外接于⊙,,,,、相交于点,点为弧的中点,连接、。
求证:为等腰三角形第二题:如图,为正方形边上一点,连接、,延长交的平行线于点,连接。
求证:第三题:已知:中,,,。
求证:第四题:已知:中,为边的中点,,。
求证:第五题:如图,四边形的两条对角线、交于点,,,,,。
求。
第六题:已知,,,。
求证:第七题:如图,切⊙于,为圆的直径,为⊙的割线,、与直线相交于、。
求证:四边形为平行四边形第八题:已知:在中,,,,。
求证:第九题:已知:正方形中,,求证:为正三角形。
第十题:已知:正方形中,、为、的中点,连接、,相交于点,连接。
求证:第十一题:如图,与都是等腰直角三角形,,,交于,求证:第十二题:已知:中,,的角平分线与的角平分线相交于点,且。
求证:第十三题:已知:在中,,,平分。
求证:第十四题:已知:中,,是的中点,过作于,连接,取中点,连接。
求证:第十五题:已知:中,,,为上一点,,连接。
求证:第十六题:已知:与均为正方形,、、、分别为、、、的中点。
求证:为正方形第十七题:如图,在三边上,向外做三角形、、,使,,。
求证:与垂直且相等。
第十八题:如图,已知是⊙的直径,是中点,、交⊙于点、,、是⊙的切线,、相交于点,连接。
求证:第十九题:如图,三角形内接于⊙,两条高、交于点,连接、。
若,,,求三角形面积。
第二十题:如图,,,,,求。
第二十一题:已知:在中,,为上一点,是的中点,。
求证:第二十二题:已知正方形,是上的一点,以为直径的圆⊙交、于、,射线、交于点。
求证:点在⊙上。
第二十三题:已知,点是内一定点,且有。
求证:是正三角形。
第二十四题:如图,过正方形的顶点的直线交、于、,与交于点,,交于点。
求证:(1);(2)第二十五题:已知:在正方形中,是上一点,交于点,交的延长线于点,连接,交于点,连接。
求证:(1)当且仅当为中点时,;(2)第二十六题:已知:与均为正方形,连接,取的中点,连接、。
求证:为等腰直角三角形第二十七题:四边形中,对角线、交于点,且,。
初中难度几何100题学习资料
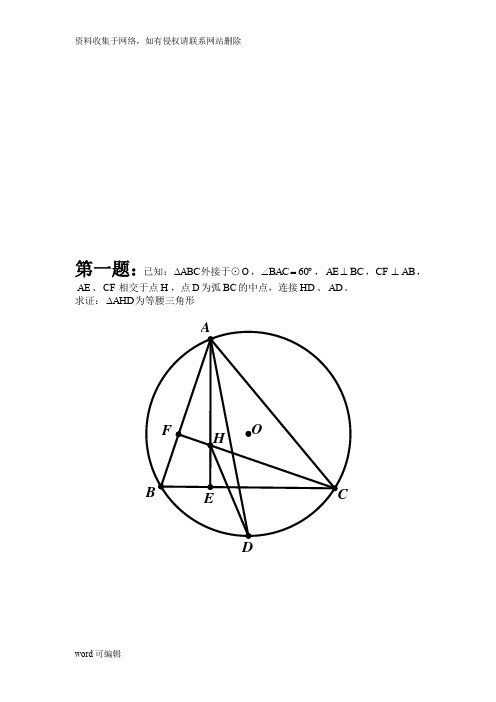
第一题:已知:ABCCF⊥,BAC,BCAE⊥,AB∆外接于⊙O,︒=∠60AE、CF相交于点H,点D为弧BC的中点,连接HD、AD。
求证:AHD∆为等腰三角形第二题:如图,F为正方形ABCD边CD上一点,连接AC、AF,延长AF交AC的平行线DE于点E,连接CE,且AC=AE。
CE求证:CFE第三题:已知:ABC ∆中,AC AB =,︒=∠20BAC ,︒=∠30BDC 。
求证:BC AD =B第四题:已知:ABC ∆中,D 为AC 边的中点,C A ∠=∠3,︒=∠45ADB 。
求证:BC AB ⊥AC第五题:如图,四边形ABCD 的两条对角线AC 、BD 交于点E ,︒=∠50BAC ,︒=∠60ABD ,︒=∠20CBD ,︒=∠30CAD ,︒=∠40ADB 。
求ACD ∠。
BD第六题:已知,︒=∠30ABC ,︒=∠60ADC ,DC AD =。
求证:222BD BC AB =+DB第七题:如图,PC切⊙O于C,AC为圆的直径,PEF为⊙O的割线,AE、AF与直线PO相交于B、D。
求证:四边形ABCD为平行四边形第八题:已知:在ABC ∆中,AC AB =,︒=∠80A ,︒=∠10OBC ,︒=∠20OCA 。
求证:OB AB =CB第九题:已知:正方形ABCD 中,︒=∠=∠15ODA OAD ,求证:OBC ∆为正三角形。
第十题:已知:正方形ABCD中,E、F为AD、DC的中点,连接BE、AF,相交于点P,连接PC。
PC求证:BC第十一题:如图,ACB ∆与ADE ∆都是等腰直角三角形,︒=∠=∠90ACB ADE ,︒=∠45CDF ,DF 交BE 于F ,求证:︒=∠90CFDEB第十二题:已知:ABC ∆中,CAB CBA ∠=∠2,CBA ∠的角平分线BD 与CAB ∠的角平分线AD 相交于点D ,且AD BC =。
求证:︒=∠60ACBA第十三题:已知:在ABC ∆中,BC AC =,︒=∠100C ,AD 平分CAB ∠。
初中联赛难度经典几何题(精编版,精选10年初中数学联赛,各地竞赛,中考压轴的高难度几何经典题)

初中几何经典难题1、已知:如图,O 是半圆的圆心,C、E 是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.求证:CD=GF.2、已知:如图,P 是正方形ABCD 内点,∠PAD=∠PDA=150.求证:△PBC 是正三角形.3、如图,已知四边形ABCD、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.APCDB AFGCEBODD 2C 2B 2A 2D 1C 1B 1C BDAA 14、已知:如图,在四边形ABCD 中,AD=BC,M、N 分别是AB、CD 的中点,AD、BC的延长线交MN 于E、F.求证:∠DEN=∠F.5、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM⊥BC 于M.(1)求证:AH=2OM;(2)若∠BAC=600,求证:AH=AO.6、设MN 是圆O 外一直线,过O 作OA⊥MN 于A,自A 引圆的两条直线,交圆于B、C 及D、E,直线EB 及CD 分别交MN 于P、Q.求证:AP=AQ.ANF ECD MB·ADHE M CBO·GA O DB ECQP NMPCGFBQADE7、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC、DE,设CD、EB 分别交MN 于P、Q.求证:AP=AQ.8、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.9、如图,四边形ABCD 为正方形,DE∥AC,AE=AC,AE 与CD 相交于F.求证:CE=CF.·O QPBDECN M·A AF DECB10、如图,四边形ABCD 为正方形,DE∥AC,且CE=CA,直线EC 交DA 延长线于F.求证:AE=AF.11、设P 是正方形ABCD 一边BC 上的任一点,PF⊥AP,CF 平分∠DCE.求证:PA=PF.12、如图,PC 切圆O 于C,AC 为圆的直径,PEF 为圆的割线,AE、AF 与直线PO 相交于B、D.求证:AB=DC,BC=AD.DEDACBFFEP C BAOD BFA EC P13、已知:△ABC 是正三角形,P 是三角形内一点,PA=3,PB=4,PC=5.求:∠APB 的度数.14、设P 是平行四边形ABCD 内部的一点,且∠PBA=∠PDA.求证:∠PAB=∠PCB.15、设ABCD 为圆内接凸四边形,求证:AB·CD+AD·BC=AC·BD.APCB PADCBCBDA16、平行四边形ABCD 中,设E、F 分别是BC、AB 上的一点,AE 与CF 相交于P,且AE=CF.求证:∠DPA=∠DPC.17、设P 是边长为1的正△ABC 内任一点,L=PA+PB+PC,求证:3L<218、已知:P 是边长为1的正方形ABCD 内的一点,求PA+PB+PC 的最小值.FPDE CBA APCB A CBPD19、P 为正方形ABCD 内的一点,并且PA=a,PB=2a,PC=3a,求正方形的边长.20、如图,△ABC 中,∠ABC=∠ACB=800,D、E 分别是AB、AC 上的点,∠DCA=300,∠EBA=200,求∠BED 的度数.ACBPDEDCB A。
初中几何难题(初二超难几何)

经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .AP C DB AFG C EBOD D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 BF1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A D 、E ,直线EB及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F . 求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F . 求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE . 求证:PA =PF .(初二)E1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5. 求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)。
初中难度几何100题

第一题:之蔡仲巾千创作已知:ABCAE⊥,ABCF⊥,AE、CFBAC,BC∠60∆外接于⊙O,︒=相交于点H,点D为弧BC的中点,连接HD、AD。
求证:AHD∆为等腰三角形第二题:如图,F为正方形ABCD边CD上一点,连接AC、AF,延长AF交AC的平行线DE于点E,连接CE,且AC=AE。
CE求证:CFE第三题:已知:ABC ∆中,AC AB =,︒=∠20BAC ,︒=∠30BDC 。
求证:BC AD =B第四题:已知:ABC ∆中,D 为AC 边的中点,C A ∠=∠3,︒=∠45ADB 。
求证:BC AB ⊥AC第五题:如图,四边形ABCD 的两条对角线AC 、BD 交于点E ,︒=∠50BAC ,︒=∠60ABD ,︒=∠20CBD ,︒=∠30CAD ,︒=∠40ADB 。
求ACD ∠。
BD第六题:已知,︒=∠30ABC ,︒=∠60ADC ,DC AD =。
求证:222BD BC AB =+DB第七题:如图,PC切⊙O于C,AC为圆的直径,PEF为⊙O的割线,AE、AF与直线PO相交于B、D。
求证:四边形ABCD为平行四边形第八题:已知:在ABC ∆中,AC AB =,︒=∠80A ,︒=∠10OBC ,︒=∠20OCA 。
求证:OB AB =CB第九题:已知:正方形ABCD 中,︒=∠=∠15ODA OAD ,求证:OBC ∆为正三角形。
第十题:已知:正方形ABCD中,E、F为AD、DC的中点,连接BE、AF,相交于点P,连接PC。
PC求证:BC第十一题:如图,ACB ∆与ADE ∆都是等腰直角三角形,︒=∠=∠90ACB ADE ,︒=∠45CDF ,DF 交BE 于F ,求证:︒=∠90CFDEB第十二题:已知:ABC ∆中,CAB CBA ∠=∠2,CBA ∠的角平分线BD 与CAB ∠的角平分线AD 相交于点D ,且AD BC =。
求证:︒=∠60ACBA第十三题:已知:在ABC ∆中,BC AC =,︒=∠100C ,AD 平分CAB ∠。
初级中学几何100题高难度版

E MA D
B
N
第三十二题:
如图, ABC 中, BD AC 于 D , E 为 BD 上一点,且 ABD 38 , CBD 68 , BCE 14 , DCE 8 ,求 DAE 的度数.
B
E
A
D
C
第三十三题:
CD 为⊙ O 的直径, A 、 B 为半圆上两点, DE 为过点 D 的切线, AB 交 DE 于 E ,连接 OE ,交 CB 于 M ,交 AC 于 N . 求证: ON OM
C
D
A
B
第四十三题:
如图,E 、F 分别是圆内接四边形 ADBC 的对角线 AB 、CD 的中点,若 DEB CEB . 求证: AFD BFD
A
D E O
F
B
C
第四十四题:
已知: AB AC , ADB 60 , BCE 30 . 求证: BA BE
A
ED
B
C
第四十五题:
已知:直角三角形 ABC , A 为直角, I 为内心, BD 、 CE 分别为两内角平分线。 IBC 的面积为 S 。求四边形 BCDE 的面积.
A
D
F E
B
C
第三题:
已知: ABC 中, AB AC , BAC 20 , BDC 30 . 求证: AD BC .
A
D
B
C
第四题:
已知: ABC 中, D 为 AC 边的中点, A 3C , ADB 45 . 求证: AB BC .
B
A
D
C
第五题:
如图,四边形 ABCD 的两条对角线 AC 、 BD 交于点 E , BAC 50 , ABD 60 , CBD 20 , CAD 30 , ADB 40 ,求 ACD .
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中教师转正必做100题
第一题:4第二题:5第三题:6第四题:7第五题:8第六题:9第七题:10第八题:11第九题:12第十题:13第十一题:14第十二题:15第十三题:16第十四题:17第十五题:18第十六题:19第十七题:20第十八题:21第十九题:22第二十题:23第二十一题:24第二十二题:25第二十三题:26第二十四题:27第二十五题:28第二十六题:29第二十七题:30第二十八题:31第二十九题:32第三十题:33第三十一题:34第三十二题:35第三十三题:36第三十四题:37第三十五题:38第三十六题:39第三十七题:40第三十八题:41第三十九题:42第四十题:43第四十一题:44第四十二题:45
第四十四题:47第四十五题:48第四十六题:49第四十七题:50第四十八题:51第四十九题:52第五十题:53第五十一题:54第五十二题:55第五十三题:56第五十四题:57第五十五题:58第五十六题:59第五十七题:60第五十八题:61第五十九题:62第六十题:63第六十一题:64第六十二题:65第六十三题:66第六十四题:67第六十五题:68第六十六题:69第六十七题:70第六十八题:71第六十九题:72第七十题:73第七十一题:74第七十二题:75第七十三题:76第七十四题:77第七十五题:78第七十六题:79第七十七题:80第七十八题:81第七十九题:82第八十题:83第八十一题:84第八十二题:85第八十三题:86第八十四题:87第八十五题:88第八十六题:89
第八十八题:91第八十九题:92第九十题:93第九十一题:94第九十二题:95第九十三题:96第九十四题:97第九十五题:98第九十六题:99第九十七题:100第九十八题:101第九十九题:102第一百题:103
第一题:
已知:外接于⊙,,,,、相交于点,点为弧的中点,连接、。
求证:为等腰三角形
第二题:
如图,为正方形边上一点,连接、,延长交的平行线于点,连接。
求证:
第三题:
已知:中,,,。
求证:
第四题:
已知:中,为边的中点,,。
求证:
第五题:
如图,四边形的两条对角线、交于点,,,,,。
求。
第六题:
已知,,,。
求证:
第七题:
如图,切⊙于,为圆的直径,为⊙的割线,、与直线相交于、。
求证:四边形为平行四边形
第八题:
已知:在中,,,,。
求证:
第九题:
已知:正方形中,,求证:为正三角形。
第十题:
已知:正方形中,、为、的中点,连接、,相交于点,连接。
求证:
第十一题:
如图,与都是等腰直角三角形,,,交于,求证:
第十二题:
已知:中,,的角平分线与的角平分线相交于点,且。
求证:
第十三题:
已知:在中,,,平分。
求证:
第十四题:
已知:中,,是的中点,过作于,连接,取中点,连接。
求证:
第十五题:
已知:中,,,为上一点,,连接。
求证:
第十六题:
已知:与均为正方形,、、、分别为、、、的中点。
求证:为正方形
第十七题:
如图,在三边上,向外做三角形、、,使,
,。
求证:与垂直且相等。
第十八题:
如图,已知是⊙的直径,是中点,、交⊙于点、,、是⊙的切线,、相交于点,连接。
求证:
第十九题:
如图,三角形内接于⊙,两条高、交于点,连接、。
若,,,求三角形面积。
第二十题:
如图,,,,,求。
第二十一题:
已知:在中,,为上一点,是的中点,。
求证:
第二十二题:
已知正方形,是上的一点,以为直径的圆⊙交、于、,射线、交于点。
求证:点在⊙上。
第二十三题:
已知,点是内一定点,且有。
求证:是正三角形。
第二十四题:
如图,过正方形的顶点的直线交、于、,与交于点,,交于点。
求证:(1);(2)
第二十五题:
已知:在正方形中,是上一点,交于点,交的延长线于点,连接,交于点,连接。
求证:(1)当且仅当为中点时,;
(2)
第二十六题:
已知:与均为正方形,连接,取的中点,连接、。
求证:为等腰直角三角形
第二十七题:
四边形中,对角线、交于点,且,。
请你猜想与产数量关系,并证明你的结论。
第二十八题:
已知:四边形中,,,,求的度数。
第二十九题:
在中,是的中点,,,求的度数。
第三十题:
在四边形中,,,,求的度数。
第三十一题:
在中,,,,、为直线上的两点,且,求的度数。
第三十二题:
如图,中,于,为上一点,且,,,,求的度数。
第三十三题:
为⊙的直径,、为半圆上两点,为过点的切线,交于,连接,交于,交于。
求证:
第三十四题:
如图,四边形中,,,,,求的度数。
第三十五题:
如图,四边形中,,,,,求的度数。
第三十六题:
如图,,、为、中点,,,。
求证:
第三十七题:
如图,在正方形中,有任意四点、、、,且、,四边形的面积为,求正方形的面积。
第三十八题:
已知,,,求。
第三十九题:
在中,,是边上一点,,,求。
第四十题:
在中,,为边上一点,为上一点,且满足。
求证:。
第四十一题:
已知,是正方形和正方形上的点、的连线,点是的中点,连接、。
求证:且。
第四十二题:
已知:,,,求证:
第四十三题:
如图,、分别是圆内接四边形的对角线、的中点,若。
求证:
第四十四题:
已知:,,。
求证:
第四十五题:
已知:直角三角形,为直角,为内心,、分别为两内角平分线。
的面积为。
求四边形的面积。
第四十六题:
,且,求的度数。
第四十七题:
如图,≌,,点在上,、交于,过作于,交于,连接并延长,交于,设,。
()
求:(1)的长(用,表示);(2)的值。
