(0775)《中学几何研究》作业一答案(1)
初等几何研究答案

《初等几何研究》作业一、填空题1、对直线a 上任意两点A 、B ,把B 以及a 上与B 在A 同侧的点的集合称作 射线(或半直线),; ,并记作 AB 。
2、在绝对几何中,外角定理的内容是: 三角形的外角大于任一不相邻的内角 。
3、第四组公理由 两 条公理组成,它们的名称分别是 度量公理(或阿基米德公理)和康托儿公理 。
4、欧氏平行公理是:对任意直线a 及其外一点A ,在a 和A 决定的平面上,至多有一条过A 与a 不相交的直线 。
5、罗氏几何公理系统与欧氏几何公理系统的共同之处是 前4组公理(或绝对几何) ,不同之处是 平行公理 。
6、几何证明的基本方法,从推理形式上分为 演绎 法与归纳法;从思维方向上分为 综合 法与分析法;从命题结构上分为 直接 证法与间接证法,其中间接证法包括 反证 法与 同一 法。
7、过反演中心的圆,其反演图形是 不过 (过或不过)反演中心的 直线 。
8、锐角三角形的所有内接三角形中,周长最短的是 垂足三角形。
9、锡瓦定理:设⊿ABC 的三边(所在直线)BC 、CA 、AB 上分别有点X 、Y 、Z ,则AX 、BY 、CZ 三线共点(包括平行)的充要条件是1=⋅⋅ZBAZYA CY XC BX 。
10、解作图问题的常用方法有: 交轨法 、三角奠基法、 代数法 、 变换法 等。
11、数学公理系统的三个基本问题是 相容性、 独立性和 完备 性.33.①答案不惟一.34.①(0,+∞),②,(0,π/2),③连续,④单调递减. 35.①平移,②旋转,③轴对称.36. ①1=⋅⋅ZB AZYA CY XC BX (或-1)37.①写出已知与求作,②分析,③作法,④证明,⑤讨论.12、对于共面的直线a和a外两点A、B,若a与(AB)相交,则称A、B在a的异侧,否则称A、B在a的同侧.13、命题:“过直线外一点,至少有一条直线与已知直线共面但不相交”是外角定理的推论.14、证明直线和圆的连续性时,主要依据了戴德金分割原理.15、罗氏平行公理是:对任意直线a及其外一点A,在a和A决定的平面上,至多有一条过A与a不相交的直线.,16、在罗氏几何中,共面的两条直线有3种关系,它们分别是平行,相交,分散.17、几何证明的通用方法一般有化归法、类比法、构造法、数形结合法、变换法、模型法等.18、等边三角形外接圆周上任一点到三顶点的连线段中,最长线段与另两条线段之和具有相等的关系.19、尺规可作图的充要条件是所求的量可用已知量的有理式或只含平方根的无理式表出.20.由公理可以证明,线段的合同关系具有反身性、对称性、传递性和可加性.21.如果线段与角对应,那么线段的中点与角的角平分线对应.22.命题:“线段小于任意一条连接其两个端点的折线”是外角定理的推论.23.绝对几何包括有四组公理,它们分别是结合公理、顺序公理、合同公理、连续公理. 24.写出一条与欧氏平行公理等价的命题:.25.在罗氏几何中,两条直线为分散线的充要条件是.26、.常用的几何变换有合同变换、相似变换、射影变换、反演变换等27.托勒密定理:四边形ABCD是圆内接四边形,则1=⋅⋅ZBAZYACYXCBX(或-1).28.请写出两条作图公法:过两点可作一条直线(或其部分)。
[0775]中学几何研究西南大学20年6月机考参考答案
![[0775]中学几何研究西南大学20年6月机考参考答案](https://img.taocdn.com/s3/m/8aef53da2e3f5727a4e9626a.png)
西南大学网络与继续教育学院课程考试试题卷
类别:网教2020年5月
课程名称【编号】:中学几何研究【0775】
A卷大作业满分:100 分
要答案:wangjiaofudao
一、解答题(任选3题,每小题20分,共60分)
1.在内角均小于的△ABC内有一点,满足。
求证:是到三顶点距离之和最小的点。
2. 设、、分别是的边、、的中点,,分别是的外心和内心。
求证:.
3. 为内一点,且,、分别在和上,当的周长最小时,求.
4. 如图,是的中线,是的中点,求的值。
二、尺规作图题(任选2题,每小题10分,共20分。
其中第1,2题只写作法,第3题只写分析和讨论)
1. 已知及外一点,过作的切线。
2.已知线段,求作一线段等于已知线段的。
3.已知的三中线的长度,求作该三角形。
三、叙述并证明梅涅劳斯定理。
(20分)。
九年级数学几何综合(一)(含答案)
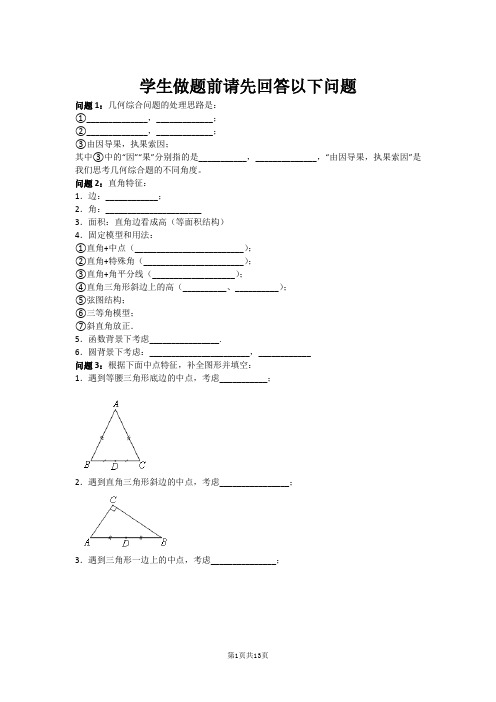
学生做题前请先回答以下问题问题1:几何综合问题的处理思路是:①______________,_____________;②______________,_____________;③由因导果,执果索因;其中③中的“因”“果”分别指的是___________,______________,“由因导果,执果索因”是我们思考几何综合题的不同角度。
问题2:直角特征:1.边:____________;2.角:______________________3.面积:直角边看成高(等面积结构)4.固定模型和用法:①直角+中点(_________________________);②直角+特殊角(_______________________);③直角+角平分线(___________________);④直角三角形斜边上的高(__________、__________);⑤弦图结构;⑥三等角模型;⑦斜直角放正.5.函数背景下考虑________________.6.圆背景下考虑:_______________________,____________问题3:根据下面中点特征,补全图形并填空:1.遇到等腰三角形底边的中点,考虑___________;2.遇到直角三角形斜边的中点,考虑________________;3.遇到三角形一边上的中点,考虑_______________;4.遇到平行线所截线段的中点,考虑___________________________;5.遇到多个中点,考虑(或构造)____________.6.在坐标系中的中点考虑________________.几何综合(一)一、单选题(共10道,每道10分)1.已知△ABC中,∠C=90°,,D是AC上一点,∠CBD=∠A,则sin∠ABD=( )A. B.C. D.答案:A解题思路:试题难度:三颗星知识点:相似三角形的判定和性质2.如图,正方形ABCD的边长为,过点A作AE⊥AC.若AE=1,连接BE,则tanE的值为( )A. B.C. D.答案:B解题思路:试题难度:三颗星知识点:解直角三角形3.如图,在菱形ABCD中,AB=3,DF=1,∠DAB=60°,∠EFG=15°,FG⊥BC,则AE=( )A. B.C. D.答案:D解题思路:试题难度:三颗星知识点:菱形的性质4.如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,AD=3,BC=5.将腰DC绕点D逆时针旋转90°至DE,连接AE,则△ADE的面积为( )A.1B.2C.3D.4答案:C解题思路:试题难度:三颗星知识点:直角梯形的性质5.如图,在△ABC中,BE平分∠ABC交AC于点E,CF平分∠ACB交AB于点F,且BE,CF 相交于点O,AG⊥BE于点G,AH⊥CF于点H.若AB=9,AC=14,BC=18,则GH的长为( )A. B.5C.3D.6答案:A解题思路:试题难度:三颗星知识点:全等三角形的判定与性质6.如图,在等腰三角形ABC中,∠ABC=90°,D为AC的中点,过点D作DE⊥DF,交AB于点E,交BC于点F.若,则AB的长为( )A.3B.6C.9D.18答案:B解题思路:试题难度:三颗星知识点:全等三角形的判定与性质7.如图,在矩形ABCD中,,BC=3,F为CD的中点,EF⊥BF交AD于点E,连接CE交BF于点G,则EG的长为( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:类倍长中线8.如图1,将矩形纸片ABCD沿过点B的直线折叠,使点A落在BC边上的点F处,折痕为BE;再沿过点E的直线折叠,使点D落在BE边上的点处,折痕为EG(如图2);再展平纸片(如图3).则图3中tanα的值为( )A. B.C. D.答案:D解题思路:试题难度:三颗星知识点:翻折变换(折叠问题)9.把一副直角三角板如图放置,已知E是AB的中点,连接CE,DE,CD,F是CD的中点,连接EF.若AB=8,则=( )A.4B.3C. D.2答案:D解题思路:试题难度:三颗星知识点:直角三角形斜边上的中线10.如图,在四边形ABCD中,AC=8,BD=6,且AC⊥BD,E,F,G,H分别是AB,BC,CD,DA的中点,则( )A.100B.64C.50D.25答案:C解题思路:试题难度:三颗星知识点:中点四边形。
中考数学复习《几何探究型问题》经典题型及测试题(含答案)

中考数学复习《几何探究型问题》经典题型及测试题(含答案)题型解读1.考查类型:①动点探究题;②平移、旋转、折叠探究题;③图形形状变化探究题.2.考查内容:①多与特殊四边形的性质、三角形全等、相似的判定和性质有关;②涉及平移、旋转或折叠的相关性质;③多与二次函数的性质有关.3.备考指导:在做此类题型时,要观察题中已知条件,并结合题设,联系相关的知识解题,对结果猜想题根据前面问题大胆猜想,往往是解题的突破口.类型一动点探究题1.如图,在Rt△ABC中,∠ACB=90°,AC=5 cm,∠BAC=60°,动点M从点B出发,在BA边上以每秒2 cm的速度向点A匀速运动,同时动点N从点C出发,在CB边上以每秒3 cm的速度向点B匀速运动,设运动时间为t秒(0≤t≤5),连接MN.(1)若BM=BN,求t的值;(2)若△MBN与△ABC相似,求t的值;(3)当t为何值时,四边形ACNM的面积最小?并求出最小值.2.如图①,菱形ABCD中,已知∠BAD=120°,∠EGF=60°,∠EGF的顶点G在菱形对角线AC上运动,角的两边分别交边BC、CD于点E、F.(1)如图②,当顶点G运动到与点A重合时,求证:EC+CF=BC;(2)知识探究:①如图③,当顶点G运动到AC中点时,探究线段EC、CF与BC的数量关系;②在顶点G 的运动过程中,若ACCG =t ,请直接写出线段EC 、CF 与BC 的数量关系(不需要写出证明过程);(3)问题解决:如图④,已知菱形边长为8,BG =7,CF =65,当t >2时,求EC 的长度.图①3.已知:如图,在矩形ABCD 中,AB =6 cm ,BC =8 cm .对角线AC ,BD 交于点O ,点P 从点A 出发,沿AD 方向匀速运动,速度为1 cm /s ;同时,点Q 从点D 出发,沿DC 方向匀速运动,速度为1 cm /s ;当一个点停止运动时,另一个点也停止运动.连接PO 并延长,交BC 于点E ,过点Q 作QF∥AC,交BD 于点F.设运动时间为t(s )(0<t<6),解答下列问题: (1)当t 为何值时,△AOP 是等腰三角形?(2)设五边形OECQF 的面积为S(cm 2),试确定S 与t 的函数关系式;(3)在运动过程中,是否存在某一时刻t ,使S 五边形OECQF ∶S △ACD =9∶16?若存在,求出t 的值;若不存在,请说明理由;(4)在运动过程中,是否存在某一时刻t ,使OD 平分∠COP?若存在,求出t 值;若不存在,请说明理由.4.某数学兴趣小组在数学课外活动中,研究三角形和正方形的性质时,做了如下探究:在△ABC 中,∠BAC =90°,AB =AC ,点D 为直线BC 上一动点(点D 不与B ,C 重合),以AD 为边在AD 右侧作正方形ADEF ,连接CF. (1)观察猜想如图①,当点D 在线段BC 上时,①BC 与CF 的位置关系为:____________. ②BC ,CD ,CF 之间的数量关系为:____________(将结论直接写在横线上). (2)数学思考如图②,当点D 在线段CB 的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明. (3)拓展延伸如图③,当点D 在线段BC 的延长线上时,延长BA 交CF 于点G ,连接GE.若已知AB =22,CD =14BC ,请求出GE 的长.类型二 平移、旋转、折叠探究题5.如图①,△ABC 是等腰直角三角形,∠BAC =90°,AB =AC ,四边形ADEF 是正方形,点B 、C 分别在边AD、AF上,此时BD=CF,BD⊥CF成立.(1)当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图②,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.(2)当△ABC绕点A逆时针旋转45°时,如图③,延长DB交CF于点H.①求证:BD⊥CF;②当AB=2,AD=32时,求线段DH的长.图①图②图③6.在△ABC中,AB=6,AC=BC=5,将△ABC绕点A按顺时针方向旋转,得到△ADE,旋转角为α(0°<α<180°),点B的对应点为点D,点C的对应点为点E,连接BD,BE.(1)如图,当α=60°时,延长BE交AD于点F.①求证:△ABD是等边三角形;②求证:BF⊥AD,AF=DF;③请直接..写出BE的长;(2)在旋转过程中,过点D作DG垂直于直线AB,垂足为点G,连接CE,当∠DAG=∠ACB,且线段DG与线段AE无公共点时,请直接..写出BE+CE的值.温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.7.已知矩形ABCD中AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.(1)如图①,已知折痕与边BC交于点O,连接AP、OP、OA,若△OCP与△PDA的面积比为1∶ 4,求边CD 的长;(2)如图②,在(1)的条件下擦去AO、OP,连接BP,动点M在线段AP上(点M不与点P、A重合),动点N 在线段AB的延长线上,且BN=PM,连接MN交PB于点F,作ME⊥BP于点E,试问当点M、N在移动过程中,线段EF的长度是否发生变化?若变化,说明变化规律,若不变,求出线段EF的长度.图①图②8.问题情境在综合与实践课上,老师让同学们以“菱形纸片的剪拼”为主题开展数学活动.如图①,将一张菱形纸片ABCD(∠BAD>90°)沿对角线AC剪开,得到△ABC和△ACD.操作发现(1)将图①中的△ACD以A为旋转中心,按逆时针方向旋转角α,使α=∠BAC,得到如图②所示的△AC′D,分别延长BC和DC′交于点E,则四边形ACEC′的形状是________;(2)创新小组将图①中的△ACD以A为旋转中心,按逆时针方向旋转角α,使α=2∠BAC,得到如图③所示的△AC′D,连接DB、C′C,得到四边形BCC′D,发现它是矩形.请你证明这个结论;实践探究(3)缜密小组在创新小组发现结论的基础上,量得图③中BC=13 cm,AC=10 cm,然后提出一个问题:将△AC′D沿着射线DB方向平移a cm,得到△A′C″D′,连接BD′,CC″,使四边形BCC″D′恰好为正方形,求a的值.请你解答此问题;(4)请你参照以上操作,将图①中的△ACD在同一平面内进行一次平移,得到△A′C′D,在图④中画出平移后构造出的新图形,标明字母,说明平移及构图方法,写出你发现的结论,不必证明.9.如图,已知一个直角三角形纸片ACB,其中∠ACB=90°,AC=4,BC=3,E、F分别是AC、AB边上的点,连接EF.(1)如图①,若将纸片ACB的一角沿EF折叠,折叠后点A落在AB边上的点D处,且使S四边形ECBF=3S△EDF,求AE的长;(2)如图②,若将纸片ACB的一角沿EF折叠,折叠后点A落在BC边上的点M处,且使MF∥CA.①试判断四边形AEMF的形状,并证明你的结论;②求EF的长;(3)如图③,若FE 的延长线与BC 的延长线交于点N ,CN =1,CE =47,求AFBF的值.10.如图①,矩形ABCD 中,AB =2,BC =5,BP =1,∠MPN =90°,将∠MPN 绕点P 从PB 处开始按顺时针方向旋转,PM 交边AB(或AD)于点E ,PN 交边AD(或CD)于点F ,当PN 旋转至PC 处时,∠MPN 的旋转随即停止.(1)特殊情形:如图②,发现当PM 过点A 时,PN 也恰好过点D , 此时,△ABP________△PCD(填“≌”或“∽”);(2)类比探究:如图③,在旋转过程中,PEPF 的值是否为定值?若是,请求出该定值;若不是,请说明理由;(3)拓展延伸:设AE =t ,△EPF 的面积为S ,试确定S 关于t 的函数关系式;当S =4.2时,求所对应的t 值.11.如图①,在△ABC中,∠ACB=90°,∠B=30°,AC=1,D为AB的中点,EF为△ACD的中位线,四边形EFGH为△ACD的内接矩形(矩形的四个顶点均在△ACD的边上).(1)计算矩形EFGH的面积;(2)将矩形EFGH沿AB向右平移,F落在BC上时停止移动.在平移过程中,当矩形与△CBD重叠部分的面积为316时,求矩形平移的距离;(3)如图③,将(2)中矩形平移停止时所得的矩形记为矩形E1F1G1H1,将矩形E1F1G1H1绕G1点按顺时针方向旋转,当H1落在CD上时停止转动,旋转后的矩形记为矩形E2F2G1H2,设旋转角为α,求cosα的值.类型三图形形状变化探究题12.如图①,②,③分别以△ABC的AB和AC为边向△ABC外作正三角形(等边三角形)、正四边形(正方形)、正五边形,BE和CD相交于点O.(1)在图①中,求证:△ABE≌△ADC.图①(2)由(1)证得△ABE≌△ADC,由此可推得在图①中∠BOC=120°,请你探索在图②中∠BOC的度数,并说明理由或写出证明过程.图②(3)填空:在上述(1)(2)的基础上可得在图③中∠BOC=________(填写度数).图③图④(4)由此推广到一般情形(如图④),分别以△ABC的AB和AC为边向△ABC外作正n边形,BE和CD仍相交于点O,猜想∠BOC的度数为____________________(用含n的式子表示).13.阅读理解:我们知道,四边形具有不稳定性,容易变形.如图①,一个矩形发生变形后成为一个平行四边形,设这个平行四边形相邻两个内角中较小的一个内角为α,我们把1sinα的值叫做这个平行四边形的变形度.(1)若矩形发生形变后的平行四边形有一个内角是120°,则这个平行四边形的变形度是________;猜想证明:(2)设矩形的面积为S1,其变形后的平行四边形面积为S2,试猜想S1,S2,1sinα之间的数量关系,并说明理由;拓展探究:(3)如图②,在矩形ABCD中,E是AD边上的一点,且AB2=AE·AD,这个矩形发生变形后为平行四边形A1B1C1D1,E1为E的对应点,连接B1E1,B1D1,若矩形ABCD的面积为4m(m>0),平行四边形A1B1C1D1的面积为2m(m>0),试求∠A1E1B1+∠A1D1B1的度数.14.已知AC ,EC 分别为四边形ABCD 和EFCG 的对角线,点E 在△ABC 内,∠CAE +∠CBE=90°. (1)如图①,当四边形ABCD 和EFCG 均为正方形时,连接BF. ①求证:△CAE∽△CBF; ②若BE =1,AE =2,求CE 的长;(2)如图②,当四边形ABCD 和EFCG 均为矩形,且AB BC =EFFC =k 时,若BE =1,AE =2,CE =3,求k 的值;(3)如图③,当四边形ABCD 和EFCG 均为菱形,且∠DAB =∠GEF=45°时,设BE =m ,AE =n ,CE =p ,试探究m ,n ,p 三者之间满足的等量关系(直接写出结果,不必写出解答过程).15.已知点O 是△ABC 内任意一点,连接OA 并延长到E ,使得AE =OA ,以OB ,OC 为邻边作▱OBFC ,连接OF ,与BC 交于点H ,再连接EF.(1)如图①,若△ABC 为等边三角形,求证:①EF⊥BC; ②EF =3BC ;(2)如图②,若△ABC 为等腰直角三角形(BC 为斜边),猜想(1)中的两个结论是否成立?若成立,直接写出结论即可;若不成立,请你直接写出你的猜想结果;(3)如图③,若△ABC 是等腰三角形,且AB =AC =kBC ,请你直接写出EF 与BC 之间的数量关系.类型一 动点探究题1. 解:(1)根据题意BM =2t ,BN =BC -3t ,而BC =5×tan 60°=5 3.∴当BM =BN 时,2t =53-3t ,解得t =103-15. (2)分类讨论:①当∠BMN =∠ACB =90°时,如解图①, △NBM ∽△ABC ,cos B =cos 30°=BM BN ,∴2t 53-3t =32,解得t =157.②当∠BNM =∠ACB =90°时,如解图②, △MBN ∽△ABC ,cos B =cos 30°=BNBM, ∴53-3t 2t =32,解得t =52. 因此当运动时间是157秒或52秒时,△MBN 与△ABC 相似.第1题解图(3)由于△ABC 面积是定值,∴当四边形ACNM 面积最小时,△MBN 面积最大, 而△MBN 的面积是S =12BM ×BN ×sin B=12×2t ×(53-3t)×12=-32t 2+532t , 由于a =-32<0, ∴当t =-5322×(-32)=52时,△MBN 面积最大,最大值是-32×(52)2+532×52=2538, 因此四边形ACNM 面积最小值是12×5×53-2538=7538.2. (1)证明:∵四边形ABCD 是菱形,∠BAD =120°,∴∠BAC =60°,∠B =∠ACF =60°,AB =BC , ∴AB =AC ,∵∠BAE +∠EAC =∠EAC +∠CAF =60°, ∴∠BAE =∠CAF , 在△BAE 和△CAF 中, ⎩⎪⎨⎪⎧∠BAE =∠CAF AB =AC ∠B =∠ACF, ∴△BAE ≌△CAF(ASA ), ∴BE =CF ,∴EC +CF =EC +BE =BC ,即EC +CF =BC ;(2)解:①线段EC ,CF 与BC 的数量关系为: EC +CF =12BC.理由如下:如解图①,过点A 作AE′∥EG ,AF ′∥GF ,分别交BC 、CD 于E′、F′.第2题解图①类比(1)可得:E′C +CF′=BC , ∵G 为AC 中点,AE ′∥EG , ∴CE CE′=CG AC =12, ∴CE =12CE′,同理可得:CF =12CF′,∴CE +CF =12CE′+12CF′=12(CE′+CF′)=12BC ,即CE +CF =12BC ;②CE +CF =1tBC ;【解法提示】类比(1)可得:E′C +CF′=BC , ∵AE ′∥EG ,ACCG =t ,∴CE CE′=CG AC =1t,∴CE =1tCE′,同理可得:CF =1tCF′,∴CE +CF =1t CE′+1t CF′=1t (CE′+CF′)=1t BC ,即CE +CF =1tBC.(3)解:如解图②,连接BD 与AC 交于点H.第2题解图②在Rt △ABH 中,∵AB =8,∠BAC =60°, ∴BH =AB·sin 60°=8×32=43, AH =CH =AB·cos 60°=8×12=4,∴GH =BG 2-BH 2=72-(43)2=1, ∴CG =4-1=3, ∴CG AC =38, ∴t =83(t >2),由(2)②得:CE +CF =1t BC ,∴CE =1t BC -CF =38×8-65=95.∴EC 的长度为95.3. 解:(1)分三种情况: ①若AP =AO ,在矩形ABCD 中,∵AB =6,BC =8, ∴AC =10,第3题解图①∴AO =CO =5,∴AP =5, ∴t =5,②若AP =PO =t , 在矩形ABCD 中, ∵AD ∥BC ,∴∠PAO =∠OCE ,∠APO =∠OEC , 又∵OA =OC ,∴△APO ≌△CEO ,∴PO =OE =t.如解图①,作AG ∥PE 交BC 于点G ,则四边形APEG 是平行四边形, ∴AG =PE =2t ,GE =AP =t. 又∵EC =AP =t ,∴BG =8-2t.在Rt △ABG 中,根据勾股定理知62+(8-2t)2=(2t)2, 解得t =258.第3题解图②③若OP =AO =5,则t =0或t =8,不合题意,舍去. 综上可知,当t =5或t =258时,△AOP 是等腰三角形.(2)如解图②,作OM ⊥BC ,垂足是M ,作ON ⊥CD ,垂足是N. 则OM =12AB =3,ON =12BC =4,∴S △OEC =12·CE·OM =12·t·3=32t ,S △OCD =12·CD·ON =12·6·4=12.∵QF ∥AC ,∴△DFQ ∽△DOC , ∴S △DFQ S △DOC =(DQ DC)2,即S △DFQ 12=(t 6)2,∴S △DFQ =13t 2,∴S 四边形OFQC =12-13t 2,∴S 五边形OECQF =S 四边形OFQC +S △OEC =12-13t 2+32t ,即S =-13t 2+32t +12(0<t <6).(3)存在.理由如下:要使S 五边形OECQF :S △ACD =9∶16,即(-13t 2+32t +12)∶(12×6×8)=9∶16,解得t 1=3,t 2=1.5,两个解都符合题意,∴存在两个t 值,使S 五边形OECQF ∶S △ACD =9∶16,此时t 1=3,t 2=1.5; (4)存在.理由如下:如解图③,作DI ⊥OP ,垂足是I ,DJ ⊥OC ,垂足是J ,第3题解图③作AG ∥PE 交BC 于点G.∵S △OCD =12·OC·DJ =12·5·DJ ,且由(2)知,S △OCD =12,∴DJ =245.∵OD 平分∠POC ,DI ⊥OP ,DJ ⊥OC , ∴DI =DJ =245=4.8.∵AG ∥PE ,∴∠DPI =∠DAG .∵AD ∥BC ,∴∠DAG =∠AGB ,∴∠DPI =∠AGB , ∴Rt △ABG ∽Rt △DIP.由(1)知,在Rt △ABG 中,BG =8-2t , ∴AB DI =BG IP ,∴64.8=8-2t IP, ∴IP =45(8-2t).在Rt △DPI 中,根据勾股定理得 (245)2+[45(8-2t)]2=(8-t)2, 解得t =11239.(t =0不合题意,舍去)4. (1)解:①BC ⊥CF ;②BC =CD +CF. 【解法提示】①∵∠BAC =∠DAF =90°, ∴∠BAD =∠CAF , 又∵AB =AC ,AD =AF , ∴△ABD ≌△ACF , ∴∠ACF =∠ABC =45°, ∵∠ACB =45°,∴∠BCF =90°,即BC ⊥CF ; ②∵△ABD ≌△ACF , ∴BD =CF , ∵BC =CD +BD , ∴BC =CD +CF.(2)解:结论①仍然成立,②不成立. ①证明:∵∠BAC =∠DAF =90°, ∴∠BAD =∠CAF ,又∵AB =AC ,AD =AF , ∴△ABD ≌△ACF ,∴∠ACF =∠ABD =180°-45°=135°, ∵∠ACB =45°, ∴∠BCF =90°,即BC ⊥CF ; ②结论为:BC =CD -CF. 证明:∵△ABD ≌△ACF , ∴BD =CF ,∵BC =CD -BD ,∴BC =CD -CF.(3)解:如解图,过点E 作EM ⊥CF 于M ,作EN ⊥BD 于点N ,过点A 作AH ⊥BD 于点H. ∵AB =AC =22,第4题解图∴BC =4,AH =12BC =2,∵CD =14BC ,∴CD =1,∵∠BAC =∠DAF =90°, ∴∠BAD =∠CAF ,又∵AB =AC ,AD =AF , ∴△ABD ≌△ACF , ∴∠ACF =∠ABC =45°, ∵∠ACB =45°, ∴∠BCF =90°,∴CN =ME ,CM =EN , ∴∠AGC =∠ABC =45°, ∴CG =BC =4,∵∠ADE =90°,∴∠ADH +∠EDN =∠EDN +∠DEN =90°, ∴∠ADH =∠DEN ,又∵∠AHC =∠DNE =90°,AD =DE , ∴△AHD ≌△DNE ,∴DN =AH =2,EN =DH =3, ∴CM =EN =3,ME =CN =3, 则GM =CG -CM =4-3=1, ∴EG =EM 2+GM 2=10.类型二 平移、旋转、折叠探究题5. (1)解:BD =CF 成立.理由如下:∵AC =AB ,∠CAF =∠BAD =θ,AF =AD , ∴△ACF ≌△ABD ,∴CF =BD.(2)①证明:由(1)得,△ACF ≌△ABD , ∴∠HFN =∠ADN , 在△HFN 与△ADN 中,∵∠HFN =∠ADN ,∠HNF =∠AND , ∴∠NHF =∠NAD =90°,第5题解图∴HD ⊥HF ,即BD ⊥CF.②解:如解图,连接DF ,延长AB ,与DF 交于点M , 在△MAD 中,∵∠MAD =∠MDA =45°, ∴∠BMD =90°.在Rt △BMD 与Rt △FHD 中, ∵∠MDB =∠HDF ,∴△BMD ∽△FHD.∵AB =2,AD =32,四边形ADEF 是正方形, ∴MA =MD =322=3,∴MB =MA -AB =3-2=1,BD =MB 2+MD 2=12+32=10, 又∵MD HD =BD FD ,即3HD =106,∴DH =9105.6. (1)①证明:∵△ABC 绕点A 顺时针方向旋转60°得到△ADE , ∴AB =AD ,∠BAD =60°, ∴△ABD 是等边三角形;②证明:由①得△ABD 是等边三角形, ∴AB =BD ,∵△ABC绕点A顺时针方向旋转60°得到△ADE,∴AC=AE,BC=DE,又∵AC=BC,∴EA=ED,∴点B,E在AD的中垂线上,∴BE是AD的中垂线,∵点F在BE的延长线上,∴BF⊥AD,AF=DF;③解:BE的长为33-4;【解法提示】由②知AF=12AD=12AB=3,AE=AC=5,BF⊥AD,由勾股定理得EF=AE2-AF2=4.在等边△ABD中,AB=6,BF⊥AD,∴BF=32AB=33,∴BE=33-4.(2)解:BE+CE的值为13;第6题解图【解法提示】如解图,∵∠DAG=∠ACB,∴∠DAB=2∠CAB.∵∠DAE=∠CAB,∴∠BAE=∠CAB,∴∠BAE=∠CBA,∴AE∥BC,∵AE=AC=BC,∴四边形ACBE是菱形,∴CE 垂直平分AB ,BE =AC =5.设CE 交AB 于M ,则CM ⊥AB ,CM =EM ,AM =BM , ∴在Rt △ACM 中,AC =5,AM =3, 由勾股定理得CM =4, ∴CE =8, ∴CE +BE =13.7. 解:(1)由矩形性质与折叠可知,∠APO =∠B =∠C =∠D =90°, ∴∠CPO +∠DPA =∠DPA +∠DAP =90°, ∴∠DAP =∠CPO , ∴△OCP ∽△PDA , ∴S △OCP S △PDA =(CP DA)2,即14=(CP8)2,∴CP =4,设CD =x ,则DP =x -4,AP =AB =CD =x , ∵AP 2-DP 2=AD 2, ∴x 2-(x -4)2=82, 解得x =10, 故CD =10. (2)第7题解图线段EF 的长度始终不发生变化,为2 5.证明:如解图,过点N 作NG ⊥PB ,与PB 的延长线相交于点G , ∵AB =AP ,∴∠APB =∠ABP =∠GBN , 在△PME 和△BNG 中, ⎩⎪⎨⎪⎧∠MEP =∠NGB =90°∠MPE =∠NBG MP =NB, ∴△PME ≌△BNG(AAS ), ∴ME =NG ,PE =BG , 在△FME 和△FNG 中, ⎩⎪⎨⎪⎧∠MEF =∠NGF ∠MFE =∠NFG ME =NG,∴△FME ≌△FNG(AAS ), ∴EF =GF , ∴EF =12EG ,∵BP =BE +EP =BE +GB =EG , ∴EF =12BP ,∵BP =BC 2+CP 2=82+42=45, ∴EF =12BP =2 5.8. (1)解:菱形.(2)证明:如解图①,作AE ⊥CC′于点E , 由旋转得AC′=AC ,∴∠CAE =∠C′AE =12α=∠BAC ,第8题解图①∵四边形ABCD 是菱形, ∴BA =BC ,BC =DC′, ∴∠BCA =∠BAC , ∴∠CAE =∠BCA , ∴AE ∥BC , 同理AE ∥DC′, ∴BC ∥DC ′,∴四边形BCC′D 是平行四边形, 又∵AE ∥BC ,∠CEA =90°, ∴∠BCC ′=180°-∠CEA =90°,∴四边形BCC′D 是矩形.(3)解:如解图①,过点B 作BF ⊥AC 于点F , ∵BA =BC ,∴CF =AF =12AC =12×10=5.在Rt △BCF 中,BF =BC 2-CF 2=132-52=12. 在△ACE 和△CBF 中,∵∠CAE =∠BCF ,∠CEA =∠BFC =90°, ∴△ACE ∽△CBF , ∴CE BF =AC BC ,即CE 12=1013, 解得CE =12013.∵AC =AC′,AE ⊥CC ′, ∴CC ′=2CE =2×12013=24013.当四边形BCC″D′恰好为正方形时,分两种情况: ①点C″在边CC′上,a =CC′-13=24013-13=7113,②点C″在边C′C 的延长线上,a =CC′+13=24013+13=40913.综上所述,a 的值为7113或40913.第8题解图②(4)解:答案不唯一,例:画出正确图形如解图②所示.平移及构图方法:将△ACD 沿着射线CA 方向平移,平移距离为12AC 的长度,得到△A ′C ′D ,连接A′B ,DC.结论:四边形A′BCD 是平行四边形.9. 解:(1)∵折叠后点A 落在AB 边上的点D 处, ∴EF ⊥AB ,△AEF ≌△DEF , ∴S △AEF =S △DEF .∵S 四边形ECBF =3S △EDF ,∴S 四边形ECBF =3S △AEF .∵S △ACB =S △AEF +S 四边形ECBF ,∴S △ACB =S △AEF +3S △AEF =4S △AEF , ∴S △AEF S △ACB =14. ∵∠EAF =∠BAC ,∠AFE =∠ACB =90°, ∴△AEF ∽△ABC , ∴S △AEF S △ABC =(AE AB )2, ∴(AE AB )2=14. 在Rt △ACB 中,∵∠ACB =90°,AC =4,BC =3, ∴AB =42+32=5, ∴(AE 5)2=14,∴AE =52.(2)第9题解图①①四边形AEMF 是菱形.证明:如解图①,∵折叠后点A 落在BC 边上的点M 处, ∴∠CAB =∠EMF ,AE =ME , 又∵MF ∥CA ,∴∠CEM =∠EMF , ∴∠CAB =∠CEM , ∴EM ∥AF ,∴四边形AEMF 是平行四边形. 又∵AE =ME ,∴四边形AEMF 是菱形.②如解图①,连接AM ,AM 与EF 交于点O ,设AE =x ,则ME =AE =x ,EC =4-x. ∵∠CEM =∠CAB ,∠ECM =∠ACB =90°, ∴△ECM ∽△ACB. ∴EC AC =EMAB , ∵AB =5,AC =4, ∴4-x 4=x5, 解得x =209,∴AE =ME =209,EC =169.在Rt △ECM 中,∵∠ECM =90°,∴CM 2=EM 2-EC 2, 即CM =EM 2-EC 2=(209)2-(169)2=43. ∵四边形AEMF 是菱形,∴OE =OF ,OA =OM ,AM ⊥EF , ∴S 菱形AEMF =4S △AOE =2OE·AO. 在Rt △AOE 和Rt △ACM 中, ∵tan ∠EAO =tan ∠MAC , ∴OE AO =CM AC. ∵CM =43,AC =4,∴AO =3OE ,∴S 菱形AEMF =6OE 2. 又∵S 菱形AEMF =AE·CM ,∴6OE 2=209×43,∴OE =2109,∴EF =4109. (3)如解图②,第9题解图②过点F 作FH ⊥CB 于点H ,在Rt △NCE 和Rt △NHF 中, ∵tan ∠ENC =tan ∠FNH , ∴EC NC =FH NH, ∵NC =1,EC =47,∴FH NH =47, 设FH =x ,则NH =74x ,∴CH =NH -NC =74x -1.∵BC =3,∴BH =BC -CH =3-(74x -1)=4-74x.在Rt △BHF 和Rt △BCA 中,∵tan ∠FBH =tan ∠ABC , ∴HF BH =CA BC , ∴x4-74x =43, 解得x =85,∴HF =85.∵∠B =∠B ,∠BHF =∠BCA =90°, ∴△BHF ∽△BCA , ∴HF CA =BFBA,即HF·BA =CA·BF , ∴85×5=4BF ,∴BF =2,∴AF =AB -BF =3, ∴AF BF =32. 10. 解:(1)△ABP ∽△PCD. 【解法提示】∵∠MPN =90°, ∴∠APB +∠DPC =90°, ∵∠B =90°,∴∠APB +∠BAP =90°, ∴∠DPC =∠BAP , 又∵∠B =∠C =90°, ∴△ABP ∽△PCD.(2)在旋转过程中,PEPF 的值为定值.如解图,过点F 作FG ⊥BC ,垂足为G.第10题解图类比(1)可得:△EBP ∽△PGF , ∴EP PF =PB FG, ∵∠A =∠B =∠FGB =90°, ∴四边形ABGF 是矩形, ∴FG =AB =2, ∵BP =1, ∴PE PF =12, 即在旋转过程中,PE PF 的值为定值12.(3)由(2)知△EBP ∽△PGF , ∴EB PG =BP GF =12, 又∵AE =t , ∴BE =2-t ,∴PG =2(2-t)=4-2t ,∴AF =BG =BP +PG =1+(4-2t)=5-2t ,∴S =S 矩形ABGF -S △AEF -S △BEP -S △PFG=2(5-2t)-12t(5-2t)-12×1×(2-t)-12×2×(4-2t)=t 2-4t +5,即S =t 2-4t +5(0≤t ≤2), 当S =4.2时,4.2=t 2-4t +5,解得:t 1=2-455,t 2=2+455(不合题意,舍去).∴t 的值是2-455.11. 解:(1)如解图①,在△ABC 中, ∵∠ACB =90°,∠B =30°,AC =1, ∴AB =2,又∵D 是AB 的中点,第11题解图①∴AD =1,CD =12AB =1,又∵EF 是△ACD 的中位线,∴EF =DF =12,在△ACD 中,AD =CD ,∠A =60°,∴△ACD 为等边三角形, ∴∠ADC =60°, 在△FGD 中,GF =DF·sin 60°=34, ∴矩形EFGH 的面积S =EF·GF =12×34=38.(2)如解图②,设矩形移动的距离为x ,则0<x ≤12,①当矩形与△CBD 重叠部分为三角形时,则0<x ≤14,重叠部分的面积S =12x·3x =316,第11题解图②∴x =24>14(舍去), ②当矩形与△CBD 重叠部分为直角梯形时,则14<x ≤12,重叠部分的面积S =34x -12×14×34=316, ∴x =38,即矩形移动的距离为38时,矩形与△CBD 重叠部分的面积是316.第11题解图③(3)如解图③,作H 2Q ⊥AB 于Q , 设DQ =m ,则H 2Q =3m , 又DG 1=14,H 2G 1=12,在Rt △H 2QG 1中, (3m)2+(m +14)2=(12)2,解得m 1=-1+1316,m 2=-1-1316<0(舍去),∴cos α=QG 1F 1G 1=-1+1316+1412=3+138.类型三 图形形状变化探究题12. (1)证明:∵△ABD 、△ACE 是等边三角形, ∴AB =AD ,AC =AE ,∠CAE =∠DAB =60°,∴∠CAE +∠BAC =∠DAB +∠BAC ,即∠BAE =∠DAC , 在△ABE 和△ADC 中, ⎩⎪⎨⎪⎧AB =AD ∠BAE =∠DAC AE =AC, ∴△ABE ≌△ADC(SAS ). (2)解:∠BOC =90°.理由如下: 由(1)得△ABE ≌△ADC ,∴∠EBA =∠CDA.∵∠FBA +∠FDA =180°,∴∠FBA -∠EBA +∠FDA +∠CDA =180°, 即∠FBO +∠FDO =180°.在四边形FBOD 中,∠F =90°, ∴∠DOB =360°-∠F -(∠FBO +∠FDO)=90°, ∴∠BOC =90°. (3)解:72°.【解法提示】∠BOC =180°-108°=72°.(4)解:180°-180°·(n -2)n.【解法提示】由(3)可知,∠BOC 度数应为180°减去正多边形内角度数. 13. 解:(1)233.【解法提示】sin 120°=32,故这个平行四边形的变形度是233. (2)1sin α=S 1S 2,理由如下: 如解图,设矩形的长和宽分别为a ,b ,其变形后的平行四边形的高为h ,第13题解图则S 1=ab ,S 2=ah ,sin α=hb ,∴S 1S 2=ab ah =b h , 又∵1sin α=b h ,∴1sin α=S 1S 2. (3)由AB 2=AE·AD ,可得A 1B 21=A 1E 1·A 1D 1,即A 1B 1A 1D 1=A 1E 1A 1B 1. 又∵∠B 1A 1E 1=∠D 1A 1B 1, ∴△B 1A 1E 1∽△D 1A 1B 1, ∴∠A 1B 1E 1=∠A 1D 1B 1, ∵A 1D 1∥B 1C 1,∴∠A 1E 1B 1=∠C 1B 1E 1,∴∠A 1E 1B 1+∠A 1D 1B 1=∠C 1B 1E 1+∠A 1B 1E 1=∠A 1B 1C 1. 由(2)结论1sin α=S 1S 2,可得1sin ∠A 1B 1C 1=4m2m =2,∴sin ∠A 1B 1C 1=12,∴∠A 1B 1C 1=30°,∴∠A 1E 1B 1+∠A 1D 1B 1=30°. 14. (1)①证明:如解图①, ∵∠ACE +∠ECB =45°,∠BCF +∠ECB =45°,第14题解图①∴∠ACE =∠BCF ,又∵四边形ABCD 和EFCG 是正方形, ∴AC BC =CECF=2, ∴△CAE ∽△CBF.②解:∵AE BF =ACBC =2,AE =2,∴BF =AE2=2, 由△CAE ∽△CBF 可得∠CAE =∠CBF , 又∵∠CAE +∠CBE =90°, ∴∠CBF +∠CBE =90°,即∠EBF =90°,第14题解图②由CE 2=2EF 2=2(BE 2+BF 2)=6, 解得CE = 6.(2)解:连接BF ,如解图②,同(1)证△CAE ∽△CBF ,可得∠EBF =90°,AC BC =AE BF, 由AB BC =EFFC=k ,可得BC ∶AB ∶AC =1∶k ∶k 2+1, CF ∶EF ∶EC =1∶k ∶k 2+1,∴CE EF =ACAB =k 2+1k ,AE BF =AC BC=k 2+1, ∴EF =kCE k 2+1,EF 2=k 2CE 2k 2+1,BF =AE k 2+1,BF 2=AE 2k 2+1,∴CE 2=k 2+1k 2×EF 2=k 2+1k2(BE 2+BF 2), ∴32=k 2+1k 2(12+22k 2+1), 解得k =104. (3)解:p 2-n 2=(2+2)m 2.【解法提示】如解图③,连接BF ,同(1)证△CAE ∽△CBF ,可得∠EBF =90°, 过点C 作CH ⊥AB 交AB 延长线于点H , 类比第(2)问得AB 2∶BC 2∶AC 2=1∶1∶(2+2),第14题解图③EF 2∶FC 2∶EC 2=1∶1∶(2+2), ∴p 2=(2+2)EF 2=(2+2)(BE 2+BF 2)=(2+2)(m 2+n 22+2)=(2+2)m 2+n 2,∴p 2-n 2=(2+2)m 2.15. 证明:(1)①连接AH ,如解图①. 第15题解图①∵四边形OBFC 是平行四边形, ∴BH =HC =12BC ,OH =HF ,∵△ABC 是等边三角形, ∴AB =BC ,AH ⊥BC ,在Rt △ABH 中,AH 2=AB 2-BH 2, ∴AH =BC 2-(12BC )2=32BC ,∵OA =AE ,OH =HF ,∴AH 是△OEF 的中位线, ∴AH =12EF ,AH ∥EF ,∴EF ⊥BC.②由①得AH =32BC ,∵AH =12EF∴32BC =12EF ,∴EF =3BC.(2)EF ⊥AB 仍然成立,EF =BC.第15题解图②【解法提示】如解图②,连接AH,∵四边形OBFC是平行四边形,∴BH=HC=12BC,OH=HF,∵△ABC是等腰直角三角形,∴AH⊥BC,在Rt△ABH中,AH2=AB2-BH2=(2BH)2-BH2=BH2,∴AH=BH=12BC,∵OA=AE,OH=HF,∴AH是△OEF的中位线,∴AH=12EF,AH∥EF,∴EF⊥BC,EF=2AH=BC.第15题解图③(3)EF=4k2-1 BC.【解法提示】如解图③,连接AH,∵四边形OBFC是平行四边形,∴BH=HC=12BC,OH=HF,∵△ABC是等腰三角形,AB=kBC,∴AH⊥BC,在Rt△ABH中,AH2=AB2-BH2=(kBC)2-(12=(k2-14)BC2,2BC)∴AH=12-1 BC,24k∵OA=AE,OH=HF,∴AH是△OEF的中位线,∴AH=12EF,AH∥EF,∴EF⊥BC,12-1 BC=12EF,24k∴EF=4k2-1 BC.。
初中数学(几何探究型问题)题库及答案

初中数学(几何探究型问题)题库及答案1.(2019•北京)在△ABC中,D,E分别是△ABC两边的中点,如果DE上的所有点都在△ABC的内部或边上,则称DE为△ABC的中内弧.例如,图1中DE 是△ABC的一条中内弧.(1)如图2,在Rt△ABC中,AB=AC=D,E分别是AB,AC的中点,画出△ABC的最长的中内弧DE,并直接写出此时DE的长;(2)在平面直角坐标系中,已知点A(0,2),B(0,0),C(4t,0)(t>0),在△ABC中,D,E分别是AB,AC的中点.①若t12=,求△ABC的中内弧DE所在圆的圆心P的纵坐标的取值范围;②若在△ABC中存在一条中内弧DE,使得DE所在圆的圆心P在△ABC的内部或边上,直接写出t的取值范围.【解析】(1)如图2,以DE为直径的半圆弧DE,就是△ABC的最长的中内弧DE,连接DE.∵∠A=90°,AB=AC=D,E分别是AB,AC的中点.∴BC sin AC B ===4,DE 12=BC 12=⨯4=2.∴弧12DE =⨯2π=π. (2)如图3,由垂径定理可知,圆心一定在线段DE 的垂直平分线上,连接DE ,作DE 垂直平分线FP ,作EG ⊥AC 交FP 于G .①当t 12=时,C (2,0),∴D (0,1),E (1,1),F (12,1).设P (12,m )由三角形中内弧定义可知,圆心线段DE 上方射线FP 上均可,∴m ≥1.∵OA =OC ,∠AOC =90°. ∴∠ACO =45°. ∵DE ∥OC .∴∠AED =∠ACO =45°.作EG ⊥AC 交直线FP 于G ,FG =EF 12=. 根据三角形中内弧的定义可知,圆心在点G 的下方(含点G )直线FP 上时也符合要求. ∴m 12≤.综上所述,m 12≤或m ≥1. ②如图4,设圆心P 在AC 上.∵P 在DE 中垂线上.∴P 为AE 中点,作PM ⊥OC 于M ,则PM 32=. ∴P (t ,32). ∵DE ∥BC .∴∠ADE =∠AOB =90°.∴AE === ∵PD =PE . ∴∠AED =∠PDE .∵∠AED +∠DAE =∠PDE +∠ADP =90°. ∴∠DAE =∠ADP . ∴AP =PD =PE 12=AE .由三角形中内弧定义知,PD ≤PM .∴12AE 32≤,AE ≤3≤3,解得:t ≤ ∵t >0. ∴0<t≤【名师点睛】此题是一道圆的综合题,考查了圆的性质,弧长计算,直角三角形性质等,给出了“三角形中内弧”新定义,要求学生能够正确理解新概念,并应用新概念解题.2.(2019•天津)在平面直角坐标系中,O为原点,点A(6,0),点B在y轴的正半轴上,∠ABO=30°.矩形CODE的顶点D,E,C分别在OA,AB,OB上,OD=2.(Ⅰ)如图①,求点E的坐标;(Ⅱ)将矩形CODE沿x轴向右平移,得到矩形C′O′D′E′,点C,O,D,E 的对应点分别为C′,O′,D′,E′.设OO′=t,矩形C′O′D′E′与△ABO重叠部分的面积为S.①如图②,当矩形C′O′D′E′与△ABO重叠部分为五边形时,C′E′,E′D′分别与AB相交于点M,F,试用含有t的式子表示S,并直接写出t的取值范围;S t的取值范围(直接写出结果即可).【解析】(Ⅰ)∵点A(6,0).∴OA=6.∵OD=2.∴AD=OA-OD=6-2=4.∵四边形CODE是矩形.∴DE∥OC.∴∠AED=∠ABO=30°.在Rt△AED中,AE=2AD=8,ED===∵OD =2.∴点E 的坐标为(2,.(Ⅱ)①由平移的性质得:O ′D ′=2,E ′D ME ′=OO ′=t ,D ′E ′∥O ′C ′∥OB . ∴∠E ′FM =∠ABO =30°.∴在Rt △MFE ′中,MF =2ME ′=2t ,FE ′===.∴S △MFE ′12=ME ′·FE ′12=⨯t 22=.∵S 矩形C ′O ′D ′E ′=O ′D ′·E ′D =∴S =S 矩形C ′O ′D ′E ′-S △MFE ′.∴S 2=-t 2,其中t 的取值范围是:0<t <2;②当S =O 'A =OA -OO '=6-t .∵∠AO 'F =90°,∠AFO '=∠ABO =30°.∴O 'F ='A =6-t ).∴S 12=(6-t )(6-t )=解得:t =6,或t =6.∴t =6S 时,如图④所示:O 'A =6-t ,D 'A =6-t -2=4-t .∴O 'G =6-t ),D 'F =4-t ).∴S 12=6-t )4-t ) 解得:t 52=.S t 的取值范围为52≤t ≤6.【名师点睛】本题是四边形综合题目,考查了矩形的性质、坐标与图形性质、勾股定理、平移的性质、直角三角形的性质、梯形面积公式等知识;本题综合性强,有一定难度,熟练掌握含30°角的直角三角形的性质时是解题的关键. 3.(2019•陕西)问题提出:(1)如图1,已知△ABC ,试确定一点D ,使得以A ,B ,C ,D 为顶点的四边形为平行四边形,请画出这个平行四边形; 问题探究:(2)如图2,在矩形ABCD 中,AB =4,BC =10,若要在该矩形中作出一个面积最大的△BPC ,且使∠BPC =90°,求满足条件的点P 到点A 的距离; 问题解决:(3)如图3,有一座塔A ,按规定,要以塔A 为对称中心,建一个面积尽可能大的形状为平行四边形的景区BCDE .根据实际情况,要求顶点B 是定点,点B到塔A的距离为50米,∠CBE=120°,那么,是否可以建一个满足要求的面积最大的平行四边形景区BCDE?若可以,求出满足要求的平行四边形BCDE的最大面积;若不可以,请说明理由.(塔A的占地面积忽略不计)【解析】(1)如图记为点D所在的位置.(2)如图.∵AB=4,BC=10,∴取BC的中点O,则OB>AB.∴以点O为圆心,OB长为半径作⊙O,⊙O一定于AD相交于P1,P2两点.连接BP1,P1C,P1O,∵∠BPC=90°,点P不能再矩形外.∴△BPC的顶点P1或P2位置时,△BPC的面积最大.作P1E⊥BC,垂足为E,则OE=3.∴AP1=BE=OB-OE=5-3=2.由对称性得AP2=8.(3)可以,如图所示,连接BD.∵A为BCDE的对称中心,BA=50,∠CBE=120°.∴BD=100,∠BED=60°.作△BDE的外接圆⊙O,则点E在优弧BD上,取BED的中点E′,连接E′B,E′D.则E′B=E′D,且∠BE′D=60°,∴△BE′D为正三角形.连接E′O并延长,经过点A至C′,使E′A=AC′,连接BC′,DC′.∵E′A⊥BD.∴四边形E′D为菱形,且∠C′BE′=120°.作EF⊥BD,垂足为F,连接EO,则EF≤EO+OA-E′O+OA=E′A.∴S△BDE12=·BD·EF12≤·BD·E′A=S△E′BD.∴S平行四边形BCDE≤S平行四边形BC′DE′=2S△E′BD=1002·m2).所以符合要求的BCDE的最大面积为2.【名师点睛】本题属于四边形综合题,考查了平行四边形的判定和性质,圆周角定理,三角形的面积等知识,解题的关键是理解题意,学会添加常用辅助线,属于中考压轴题.4.(2019•海南)如图,在边长为1的正方形ABCD中,E是边CD的中点,点P 是边AD上一点(与点A、D不重合),射线PE与BC的延长线交于点Q.(1)求证:△PDE≌△QCE;(2)过点E作EF∥BC交PB于点F,连结AF,当PB=PQ时.①求证:四边形AFEP是平行四边形;②请判断四边形AFEP是否为菱形,并说明理由.【解析】(1)∵四边形ABCD是正方形.∴∠D=∠ECQ=90°.∵E是CD的中点.∴DE=CE.又∵∠DEP=∠CEQ.∴△PDE≌△QCE.(2)①∵PB=PQ.∴∠PBQ=∠Q.∵AD∥BC.∴∠APB=∠PBQ=∠Q=∠EPD.∵△PDE≌△QCE.∴PE=QE.∵EF∥BQ.∴PF=BF.∴在Rt△P AB中,AF=PF=BF.∴∠APF=∠P AF.∴∠P AF=∠EPD.∴PE∥AF.∵EF∥BQ∥AD.∴四边形AFEP是平行四边形;②四边形AFEP不是菱形,理由如下:设PD=x,则AP=1-x.由(1)可得△PDE≌△QCE.∴CQ=PD=x.∴BQ=BC+CQ=1+x.∵点E、F分别是PQ、PB的中点.∴EF是△PBQ的中位线.∴EF12=BQ12x+=.由①知AP=EF,即1-x12x+ =.解得x1 3 =.∴PD13=,AP23=.在Rt△PDE中,DE1 2 =.∴PE==∴AP≠PE.∴四边形AFEP不是菱形.【名师点睛】本题是四边形的综合问题,解题的关键是掌握正方形的性质、全等三角形的判定与性质、直角三角形的性质、平行四边形与菱形的判定、性质等知识点.5.(2019•江西)在图1,2,3中,已知ABCD,∠ABC=120°,点E为线段BC 上的动点,连接AE,以AE为边向上作菱形AEFG,且∠EAG=120°.(1)如图1,当点E与点B重合时,∠CEF=__________°;(2)如图2,连接AF.①填空:∠F AD__________∠EAB(填“>”“<”“=”);②求证:点F在∠ABC的平分线上.(3)如图3,连接EG,DG,并延长DG交BA的延长线于点H,当四边形AEGH是平行四边形时,求BC的值.AB【解析】(1)∵四边形AEFG是菱形.∴∠AEF=180°-∠EAG=60°.∴∠CEF=∠AEC-∠AEF=60°.故答案为:60°.(2)①∵四边形ABCD是平行四边形.∴∠DAB=180°-∠ABC=60°.∵四边形AEFG是菱形,∠EAG=120°.∴∠F AE=60°.∴∠F AD=∠EAB.故答案为:=.②如图,作FM⊥BC于M,FN⊥BA交BA的延长线于N.则∠FNB=∠FMB=90°.∴∠NFM=60°,又∠AFE=60°.∴∠AFN=∠EFM.∵EF=EA,∠F AE=60°.∴△AEF为等边三角形.∴F A=FE.在△AFN和△EFM中,AFN EFMFNA FME FA FE∠=∠⎧⎪∠=∠⎨⎪=⎩.∴△AFN≌△EFM(AAS)∴FN=FM,又FM⊥BC,FN⊥BA.∴点F在∠ABC的平分线上.(3)如图.∵四边形AEFG是菱形,∠EAG=120°.∴∠AGF=60°.∴∠FGE=∠AGE=30°.∵四边形AEGH为平行四边形.∴GE∥AH.∴∠GAH=∠AGE=30°,∠H=∠FGE=30°.∴∠GAN=90°,又∠AGE=30°.∴GN=2AN.∵∠DAB=60°,∠H=30°.∴∠ADH=30°.∴AD=AH=GE.∵四边形ABCD为平行四边形.∴BC=AD.∴BC=GE.∵四边形ABEH为平行四边形,∠HAE=∠EAB=30°.∴平行四边形ABEN为菱形.∴AB=AN=NE.∴GE=3AB.∴BCAB3.【名师点睛】本题考查的是相似三角形的判定和性质、全等三角形的判定和性质、菱形的性质、平行四边形的性质,掌握全等三角形的判定定理和性质定理、菱形的性质、直角三角形的性质是解题的关键.6.(2019•宁夏)如图,在△ABC中,∠A=90°,AB=3,AC=4,点M,Q分别是边AB,BC上的动点(点M不与A,B重合),且MQ⊥BC,过点M作BC的平行线MN,交AC于点N,连接NQ,设BQ为x.(1)试说明不论x为何值时,总有△QBM∽△ABC;(2)是否存在一点Q,使得四边形BMNQ为平行四边形,试说明理由;(3)当x为何值时,四边形BMNQ的面积最大,并求出最大值.【解析】(1)∵MQ⊥BC.∴∠MQB=90°.∴∠MQB=∠CAB,又∠QBM=∠ABC.∴△QBM∽△ABC.(2)当BQ=MN时,四边形BMNQ为平行四边形.∵MN∥BQ,BQ=MN.∴四边形BMNQ为平行四边形.(3)∵∠A=90°,AB=3,AC=4.∴BC==5.∵△QBM∽△ABC.∴QB QM BMAB AC BC==,即345x QM BM==.解得,QM43=x,BM53=x.∵MN∥BC.∴MN AMBC AB=,即53353xMN-=.解得,MN=525 9 -x.则四边形BMNQ的面积12=⨯(5259-x+x)43⨯x3227=-(x4532-)27532+.∴当x4532=时,四边形BMNQ的面积最大,最大值为7532.【名师点睛】本题考查的是相似三角形的判定和性质、平行四边形的判定、二次函数的性质,掌握相似三角形的判定定理、二次函数的性质是解题的关键.7.(2019•安徽)如图,Rt△ABC中,∠ACB=90°,AC=BC,P为△ABC内部一点,且∠APB=∠BPC=135°.(1)求证:△P AB∽△PBC;(2)求证:P A=2PC;(3)若点P到三角形的边AB,BC,CA的距离分别为h1,h2,h3,求证h12=h2·h3.【解析】(1)∵∠ACB=90°,AB=BC.∴∠ABC=45°=∠PBA+∠PBC.又∠APB=135°.∴∠P AB+∠PBA=45°.∴∠PBC=∠P AB.又∵∠APB=∠BPC=135°.(2)∵△P AB ∽△PBC .∴PA PB ABPB PC BC==. 在Rt △ABC 中,AB =AC .∴ABBC= ∴PB PA ==,. ∴P A =2PC .(3)如图,过点P 作PD ⊥BC ,PE ⊥AC 交BC 、AC 于点D ,E .∴PF =h 1,PD =h 2,PE =h 3. ∵∠CPB +∠APB =135°+135°=270°. ∴∠APC =90°. ∴∠EAP +∠ACP =90°.又∵∠ACB =∠ACP +∠PCD =90°. ∴∠EAP =∠PCD . ∴Rt △AEP ∽Rt △CDP .∴2PE APDP PC==,即322h h =. ∴h 3=2h 2.∴12h ABh BC ==.∴12h .∴2212222322h h h h h h ==⋅=.即:h 12=h 2·h 3.【名师点睛】此题主要考查了相似三角形的判定和性质,等腰直角三角形的性质,判断出∠EAP =∠PCD 是解本题的关键.8.(2019•重庆A 卷)如图,在平行四边形ABCD 中,点E 在边BC 上,连结AE ,EM ⊥AE ,垂足为E ,交CD 于点M ,AF ⊥BC ,垂足为F ,BH ⊥AE ,垂足为H ,交AF 于点N ,点P 是AD 上一点,连接CP .(1)若DP =2AP =4,CP =CD =5,求△ACD 的面积. (2)若AE =BN ,AN =CE ,求证:AD=+2CE .【解析】(1)作CG ⊥AD 于G ,如图1所示:设PG =x ,则DG =4-x .在Rt △PGC 中,GC 2=CP 2-PG 2=17-x 2.在Rt△DGC中,GC2=CD2-GD2=52-(4-x)2=9+8x-x2.∴17-x2=9+8x-x2.解得:x=1,即PG=1.∴GC=4.∵DP=2AP=4.∴AD=6.∴S△ACD12=⨯AD×CG12=⨯6×4=12.(2)连接NE,如图2所示:∵AH⊥AE,AF⊥BC,AE⊥EM.∴∠AEB+∠NBF=∠AEB+∠EAF=∠AEB+∠MEC=90°.∴∠NBF=∠EAF=∠MEC.在△NBF和△EAF中,NBF EAFBFN EFA AE BN∠=∠⎧⎪∠=∠⎨⎪=⎩.∴△NBF≌△EAF.∴BF=AF,NF=EF.∴∠ABC=45°,∠ENF=45°,FC=AF=BF.∴∠ANE=∠BCD=135°,AD=BC=2AF.在△ANE和△ECM中,MEC EAF AN ECANE ECM ∠=∠⎧⎪=⎨⎪∠=∠⎩.∴△ANE≌△ECM.∴CM=NE.又∵NF2=NE2=MC.∴AF2=MC+EC.∴AD=+2EC.【名师点睛】本题考查了平行四边形的性质、全等三角形的判定与性质、勾股定理、三角形面积公式等知识;熟练掌握平行四边形的性质,证明三角形全等是解题的关键.。
中学数学研究在线测试答案

中学数学研究在线测试答案第一题、单项选择题(每题1分,5道题共5分)第二题、多项选择题(每题2分,5道题共10分)1、用0,1,2,3,4五个数字组数,则下列结论正确的有:A、可以组成120个没有重复数字的五位数;B、可以组成96个没有重复数字的五位数;C、可以组成60个没有重复数字的四位偶数;D、可以组成60个没有重复数字的四位奇数;E、可以组成36个没有重复数字的四位偶数;2、a,b,c,d,e五人排成一排,则下列结论正确的有:A、a不在两端的排法有96种;B、a不在两端的排法有72种;C、a,b相邻的排法有48种;D、a,b不相邻的排法有72种;E、a,b不在两端的排法有36种。
3、a,b,c三位先生和d,e,f三位女士围着圆桌就坐,则下列结论正确的有:A、六人围着圆桌就坐共有120种不同的就坐方式;B、六人围着圆桌就坐共有720种不同的就坐方式;C、若a,b相邻共有48种不同就坐方式;D、若男、女相间就坐共有6种不同就坐方式;E、如男、女相间就坐共有9种不同就坐方式。
4、从1,2,3,4,5,6,7,8,9,10中任取两个不同的数,则下列结论正确的有:A、乘积能被2整除的数对有45对;B、和能被2整除的有20对;C、和能被2整除的有40对;D、和能被3整除的有10对;E、积能被3整除的有27对;5、把4人分别按下列条件分组,则正确的结论有:A、第一组3人,第二组1人的分法数为4种;B、一个组3人,一个组1人的分法数为4种;C、平均分成两组,每组2人的分法数为3种;D、第一组2人。
第二组2人的分法数为3种;E、第一组2人。
第二组2人的分法数为6种.第三题、判断题(每题1分,5道题共5分)1、由数码1,2,3,4可以组成228个大于1234的四位数。
正确错误2、五元不定方程x+y+z+w+u=8共有495组非负整数解组。
正确错误3、a,b,c,d,e五人围着一张圆桌而坐,若限定a,b不相邻,则不同的坐法数是12种。
西南大学网络与继续教育《中学几何研究》作业及答案

(0775)《中学几何研究》作业4一、填空题:1.欧氏几何的平行公理为 。
2.几何轨迹的纯粹性是指 。
3.一个公理化系统需解决三个基本问题,而首要的是 。
4.已知ABC ∆的三边长分别为6、7、9,则ABC S ∆= 。
5.复数210iz e π=,则||z = 。
6.图形F 经对称变换变为图形F ',其对称轴为g ,该变换可记为 。
7.设A '、B '、C '是ABC ∆三边BC 、CA 、AB 上的点,则AA '、BB '、CC '相交于一点的充要条件 。
8.到两定点距离的平方差为常量的点的轨迹是一条直线,该直线称为 。
9.求解一个作图题的基本步骤是 。
二、解答下列各小题:(1)在圆内接四边形ABCD 中,已知BC CD =。
求证:22AC AB AD BC =⋅+.(2)作图题(只写作法):已知ABC ∆,求作ABC ∆的外接圆。
二、简述《几何原本》的不足之处。
三、填空题:1.过平面上直线外一点,有且只有一条直线与已知直线相平行。
2.轨迹上的点均满足条件。
3.相容性问题。
4.5.10。
6.()s g F F '−−−→. 7.1AC BA CB C B A C B A'''⋅⋅='''. 8.等差幂线。
9.分析、作法、证明、讨论。
二、解答下列各小题:(1)证明:ABCD ABD BCD S S S ∆∆=+ 而211sin sin 22ABD BCD S S AB AD BCD BC BCD ∆∆+=⋅∠+∠ (∵BC =CD ) 11sin sin sin 22ABCDS AC BD AC d BCD θθ=⋅=⋅∠⋅(其中d 为圆的直径)11sin sin(12)sin sin(14)22AC BCD d AC BCD d =⋅∠⋅⋅∠+∠=⋅∠⋅⋅∠+∠ 211sin sin 22AC BCD AC AC BCD =⋅∠⋅=∠ ∴22AC AB AD BC =⋅+.第(1)题图(2)作法:作BC 的中垂线l 和AC 的中垂线m ,l 与m 交于点O ,以O 为圆心,OA 为半径作圆(,)O OA 即为所求。
初等几何研究作业参考答案

《初等几何研究》作业参考答案一.填空题1.①射线(或半直线),②。
2. ①两,②度量公理(或阿基米德公理)和康托儿公理。
3.①前4组公理(或绝对几何),②平行公理。
4.①平移,②旋转,③轴对称. 5.1=⋅⋅ZBAZYA CY XC BX 。
6.①交轨法,②三角奠基法,③代数法,④变换法。
7.①反身性、②对称性、③传递性、④可加性. 8.外角. 9.答案不惟一.10.①演绎,②综合,③直接,④反证,⑤同一; 11.1=⋅⋅ZBAZYA CY XC BX .(答-1也对) 12. ①过两点可作一条直线(或其部分),②已知圆心和半径可作一圆(或其部分). 13.①不共线的三点A 、B 、C 及(AB)、(BC)、(CA)构成的点的集合。
14.连续. 15.答案不惟一. 16.①不过,②圆.17.1=⋅⋅ZB AZYA CY XC BX (或-1).18.①写出已知与求作,②分析,③作法,④证明,⑤讨论. 19.①相容,②独立,③完备.20.合同变换、相似变换、射影变换、反演变换等21.对任意直线a 及其外一点A ,在a 和A 决定的平面上,至少有两条过A 与a 不相交的直线. 22.①代数,②解析,③三角,④面积,⑤复数,⑥向量. 23.相等。
24.所求的量可用已知量的有理式或只含平方根的无理式表出. 二.问答题1.对于公理系统∑,若有一组具体事物M ,其性质是已知的,在规定∑中每一个基本概念指M 中某一具体事物后,可验证∑中每个公理在M 中都成立,则称M 为公理系统∑的一个模型;2.①若AB ≡B A '',则d(AB)=d(B A '');②当C BA ˆ时,有d(AB)+d(BC)=d(AC). 3.命题“三角形的内角和不大于两个直角” 与欧氏平行公理不等价。
4.结合,介于,合同;结合——即有公共点,介于——即在…之间,合同——相等或完全相等. 5.长度、角度、相等、全等、运动、移置、叠合、重合等.6.由第五公设引出了该公理独立性的问题,对该问题的研究导致了非欧几何等结果的产生. 7.通常用“在……上”、“属于”、“通过”等语句来表述。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(0775)《中学几何研究》作业一答案
一、填空题:
1.对于一个公理化系统,其公理的选择应符合三个条件,即相容性、独立性和完备性。
2.黎曼几何的平行公理为过平面上直线外一点,没有直线与已知直线相平行。
3.希尔伯特在其巨著《几何基础》中,建立了完备化的公理系统,其五组基本公理 是关联公理、顺序公理、合同公理、平行公理及连续公理。
4.已知ABC ∆的外接圆半径为R ,三边长分别为,,a b c ,则ABC S ∆=
4abc R 。
5.复数(cos sin )z r i θθ=+,该复数的指数形式为i z re θ=。
6.将ABC ∆顺时针绕点O 旋转30得A B C '''∆,该变换可记为(0,30)R ABC A B C -'''∆−−−−→∆。
7.设A '、B '、C '是ABC ∆的边BC 、CA 、AB 所在直线上的点,则A '、B '、C '共线的充要条件是1AC BA CB C B A C B A
'''⋅⋅='''。
8.轨迹命题证明的两面性包括完备性和纯粹性。
9.人们常说的尺规作图不可能的三个古典问题是倍立方问题、三等分任意角问题、化圆为方问题。
二、在△ABC 内任取一点P ,直线AP 、BP 、CP 分别交BC 、CA 、AB 于D 、E 、F. 求证:
1AF BD CE BF CD AE
⋅⋅=
第二题图
证明:CPA CPB S AF BF S ∆∆=,APB APC S BD CD S ∆∆=,BPC BPA S CE AE S ∆∆= ∴
1PCA PBC PAB PCB PAC PAB
S S S AF BD CE BF CD AE S S S ∆∆∆∆∆∆⋅⋅=⋅⋅=。
三、作图题(只写作法):用尺规求作三角形ABC ,已知,,a b c h m m 。
作法:① 任作直线L ,在其上取一点M ,作GM L ⊥且13a GM h =; ② 以G 为圆心,23b m 及23
c m 为半径作圆弧,分别交L 于B 、C 两点; ③ 延长BG 至D ,使b BD m =,延长CG 至E ,使c CE m =; ④ 延长BE 和CD ,交点为A ,ABC ∆完成。
四、联系中学教学实际,谈谈如何运用运动的观点进行几何教学。
