河南省安阳市滑县2015-2016学年七年级(下)期中数学试卷(解析版)
2015-2016第二学期期中七年级数学参考答案

2015—2016学年度第二学期期中质量评估试题七年级数学参考答案及评分标准11. 9; 12. 80°; 13.(5,0); 14. 4; 15. 100°;16. 一 三、解答题(一)17. 解:34)2(3-----=3+2-2-3 ……………4分 =0 ……………6分 18. 解:∵a ∥b∴∠2=∠3 ……………2分 ∵∠1+∠3=180°∴∠1+∠2=180° ……………4分 ∴∠2=180°-∠1 ∵∠1=118°∴∠2=180°-118°=62° ……………6分 19.(1)图(略) 图……………4分(2)A 1(0,6);B 1(-1,2) ……………6分 四、解答题(二) 20. 解: )223(328)2(32---+-+-=2232322+--+- ……………4分 =2 ……………7分 21. 解:∵∠1=∠2∴AB ∥CD ……………2分 ∴∠3+∠4=180° ……………4分 ∴∠4=180°-∠3 ……………6分 ∵∠3=108°∴∠4=180°-108°=72° ……………7分 22.(每空1分)∵AB ∥DC (已知)∴∠1=∠CFE (两直线平行,同位角相等)……………2分 ∵AE 平分∠BAD (已知)∴∠1=∠2(角平分线的定义) ……………4分 ∴∠2=∠CFE ……………5分 ∵∠CFE=∠E (已知)∴∠2=∠E …………6分 ∴AD ∥BC (内错角相等,两直线平行). …………7分五、解答题(三) 23. 解:100)1(2=-x101±=-x …………4分 110+±=x11=x …………7分或9-=x …………9分24. 证明:∵DE ‖BC (已知)∴∠ADE =∠ABC (两直线平行,同位角相等) …………2分 ∵DF 、BE 分别平分∠ADE 、∠ABC ∴∠ADF =12∠ADE∠ABE =12∠ABC (角平分线的定义) …………4分∴∠ADF =∠ABE …………5分∴ DF ‖BE (同位角相等,两直线平行) …………7分 ∴∠FDE =∠DEB. (两直线平行,内错角相等) …………9分 25. 解:(1)C (0,2),D (4,2),…………2分(2)依题意,得S 四边形ABDC =AB ×OC=4×2=8; …………3分 (3)存在. …………4分。
2016年河南省安阳市滑县七年级下学期数学期中试卷与解析答案

2015-2016学年河南省安阳市滑县七年级(下)期中数学试卷一.选择题1.(3分)下列各图中,∠1与∠2是对顶角的是()A.B.C.D.2.(3分)如图,如果AB∥CD,那么图中相等的内错角是()A.∠1与∠5,∠2与∠6 B.∠3与∠7,∠4与∠8C.∠5与∠1,∠4与∠8 D.∠2与∠6,∠7与∠33.(3分)下列结论正确的是()A.64的立方根是±4 B.﹣没有立方根C.立方根等于本身的数是0 D.=﹣4.(3分)下列计算正确的是()A.B.C.D.5.(3分)直角坐标系中,点P(x,y)在第三象限,且P到x轴和y轴的距离分别为3、7,则点P的坐标为()A.(﹣3,﹣7)B.(﹣7,﹣3)C.(3,7) D.(7,3)6.(3分)已知点P(0,a)在y轴的负半轴上,则点Q(﹣a2﹣1,﹣a+1)在()A.第一象限B.第二象限C.第三象限D.第四象限7.(3分)如图,直线AB∥CD,直线EF分别交直线AB、CD于点E、F,过点F 作FG⊥FE,交直线AB于点G,若∠1=42°,则∠2的大小是()A.56°B.48°C.46°D.40°8.(3分)把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在MN的位置上,若∠EFG=55°,则∠2=()A.105 B.110 C.95 D.120二.填空题9.(3分)的算术平方根是.10.(3分)如果∠A与∠B的两边分别平行,且∠A比∠B的3倍少36°,则∠A 的度数是.11.(3分)若+|b+1|+(c+1)2=0,则a+b﹣c=.12.(3分)已知点A(3a+5,a﹣3)在二、四象限的角平分线上,则a=.13.(3分)已知点M在y轴上,纵坐标为5,点P(3,﹣2),则△OMP的面积是.14.(3分)一个正数x的平方根分别是2a﹣3与5﹣a,x等于.15.(3分)如图,已知AB∥CD∥EF,则∠x、∠y、∠z三者之间的关系是.三.解答题16.(8分)计算:(1)||+|﹣1|﹣|3|(2)﹣++.17.(8分)求下列各式中的x.(1)4x2﹣16=0(2)27(x﹣3)3=﹣64.18.(8分)已知2a﹣1的平方根是±3,3a+b﹣1的算术平方根是4,求12a+2b 的立方根.19.(8分)如图,在△ABC中,三个顶点的坐标分别为A(﹣5,0),B(4,0),C(2,5),将△ABC沿x轴正方向平移2个单位长度,再沿y轴沿负方向平移1个单位长度得到△EFG.(1)求△EFG的三个顶点坐标.(2)求△EFG的面积.20.(10分)如图,已知AB∥CD,EF与AB、CD分别相交于点E、F,∠BEF与∠EFD的平分线相交于点P,求证:EP⊥FP.21.(10分)如图,∠1+∠2=180°,∠DAE=∠BCF,DA平分∠BDF.(1)AE与FC会平行吗?说明理由.(2)AD与BC的位置关系如何?为什么?(3)BC平分∠DBE吗?为什么?22.(10分)如图,已知AD⊥BC,FG⊥BC,垂足分别为D、G.且∠1=∠2,猜想:∠BDE与∠C有怎样的关系?说明理由.23.(13分)如图所示,已知AB∥CD,分别探究下面图形中∠APC,∠PAB,∠PCD的关系,请你从四个图形中任选一个,说明你所探究的结论的正确性.①结论:(1)(2)(3)(4)②选择结论,说明理由.2015-2016学年河南省安阳市滑县七年级(下)期中数学试卷参考答案与试题解析一.选择题1.(3分)下列各图中,∠1与∠2是对顶角的是()A.B.C.D.【解答】解:根据对顶角的定义可知:只有C选项的是对顶角,其它都不是.故选:C.2.(3分)如图,如果AB∥CD,那么图中相等的内错角是()A.∠1与∠5,∠2与∠6 B.∠3与∠7,∠4与∠8C.∠5与∠1,∠4与∠8 D.∠2与∠6,∠7与∠3【解答】解:∵∠1与∠5,∠4与∠8是直线AD、BC被AC所截得到的内错角,而AD、BC的位置关系不确定,∴∠1与∠5,∠4与∠8的数量关系也不确定,故A、B、C错误;D、∵∠2与∠6是平行线AB、CD被AC所截得到的内错角,∠3与∠7是平行线AB、CD被BD所截得到的内错角,由平行线的性质可得,它们相等,故正确.故选:D.3.(3分)下列结论正确的是()A.64的立方根是±4 B.﹣没有立方根C.立方根等于本身的数是0 D.=﹣【解答】解:A、64的立方根是4,故本选项错误;B、﹣的立方根是﹣,故本选项错误;C、立方根等于它本身的数是0、1、﹣1,故本选项错误;D、=﹣3,﹣=﹣3,故本选项正确;故选:D.4.(3分)下列计算正确的是()A.B.C.D.【解答】解:A、0.53=0.125,故选项错误;B、应取负号,故选项错误;C、∵等于,∴的立方根等于,故选项正确;D、应取正号,故选项错误.故选:C.5.(3分)直角坐标系中,点P(x,y)在第三象限,且P到x轴和y轴的距离分别为3、7,则点P的坐标为()A.(﹣3,﹣7)B.(﹣7,﹣3)C.(3,7) D.(7,3)【解答】解:∵点P(x,y)在第三象限,∴P点横纵坐标都是负数,∵P到x轴和y轴的距离分别为3、7,∴点P的坐标为(﹣7,﹣3).故选:B.6.(3分)已知点P(0,a)在y轴的负半轴上,则点Q(﹣a2﹣1,﹣a+1)在()A.第一象限B.第二象限C.第三象限D.第四象限【解答】解:∵点P(0,a)在y轴的负半轴上,∴a<0,∴﹣a2﹣1<0,﹣a+1>0,∴点Q在第二象限.故选:B.7.(3分)如图,直线AB∥CD,直线EF分别交直线AB、CD于点E、F,过点F 作FG⊥FE,交直线AB于点G,若∠1=42°,则∠2的大小是()A.56°B.48°C.46°D.40°【解答】解:∵AB∥CD,∴∠3=∠1=42°,∵FG⊥FE,∴∠GFE=90°,∴∠2=180°﹣90°﹣42°=48°.故选:B.8.(3分)把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在MN的位置上,若∠EFG=55°,则∠2=()A.105 B.110 C.95 D.120【解答】解:由折叠的性质可知ME∥NF,∴∠BGM=∠GFN.∵2∠EFG+∠GFN=180°,且∠EFG=55°,∴∠BGM=∠GFN=180°﹣2×55°=70°,又∵∠2+∠BGM=180°,∴∠2=110°.故选:B.二.填空题9.(3分)的算术平方根是3.【解答】解:∵=9,又∵(±3)2=9,∴9的平方根是±3,∴9的算术平方根是3.即的算术平方根是3.故答案为:3.10.(3分)如果∠A与∠B的两边分别平行,且∠A比∠B的3倍少36°,则∠A 的度数是18°或126°.【解答】解:∵∠A与∠B的两边分别平行,∴∠A与∠B相等或互补.分两种情况:①当∠A+∠B=180°时,∠A=3∠B﹣36°,解得:∠A=126°;②当∠A=∠B,∠A=3∠B﹣36°,解得:∠A=18°.所以∠A=18°或126°.故答案为18°或126°.11.(3分)若+|b+1|+(c+1)2=0,则a+b﹣c=2.【解答】解:根据题意得,a﹣2=0,b+1=0,c+1=0,解得a=2,b=﹣1,c=﹣1,所以,a+b﹣c=2﹣1﹣(﹣1)=2﹣1+1=2.故答案为:2.12.(3分)已知点A(3a+5,a﹣3)在二、四象限的角平分线上,则a=﹣.【解答】解:∵点A(3a+5,a﹣3)在二、四象限的角平分线上,∴3a+5+a﹣3=0,∴a=﹣.故答案为:﹣.13.(3分)已知点M在y轴上,纵坐标为5,点P(3,﹣2),则△OMP的面积是7.5.【解答】解:如图所示:由题意可得,MO=5,△OMP的面积是:×5×3=7.5.故答案为:7.5.14.(3分)一个正数x的平方根分别是2a﹣3与5﹣a,x等于49.【解答】解:∵正数x的平方根分别是2a﹣3与5﹣a,∴2a﹣3+5﹣a=0,解得a=﹣2,∴5﹣a=5﹣(﹣2)=7,∴x=72=49.故答案为:49.15.(3分)如图,已知AB∥CD∥EF,则∠x、∠y、∠z三者之间的关系是x=180°+z ﹣y.【解答】解:∵CD∥EF,∴∠CEF=180°﹣y,∵AB∥EF,∴∠x=∠AEF=∠z+∠CEF,即x=180°+z﹣y.故答案为:x=180°+z﹣y.三.解答题16.(8分)计算:(1)||+|﹣1|﹣|3|(2)﹣++.【解答】解:(1)原式=﹣+﹣1﹣3+=2﹣4;(2)原式=﹣(﹣2)+5+2=2+5+2=9.17.(8分)求下列各式中的x.(1)4x2﹣16=0(2)27(x﹣3)3=﹣64.【解答】解(1)4x2=16,x2=4x=±2;(2)(x﹣3)3=﹣,x﹣3=﹣x=.18.(8分)已知2a﹣1的平方根是±3,3a+b﹣1的算术平方根是4,求12a+2b 的立方根.【解答】解:∵2a﹣1的平方根是±3,∴2a﹣1=(±3)2,解得a=5;∵3a+b﹣1的算术平方根是4,∴3a+b﹣1=16,把a=5代入得,3×5+b﹣1=16,解得b=2,∴12a+2b=12×5+4=64,∴=4,即12a+2b的立方根是4.19.(8分)如图,在△ABC中,三个顶点的坐标分别为A(﹣5,0),B(4,0),C(2,5),将△ABC沿x轴正方向平移2个单位长度,再沿y轴沿负方向平移1个单位长度得到△EFG.(1)求△EFG的三个顶点坐标.(2)求△EFG的面积.【解答】解:(1)如下图:E(﹣3,﹣1)、F(6,﹣1)、G(4,4);(2)如上图,过C作CH⊥AB.∵△EFG是由△ABC沿x轴正方向平移2个单位长度,再沿y轴沿负方向平移1个单位长度得到的.∴△EFG≌△ABC,∴S=S△ABC,△EFG∵AB=|4﹣(﹣5)|=9,CH=|5﹣0|=5,∴S=AB•CH△ABC=×9×5即S=S△ABC=.△EFG20.(10分)如图,已知AB∥CD,EF与AB、CD分别相交于点E、F,∠BEF与∠EFD的平分线相交于点P,求证:EP⊥FP.【解答】证明:∵AB∥CD,∴∠BEF+∠EFD=180°,又EP、FP分别是∠BEF、∠EFD的平分线,∴∠PEF=∠BEF,∠EFP=∠EFD,∴∠PEF+∠EFP=(∠BEF+∠EFD)=90°,∴∠P=180°﹣(∠PEF+∠EFP)=180°﹣90°=90°,即EP⊥FP.21.(10分)如图,∠1+∠2=180°,∠DAE=∠BCF,DA平分∠BDF.(1)AE与FC会平行吗?说明理由.(2)AD与BC的位置关系如何?为什么?(3)BC平分∠DBE吗?为什么?【解答】解:(1)平行;证明:∵∠2+∠CDB=180°,∠1+∠2=180°,∴∠CDB=∠1,(2)平行,证明:∵AE∥FC,∴∠CDA+∠DAE=180°,∵∠DAE=∠BCF∴∠CDA+∠BCF=180°,∴AD∥BC.(3)平分,证明:∵AE∥FC,∴∠EBC=∠BCF,∵AD∥BC,∴∠BCF=∠FDA,∠DBC=∠BDA,又∵DA平分∠BDF,即∠FDA=∠BDA,∴∠EBC=∠DBC,∴BC平分∠DBE.22.(10分)如图,已知AD⊥BC,FG⊥BC,垂足分别为D、G.且∠1=∠2,猜想:∠BDE与∠C有怎样的关系?说明理由.【解答】解:∠BDE=∠C.理由如下:∵AD⊥BC,FG⊥BC,∴AD∥FG,∴∠1=∠3,∴∠2=∠3,∴DE∥AC,∴∠BDE=∠C.23.(13分)如图所示,已知AB∥CD,分别探究下面图形中∠APC,∠PAB,∠PCD的关系,请你从四个图形中任选一个,说明你所探究的结论的正确性.①结论:(1)∠APC+∠PAB+∠PCD=360°(2)∠APC=∠PAB+∠PCD(3)∠PCD=∠APC+∠PAB(4)∠PAB=∠APC+∠PCD②选择结论(1),说明理由.【解答】解:①(1)过点P作PE∥AB,则AB∥PE∥CD,∴∠1+∠PAB=180°,∠2+∠PCD=180°,∴∠APC+∠PAB+∠PCD=360°;(2)过点P作直线l∥AB,∵AB∥CD,∴AB∥PE∥CD,∴∠PAB=∠3,∠PCD=∠4,∴∠APC=∠PAB+∠PCD;(3)∵AB∥CD,∴∠PEB=∠PCD,∵∠PEB是△APE的外角,∴∠PEB=∠PAB+∠APC,∴∠PCD=∠APC+∠PAB;(4)∵AB∥CD,∴∠PAB=∠PFD,∵∠PFD是△CPF的外角,∴∠PCD+∠APC=∠PFD,∴∠PAB=∠APC+∠PCD.②选择结论(1),证明同上.赠送:初中数学几何模型举例【模型四】几何最值模型:图形特征:BAPl运用举例:1. △ABC中,AB=6,AC=8,BC=10,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为AP的中点,则MF的最小值为EM FB2.如图,在边长为6的菱形ABCD中,∠BAD=60°,E为AB的中点,F为AC上一动点,则EF+BF的最小值为_________。
河南省安阳市滑县2015-2016学年七年级(下)期中地理试卷(解析版)

最大最全最精的教育资源网2015-2016 学年河南省安阳市滑县七年级(下)期中地理试卷一、单项选择题(每题 2 分,共 50 分.)1.亚洲散布最广的天气种类是()A .温带季民风候B .亚热带季民风候C.热带季民风候 D .温带大陆性天气2.亚洲的主要地形是()A .高原、山地B.平原、丘陵C.高原、盆地D.平原、山地3.不属于穿过白令海峡“三线”的是()A .俄罗斯与美国的分解线B .国际日期更改线C.亚洲与北美洲的分界限 D .亚洲与加拿大的分界限4.“北京时间”是采纳北京所在的()A .东 6 区的区时B .东 7 区的区时C .东 8 区的区时D .东 9 区的区时5.以下哪一个大洲没有热带()A .亚洲B .北美洲C.南美洲D.欧洲6.苏伊士运河交流了()A .地中海和大西洋B .地中海和黑海C.大西洋和太平洋 D .地中海和红海7.世界上国家个数最多的大洲是()A .非洲B .亚洲C .欧洲D .大洋洲8.世界各大洲中,均匀人口自然增加率最高的洲是()A .亚洲B .非洲C .大洋洲D .南美洲9.湄公河号称“亚洲的多瑙河”,此称呼主要针对湄公河的什么特色而言()A .是亚洲流量最丰富的河流 B .是亚洲最长的河流C.是亚洲流经国家最多的河流 D .是亚洲航运最发达的河流10.世界上最润湿的大洲是()A .欧洲B .南美洲C.亚洲 D .北美洲11.东非大裂谷的成因是()A .板块碰撞B .板块张裂C .外力侵害D .人工开凿12.世界上最湿热的大洲是()A .亚洲B .非洲C .南美洲D .欧洲13.玉米的原产地是()A .中国B .美国C .墨西哥D .巴西14.连结太平洋和印度洋的近来通道是()A .苏伊士运河B.霍尔木兹海峡 C .马六甲海峡D.台湾海峡15.马来群岛的主要天气种类是()A .热带雨林天气B .热带季民风候C.亚热带季民风候 D .热带草原天气16.东南亚独一的内地国是()A .缅甸B .老挝C .越南D .柬埔寨17.中南半岛的地形特色是()A .河山相间,纵列散布B.地形曲折,火山众多最大最全最精的教育资源网C.南高北低,以平原为主 D .西高东低,以高原为主18.世界上最长的山脉是()A .喜马拉雅山B.落基山C.安第斯山 D .阿尔卑斯山19.世界最大的平原是()A .密西西比河平原B .亚马孙平原C.东欧平原 D .西西伯利亚平原20.以下国家不属于西亚地域的是()A .沙特阿拉伯B.巴基斯坦 C .阿富汗D.伊拉克21.西亚农业发展的主要限制要素是()A .高温B .干旱C .劳动力不足D.生产技术落伍22.西亚的很多矛盾、战争因抢夺资源而起,以下哪两种资源常常惹起“西亚形势不稳(”)A .铁矿、煤矿B.铜矿、天然气 C .土地、金矿D.石油、淡水23.法国、德国的国都分别是()A .伦敦、柏林B.伦敦、巴黎C.巴黎、柏林D.巴黎、伦敦24.欧洲西部以风车和郁金香而有名于世的是()A .英国B .芬兰C .荷兰D .波兰25.挪威沿海幽静波折的峡湾和芬兰不计其数的湖泊的形成原由主假如()A .流水作用B .风力作用C .冰川作用D .海浪作用二、填空题.(每空 1 分,共 20 分.)26.世界上边积最大的洲是,亚洲和欧洲的大陆部分连为一体,全称大陆.27.国际上规定大概以度经线作为国际日期更改线,向东超出这条线,日期要(加、减)一天.28.位于非洲北部的荒漠,是世界面积最大的荒漠.29.习惯上,人们把作为区分北美洲与南美洲的分界限.30.北美洲地形:三大南北纵列带:西部高大山系;中部广阔的;东部低缓的高原山地.31.南美洲的天气种类以天气和天气为主.32.“世界人种大熔炉”是洲.33.东南亚主要的粮食作物是.34.世界上国外华人散布最集中的地域是.35.南亚经济发展最快的国家是.36.伊斯兰教、基督教、犹太教都把看作圣城.37.西亚的石油主要输往西欧以及、等国家.38.从经济发展水平看,欧洲西部的国家大多半属于国家.三、综合题.(每空 1 分,共 30 分.)39.读非洲天气种类图,达成以下问题.(1)填出图中序号表示的天气种类:①天气;②天气;③天气;④天气.(2 )非洲因为(纬线)横穿中部,所以非洲天气拥有散布特色.(3 )非洲天气种类中散布面积最广的有天气和天气.最大最全最精的教育资源网(4)刚果盆地位于天气区(填序号).(5)在赤道邻近的乞力马扎罗山,山顶终年覆盖着厚厚的积雪,原由是.40.读南亚地形图,回答以下问题.(1)图中序号所代表的地形区为:①平原;②平原;③河;④山脉;⑤高原.(2)图中⑥代表岛.(3)此中④山脉有世界最高的山岳为.(4)从图中可看出南亚的地形可分为三大地形区,北部为,中部为,南部为.41.读西亚地域图,回答以下问题:(1)图中交流①海和②海的是⑤海峡.(2 )将海湾③湾四周的石油运往美国,走最短线路,先后经过霍尔木兹海峡﹣阿拉伯海﹣红海﹣④运河﹣地中海﹣直布罗陀海峡﹣大西洋﹣美国.(3 )有名产油国⑥ 是.(4 )⑦ 国所在的半岛是半岛,它是世界上最大的半岛.(5)图中⑧是海,它是世界上最大的湖泊.(6 )西亚地处“五海三洲之地”,此中的三洲是指亚洲、洲和非洲.(7)西亚在发展节水农业方面获得明显成绩的国家是.2015-2016 学年河南省安阳市滑县七年级(下)期中地理试卷参照答案与试题分析一、单项选择题(每题 2 分,共 50 分.)1.亚洲散布最广的天气种类是()A .温带季民风候B .亚热带季民风候C.热带季民风候 D .温带大陆性天气【考点】亚洲的天气.【剖析】亚洲面积广大,地跨寒、温、热三带,且地形复杂多样,除温带大海性天气外,世界上的各样天气在亚洲都有散布.【解答】解:亚洲各地距海远近不一样,加上气流和地形等要素的影响,干湿差别悬殊.这里有降水丰沛的世界“雨极”,也有终年滴水不下的干旱地带.整体上看,亚洲天气的大陆性特色明显,温带大陆性天气散布最为宽泛.应选: D.2.亚洲的主要地形是()A .高原、山地B.平原、丘陵C.高原、盆地D.平原、山地【考点】亚洲的地形、地势及其影响.【剖析】亚洲地面起伏很大,中部高,四周低,地形以高原、山地为主,亚洲是世界上除南极洲外均匀海拔高度最高的大洲.【解答】解:亚洲地面起伏很大,中部高,四周低,地形以高原、山地为主.应选: A.3.不属于穿过白令海峡“三线”的是()A .俄罗斯与美国的分解线B .国际日期更改线C.亚洲与北美洲的分界限 D .亚洲与加拿大的分界限【考点】洲界限.【剖析】白令海峡是亚洲与北美洲的洲界限、俄罗斯与美国的国界限和日界限.【解答】解:白令海峡是北冰洋与太平洋之间的独一通道,水道中央有亚洲与北美洲的洲界限、俄罗斯与美国的国界限、国际日起更改线三线穿过.应选: D.4.“北京时间”是采纳北京所在的()A .东 6 区的区时B .东 7 区的区时C .东 8 区的区时D .东 9 区的区时【考点】我国的地理地点及特色.【剖析】世界时区的区分以本初子午线为标准.从西经7°30'到东经 7°30'(经度间隔为15°)为零地域.由零时区的两个界限分别向东和向西,每隔经度15°划一个时区,东、西各划出12 个时区,东十二时区与西十二时区相重合;全世界共区分红24 个时区.【解答】解:我国幅员辽阔,从西到东横跨东五、东六、东七、东八和东九五个时区.中华人民共和国建立此后,全国一致采纳国都北京所在的东八时区的区时作为标准时间,称为北京时间.依照题意.应选: C.5.以下哪一个大洲没有热带()A .亚洲B .北美洲C.南美洲D.欧洲【考点】七大洲的地理散布和概略.【剖析】世界七大洲中,亚洲、南美洲、非洲、大洋洲、北美洲都有热带天气散布,都有阳光直射现象,欧洲和南极洲没有热带即没有阳光直射现象.【解答】解:世界七大洲中,亚洲、南美洲、非洲、大洋洲、北美洲都有热带天气散布,欧洲和南极洲没有热带散布.应选项 D 切合题意.应选: D.6.苏伊士运河交流了()A .地中海和大西洋B .地中海和黑海C.大西洋和太平洋 D .地中海和红海【考点】洲界限.【剖析】地球上的陆地被大海切割成六个大块和很多小块,面积较大的陆地叫大陆,面积较小的陆地叫岛屿,大陆和它邻近的岛屿合称大洲.全世界共有七大洲,按面积由大到小摆列分别为:亚洲、非洲、北美洲、南美洲、南极洲、欧洲和大洋洲.七大洲之间有的相连,有的被运河或海峡切割.【解答】解:苏伊士运河是亚洲与非洲的分界限,交流了红海和地中海两个海疆.依照题意.应选: D.7.世界上国家个数最多的大洲是()A .非洲B .亚洲C .欧洲D .大洋洲【考点】七大洲的地理散布和概略.【剖析】各大洲国家和地域的数量是:亚洲49 个;非洲54 个;南美洲12 个;北美州23 个;大洋洲 14 个;欧洲 43 个.能够看出,在世界七大洲中,国家和地域的数量最多的是非洲.【解答】解:在世界七大洲中,国家和地域的数量最多的是非洲.应选: A.8.世界各大洲中,均匀人口自然增加率最高的洲是()A .亚洲B .非洲C .大洋洲D .南美洲【考点】七大洲的地理散布和概略.【剖析】非洲是世界上人口自然增加率最高的大洲.【解答】解:非洲是世界上人口自然增加率最高的大洲.应选: B.9.湄公河号称“亚洲的多瑙河”,此称呼主要针对湄公河的什么特色而言()A .是亚洲流量最丰富的河流B .是亚洲最长的河流C.是亚洲流经国家最多的河流 D .是亚洲航运最发达的河流【考点】亚洲的河湖.【剖析】亚洲河网散布主要有两大特色:一是大河多起源于中部的高原山地,顺地势呈放射状向四周奔腾入海;二是内流区面积广大.亚洲中部的锡尔河和阿姆河注入咸海,是世界上两条有名的内流河.【解答】解:亚洲的大江大河好多.长江的长度和流量都居亚洲首位,世界第三.湄公河在我国境内称澜沧江,是亚洲流经国家最多的一条国际河流,被称为“”亚洲的多瑙河.应选: C.10.世界上最润湿的大洲是()A .欧洲B .南美洲C.亚洲 D .北美洲【考点】七大洲的地理散布和概略.【剖析】地球上的陆地被大海切割成六个大块和很多小块,面积较大的陆地叫大陆,面积较小的陆地叫岛屿,大陆和它邻近的岛屿合称大洲.全世界共有七大洲,按面积由大到小摆列分别为:亚洲、非洲、北美洲、南美洲、南极洲、欧洲和大洋洲.【解答】解:南美洲天气种类以热带雨林天气和热带稀树草原天气为主,降水丰沛,大多半地域的年降水量在1000 毫米以上,是世界上最润湿的大洲.依照题意.应选: B.11.东非大裂谷的成因是()A .板块碰撞B .板块张裂C .外力侵害D .人工开凿【考点】非洲的主要岛屿、山脉、裂谷、河流.【剖析】板块运动学说以为,有岩石构成的地球表层其实不是一块整体,而是由六大板块拼合而成,板块之间有的碰撞挤压,有的张裂拉伸.【解答】解:地球上分为六大板块,它们之间有的碰撞挤压,有的张裂拉伸.板块张裂会形成裂谷或新的大海,板块互相挤压碰撞则会形成高大的山脉.非洲板块与印度洋板块张裂拉伸形成东非裂谷带.应选: B.12.世界上最湿热的大洲是()A .亚洲B .非洲C .南美洲D .欧洲【考点】七大洲的地理散布和概略.【剖析】地球上的陆地被大海切割成六个大块和很多小块,面积较大的陆地叫大陆,面积较小的陆地叫岛屿,大陆和它邻近的岛屿合称大洲.全世界共有七大洲,按面积由大到小摆列分别为:亚洲、非洲、北美洲、南美洲、南极洲、欧洲和大洋洲.【解答】解:世界上最湿热的大洲是南美洲,该洲天气种类以热带雨林天气和热带稀树草原天气为主.依照题意.应选: C.13.玉米的原产地是()A .中国B .美国C .墨西哥D .巴西【考点】世界上的国家和地域概略.【剖析】北美洲的墨西哥是玉米的原产地,玉米是该国主要的粮食作物.【解答】解:玉米的原产地是墨西哥.应选: C.14.连结太平洋和印度洋的近来通道是()A .苏伊士运河B.霍尔木兹海峡 C .马六甲海峡D.台湾海峡【考点】洲界限.【剖析】马六甲海峡位于马来半岛和苏门答腊岛之间,是交流太平洋与印度洋的天然水道,也是连结欧洲、印度洋沿岸港口与太平洋西岸港口的重要航道.【解答】解:连结太平洋和印度洋的近来通道是马六甲海峡,选项ABD 不切合题意.应选: C.15.马来群岛的主要天气种类是()A .热带雨林天气B .热带季民风候C.亚热带季民风候 D .热带草原天气【考点】世界主要天气种类及其散布概略.【剖析】依据东南亚的天气种类散布及特色解答.【解答】解:东南亚位于亚洲的东南部,包含中南半岛和马来群岛两大多半.马来群岛终年酷热多雨,属于热带雨林天气.应选: A.16.东南亚独一的内地国是()A .缅甸B .老挝C .越南D .柬埔寨【考点】东南亚主要国家和国都.【剖析】东南亚位于亚洲的东南部,包含中南半岛和马来群岛的大多半.东南亚处在亚洲与大洋洲、印度洋与太平洋的“”十字路口,是世界大海运输和航空运输的重要枢纽.【解答】解:东南亚主要的国家有越南、老挝、缅甸、泰国、新加坡、马来西亚、印度尼西亚等,此中该区独一的内地国是老挝.应选: B.17.中南半岛的地形特色是()A .河山相间,纵列散布B.地形曲折,火山众多C.南高北低,以平原为主 D .西高东低,以高原为主【考点】东南亚的自然地理特色.【剖析】东南亚位于亚洲的东南部,包含中南半岛和马来群岛的大多半.【解答】解:中南半岛因在中国以南而得名;中南半岛北部地势高峻,与我国山川相连,高山和大河由北向南延长,形成河山相间、纵列散布的地表形态;中南半岛河流的上游奔跑在崇山峻岭之中,储藏着丰富的水力资源.应选: A.18.世界上最长的山脉是()A .喜马拉雅山B.落基山C.安第斯山 D .阿尔卑斯山【考点】主要地形区.【剖析】世界上最长的山脉是南美洲的安第斯山脉,世界上最高大的山脉是亚洲的喜马拉雅山脉.【解答】解:世界上最长的山脉是南美洲的安第斯山脉,长达9000 多千米.应选: C.19.世界最大的平原是()A .密西西比河平原B .亚马孙平原C.东欧平原 D .西西伯利亚平原【考点】主要地形区.【剖析】世界上最大的平原是南美洲的亚马孙平原,主要属于热带雨林天气.【解答】解:世界上最大的平原是亚马孙平原,主要由亚马孙河冲积形成.应选: B.20.以下国家不属于西亚地域的是()A .沙特阿拉伯B.巴基斯坦 C .阿富汗D.伊拉克【考点】西亚的国家和城市.【剖析】西亚地处“三洲五海”之地,向来是东西方交通要道.【解答】解: A 、沙特阿拉伯属于西亚.故不切合题意.B、巴基斯坦位于南亚.故切合题意.C、阿富汗位于西亚.故不切合题意.D、伊拉克位于西亚.故不切合题意.应选: B.21.西亚农业发展的主要限制要素是()A .高温B .干旱C .劳动力不足D.生产技术落伍【考点】基础设备建设和生态环境保护的重要意义.【剖析】西亚和北非地处三洲、五海和两洋之地,自古以来就是东西方交通要道.地形以高原为主,天气酷热,降水较少,荒漠广布,发展农业主要靠浇灌;居民大多为阿拉伯人,信奉伊斯兰教.【解答】解:西亚主要天气是热带荒漠天气,天气干燥,降水稀罕,农业发展的主要限制因素干旱.应选项 B 切合题意.应选: B.22.西亚的很多矛盾、战争因抢夺资源而起,以下哪两种资源常常惹起“西亚形势不稳(”)A .铁矿、煤矿B.铜矿、天然气 C .土地、金矿D.石油、淡水【考点】西亚复杂的民族和宗教问题对政治的影响.【剖析】民族矛盾、宗教文化纠葛、国土纷争、对石油和水资源的抢夺,是西亚地域发生战争和矛盾的重要要素.崇奉犹太教的以色列和周边的阿拉伯国家的土地之争、宗教之争由来已久,并愈演愈烈,成为西亚问题的重点.【解答】解:西亚地域有丰富的石油资源,各国为抢夺石油资源而引起矛盾,致使各国之间为石油而战;西亚地域水资源缺少,有限的水资源散布不均匀,多国共用,各国为抢夺水权而产生矛盾,致使各国为淡水而战.应选: D.23.法国、德国的国都分别是()A .伦敦、柏林B.伦敦、巴黎C.巴黎、柏林D.巴黎、伦敦【考点】世界上的国家和地域概略.【剖析】熟记欧洲各国及其国都是解题重点.【解答】解:法国的国都是巴黎;德国的国都柏林.应选: C.24.欧洲西部以风车和郁金香而有名于世的是()A .英国B .芬兰C .荷兰D .波兰【考点】欧洲西部的文化景观、旅行胜地与旅行业.【剖析】欧洲西部的自然和人文旅行资源异样丰富.挪威陡峻幽静的峡湾、瑞士冰雪皑皑的山岳、西班牙阳光绚烂的海滩、法国风景如画的田园、风光旖旎;千年古都罗马、音乐之都维也纳、艺术之都巴黎,精深典雅;古老的城堡、威严的教堂、为数众多的博物馆,风格各异;西班牙的斗牛场、意大利的狂欢日以及慕尼黑的啤酒节.【解答】解:想赏析花卉与风车,应当去荷兰.应选: C.25.挪威沿海幽静波折的峡湾和芬兰不计其数的湖泊的形成原由主假如()A .流水作用B .风力作用C .冰川作用D .海浪作用【考点】欧洲冰川作用下的地形.【剖析】欧洲是世界上海岸线最波折的大洲,欧洲因为冰川作用形成的地貌有阿尔卑斯山脉挺秀的山峰、东欧平原上波状起伏的丘陵、挪威沿海幽静波折的峡湾等.【解答】解:挪威沿海幽静波折的峡湾和芬兰不计其数的湖泊的形成原由主假如冰川作用.应选: C.二、填空题.(每空 1 分,共20 分.)26.世界上边积最大的洲是亚洲,亚洲和欧洲的大陆部分连为一体,全称亚欧大陆.【考点】七大洲的地理散布和概略.【剖析】地球上的陆地被大海切割成六个大块和很多小块,面积较大的陆地叫大陆,面积较小的陆地叫岛屿,大陆和它邻近的岛屿合称大洲.全世界共有七大洲,按面积由大到小摆列分别为:亚洲、非洲、北美洲、南美洲、南极洲、欧洲和大洋洲.【解答】解:七大洲中,亚洲面积约4400 万千米2,是世界第一大洲.亚洲和欧洲的大陆部分连为一体,全称亚欧大陆,是世界上最大的大陆.依照题意.故答案为:亚洲;亚欧.27.国际上规定大概以180 度经线作为国际日期更改线,向东超出这条线,日期要减(加、减)一天.【考点】国际日期更改线与北京时间.【剖析】日界限,又称国际日期更改线,原则上以180°经线作为日界限,是地球上“今日”“”和昨天的分界限.【解答】解:日界限,又称国际日期更改线.大概上与经度180°相符合,凡从西向东超出该线,日期减一天;相反,从东向西超出该线,日期加一天.故答案为: 180;减.28.位于非洲北部的撒哈拉荒漠,是世界面积最大的荒漠.【考点】北非的主要海峡、荒漠和河流.【剖析】非洲位于亚洲的西南面、东半球的西南部,地跨赤道南北.东濒印度洋,西临大西洋,北隔地中海与欧洲相望,东北隅以狭长的红海与苏伊士运河紧邻亚洲.最大最全最精的教育资源网【解答】解:“撒哈拉”,阿拉伯语意为“大荒漠”.撒哈拉荒漠北起非洲北部的阿特拉斯山脉,南至苏丹草原带,宽1300~ 2200 千米;西自傲西洋边,东达红海沿岸,长4800 千米,面积达 770 多万平方千米,是世界上边积最大的荒漠.依照题意.故答案为:撒哈拉.29.习惯上,人们把巴拿马运河作为区分北美洲与南美洲的分界限.【考点】洲界限.【剖析】大洲之间常常以山脉、河流、湖泊、运河、海峡等地理事物为分界限.【解答】解:北美洲与南美洲的分界限是巴拿马运河,该运河交流了太平洋和大西洋.故答案为:巴拿马运河.30.北美洲地形:三大南北纵列带:西部高大山系;中部广阔的平原;东部低缓的高原山地.【考点】北美的主要地形区及散布特色.【剖析】美洲大陆是一块整体.人们在美洲大陆中部中美地峡的最狭小部位开凿了巴拿马运河,习惯上以它作为区分北美洲与南美洲的界限.北美洲位于西半球北部,面积2400 多万平方千米,在各大洲中列第 3 位.【解答】解:北美洲均匀海拔较高,地势起伏较大,地形分为三大南北纵列带:西部是高大的山系,中部是广阔的平原,东部是低缓的高地.故答案为:平原.31.南美洲的天气种类以热带雨林天气和热带草原天气为主.【考点】拉丁美洲的暖湿天气特色及独有的动植物.【剖析】南美洲热带范围广阔,温带面积不大,寒带缺失.天气种类以热带雨林天气和热带稀树草原天气散布最广.南美洲降水充足,大多半地域的年降水量在 1 000 毫米以上,是世界上最润湿的大洲.【解答】解:南美洲热带范围广阔,温带面积不大,寒带缺失.天气种类以热带雨林天气和热带草原天气散布最广.故答案为:热带雨林;热带草原.32.“世界人种大熔炉”是南美洲.【考点】拉丁美洲的居民与语种.【剖析】南美洲号称“世界人种大熔炉”.【解答】解:南美洲以前长久沦为殖民地,各样人种混居通婚,混血人最多,号称“世界人种大熔炉”.故答案为:南美.33.东南亚主要的粮食作物是水稻.【考点】东南亚的自然地理特色.【剖析】东南亚各国广泛栽种水稻,稻米是当地居民的主要粮食,也是传统的出口产品,泰国、越南、缅甸是世界上重要的稻米出口国.【解答】解:东南亚各国广泛栽种水稻,稻米是当地居民的主要粮食.故答案为:水稻.最大最全最精的教育资源网34.世界上国外华人散布最集中的地域是东南亚.【考点】东南亚华侨和华人在当地的重要影响.【剖析】东南亚是世界上人口浓密的地域之一.人口集中散布在大河两岸的冲积平原、河口三角洲以及沿海平原,而山区和岛屿的热带雨林地域则人口稀罕.【解答】解:东南亚是世界上国外华人散布最集中的地域,总人数在2000 万以上. 19 世纪后期到 20 世纪早期,我国东南沿海一带,特别是广东、福建两省,有大批人口“下南洋”谋生.他们中大多半人获得了所在国国籍,被称为华人.还有少量人保存了中国国籍,属于华侨.华人和华侨在东南亚各国人口中占较大比重.比如,新加坡占76%,马来西亚占 35%.故答案为:东南亚.35.南亚经济发展最快的国家是印度.【考点】南亚的半岛、地形区、河流、国家和国都.【剖析】南亚指位于亚洲南部喜马拉雅山脉中、西段与印度洋之间的广大地域.它东濒孟加拉湾,西滨阿拉伯海,总面积约430 万平方千米.南亚次大陆上有印度、巴基斯坦、孟加拉国、尼泊尔、不丹 5 个国家和克什米尔地域,印度洋中有斯里兰卡和马尔代夫两个岛国.【解答】解:南亚都是发展中国家.第二次世界大战后,工业发展较快,大多以纺织、食品等传统的轻工业为主.印度是南亚经济发展最快的一个国家.印度独立后,在本来利用煤、铁资源发展重工业的基础上,电子、汽车制造、原子能、航空航天等新兴工业渐渐兴起.近来几年来,印度的电脑软件家产在世界上据有重要的地位.依据题意.故答案为:印度.36.伊斯兰教、基督教、犹太教都把耶路撒冷看作圣城.【考点】西亚的民族和宗教.【剖析】西亚地处亚、非、欧三大洲的交界地带,位于阿拉伯海、红海、地中海、黑海和里海(内地湖)之间,联系亚洲、欧洲和非洲,所以被称为“五海三洲之地”.一般把阿拉伯人占多半的国家称为阿拉伯国家.西亚是世界上阿拉伯人的主要聚居地域之一.【解答】解:西亚是伊斯兰教的起源地,阿拉伯人广泛信仰伊斯兰教.沙特阿拉伯的古城麦加,是伊斯兰教首创人穆罕默德的出生地.作为伊斯兰教第一圣地,每年到麦加朝觐的穆斯林多达数百万.麦加大清真寺是世界上规模最大的清真寺.西亚也是基督教和犹太教的起源地.伊斯兰教、基督教和犹太教都把耶路撒冷奉为圣城.故答案为:耶路撒冷.37.西亚的石油主要输往西欧以及美国、日本等国家.【考点】西亚的石油生产及意义.【剖析】西亚的石油资源主要散布在波斯湾及其沿岸地域.沙特阿拉伯、伊朗、科威特和伊拉克是世界重要的产油国.【解答】解:西亚是世界上石油储量最为丰富、石油产量和输出量最多的地域.西亚石油的探明储量约占世界石油总探明储量的一半以上,石油产量往常占世界总产量的1/4.西亚各国所产石油的 90% 供出口,出口量占世界石油出口量的 3/5.西亚的石油主要输往西欧、美国和日本.故答案为:美国;日本.38.从经济发展水平看,欧洲西部的国家大多半属于发达国家.【考点】欧洲西部的主要港口、国家和国都.。
2015—2016学年度第二学期七年级数学期中考试试题
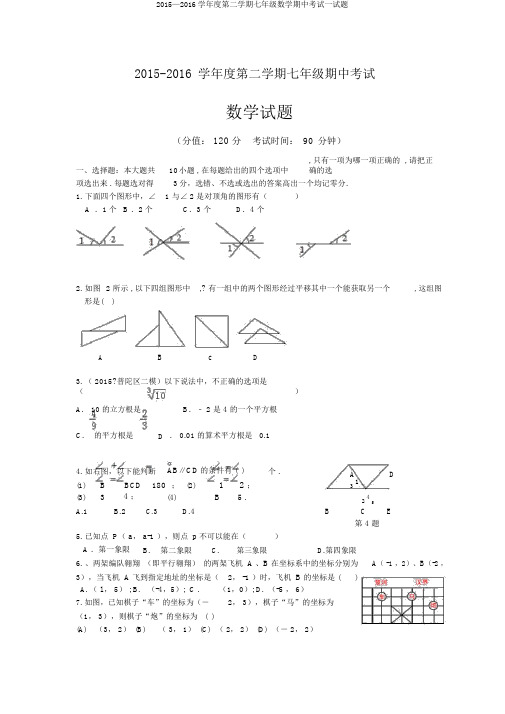
2015-2016 学年度第二学期七年级期中考试数学试题(分值: 120 分考试时间:90分钟)一、选择题:本大题共10小题 , 在每题给出的四个选项中, 只有一项为哪一项正确的 , 请把正确的选项选出来 . 每题选对得3分,选错、不选或选出的答案高出一个均记零分.1. 下面四个图形中,∠ 1 与∠ 2 是对顶角的图形有()A .1个B .2个C.3 个D.4 个2. 如图 2 所示 , 以下四组图形中形是( ),? 有一组中的两个图形经过平移其中一个能获取另一个, 这组图A B C D3. ( 2015?普陀区二模)以下说法中,不正确的选项是()A. 10 的立方根是B.﹣ 2 是 4 的一个平方根C.的平方根是D. 0.01 的算术平方根是 0.14. 如右图,以下能判断AB∥CD的条件有( )个 .A D(1)B BCD180; (2)1 2 ; 3 1(3)3 4 ;(4)B 5 .2 4 5A.1B.2C.3D.4B C E第 4 题5. 已知点 P( a, a-1 ),则点 p 不可以能在()A .第一象限 B.第二象限 C.第三象限 D.第四象限6. 、两架编队翱翔(即平行翱翔)的两架飞机A、B在坐标系中的坐标分别为A(-1,2)、B(-2,3),当飞机A飞到指定地址的坐标是(2, -1 )时,飞机B的坐标是 ()A. ( l , 5) ;B.(-4,5); C .(1,0); D. (-5 , 6)7. 如图,已知棋子“车”的坐标为(-2, 3),棋子“马”的坐标为(1, 3),则棋子“炮”的坐标为 ( )(A)(3, 2) (B)( 3, 1) (C)( 2, 2) (D)(- 2, 2)8. 若 x|2m﹣3| +(m﹣ 2) y=6 是关于 x、 y 的二元一次方程,则m的值是()A.1B.任何数C. 2D.1 或 2x4y)9、若方程组中的 x 是 y 的 2 倍,则 a 等于(2x y 2aA.- 9B. 8C.- 7D.- 610.如图,周长为 34cm的长方形 ABCD被分成7 个形状大小完好同样的小长方形,则长方形ABCD的面积为()22C 22A . 49cm B.68cm. 70cm D.74cmA DB C二、填空题:本大题共10 小题,共30 分,只要求填写最后结果,每题填对得 3 分.11。
2015-2016学年七年级下学期期中联考数学试题(含答案)

2015-2016学年七年级下数学期中测试题数 学 试 题(含答案)一、填空题(每题2分共24分)1. 在同一平面内,两条直线有 种位置关系,它们是 ;2.若直线a//b ,b//c ,则 ,其理由是 ;3.如图1直线AB ,CD ,EF 相交与点O ,图中AOE ∠的对顶角是 ,COF ∠的邻补角是 。
4.如图2,要把池中的水引到D 处,可过D 点引CD ⊥AB 于C ,然后沿CD 开渠,可使所开渠道最短,试说明设计的依据: ;5.点P (-2,3)关于X 轴对称点的坐标是 。
关于原点对称点的坐标是 。
6.把“对顶角相等”写成“如果……那么……”的形式为 。
7.如图4,170=∠,270=∠,388=∠,则4=∠_____________. 8 . 若点M (a+5,a-3)在y 轴上,则点M 的坐标为 。
9.若P (X ,Y )的坐标满足XY >0,且X+Y<0,则点P 在第 象限 。
0. 如图5,AB CD ∥,BC DE ∥,则∠B 与∠D 的关系是_____________.ABCD 图2A FC EB D图1OAB DC12 图3 图43142图4c ba5 4 32 1 图6 图511.若│x2-25│+3y -=0,则x=_______,y=_______.12.如图3,四边形ABCD 中,12∠∠与满足 关系时AB//CD ,当 时AD//BC(只要写出一个你认为成立的条件)。
二、 选择题 (下列各小题的四个选项中,有且只有一个是符合题意的,把你认为符合题意的答案代号填入答题表中,每小题2分,共12分) 题 号 1 2 3 4 56 答 案1.下列各图中,∠1与∠2是对顶角的是:( )2.一个三角形的三个内角中( )A. 至少有一个等于90°B. 至少有一个大于90°C. 不可能有两个大于89°D. 不可能都小于60°3.如图7,一条公路修到湖边时,需拐弯绕湖而过,如果第一次拐 的角∠A 是120°,第二次拐的角 ∠B 是150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C 是( ) A、150°B、140°C、130° D、120°4.在直角坐标系中,点P (-2,3)向右平移3个单位长度后的坐标为( ) A .(3,6) B.(1,3) C.(1,6) D.(3,3) 5. 如图6 下列条件中,不能判断直线a//b 的是( )A 、∠1=∠3B 、∠2=∠3C 、∠4=∠5D 、∠2+∠4=180° 6.在实数范围内,下列判断正确的是 ( ) (A) .若m=n,则n m = (B) .若22b a >, 则b a >(C) .若2a =2)(b ,则b a = (D) .若3a =3b ,则b a =7.16的平方根是( )(A )2 (B )4 (C )- 2或2 (D )- 4或48. 若a 是(-3)2的平方根,则3a 等于( ) (A )-3 (B )33 (C )33或-33 (D )3或-3三.作图题。
河南省安阳市滑县大寨一中七年级数学下学期第一次月考试卷(含解析) 新人教版

2015-2016学年河南省安阳市滑县大寨一中七年级(下)第一次月考数学试卷一、选择题(共10小题,每小题3分,满分30分)1.下列命题中,是真命题的是()A.同位角相等B.邻补角一定互补C.相等的角是对顶角D.有且只有一条直线与已知直线垂直2.在同一平面内,不重合的两条直线的位置关系是()A.平行 B.相交C.平行或相交D.平行、相交或垂直3.下列各图中,∠1与∠2是对顶角的是()A.B. C.D.4.已知,∠1与∠2互为邻补角,∠1=140°,则∠2的余角的度数为()A.30° B.40° C.50° D.100°5.平面内四条直线最少有a个交点,最多有b个交点,则a+b=()A.6 B.4 C.2 D.06.下列说法正确的是()A.1的平方根是1B.6是36的算术平方根C.同一平面内的三条直线满足a⊥b,b⊥c,则a⊥cD.两直线被第三条直线所截,内错角相等7.已知,如图,三角形ABC中,∠BAC=90°,AD⊥BC于D,则图中相等的锐角的对数有()A.4对B.3对C.2对D.1对8.如图,点E在BC的延长线上,则下列条件中,不能判定AB∥CD的是()A.∠3=50°,∠4=50°B.∠B=40°,∠DCB=140°C.∠1=60°,∠2=60°D.∠D+∠DAB=180°9.如图,AB∥EF,BC∥DE,∠B=70°,则∠E的度数为()A.90° B.110°C.130°D.160°10.如图,AB∥CD∥EF,∠ABE=38°,∠ECD=110°,则∠BEC的度数为()A.42° B.32° C.62° D.38°二、填空题(共8小题,每小题4分,满分32分)11.36的平方根是;的算术平方根是.12.用“<”或“>”填空: +1 4.13.点到直线的距离是指这点到这条直线的.14.把命题“等角的补角相等”改写成“如果…那么…”的形式是.15.一个正数的平方根为2﹣m与3m﹣8,则m的值为.16.在同一平面内如图,EG∥BC,CD交EG于点F,那么图中与∠1相等的角共有个.17.如图,已知:∠1=∠2,∠3=108°,则∠4的度数为.18.如果两条平行线被第三条直线所截,那么同位角的平分线的位置关系是.三、解答题(共5小题,满分58分)19.如图,∠AOB内一点P:(1)过点P画PC∥OB交OA于点C,画PD∥OA交OB于点D;(2)写出两个图中与∠O互补的角;(3)写出两个图中与∠O相等的角.20.求下列各式中的x的值:(1)x2﹣81=0(2)36x2﹣49=0.21.如图,已知∠A=∠F,∠C=∠D,可以证明BD∥CE.在下列括号中填写推理理由证明:∵∠A=∠F∴AC∥DF()∴∠C+∠=180°()∵∠C=∠D∴∠D+∠DEC=180°()∴BD∥CE ().22.小明打算用一块面积为900cm2的正方形木板,沿着边的方向裁出一个长方形面积为588cm2桌面,并且的长宽之比为4:3,你认为能做到吗?如果能,计算出桌面的长和宽;如果不能,请说明理由.23.如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数.2015-2016学年河南省安阳市滑县大寨一中七年级(下)第一次月考数学试卷参考答案与试题解析一、选择题(共10小题,每小题3分,满分30分)1.下列命题中,是真命题的是()A.同位角相等B.邻补角一定互补C.相等的角是对顶角D.有且只有一条直线与已知直线垂直【考点】命题与定理.【分析】分析是否为真命题,需要分别分析各题设是否能推出结论,从而利用排除法得出答案.【解答】解:A、两直线平行,同位角相等,故此选项错误;B、根据邻补角的定义,故此选项正确;C、相等的角不一定是对顶角,故此选项错误;D、过直线外一点,有且只有一条直线与已知直线垂直,故此选项错误.故选:B.【点评】此题主要考查了命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.2.在同一平面内,不重合的两条直线的位置关系是()A.平行 B.相交C.平行或相交D.平行、相交或垂直【考点】平行线.【专题】常规题型.【分析】根据直线的位置关系解答.【解答】解:在同一平面内,不重合的两条直线只有两种位置关系,是平行或相交,所以在同一平面内,不重合的两条直线的位置关系是:平行或相交.故选C.【点评】本题考查了两直线的位置关系,需要特别注意,垂直是相交特殊形式,在同一平面内,不重合的两条直线只有平行或相交两种位置关系.3.下列各图中,∠1与∠2是对顶角的是()A.B. C.D.【考点】对顶角、邻补角.【分析】根据对顶角的定义对各选项分析判断后利用排除法求解.【解答】解:A、∠1与∠2不是对顶角,故A选项错误;B、∠1与∠2是对顶角,故B选项正确;C、∠1与∠2不是对顶角,故C选项错误;D、∠1与∠2不是对顶角,故D选项错误.故选:B.【点评】本题主要考查了对顶角的定义,熟记对顶角的图形是解题的关键.4.已知,∠1与∠2互为邻补角,∠1=140°,则∠2的余角的度数为()A.30° B.40° C.50° D.100°【考点】对顶角、邻补角.【分析】根据互为邻补角的两个角的和等于180°求出∠2,再根据互为余角的两个角的和等于90°列式计算即可得解.【解答】解:∵∠1与∠2互为邻补角,∠1=140°,∴∠2=180°﹣∠1=180°﹣140°=40°,∴∠2的余角的度数为90°﹣40°=50°.故选C.【点评】本题考查了邻补角和余角的定义,是基础题,熟记概念是解题的关键.5.平面内四条直线最少有a个交点,最多有b个交点,则a+b=()A.6 B.4 C.2 D.0【考点】直线、射线、线段.【专题】计算题.【分析】当所有直线两两平行时交点个数最少;交点最多时根据交点个数公式代入计算即可求解;依此得到a、b的值,再相加即可求解.【解答】解:交点个数最多时, ==6,最少有0个.所以b=6,a=0,所以 a+b=6.故选:A.【点评】本题考查了相交线的交点问题,熟记公式是解题的关键.6.下列说法正确的是()A.1的平方根是1B.6是36的算术平方根C.同一平面内的三条直线满足a⊥b,b⊥c,则a⊥cD.两直线被第三条直线所截,内错角相等【考点】算术平方根;平方根;垂线;同位角、内错角、同旁内角.【分析】根据平方根的概念、平行公理和平行线的性质判断即可.【解答】解:1的平方根是±1,A错误;6是36的算术平方根,B正确;同一平面内的三条直线满足a⊥b,b⊥c,则a∥c,C错误;两直线被第三条直线所截,内错角不一定相等,D错误,故选:B.【点评】本题考查的是平方根、算术平方根的概念、垂直的定义,正确理解相关的概念和性质是解题的关键.7.已知,如图,三角形ABC中,∠BAC=90°,AD⊥BC于D,则图中相等的锐角的对数有()A.4对B.3对C.2对D.1对【考点】直角三角形的性质.【分析】根据直角三角形两锐角互余和同角的余角相等写出相等的角即可.【解答】解:相等的锐角有:∠B=∠CAD,∠C=∠BAD共2对.故选C.【点评】本题考查了直角三角形两锐角互余的性质,熟记性质并准确识图是解题的关键.8.如图,点E在BC的延长线上,则下列条件中,不能判定AB∥CD的是()A.∠3=50°,∠4=50°B.∠B=40°,∠DCB=140°C.∠1=60°,∠2=60°D.∠D+∠DAB=180°【考点】平行线的判定.【分析】直接利用平行线的判定定理判定,即可求得答案,注意排除法在解选择题中的应用.【解答】解:A、∵∠3=50°,∠4=50°,∴∠3=∠4,∴AD∥BC,故错误;B、∵∠B=40°,∠DCB=140°,∴∠B+∠DCB=180°,∴AB∥CD,正确;C、∵∠1=60°,∠2=60°,∴∠1=∠2,∴AB∥CD,正确;D、∵∠D+∠DAB=180°,∴AB∥CD,正确.故选A.【点评】此题考查了平行线的判定.此题比较简单,注意掌握数形结合思想的应用.9.如图,AB∥EF,BC∥DE,∠B=70°,则∠E的度数为()A.90° B.110°C.130°D.160°【考点】平行线的性质.【专题】计算题.【分析】首先根据BC∥DE,依据两直线平行,同位角相等求得∠1的度数,然后根据AB∥EF,依据两直线平行,同旁内角互补即可求解.【解答】解:∵BC∥DE,∴∠1=∠B=70°,∵AB∥EF,∴∠E+∠1=180°,∴∠E=180°﹣∠1=180°﹣70°=110°.故选B.【点评】本题利用了平行线的性质:两直线平行,同位角相等;两直线平行,同旁内角互补.10.如图,AB∥CD∥EF,∠ABE=38°,∠ECD=110°,则∠BEC的度数为()A.42° B.32° C.62° D.38°【考点】平行线的性质.【分析】由AB∥CD∥EF,∠ABE=38°,∠ECD=110°,根据平行线的性质,即可求得∠BEF与∠CEF 的度数,继而求得答案.【解答】解:∵AB∥CD∥EF,∠ABE=38°,∠ECD=110°,∴∠BEF=∠ABE=38°,∠CEF=180°﹣∠ECD=70°,∴∠BEC=∠CEF﹣∠BEF=32°.故选B.【点评】此题考查了平行线的性质.此题难度不大,注意掌握数形结合思想的应用.二、填空题(共8小题,每小题4分,满分32分)11.36的平方根是±6 ;的算术平方根是.【考点】算术平方根;平方根.【分析】根据平方根的定义和算术平方根的定义进行计算即可得解.【解答】解:∵(±6)2=36,∴36的平方根是±6;∵()2=,∴的平方根是.故答案为:±6;.【点评】本题考查了算术平方根、平方根的定义,是基础题,熟记概念是解题的关键.12.用“<”或“>”填空: +1 >4.【考点】实数大小比较.【分析】首先估算出的取值范围,再进一步确定+1的范围,进一步得出结论解决问题.【解答】解:∵3<<4,∴4<+1<5,所以+1>4.故答案为:>.【点评】此题考查实数的大小比较,估算的取值范围是解决问题的关键.13.点到直线的距离是指这点到这条直线的垂线段的长度.【考点】点到直线的距离.【分析】根据点到直线的距离的定义解答.【解答】解:点到直线的距离是指这点到这条直线的:垂线段的长度.故答案为:垂线段的长度.【点评】本题考查了点到直线的距离的定义,是基础题,熟记概念是解题的关键.14.把命题“等角的补角相等”改写成“如果…那么…”的形式是如果两个角是等角的补角,那么它们相等.【考点】命题与定理.【分析】命题中的条件是两个角相等,放在“如果”的后面,结论是这两个角的补角相等,应放在“那么”的后面.【解答】解:题设为:两个角是等角的补角,结论为:相等,故写成“如果…那么…”的形式是:如果两个角是等角的补角,那么它们相等.故答案为:如果两个角是等角的补角,那么它们相等.【点评】本题主要考查了将原命题写成条件与结论的形式,“如果”后面是命题的条件,“那么”后面是条件的结论,解决本题的关键是找到相应的条件和结论,比较简单.15.一个正数的平方根为2﹣m与3m﹣8,则m的值为 3 .【考点】平方根.【分析】根据一个正数的平方根有两个,它们互为相反数,根据互为相反数的两个数的和为0,可得答案.【解答】解:一个正数的平方根为2﹣m与3m﹣8,(2﹣m)+(3m﹣8)=0m=3,故答案为:3.【点评】本题考查了平方根,注意一个正数的两个平方根的和为0.16.在同一平面内如图,EG∥BC,CD交EG于点F,那么图中与∠1相等的角共有 2 个.【考点】平行线的性质.【分析】根据两直线平行,同位角相等,内错角相等找出与∠1相等的角即可.【解答】解:如图,∵EG∥BC,∴∠1=∠2,∠1=∠3,∴与∠1相等的角有2个角.故答案为:2.【点评】本题考查了平行线的性质,熟记性质并准确识图,找出∠1的同位角、内错角是解题的关键.17.如图,已知:∠1=∠2,∠3=108°,则∠4的度数为72°.【考点】平行线的判定与性质.【分析】根据“同位角相等,两直线平行”判定AB∥CD,然后由“两直线平行,同旁内角互补”得到∠3+∠4=180°,由此易求∠4的度数.【解答】解:如图,∵∠1=∠2,∴AB∥CD,∴∠3+∠4=180°.又∵∠3=108°,∴∠4=72°.故答案是:72°.【点评】此题考查了平行线的判定与性质.平行线的判定是由角的数量关系判断两直线的位置关系.平行线的性质是由平行关系来寻找角的数量关系.18.如果两条平行线被第三条直线所截,那么同位角的平分线的位置关系是平行.【考点】平行线的性质;同位角、内错角、同旁内角.【分析】根据两直线平行,同位角相等,即可得一组同位角相等即∠FEB=∠GFD,又由角平分线的性质求得∠1=∠2,然后根据同位角相等,两直线平行,即可求得答案.【解答】解:∵AB∥CD,∴∠FEB=∠GFD,∵EM与FN分别是∠FEM与∠GFD的平分线,∴∠1=∠FEB,∠2=∠GFD,∴∠1=∠2,∴EM∥FN.故答案为:平行.【点评】本题考查了平行线性质的应用,注意:平行线的性质有:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补.三、解答题(共5小题,满分58分)19.如图,∠AOB内一点P:(1)过点P画PC∥OB交OA于点C,画PD∥OA交OB于点D;(2)写出两个图中与∠O互补的角;(3)写出两个图中与∠O相等的角.【考点】作图—基本作图;余角和补角;平行线的性质.【分析】(1)根据平行线的画法画图即可;(2)根据平行线的性质:两直线平行,同旁内角互补可得答案;(3)根据平行线的性质:两直线平行,同位角相等可得答案.【解答】解:(1)如图所示:(2)与∠O互补的角有∠PDO,∠PCO;(3)与∠O相等的角有∠PDB,∠PCA.【点评】此题主要考查了平行线的画法,以及平行线的性质,关键是掌握平行线性质定理;定理1:两直线平行,同位角相等.定理2:两直线平行,同旁内角互补.定理3:两直线平行,内错角相等.20.求下列各式中的x的值:(1)x2﹣81=0(2)36x2﹣49=0.【考点】立方根.【分析】(1)根据移项,可得乘方的形式,根据开方,可得答案;(2)根据移项,等式的性质,可得乘方的形式,根据开方,可得答案.【解答】解:(1)x2=81,x=±9;(2)36x2=49,xx=±.【点评】本题考查了平方根,先化成乘方的形式,再开方运算.21.如图,已知∠A=∠F,∠C=∠D,可以证明BD∥CE.在下列括号中填写推理理由证明:∵∠A=∠F∴AC∥DF(内错角相等,两直线平行)∴∠C+∠DEC =180°(两直线平行,同旁内角互补)∵∠C=∠D∴∠D+∠DEC=180°(等量代换)∴BD∥CE (同旁内角互补,两直线平行).【考点】平行线的判定与性质.【专题】推理填空题.【分析】由已知的一对内错角相等,利用内错角相等两直线平行得出AC与DF平行,再由两直线平行内错角相等得到∠D=∠1,而∠C=∠D,等量代换得到一对同位角相等,利用同位角相等两直线平行即可得到BD与CE平行.【解答】证明:∵∠A=∠F∴AC∥DF(内错角相等,两直线平行)∴∠C+∠DEC=180°(两直线平行,同旁内角互补)∵∠C=∠D∴∠D+∠DEC=180°(等量代换)∴BD∥CE (同旁内角互补,两直线平行).故答案是:内错角相等,两直线平行;DEC;两直线平行,同旁内角互补;等量代换;同旁内角互补,两直线平行【点评】此题考查了平行线的判定与性质,属于推理型填空题,熟练掌握平行线的判定与性质是解本题的关键.22.小明打算用一块面积为900cm2的正方形木板,沿着边的方向裁出一个长方形面积为588cm2桌面,并且的长宽之比为4:3,你认为能做到吗?如果能,计算出桌面的长和宽;如果不能,请说明理由.【考点】算术平方根.【专题】计算题.【分析】根据长方形的面积,可得一个元二次方程,根据解方程,可得长方形的边长,根据长方形的边长与正方形的边长的比,可得答案.【解答】解:能做到,理由如下设桌面的长和宽分别为4x(cm)和3x(cm),根据题意得,4x×3x=588.12x2=588x2=49,x>0,x==7∴4x=4×7=28 (cm) 3x=3×7=21(cm)∵面积为900cm2的正方形木板的边长为30cm,28cm<30cm∴能够裁出一个长方形面积为588 cm2并且长宽之比为4:3的桌面,答:桌面长宽分别为28cm和21cm.【点评】本题考查了算术平方根,开平方是求边长的关键,注意算术平方根都是非负数.23.如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数.【考点】平行线的判定与性质.【分析】推出EF∥BC,根据平行线性质求出∠ACB,求出∠FCB,根据角平分线求出∠ECB,根据平行线的性质推出∠FEC=∠ECB,代入即可.【解答】解:∵EF∥AD,AD∥BC,∴EF∥BC,∴∠ACB+∠DAC=180°,∵∠DAC=120°,∴∠ACB=60°,又∵∠ACF=20°,∴∠FCB=∠ACB﹣∠ACF=40°,∵CE平分∠BCF,∴∠BCE=20°,∵EF∥BC,∴∠FEC=∠ECB,∴∠FEC=20°.【点评】本题考查了平行线的性质和判定,平行公理及推论,注意:平行线的性质有①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补.。
2015-2016年七年级第二学期期中考试数学试题
七年级下数学期中测试数学试题姓名 __________ 班级 _________ 分数 _____________一、选择题:1.计算(-a 2)3的结果是----------------------------------------------------------------------【 】A .-a 5 B. a 5 C .-a 6 D. a 62、如图,已知直线a 、b 被直线c 所截,a ∥b ,∠1=130°,则 ∠2=【 】A. 130°B. 50°C.40°D.60° 3.李老师骑车外出办事,离校不久便接到学校到他返校的紧急电话,李老师急忙赶回学校.下面四个图象中,描述李老师与学校距离的图象是---------------------------------【 】 4、下列各题中, 能用平方差公式的是 :---------------------------------------------------【 】 A.(-a -2b)(a +2b) B.(a -2b)( -a +2b)C.( -a -2b)( -a -2b)D. ( a -2b)(a +2b)5.已知:如图,AB CD ⊥,垂足为O ,EF 为过点O 的 一条直线,则1∠与2∠的关系一定成立的是---【 】 A .相等 B .互余C .互补D .互为对顶角6.在某次实验中,测得两个变量m 和v 之间的4组对应数据如下表:则m 与v 之间的关系是下列哪个( )A .v=4mB .v=4m ﹣1C .v=2m+2D .v=3m+1 7. 计算(-0.5)2007×22009的结果是---------------------------------------------------------- 【 】A .-4B .0.25C .4D .-0.258.已知,3,5=-=+xy y x 则=+22y x --------------------------------------------------- 【 】A 、25B 、25-C 、19D 、19-9.“龟兔赛跑”讲述了这样的故事:领先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达终点、用s 1、s 2分别表示乌龟和兔子所行的路程,t 为时间,则下列图象中与故事情节相吻合的是------------------------------------------------------------------------------------------------------ 【 】m 1 2 34 v471013ABC DEF 2 1 OA. B. C. D.A .B .C .D .10.已知,5,3==bax x 则=-ba x----------------------------------------------------------------【 】A 、35B 、109 C 、53D 、1511.小明利用计算机设计了一个计算程序,输入和输出的数据如下: 输入 (1)2345… 输出…2152 103 174 265 …那么,当输入数据8时,输出的数据是-------------------------------------------------------------【 】A.168B.638 C.658 D.278 12.如图,图象(折线OEFPMN )描述了某汽车在行驶过程中速度与时间的函数关系,下列说法中错误的是--------------------【 】 A .第3分时汽车的速度是40千米/时B .第12分时汽车的速度是0千米/时C .从第3分到第6分,汽车行驶了120千米D .从第9分到第12分,汽车的速度从60千米/时减少到0千米/时二、填空题:13.计算:()=⨯--152006 。
2015-2016学年七年级第 二学期期中考试数学试题(含答案)
2015-2016学年七年级下数学期中测试题数 学 试 题(含答案)(考试时间:120分钟 满分:100分) 一、选择题:(每小题3分,共30分.)1.下列图形中,不能通过其中一个四边形平移得到的是 ( )2.下列计算:①2n n n a a a ⋅=; ②1266a a a =+; ③33)(ab ab =;④428a a a =÷;⑤22))((b a b a b a +-=---;⑥22293)3(y xy x y x +-=-其中正确的个数为 ( )A .3B .2C .1D .03.下列等式由左边到右边的变形中,属于因式分解的是 ( )A .1)1)(1(2-=-+a a aB .22)3(96-=+-a a a C .1)2(122++=++x x x x D .y x y x y x 222343618∙-=- 4.若-个多边形的内角和等于它的外角和的两倍,则这个多边形的边数为 ( ) A .6 B .7 C .8 D .92·1·c·n·j·y5.若(x +5)(2x -n )=2x2+mx -15,则 ( ) A .m =-7,n =3 B .m =7,n =-3 C .m =-7,n =-3 D .m =7,n =36.如图,如下四个条件:①∠B +∠BCD =180°,②∠1=∠2,③∠3=∠4,④∠B =∠5,其中能判定AB ∥CD 的条件的个数有 ( ) A .1 B .2 C .3 D .4第6题 第7题 第9题7.将一副直角三角板,按如图所示叠放在一起,则图中∠α为 ( ) A. 45° B. 60° C. 75° D. 90°8.在△ABC 中,∠A=2∠B=3∠C,则△ABC 是 ( )A .锐角三角形B .直角三角形C .钝角三角形D .都有可能 9.如图,△ABC 的面积为1.第一次操作:分别延长AB,BC,CA 至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过2015,最少经过 次操作 . ( )第17题图 A .6 B .5C .4D .310.∑表示数学中的求和符号,主要用于求多个数的和,∑下面的小字,1i =表示从1开始求和;上面的小字,如n 表示求和到n 为止.即1231nini xx x x x ==++++∑….则()211ni i=-∑表示( ) A .n2-1 B . 12+22+32+…+n2-(1+2+3+…+ n ) C .12+22+32+…+n2-nD . 12+22+32+…+2i - i二、填空题:(每空2分,共16分.) 11. 计算:(-2xy )3= .12.甲型H7N9流感病毒的直径大约为0.000 000 08米,用科学记数法表示为 米.13.三角形两边长分别为2和8,若该三角形第三边长为奇数,则该三角形的第三边为 .14.已知m>0,如果16)1(22+-+x m x 是一个完全平方式,那么m 的值为 . 15.如图,将一块长方形纸条折成如图的形状,若已知∠1=110°,则∠2= °.16.如图,在△ABC 中,已知∠ABC=50°,∠ACB=60°,BE 是AC 边上的高,CF 是AB 边上的高,H 是BE 和CF 的交点,则∠BHC= °.17.如图,在△ABC 中E 是BC 上的一点,EC =2EB ,点D 是AC 的中点,AE 、BD 交于点F ,AF =3FE ,若△ABC 的面积为18,给出下列命题:①△ABE 的面积为6;②△ABF 的面积和四边形DFEC 的面积相等;③点F 是BD 的中点;④四边形DFEC 的面积为152.其中,正确的结论有 .(把你认为正确的结论的序号都填上)18.如图,长方形ABCD 中,AB=4cm ,BC=3cm ,点E 是CD 的中点,动点P 从A 点出发,以 每秒1cm 的速度沿A →B →C →E 运动,最终到达点E .若点P 运动的时间为x 秒,那么 当x=_ ___时,△APE 的面积等于52cm . 三、解答题(本大题共10小题,共54分.) 19. 计算或化简:(本题共9分,每小题3分)(1)-22+(-21)-2-(π-5)0-|-4| (2)2244223)2()(a a a a a ÷+∙--第18题图E C D A B P第15题图 第16题图(3))32)(32(c b a c b a -+++20.因式分解:(本题共9分,每小题3分)(1))(6)(3a b y b a x --- (2)6442-x(3)22216)4(x x -+21.先化简,再求值(本题共4分)(2x+y )2—(2x-y )(2x+y )—4xy ;其中x=2015,y=-1.22.(本题共4分)若x +y =3,且(x +2)(y +2)=12. (1)求xy 的值; (2)求x2-xy +y2的值.23.(本题共4分)已知以2m a =,4n a =,32k a =,求kn m a -+23的值.24.(本题共5分)在正方形网格中,每个小正方形的边长都为1个单位长度,△ABC 的三个顶点的位置如图所示,现将△ABC 平移后得△EDF ,使点B 的对应点为点D ,点A 对应点为点E . (1)画出△EDF ;(2)线段BD 与AE 有何关系?_________ ___;(3)连接CD 、BD ,则四边形ABDC 的面积为_______.21世纪教育网25.(本题共5分)如图,已知∠DAB+∠D=180°,AC 平分∠DAB ,且∠CAD=25°,∠B=95° 求(1)∠DCA 的度数;(2)∠DCE 的度数.26. (本题6分)先阅读下面的内容,再解决问题.例题:若m2+2mn +2n2-6n +9=0,求m 和n 的值. 解:∵m2+2mn +2n2—6n +9=0 ∴m2+2mn +n2+n2-6n +9=0 ∴(m +n)2+(n -3)2=0 ∴m +n =0,n -3=0 即m =-3,n =3(1)若x2+2y2-2xy +4y +4=0,求yx 的值.(2)已知a ,b ,c 是△ABC 的三边长,且满足a2+b2-10a -8b +41=0,且c 是△ABC 中最长的边,求c 的取值范围.27.(本题共8分)(1)如图1的图形我们把它称为“8字形”,请说明A B C D∠+∠=∠+∠;图1O ABC D图4P OABCDE F图3P OA B CD E F 图5POABCDE(2)阅读下面的内容,并解决后面的问题:如图2, AP 、CP 分别平分∠BAD. ∠BCD ,若∠ABC=36°,∠ADC=16°,求∠P 的度数; 解:∵AP 、CP 分别平分∠BAD. ∠BCD ∴∠1=∠2,∠ 3=∠4由(1)的结论得: 3124P B P D ∠+∠=∠+∠⎧⎨∠+∠=∠+∠⎩①②①+②,得2∠P+∠2+∠3=∠1+∠4+∠B+∠D∴∠P =21(∠B+∠D)=26°.①如图3,直线AP 平分∠BAD 的外角∠FAD ,CP 平分∠BCD 的外角∠BCE ,若∠ABC=36°,∠ADC=16°,请猜想P ∠的度数,并说明理由.②在图4中,直线AP 平分∠BAD 的外角∠FAD ,CP 平分∠BCD 的外角∠BCE ,猜想∠P 与∠B 、∠D 的关系,直接写出结论,无需说明理由.③在图5中,AP 平分∠BAD ,CP 平分∠BCD 的外角∠BCE ,猜想∠P 与∠B 、∠D 的关系,直接写出结论,无需说明理由.4321图2OPAB CD初一年级数学学科期中考试答案 选择题:D,C,B,A,D C,C,C,C,B 填空题:11.338-y x 12. 8×810- 13. 7,9 14.5 15.55゜ 16.110゜ 17.①③④ 18.5310,三.解答题:19.计算或化简:(1)原式=-4+4-1-4 2分(2)原式=6a -6a +48a ÷2a 1分(3)原式=(a+2b)2-(3c)22分=-5 3分 =6a -6a +46a 2 分 =2244b ab a ++-9c 2 3分=46a 3分 20.因式分解:(1)原式=3x(a-b)+6y(a-b) 1分(2)原式=4(2x -16)1分(3)原式=(2x +4+4y )(2x +4-4y) 2分=3(a-b)(x+2y) 3分 =4(x+2)(x-2) 3分 =(x+2)2(x-2)23分21.原式=22y 2分 当y=-1时,原式=2 4分 22.(1)xy=2 2分 (2)22y xy x +-=3 4分23. 4 4分24.(1)画图1分 (2)BD=AE, BD//AE 3分 (3)6 5分 25. 解:(1)∵∠DAB+∠D=180°, ∴AB ∥CD ,∴∠ACD=∠BAC , ∵AC 平分∠DAB , ∴∠DAC=∠BAC , ∴∠DAC=∠DCA , ∵∠CAD=25°, ∴∠DCA=25°;3分 (2)∵AB ∥CD , ∴∠ECD=∠B ; ∵∠B=95,∴∠DCE=95°. 5分26.解(1)∵x2+2y2-2xy+4y+4=0 ∴x2-2xy+y2+y2+4y+4=0∴(x-y )2+(y+2)2=0, 1分 ∴x-y=0,y+2=0,图3P OABC DEF 1 23 4解得x=-2,y=-2, 2分∴xy=(-2)-2=413分(2)∵a2+b2-10a-8b+41=0 ∴a2-10a+25+b2-8b+16=0, ∴(a-5)2+(b-4)2=0,4分 ∴a-5=0,b-4=0, 解得a=5,b=4,5分∵c 是△ABC 中最长的边, ∴5≤c <9. 6分27.(1)∵∠A+∠B+∠AOB=180° ∠C+∠D+∠COD=180゜∴∠A+∠B+∠AOB=∠C+∠D+∠COD ∵∠AOB=∠COD∴∠A+∠B=∠C+∠D 2分 (2) ∠P=26゜ 3分∵AP 平分BAD ∠的外角FAD ∠,CP 平分BCD ∠的外角BCE ∠, ∴12∠=∠,34∠=∠由(1)的结论得:∠PAD+∠P= ∠PCD+∠D ①∠PAB+∠P= ∠PCB+∠B ② ∵∠PAB=∠1,∠1=∠2∴∠PAB=∠2∴∠2+∠P= ∠3+∠B ③+③得∠2+∠P +∠PAD+∠P = ∠3+∠B +∠PCD+∠D 2∠P +180° = ∠B+∠D+180°∴∠P = (21∠B+∠D )=26° 6分 (3)∠p=180゜-(21∠B+∠D ) 7分 (4)∠p=90゜+(21∠B+∠D ) 8分。
【初中数学】2015-2016学年河南省安阳市滑县实验中学七年级(上)期中数学试卷(解析版) 人教版
2015-2016学年河南省安阳市滑县实验中学七年级(上)期中数学试卷一、选择题(每小题3分,共30分)1.﹣3的相反数是()A.3 B.﹣3 C.±3 D.2.如果收入15元记作+15元,那么支出20元记作()元.A.+5 B.+20 C.﹣5 D.﹣203.我国建造的长江三峡水电站,估计总装机容量达16780000千瓦,16780000用科学记数法表示为()A.16.7×106 B.1.68×107 C.1.678×107D.1.678×1084.﹣、﹣、﹣的大小顺序是()A.﹣<﹣<﹣B.﹣<﹣<﹣C.﹣<﹣<﹣D.﹣<﹣<﹣5.下列不是同类项的一组是()A.﹣1与B.2mn与2mnp C.5ab与﹣3ba D.x2y与6yx26.已知有理数a、b在数轴上的位置如图所示,下列结论正确的是()A.a>b B.ab<0 C.b﹣a>0 D.a+b>07.下列各式中,是二次三项式的是()A.x2+y2+x﹣y B.a2﹣3 C.32+a+ab D.32+3+18.冬季某天我国三个城市的最高气温分别是﹣10℃,1℃,﹣7℃,它们任意两城市中最大的温差是()A.11℃B.17℃C.8℃D.3℃9.将代数式xy2+合并同类项,结果是()A.x2y B.x2y+5xy2C.x2y D.x2y+x2y+5xy210.已知|a|=﹣a,则a是()A.正数B.负数C.负数或0 D.正数或0二、填空题(每小题3分,共30分)11.单项式﹣2a2b的系数是,次数是.12.﹣0.25的倒数是,若|a|=|﹣4|,则a=.13.比较大小:﹣|﹣2.5| (﹣5)2.14.比a的2倍大1的数,列式为.15.绝对值小于2的非负整数是.16.若2x6﹣m y4与﹣3x3y2n是同类项,则(m﹣n)2015=.17.在数轴上距原点3个单位长度的点表示的数是.18.若x3+(m+1)x2﹣3没有二次项,则m的值是.19.a*b=a+2b+3,则(﹣2)*的值为.20.用代数式表示:买一个球拍需要a元,买一根跳绳需要b元,则分别购买50个球拍和50根跳绳,共需元.三、解答题(21题每小题20分,22-23题每小题20分,共32分)21.计算:(1)(﹣48)+(﹣2)3﹣(﹣25)×(﹣4)+(﹣2)2;(2)||+(﹣3)﹣×(﹣3);(3)﹣12﹣6×(﹣)2+(﹣5)×(﹣3);(4)(﹣)×24.22.先化简,再求值:(4a2﹣3a)﹣2(a2+2a﹣1)﹣(a2+a+1),其中a=﹣3.23.已知A=3a2﹣3ab+b2,B=3a2﹣2ab,C=a2﹣ab,其中a,b满足|a﹣2|+(b+1)2=0,试计算A﹣2B+3C的值.四、解答题(24题8分,25题10分,26题10分,满分28分)24.为体现社会对教师的尊重,教师节这天上午,出租车司机小王在东西走向的公路上免费接送老师.如果规定向东为正,向西为负,出租车的行程如下.(单位:千米)+15,﹣4,+13,﹣10,﹣12,+3,﹣13,﹣17(1)当最后一名老师到达目的地时,小王距离开始接送第一位老师之前的地点的距离是多少?(2)若出租车的耗油量为0.4升/千米,这天上午出租车共耗油多少升?25.某工厂第一车间有x人,第二车间比第一车间人数的少30人.(1)第二车间有多少人?(2)如果从第二车间调出10人到第一车间,那么调动后,第一车间的人数比第二车间多多少人?26.大客车上原有(3a﹣b)人,中途下车一半人,又上车若干人,使车上共有乘客(8a﹣5b)人.问中途上车乘客是多少人当a=10,b=8时,上车乘客是多少人?2015-2016学年河南省安阳市滑县实验中学七年级(上)期中数学试卷参考答案与试题解析一、选择题(每小题3分,共30分)1.﹣3的相反数是()A.3 B.﹣3 C.±3 D.【考点】相反数.【分析】依据相反数的概念求解.相反数的定义:只有符号不同的两个数互为相反数,0的相反数是0.【解答】解:﹣3的相反数就是3.故选A.2.如果收入15元记作+15元,那么支出20元记作()元.A.+5 B.+20 C.﹣5 D.﹣20【考点】正数和负数.【分析】在一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示.【解答】解:“正”和“负”相对,所以如果收入15元记作+15元,那么支出20元记作﹣20元.故选D.3.我国建造的长江三峡水电站,估计总装机容量达16780000千瓦,16780000用科学记数法表示为()A.16.7×106 B.1.68×107 C.1.678×107D.1.678×108【考点】科学记数法—表示较大的数.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.【解答】解:将16780000用科学记数法表示为:1.678×107.故选:C.4.﹣、﹣、﹣的大小顺序是()A.﹣<﹣<﹣B.﹣<﹣<﹣C.﹣<﹣<﹣D.﹣<﹣<﹣【考点】有理数大小比较.【分析】将三个数通分,再利用负数比较大小的规则进行比较,即可得出结论.【解答】解:∵4、6、8的最小公倍数为24,∴﹣=﹣,﹣=﹣,﹣=﹣,又∵18<20<21,∴有﹣>﹣>﹣,故选A.5.下列不是同类项的一组是()A.﹣1与B.2mn与2mnp C.5ab与﹣3ba D.x2y与6yx2【考点】同类项.【分析】利用同类项定义判断即可.【解答】解:同类项的有﹣1和,5ab和﹣3ba,x2y与6yx2,不是同类项的是2mn和2mnp,故选B6.已知有理数a、b在数轴上的位置如图所示,下列结论正确的是()A.a>b B.ab<0 C.b﹣a>0 D.a+b>0【考点】数轴.【分析】由数轴可得b<a<0,从而可以判断选项中的结论是否正确,从而可以解答本题.【解答】解:∵由数轴可得,b<a<0,∴a>b,(故A正确);ab>0,(故B错误);b﹣a<0,(故C错误);a+b<0,(故D错误).故选A.7.下列各式中,是二次三项式的是()A.x2+y2+x﹣y B.a2﹣3 C.32+a+ab D.32+3+1【考点】多项式.【分析】找到单项式的最高次数是2的,整个式子由3个单项式组成的多项式即可.【解答】解:A、是二次四项式,故本选项错误;B、是分式,故本选项错误;C、是二次三项式,正确;D、32+3+1=13,是常数,故本选项错误;故选:C.8.冬季某天我国三个城市的最高气温分别是﹣10℃,1℃,﹣7℃,它们任意两城市中最大的温差是()A.11℃B.17℃C.8℃D.3℃【考点】正数和负数;有理数的加法;有理数的减法.【分析】根据最大的温差=最高气温﹣最低气温可得.【解答】解:任意两城市中最大的温差是1﹣(﹣10)=1+10=11℃.故选A.9.将代数式xy2+合并同类项,结果是()A.x2y B.x2y+5xy2C.x2y D.x2y+x2y+5xy2【考点】合并同类项.【分析】根据合并同类项的运算法则进行解答即可.【解答】解:xy2+=x2y;故选C.10.已知|a|=﹣a,则a是()A.正数B.负数C.负数或0 D.正数或0【考点】绝对值.【分析】根据绝对值的性质:正数的绝对值是它本身,负数的绝对值是它的相反数,0的绝对值是0.即可判断.【解答】解:|a|=﹣a,即a的绝对值是它的相反数,则a是负数或0.故选C.二、填空题(每小题3分,共30分)11.单项式﹣2a2b的系数是﹣2,次数是3.【考点】单项式.【分析】根据单项式的系数和次数的定义即可作出判断.【解答】解:﹣2a2b的系数是﹣2,次数是2+1=3.12.﹣0.25的倒数是﹣4,若|a|=|﹣4|,则a=±4.【考点】倒数;绝对值.【分析】根据倒数的性质,互为倒数的两个数积为1;绝对值的定义,一个正数的绝对值是它本身,一个负数的绝对值是它的相反数,0的绝对值是0,求解即可.【解答】解:﹣0.25的倒数是﹣4,若|a|=|﹣4|,则a=±4,故答案为:﹣4,±4.13.比较大小:﹣|﹣2.5| <(﹣5)2.【考点】有理数大小比较.【分析】先计算﹣|﹣2.5|=﹣2.5,(﹣5)2=25,然后根据正数大于零,负数小于零即可得到它们的大小关系.【解答】解:∵﹣|﹣2.5|=﹣2.5,(﹣5)2=25,∴﹣|﹣2.5|<(﹣5)2.故答案为<.14.比a的2倍大1的数,列式为2a+1.【考点】列代数式.【分析】根据题意列式即可.【解答】解:故答案为:2a+115.绝对值小于2的非负整数是0,1.【考点】绝对值.【分析】根据绝对值的意义及非负整数就是正整数或0解答.【解答】解:绝对值小于2的非负整数有:0、1.故答案为:0,1.16.若2x6﹣m y4与﹣3x3y2n是同类项,则(m﹣n)2015=1.【考点】同类项.【分析】根据同类项的定义(所含字母相同,相同字母的指数相同),求出n,m的值,再代入代数式计算即可.【解答】解:∵2x6﹣m y4与﹣3x3y2n是同类项,∴6﹣m=3,2n=4,∴m=3,n=2,∴(m﹣n)2015=1,故答案为:1.17.在数轴上距原点3个单位长度的点表示的数是±3.【考点】数轴.【分析】在数轴上,+3和﹣3到原点0的距离都等于3,据此进行填空即可.【解答】解:在数轴上距原点3个单位长度的点表示的数是±3.故答案为:±3.18.若x3+(m+1)x2﹣3没有二次项,则m的值是﹣1.【考点】多项式.【分析】根据题意列出关于m的方程,求解即可.【解答】解:∵x3+(m+1)x2﹣3没有二次项,∴m+1=0,∴m=﹣1,故答案为﹣1.19.a*b=a+2b+3,则(﹣2)*的值为3.【考点】有理数的混合运算.【分析】根据*的含义,以及有理数的混合运算的运算方法,求出(﹣2)*的值为多少即可.【解答】解:(﹣2)*=×(﹣2)+2×+3=3故答案为:3.20.用代数式表示:买一个球拍需要a元,买一根跳绳需要b元,则分别购买50个球拍和50根跳绳,共需50(a+b)元.【考点】列代数式.【分析】根据总钱数=一个球拍的价格×球拍的个数+一根跳绳的价格×跳绳的根数,即可列出共需的钱数.【解答】解:根据题意列得:50a+50b=50(a+b)元,则分别购买50个球拍和50根跳绳,共需50(a+b)元.故答案为:50(a+b).三、解答题(21题每小题20分,22-23题每小题20分,共32分)21.计算:(1)(﹣48)+(﹣2)3﹣(﹣25)×(﹣4)+(﹣2)2;(2)||+(﹣3)﹣×(﹣3);(3)﹣12﹣6×(﹣)2+(﹣5)×(﹣3);(4)(﹣)×24.【考点】有理数的混合运算.【分析】(1)首先计算乘方、然后计算乘法,最后进行加减计算即可;(2)首先去掉绝对值,然后计算乘法,最后进行加减计算;(3)首先计算乘方、然后计算乘法,最后进行加减计算即可;(4)把除法转化为乘法,利用分配律计算,然后计算乘法,最后进行加减即可.【解答】解:(1)原式=﹣48﹣8﹣25×4+4=﹣48﹣8﹣100+4=﹣156+4=﹣152;(2)原式=﹣3+×=﹣3+=﹣;(3)原式=﹣1﹣6×+15=﹣1﹣+15=14﹣(4)原式=﹣×24+×24﹣×24+×24=﹣12+4﹣9+10=﹣21+14=﹣7.22.先化简,再求值:(4a2﹣3a)﹣2(a2+2a﹣1)﹣(a2+a+1),其中a=﹣3.【考点】整式的加减—化简求值.【分析】原式去括号合并得到最简结果,把a的值代入计算即可求出值.【解答】解:原式=4a2﹣3a﹣2a2﹣4a+2﹣a2﹣a﹣1=a2﹣8a+1,当a=﹣3时,原式=9+24+1=34.23.已知A=3a2﹣3ab+b2,B=3a2﹣2ab,C=a2﹣ab,其中a,b满足|a﹣2|+(b+1)2=0,试计算A﹣2B+3C的值.【考点】整式的加减—化简求值;非负数的性质:绝对值;非负数的性质:偶次方.【分析】把A,B,C代入A﹣2B+3C中,去括号合并得到最简结果,利用非负数的性质求出a 与b的值,代入计算即可求出值.【解答】解:∵A=3a2﹣3ab+b2,B=3a2﹣2ab,C=a2﹣ab,∴A﹣2B+3C=3a2﹣3ab+b2﹣6a2+4ab+3a2﹣3ab=﹣2ab+b2,∵|a﹣2|+(b+1)2=0,∴a=2,b=﹣1,则原式=4+1=5.四、解答题(24题8分,25题10分,26题10分,满分28分)24.为体现社会对教师的尊重,教师节这天上午,出租车司机小王在东西走向的公路上免费接送老师.如果规定向东为正,向西为负,出租车的行程如下.(单位:千米)+15,﹣4,+13,﹣10,﹣12,+3,﹣13,﹣17(1)当最后一名老师到达目的地时,小王距离开始接送第一位老师之前的地点的距离是多少?(2)若出租车的耗油量为0.4升/千米,这天上午出租车共耗油多少升?【考点】正数和负数.【分析】(1)根据有理数的加法运算,将所有数据相加即可;(2)根据行车就耗油,可得到耗油量.【解答】解:∵(1)15﹣4+13﹣10﹣12+3﹣13﹣17=﹣25,∴当最后一名老师到达目的地时,小王距离开始接送第一位老师之前的地点的距离是25千米(2)|+15|+|﹣4|+|+13|+|﹣10|+|﹣12|+|+3|+|﹣13|+|﹣17|=87,87×0.4=34.8(升).答:这天上午出租车共耗油34.8升.25.某工厂第一车间有x人,第二车间比第一车间人数的少30人.(1)第二车间有多少人?(2)如果从第二车间调出10人到第一车间,那么调动后,第一车间的人数比第二车间多多少人?【考点】列代数式.【分析】(1)根据第二车间比第一车间人数的少30人即可表示第二车间的人数;(2)注意从第二车间调出10人,则第二车间少10人,第一车间多10人.分别表示出两个车间的人数后再进一步计算.【解答】解:(1)第二车间有(x﹣30)人.(2)(x+10)﹣(x﹣30﹣10)=x+10﹣x+30+10=x+50∴第一车间的人数比第二车间多(x+50)人.26.大客车上原有(3a﹣b)人,中途下车一半人,又上车若干人,使车上共有乘客(8a﹣5b)人.问中途上车乘客是多少人当a=10,b=8时,上车乘客是多少人?【考点】列代数式;代数式求值.【分析】原有(3a﹣b)人,中途下车(3a﹣b)人,又上车若干人后车上共有乘客(8a﹣5b)人.中途上车乘客数=车上共有乘客数﹣中途下车人数,所以中途上车乘客为,把a=10,b=8代入上式可得上车乘客人数.【解答】解:中途上车乘客是(8a﹣5b)﹣(3a﹣b)=(人),当a=10,b=8时,上车乘客是29人.2016年12月12日。
2015—2016学年度第二学期期中考试七年级数学试卷及答案
2015--2016学年度第二学期期中考试七年级数学试卷一、选择题(本题有5小题目,每小题3分,共15分;请你将正确答案的代号填入答题卷相应的括号中)1、如图,直线a ∥b ,∠1=37º,则∠2的度数是( )(A )57º (B )37º (C )143º (D )53º2、下列个组数中,是方程⎩⎨⎧=-=+13y x y x 的解的是( ) (A )⎩⎨⎧==12y x (B )⎩⎨⎧==13y x (C )⎩⎨⎧-==13y x (D )⎩⎨⎧==21y x3、如图,点A 的坐标是( )(A )(2,-2) (B )(-2,2)(C )(0,2) (D )(-2,0)4、若⎩⎨⎧==13y x 是方程32=-ay x 的一组解,则a 的值是()(A )1 (B )2 (C )3 (D )4,如果,1-), 所在位置的坐标为 (1,1-),所在() (A )(0,0) (B )(1,1)(C )(2,1) (D )(1,2)二、、填空题(本题共有5小题,每小题4分,共20分;请你将正确的答案填在答题卷相应的横线上)6、如图,直线a ,b 相交于点O ,∠1=43º,则∠2= º,∠3= º;7、请你写出方程1-=-y x 的一组整数解;8、点)3,5(-A 在第 象限,点)3,1(-B 在第 象限;9、如图,若∠1=∠2,则互相平行的线段是_____________;10、把点A (-4,2)向右平移3个单位长度得A1的坐标是 ;把点B (-4,2)向下平移3个单位长度得B2的坐标是 ;三、解答题(本题共5题,每小题6分,共30分)11、如图,直线a 、b 被直线c 所截若∠1=30°,∠2=150°,试说明a 与b 的位置关系。
12、解方程组 ⎩⎨⎧+==+y x y x 293213、解方程组 ⎩⎨⎧=-=+827y x y x14、如图,AD ∥BC ,AD 平分∠EAC ,∠EAD=50°,求∠B 和∠C 的度数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015-2016学年河南省安阳市滑县七年级(下)期中数学试卷一.选择题1.下列各图中,∠1与∠2是对顶角的是()A.B.C. D.2.如图,如果AB∥CD,那么图中相等的内错角是()A.∠1与∠5,∠2与∠6 B.∠3与∠7,∠4与∠8C.∠5与∠1,∠4与∠8 D.∠2与∠6,∠7与∠33.下列结论正确的是()A.64的立方根是±4 B.﹣没有立方根C.立方根等于本身的数是0 D.=﹣4.下列计算正确的是()A.B.C.D.5.直角坐标系中,点P(x,y)在第三象限,且P到x轴和y轴的距离分别为3、7,则点P的坐标为()A.(﹣3,﹣7)B.(﹣7,﹣3)C.(3,7)D.(7,3)6.已知点P(0,a)在y轴的负半轴上,则点Q(﹣a2﹣1,﹣a+1)在()A.第一象限 B.第二象限 C.第三象限 D.第四象限7.如图,直线AB∥CD,直线EF分别交直线AB、CD于点E、F,过点F作FG⊥FE,交直线AB于点G,若∠1=42°,则∠2的大小是()A.56°B.48°C.46°D.40°8.把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在MN的位置上,若∠EFG=55°,则∠2=()A.105 B.110 C.95 D.120二.填空题9.的算术平方根是.10.如果∠A与∠B的两边分别平行,且∠A比∠B的3倍少36°,则∠A的度数是.11.若+|b+1|+(c+1)2=0,则a+b﹣c=.12.已知点A(3a+5,a﹣3)在二、四象限的角平分线上,则a=.13.已知点M在y轴上,纵坐标为5,点P(3,﹣2),则△OMP的面积是.14.一个正数x的平方根分别是2a﹣3与5﹣a,x等于.15.如图,已知AB∥CD∥EF,则∠x、∠y、∠z三者之间的关系是.三.解答题16.计算:(1)||+|﹣1|﹣|3|(2)﹣++.17.求下列各式中的x.(1)4x2﹣16=0(2)27(x﹣3)3=﹣64.18.已知2a﹣1的平方根是±3,3a+b﹣1的算术平方根是4,求12a+2b的立方根.19.如图,在△ABC中,三个顶点的坐标分别为A(﹣5,0),B(4,0),C(2,5),将△ABC沿x轴正方向平移2个单位长度,再沿y轴沿负方向平移1个单位长度得到△EFG.(1)求△EFG的三个顶点坐标.(2)求△EFG的面积.20.如图,已知AB∥CD,EF与AB、CD分别相交于点E、F,∠BEF与∠EFD的平分线相交于点P,求证:EP⊥FP.21.如图,∠1+∠2=180°,∠DAE=∠BCF,DA平分∠BDF.(1)AE与FC会平行吗?说明理由.(2)AD与BC的位置关系如何?为什么?(3)BC平分∠DBE吗?为什么?22.如图,已知AD⊥BC,FG⊥BC,垂足分别为D、G.且∠1=∠2,猜想:∠BDE与∠C 有怎样的关系?说明理由.23.如图所示,已知AB∥CD,分别探究下面图形中∠APC,∠PAB,∠PCD的关系,请你从四个图形中任选一个,说明你所探究的结论的正确性.①结论:(1)(2)(3)(4)②选择结论,说明理由.2015-2016学年河南省安阳市滑县七年级(下)期中数学试卷参考答案与试题解析一.选择题1.下列各图中,∠1与∠2是对顶角的是()A.B.C. D.【考点】对顶角、邻补角.【分析】根据对顶角的定义作出判断即可.【解答】解:根据对顶角的定义可知:只有丙图中的是对顶角,其它都不是.故选:C.2.如图,如果AB∥CD,那么图中相等的内错角是()A.∠1与∠5,∠2与∠6 B.∠3与∠7,∠4与∠8C.∠5与∠1,∠4与∠8 D.∠2与∠6,∠7与∠3【考点】平行线的性质.【分析】找出平行线AB、CD被AC所截得到的内错角是∠2、∠6,被BD所截得到的内错角是∠3,∠7.【解答】解:∵∠1与∠5,∠4与∠8是直线AD、BC被AC所截得到的内错角,而AD、BC的位置关系不确定,∴∠1与∠5,∠4与∠8的数量关系也不确定,故A、B、C错误;D、∵∠2与∠6是平行线AB、CD被AC所截得到的内错角,∠3与∠7是平行线AB、CD 被BD所截得到的内错角,由平行线的性质可得,它们相等,故正确.故选D.3.下列结论正确的是()A.64的立方根是±4 B.﹣没有立方根C.立方根等于本身的数是0 D.=﹣【考点】立方根.【分析】根据立方根的定义求出每个数(如64、﹣、±1、0,﹣27、27)的立方根,再判断即可.【解答】解:A、64的立方根是4,故本选项错误;B、﹣的立方根是﹣,故本选项错误;C、立方根等于它本身的数是0、1、﹣1,故本选项错误;D、=﹣3,﹣=﹣3,故本选项正确;故选D.4.下列计算正确的是()A.B.C.D.【考点】立方根.【分析】A、B、C、D都可以直接根据立方根的定义求解即可判定.【解答】解:A、0.53=0.625,故选项错误;B、应取负号,故选项错误;C、∵等于,∴的立方根等于,故选项正确;D、应取正号,故选项错误.故选C5.直角坐标系中,点P(x,y)在第三象限,且P到x轴和y轴的距离分别为3、7,则点P的坐标为()A.(﹣3,﹣7)B.(﹣7,﹣3)C.(3,7)D.(7,3)【考点】点的坐标.【分析】根据点P所在象限先确定P点横纵坐标都是负数,根据P到x轴和y轴的距离确定点的坐标.【解答】解:∵点P(x,y)在第三象限,∴P点横纵坐标都是负数,∵P到x轴和y轴的距离分别为3、7,∴点P的坐标为(﹣7,﹣3).故选:B.6.已知点P(0,a)在y轴的负半轴上,则点Q(﹣a2﹣1,﹣a+1)在()A.第一象限 B.第二象限 C.第三象限 D.第四象限【考点】点的坐标.【分析】根据y轴负半轴上点的纵坐标是负数求出a的取值范围,再求出点Q的横坐标与纵坐标的正负情况,然后求解即可.【解答】解:∵点P(0,a)在y轴的负半轴上,∴a<0,∴﹣a2﹣1<0,﹣a+1>0,∴点Q在第二象限.故选B.7.如图,直线AB∥CD,直线EF分别交直线AB、CD于点E、F,过点F作FG⊥FE,交直线AB于点G,若∠1=42°,则∠2的大小是()A.56°B.48°C.46°D.40°【考点】平行线的性质.【分析】根据两直线平行,同位角相等可得∠3=∠1,再根据垂直的定义可得∠GFE=90°,然后根据平角等于180°列式计算即可得解.【解答】解:∵AB∥CD,∴∠3=∠1=42°,∵FG⊥FE,∴∠GFE=90°,∴∠2=180°﹣90°﹣42°=48°.故选:B.8.把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在MN的位置上,若∠EFG=55°,则∠2=()A.105 B.110 C.95 D.120【考点】平行线的性质.【分析】根据折叠的性质可知ME∥NF,由ME∥NF可得出∠BGM=∠GFN,再分解平角通过计算得出∠BGM的度数,根据∠BGM与∠2互补即可得出结论.【解答】解:由折叠的性质可知ME∥NF,∴∠BGM=∠GFN.∵2∠EFG+∠GFN=180°,且∠EFG=55°,∴∠BGM=∠GFN=180°﹣2×55°=70°,又∵∠2+∠BGM=180°,∴∠2=110°.故选B.二.填空题9.的算术平方根是3.【考点】算术平方根.【分析】首先根据算术平方根的定义求出的值,然后即可求出其算术平方根.【解答】解:∵=9,又∵(±3)2=9,∴9的平方根是±3,∴9的算术平方根是3.即的算术平方根是3.故答案为:3.10.如果∠A与∠B的两边分别平行,且∠A比∠B的3倍少36°,则∠A的度数是18°或126°.【考点】平行线的性质.【分析】由∠A与∠B的两边分别平行,即可得∠A与∠B相等或互补,然后分两种情况,分别从∠A与∠B相等或互补去分析,求得方程组,解方程组即可求得∠A的度数.【解答】解:∵∠A与∠B的两边分别平行,∴∠A与∠B相等或互补.分两种情况:①当∠A+∠B=180°时,∠A=3∠B﹣36°,解得:∠A=126°;②当∠A=∠B,∠A=3∠B﹣36°,解得:∠A=18°.所以∠A=18°或126°.故答案为18°或126°.11.若+|b+1|+(c+1)2=0,则a+b﹣c=2.【考点】非负数的性质:算术平方根;非负数的性质:绝对值;非负数的性质:偶次方.【分析】根据非负数的性质列式求出a、b、c的值,然后代入代数式进行计算即可得解.【解答】解:根据题意得,a﹣2=0,b+1=0,c+1=0,解得a=2,b=﹣1,c=﹣1,所以,a+b﹣c=2﹣1﹣(﹣1)=2﹣1+1=2.故答案为:2.12.已知点A(3a+5,a﹣3)在二、四象限的角平分线上,则a=﹣.【考点】坐标与图形性质.【分析】根据二、四象限的角平分线上,点的特点即可.【解答】解:∵点A(3a+5,a﹣3)在二、四象限的角平分线上,∴3a+5+a﹣3=0,∴a=﹣.13.已知点M在y轴上,纵坐标为5,点P(3,﹣2),则△OMP的面积是7.5.【考点】坐标与图形性质;三角形的面积.【分析】根据题意画出图形,进而利用三角形面积求法得出答案.【解答】解:如图所示:由题意可得,MO=5,△OMP的面积是:×5×3=7.5.故答案为:7.5.14.一个正数x的平方根分别是2a﹣3与5﹣a,x等于49.【考点】平方根.【分析】根据正数的两个平方根互为相反数列式求出a的值,然后再根据平方根的定义进行计算即可得解.【解答】解:∵正数x的平方根分别是2a﹣3与5﹣a,∴2a﹣3+5﹣a=0,解得a=﹣2,∴5﹣a=5﹣(﹣2)=7,∴x=72=49.故答案为:49.15.如图,已知AB∥CD∥EF,则∠x、∠y、∠z三者之间的关系是x=180°+z﹣y.【考点】平行线的性质.【分析】根据两直线平行,同旁内角互补求出∠CEF,再根据两直线平行,内错角相等即可得到∠x=∠AEF.【解答】解:∵CD∥EF,∴∠CEF=180°﹣y,∵AB∥EF,∴∠x=∠AEF=∠z+∠CEF,即x=180°+z﹣y.故答案为:x=180°+z﹣y.三.解答题16.计算:(1)||+|﹣1|﹣|3|(2)﹣++.【考点】实数的运算.【分析】(1)根据绝对值的意义去绝对值得到原式=﹣+﹣1﹣3+,然后合并即可;(2)先进行开方运算得到原式=﹣(﹣2)+5+2,然后进行加法运算.【解答】解:(1)原式=﹣+﹣1﹣3+=2﹣4;(2)原式=﹣(﹣2)+5+2=2+5+2=9.17.求下列各式中的x.(1)4x2﹣16=0(2)27(x﹣3)3=﹣64.【考点】立方根;平方根.【分析】(1)根据移项,可得平方的形式,根据开平方,可得答案;(2)根据等式的性质,可得立方的形式,根据开立方,可得答案.【解答】解(1)4x2=16,x2=4x=±2;(2)(x﹣3)3=﹣,x﹣3=﹣x=.18.已知2a﹣1的平方根是±3,3a+b﹣1的算术平方根是4,求12a+2b的立方根.【考点】立方根;平方根;算术平方根.【分析】分别根据2a﹣1的平方根是±3,3a+b﹣1的算术平方根是4,求出a、b的值,再求出12a+2b的值,求出其立方根即可.【解答】解:∵2a﹣1的平方根是±3,∴2a﹣1=(±3)2,解得a=5;∵3a+b﹣1的算术平方根是4,∴3a+b﹣1=16,把a=5代入得,3×5+b﹣1=16,解得b=2,∴12a+2b=12×5+4=64,∴=4,即12a+2b的立方根是4.19.如图,在△ABC中,三个顶点的坐标分别为A(﹣5,0),B(4,0),C(2,5),将△ABC沿x轴正方向平移2个单位长度,再沿y轴沿负方向平移1个单位长度得到△EFG.(1)求△EFG的三个顶点坐标.(2)求△EFG的面积.【考点】三角形的面积;作图-平移变换.【分析】(1)按照题目要求,画出平移后的三角形,即可得出△EFG的三点坐标,或根据平移公式也可直接得出平移后三角形的三个顶点坐标;(2)根据已知条件,△EFG≌△ABC,所以有S△EFG=S△ABC,只需求出S△ABC即可,根据三角形的面积公式,易知底边AB的长度,高为点C到AB的距离,即为点C的纵坐标.【解答】解:(1)如下图:E(﹣3,﹣1)、F(6,﹣1)、G(4,4);(2)如上图,过C作CH⊥AB.∵△EFG是由△ABC沿x轴正方向平移2个单位长度,再沿y轴沿负方向平移1个单位长度得到的.∴△EFG≌△ABC,∴S△EFG=S△ABC,∵AB=|4﹣(﹣5)|=9,CH=|5﹣0|=5,∴S△ABC=AB•CH=×9×5=;即S△EFG=S△ABC=.20.如图,已知AB∥CD,EF与AB、CD分别相交于点E、F,∠BEF与∠EFD的平分线相交于点P,求证:EP⊥FP.【考点】三角形内角和定理;角平分线的定义;平行线的性质.【分析】要证EP⊥FP,即证∠PEF+∠EFP=90°,由角平分线的性质和平行线的性质可知,∠PEF+∠EFP=(∠BEF+∠EFD)=90°.【解答】证明:∵AB∥CD,∴∠BEF+∠EFD=180°,又EP、FP分别是∠BEF、∠EFD的平分线,∴∠PEF=∠BEF,∠EFP=∠EFD,∴∠PEF+∠EFP=(∠BEF+∠EFD)=90°,∴∠P=180°﹣(∠PEF+∠EFP)=180°﹣90°=90°,即EP⊥FP.21.如图,∠1+∠2=180°,∠DAE=∠BCF,DA平分∠BDF.(1)AE与FC会平行吗?说明理由.(2)AD与BC的位置关系如何?为什么?(3)BC平分∠DBE吗?为什么?【考点】平行线的判定.【分析】(1)∠1+∠2=180°而∠2+∠CDB=180°,则∠CDB=∠1,根据同位角相等,两直线平行,求得结论;(2)要说明AD与BC平行,只要说明∠BCF+∠CDA=180°即可.而根据AE∥FC可得:∠CDA+∠DEA=180°,再据∠DAE=∠BCF就可以证得.(3)BC平分∠DBE即说明∠EBC=∠DBC是否成立.根据AE∥FC,可得:∠EBC=∠BCF,据AD∥BC得到:∠BCF=∠FAD,∠DBC=∠BAD,进而就可以证出结论.【解答】解:(1)平行;证明:∵∠2+∠CDB=180°,∠1+∠2=180°,∴∠CDB=∠1,∴AE∥FC.(2)平行,证明:∵AE∥FC,∴∠CDA+∠DAE=180°,∵∠DAE=∠BCF∴∠CDA+∠BCF=180°,∴AD∥BC.(3)平分,证明:∵AE∥FC,∴∠EBC=∠BCF,∵AD∥BC,∴∠BCF=∠FDA,∠DBC=∠BDA,又∵DA平分∠BDF,即∠FDA=∠BDA,∴∠EBC=∠DBC,∴BC平分∠DBE.22.如图,已知AD⊥BC,FG⊥BC,垂足分别为D、G.且∠1=∠2,猜想:∠BDE与∠C 有怎样的关系?说明理由.【考点】平行线的判定与性质.【分析】由题意可知AD∥FG,然后,结合已知条件即可推出∠2=∠3,推出DE∥AC,即可推出结论.【解答】解:∠BDE=∠C.理由如下:∵AD⊥BC,FG⊥BC,∴AD∥FG,∴∠1=∠3,∵∠1=∠2,∴∠2=∠3,∴DE∥AC,∴∠BDE=∠C.23.如图所示,已知AB∥CD,分别探究下面图形中∠APC,∠PAB,∠PCD的关系,请你从四个图形中任选一个,说明你所探究的结论的正确性.①结论:(1)∠APC+∠PAB+∠PCD=360°(2)∠APC=∠PAB+∠PCD(3)∠PCD=∠APC+∠PAB(4)∠PAB=∠APC+∠PCD②选择结论(1),说明理由.【考点】平行线的性质.【分析】①(1)过点P作PE∥AB,则AB∥PE∥CD,再根据两直线平行同旁内角互补即可解答;(2)过点P作l∥AB,则AB∥CD∥l,再根据两直线内错角相等即可解答;(3)根据AB∥CD,可得出∠PEB=∠PCD,再根据三角形外角的性质进行解答;(4)根据AB∥CD,可得出∠PAB=∠PFD,再根据∠PFD是△CPF的外角,由三角形外角的性质进行解答;②选择①中任意一个进行证明即可.【解答】解:①(1)过点P作PE∥AB,则AB∥PE∥CD,∴∠1+∠PAB=180°,∠2+∠PCD=180°,∴∠APC+∠PAB+∠PCD=360°;(2)过点P作直线l∥AB,∵AB∥CD,∴AB∥PE∥CD,∴∠PAB=∠3,∠PCD=∠4,∴∠APC=∠PAB+∠PCD;(3)∵AB∥CD,∴∠PEB=∠PCD,∵∠PEB是△APE的外角,∴∠PEB=∠PAB+∠APC,∴∠PCD=∠APC+∠PAB;(4)∵AB∥CD,∴∠PAB=∠PFD,∵∠PFD是△CPF的外角,∴∠PCD+∠APC=∠PFD,∴∠PAB=∠APC+∠PCD.②选择结论(1),证明同上.2016年5月21日。
