后方交会测量原理及其程序实现
后方交会法流程

后方交会法流程后方交会法呀,这可有点小意思呢。
后方交会法是一种在测量里挺有用的方法哦。
咱先说一下啥是后方交会法的基本原理吧。
它就是通过在未知点上设站,然后观测三个或者更多的已知控制点,根据这些观测数据来计算出这个未知点的坐标。
这就好比你在一个陌生的地方,你能看到周围几个你认识的标志性建筑,然后根据你看这些建筑的角度啊之类的信息,就能知道自己在啥位置啦。
那它的具体操作流程是啥样的呢?一、前期准备工作。
咱们得先准备好测量仪器呀,像全站仪这些,这就像是战士上战场要带好武器一样重要。
而且要保证仪器的状态良好,要是仪器出了问题,那后面测量出来的数据可就不准啦。
同时呢,还要拿到那些已知控制点的坐标资料,这可是关键的参考信息,没有这些,就像没了地图的旅行者,完全不知道方向呢。
二、设站。
把全站仪安置在这个未知点上,这个未知点的选择也有点小讲究哦。
要选择一个视野开阔的地方,这样才能很好地观测到那些已知控制点。
要是周围都是遮挡物,那可就没法好好测量啦。
在设站的时候呢,要把仪器调平,这一步可不能马虎,如果仪器没有调平,就像盖房子没有打好地基,后面的数据肯定是错得离谱。
三、观测已知控制点。
接下来就是观测那些已知控制点啦。
要仔细地测量每个控制点的水平角和垂直角之类的数据。
测量的时候要认真哦,多测几次取个平均值就更好啦,这样可以减少误差。
就像你做数学题,多检查几遍答案就更准确啦。
而且观测的时候要按照一定的顺序,这样不容易乱,也方便后面整理数据。
四、数据记录与整理。
把观测到的数据认真地记录下来,这可关系到最后的计算结果呢。
要是记录错了一个数字,那就像做饭放错了盐一样,整个味道就不对啦。
记录完之后呢,要检查一下有没有遗漏或者错误的地方。
然后根据这些数据开始计算未知点的坐标啦。
这个计算过程可能有点复杂,不过现在有很多软件可以帮助我们计算,但是咱也得知道计算的原理呀,不能完全依赖软件。
五、精度检查。
计算出坐标之后呢,可不能就这么完事儿了。
全站仪后方交会法步骤和高程测量步骤

1、角度测量(angle observation)(1)功能:可进行水平角、竖直角的测量。
(2)方法:与经纬仪相同,若要测出水平角∠AOB ,则:1)当精度要求不高时:瞄准A 点——置零(0 SET )——瞄准B 点,记下水平度盘HR 的大小。
2)当精度要求高时:——可用测回法(method of observation set )。
操作步骤同用经纬仪操作一样,只是配置度盘时,按“置盘”(H SET )。
2、距离测量(distance measurement )PSM 、PPM 的设置——测距、测坐标、放样前。
1)棱镜常数(PSM )的设置。
一般:PRISM=0 (原配棱镜),-30mm (国产棱镜)2)大气改正数(PPM )(乘常数)的设置。
输入测量时的气温(TEMP )、气压(PRESS ),或经计算后,输入PPM 的值。
(1)功能:可测量平距HD 、高差VD 和斜距SD (全站仪镜点至棱镜镜点间高差及斜距)(2)方法:照准棱镜点,按“测量”(MEAS )。
3、坐标测量(coordinate measurement )(1)功能:可测量目标点的三维坐标(X ,Y ,H )。
(2)测量原理任意架仪器,先设置仪器高为0,棱镜高是多少就是多少,棱镜拿去直接放在已知点上测高差,测得的高差为棱镜头到仪器视线的高差,当然,有正有负了,然后拿出计算器用已知点加上棱镜高,再加上或减去(因为有正有负)测得的高差就是仪器的视线高啊,因为仪器高为0,所以这个数字就是你的测站点高程,进测站点把它改成这个数字就行了,改完测站点了一般情况下都要打一下已知点复核一下。
若输入:方位角,测站坐标(,);测得:水平角和平距。
则有:方位角:坐标:若输入:测站S 高程,测得:仪器高i ,棱镜高v ,平距,竖直角,则有:高程:(3)方法:输入测站S (X ,Y ,H ),仪器高i ,棱镜高v ——瞄准后视点B ,将水平度盘读数设置为——瞄准目标棱镜点T ,按“测量”,即可显示点T 的三维坐标。
全站仪后方交会标准差算法 -回复

全站仪后方交会标准差算法-回复全站仪后方交会标准差算法是一种用于测量和校正地形和地形图数据中错误的算法。
本文将详细介绍后方交会的概念、全站仪的基本原理、后方交会标准差算法的步骤和计算方法。
一、后方交会的概念后方交会是一种测量方法,通过在地面上放置全站仪进行观测,然后根据观测数据和相关的地理位置信息,计算出地面上各个点的坐标位置。
后方交会在土地测量、工程测量、地形图绘制等领域都有广泛的应用。
二、全站仪的基本原理全站仪是一种精密的测量仪器,通过自动和手动调整观测仪器的参数,利用角度和距离观测测量点的水平和垂直角度以及与仪器的距离。
观测数据经过处理后,可以确定测量点的坐标位置。
全站仪具有快速、精确、全面和高效的特点,广泛应用于各种测量任务中。
三、后方交会标准差算法的步骤后方交会标准差算法包括以下几个步骤:1.观测数据采集:使用全站仪对目标点进行观测,记录水平角、垂直角和斜距数据。
观测过程中需要注意仪器的稳定和准确对准。
2.观测数据处理:按照测量次序和观测数据的特点,对观测数据进行处理和整理。
这包括数据的去除、筛选和修正等。
3.观测数据校正:根据已知和控制点的坐标,使用观测数据进行校正。
这个过程中需要使用后方交会标准差算法对数据进行处理。
4.测量点坐标计算:利用已校正的观测数据,结合先前测量的控制点坐标,使用三角法或其他测量计算方法,计算出待测点的坐标位置。
5.检查和调整:对计算得到的测量点坐标进行检查和调整,保证测量结果的准确性和可靠性。
如果发现误差较大或不符合预期要求,需要进行进一步的观测和调整。
四、后方交会标准差算法的计算方法后方交会标准差算法用于对观测数据进行处理和校正,以提高测量结果的精度。
其计算方法如下:1.计算观测数据的平均值:对每次观测数据的水平角、垂直角和斜距进行平均,得到平均值。
2.计算观测数据的中误差:对每次观测数据与平均值之差的平方进行求和,并除以总观测次数减1,得到中误差。
3.计算观测数据的方差:观测数据的方差等于中误差的平方。
摄影测量学空间后方交会实验报告

摄影测量学实验报告实验一、单像空间后方交会学院:建测学院班级:测绘082姓名:肖澎学号: 15一.实验目的1.深入了解单像空间后方交会的计算过程;2.加强空间后方交会基本公式和误差方程式,法线方程式的记忆;3.通过上机调试程序加强动手能力的培养。
二.实验原理以单幅影像为基础,从该影像所覆盖地面范围内若干控制点和相应点的像坐标量测值出发,根据共线条件方程,求解该影像在航空摄影时刻的相片外方位元素。
三.实验内容1.程序图框图2.实验数据(1)已知航摄仪内方位元素f=153.24mm,Xo=Yo=0。
限差0.1秒(2)已知4对点的影像坐标和地面坐标:3.实验程序using System;using System.Collections.Generic;using System.Linq;using System.Text;namespace ConsoleApplication3{class Program{static void Main(){//输入比例尺,主距,参与平参点的个数Console.WriteLine("请输入比例尺分母m:\r");string m1 = Console.ReadLine();double m = (double)Convert.ToSingle(m1);Console.WriteLine("请输入主距f:\r");string f1 = Console.ReadLine();double f = (double)Convert.ToSingle(f1);Console.WriteLine("请输入参与平差控制点的个数n:\r");string n1 = Console.ReadLine();int n = (int)Convert.ToSingle(n1);//像点坐标的输入代码double[] arr1 = new double[2 * n];//1.像点x坐标的输入for (int i = 0; i < n; i++){Console.WriteLine("请输入已进行系统误差改正的像点坐标的x{0}值:\r", i+1);string u = Console.ReadLine();for (int j = 0; j < n; j += 2){arr1[j] = (double)Convert.ToSingle(u);}}//2.像点y坐标的输入for (int i = 0; i < n; i++){Console.WriteLine("请输入已进行系统误差改正的像点坐标的y{0}值:\r", i+1);string v = Console.ReadLine();for (int j = 1; j < n; j += 2){arr1[j] = (double)Convert.ToSingle(v);}}//控制点的坐标输入代码double[,] arr2 = new double[n, 3];//1.控制点X坐标的输入for (int j = 0; j < n; j++){Console.WriteLine("请输入控制点在地面摄影测量坐标系的坐标的X{0}值:\r", j+1);string u = Console.ReadLine();arr2[j , 0] = (double)Convert.ToSingle(u);}//2.控制点Y坐标的输入for (int k = 0; k < n; k++){Console.WriteLine("请输入控制点在地面摄影测量坐标系的坐标的Y{0}值:\r", k+1);string v = Console.ReadLine();arr2[k , 1] = (double)Convert.ToSingle(v);}//3.控制点Z坐标的输入for (int p =0; p < n; p++){Console.WriteLine("请输入控制点在地面摄影测量坐标系的坐标的Z{0}值:\r", p+1);string w = Console.ReadLine();arr2[p , 2] = (double)Convert.ToSingle(w);}//确定外方位元素的初始值//1.确定Xs的初始值:double Xs0 = 0;double sumx = 0;for (int j = 0; j < n; j++){double h = arr2[j, 0];sumx += h;}Xs0 = sumx / n;//2.确定Ys的初始值:double Ys0 = 0;double sumy = 0;for (int j = 0; j < n; j++){double h = arr2[j, 1];sumy += h;}Ys0 = sumy / n;//3.确定Zs的初始值:double Zs0 = 0;double sumz = 0;for (int j = 0; j <= n - 1; j++){double h = arr2[j, 2];sumz += h;}Zs0 = sumz / n;doubleΦ0 = 0;doubleΨ0 = 0;double K0 = 0;Console.WriteLine("Xs0,Ys0,Zs0,Φ0,Ψ0,K0的值分别是:{0},{1},{2},{3},{4},{5}", Xs0, Ys0, Zs0, 0, 0, 0);//用三个角元素的初始值按(3-4-5)计算各方向余弦值,组成旋转矩阵,此时的旋转矩阵为单位矩阵I:double[,] arr3 = new double[3, 3];for (int i = 0; i < 3; i++)arr3[i, i] = 1;}double a1 = arr3[0, 0]; double a2 = arr3[0, 1]; double a3 = arr3[0, 2];double b1 = arr3[1, 0]; double b2 = arr3[1, 1]; double b3 = arr3[1, 2];double c1 = arr3[2, 0]; double c2 = arr3[2, 1]; double c3 = arr3[2, 2];/*利用线元素的初始值和控制点的地面坐标,代入共线方程(3-5-2),* 逐点计算像点坐标的近似值*///1.定义存放像点近似值的数组double[] arr4 = new double[2 * n];//----------近似值矩阵//2.逐点像点坐标计算近似值//a.计算像点的x坐标近似值(x)for (int i = 0; i < 2 * n; i += 2){for (int j = 0; j < n; j++){arr4[i] = -f * (a1 * (arr2[j, 0] - Xs0) + b1 * (arr2[j, 1] - Ys0) + c1 * (arr2[j, 2] - Zs0)) / (a3 * (arr2[j, 0] - Xs0) + b3 * (arr2[j, 1] - Ys0) + c3 * (arr2[j, 2] - Zs0)); }}//b.计算像点的y坐标近似值(y)for (int i = 1; i < 2 * n; i += 2){for (int j = 0; j < n; j++){arr4[i] = -f * (a2 * (arr2[j, 0] - Xs0) + b2 * (arr2[j, 1] - Ys0) + c2 * (arr2[j, 2] - Zs0)) / (a3 * (arr2[j, 0] - Xs0) + b3 * (arr2[j, 1] - Ys0) + c3 * (arr2[j, 2] - Zs0)); }}//逐点计算误差方程式的系数和常数项,组成误差方程:double[,] arr5 = new double[2 * n, 6]; //------------系数矩阵(A)//1.计算dXs的系数for (int i = 0; i < 2 * n; i += 2){arr5[i, 0] = -1 / m; //-f/H == -1/m}//2.计算dYs的系数for (int i = 1; i < 2 * n; i += 2){arr5[i, 1] = -1 / m; //-f/H == -1/m}//3.a.计算误差方程式Vx中dZs的系数for (int i = 0; i < 2 * n; i += 2)arr5[i, 2] = -arr1[i] / m * f;}//3.b.计算误差方程式Vy中dZs的系数for (int i = 1; i < 2 * n; i += 2){arr5[i, 2] = -arr1[i] / m * f;}//4.a.计算误差方程式Vx中dΦ的系数for (int i = 0; i < 2 * n; i += 2){arr5[i, 3] = -f * (1 + arr1[i] * arr1[i] / f * f);}//4.a.计算误差方程式Vy中dΦ的系数for (int i = 1; i < 2 * n; i += 2){arr5[i, 3] = -arr1[i - 1] * arr1[i] / f;}//5.a.计算误差方程式Vx中dΨ的系数for (int i = 0; i < 2 * n; i += 2){arr5[i, 4] = -arr1[i] * arr1[i + 1] / f;}//5.b.计算误差方程式Vy中dΨ的系数for (int i = 1; i < 2 * n; i += 2){arr5[i, 4] = -f * (1 + arr1[i] * arr1[i] / f * f);}//6.a.计算误差方程式Vx中dk的系数for (int i = 0; i < 2 * n; i += 2){arr5[i, 5] = arr1[i + 1];}//6.b.计算误差方程式Vy中dk的系数for (int i = 1; i < 2 * n; i += 2){arr5[i, 5] = -arr1[i - 1];}//定义外方位元素组成的数组double[] arr6 = new double[6];//--------------------外方位元素改正数矩阵(X)//定义常数项元素组成的数组double[] arr7 = new double[2 * n];//-----------------常数矩阵(L)//计算lx的值for (int i = 0; i < 2 * n; i += 2)arr7[i] = arr1[i] - arr4[i]; //将近似值矩阵的元素代入}//计算ly的值for (int i = 1; i <= 2 * (n - 1); i += 2){arr7[i] = arr1[i] - arr4[i]; //将近似值矩阵的元素代入}/* 对于所有像点的坐标观测值,一般认为是等精度量测,所以权阵P为单位阵.所以X=(ATA)-1ATL *///1.计算ATdouble[,] arr5T = new double[6, 2 * n];for (int i = 0; i < 6; i++){for (int j = 0; j < 2 * n; j++){arr5T[i, j] = arr5[j, i];}}//A的转置与A的乘积,存放在arr5AA中double[,] arr5AA = new double[6, 6];for (int i = 0; i < 6; i++){for (int j = 0; j < 6; j++){arr5AA[i, j] = 0;for (int l = 0; l < 2 * n; l++){arr5AA[i, j] += arr5T[i, l] * arr5[l, j];}}}nijuzhen(arr5AA);//arr5AA经过求逆后变成原矩阵的逆矩阵//arr5AA * arr5T存在arr5AARATdouble[,] arr5AARAT = new double[6, 2 * n];for (int i = 0; i < 6; i++){for (int j = 0; j < 2 * n; j++){arr5AARAT[i, j] = 0;for (int p = 0; p < 6; p++){arr5AARAT[i, j] += arr5AA[i, p] * arr5T[p, j];}}}//计算arr5AARAT x L,存在arrX中double[] arrX = new double[6];for (int i = 0; i < 6; i++){for (int j = 0; j < 1; j++){arrX[i] = 0;for (int vv = 0; vv < 6; vv++){arrX[i] += arr5AARAT[i, vv] * arr7[vv];}}}//计算外方位元素值double Xs, Ys, Zs, Φ, Ψ, K;Xs = Xs0 + arrX[0];Ys = Ys0 + arrX[1];Zs = Zs0 + arrX[2];Φ = Φ0 + arrX[3];Ψ = Ψ0 + arrX[4];K = K0 + arrX[5];for (int i = 0; i <= 2; i++){Xs += arrX[0];Ys += arrX[1];Zs += arrX[2];Φ += arrX[3];Ψ += arrX[4];K += arrX[5];}Console.WriteLine("Xs,Ys,Zs,Φ,Ψ,K的值分别是:{0},{1},{2},{3},{4},{5}", Xs0, Ys0, Zs0, Φ, Ψ, K);Console.Read();}//求arr5AA的逆矩public static double[,] nijuzhen(double[,] a) {double[,] B = new double[6, 6];int i, j, k;int row = 0;int col = 0;double max, temp;int[] p = new int[6];for (i = 0; i < 6; i++){p[i] = i;B[i, i] = 1;}for (k = 0; k < 6; k++){//找主元max = 0; row = col = i;for (i = k; i < 6; i++){for (j = k; j < 6; j++){temp = Math.Abs(a[i, j]);if (max < temp){max = temp;row = i;col = j;}}}//交换行列,将主元调整到k行k列上if (row != k){for (j = 0; j < 6; j++){temp = a[row, j];a[row, j] = a[k, j];a[k, j] = temp;temp = B[row, j];B[row, j] = B[k, j];B[k, j] = temp;i = p[row]; p[row] = p[k]; p[k] = i; }if (col != k){for (i = 0; i < 6; i++){temp = a[i, col];a[i, col] = a[i, k];a[i, k] = temp;}}//处理for (j = k + 1; j < 6; j++){a[k, j] /= a[k, k];}for (j = 0; j < 6; j++){B[k, j] /= a[k, k];a[k, k] = 1;}for (j = k + 1; j < 6; j++){for (i = 0; j < k; i++){a[i, j] -= a[i, k] * a[k, j];}for (i = k + 1; i < 6; i++){a[i, j] -= a[i, k] * a[k, j];}}for (j = 0; j < 6; j++){for (i = 0; i < k; i++){B[i, j] -= a[i, k] * B[k, j];}for (i = k + 1; i < 6; i++){B[i, j] -= a[i, k] * B[k, j];}for (i = 0; i < 6; i++) {a[i, k] = 0;a[k, k] = 1;}}//恢复行列次序for (j = 0; j < 6; j++){for (i = 0; i < 6; i++) {a[p[i], j] = B[i, j]; }}for (i = 0; i < 6; i++){for (j = 0; j < 6; j++) {a[i, j] = a[i, j];}}return a;}4.实验结果四.实验总结此次实验让我深入了解单像空间后方交会的计算过程,加强了对空间后方交会基本公式和误差方程式,法线方程式的记忆。
全站仪后方交会步骤

全站仪后方交会步骤在测量工程中,后方交会是一种常用的数据处理方法,用于确定点的坐标。
全站仪后方交会是通过使用全站仪进行测量,然后将测得的数据进行计算和处理,以确定点的坐标。
下面将介绍全站仪后方交会的步骤。
1. 收集测量数据在进行全站仪后方交会之前,首先需要进行测量。
使用全站仪进行测量,可以测量出目标点与其他已知点之间的水平角度、垂直角度和距离等数据。
这些数据将作为后方交会的基础。
2. 计算方位角在进行后方交会之前,需要确定目标点所在的方位角。
方位角是指目标点与基准点之间的水平角度。
可以通过在全站仪上设置一个已知点为基准点,然后测量目标点与基准点之间的水平角度来确定方位角。
3. 计算坐标增量在计算目标点坐标之前,需要计算方位角和水平角度之间的差异。
通过将测量数据中的方位角和角度减去基准点的方位角和角度,可以得到目标点的水平角度差和垂直角度差。
这些差值将被用于计算目标点的坐标增量。
4. 计算目标点坐标通过在基准点上测量已知点的坐标,并将基准点的坐标增量加上目标点的坐标增量,可以计算出目标点的坐标。
这样,就可以确定目标点的水平坐标和垂直坐标。
5. 检查数据完成全站仪后方交会后,应该对计算出的数据进行检查。
检查的目的是确保数据的准确性和一致性。
可以通过对已知点进行再次测量和计算,来验证计算出的目标点的坐标是否正确。
如果数据有误,应该重新检查和计算。
6. 绘制图形最后,可以使用计算出的目标点的坐标来绘制图形。
可以使用计算机辅助设计(CAD)软件或手绘来完成此任务。
根据测量数据和计算结果,可以绘制出点的坐标和连接线,从而形成一个完整的图形。
总结:全站仪后方交会是一种确定点坐标的常用方法。
通过收集测量数据、计算方位角和角度差、计算坐标增量,并最终计算目标点坐标,可以确定目标点的水平坐标和垂直坐标。
在进行这一过程的过程中,需要重视数据的准确性和一致性,并进行数据的检查和验证。
最后,通过绘制图形来展示计算出的结果。
摄影测量实验报告(空间后方交会—前方交会)
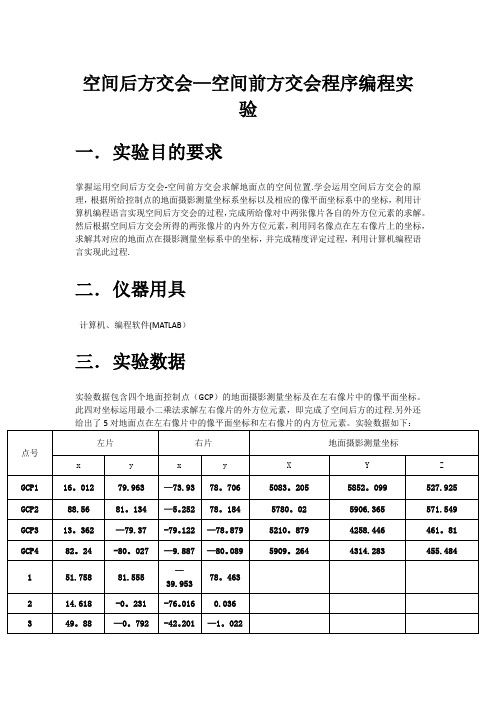
空间后方交会—空间前方交会程序编程实验一.实验目的要求掌握运用空间后方交会-空间前方交会求解地面点的空间位置.学会运用空间后方交会的原理,根据所给控制点的地面摄影测量坐标系坐标以及相应的像平面坐标系中的坐标,利用计算机编程语言实现空间后方交会的过程,完成所给像对中两张像片各自的外方位元素的求解。
然后根据空间后方交会所得的两张像片的内外方位元素,利用同名像点在左右像片上的坐标,求解其对应的地面点在摄影测量坐标系中的坐标,并完成精度评定过程,利用计算机编程语言实现此过程.二.仪器用具计算机、编程软件(MATLAB)三.实验数据实验数据包含四个地面控制点(GCP)的地面摄影测量坐标及在左右像片中的像平面坐标。
此四对坐标运用最小二乘法求解左右像片的外方位元素,即完成了空间后方的过程.另外还给出了5对地面点在左右像片中的像平面坐标和左右像片的内方位元素。
实验数据如下:内方位元素:f=152。
000mm,x0=0,y0=0 四.实验框图此过程完成空间后方交会求解像片的外方位元素,其中改正数小于限差(0。
00003,相当于0。
1'的角度值)为止。
在这个过程中采用迭代的方法,是外方位元素逐渐收敛于理论值,每次迭代所得的改正数都应加到上一次的初始值之中。
在空间后方交会中运用的数学模型为共线方程确定Xs,Ys,Zs的初始值时,对于左片可取地面左边两个GCP的坐标的平均值作为左片Xs 和Ys的初始值,取右边两个GCP的坐标平均值作为右片Xs 和Ys的初始值。
Zs可取地面所有GCP的Z坐标的平均值再加上航高.空间前方交会的数学模型为:五.实验源代码function Main_KJQHFJH()global R g1 g2 m G a c b1 b2;m=10000;a=5;c=4;feval(@shuru);%调用shuru()shurujcp()函数完成像点及feval(@shurujcp);%CCP有关数据的输入XYZ=feval(@MQZqianfangjh); %调用MQZqianfangjh()函数完成空间前方、%%%%%% 单位权中误差%%%%%后方交会计算解得外方位元素global V1 V2;%由于以上三个函数定义在外部文件中故需VV=[]; %用feval()完成调用过程for i=1:2*cVV(i)=V1(i);VV(2*i+1)=V2(i);endm0=sqrt(VV*(VV’)/(2*c-6));disp('单位权中误差m0为正负:’);disp(m0); %计算单位权中误差并将其输出显示输入GCP像点坐标及地面摄影测量坐标系坐标的函数和输入所求点像点坐标函数:function shurujcp()global c m;m=input(’摄影比例尺:');%输入GCP像点坐标数据函数并分别将其c=input('GCP的总数=');%存入到不同的矩阵之中disp('GCP左片像框标坐标:');global g1;g1=zeros(c,2);i=1;while i<=cm=input('x=');n=input('y=');g1(i,1)=m;g1(i,2)=n;i=i+1;enddisp('GCP右片像框标坐标:’);global g2;g2=zeros(c,2);i=1;while i〈=cm=input('x=’);n=input('y=’);g2(i,1)=m;g2(i,2)=n;i=i+1;end%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function shuru()global a;a=input('计算总像对点数='); %完成想计算所需的像平面坐标global b1;%坐标输入,存入不同的矩阵中b1=zeros(a,2);disp('左片像点坐标:')i=1;while i〈=am=input('x=’);n=input(’y=’);b1(i,1)=m;b1(i,2)=n;i=i+1;end%%global b2;b2=zeros(a,2);disp(’右片像点坐标:')i=1;while i〈=am=input('x=’);n=input('y=’);b2(i,1)=m;b2(i,2)=n;i=i+1;end%%global c;c=input(’GCP的总数=');disp('GCP摄影测量系坐标:’)global G;G=zeros(3,c);i=1;while i〈=cm=input(’X=');n=input(’Y=');v=input(’Z=');G(i,1)=m;G(i,2)=n;G(i,3)=v;i=i+1;end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%空间前方交会和后方交会函数:function XYZ=MQZqianfangjh()global R1 R2 a f b1 b2 Ra Rb;global X1 X2;R1=Ra;R2=Rb;R1=zeros(3,3);R2=zeros(3,3);global g1 g2 G V1 V2 V WF c QXX QXX1 QXX2;xs0=(G(1,1)+G(3,1))/2;ys0=(G(1,2)+G(3,2))/2;[Xs1,Ys1,Zs1,q1,w1,k1 R]=houfangjh(g1,xs0,ys0);%对左片调用后方交会函数R1=R;V1=V;WF1=WF;QXX1=QXX;save '左片外方位元素为。
后方交会测量原理及其程序实现

后方交会测量原理及其程序实现
摘要本文针对后方交会测量原理的定义、意义进行了概述,并归纳总结了后方交会测量原理的3种常见情况。
然后利用Visual Basic 6.0软件作为平台,对这3种情况进行了程序实现。
关键词后方交会;余弦定理;测边交会;边角交会;Visual Basic 6.0
0 引言
随着计算机的广泛普及和各种计算机语言的不断完善,利用计算机语言编制一些测量中常用的程序,以此来解决实地工作中的计算问题,深获测绘工作者的青睐。
本文总结了后方交会测量原理的几种情况,并尝试利用Visual Basic 6.0编写了后方交会测量原理的计算程序,在实地工作中得到了很好的应用。
1 后方交会测量原理
1.1 余切公式
根据A、B、C三个已知点的坐标(XA,YA)、(X B ,YB)、(XC,YC)及两个水平观测角α、β,计算出已知点到未知点的坐标方位角(这里以αBP 为例)。
然后根据这个坐标方位角及已知坐标增量和α、β角求出已知点到未知点的坐标增量,最后求得未知点的坐标XP,YP。
由图1可知,CP、BP、AP三条直线的方程式为
式中:为B点至P点的坐标方位角;
为A点坐标;
为B点坐标;
为C点坐标;
为P点坐标。
类似的计算方法还有赫尔默特公式(重心公式)等,这里就不再详述。
在此特别强调后方交会危险圆的问题:如图2所示,当未知点P在3个已知点所在的圆上移动时,总有下列式子成立,
即α和β固定不变,它说明此时仅有α、β这两个角和3个已知点不能唯一确定P点位置,因此称3个已知点所在的圆为后方交会危险圆。
当P点位于危险圆时,无论用何种后方交会公式,均无法求出P点坐标。
后方交会在施工测量中的应用与分析(图文)

后方交会在施工测量中的应用与分析(图文)后方交会法是测量学中广泛应用的一种几何测量方法,它可以用于对已知控制点的坐标及其相对位置关系进行测量,以推算待测对象的坐标。
在施工测量中,后方交会法常用于测量建筑物、道路、桥梁、隧道等工程结构的坐标,以保证这些结构的建造精度和安全性。
本文将介绍后方交会法在施工测量中的应用及其分析。
什么是后方交会法后方交会法是测量学中一种基本的几何测量方法,它利用已知控制点的坐标及其相对位置关系,通过测量目标物体上特定点的定向角、仰角和水平距离,从而推算出目标点的空间坐标。
后方交会法的基本步骤包括:观测控制点,计算控制点坐标,测量特定目标点的定向角、仰角和水平距离,推算目标点坐标,最后通过重算检查误差,保证准确性。
后方交会法的主要优点在于:适用范围广,可用于较大的空间距离,操作简便,精度高。
后方交会法在施工测量中的应用后方交会法在施工测量中的应用范围广泛,通常用于以下情况:1.建筑结构的定位和测量。
后方交会法可以用于建筑物立面的测量,如门、窗、墙角等标志性结构的位置和高度测量。
此外,后方交会法可用于逐层扫描建筑物自上而下的高程数据收集,以获取建筑物的立体信息。
2.道路、桥梁、隧道等工程结构的坐标测量。
后方交会法可用于收集地球表面上的架桥点坐标,以及地面各点之间的相对位置关系;同时,也可用于隧道和地下建筑物的GPS定位和导向。
3.土地测量。
后方交会法可用于土地界址的位置识别和土地面积的测量。
后方交会法在施工测量中的分析后方交会法在施工测量中的具体应用需要进行相应的分析,主要包括三个方面:观测条件的分析后方交会法在施工测量中需要满足一定的观测条件,观测条件的不同会对测量结果带来不同的影响。
例如,观测点数量的不足、观测角度的不合理等因素都会降低测量结果的精度。
因此,在施工测量前需要进行观测条件的充分分析,并选择合适的设备和方案。
推算过程的优化后方交会法在施工测量中的推算过程需要进行优化,以提高测量精度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
后方交会测量原理及其程序实现
摘要本文针对后方交会测量原理的定义、意义进行了概述,并归纳总结了后方交会测量原理的3种常见情况。
然后利用visual basic 6.0软件作为平台,对这3种情况进行了程序实现。
关键词后方交会;余弦定理;测边交会;边角交会;visual basic 6.0
中图分类号p2 文献标识码a 文章编号 1674-6708(2011)41-0174-02
0 引言
随着计算机的广泛普及和各种计算机语言的不断完善,利用计算机语言编制一些测量中常用的程序,以此来解决实地工作中的计算问题,深获测绘工作者的青睐。
本文总结了后方交会测量原理的几种情况,并尝试利用visual basic 6.0编写了后方交会测量原理的计算程序,在实地工作中得到了很好的应用。
1 后方交会测量原理
1.1 余切公式
根据a、b、c三个已知点的坐标(xa,ya)、(x b ,yb)、(xc,yc)及两个水平观测角α、β,计算出已知点到未知点的坐标方位角(这里以αbp 为例)。
然后根据这个坐标方位角及已知坐标增量和α、β角求出已知点到未知点的坐标增量,最后求得未知点的坐标xp,yp。
由图1可知,cp、bp、ap三条直线的方程式为
式中:为b点至p点的坐标方位角;
为a点坐标;
为b点坐标;
为c点坐标;
为p点坐标。
类似的计算方法还有赫尔默特公式(重心公式)等,这里就不再详述。
在此特别强调后方交会危险圆的问题:如图2所示,当未知点p 在3个已知点所在的圆上移动时,总有下列式子成立,即α和β固定不变,它说明此时仅有α、β这两个角和3个已知点不能唯一确定p点位置,因此称3个已知点所在的圆为后方交会危险圆。
当p点位于危险圆时,无论用何种后方交会公式,均无法求出p点坐标。
实际作业中,即使p点不正好在危险圆上,而是接近危险圆时,计算结果也会有较大的误差。
因此,一般规定:不得在之间。
1.2 测边交会
测得未知点p至两已知点a、b的水平距离为s1和s2。
根据已知点坐标可反算出ab间的坐标方位角和边长s0。
在△abp中用余弦定理可求得。
当两个已知点a、b之间互不通视的情况下,由未知点p测得与两已知点a、b之间的夹角θ和pa的距离s1,从而便可求出为未知
点p的坐标。
如图:在△abp中,应用正弦定理可求得b角
从而可计算角a和ap的方位角
待定点p的坐标为:
精度分析可以证明,b角较小,越接近时,交会点的精度较高。
所以,布设控制点时,应当注意这一点,一般应尽可能测量距待定点较近的边长。
2 后方交会原理的应用
随着科技的发展,在袖珍机广泛普及的今天,后方交会不仅能够解决实际工作中控制点相互不通视的困难,而且实践证明这种效果很好。
本文以2010年绍兴市王坛镇水利工程的施工控制网加密为例,来介绍后方交会在实地工程中的应用。
由于王坛镇多山、多林,所以我们在控制网加密过程中受到了地理条件的限制,经常会碰到首级控制点之间相互不通视或通视条件不好,为此我们采用了后方交会的办法解决施测过程中遇到的困难。
首先在互不通视的两个首级控制点wi02和wi03之间选择一个合时的位置打桩,在此建立一个加密图根点p。
然后运用边交会的方法,用测距仪测出pwi02、pwi03的距离s1、s2。
为了减小测量误差,我们采用3个人,每次观测3次的方法,从测量结果中剔除粗差,然后取其均值。
最后把采集的数据输入程序中,从而便可快
速求得p点的坐标。
在实际生产过程中取得了很好的效果。
3 程序的实现
3.1 程序的设计流程
通过对以上几种后方交会测量原理的总结,笔者采用visual basic6.0作为平台,编写了简单的计算程序。
3.2 工具界面
根据后方交会3种不同的情况,软件工具的功能分为3个部分,即判断运用的交会方法、数据的录入和结果的输出。
这里有3个命令按钮,分别输入相应的已知数据,运行相应的命令按钮,进而可以求得未知点p的坐标。
根据程序的功能和流程图,笔者设计了如下程序界面,如图3所示。
4 结论
后方交会在测量史上有着重要的意义,在野外测绘工作中被广泛应用。
从本文的编程尝试来看,将一些常用的测量计算,编制成具有简单界面的程序既简单又经济,而且又是行之有效的。
通过对这些交会方法的总结和程序的实现,从而使我们的思维也更加开阔,对后方交会测量原理有了一个清晰的认识。
参考文献
[1]赵夫来.现代测量学[m].解放军出版社,2003.
[2]孙现申.工程测量学[m].解放军出版社,2004.。
