变位斜齿轮设计计算,重合度计算
斜齿轮设计

1. 变位齿轮的几何尺寸
Z、m、α与标准齿轮相同 2. 变位齿轮的传动类型
高变位传动
角变位传动
正传动 负传动
3. 变位齿轮传动的设计步骤
3.8 齿轮常见的失效形式与设计准则
一、常见失效形式
轮齿拆断 齿面胶合
齿面点蚀 齿面磨损 齿面塑性变形
二、设计准则 1、对一般工况下的齿轮传动,其设计准则是: 保证足够的齿根弯曲疲劳强度,以免发生齿根折断。 保证足够的齿面接触疲劳强度,以免发生齿面点蚀。 2、对高速重载齿轮传动,除以上两设计准则外,还应按齿面抗胶合能力的准则进行设计。
da
dad2ha
hf
hf 1.25mn
df
df d2hf
h
hh ahf2 .2m 5 n
a a 1 2 ( d 1 d 2 ) 1 2 m t( z 1 z 2 ) 2 c m no ( z 1 s z 2 )
返回
标准直齿锥齿轮传动的主要几何尺寸计算公式
结语
谢谢大家!
齿轮齿根附近的渐开线齿廓将被切去一部分,这种现象称为根切。
力求避免
二、标准外啮合直齿轮的最少齿数
要使被切齿轮不产生根切,刀具的齿项线不得超过N点,即
斜齿轮正确啮合的条件和重合度

个中心距称为标准中心距,按照标准中心距进行安 装称标准安装。
11
a
6-4 渐开线齿轮的啮合传动
2.齿轮齿条啮合
齿轮齿条啮合时,相当于齿轮的分度圆与齿条的节圆作纯滚动。 标准安装时,齿条的节线与齿轮的分度圆相切。
此时, 当齿' 条圆离或靠近齿轮§6-1 §6-2 §6-3 §6-4 §6-5 §6-6 §6-7 §6-8 §6-9 §6-10 §6-11 §6-12 §6-13
齿轮传动的特点、应用与分类
渐开线的形成原理和特性
渐开线齿轮的参数及几何尺寸
渐开线齿轮的啮合传动
渐开线齿轮的切齿原理
根切现象与最少齿数
渐开线变位齿轮概述
6
a
6-3 渐开线齿轮的参数及几何尺寸
渐开线标准直齿圆柱齿轮几何尺寸公式表
名称
代号
公
式
分度圆直径
d
d1=mz1 d2=mz2
基圆直径 齿顶高 齿根高
齿顶圆直径 齿根圆直径
db
db1=mz1cos、 db2=mz2cos
ha
ha = ha*m
hf
hf = (ha* + c* )m
da
da1 d1 2ha m(z1 2ha* )
9
a
6-4 渐开线齿轮的啮合传动
一、正确啮合条件
两齿轮的正确啮合条件为:m1m2 m
12
即啮合条件为:两轮的模数和压力角必须分别相等。
二、连续传动条件 连续传动的条件为:B1B2 >= Pb
也可表示为: >= 1(即齿轮传动的重合度大 于等于1,一般取 =(1.1~1.4)
10
斜齿轮重合度啮合时间

斜齿轮重合度啮合时间
斜齿轮的重合度是指齿轮啮合时,在原始位置的两个齿的垂直间距,也可以理解为齿轮啮合时齿与齿之间的间隙。
斜齿轮的重合度的计算公式为:H = h*tanθ
其中,H表示重合度,h表示齿高,θ表示压力角。
齿轮的啮合时间是指齿轮从开始接触到完全啮合所经过的时间。
齿轮的啮合时间取决于齿轮的尺寸、齿数、轮齿面的质量、转速等因素,一般而言,啮合时间较短的齿轮具有更好的运动平稳性和传动效率。
啮合时间的计算可以通过分析齿轮的几何形状和运动学特性得到,也可以通过实验测量得到。
具体的计算方法需要根据齿轮的具体参数和运动状态进行分析,一般通过CAD软件或者专业的工程计算软件进行计算。
(完整版)齿轮强度校核及重合度计算(已优化)

深
参考表16.2-47选定
2
10 NL
6
0 .0191
参考GB/T3480-1997表14-1-98,按剃齿齿轮副选取
0.942 1550
15000000 0.962
1
12 工作硬化系数
ZW 图14-1-90或计算,大齿轮齿面硬度HBS>470
1
13 尺寸系数 14 最小安全系数
ZX 表14-1-99,按mn<7选取/
1.65105 大齿轮轴向重合度
εβ
传动比
u
3.929 节圆端面压力角
αt
齿轮为7级精度,齿形齿向均作修形,剃齿
齿轮上圆周力 N
节点线速度
mm/s
序号
输入系数
Ft v 代号
2T
d1
n d1
说明
16951 2.06 齿轮1
1 使用系数
Ka
参照表14-1-71说明
1
2 动载系数
Kv
1
K
K1 A
d
mtΒιβλιοθήκη z1mn z1 cos
径da
a
mn 2 cos
(z1 z2 )
角
αt
d a d 2ha
db d b d cos t
ha (ha*n x)mn
t arctan(tan n / cos )
28.5
3.43
28.5
3.43
48.02 188.65
4.5 3.2277
57.02
118.34 195.11
Ft b
K2
Z V 100
u2 1 u2
K1 K1、K2按表16.2-39查取,7级精度斜齿轮 K2 3 齿向载荷分布系数 KHβ、KF 参照表14-1-88/89说明按修形齿轮选取
第五章 齿轮机构及其设计习题解答

5.1 设已知一对渐开线齿轮的基圆、齿顶圆及主动轮1的角速度1ω的方向如图5.4(a )所示。
试作出啮合线,并指出理论啮合线和实际啮合线。
【分析】根据渐开线的性质,啮合线必和两轮的基圆相切,由于1ω逆时针方向旋转,故其应切于轮1基圆的左下方和轮2的右上方,设切点分别为1N 、212N N N ,与轮1和轮2齿顶圆的交点分别为21B B 和,则21N N 为理论啮合线,21B B 为实际啮合线。
解:如图5.4(b )所示。
【评注】本题主要考查对渐开线齿轮啮合原理和渐开线的性质及其相关知识的理解。
(a) (b)图5.45.2 在图 5.5所示轮系中,已知系杆H 为输入端,1000=H n min /r ,而齿轮4为输出端,min /104r n =,它们的转向如图所示。
20mm,3,99,101321=====αm z z z ,且均为直齿圆柱齿轮。
试求:(1)轮4的齿数4z ?(2)若齿轮1、2采用标准齿轮传动,求齿轮3、4的啮合角,说明无侧隙啮合时采用的传动类型。
(3)若齿轮1、2采用标准齿轮,而齿轮3、4改用斜齿圆柱齿轮,法面模数mm 3=n m ,3、4轮的β角应为多少?【分析】本题第一问涉及行星轮系传动比的计算,关于这方面的内容在第11章中将专门讨论。
其余二问涉及到齿轮传动与啮合角的关系,斜齿轮传动的中心距计算公式等,有关公式应当在理解基础上能够记住。
解:(1)求轮4的齿数。
21431441z z z z n n n n i H H H⋅=--=10010001010009910199412134=+⨯⨯=--⋅=HH n n n n z z z z图5.5(2)计算啮合角。
1,2为标准齿轮 mm 30023)10199(2)(2112=⨯+=+=mz z a而 mm 5.29823)10099(2)(4334=⨯+=+=mz z a要使轮系满足同心条件,则mm,300'34=a 故3,4轮的啮合角'34a 为 ︒=︒==773.2030020cos 5.298cos arccos1234'34a a a α由于mm 5.2983003412'34=>==a a a 故为正传动。
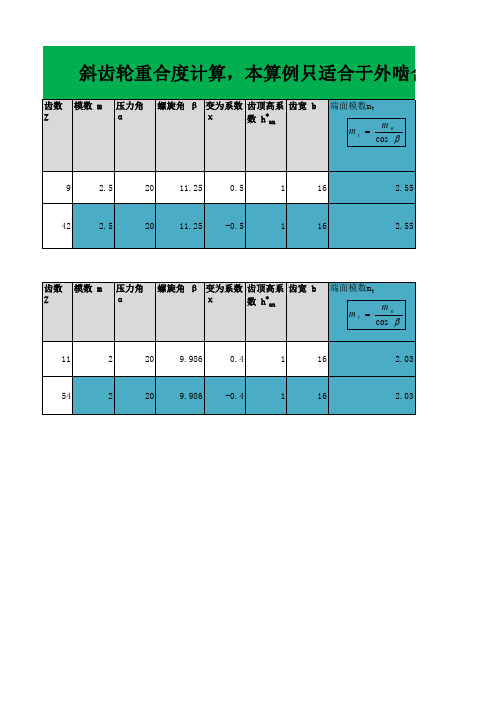
变位斜齿轮设计计算 重合度计算
1.34748596
0.39743474
1.7449207
端面重合度 εα
纵向重合度εβ
1 2
z1tan at1
tan t z2 tan at2
tan t
b sin mn
总重合度ε
γ
1.436109828
χ
数 h*an
端面模数mt
mt
mn cos
11
2
20
9.986
0.4
1
16
2.03
54
2
20
9.986 -0.4
1
16
2.03
于外啮合齿轮
分度圆直径 d
d
mt z1
mn z1 cos
齿顶高 ha
齿顶圆直径da 中心距 a
ha (ha*n x)mn d a d 2 h a
0.441578671 1.8776885
当量齿数zv
z v z 1 / cos 3
9.54 44.52
当量齿数zv
z v z 1 / cos 3
11.52 56.53
a
mn 2 cos
( z1
z2 )
22.94 107.06
3.75 1.25
30.44 109.56
65.00
分度圆直径 d
d
mt z1
mn z1 cos
齿顶高 ha
齿顶圆直径da 中心距 a
ha (ha*n x)mn d a d s
( z1
tan t
斜齿轮端面重合度计算公式

斜齿轮端面重合度计算公式斜齿轮端面重合度是指两个相互啮合的斜齿轮端面上的齿廓重合程度。
它是衡量齿轮传动质量的一个重要指标。
1.螺旋角系数法计算公式:假设A、B两个齿轮的模数分别为m1、m2,齿数分别为z1、z2,螺旋角分别为β1、β2。
螺旋方程为:cos(β1)/m1=cos(β2)/m2斜齿轮的端面重合度系数(σ)可根据以下公式计算:σ=(2*h)/(t1+t2)其中,h为齿高,t1和t2分别为齿槽高度。
它们的计算方式为:h=2*m1t1=h*tan(β1)t2=h*tan(β2)最终,斜齿轮端面重合度可以用以下公式计算:σ=(4*m)/(z1+z2)其中,m为AB两齿轮的法向模数的均值,计算方式为:m=(m1+m2)/22.模数系数法计算公式:假设A、B两个齿轮的模数分别为m1、m2,齿数分别为z1、z2。
斜齿轮的端面重合度系数(σ)可根据以下公式计算:σ=(2*h)/(t1+t2)其中,h为齿高,t1和t2分别为齿槽高度。
它们的计算方式为:h=2*m1t1=h*cos(α1)t2=h*cos(α2)其中,α1和α2分别为A、B两个齿轮齿槽线与轴线夹角的一半。
它们的计算方式为:α1=arctan(cos(β1)*tan(φ1))α2=arctan(cos(β2)*tan(φ2))其中,φ1和φ2分别为齿槽线与轴线的夹角。
它们的计算方式为:φ1=arctan(tan(β1)/cos(α1))φ2=arctan(tan(β2)/cos(α2))最终,斜齿轮端面重合度可以用以下公式计算:σ=(4*m)/(z1+z2)其中,m为AB两齿轮的法向模数的均值,计算方式为:m=(m1+m2)/2以上就是斜齿轮端面重合度计算的两种常见方法,根据具体情况选择适合的计算方法。
斜齿轮设计(史上最详细的计算过程,有图有表有计算)

例题:已知小齿轮传递的额定功率P=95 KW,小斜齿轮转速n1=730 r/min,传动比i=3.11,单向运转,满载工作时间35000h。
1.确定齿轮材料,确定试验齿轮的疲劳极限应力参考齿轮材料表,选择齿轮的材料为:小斜齿轮:38S i M n M o,调质处理,表面硬度320~340HBS(取中间值为330HBS)大斜齿轮:35S i M n, 调质处理, 表面硬度280~300HBS(取中间值为290HBS)注:合金钢可提高320~340HBS由图16.2-17和图16.2-26,按MQ级质量要求选取值,查得齿轮接触疲劳强度极限σHlim及基本值σFE:σHlim1=800Mpa, σHlim2=760MpaσFE1=640Mpa, σFE2=600Mpa2.按齿面接触强度初步确定中心距,并初选主要参数:按公式表查得:a≥476(u+1)√KT1φa σHP2u3 1)小齿轮传递扭矩T1:T1=9550×Pn1=9549×95730=1243N.m2)载荷系数K:考虑齿轮对称轴承布置,速度较低,冲击负荷较大,取K=1.63)查表16.2-01齿宽系数φα:取φα=0.44)齿数比u=Z2/Z1=3.115)许用接触应力σHP:σHP =σHlimS Hmin查表16.2-46,取最小安全系数s Hmin=1.1,按大齿轮计算σHP2=σHlim2S Hmin2=7601.1MPa=691MPa6)将以上数据代入计算中心距公式:a≥476(3.11+1)√ 1.6×12430.4×6912×3.113=292.67mm取圆整为标准中心距a =300mm7)确定模数:按经验公式m n=(0.007~0.02)α=(0.007~0.02)x300mm=2.1~6mm 取标准模数m n=4mm8)初选螺旋角β=9°,cosβ= cos9°=0.9889)确定齿数:z1=2acosβm n(u+1)=2×300×0.9884×(3.11+1)=36.06Z2=Z1i=36.03×3.11=112.15 Z1=36,Z2=112 实际传动比i实=Z2/Z1=112/36=3.111 10)求螺旋角β:cosβ=m n(Z1+Z2)2a =4×(36+112)2×300=0.98667,所以β=9°22’11)计算分度圆直径:d1=m n Z1cosβ=4×360.98667=145.946mmd2=m n Z2cosβ=4×1120.98667=454.053mm12)确定齿宽:b=Фα×a =0.4×300=120mm 13)计算齿轮圆周速度:V=πd1n160×1000=π×145.946×73060×100=5.58m/s根据齿轮圆周速度,参考表16.2-73,选择齿轮精度等级为8-7-7 (GB10095-2002)3.校核齿面接触疲劳强度根据σH=Z H Z E Zεβ√F1bd1u+1uK A×K V×K Hβ×K Ha1)分度圆上的圆周F1:F1=2T1d1=2×1243×103145.946=17034N2)使用系数K A:查表16.2-36,K A=1.5 3)动载荷系数K V:K V=1+(K1K A F1b+K2)Z1V100√u21+u2查表16.2-39得K1=23.9,K2=0.0087代入上式得K V =1+(23.91.5×17034120+0.0087)36×5.58100√ 3.1121+3.112 =1.234)接触强度计算的齿向载荷分布系数K H β,根据表16.2-40,装配时候检验调整:K Hβ=1.15+0.18×(b d 1)2+0.31×10−3×b=1.15+0.18×(120145.946)2+0.31×10−3×120=1.2695)齿间载荷分配系数K H α:查表16.2-42,得:K A F t b=1.5×17034120=213 N/mm 2,K H α=1.16)节点区域系数Z H ,查图16.2-15,Z H =2.477)弹性系数Z E ,查表16.2-43,Z E =189.8√MPa8)接触强度计算的重合度与螺旋角系数Zεβ:当量齿数:Z V1=Z1COS3β=360.986673=37.5Z V2=Z2COS3β=1120.986673=116.6当量齿轮的端面重合度εav:εav=εaI+εaII ,查图16.2-10,分别得到εaI=0.83,εaII=0.91,εav:εav=εaI+εaII=0.83+0.91=1.74按 φm=bm =1204=30, β=9°22’,查图16.2-11,得εβ=1.55按εav= 1.74,εβ=1.55,β=9°22`,查图16.2-16,得Zεβ=0.76 9)将以上数据代入公式计算接触应力σH=2.47×189.8×0.76×√17034120×145.946×3.11+13.11× √1.5×1.23×1.27×1.1=649MPa10)计算安全系数S H根据表16.2-34,S H=σHlimZ HT Z LVR Z W Z XσH寿命系数Z NT:按式16.2-10N1=60n1K h=60×730×1×35000=1.533×109N2=N1i=1.533×1093.11=4.93×108对调质钢(允许有一点的点蚀),查图16.2-18,Z NT1=0.98,Z NT2=1.04滑油膜影响系数Z LVR ,:按v=5.58m/s选用220号齿轮油,其运动粘度V40=220mm2/s查图16.2-19, Z得LVR =0.95工作硬化系数Z W,:因小齿轮未硬化处理,齿面未光整,故Z W=1尺寸系数Z X:查图16.2-22,Z X =1 将各参数代入公式计算安全系数S HS H1=σHlim1Z NT1Z LVRσH Z w Z X=800×0.98×0.95×1649=1.13S H2=σHlim2Z NT2Z LVRσH Z w Z X=760×1.04×0.95×1649=1.16根据表16.2-46,一般可靠度S Hmin=1~1.1,S H>S Hmin,故安全。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0.39743474
1.7449207
端面重合度 ε
α
纵向重合度ε
β
总重合度ε
γ
b sin db 1 arccos z tan tan z tan tan at1 t 2 at 2 t m d a 2 1 n
端面模数mt
mt
mn cos
11
2
20
9.986
0.4
1
16
2.03
54
2
20
9.986
-0.4
1
16
2.03
于外啮合齿轮
分度圆直径 d 齿顶高 ha 齿顶圆直径da 中心距 a
d m t z1
m n z1 * dm h ( h x) a n a an cos
d 2ha
斜齿轮重合度计算,本算例只适合于外啮合齿轮
齿数 Z 模数 m 压力角 α 螺旋角 β 变为系数 齿顶高系 齿宽 b * χ 数 h an 端面模数mt
mt
mn cos
9
2.5
20
11.25
0.5
1
16
2.55
42
2.5
20
11.25
-0.5
1
16
2.55
齿数 Z
模数 m
压力角 α
螺旋角 β
变为系数 齿顶高系 齿宽 b χ 数 h* an
22.34
27.94 66.00
109.66
1.2
112.06
端面压力角 α
t
基圆直径 db
齿顶圆压力角α
at
mn d b ) d cos ( z1 z2 ) t arctan(tan n / cos cos
20.36
t a arccos
db da
21.51
45.05
1.436109828
0.441578671
1.8776885
当量齿数zv
ቤተ መጻሕፍቲ ባይዱ
z v z 1 / cos
3
9.54
44.52
当量齿数zv
z v z 1 / cos
11.52
3
56.53
20.36
100.37
23.63
端面压力角 α
t
基圆直径 db
齿顶圆压力角α
at
mn d b ) d cos ( z1 z2 ) t arctan(tan n / cos cos
20.28
t a arccos
db da
20.95
41.41
20.28
102.86
23.38
端面重合度 ε
α
纵向重合度ε
β
总重合度ε
γ
b sin db 1 arccos z tan tan z tan tan at1 t 2 at 2 t m d a 2 1 n
1.34748596
a
mn ( z1 z 2 ) 2 cos
22.94
3.75
30.44 65.00
107.06
1.25
109.56
分度圆直径 d
齿顶高 ha
齿顶圆直径da
中心距 a
d m t z1
m n z1 * da a ( han x ) m n cosh
2.8
d 2ha
a
mn ( z1 z 2 ) 2 cos
