运筹学-图论
运筹学课件:第7章 图论与网络分析-第1,2节

v1
v2 a
v3
v4 c
b v1
a
v2
b
v3
d
d
v4
c
第2节 最小树问题
一、树及其性质 定义1: 无圈的连通图称为树。树一般用T表示。
定理1: 任给树T=(V,E),若P(T)≥2,则 T中至少有两个悬挂点。
证明:设µ=(v1,v2,…,vk)是G中含边数最多的 一条初等链,因P(T)≥2,并且T是连通的, 故链µ中至少有一条边,从而v1与vk是不同的 。
不少数学家都尝试去解析这个事例。而这些解析,最 后发展成为了数学中的图论。
例:中国邮路问题 一个邮递员送信,要走完他所负责的全部街道分送
信件,最后返回邮局。邮递员都会本能地以尽可能少的 行程完成送信任务。
问题:他如何走?
点:路口; 边:两路口之间道路,第i条道路长ei。
问题:求一个圈,过每边至少一次,并使圈长度最短。
由于T是树,由定义知T连通且无圈。只须证明m=n-1。
归纳法: 当n=2时,由于T是树,所以两点间显然有且 仅有一条边,满足m=n-1。
假设 n=k-1时命题成立,即有k-1个顶点时,T有k-2条边。
当n=k时,因为T连通无圈,k个顶点中至少有一个点次 为1。设此点为u,即u为悬挂点,设连接点u的悬挂边 为[v,u],从T中去掉[v,u]边及点u ,不会影响T的连 通性,得图T’,T’为有k-1个顶点的树,所以T’有k-2条 边,再把( v,u)、点u加上去,可知当T有k个顶点 时有k-1条边。
4
2
v4
94
v2
3
v3 8
0 9 2 4 7 9 0 3 4 0 其权矩阵为: A 2 3 0 8 5 4 4 8 0 6 7 0 5 6 0
图论知识点

图论知识点摘要:图论是数学的一个分支,它研究图的性质和应用。
图由节点(或顶点)和连接这些节点的边组成。
本文将概述图论的基本概念、类型、算法以及在各种领域的应用。
1. 基本概念1.1 节点和边图由一组节点(V)和一组边(E)组成,每条边连接两个节点。
边可以是有向的(指向一个方向)或无向的(双向连接)。
1.2 路径和环路径是节点的序列,其中每对连续节点由边连接。
环是一条起点和终点相同的路径。
1.3 度数节点的度数是与该节点相连的边的数量。
对于有向图,分为入度和出度。
1.4 子图子图是原图的一部分,包含原图的一些节点和连接这些节点的边。
2. 图的类型2.1 无向图和有向图无向图的边没有方向,有向图的每条边都有一个方向。
2.2 简单图和多重图简单图是没有多重边或自环的图。
多重图中,可以有多条边连接同一对节点。
2.3 连通图和非连通图在无向图中,如果从任意节点都可以到达其他所有节点,则称该图为连通的。
有向图的连通性称为强连通性。
2.4 树树是一种特殊的连通图,其中任意两个节点之间有且仅有一条路径。
3. 图的算法3.1 最短路径算法如Dijkstra算法和Bellman-Ford算法,用于在加权图中找到从单个源点到所有其他节点的最短路径。
3.2 最大流最小割定理Ford-Fulkerson算法用于解决网络流中的最大流问题。
3.3 匹配问题如匈牙利算法,用于解决二分图中的匹配问题。
4. 应用4.1 网络科学图论在网络科学中有广泛应用,如社交网络分析、互联网结构研究等。
4.2 运筹学在运筹学中,图论用于解决物流、交通网络优化等问题。
4.3 生物信息学在生物信息学中,图论用于分析蛋白质相互作用网络、基因调控网络等。
5. 结论图论是数学中一个非常重要和广泛应用的领域。
它不仅在理论上有着深刻的内涵,而且在实际应用中也发挥着关键作用。
随着科技的发展,图论在新的领域中的应用将会不断涌现。
本文提供了图论的基础知识点,包括概念、图的类型、算法和应用。
数学建模-图论

如例2中球队胜了,可从v1引一条带箭头的连线到v2,每 场比赛的胜负都用带箭头的连线标出,即可反映五个球队比 赛的胜负情况。如下图
v5
v1
v2 v3
v4
Байду номын сангаас
由图可知, v1三胜一 负, v4打了三场球, 全负等等
类似胜负这种非对称性的关系,在生产和生活中也是常见 的,如交通运输中的“单行线”,部门之间的领导和被领导关 系,一项工程中各工序之间的先后关系等等。
B
哥尼斯堡七桥问题
从某点出发通过每座桥且每桥只通过一次回到起点 A B D
建模:
C
A B D C
点——陆地 岛屿 边——桥
后来,英国数学家哈密尔顿在1856年提出“周游世界”的 问题:一个正十二面体,20个顶点分别表示世界上20个大城市, 要求从某个城市出发,经过所有城市一次而不重复,最后回到出 发地.这也是图论中一个著名的问题. “四色问题”也是图论中的著名问题:地图着色时,国境 线相邻的国家需要着上不同的颜色,最少需要几种颜色?1976 年,美国人阿佩尔和哈肯用计算机运行1200个小时,证明4种颜 色就够了.但至今尚有争议.
图论起源
图论最早处理的问题是哥尼 斯堡城的七桥问题:18世纪在哥 尼斯堡城(今俄罗斯加里宁格勒) 有一条名叫普莱格尔(Pregel) 的河流横经其中,河上有7座桥, 将河中的两个岛和河岸连结。
C A D
城中的居民经常沿河过桥 散步,于是提出了一个问 题:能否一次走遍7座桥, 后来有人请教当时的大数学家 而每座桥只许通过一次, 欧拉,欧拉用图论的方法证明这个问 最后仍回到起始地点? 题无解,同时他提出并解决了更为一 般的问题,从而奠定了图论的基础, 欧拉也被誉为“图论之父”.
哈尔滨工业大学运筹学教案教案_图论2

的一个不含圈的支撑子图Gk,于是Gk是G的一个支撑
树。
(一)破圈法
(二)避圈法 在图中任取一条边e1,找一条与e1不构成圈的边e2, 再找一条与{e1,e2}不构成圈的边e3。一般设已有{e1, e2,…,ek},找一条与{e1,e2,…,ek}中任何一些边 不构成圈的边ek+1,重复这个过程,直到不能进行为 止。
证明:必要性 因T是连通的,故任两个点之
间至少有一条链。但如果某两个点之间有两条链
的话,那么图T中含有圈,这与树的定义矛盾,从 而任两个点之间恰有一条链。
充分性 设图T中任两个点之间恰有一条链, 那么易见T是连通的,如果T中含有圈,那么这个 圈上的两个顶点之间有两条链,这与假设矛盾,
故T不含圈,于是T是树。
证明:(1)→(2) 由于T是树,由定义知T连通且无圈。只须证明m=n-1。 归纳法:当n=2时,由于T是树,所以两点间显然有且 仅有一条边,满足m=n-1。 假设 n=k-1时命题成立,即有k-1个顶点时,T有 k-2条边。 当n=k时,因为T连通无圈,k个顶点中至少有一 个点次为1。设此点为u,即u为悬挂点,设连接点u的 悬挂边为[v,u],从T中去掉[v,u]边及点u ,不会影 响T的连通性,得图T’,T’为有k-1个顶点的树,所以 T’有k-2条边,再把( v,u)、点u加上去,可知当T 有k个顶点时有k-1条边。
现证v1是悬挂点,即d(v1)=1。
反证法:如d(v1)≥2,则存在边[v1,vm],使m≠2,
v1
若vm不在µ 上,
v2
vk
vm
那么(vm,v1,v2,…,vk)比µ链边数多一条, 与µ 是边数最多的链矛盾。 若vm在µ 上
v1
v2
vm
图论在运筹学中的名词解释

图论在运筹学中的名词解释一、引言运筹学是一门研究复杂问题的学科,它借助各种数学方法和技术,帮助我们做出最佳的决策。
图论作为运筹学的重要工具之一,被广泛应用于解决各类实际问题。
本文将就图论在运筹学中的几个重要名词进行解释和探讨。
二、图图是图论的核心概念之一。
它由一组顶点和连接这些顶点的边组成。
在运筹学中,图可以用来描述和分析各种现实场景。
比如,交通网络可以用图来表示,道路是边,路口是顶点;社交网络可以用图来表示,用户是顶点,社交关系是边。
通过构建和分析图,我们可以揭示事物之间的关联性和特征,并利用这些信息进行决策。
三、路径路径是图论中一个重要概念。
它指的是在图中顶点之间连接的一系列边的序列。
在运筹学中,路径常常被用来表示两个顶点之间的最佳路线或最优解。
比如,在物流配送中,我们需要找到从仓库到目的地的最短路径,以最大程度地降低运输成本和时间。
通过图论的路径算法,我们可以高效地找到这样的最短路径,为物流管理提供有效支持。
四、最小生成树最小生成树是一种特殊的图结构,它是原图的一个子图,包含了所有顶点,但只有足够的边连接这些顶点,并使得整个图的总权重最小。
在运筹学中,最小生成树常常被用于解决资源分配和网络设计等问题。
比如,在电力输送系统中,我们需要将发电站和各个消费点以最短的电网连接起来,以确保电能的高效分配和传输。
通过构建最小生成树,我们可以优化电网的布局,降低能源损耗,提高供电可靠性。
五、网络流网络流是图论中的一个重要概念,它用来描述在一个有向图中通过各个边所能承载的最大流量。
在运筹学中,网络流被广泛应用于流程设计和资源调度问题。
比如,在工厂生产调度中,我们需要在供应链上对原材料、组件和成品进行优化配送,以实现最佳生产效率和降低成本。
通过分析网络流,我们可以确定各个节点的产能和需求,从而优化生产计划和物流调度。
六、最短路径最短路径是图论中的一个重要问题,即在图中找到连接两个顶点的最短路径。
在运筹学中,最短路径经常被用于解决物流和通信等问题。
华南理工大学 运筹学 第7章 图论-2(简) 工商管理学院

节点标号—对已标号未检查的节点v1,对与其相邻 、未标号的节点v4(前向非饱和弧)进行标号。
[+vs,4]
(7,3) v1 (7,2)
[+v1,4]
v4 (9,6)
(5,1) v2
[-, ∞]
vs
(8,4)
(4,0) (7,1) (16,5) (6,4) v5
18
(10,4)
vt
(4,0)
(10,4)
[-, ∞]
vs
(10,4)
(4,0) (10,4) v3
(16,5)
(6,4) v5
22
Ford-Fulkerson标号算法示例1
(第2轮迭代) 1-搜索过程:
节点标号—对节点v4(前向非饱和弧)进行标号。
[+vs,1]
(7,6) v1 (7,5)
[+v1,1]
v4 (9,9)
(5,1) v2
图G为流量网络。
2
最大流问题示例1
Petro公司的天然气管道输送网络:vs为Petro公 司的制气厂,vt为输送目的地的储气库,其它 中间节点为流量检测和控制站。各点间的弧代 表输送管道,其权值的两个数字分别表示容量 和当前的流量。问:如何利用输送管道,可以 使从制气厂运输到目的地的天然气最多?
(1) 已标号已检查;(2)已标号未检查;(3)未标号。
检查是指从一个已取得标号、未检查的节点vi 出发,搜寻与之邻接的其它未取得标号的节点 vj ,并根据vi的标号计算得到vj的标号。
7
Ford-Fulkerson标号算法
节点vj的标号为[+vi,θj]或[−vi,θj]:
运筹学-第六章 图论1

哥尼斯堡七桥问题 哥尼斯堡( 现名加里宁格勒) 哥尼斯堡 ( 现名加里宁格勒 ) 是 欧洲一个城市, Pregei河把该城分 欧洲一个城市 , Pregei 河把该城分 成两部分, 河中有两个小岛, 成两部分 , 河中有两个小岛 , 十八 世纪时, 世纪时 , 河两边及小岛之间共有七 座桥, 当时人们提出这样的问题: 座桥 , 当时人们提出这样的问题 : 有没有办法从某处( 出发, 有没有办法从某处 ( 如 A ) 出发 , 经过各桥一次且仅一次最后回到原 地呢? 地呢?
v2 5 0 v1
2 7 5
7 2
v5 v4
6 1 2 4
7
3
7 v3
v7
6
v6 6 2 与v1、V2、v3、v6、 v4 、v5相邻的点有v7 L17=min{L15+d57,L16+d67} =min{7+3,6+6}=10
v2 5 0 v1
2 7 5
7 2
v5 v4
6 1 2 4
7
3
7 v3
④重复上述步骤,直至全部的点 重复上述步骤,
都标完。 都标完。
例:如下图中从v1到v7的最短路。 v2
5 7 2
v5 v4
6 1 2 4 6 3
v1
2 7
v7 v6
v3
v2 0 v1
2 7 5
7 2
v5 v4
6 1 2 4 6 3
v3
v7
2
v6
与v1、v3相邻的点有v2、v4、v6 L1p=min{L11+d12,L13+d34,L13+d36} =min{0+5,2+7,2+4}=5=L12
运筹学上机试题5-图论
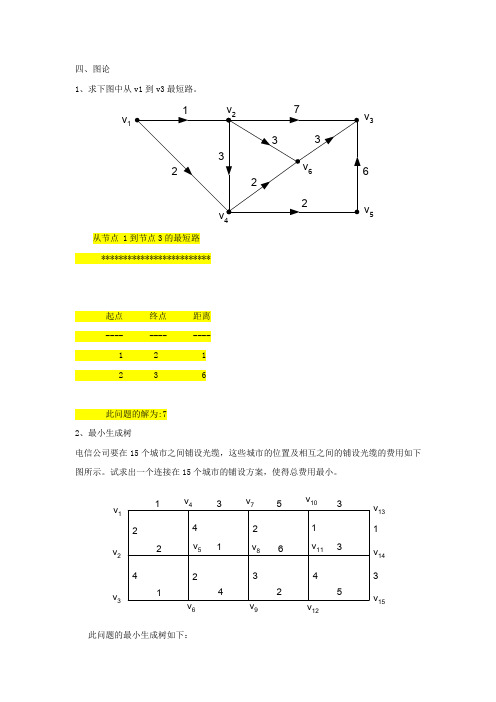
四、图论1、求下图中从v1到v3最短路。
v 1v 3v 546从节点 1到节点3的最短路 *************************起点 终点 距离 ---- ---- ---- 1 2 1 2 3 6此问题的解为:7 2、最小生成树电信公司要在15个城市之间铺设光缆,这些城市的位置及相互之间的铺设光缆的费用如下图所示。
试求出一个连接在15个城市的铺设方案,使得总费用最小。
v 1v 2v 3v 4v 5v 6v 7v 8v 9v 10v 11v 12v 13v 14v 152241131456422323135134此问题的最小生成树如下:*************************起点终点距离---- ---- ----1 4 11 2 22 5 25 8 15 6 26 3 18 7 28 9 39 12 212 11 411 10 110 13 313 14 114 15 3此问题的解为:283、最短路问题例. 求下图中从v1到各点的最短路,并指出有哪些点是不可达到的。
vv7v8v4从节点 1到节点2的最短路*************************起点终点距离---- ---- ---- 1 2 4此问题的解为:41到3没有路1到4没有路从节点 1到节点5的最短路*************************起点终点距离 ---- ---- ---- 1 5 1此问题的解为:1从节点 1到节点6的最短路*************************起点终点距离 ---- ---- ---- 1 5 1 5 6 6此问题的解为:7从节点 1到节点7的最短路*************************起点终点距离 ---- ---- ---- 1 7 3此问题的解为:3从节点 1到节点8的最短路*************************起点终点距离 ---- ---- ---- 1 5 1 5 6 66 8 3此问题的解为:104、最短路问题有6个村庄,各村庄的距离如下图所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
.
主要内容:
1 图的基本概念与基本定理 2 树和最小支撑树 3 最短路问题 4 最大流问题 5 最小费用流问题
.
什么是图?
图论中所谓的图是由一些点(vertices),和一 些连接兩点的边(edges)所形成的
.
5.1 图的基本概念与基本定理
图论是应用非常广泛的运筹学分支,它已经广 泛地应用于物理学控制论、信息论、工程技术、交 通运输、经济管理、电子计算机等各项领域。对于 科学研究、市场和社会生活中的许多问题,可以同 图论的理论和方法来加以解决。例如:各种通信线 路的架设,输油管道的铺设,铁路或者公路交通网 络的合理布局等问题,都可以应用图论的方法,简 便、快捷地加以解决问题。
.
图的基本概念
如果两个端点之间有两条以上的边,那么
称 为 它 们 为 多 重 边 , 如 图 5.4 中 的 边
[v1 ,v2] ,[v2 ,v1]。
v1
v2
v3 v4
.
一个无环,无多重边的图称为简单图, 一个无环,有多重边的图称为多重图。
v2(3)
v3(3)
(2)
v5
v1(2) v4(4) 简单图
v2 v
v
4
v
1
6
v3
v5
.
从以上的几个例子可以看出,我们用点和点 之间的线所构成的图,反映实际生产和生活中的
某些特定对象之间的特定关系。通常用点表示研 究对象,用点与点之间的线表示研究对象之间
的特定关系。由于在一般情况下,图中对象的相 对位置如何,点与点之间线的长短曲直,对于反 映研究对象之间的关系,显的并不重要,因此, 图论中的图与几何图、工程图等本质上是不同的。
v2 (3) v3 (3)
(2)
v5
(4)
v1
v4(6) 多重图
.
以点v为端点的边的个数称为点v的度(次),记 作 d(v), 如 图 5.4 中 d(v1)=3 , d(v2 )=4 , d(v3 )=4 , d(v4 )=3。
[v2 ,v4], [v3 ,v3]}
v3 v4
图 5.4
.
图5.5 是一个有向图D=(V,A)
其中V={v1 ,v2 ,v3 ,v4 ,v5 ,v6 ,v7} A={(v1,v2),(v1,v3),(v3 ,v2)(v3 ,v4),(v2 ,v4),(v4 ,v5), (v4 ,v6),(v5 ,v3),(v5 ,v4), (v5 ,v6),(v6 ,v7)}
图,记作D=(V, A),其中V表示有向图D的点集合,A表 示有向图D的弧集合。一条方向从vi 指向vj 的弧,记作 (vi , vj)。
.
图5.4是一个无向图G=(V,E),
其中V={v1 , v2 , v3 , v4}
v1
v2
E={[v1 , v2],[v2 ,v1],[v2 ,v3],
[v3 ,v4],[v1 ,v4],
郑州
济南 徐州
青岛 连云港
重庆
武汉 南京
上海
图5.3
.
例5.2 有六支球队进行足球比赛,我们分别用
点v1 ,…,v6表示这六支球队,它们之间的比赛情 况,也可以用图反映出来,已知v1队战胜v2 队,v2 队战胜v3 队,v3 队战胜v5队,如此等等。这个胜负
情况,可以用图5.3所示的有向图反映出来
C
A
B
D
.
哥尼斯堡七橋問題可以看成是:对这样一个封闭
的图形C ,是否可以一笔画完成它并且回到原点
A
B
D
数学家欧拉(Euler, 1707-1783) 于1736年严格地证明了上述哥尼斯 堡七桥问题无解,并且由此开创了图论的典型思维方式及论证方式
.
即能否从某一点开始不重复地一笔画出这个图形, 最终回到原点。欧拉在他的论文中证明了这是不可 能的,因为这个图形中每一个顶点都与奇数条边相 连接,不可能将它一笔画出,这就是古典图论中的 第一个著名问题。
.
Königsberg (Koenigsberg)
哥尼斯堡,原为东 普鲁士 (Prussia) 首 府,现属俄罗斯(飞 地),名为加里宁格
勒(Kaliningrad)
.
.
哥尼斯堡七桥问題: 要如何走过每座桥 恰一次,再返回出发点?
普瑞格爾河
.
哥尼斯堡七桥问题
C
A
B
D
.
哥尼斯堡七桥问题可简化为以下图形 其中的四个顶点都是奇顶点
v3
v5
v7
v1 v6
v2
v4
图 5.5
.
图的基本概念
一 个 图 G 或 有 向 图 D 中 的 点 数 , 记 作 P(G) 或 P(D),简记作P;边数或者弧数,记作q(G)或者 q(D),简记作q 。 如果边[vi ,vj] E ,那么称vi , vj 是边的端点, 或者vi ,vj是相邻的。如果一个图G中,一条边的 两个端点是相同的,那么称为这条边是环,如图 5.4中的边[v3 ,v3]是环。
在实际的生产和生活中,人们为了反映事物 之间的关系,常常在纸上用点和线来画出各式各样 的示意图。
.
图论应用举例
例如,在组织生产中,为完成某项任务,各工序之 间怎样衔接,才能使生产任务完成得既快又好。
一个邮递员送信,要走完他负责投递的全部街道, 完成任务后回到邮局,应该按照怎样的路线走,所 走的路程最短。
.
关于图的第一篇论文是瑞士数学家欧拉(E. Euler) 在1736年发表的解决“哥尼斯堡” 七桥难题的论文。
德国的哥尼斯堡城有一条普雷格尔河,河中有 两个岛屿,河的两岸和岛屿之间有七座桥相互连接, 当地的居民热衷于这样一个问题:一个散步者如何 能够走过这七座桥,并且每座桥只能走过一次,最 终回到原出发地。尽管试验者很多,但是都没有成 功。为了寻找答案,1736年欧拉将这个问题抽象成 图所示图形的一笔画问题。
各种通信网络的合理架设 交通网络的合理分布等
.
生 活 中 的 一 些 例 子
.
台大网路架构图
.
例5.1 图5.2是我国北京、上海、重庆等十四个城市之间的
铁路交通图,这里用点表示城市,用点与点之间的线表示城 市之间的铁路线。诸如此类还有城市中的市政管道图,民用 航空线图等等。
北京
太原
石家庄
பைடு நூலகம்天津 塘沽
.
图的基本概念
图论中的图是由点、点与点之间的线所组成的。通常, 我们把点与点之间不带箭头的线叫做边,带箭头的线叫 做弧。
如果一个图是由点和边所构成的,那么称为无向图,
记作G=(V,E),其中V表示图G 的点集合,E表示图G的
边集合。连接点vi , vj V 的边记作[vi , vj],或者[vj , vi]。 如果一个图是由点和弧所构成的,那么称为它为有向
