新人教版八年级数学上册滚动周练卷三同步训练(附答案)
「最新」八年级数学上册滚动周练卷三-可编辑修改

滚动周练卷(三)[时间:45分钟 测试范围:13.1~13.2 分值:100分]一、选择题(每题5分,共30分)1.[2016·松北模拟]下列平面图形中,不是轴对称图形的是( )A B C D2.[2016·奉贤区二模]下列说法中,正确的是( ) A .关于某条直线对称的两个三角形一定全等 B .两个全等三角形一定关于某条直线对称 C .面积相等的两个三角形一定关于某条直线对称 D .周长相等的两个三角形一定关于某条直线对称3.[2016春·户县期末]如图1,△ABC 与△A ′B ′C ′关于直线l 成轴对称,则下列结论中错误的是( )图1A .AB =A ′B ′ B .∠B =∠B ′C .AB ∥A ′C ′D .直线l 垂直平分线段AA ′4.[2016·龙岩模拟]如图2,在△ABC 中,分别以点A ,B 为圆心,大于12AB 的长为半径画弧,两弧分别交于点D ,E ,则直线DE 是( )图2A .∠A 的平分线B.AC边的中线C.BC边的高线D.AB边的垂直平分线5.[2016·深圳期末]如图3,△ABC中,AB的垂直平分线交AC于D,如果AC=5 cm,BC=4 cm,那么△DBC的周长是( )图3A.6 cm B.7 cm C.8 cm D.9 cm6.[2016·邹城市一模]若点A(a-2,3)和点B(-1,b+5)关于y轴对称,则点C(a,b)在( ) A.第一象限 B.第二象限C.第三象限 D.第四象限二、填空题(每题4分,共24分)7.[2016·临河校级月考]在直角坐标系中,点P(-3,2)关于x轴对称的点Q的坐标是__ __.8.下面是在计算器上出现的一些数字,其中是轴对称图形的是__ _.图49.[2016·黄岛期末]如图5,点P在∠AOB内,点M,N分别是点P关于AO,BO的对称点,若△PEF的周长等于20 cm,则MN的长为__ __.图510.[2016·永新期末]如图6,AD是△ABC的对称轴,点E,F是AD上的两点,若BD=2,AD=3,则图中阴影部分的面积是__ __.图611.[2016·祁阳期末]△ABC与△DEF关于直线m对称,AB=4,BC=6,△DEF的周长是15,则AC=__ __.12.[2016·江阴期中]如图7,△ABC的边BC的垂直平分线MN交AC于D,若△ADB的周长是10 cm,AB=4 cm,则AC=____cm.图7三、解答题(共46分)13.(8分)[2016·玄武期末]如图8,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).(1)画出△ABC关于y轴的对称图形△A1B1C1;(2)画出△A1B1C1沿x轴向右平移4个单位长度后得到的△A2B2C2;(3)如果AC上有一点M(a,b),请写出经过上述两次变换所得的对应边A2C2上的点M2的坐标.14.(8分)[2016·西市期中]电信部门要修建一座电视信号发射塔P,按照设计要求,发射塔P 到两城镇A,B的距离必须相等,到两条高速公路m和n的距离也必须相等.请在图中作出发射塔P的位置(尺规作图,不写作法,保留作图痕迹).15.(10分)[2016·青海期中]已知A(a+b,1),B(-2,2a-b),若点A,B关于x轴对称,求a,b的值.16.(10分)[2016·历下区一模]如图10,在△ABC中,∠ACB=90°,BE平分∠ABC交AC于点E,DE垂直平分AB于D.求证:BE+DE=AC.图1017.(10分)如图11,已知OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.求证:图11(1)PO平分∠APB;(2)OP是AB的垂直平分线.参考答案1.A 2.A 3.C 4.D 5.D 6.D7.(-3,-2) 8.2005 9.20 cm 10.3 11.5 12.613.解:(1)如答图所示:△A1B1C1即为所求;第13题答图(2)如答图所示:△A2B2C2即为所求;(3)M 2(-a +4,b ). 14.第14题答图解:设两条公路相交于O 点.P 应为线段AB 的垂直平分线与∠MON 的平分线交点或与∠QON 的平分线交点.如答图,满足条件的点有两个,即P ,P ′.15.解:∵A (a +b ,1),B (-2,2a -b )关于x 轴对称, ∴⎩⎪⎨⎪⎧a +b =-2,①2a -b =-1,②①+②得,3a =-3, 解得a =-1,将a =-1代入①得,-1+b =-2, 解得b =-1, ∴a =-1,b =-1.16.证明:∵∠ACB =90°,∴AC ⊥BC , ∵ED ⊥AB ,BE 平分∠ABC , ∴CE =DE , ∵DE 垂直平分AB , ∴AE =BE , ∵AE +CE =AC , ∴BE +DE =AC .17.证明:(1)∵OP 平分∠AOB ,PA ⊥OA ,PB ⊥OB ,∴PA =PB ,在Rt△AOP 和Rt△BOP 中,⎩⎪⎨⎪⎧PA =PB ,OP =OP ,∴Rt△AOP≌Rt△BOP,∴∠APO=∠BPO,即PO平分∠APB;(2)∵Rt△AOP≌Rt△BOP,∴OA=OB,又∵PA=PB,∴OP是AB的垂直平分线.。
2017-2018学年八年级上数学第三周测试卷(有答案)-(新课标人教版)AKwKAH

第三周九年级数学作业(2017年9月15日)班级 年 班 姓名__________ 家长签字____________ 分数_____________一、选择题(每空2分,共10分)1.下列各式中,是二次函数的是( )A .1x 2y +-=B .23x 2x 4y -=C .1x 1y 2+=D .2x 3y 2+= 2.下列四个二次函数:①2x y =,②2x 2y -=,③2x 21y =,④2x 3y =,其中抛物线开口从大到小的排列顺序是( )A .③①②④B .②③①④C .④②①③D .④①③②3.二次函数y=mx ²+m-2的图像的顶点在y 轴的负半轴上,且开口向上,则m 的取值范围是( )A.m >2B.m <2C.0<m <2D.m <04.二次函数2x y =的图象向右平移2个单位长度,得到新的图象的二次函数的表达式是( )A .2x y 2-=B .2)2x (y -=C .2x y 2+=D .2)2x (y +=5.函数2ax y =与b ax y +=(0a ≠,b<0)在同一坐标系中的大致图象为( )二、填空题(每空2分,共40分) 6.已知4a a 2x )2a (y -+-=是关于x 的二次函数,则a 的值为____________。
7.对于二次函数1x 2y 2+=,当1x -=时,=y ________,当19y =时,=x ________。
8.函数2x 8y -=的图象形状是________,开口向_____,对称轴是_______,顶点坐标是________;当x>0时,y 随x 的增大而_______,当x<0时,y 随x 的增大而_______。
9.函数3x 4y 2--=的图象形状是________,开口向_____,对称轴是_______,顶点坐标是________;当x_____0时,y 随x 的增大而减小,当x_____时,y 有最_____值,是=y _____,这个函数是由2x 4y -=的图象向_____平移_____个单位长度就可以得到了。
第10周——2022-2023学年人教版数学八年级上册周周测(含答案)

第十周——2022-2023学年人教版数学八年级上册周周测1.若M是关于x的三次多项式,N是关于x的五次多项式,则下列说法正确的是( )A.是关于x的八次多项式B.是关于x的二次多项式C.是关于x的八次多项式D.是关于x的十五次多项式2.下列多项式相乘,结果为的是( )A. B. C. D.3.已知,则的值等于( )A.-1B.0C.1D.无法确定4.下列计算错误的是( )A. B.C. D.5.若的结果中不含x的一次项,则p与q的关系是( )A. B. C. D.6.下列运算正确的是( )A. B.C. D.7.若,则A,B的大小关系为( )A. B. C. D.无法确定8.若的展开式中常数项为-2,且不含项,则展开式中次项的系数为( )A.-2B.2C.3D.-39.若中不含x的三次项,则_________.10.已知,则___________.11.若,其中a,b为整数,则的值为_________.12.计算:(1);(2);(3).答案以及解析1.答案:C解析:是关于x的五次多项式;故选项A错误;是关于x的五次多项式,故选项B错误;是关于x的八次多项式,故选项C正确,选项D错误.故选C.2.答案:C解析:A项,;B项,;C项,; D项,.故选C.3.答案:C解析:,原式,故选C.4.答案:D解析:,故D项计算错误.故选D.5.答案:C解析:,结果中不含x的一次项,.故选C.6.答案:D解析:选项A中,,故错误;选项B中,,故错误;选项C中,,故错误;选项D中,,故正确.7.答案:A解析:因为,所以,所以.故选A.8.答案:D解析:,因为展开式中常数项为-2,且不含项,所以,所以,所以一次项的系数为.故选D.9.答案:解析:,因为中不含x的三次项,所以,解得.10.答案:2解析:当时,.11.答案:4解析:,,,,,解得,,.12.答案:(1)原式.(2)原式.(3)原式.。
新人教版数学八年级上册 周滚动练(13.1~13.2)

周滚动练( 13.1~13.2)( 时间:45分钟满分:100分)一、选择题( 每小题4分,共28分)1.点A( 3,5 )关于x轴对称的点的坐标为( A)A.( 3,-5 )B.( -3,-5 )C.( -3,5 )D.( -5,3 )2.下列交通标志中,是轴对称图形的是( C)3.等腰直角三角形是轴对称图形,它的对称轴有( A)A.1条B.2条C.3条D.无数条4.把一个图形先沿着一条直线进行轴对称变换,再沿着与这条直线平行的方向平移,我们把这样的图形变换叫做滑动对称变换.在自然界和日常生活中,大量地存在这种图形变换( 如图1 ).结合轴对称变换和平移变换的有关性质,你认为在滑动对称变换过程中,两个对应三角形( 如图2 )的对应点所具有的性质是( B)A.对应点连线与对称轴垂直B.对应点连线被对称轴平分C.对应点连线被对称轴垂直平分D.对应点连线互相平行5.如图,在Rt△ABC中,∠C=90°,DE垂直平分AB,垂足为E,交AC于点D,连接BD,且DE∶BD=1∶2.若DE=2,则AC的值为( B)A.4B.6C.8D.106.到三角形三个顶点的距离相等的点是( D)A.三条角平分线的交点B.三边中线的交点C.三边上高所在直线的交点D.三边的垂直平分线的交点7.如图,∠ABC=50°,AD垂直平分线段BC于点D,∠ABC的平分线BE交AD于点E,连接EC,则∠AEC的度数是( A)A.115°B.105°C.75°D.50°二、填空题( 每小题5分,共20分)8.如图,D,E分别为△ABC的两边AB,AC上的点,将△ABC沿线段DE折叠,使点A落在BC边上的点F处.已知DE∥BC,∠B=55°,则∠BDF=70°.9.如图,在△ABC中,∠C=90°,BD平分∠ABC,交AC于点D.若AB=10,CD=3,则△ABD的面积是15.10.( 改编)甲和乙下棋,甲执圆子,乙执方子.如图,棋盘中心方子的位置用( 2,0 )表示,左下角方子的位置用( 1,-1 )表示,甲将第4枚圆子放入棋盘后,所有棋子构成一个轴对称图形,则他放的位置是( 2,1 ).11.如图,在3×3的正方形网格中,已有两个小正方形被涂黑,再将图中其余的小正方形任意涂黑一个,使整个图案构成一个轴对称图形的涂法有5种.三、解答题( 共52分)12.( 8分)如图所示,在平面直角坐标系xOy中,A( -1,5 ),B( -3,0 ),C( -4,3 ).( 1 )作出△ABC关于y轴对称的图形△A'B'C';( 2 )写出点C关于y轴的对称点C'的坐标.解:( 1 )图略.( 2 )C'( 4,3 ).13.( 10分)如图,在四边形ABCD中,∠BAD=∠BCD=90°,BC=DC.延长AD到点E,使DE=AB.( 1 )求证:∠ABC=∠EDC;( 2 )连接AC,求证:△ABC≌△EDC.证明:( 1 )在四边形ABCD中,∵∠BAD=∠BCD=90°,∴∠B+∠ADC=180°,又∵∠CDE+∠ADC=180°,∴∠ABC=∠EDC.( 2 )由( 1 )证得∠ABC=∠EDC,在△ABC和△EDC中,∴△ABC≌△EDC( SAS ).14.( 10分)如图,已知线段AB.( 1 )用尺规作图的方法作出线段AB的垂直平分线l( 保留作图痕迹,不要求写出作法); ( 2 )在( 1 )中所作的直线l上任意取两点M,N( 线段AB的上方),连接AM,AN,BM,BN.求证:∠MAN=∠MBN.略15.( 12分)如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C'的位置上.( 1 )折叠后,DC的对应线段是BC',CF的对应线段是C'F;( 2 )若∠1=50°,求∠2,∠3的度数;( 3 )若AE=6,求CF的长度.解:( 2 )∠2=50°,∠3=80°.( 3 )在长方形ABCD中,根据折叠得BC'=DC,CF=C'F,∠C'=∠C,∠EBC'=∠D=90°,∴∠ABC=∠EBC',∴∠ABE=∠C'BF.又∵AB=DC=BC',∠A=∠C',∴△ABE≌△C'BF( ASA ),∴C'F=AE,∴CF=C'F=AE=6.16.( 12分)如图,已知△ABC中BC边的垂直平分线DE与∠BAC的平分线交于点E,EF⊥AB,交AB的延长线于点F,EG⊥AC交AC于点G.求证:( 1 )BF=CG;( 2 )AF=( AB+AC).证明:( 1 )连接BE,CE.∵AE平分∠BAC,EF⊥AB,EG⊥AC,∴EF=EG.∵DE垂直平分BC,∴EB=EC.在Rt△EFB和Rt△EGC中,∴Rt△EFB≌Rt△EGC( HL ),∴BF=CG.( 2 )∵BF=CG,∴AB+AC=AB+BF+AG=AF+AG.易证Rt△AEF≌Rt△AEG( HL ),∴AF=AG=( AB+AC).。
第8周——2022-2023学年人教版数学八年级上册周周测(含答案)
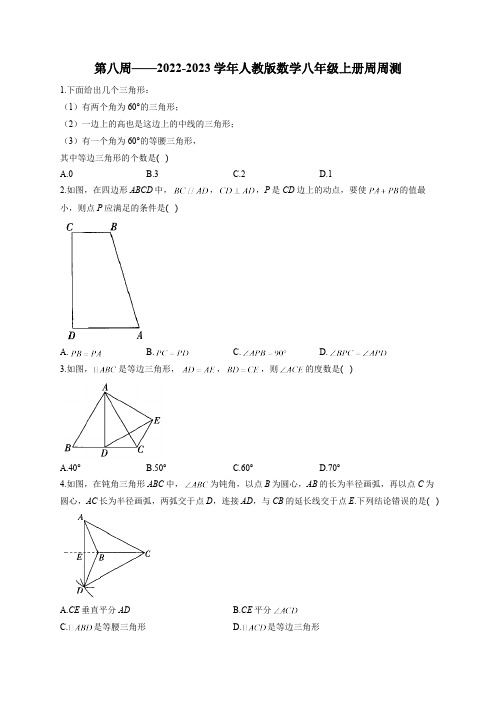
第八周——2022-2023学年人教版数学八年级上册周周测1.下面给出几个三角形:(1)有两个角为60°的三角形;(2)一边上的高也是这边上的中线的三角形;(3)有一个角为60°的等腰三角形,其中等边三角形的个数是( )A.0B.3C.2D.12.如图,在四边形ABCD中,,,P是CD边上的动点,要使的值最小,则点P应满足的条件是( )A. B. C. D.3.如图,是等边三角形,,,则的度数是( )A.40°B.50°C.60°D.70°4.如图,在钝角三角形ABC中,为钝角,以点B为圆心,AB的长为半径画弧,再以点C为圆心,AC长为半径画弧,两弧交于点D,连接AD,与CB的延长线交于点E.下列结论错误的是( )A.CE垂直平分ADB.CE平分C.是等腰三角形D.是等边三角形5.如图,牧童在A处放牛,其家在B处,A、B到河岸的距离分别为AC的长和BD的长,且,若点A到河岸CD的中点的距离为500米,则牧童从A处把牛牵到河边饮水再回家,最短距离是( )A.750米B.1000米C.1500米D.2000米6.如图,在等边中,BD平分交AC于点D,过点D作于点E,且,则AB的长为( )A.3B.4.5C.6D.7.57.如图,CD是的角平分线,的面积为12,BC的长为6,点E,F分别是CD,AC上的动点,则的最小值是( )A.6B.4C.3D.28.如图,等边三角形ABC的边长为4,AD是BC边上的中线,F是AD上的动点,E是AC边上一点.若,则取得最小值时,的度数为( )A.15°B.22.5°C.30°D.45°9.如图,在等边中,BD为AC边上的中线,CE为的平分线,BD、CE交于点M,则___________°.10.如图,在等边中,,点O在AC上,且,点P是AB上一动点,连接OP,将线段OP绕点O逆时针旋转60°得到线段OD.要使点D恰好落在BC上,则AP的长是____________.11.如图,直线m是中BC边的垂直平分线,点P是直线m上的动点.若,,,则的周长的最小值是_____________.12.如图,A,B,C是平面内三点.(1)按要求作图:①作射线BC,过点B作直线l,使A,C两点在直线l两旁;②点P为直线l上任意一点,点Q为射线BC上任意一点,连接线段AP,PQ.(2)在(1)所作图形中,若点A到直线l的距离为2,点A到直线BC的距离为5,点A,B之间的距离为8,点A,C之间的距离为6,求的最小值,并写出其依据.答案以及解析1.答案:C解析:易知(1)有两个角为60°的三角形的三个内角都是60°,(3)有一个角是60°的等腰三角形是等边三角形,所以(1)(3)为等边三角形,故等边三角形的个数是2.2.答案:D解析:如图所示,作点A关于CD的对称点,连接,交CD于点P,连接AP,则的最小值为的长,点P即为所求.点与点A关于CD对称,,,,故D符合题意.由图可知,选项A和选项B不成立,而C只有在时才成立,故选项C不一定成立.故选D.3.答案:C解析:是等边三角形,,,在和中,,,,故选C.4.答案:D解析:由题意可得,,直线CB是AD的垂直平分线,即CE垂直平分AD,故A选项结论正确;CE垂直平分AD,,,,即CE平分,故B选项结论正确;,是等腰三角形,故C选项结论正确;AD与AC不一定相等,不一定是等边三角形,故D选项结论错误.故选D.5.答案:B解析:作A关于CD的对称点,连接交CD于P,则,,,在和中,,,,,P为CD的中点,米,米.6.答案:C解析:是等边三角形,,,,,,,BD平分,,.7.答案:B解析:如图,作点A关于CD的对称点H.CD是的角平分线,点H一定在BC上.过H作于F,交CD于E,此时的值最小,的最小值.过A作于G.的面积为12,BC的长为6,,CD垂直平分AH,,,,的最小值是4,故选B.8.答案:C解析:如图,连接交于点是等边三角形的中线,,此时的值最小.是的中点.是等边三角形,平分,.,.故选C.9.答案:60解析:是等边三角形,,BD为AC边上的中线,CE为的平分线,,,.10.答案:6解析:,,.在和中,,,,.11.答案:10解析:直线m垂直平分BC,B、C两点关于直线m对称,如图,设直线m交AB于D,连接CD,则.当P和D重合时,的值最小,最小值等于AB的长,的周长的最小值是.12.答案:(1)(作法不唯一)如图所示,射线BC,直线l,线段AP,PQ即为所求.(2)如图,过点A作于点Q,交直线l于点P,此时的值最小.因为点A到直线BC的距离为5,所以的最小值为5,依据是垂线段最短.。
2019最新八年级数学上册滚动周练卷三

八年级数学上册滚动周练卷三
[时间:45分钟测试范围:13.1~13.2 分值:100分]
一、选择题(每题5分,共30分)
1.[2016·松北模拟]下列平面图形中,不是轴对称图形的是( )
A B C D
2.[2016·奉贤区二模]下列说法中,正确的是( )
A.关于某条直线对称的两个三角形一定全等
B.两个全等三角形一定关于某条直线对称
C.面积相等的两个三角形一定关于某条直线对称
D.周长相等的两个三角形一定关于某条直线对称
3.[2016春·户县期末]如图1,△ABC与△A′B′C′关于直线l成轴对称,则下列结论中错误的是( )
图1
A.AB=A′B′
B.∠B=∠B′
C.AB∥A′C′
D.直线l垂直平分线段AA′
4.[2016·龙岩模拟]如图2,在△ABC中,分别以点A,B为圆心,大于AB的长为半径画弧,两弧分别交于点D,E,则直线DE是( )
图2
A.∠A的平分线
B.AC边的中线
C.BC边的高线
D.AB边的垂直平分线
5.[2016·深圳期末]如图3,△ABC中,AB的垂直平分线交AC 于D,如果AC=5 cm,BC=4 cm,那么△DBC的周长是( )
图3。
八年级数学上学期周练试卷三含解析[新人教版]
![八年级数学上学期周练试卷三含解析[新人教版]](https://img.taocdn.com/s3/m/3f3350aa1711cc7931b716fd.png)
2015-2016学年四川省成都市嘉祥外国语学校八年级(上)周练数学试卷(三)一、用心选一选(每题3分,共30分)1.下列计算中,错误的是()A.﹣62=﹣36 B.()2=C.(﹣4)3=﹣64 D.(﹣1)100+(﹣1)1000=02.数轴上点A表示﹣4,点B表示2,则表示A,B两点间的距离的算式是()A.﹣4+2 B.﹣4﹣2 C.2﹣(﹣4)D.2﹣43.设x是有理数,那么下列各式中一定表示正数的是()A.2008x B.x+2008 C.|2008x| D.|x|+20084.下列各对数中,数值相等的是()A.﹣27与(﹣2)7B.﹣32与(﹣3)2C.﹣3×23与﹣32×2 D.﹣(﹣3)2与﹣(﹣2)35.若x的相反数是3,|y|=5,则x+y的值为()A.﹣8 B.2 C.8或﹣2 D.﹣8或26.已知a、b、c、d是互不相等的整数,且abcd=9,则a+b+c+d的值等于()A.0 B.4 C.8 D.不能求出7.如果a、b互为相反数,c、d互为倒数,m的绝对值为2,那么a+b+m2﹣cd的值为()A.3 B.±3 C.3±D.4±8.当a<0,化简,得()A.﹣2 B.0 C.1 D.29.下列结论不正确的是()A.若a>0,b>0,则a+b>0 B.若a<0,b<0,则a+b<0C.若a>0,b<0,则|a|>|b|,则a+b>0 D.若a<0,b>0,且|a|>|b|,则a+b>0 10. ++++…+的值为()A.1 B.C.1﹣D.二、填空题(11-14每题4分,共16分)11.计算:(﹣1)2008+(﹣1)2009÷|﹣1|= .12.如果a是7的相反数,b比a的相反数小﹣3,则b比a大.13.一口深井,井底有一只青蛙,这只青蛙白天沿着井壁向上爬3米,夜间又落下2米,到了第十天的下午,这只青蛙恰好爬到井口,则这口井的深度是.14.三个有理数a、b、c满足abc<0,a+b+c>0,当x=19÷(﹣7)﹣6÷(﹣7)+15÷(﹣7)时,x的值为.三、计算题15.①|﹣6+2|+(﹣8 )+|﹣3﹣|;②19÷(﹣7)﹣6÷(﹣7)+15÷(﹣7)③(﹣22)+3×(﹣1)6﹣(﹣2)④(﹣2)2010×(﹣)2009+(﹣6)×7⑤﹣12﹣[1+(﹣12)÷6]2×(﹣)3⑥×6﹣(﹣+)×18﹣×6⑦++…+⑧(﹣2)2015+(﹣2)2016.四、解答题16.已知|x﹣1|=2,(y+2)2=9,求xy﹣2y的值.17.若|a|=1,|b|=2,|c|=4,且|a+b﹣c|=a+b﹣c,求a+b+c的值.18.已知有理数a、b、c在数轴上所对应的点位置如图所示,原点为O.试化简|a+2b|﹣|a ﹣c|﹣|c﹣2b|+|c﹣b|.19.读一读:式子“1+2+3+4+5+…+100”表示1开始的100个连续自然数的和.由于上述式子比较长,书写也不方便,为了简便起见,我们可以将“1+2+3+4+5+…+100”表示为n,这里“”是求和符号.例如:1+3+5+7+9+…+99,即从1开始的100以内的连续奇数的和,可表示为(2n﹣1);又如13+23+33+43+53+63+73+83+93+103可表示为n3.通过对上以材料的阅读,请解答下列问题.(1)2+4+6+8+10+…+100(即从2开始的100以内的连续偶数的和)用求和符合可表示为;(2)计算(n﹣1).五、填空题20.定义a⊙b=是有理数范围内的一种运算,则(⊙)⊙= .21.若a,b为有理数,下列判断正确的个数有(填序号)(1)|m+1|+2总是正数;(2)a2+(ab﹣4)2总是正数;(3)5+(mn﹣5)2的最大值为5;④2﹣(mn+3)2的最大值为3.22.观察下列数:﹣1,2,﹣3,4,﹣5,6,﹣7,…,将这列数排成下列形式:﹣12﹣3 4﹣5 6﹣7 8﹣910﹣11 12﹣13 14﹣15 16…按照上述规律排下去,那么第11行从左边第9个数是;﹣2015在第行.23.若a,b,c为整数,且|a﹣b|+|c﹣a|=1,求|a﹣b|+|b﹣c|+|c﹣a|的值.24.有理数a,b,c均不为0,且a+b+c=0,设,试求x19﹣99x+2009的值.2015-2016学年四川省成都市嘉祥外国语学校八年级(上)周练数学试卷(三)参考答案与试题解析一、用心选一选(每题3分,共30分)1.下列计算中,错误的是()A.﹣62=﹣36 B.()2=C.(﹣4)3=﹣64 D.(﹣1)100+(﹣1)1000=0【考点】有理数的乘方.【分析】根据有理数的乘方的定义对各选项分别进行计算,然后利用排除法求解.【解答】解:A、﹣62=﹣36,故本选项错误;B、()2=,故本选项错误;C、(﹣4)3=﹣64,故本选项错误;D、(﹣1)100+(﹣1)1000=1+1=2,故本选项正确.故选D.2.数轴上点A表示﹣4,点B表示2,则表示A,B两点间的距离的算式是()A.﹣4+2 B.﹣4﹣2 C.2﹣(﹣4)D.2﹣4【考点】数轴.【分析】此题可借助数轴用数形结合的方法求解.结合图形:点A在数轴负方向上,点B 在数轴正方向上,A,B两点间的距离通过有理数减法求得.【解答】解:由数轴得,表示A,B两点间的距离的算式是2﹣(﹣4).故选C.3.设x是有理数,那么下列各式中一定表示正数的是()A.2008x B.x+2008 C.|2008x| D.|x|+2008【考点】非负数的性质:绝对值.【分析】根据任何一个数的绝对值都为非负数,再进行选择即可.【解答】解:A、当x≤0时,2008x<0,故A错误;B、当x≤﹣2008时,x+2008≤0,故B错误;C、当x=0时,2008x=0,故C错误;D、|x|≥0,则|x|+2008>0,故D正确,故选D.4.下列各对数中,数值相等的是()A.﹣27与(﹣2)7B.﹣32与(﹣3)2C.﹣3×23与﹣32×2 D.﹣(﹣3)2与﹣(﹣2)3【考点】有理数的乘方.【分析】根据有理数乘方的法则对个选项的值进行逐一判断,找出数值相同的项.【解答】解:A、根据有理数乘方的法则可知,(﹣2)7=﹣27,故A选项符合题意;B、﹣32=﹣9,(﹣3)2=9,故B选项不符合题意;C、﹣3×23=﹣24,﹣32×2=﹣18,故C选项不符合题意;D、﹣(﹣3)2=﹣9,﹣(﹣2)3=8,故D选项不符合题意.故选:A.5.若x的相反数是3,|y|=5,则x+y的值为()A.﹣8 B.2 C.8或﹣2 D.﹣8或2【考点】绝对值;相反数.【分析】首先根据相反数,绝对值的概念分别求出x、y的值,然后代入x+y,即可得出结果.【解答】解:x的相反数是3,则x=﹣3,|y|=5,y=±5,∴x+y=﹣3+5=2,或x+y=﹣3﹣5=﹣8.则x+y的值为﹣8或2.故选:D.6.已知a、b、c、d是互不相等的整数,且abcd=9,则a+b+c+d的值等于()A.0 B.4 C.8 D.不能求出【考点】有理数的乘法.【分析】根据题意可得出这四个数的值,继而可以确定这四个数的和.【解答】解:由题意得:这四个数小于等于9,且互不相等.再由乘积为9可得,四个数中必有3和﹣3,∴四个数为:1,﹣1,3,﹣3,和为0.故选A.7.如果a、b互为相反数,c、d互为倒数,m的绝对值为2,那么a+b+m2﹣cd的值为()A.3 B.±3 C.3±D.4±【考点】代数式求值;相反数;倒数.【分析】由题意a、b互为相反数,c、d互为倒数,m的绝对值为2,可知a+b=0,cd=1,|m|=2,把其代入a+b+m2﹣cd,从而求解.【解答】解:∵a、b互为相反数,c、d互为倒数,m的绝对值为2,∴a+b=0,cd=1,m2=4,∴a+b+m2﹣cd=0+4﹣1=3,故选A.8.当a<0,化简,得()A.﹣2 B.0 C.1 D.2【考点】绝对值;有理数的混合运算.【分析】负数的绝对值去绝对值符号时,代数式的符号改变.【解答】解:∵a<0,∴原式==﹣2.故选A.9.下列结论不正确的是()A.若a>0,b>0,则a+b>0 B.若a<0,b<0,则a+b<0C.若a>0,b<0,则|a|>|b|,则a+b>0 D.若a<0,b>0,且|a|>|b|,则a+b>0 【考点】有理数的加法.【分析】根据有理数的加法法则,举反例,排除错误选项,从而得出正确结果.【解答】解:∵b=2,a=﹣3,∴a+b=﹣1,∴D都错误;∴A、B、C正确.故选D.10. ++++…+的值为()A.1 B.C.1﹣D.【考点】分式的混合运算.【分析】根据+==1﹣, ++==1﹣,即可得出规律,从而得出正确选项.【解答】解:∵+=, +==1﹣,∴++++…+=1﹣;故选C.二、填空题(11-14每题4分,共16分)11.计算:(﹣1)2008+(﹣1)2009÷|﹣1|= 0 .【考点】有理数的混合运算.【分析】先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.【解答】解:(﹣1)2008+(﹣1)2009÷|﹣1|=1﹣1÷1=1﹣1=0.故答案为:0.12.如果a是7的相反数,b比a的相反数小﹣3,则b比a大17 .【考点】相反数.【分析】根据相反数,即可解答.【解答】解:∵a是7的相反数,∴a=﹣7,∵b比a的相反数小﹣3,∴b=7﹣(﹣3)=10,∴b﹣a=10﹣(﹣7)=17,故答案为:17.13.一口深井,井底有一只青蛙,这只青蛙白天沿着井壁向上爬3米,夜间又落下2米,到了第十天的下午,这只青蛙恰好爬到井口,则这口井的深度是12米.【考点】有理数的混合运算.【分析】每天上升的深度为(3﹣2)米,到第十天时井的深度为9×(3﹣2)+3,利用有理数运算法则进行计算.【解答】解:这口井的深度是9×(3﹣2)+3=12米.14.三个有理数a、b、c满足abc<0,a+b+c>0,当x=19÷(﹣7)﹣6÷(﹣7)+15÷(﹣7)时,x的值为﹣4 .【考点】有理数的混合运算.【分析】原式先计算除法运算,再计算加减运算,即可确定出x的值.【解答】解:x=19÷(﹣7)﹣6÷(﹣7)+15÷(﹣7)=﹣+﹣=﹣4,故答案为:﹣4三、计算题15.①|﹣6+2|+(﹣8 )+|﹣3﹣|;②19÷(﹣7)﹣6÷(﹣7)+15÷(﹣7)③(﹣22)+3×(﹣1)6﹣(﹣2)④(﹣2)2010×(﹣)2009+(﹣6)×7⑤﹣12﹣[1+(﹣12)÷6]2×(﹣)3⑥×6﹣(﹣+)×18﹣×6⑦++…+⑧(﹣2)2015+(﹣2)2016.【考点】有理数的混合运算.【分析】①原式利用绝对值的代数意义化简,计算即可得到结果;②原式先计算乘除运算,再计算加减运算即可得到结果;③原式先计算乘方运算,再计算乘法运算,最后算加减运算即可得到结果;④原式逆用积的乘方运算法则变形,计算即可得到结果;⑤原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果;⑥原式先计算乘法运算,再计算加减运算即可得到结果;⑦原式利用拆项法变形后,计算即可得到结果;⑧原式提取公因式,计算即可得到结果.【解答】解:①原式=3﹣8+3=7﹣8=﹣;②原式=﹣+﹣=﹣4;③原式=﹣4+3+2=1;④原式=(﹣2)×(2×)2009+(﹣7+)×7=﹣2﹣49+=﹣50;⑤原式=﹣1﹣(1﹣2)2×(﹣)=﹣1﹣×(﹣)=﹣1+=﹣;⑥原式=(﹣)×6﹣(14﹣15+7)=15﹣14+15﹣7=9;⑦原式=(﹣+﹣+…+﹣)=(﹣)=;⑧原式=(﹣2)2015×(1﹣2)=22015.四、解答题16.已知|x﹣1|=2,(y+2)2=9,求xy﹣2y的值.【考点】代数式求值.【分析】利用绝对值的代数意义,以及平方根的定义求出x与y的值,即可确定出xy﹣2y 的值.【解答】解:∵|x﹣1|=5,∴x=﹣4或x=6,∵(y+2)2=9,∴y=﹣5或y=1,当x=﹣4,y=﹣5时,xy﹣2y=20+10=30;当x=﹣4,y=1时,xy﹣2y=﹣4﹣2=﹣6;当x=6,y=﹣5时,xy﹣2y=﹣30+10=﹣20;当x=6,y=1时,xy﹣2y=6﹣2=4.则xy﹣2y的值是30或﹣6或﹣20或4.17.若|a|=1,|b|=2,|c|=4,且|a+b﹣c|=a+b﹣c,求a+b+c的值.【考点】绝对值.【分析】根据绝对值先求出a,b,c的值,再进行分类讨论,即可解答.【解答】解:∵|a|=1,|b|=2,|c|=4,∴a=±1,b=±2,c=±4,∵|a+b﹣c|=a+b﹣c,∴或或或∴a+b+c的值为﹣1或﹣5或﹣3或﹣7.18.已知有理数a、b、c在数轴上所对应的点位置如图所示,原点为O.试化简|a+2b|﹣|a ﹣c|﹣|c﹣2b|+|c﹣b|.【考点】整式的加减;数轴;绝对值.【分析】根据数轴上点的位置判断出绝对值里边式子的正负,利用绝对值的代数意义化简,计算即可得到结果.【解答】解:根据数轴上点的位置得:a<b<0<c,∴a+2b<0,a﹣c<0,c﹣2b>0,c﹣b>0,则原式=﹣a﹣2b+a﹣c﹣c+2b+c﹣b=﹣c﹣b.19.读一读:式子“1+2+3+4+5+…+100”表示1开始的100个连续自然数的和.由于上述式子比较长,书写也不方便,为了简便起见,我们可以将“1+2+3+4+5+…+100”表示为n,这里“”是求和符号.例如:1+3+5+7+9+…+99,即从1开始的100以内的连续奇数的和,可表示为(2n﹣1);又如13+23+33+43+53+63+73+83+93+103可表示为n3.通过对上以材料的阅读,请解答下列问题.(1)2+4+6+8+10+…+100(即从2开始的100以内的连续偶数的和)用求和符合可表示为;(2)计算(n﹣1).【考点】规律型:数字的变化类.【分析】(1)根据求和符号的含义和表示方法,判断出2+4+6+8+10+…+100(即从2开始的100以内的连续偶数的和)用求和符合可表示为多少即可.(2)根据等差数列的求和方法,求出(n﹣1)的值是多少即可.【解答】解:(1)2+4+6+8+10+…+100(即从2开始的100以内的连续偶数的和)用求和符合可表示为:.(2)(n﹣1)=(2+4+6+…+40)﹣20=×﹣20=210﹣20=190故答案为:.五、填空题20.定义a⊙b=是有理数范围内的一种运算,则(⊙)⊙= 1 .【考点】有理数的混合运算.【分析】首先理解a⊙b=的运算法则,然后求出(⊙),再根据刚刚求出结果利用运算法则去求最后的结果.【解答】解:∵(⊙)==,∴(⊙)⊙=⊙==1.故答案为:1.21.若a,b为有理数,下列判断正确的个数有(1)(4)(填序号)(1)|m+1|+2总是正数;(2)a2+(ab﹣4)2总是正数;(3)5+(mn﹣5)2的最大值为5;④2﹣(mn+3)2的最大值为3.【考点】非负数的性质:偶次方;非负数的性质:绝对值.【分析】根据绝对值、偶次方的非负性进行判断即可.【解答】解:∵|m+1|≥0,∴|m+1|+2>0,即|m+1|+2总是正数,(1)正确;a2≥0,(ab﹣4)2,≥0,则a2+(ab﹣4)2≥0,即a2+(ab﹣4)2总是非负数,(2)错误;5+(mn﹣5)2的最小值为5,(3)错误;2﹣(mn+3)2的最大值为3,(4)正确,故答案为:(1)(4).22.观察下列数:﹣1,2,﹣3,4,﹣5,6,﹣7,…,将这列数排成下列形式:﹣12﹣3 4﹣5 6﹣7 8﹣910﹣11 12﹣13 14﹣15 16…按照上述规律排下去,那么第11行从左边第9个数是﹣109 ;﹣2015在第45 行.【考点】规律型:数字的变化类.百度文库- 让每个人平等地提升自我【分析】由数字的排列可知:每行的最后一个数的绝对值是所在行数的平方,奇数为负,偶数为正,由此规律求得第10行的最后数字是102,再加上9就是第11行从左边第9个数字;由442=1936<2015<452=2025,可得﹣2015在第45行.【解答】解:根据每行的最后一个数的绝对值是所在行数的平方,所以第10行最后一个数字的绝对值是:10×10=100,第11行从左边第9个数是:100+9=109.∵442=1936,452=2025,﹣2015=﹣,∴﹣2015在第45行.故答案为﹣109;45.23.若a,b,c为整数,且|a﹣b|+|c﹣a|=1,求|a﹣b|+|b﹣c|+|c﹣a|的值.【考点】绝对值.【分析】由a、b、c为整数,且|a﹣b|+|c﹣b|=1,分两种情况①|a﹣b|=0,|c﹣a|=1,②|a ﹣b|=1,|c﹣a|=0求解出|b﹣c|的值,即可解答.【解答】解:∵a、b、c为整数,且|a﹣b|+|c﹣a|=1,∴①|a﹣b|=0,|c﹣a|=1,即a=b,|c﹣b|=|c﹣a|=1,|b﹣c|=1,②|a﹣b|=1,|c﹣a|=0,即c=a,|a﹣b|=|c﹣b|=|b﹣c|=1,综上所述|b﹣c|=1.∴|a﹣b|+|b﹣c|+|c﹣a|=1+1=2.24.有理数a,b,c均不为0,且a+b+c=0,设,试求x19﹣99x+2009的值.【考点】分式的加减法.【分析】根据题意可得a,b,c中不能全同号,必有一正两负或两正一负与a=﹣(b+c),b=﹣(c+a),c=﹣(a+b),则可得的值为两个+1,一个﹣1或两个﹣1,一个+1,即可求得x的值,代入即可求得答案.【解答】解:∵有理数a,b,c均不为0,且a+b+c=0,∴a,b,c中不能全同号,必有一正两负或两正一负,∴a=﹣(b+c),b=﹣(c+a),c=﹣(a+b),即,∴中必有两个同号,另一个符号与其相反,∴的值为两个+1,一个﹣1或两个﹣1,一个+1,∴x=1,∴原式=1﹣99+2009=1911.11。
2023-2024学年全国初中八年级上数学新人教版同步练习(含解析)

2023-2024学年全国八年级上数学同步练习考试总分:36 分 考试时间: 120 分钟学校:__________ 班级:__________ 姓名:__________ 考号:__________注意事项:1.答题前填写好自己的姓名、班级、考号等信息; 2.请将答案正确填写在答题卡上;卷I (选择题)一、 选择题 (本题共计 5 小题 ,每题 3 分 ,共计15分 )1. 将下列长度的三根木棒首尾顺次连接,能组成三角形的是 A.,,B.,,C.,,D.,,2. 一个三角形任意一边上的高都是这边上的中线,则对这个三角形最准确的判断是( )A.等腰三角形B.直角三角形C.等腰直角三角形D.等边三角形3. 作中边上的高,下列作法正确的是 A. B. C.()1248641265336△ABC BC AD ()D.4. 在下列各图形中,分别画出了中边上的高,其中正确的是( ) A. B. C. D.5. 已知三角形的两边长分别为和,则下列数据中能作为第三边长的是( )A.B.C.D.卷II (非选择题)二、 填空题 (本题共计 5 小题 ,每题 3 分 ,共计15分 )6.如图,在中,,,为中线,则与的周长之差________.△ABC BC AD 5934514△ABC AB =2013AC =2010AD △ABD △ACD =7. 若等腰三角形的两边长分别为和,则它的周长为__________;若等腰三角形的两边长分别是和,则它的周长为________.8. 已知等腰三角形的两条边长分别是和,则此三角形的周长为________.9. 如图,是的中位线,是的中点,的延长线交于点,则________.10.如图,在中,,,为中点,则线段的范围是________.三、 解答题 (本题共计 2 小题 ,每题 3 分 ,共计6分 )11. 已知,在中,==,平分,点是的中点,在上取点,使得=,与的延长线交于点.(1)当=时,①求的长;②求的大小.(2)当时,探究与的数量关系.12. 若等腰三角形一腰上的中线把它的周长分为或的两部分,求这个等腰三角形的底边和腰的长.373436DE △ABC M DE CM AB N :=S △DMN S 四边形ANME D △ABC AB AC 5AD ∠BAC M AC AD E DE AM EM DC F ∠BAC 90∘AE ∠F ∠BAC ≠90∘∠F ∠BAC 6cm 9cm参考答案与试题解析2023-2024学年全国八年级上数学同步练习一、 选择题 (本题共计 5 小题 ,每题 3 分 ,共计15分 )1.【答案】B【考点】三角形三边关系【解析】根据三角形三边关系定理:三角形两边之和大于第三边进行分析即可.【解答】解:、,不能组成三角形,故此选项错误;、,能组成三角形,故此选项正确;、,不能组成三角形,故此选项错误;、,不能组成三角形,故此选项错误.故选.2.【答案】D【考点】等边三角形的判定【解析】根据等腰三角形的性质易得这个三角形的三边都相等,然后根据等边三角形的判定方法可得这个三角形必为等边三角形.【解答】解:∵一个三角形任意一边上的高都是这边上的中线,即三角形任意一边上的高与中线重合,∴这个三角形的三边都相等,∴这个三角形必为等边三角形.故选.3.A 1+2<4B 6+4>8C 6+5<12D 3+3=6B DD【考点】三角形的高【解析】从三角形的一个顶点向它的对边引垂线,从顶点到垂足之间的线段是三角形的高,据此作高.【解答】解:根据高的定义:从三角形的一个顶点向它的对边引垂线,从顶点到垂足之间的线段是三角形的高,可得,正确.故选.4.【答案】D【考点】三角形的高【解析】根据三角形高的定义,逐项判定即可.【解答】解:过一个顶点作垂直于它对边所在直线的线段,叫做三角形的高线.作中边上的高过点且垂直于对边,只有选项正确.故选.5.【答案】C【考点】三角形三边关系【解析】利用两边之和大于第三边,两边之差小于第三边即可求解D D △ABC BC AD A BC D D解:设第三边长为,则,即,满足条件的只有选项.故选.二、 填空题 (本题共计 5 小题 ,每题 3 分 ,共计15分 )6.【答案】【考点】三角形的角平分线、中线和高【解析】根据三角形中线的定义可得,然后根据三角形的周长公式列式计算即可得解.【解答】解:∵为中线,∴,∴与的周长之差,∵,,∴与的周长之差.故答案为:.7.【答案】,或【考点】三角形三边关系【解析】此题暂无解析【解答】解:当等腰三角形的腰长为,底边为时,不满足三角形的三边关系.当等腰三角形的腰长为,底边为时,满足三角形的三边关系则该等腰三角形的周长.所以当等腰三角形的两边长分别为和时,它的周长为.当等腰长为,底边为时,满足三角形的三边关系,则该等腰三角形的周长.当等腰三角形的腰长为,底边为时,满足三角形的三边关系,则该等腰三角形的周长x 9−5<x <9+54<x <14C C 3BD =CD AD BD =CD △ABD △ACD =(AB +AD +BD)−(AC+AD+CD)=AB −AC AB =2013AC =2010△ABD △ACD =2013−2010=331711103773=7+7+3=17371734=3+3+4=1043.所以当等腰三角形的两边长分别为和,则它的周长为和.故答案为,和.8.【答案】【考点】等腰三角形的判定与性质三角形三边关系【解析】因为已知长度为和两边,没由明确是底边还是腰,所以有两种情况,需要分类讨论.【解答】解:当为底时,其它两边都为,,,可以构成三角形,周长为;当为腰时,其它两边为和,∵,所以不能构成三角形,故舍去,∴答案只有.故答案为:.9.【答案】【考点】平行线分线段成比例三角形中位线定理【解析】此题暂无解析【解答】此题暂无解答10.【答案】【答【考点】=4+4+3=11341011171011153636366153363+3=615151∶53<AD <6三角形三边关系【解析】延长至,使,根据三角形中线的定义可得,然后利用“边角边”证明和全等,根据全等三角形对应边相等可得,再根据三角形的任意两边之和大于第三边,任意两边之差小于第三边求出.的范围,然后求解即可.【解答】解:如图,延长至,使:是中边上的中线,.在和中,:故答案为:三、 解答题 (本题共计 2 小题 ,每题 3 分 ,共计6分 )11.【答案】当=时,①=;②连接.∵=,=,平分,∴,=.∵点是的中点,∴===,,∴==,∴=,∴==;当时,=.理由如下:∵=,平分,∴=.设=,则=.∵点是的中点,∴===,∴==,AD E DE =AD BD =CD △ABD △ECD CE =AB AE AD E DE =ADAD △ABC BC BD =CD△ABD △ECD AD =DE∠ADB =∠EDCBD =CD△ABD ≅△ECD(SAS)CE =AB =9AC =39+3=129−3=66<AE <123<AD <63<AD <6C∠BAC 90∘AE AD −DE =AB −DE =−2–√252–√252DM AB AC ∠BAC 90∘AD ∠BAC AD ⊥BC AD DC M AC DM MC AM DE DM ⊥AC ∠MDC ∠MDE 45∘∠DEM =(−)12180∘45∘67.5∘∠F −90∘67.5∘22.5∘∠BAC ≠90∘∠BAC 4∠F AB AC AD ∠BAC ∠ADC 90∘∠BAC 4x ∠DAC 2x M AC DM MC AM DE ∠ADM ∠DAC 2x DEM =(−2x)1∴=,∴===,∴=.【考点】等腰三角形的性质【解析】(1)①先根据等腰直角三角形的性质求出,根据线段中点的定义得出=,再代入=即可;②连接,根据等腰直角三角形的性质以及已知条件得出,=,===,,==,利用三角形内角和定理以及等边对等角求出=,那么==;(2)当时,先根据等腰三角形的性质得出=.设=,则=.根据直角三角形斜边中线的性质得出===,利用三角形内角和定理以及等边对等角求出==,=,那么===,从而得出=.【解答】当=时,①=;②连接.∵=,=,平分,∴,=.∵点是的中点,∴===,,∴==,∴=,∴==;当时,=.理由如下:∵=,平分,∴=.∠DEM =(−2x)12180∘−x 90∘∠F −DEM 90∘−(−x)90∘90∘x ∠BAC 4∠F AD =AB =2–√252–√2DE AM =52AE AD −DE DM AD ⊥BC AD DC DM MC AM DE DM ⊥AC ∠MDC ∠MDE 45∘∠DEM =(−)12180∘45∘67.5∘∠F −90∘67.5∘22.5∘∠BAC ≠90∘∠ADC 90∘∠BAC 4x ∠DAC 2x DM MC AM DE ∠ADM ∠DAC 2x ∠DEM =(−2x)12180∘−x 90∘∠F −DEM 90∘−(−x)90∘90∘x ∠BAC 4∠F ∠BAC 90∘AE AD −DE =AB −DE =−2–√252–√252DM AB AC ∠BAC 90∘AD ∠BAC AD ⊥BC AD DC M AC DM MC AM DE DM ⊥AC ∠MDC ∠MDE 45∘∠DEM =(−)12180∘45∘67.5∘∠F −90∘67.5∘22.5∘∠BAC ≠90∘∠BAC 4∠F AB AC AD ∠BAC ∠ADC 90∘∠BAC ∠DAC设=,则=.∵点是的中点,∴===,∴==,∴=,∴===,∴=.12.【答案】解:设等腰三角形的腰长、底边长分别为,.依题意,得 或 解得’或故这个等腰三角形的腰长为,底边长为 或腰长为,底边长为.【考点】等腰三角形的性质与判定【解析】此题暂无解析【解答】解:设等腰三角形的腰长、底边长分别为,.依题意,得 或 解得’或故这个等腰三角形的腰长为,底边长为 或腰长为,底边长为.∠BAC 4x ∠DAC 2x M AC DM MC AM DE ∠ADM ∠DAC 2x ∠DEM =(−2x)12180∘−x 90∘∠F −DEM 90∘−(−x)90∘90∘x ∠BAC 4∠F xcm ycm x +x =9,12x +y =612 x +x =6,12x +y =912{x =6y =3{x =4y =76cm 3cm 4cm 7cm xcm ycm x +x =9,12x +y =612 x +x =6,12x +y =912{x =6y =3{x =4y =76cm 3cm 4cm 7cm。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
滚动周练卷(三)
[时间:45分钟 测试范围:13.1~13.2 分值:100分]
一、选择题(每题5分,共30分)
1.[2016·松北模拟]下列平面图形中,不是轴对称图形的是( )
A B C D
2.[2016·奉贤区二模]下列说法中,正确的是( ) A .关于某条直线对称的两个三角形一定全等 B .两个全等三角形一定关于某条直线对称 C .面积相等的两个三角形一定关于某条直线对称 D .周长相等的两个三角形一定关于某条直线对称
3.[2016春·户县期末]如图1,△ABC 与△A ′B ′C ′关于直线l 成轴对称,则下列结论中错误的是( )
图1
A .A
B =A ′B ′ B .∠B =∠B ′
C .AB ∥A ′C ′
D .直线l 垂直平分线段AA ′
4.[2016·龙岩模拟]如图2,在△ABC 中,分别以点A ,B 为圆心,大于1
2AB 的长为半径画弧,
两弧分别交于点D ,E ,则直线DE 是( )
图2
A .∠A 的平分线
B .A
C 边的中线
C.BC边的高线
D.AB边的垂直平分线
5.[2016·深圳期末]如图3,△ABC中,AB的垂直平分线交AC于D,如果AC=5 cm,BC=4 cm,那么△DBC的周长是( )
图3
A.6 cm B.7 cm C.8 cm D.9 cm
6.[2016·邹城市一模]若点A(a-2,3)和点B(-1,b+5)关于y轴对称,则点C(a,b)在( ) A.第一象限 B.第二象限
C.第三象限 D.第四象限
二、填空题(每题4分,共24分)
7.[2016·临河校级月考]在直角坐标系中,点P(-3,2)关于x轴对称的点Q的坐标是__ __.8.下面是在计算器上出现的一些数字,其中是轴对称图形的是__ _.
图4
9.[2016·黄岛期末]如图5,点P在∠AOB内,点M,N分别是点P关于AO,BO的对称点,若△PEF的周长等于20 cm,则MN的长为__ __.
图5
10.[2016·永新期末]如图6,AD是△ABC的对称轴,点E,F是AD上的两点,若BD=2,AD =3,则图中阴影部分的面积是__ __.
图6
11.[2016·祁阳期末]△ABC与△DEF关于直线m对称,AB=4,BC=6,△DEF的周长是15,则AC=__ __.
12.[2016·江阴期中]如图7,△ABC的边BC的垂直平分线MN交AC于D,若△ADB的周长是10 cm,AB=4 cm,则AC=____cm.
图7
三、解答题(共46分)
13.(8分)[2016·玄武期末]如图8,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).
(1)画出△ABC关于y轴的对称图形△A1B1C1;
(2)画出△A1B1C1沿x轴向右平移4个单位长度后得到的△A2B2C2;
(3)如果AC上有一点M(a,b),请写出经过上述两次变换所得的对应边A2C2上的点M2的坐标.
14.(8分)[2016·西市期中]电信部门要修建一座电视信号发射塔P,按照设计要求,发射塔P到两城镇A,B的距离必须相等,到两条高速公路m和n的距离也必须相等.请在图中作出发射
塔P的位置(尺规作图,不写作法,保留作图痕迹).
15.(10分)[2016·青海期中]已知A(a+b,1),B(-2,2a-b),若点A,B关于x轴对称,
求a,b的值.
16.(10分)[2016·历下区一模]如图10,在△ABC中,∠ACB=90°,BE平分∠ABC交AC于点E,DE垂直平分AB于D.求证:BE+DE=AC.
图10
17.(10分)如图11,已知OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.求证:
图11
(1)PO平分∠APB;
(2)OP是AB的垂直平分线.
参考答案
1.A 2.A 3.C 4.D 5.D 6.D
7.(-3,-2) 8.2005 9.20 cm 10.3 11.5 12.6
13.解:(1)如答图所示:△A1B1C1即为所求;
第13题答图
(2)如答图所示:△A2B2C2即为所求;
(3)M2(-a+4,b).
14.
第14题答图
解:设两条公路相交于O 点.P 应为线段AB 的垂直平分线与∠MON 的平分线交点或与∠QON 的平分线交点.如答图,满足条件的点有两个,即P ,P ′.
15.解:∵A (a +b ,1),B (-2,2a -b )关于x 轴对称, ∴⎩⎪⎨
⎪
⎧a +b =-2,①2a -b =-1,②
①+②得,3a =-3, 解得a =-1,
将a =-1代入①得,-1+b =-2, 解得b =-1, ∴a =-1,b =-1.
16.证明:∵∠ACB =90°,∴AC ⊥BC , ∵ED ⊥AB ,BE 平分∠ABC , ∴CE =DE , ∵DE 垂直平分AB , ∴AE =BE , ∵AE +CE =AC , ∴BE +DE =AC .
17.证明:(1)∵OP 平分∠AOB ,
PA ⊥OA ,PB ⊥OB ,
∴PA =PB ,
在Rt△AOP 和Rt△BOP 中,
⎩
⎪⎨⎪⎧PA =PB ,OP =OP , ∴Rt△AOP ≌Rt△BOP ,
∴∠APO =∠BPO ,即PO 平分∠APB ; (2)∵Rt△AOP ≌Rt△BOP ,
∴OA=OB,又∵PA=PB,∴OP是AB的垂直平分线.。
