第九章 习题及答案教学文稿
管理学第九章课后习题答案

管理学第九章课后习题答案在管理学的学习过程中,课后习题是非常重要的一部分。
通过解答习题,我们可以更好地理解和掌握课堂上所学到的知识。
本文将为大家提供管理学第九章课后习题的答案,希望能够对大家的学习有所帮助。
第一题:什么是组织结构?它的作用是什么?组织结构是指组织中各个部门、岗位和个人之间的关系和相互联系的方式和形式。
它决定了组织中权力和责任的分配、信息流动的路径以及决策的层次和过程。
组织结构的作用是实现组织的目标和任务,提高组织的效率和竞争力。
第二题:什么是职权集中和职权分散?它们各自的特点是什么?职权集中是指权力和决策集中在组织的高层管理者手中。
这种结构下,高层管理者对组织的各项决策和权力具有绝对控制权,下属只需按照上级的指示执行即可。
职权集中的特点是决策速度快,执行效率高,适用于环境变化较快的情况。
职权分散是指权力和决策下放到组织的各个层级和部门。
这种结构下,下属具有一定的自主权和决策权,可以根据自己的判断和能力来执行任务。
职权分散的特点是灵活性强,适应性好,能够充分发挥下属的创造力和积极性。
第三题:什么是部门化组织结构?它的优缺点是什么?部门化组织结构是指将组织按照不同的职能或任务划分为若干个部门,每个部门负责特定的职能或任务。
部门化组织结构的优点是可以实现各个部门的专业化和分工,提高工作效率;可以便于管理者对各个部门进行监督和控制;可以适应不同的环境和任务需求。
缺点是部门之间的沟通和协调相对困难,可能会导致信息不畅通和决策不一致的问题。
第四题:什么是跨国公司?它的特点和挑战是什么?跨国公司是指在一个以上国家开展业务和经营活动的企业。
跨国公司的特点是具有全球化的视野和战略,可以在不同的国家和市场中获取资源和市场份额;具有多元化的文化和团队,可以融合不同国家和地区的人才和经验;具有全球化的供应链和价值链,可以实现资源的优化配置和价值的最大化。
跨国公司面临的挑战包括文化差异和管理难题,需要处理不同国家和地区的文化差异和管理方式;法律和政策风险,需要遵守不同国家和地区的法律和政策;市场和竞争压力,需要在全球市场中与其他跨国公司竞争。
结构化学课后答案第9章晶体的结构习题解答

第9章 晶体结构和性质习题解答【9.1】若平面周期性结构系按下列单位并置重复堆砌而成,试画出它们的点阵结构,并指出结构基元。
●●●●●●●●●●●●●●●●●●●●○○○○○○○○○○○○○○○○○○○○○○○○○○○○○○○○○○○○○○○解:用虚线画出点阵结构如下图,各结构基元中圈和黑点数如下表:1234567○○○○○○○○○○○○○○○○○○○○○○○○○○○○○○○○○○○○○○○●●●●●●●●●●●●●●●●●●●●图序号 1 2 3 4 5 6 7 结构基元数 1 1 1 1 1 1 1 黑点数 1 1 1 1 0 2 4 圈数1112313【评注】 从实际周期性结构中抽取出点阵的关键是理解点阵的含义,即抽取的点按连接其中任意两点的向量平移后必须能够复原。
如果不考虑格子单位的对称性,任何点阵均可划出素单位来,且素单位的形状并不是唯一的,但面积是确定不变的。
如果考虑到格子单位的对称形,必须选取正当单位,即在对称性尽量高的前提下,选取含点阵点数目尽量少的单位,也即保持格子形状不变的条件下,格子中点阵点数目要尽量少。
例如,对2号图像,如果原图是正方形,对应的正当格子单位应该与原图等价(并非现在的矩形素格子),此时结构基元包含两个黑点与两个圆圈。
【9.2】有一AB 型晶体,晶胞中A 和B 的坐标参数分别为(0,0,0)和(12,12,12)。
指明该晶体的空间点阵型式和结构基元。
解:晶胞中只有一个A 和一个B ,因此不论该晶体属于哪一个晶系,只能是简单点阵,结构基元为一个AB 。
【9.3】已知金刚石立方晶胞的晶胞参数a =356.7pm 。
请写出其中碳原子的分数坐标,并计算C —C 键的键长和晶胞密度。
解:金刚石立方晶胞中包含8个碳原子,其分数坐标为:(0,0,0),1(2,12,0),(12,0,1)2,(0,12,1)2,(14,14,1)4,3(4,34,1)4,(34,14,3)4,(14,34,3)4(0,0,0)与(14,14,14)两个原子间的距离即为C -C 键长,由两点间距离公式求得:C-C 356.7154.4pm r ====密度-13-10323-1812.0g mol 3.51 g cm (356.710cm)(6.022 10mol )A ZM D N V -⨯⋅==⋅⨯⨯⨯ 【9.4】立方晶系金属钨的粉末衍射线指标如下:110,200,211,220,310,222,321,400。
高等数学(同济第七版)第九章课后答案

-.《高"tt雪;')( ;r,乞履>rm习IA全航44, ’ ’i,、、J·.,-一,rr-T令,,、-M-·.‘FEE-’‘....l i··付守年,2-·’、fp····.,...、付’创刊令,-2、.四.,。
-H‘.,.JA、。
当”、句,‘-、,.-.-----号ri咱也k fi'l企:,i(r'J ;(,) f尔1’在.i!Iii i ra、2所l'..t全微分r.. l.主R F列的数的全做分:l I ) :二X)... ...:.. ; (2):=··-:14)u=‘., .( 3): sτ兰==:、f叶’.,.I·.·、-= .,ii: ”l' .‘Ez---虫”·飞”( I ) I晏为t;_=(,-干)‘1曹寸、-于)r1r.ii·i i·dz =ι二,I x+ , _ •h,,店,问向f t:l曾il=,l: \-二-.....,..,.h’,:1 2 l I崎').J...+二二,I‘冉、,1: d‘。
‘1’fr l'..lt、,I‘.“i,)dε =-飞、··....( l、牛+‘.}‘ii:_ -J '们飞!-+\1、厅可丁2( 3 > I叫11• , Iv飞+,--,--咱自---,电·、,、句’‘‘. t I--,l:,l 1、·"l1..t..1...-F‘{’. .,..,.,1: ·=、·,1‘φ. • ,I,A‘.11.,MFa,.’}iuyt吁《-Itl48 一、o,�舷学’{第七版)"F筋习忍金’E8ε27.6 一二一一-二I.JO 号i S 2 127. 8 !:, · 12.钊JU 1: l校纷iaF I乎):内政之佣的地(,j i克i:丁j宫。
高等数学课后习题答案--第九章

9. 设 x n >0,
10. 讨论下列级数的收敛性(包括条件收敛与绝对收敛)
182
⑴ ⑶ ⑸ ⑺ ⑼
x sin ; n n =1 ∞ n (−1) n −1 n −1 ; ∑ 3 n =1 n +1 ∞ (−1) ( x > 0 ); ∑ n =1 n + x
∑ (−1)
∞
n +1
⑵ ⑷ ⑹ ⑻ ⑽
180
(4) (6)
∑
∞
∞
n =1 ∞
∑
n =1
ln n ln n 1 ln n 1 n 1 , = = 3 . 收敛; < 2 2 n n n n n n n2 1 1 1 , < , 收敛; n ln (n + 2) ln(n + 2) 2
n
(5)
收敛;
(7) (8) (13) (14)
∑ (
n =1
n −1
)
n
发散
由于 lim (10
a −1
1 n
n →∞
= ln a , 而 n n − 1 > n a − 1 ;
(11)
发散;
∑
n =1
∞
∞
∑
n =1
( n + 1 − n − 1 ), ( n + 1 − (2n − n + 1 − n − 1) = (n −
2 2 2 2 2
(9) 收敛;
收敛;
5.利用级数收敛的必要条件,证明: nn (1) lim = 0, (2) n →∞ ( n !) 2
∞
n →∞
lim
( 2 n) ! = 0. 2 n ( n +1)
第九章课后题答案

《第九章压强》《9.1压强》1.估测你站立时对地面的压强。
根据你的体重可以得到你对地面的压力,再测量你站立时鞋底和地面的接触面积。
为简单起见,假设双脚站立时,整个鞋印范围都与地面接触(如图)。
测量时,在方格纸上画出鞋底的轮廓,看鞋底占有多少个小格(不满一个时,大于半格的算一格,小于半格的不算),再乘以每一小格的面积。
根据得到的数据,计算你对地面的压强。
如果图中每个小格的边长是1cm,某同学的质量为 50kg,他对地面的压强是多大?与你对地面的压强相比哪个大?-4 2 -2 2S=133x1x10 m x2=2.66 xIO mF=G=mg=50kg x9.8N/kg=490N£.=——490 -------- = x 4P a x hH 1.84 10 Ha° 22.66 10 m略2.解释下列现彖锯、剪刀、斧头,用过一段时间就要磨一磨,为什么?书包为什么要用宽的背带, 用细绳?啄木鸟有个坚硬而细长的嘴,这对它的生存为什么特别重要?(1)通过减小受力面积来增大压强;(2)通过增大受力面积来减小压强;(3)由于受力面积小,可以对树产生较大的压强。
再加上比较坚硬,更容易将树啄开,捉到树内的小虫子。
3.骆驼的体重比马大不了一倍,而它的脚掌面积是马蹄的三倍。
这位它在沙漠行走提供了什么有利条件?骆驼与马虽然对地产生的压力差不到一倍,但由于骆驼与沙漠的受力面积却是马蹄与沙漠的受力面积的三倍,根据P F可知,骆驼对地面的压强要比马蹄对沙漠的压强小,使得骆驼在沙漠上行走时不易陷入沙屮。
召图钉尖的面积是 5x102,手指对钉帽的压力使 20N,手4.一个图钉帽的面积是0.8cmcm _ Y对图钉帽的压强和佟I钉矣对墙的压强各是多少?而不F 20N25 1Q5 Pa= -5-=0.8 10 4 =帽X _ 2mF 20NP 小 5 8 8墙S 4 10 Pa墙284 10Pa10 m《9.2液体的压强》1.一个空的塑料药瓶,瓶口扎上橡皮膜,竖直的浸入水中,一次瓶口朝上,一次瓶口朝下, 这两次药瓶在水里的位置相同(如图)。
高等数学 课后习题答案第九章
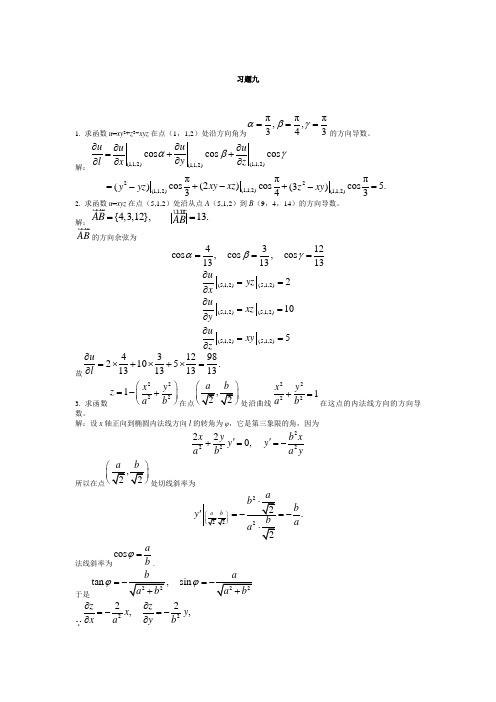
习题九1. 求函数u =xy 2+z 3-xyz 在点(1,1,2)处沿方向角为πππ,,343αβγ===的方向导数。
解:(1,1,2)(1,1,2)(1,1,2)cos cos cos u u u uy l x z αβγ∂∂∂∂=++∂∂∂∂22(1,1,2)(1,1,2)(1,1,2)πππcoscos cos 5.(2)()(3)343xy xz y yz z xy =++=---2. 求函数u =xyz 在点(5,1,2)处沿从点A (5,1,2)到B (9,4,14)的方向导数。
解:{4,3,12},13.AB AB ==AB的方向余弦为4312cos ,cos ,cos 131313αβγ=== (5,1,2)(5,1,2)(5,1,2)(5,1,2)(5,1,2)(5,1,2)2105uyz x uxz yuxy z ∂==∂∂==∂∂==∂故4312982105.13131313u l∂=⨯+⨯+⨯=∂ 3. 求函数22221x y z a b ⎛⎫=-+ ⎪⎝⎭在点处沿曲线22221x y a b +=在这点的内法线方向的方向导数。
解:设x 轴正向到椭圆内法线方向l 的转角为φ,它是第三象限的角,因为2222220,x y b x y y a b a y ''+==-所以在点处切线斜率为2.b y a a '==-法线斜率为cos ab ϕ=.于是tan sin ϕϕ== ∵2222,,z z x y x a y b ∂∂=-=-∂∂∴2222zl a b⎛∂=--=∂⎝4.研究下列函数的极值:(1)z=x3+y3-3(x2+y2); (2)z=e2x(x+y2+2y);(3)z=(6x-x2)(4y-y2); (4)z=(x2+y2)22()e x y-+;(5)z=xy(a-x-y),a≠0.解:(1)解方程组22360360xyz x xz y y⎧=-=⎪⎨=-=⎪⎩得驻点为(0,0),(0,2),(2,0),(2,2).z xx=6x-6, z xy=0, z yy=6y-6在点(0,0)处,A=-6,B=0,C=-6,B2-AC=-36<0,且A<0,所以函数有极大值z(0,0)=0.在点(0,2)处,A=-6,B=0,C=6,B2-AC=36>0,所以(0,2)点不是极值点.在点(2,0)处,A=6,B=0,C=-6,B2-AC=36>0,所以(2,0)点不是极值点.在点(2,2)处,A=6,B=0,C=6,B2-AC=-36<0,且A>0,所以函数有极小值z(2,2)=-8.(2)解方程组222e(2241)02e(1)0xxxyz x y yz y⎧=+++=⎪⎨=+=⎪⎩得驻点为1,12⎛⎫-⎪⎝⎭.22224e(21)4e(1)2exxxxxyxyyz x y yz yz=+++=+=在点1,12⎛⎫-⎪⎝⎭处,A=2e,B=0,C=2e,B2-AC=-4e2<0,又A>0,所以函数有极小值e1,122z⎛⎫=--⎪⎝⎭. (3) 解方程组22(62)(4)0(6)(42)0xyz x y yz x x y⎧=--=⎪⎨=--=⎪⎩得驻点为(3,2),(0,0),(0,4),(6,0),(6,4).Z xx=-2(4y-y2),Z xy=4(3-x)(2-y)Z yy=-2(6x-x2)在点(3,2)处,A=-8,B=0,C=-18,B2-AC=-8×18<0,且A<0,所以函数有极大值z(3,2)=36. 在点(0,0)处,A=0,B=24,C=0,B2-AC>0,所以(0,0)点不是极值点.在点(0,4)处,A=0,B=-24,C=0,B2-AC>0,所以(0,4)不是极值点.在点(6,0)处,A=0,B=-24,C=0,B2-AC>0,所以(6,0)不是极值点.在点(6,4)处,A=0,B=24,C=0,B2-AC>0,所以(6,4)不是极值点.(4)解方程组2222()22()222e(1)02e(1)0x yx yx x yy x y-+-+⎧--=⎪⎨--=⎪⎩得驻点P0(0,0),及P(x0,y0),其中x02+y02=1,在点P0处有z=0,而当(x,y)≠(0,0)时,恒有z>0,故函数z在点P0处取得极小值z=0.再讨论函数z=u e-u由de(1)duzuu-=-,令ddzu=得u=1,当u>1时,ddzu<;当u<1时,ddzu>,由此可知,在满足x 02+y 02=1的点(x 0,y 0)的邻域内,不论是x 2+y 2>1或x 2+y 2<1,均有2222()1()e e x y z x y -+-=+≤.故函数z 在点(x 0,y 0)取得极大值z =e -1(5)解方程组(2)0(2)0x y z y a x y z x a y x =--=⎧⎨=--=⎪⎩ 得驻点为12(0,0),,33a a P P ⎛⎫⎪⎝⎭z xx =-2y , z xy =a -2x -2y , z yy =-2x .故z 的黑塞矩阵为222222ya x y H a x y x ---⎡⎤=⎢⎥---⎣⎦ 于是122033(),().0233aa a H P H P a a a ⎡⎤--⎢⎥⎡⎤==⎢⎥⎢⎥⎣⎦⎢⎥--⎢⎥⎣⎦ 易知H (P 1)不定,故P 1不是z 的极值点,H (P 2)当a <0时正定,故此时P 2是z 的极小值点,且3,2733a a a z ⎛⎫=⎪⎝⎭,H (P 2)当a >0时负定,故此时P 2是z 的极大值点,且3,2733a a a z ⎛⎫=⎪⎝⎭.5. 设2x 2+2y 2+z 2+8xz -z +8=0,确定函数z =z (x ,y ),研究其极值。
习题解答 第九章 欧氏空间(定稿)

当且仅当 与 线性相关时,等号成立. 2. 标准正交基
定义 6 称欧氏空间 V 中一组两两正交的非零向量组1,2 , ,m 为一个正交向量组. 定义 7 设1,2,L ,n 是 n 维欧氏空间 V 中的一组基,若它们两两正交,则称 1,2,L ,n 为 V 的一组正交基;若正交基中的向量1,2,L ,n 都为单位向量,则称为标
n
( A, A) 0 ai2j 0 A 0 i, j1
此即证V是欧式空间。
(1)证:Eij是(i, j)元为1,其余一元皆为0的n阶方阵,那么可证 B11 E11, B12 E12 E21,L , B1n E1n En1 B22 E22 , B2n E2n En2 ,L , Bnn Enn 为V的一组基,于是
故○1 成立,且
V =S (S )
故S和(S)是同一子空间S的正交补,由正交补的唯一性,即证 ○2 .
4.设 是欧式空间V的线性变换,设 是V的一个变换,且, V ,都有(( ), )=(,( )). 证明:
(1) 是V的线性变换 (2)的值域 Im 等于的核ker的正交补。
四、典型题解析
例1.设A, B是n阶实对称阵,定义
(A, B) trAB
○1
证明:所有n阶实对称阵V 关于( A, B)成一欧式空间。 (1)求V的维数。 (2)求使trA=0的空间S的维数。 (3)求S的维数。
证 首先可证V {A Rnn | A A}是R上的一个线性空间。 再证○1 是V 的内积,从而得证V 是关于内积○1 的欧式空间. 事实上A,B,CV ,k R,有
部编数学七年级下册第9章不等式与不等式组(解析版)含答案

第9章 不等式与不等式组一、单选题1.如图在数轴上表示是哪一个不等式的解( )A .1x ³-B .1x £-C . 2.5x ³-D . 2.5x £-【答案】A 【分析】直接根据数轴写出不等式的解集,判断即可.【详解】解:根据数轴可得:1x ³-,故选:A .【点睛】本题考查了在数轴上表示不等式的解集,不等式的解集在数轴上表示的方法是“,>³”向右画,“,<£”向左画,注意在表示解集时,“,³£”要用实心圆点表示;“,<>”要用空心圆点表示.2.“x 的2倍与3的和是非负数”列成不等式为( )A .230x +³B .230x +>C .230x +£D .230x +<【答案】A【分析】非负数就是大于或等于零的数,再根据x 的2倍与3的和是非负数列出不等式即可.【详解】解:“x 的2倍与3的和是非负数”列成不等式为:230,x +³故选:.A 【点睛】本题考查的是列不等式,掌握“非负数是正数或零,用不等式表示就是大于或等于零”是解题的关键.3.某次篮球联赛中,火炬队与月亮队要争夺一个出线权,火炬队目前的战绩是17胜13负(其中有1场以4分之差负于月亮队),后面还要比赛6场(其中包括再与月亮队比赛1场);月亮队目前的战绩是15胜16负,后面还要比赛5场.如果火炬队在后面对月亮队1场比赛中至少胜月亮队5分,那么它在后面的其他比赛中至少胜( )场就一定能出线?A .1B .2C .3D .4【答案】A【分析】利用火炬队在后面对月亮队1场比赛中至少胜月亮队5分,则火炬队胜场数不低于月亮队列出不等式即可得出答案.【详解】解设火炬队在后面的比赛中胜x 场就一定能出线.∵火炬队在后面对月亮队1场比赛中至少胜月亮队5分,那么火炬队目前的战绩是18胜13负,后面还要比赛5场;月亮队目前的战绩为15胜17负,后面还要比赛4场;月亮队在后面的比赛中至多胜4场,所以整个比赛它至多胜15419+=场.需有1819x +³.解得1³x .因此火炬队在后面的比赛中至少胜1场就一定能出线,故选:A .【点睛】本题考查的是一元一次不等式的应用,解题关键是设出未知数再根据题意列出不等式.4.已知方程组2420x ky x y +=ìí-=î有正数解,则k 的取值范围是( )A .4k <B .4k >C .4k <-D .4k >-【答案】D【分析】先将方程组标号,用含y 的代数式表示x ,利用代入消元法求出44+y k=,根据方程组2420x ky x y +=ìí-=î有正数解,可得不等式404+y k =>,解不等式即可.【详解】解:2420x ky x y +=ìí-=î①②,由方程20x y -=变形得2x y =③,把③代入①得44y ky +=,解得44+y k=,方程组2420x ky x y +=ìí-=î有正数解,∴404+y k=,∴4+0k >,∴4k >-.故选择D .【点睛】本题考查二元一次方程组的解法与不等式综合运用题,掌握二元一次方程组的解法与不等式的解法是解题关键.5.若()1a b x a +>+的解集是1x <,则a 必须满足是( )A .0a <B .1a >-C .1a <-D .1a £【答案】C【分析】由()1a b x a +>+的解集是1x <,可得0a b +<,再利用不等式的解集可得11a a b+=+,再利用两数相除,同号得正,可得10a +<,从而可得答案.【详解】解:Q ()1a b x a +>+的解集是1x <,\ 0a b +<,\ 不等式的解集为:x <1,a a b++ \ 11a a b +=+,∴10a +<,∴a <1,-故选:.C 【点睛】本题考查的是利用不等式的基本性质解不等式,以及利用不等式的解集确定字母系数的范围,掌握不等式的基本性质是解题的关键.6.不等式324x -<中,x 可取的最大整数值是( )A .0B .1C .2D .3【答案】B【分析】首先解不等式,再从不等式的解集中找出适合条件的最大正整数即可.【详解】解:324x -<,342x <+36x <2x <,\最大整数解是1.故选为:B .【点睛】本题考查解一元一次不等式,一元一次不等式的整数解,正确解不等式,求出解集是解答本题的关键.7.如图,天平右盘中的每个砝码的质量都是1g ,则物体A 的质量m (g )的取值范围在数轴上可表示( )A .B .C .D .【答案】D【分析】根据图示,可得不等式组的解集,可得答案.【详解】解:由图示得1A >,2A <,故选:D .【点睛】本题考查了在数轴上表示不等式的解集,先求出不等式的解集,再在数轴上表示出来,注意,不包括点1、2,用空心点表示.8.若数a 使关于x 的方程12ax +=﹣73x ﹣1有非负数解,且关于y 的不等式组172222212y y y a y--ì-<ïíï+>-î恰好有两个偶数解,则符合条件的所有整数a 的和是( )A .﹣22B .﹣18C .11D .12【答案】B【分析】依题意,表示出分式方程的解,由分式方程有非负数解确定出a 的值,表示不等式组的解集,由不等式组恰好有两个偶数解,得到a 的值即可.【详解】由题知:原式:17123ax x +=-- ,去分母得:33146ax x +=--,得:9314x a =-+,又关于x 的方程17123ax x +=--有非负数解,∴ 3140a +<,∴ 143a <-;不等式组整理得:414y a y <ìïí->ïî,解得:144a y -<<,由不等式组有解且恰好有两个偶数解,得到偶数解为2,0;∴ 1204a --£<,可得71a -£<∴1473a -£<-,则满足题意a 的值有﹣7,﹣6,﹣5,则符合条件的所有整数a 的和是﹣18.故选:B ;【点睛】本题考查一元一次不等式组的整数解、一元一次方程的解,难点在熟练掌握求解的运算过程.9.已知关于x ,y 的方程组343x y a x y a+=-ìí-=î,其中31a -££,下列结论:①当2a =-时,x ,y 的值互为相反数;②51x y =ìí=-î是方程组的解;③当1a =-时,方程组的解也是方程1x y +=的解;④若14y ££,则30a -££.其中正确的是( )A .①②B .②③C .②③④D .①③④【答案】D【分析】将原方程求解,用a 表示x 和y ,然后根据a 的取值范围,求出x 和y 的取值范围,然后逐一判断每一项即可.【详解】由343x y a x y a +=-ìí-=î,解得121x a y a=+ìí=-î∵31a -££∴53x -££,04y ££①当2a =-时,解得33x y =-ìí=î,故①正确;②51x y =ìí=-î不是方程组的解,故②错误;③当1a =-时,解得12x y =-ìí=î,此时1x y +=,故③正确;④若14y ££,即114a £-£,解得30a -££,故④正确;故选D .【点睛】本题考查了二元一次方程组,解一元一次不等式,熟练掌握二元一次方程组的解法和不等式的解法是本题的关键.10.如图的宣传单为莱克印刷公司设计与印刷卡片计价方式的说明,妮娜打算请此印刷公司设计一款母亲节卡片并印刷,她再将卡片以每张15元的价格贩售.若利润等于收入扣掉成本,且成本只考虑设计费与印刷费,则她至少需印多少张卡片,才可使得卡片全数售出后的利润超过成本的2成?( )A .112B .121C .134D .143【答案】C 【详解】分析:设妮娜需印x 张卡片,根据利润=收入﹣成本结合利润超过成本的2成,即可得出关于x 的一元一次不等式,解之即可得出x 的取值范围,取其内最小的整数即可得出结论.详解:设妮娜需印x 张卡片,根据题意得:15x ﹣1000﹣5x >0.2(1000+5x ),解得:x >13313,∵x 为整数,∴x≥134.答:妮娜至少需印134张卡片,才可使得卡片全数售出后的利润超过成本的2成.故选C .点睛:本题考查了一元一次不等式的应用,根据各数量之间的关系,正确列出一元一次不等式是解题的关键.二、填空题11.已知等腰三角形的周长为12cm ,则这个等腰三角形的腰长x 的范围是________.【答案】3cm 6cmx <<【分析】设等腰三角形的底边长为y cm ,根据三角形三边的不等关系及周长,可得关于x 的不等式,解不等式即可.【详解】设等腰三角形的底边长为y cm ,由已知得2x y >,212x y +=,∴2122x x >-,解得:x >3,∵y =12-2x >0,∴x <6∴36x <<故答案为:36cm x cm<<【点睛】本题是一元一次不等式的简单应用,考查了三角形三边的不等关系、等腰三角形的定义,解一元一次不等式,关键是清楚三角形三边的不等关系及实际问题中三角形的边长为正这个隐含条件.12.商店为了对某种商品促销,将定价为3元的商品,以下列方式优惠销售:若购买不超过5件,按原价付款;若一次性购买5件以上,超过部分打八折.现有27元钱,最多可以购买该商品的件数是________.【答案】10件【分析】设购买该商品x 件,先判断购买件数在5件之上,再根据总价=3×5+3×0.8×超过5件的数量,结合总价不超过27元,即可得出关于x 的一元一次不等式,求出x 的解集即可得出结论.【详解】解:设购买该商品x 件,因为共有27元,所以最多购买的件数超过5件,依题意得:3×5+3×0.8(x -5)≤27,解得:x ≤10,故答案为:10件.【点睛】本题考查了一元一次不等式的应用,根据各数量之间的关系,正确列出一元一次不等式是解题的关键.13.不等式23510x x -³-的正整数解________.【答案】1和2【分析】求出不等式的解集,然后在解集中找出正整数即可.【详解】解:23510x x -³-解得:73x £,∴符合条件的正整数为:1和2,故答案为:1和2.【点睛】本题考查了求一元一次不等式的整数解,正确求出不等式的解集是解题的关键.14.已知关于x 的不等式组0321x a x -³ìí->-î有9个整数解,则a 的取值范围是________.【答案】87a -<£-【分析】首先确定不等式组的解集,根据整数解的个数就可以确定有哪些整数解,根据解的情况可以得到关于a 的不等式,从而求出a 的范围.【详解】解:0321x a x -³ìí->-î解不等式组可得2a x £<,∴9个整数解为1,0,1-,2-,3-,4-,5-,6-,7-,∴87a -<£-.故答案为:87a -<£-【点睛】本题主要考查了学生对不等式组知识点的掌握,先求出不等式组范围,再根据具体解逆推出a 的取值范围.15.382x -的值不大于7x -的值,x 的取值范围是________.【答案】6x £【分析】根据题意列出不等式,解不等式即可.【详解】由题意,得:3872x x -£-解得:6x £故答案为:6x £【点睛】本题考查了一元一次不等式的应用,关键是理解不大于即小于或等于.16.已知0a <,10b -<<,请将a ,ab ,2ab 从小到大依次排列________.【答案】2a ab ab<<【分析】根据不等式的性质和乘法法则进行判断即可.【详解】解:∵a <0, b <0,∴ab >0,∵﹣1<b <0,∴0<b 2<1;两边同时乘a ,0>ab 2>a ,∴a <ab 2<ab .【点睛】本题考查了不等式的性质,明确(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变.(2)不等式两边乘(或除以)同一个正数,不等号的方向不变.(3)不等式两边乘(或除以)同一个负数,不等号的方向改变是解题关键.17.当m ________时,代数式342423m m +--的值是非负数.【答案】4³-【分析】根据题意,列出不等式解不等式即可.【详解】依题意342423m m +--0³去分母得:()()3342240m m +--³去括号得:912480m m +-+³移项,合并同类项得:520m ³-化系数为1,得:4m ³-故答案为:4³-【点睛】本题考查了解一元一次不等式,掌握解一元一次不等式的步骤是解题的关键.18.定义一种法则“Ä”如下:()()a a b a b b a b >ìÄ=í£î,如:122Ä=,若(25)33m -Ä=,则m 的取值范围是_______.【答案】4m £【分析】根据题意可得2m ﹣5≤3,然后求解不等式即可.【详解】根据题意可得,∵(2m -5)⊕3=3,∴2m ﹣5≤3,解得:m≤4故答案为4m £.【点睛】本题主要考查解一元一次不等式,解此题的关键在于准确理解题中新定义法则的运算规律,得到一元一次不等式.三、解答题19.解下列不等式,并把它们的解集在数轴上表示出来:(1)3(27)23+>x ;(2)124(31)2(216)x x --£-;(3)325153x x +-<-;(4)213153212x x ---³.【答案】(1)13x >;(2)3x ³;(3)7x >;(4)310x £-,见解析【分析】(1)去括号,移项、合并同类项,系数化为1求得一元一次不等式的解集,再根据所求解集在数轴上表示即可;(2)去括号,移项、合并同类项,系数化为1求得一元一次不等式的解集,再根据所求解集在数轴上表示即可;(3)去分母,去括号,移项、合并同类项,系数化为1求得一元一次不等式的解集,再根据所求解集在数轴上表示即可;(4)去分母,去括号,移项、合并同类项,系数化为1求得一元一次不等式的解集,再根据所求解集在数轴上表示即可;【详解】(1)去括号,得:62123x +>,移项、合并同类项,得:62x >,系数化为1,得:13x >,在数轴上表示不等式解集,如图:(2)去括号,得:1212+4432x x -£-,移项、合并同类项,得:1648x -£-,系数化为1,得:3x ³,在数轴上表示不等式解集,如图:;(3)去分母,得:()()3352515x x +<--,去括号,得:39102515x x +<--,移项、合并同类项,得:749x -<-,系数化为1,得:7x >,在数轴上表示不等式解集,如图:;(4)去分母,得:()()4216315x x ---³,去括号,得:841865x x --+³,移项、合并同类项,得:103x -³,系数化为1,得:310x £-,在数轴上表示不等式解集,如图:.【点睛】本题考查解一元一次不等式及用数轴表示不等式的解集,解题的关键是熟练掌握解一元一次不等式的一般步骤:去分母,去括号,移项、合并同类项,系数化为1.20.赵军说不等式2a a >永远不会成立,因为如果在这个不等式两边同除以a ,就会出现12>这样的错误结论.他的说法对吗?【答案】不对,见解析【分析】根据不等式的性质可知当0a <时,不等号方向发生改变即可求解.【详解】解:赵军的说法不对.理由如下:当0a <时,根据不等式的性质:“不等式的两边同时除以一个负数,不等号的方向改变”可知此时得到:12<.【点睛】本题考查一元一次不等式的基本性质:不等式两边同时除以一个负数,不等号的方向发生改变,熟练掌握不等式的性质是解题的关键.21.解不等式组()262311x x x x ì-£ï>-íï-<+î①②③,请结合题意,完成本题的解答.(1)解不等式①,得 ,依据是: .(2)解不等式③,得 .(3)把不等式①、②和③的解集在数轴上表示出来.(4)从图中可以找出三个不等式解集的公共部分,得不等式组的解集 .【答案】(1)x≥﹣3、不等式的性质3;(2)x <2;(3)作图见解析;(4)﹣2<x <2.【详解】试题分析:分别求出每一个不等式的解集,根据各不等式解集在数轴上的表示,确定不等式组的解集.试题解析:(1)解不等式①,得x ≥﹣3,依据是:不等式的性质3,故答案为x≥﹣3、不等式的性质3;(2)解不等式③,得x <2,故答案为x <2;(3)把不等式①,②和③的解集在数轴上表示出来,如图所示:(4)从图中可以找出三个不等式解集的公共部分,得不等式组的解集为:﹣2<x <2,故答案为﹣2<x <2.【点睛】本题考查了解一元一次不等式组、在数轴上表示不等式的解集,关键是先求出每个不等式的解集,分别在数轴上表示每一个不等式的解集,然后再确定出不等式组的解集.22.一艘轮船从某江上游的A 地匀速行驶到下游的B 地用了10h ,从B 地匀速返回A 地用了不到12h ,这段江水流速为3km /h ,轮船在静水里的往返速度v 不变,v 满足什么条件?【答案】v 满足的条件是大于33千米每小时.【分析】直接利用总路程不变得出不等关系进而得出答案.【详解】解:由题意得,从A 到B 的速度为:()3v +千米/时,从B 到A 的速度为:()3v -千米/时∵从B 地匀速返回A 地用了不到12小时,∴()()123103v v ->+,解得:33v >.答:v 满足的条件是大于33千米每小时.【点睛】此题主要考查了一元一次不等式的实际应用,正确得出不等关系是解题关键.23.每年的5月20日是中国学生营养日,某校社会实践小组在这天开展活动,调查快餐营养情况.他们从食品安全监督部门获取了一份快餐的信息.根据此信息,解答下列问题:1.快餐的成分:蛋白质,脂肪、矿物质、碳水化合物;2.快餐总质量为400g ;3.脂肪所占的百分比为5%;4.所含蛋白质质量是矿物质质量的4倍.(1)求这份快餐中所含脂肪质量;(2)若碳水化合物占快餐总质量的40%,求这份快餐所含蛋白质的质量;(3)若这份快餐中蛋白质和碳水化合物所占百分比的和不高于85%,求其中所含碳水化合物质量的最大值.【答案】(1)20g ;(2)176g ;(3)180g【分析】(1)用总质量乘以5%即可;(2)设所含矿物质的质量为g x ,根据题意列方程42040040%400x x +++´=,求出解即可得到答案;(3)设所含矿物质的质量为g y ,则所含碳水化合物的质量为(3805)g -y ,根据题意列不等式解答.【详解】解:(1)这份快餐中所含脂肪质量为4005%=20´(g );(2)设所含矿物质的质量为g x ,由题意得42040040%400x x +++´=,解得44x =,故4176=x .∴这份快餐所含蛋白质的质量为176g ;(3)设所含矿物质的质量为g y ,则所含碳水化合物的质量为(3805)g -y ,∴4(3805)40085%+-£´y y ,解得40y ³,故3805180-£y .∴所含碳水化合物质量的最大值为180g .【点睛】本题主要考查学生用不等式解决实际问题的能力,列一元一次方程解决实际问题,正确理解题意设定未知数列出方程及不等式是解题的关键.24.某电器超市销售每台进价分别为160元、120元的A 、B 两种型号的电风扇,如表是近两周的销售情况:销售数量销售时段A 种型号B 种型号销售收入第一周3台4台1200元第二周5台6台1900元(进价、售价均保持不变,利润=销售收入﹣进货成本)(1)求A 、B 两种型号的电风扇的销售单价;(2)若超市准备用不多于7500元的金额再采购这两种型号的电风扇共50台,求A 种型号的电风扇最多能采购多少台?(3)在(2)的条件下,超市销售完这50台电风扇能否实现利润超过1850元的目标?若能,请给出相应的采购方案;若不能,请说明理由.【答案】(1)A 、B 两种型号电风扇的销售单价分别为200元、150元;(2)超市最多采购A 种型号电风扇37台时,采购金额不多于7500元;(3)在(2)的条件下超市能实现利润超过1850元的目标.相应方案有两种:当a =36时,采购A 种型号的电风扇36台,B 种型号的电风扇14台;当a =37时,采购A 种型号的电风扇37台,B 种型号的电风扇13台.【分析】(1)设A 、B 两种型号电风扇的销售单价分别为x 元、y 元,列二元一次方程组,解方程组即可得到答案;(2)设采购A 种型号电风扇a 台,则采购B 种型号电风扇(50﹣a )台,利用超市准备用不多于7500元,列不等式160a +120(50﹣a )≤7500,解不等式可得答案;(3)由超市销售完这50台电风扇实现利润超过1850元,列不等式(200﹣160)a +(150﹣120)(50﹣a )>1850,结合(2)问,得到a 的范围,由a 为非负整数,从而可得答案.【详解】解:(1)设A 、B 两种型号电风扇的销售单价分别为x 元、y 元,依题意得:341200561900x y x y +=ìí+=î①②,①5´-②3´得:2300,y =150,y \=把150y =代入①得:200,x =解得:200150x y =ìí=î,答:A 、B 两种型号电风扇的销售单价分别为200元、150元.(2)设采购A 种型号电风扇a 台,则采购B 种型号电风扇(50﹣a )台.依题意得:160a +120(50﹣a )≤7500,401500,a \£解得:a ≤1372.因为:a 为非负整数,所以:a 的最大整数值是37.答:超市最多采购A 种型号电风扇37台时,采购金额不多于7500元.(3)根据题意得:(200﹣160)a +(150﹣120)(50﹣a )>1850,10a \>350,解得:a >35,∵a ≤1372,35\<a 1372£,Q a 为非负整数,36a =或37.a =∴在(2)的条件下超市能实现利润超过1850元的目标.相应方案有两种:当a =36时,采购A 种型号的电风扇36台,B 种型号的电风扇14台;当a =37时,采购A 种型号的电风扇37台,B 种型号的电风扇13台.【点睛】本题考查的是二元一次方程组的应用,一元一次不等式,一元一次不等式组的应用的方案问题,掌握以上知识是解题的关键.25.对于三个数a ,b ,c ,M{a ,b ,c}表示a ,b ,c 这三个数的平均数,min{a ,b ,c}表示a ,b ,c 这三个数中最小的数,如:1234{1,2,3}33M -++-==,min {﹣1,2,3}=﹣1;121{1,2,}33a a M a -+++-==,min {﹣1,2,a }=(1)11a a a £-ìí->-î;解决下列问题:(1)填空:min {﹣22,2﹣2,20130}= ;(2)若min {2,2x +2,4﹣2x }=2,求x 的取值范围;(3)①若M {2,x +1,2x }=min {2,x +1,2x },那么x = ;②根据①,你发现结论“若M {a ,b ,c }=min {a ,b ,c },则 ”(填a ,b ,c 的大小关系);③运用②解决问题:若M {2x +y +2,x +2y ,2x ﹣y }=min {2x +y +2,x +2y ,2x ﹣y },求x +y 的值.【答案】(1)-4;(2)01x ££;(3)①1;②a =b =c ;③-4【分析】(1)先求出﹣22,2﹣2,20130这些数的值,再根据运算规则即可得出答案;(2)先根据运算规则列出不等式组,再进行求解即可得出答案;(3)根据题中规定的M {a 、b 、c }表示这三个数的平均数,min {a 、b 、c }表示a 、b 、c 这三个数中的最小数,列出方程组即可求解.【详解】(1)∵﹣22=﹣4,2﹣2=14,20130=1,∴min {﹣22,2﹣2,20130}=﹣4;故答案为:﹣4;(2)由题意得:222422x x +³ìí-³î,解得:0≤x ≤1,则x 的取值范围是0≤x ≤1;故答案为0≤x ≤1;(3)①M {2,x +1,2x }=2123x x +++=x +1=min {2,x +1,2x },∴1212x x x +£ìí+£î,∴11x x £ìí³î,∴x =1.②若M {a ,b ,c }=min {a ,b ,c },则a =b =c ;③根据②得:2x +y +2=x +2y =2x ﹣y ,解得:x=﹣3,y=﹣1,则x+y=﹣4.故答案为:①1;②a=b=c;③﹣4.【点睛】本题主要考查了一元一次不等式组及二元一次方程组的应用,读懂题目信息并理解新定义“M”与“min”的意义是解题的关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第九章习题及答案第九章习题一、选择题1.以下选项中不能正确把cl定义成结构体变量的是( )A)typedef struct B)struct color cl{ int red; { int red;int green; int green;int blue; int blue;} COLOR; COLOR cl; };C)struct color D)struct{ int red; { int red;int green; int green;int blue; int blue;} cl; } cl;2.有以下说明和定义语句struct student{ int age; char num[8];};struct student stu[3]={{20,"200401"},{21,"200402"},{10\9,"200403"}};struct student *p=stu;以下选项中引用结构体变量成员的表达式错误的是( )A) (p++)->num B)p->num C)(*p).num D)stu[3].age3.有以下结构体说明、变量定义和赋值语句struct STD{char name[10];int age;char sex;}s[5],*ps;ps=&s[0];则以下scanf函数调用语句中错误引用结构体变量成员的是( )。
A)scanf(“%s”,s[0].name);B)scanf(“%d”,&s[0].age);C)scanf(“%c”,&(ps->sex)); D)scanf(“%d”,ps->age);4.以下叙述中错误的是()A)可以通过typedef增加新的类型B)可以用typedef将已存在的类型用一个新的名字来代表C)用typedef定义新的类型名后,原有类型名仍有效D)用typedef可以为各种类型起别名,但不能为变量起别名5.有以下程序段()typedef struct node { int data; struct node *next; } *NODE;NODE p;以下叙述正确的是(C)A)p是指向struct node结构变量的指针的指针B)NODE p;语句出错C)p是指向struct node结构变量的指针D)p是struct node结构变量6.若有以下定义和语句union data{ int i; char c; float f;}x;int y;则以下语句正确的是( )。
A)x=10.5;B)x.c=101; C)y=x;D)printf(“%d\n”,x); 7.有以下程序main(){ union { unsigned int n;unsigned char c;}u1;ul.c=`A`;printf("%c\n",u1.n);}执行后输出结果是()A) 产生语法错 B) 随机值 C) A D) 658.有以程序#include <stdio.h>#include <string.h>typedef struct { char name[9]; char sex; float score[2]; } STU;void f( STU a){ STU b={“Zhao” ,’m’,85.0,90.0} ; int i;strcpy(,);a.sex=b.sex;for(i=0;i<2;i++) a.score[i]=b.score[i];}main(){ STU c={“Qian”,’p’,95.0,92.0};f(c); printf(“%s,%c,%2.0f,%2.0f\n”,,c.sex,c.score[0],c.score[1]);}程序的运行结果是A)Qian,p,95,92 B) Qian,m,85,90C)Zhao,p,95,92 D) Zhao,m,85,909.现有以下结构体说明和变量定义,如图所示,指针p,q,r分别指向一个链表中连续的三个结点。
struct node{char data;struct node *next;}*p,*q,*r;现要将q和r所指结点交换前后位置,同时要保持链表的连续,以下不能完成此操作的语句是A)q->next=r->next; p->next=r; r->next=q;B) p->next=r; q->next=r->next; r->next=q;C) q->next=r->next; r->next=q; p->next=r;D) r->next=q; p->next=r; q-next=r->next;10.有以下程序段struct st{ int x; int *y;}*pt:int a[]={1,2},b[]={3,4};struct st c[2]={10,a,20,b};pt=c;以下选项中表达式的值为11的是( )A) *pt->y B) pt->x C) ++pt->x D) (pt++)->x二、填空题1.设有说明struct DATE{int year;int month; int day;};请写出一条定义语句,该语句定义d为上述结构体变量,并同时为其成员year、month、day 依次赋初值2006、10、1。
2.已有定义如下:struct node{ int data;struct node *next;} *p;以下语句调用malloc函数,使指针p指向一个具有struct node类型的动态存储空间。
请填空。
p = (struct node *)malloc( );3.以下程序中函数fun的功能是:统计person所指结构体数组中所有性别(sex)为M的记录的个数,存入变量n中,并做为函数值返回。
请填空:#include<stdio.h>#define N 3typedef struct{int num;char nam[10]; char sex;}SS;int fun(SS person[]){int i,n=0;for(i=0;i<N;i++)if( ==’M’ ) n++;return n;}main(){SS W[N]={{1,”AA”,’F’},{2,”BB”,’M’},{3,”CC”,’M’}}; int n;n=fun(W); printf(“n=%d\n”,n);}4.以下程序运行后的输出结果是( ) 。
struct NODE{ int k;struct NODE *link;};main(){ struct NODE m[5],*p=m,*q=m+4;int i=0;while(p!=q){p->k=++i; p++;q->k=i++; q--;}q->k=i;for(i=0;i<5;i++) printf("%d",m[i].k);printf("\n");}5.以下程序的功能是:建立一个带有头结点的单向链表,并将存储在数组中的字符依次转储到链表的各个结点中,请从与下划线处号码对应的一组选若中选择出正确的选项。
#includestuct node{ char data; struct node *next;};(1) CreatList(char *s){ struct node *h,*p,*q);h=(struct node *) malloc(sizeof(struct node));p=q=h;while(*s!='\0'){ p=(struct node *) malloc(sizeof(struct node));p->data= (2) ;q->next=p;q= (3) ;s++;}p->next='\0';return h;}main(){ char str[]="link list";struct node *head;head=CreatList(str);...}三、编程题1. 定义一个能正常反映教师情况的结构体teacher,包含教师姓名、性别、年龄、所在部门和薪水;定义一个能存放两人数据的结构体数组tea,并用如下数据初始化:{{“Mary “, ‘W’,40, ‘Computer’ , 1234 },{“Andy“, ‘M’,55, ‘English’ , 1834}};要求:分别用结构体数组tea和指针p输出各位教师的信息,写出完整定义、初始化、输出过程。
2.定义一个结构体变量(包括年、月、日)。
计算该日在本年中是第几天,注意闰年问题。
3.构建简单的手机通讯录,手机通讯录包括信息(姓名、年龄、联系电话),要求实现新建、查询功能。
假设通信录最多容纳50名联系人信息。
4.建立一个教师链表,每个结点包括学号(no),姓名(name[8]),工资(wage),写出动态创建函数creat和输出函数print。
5.在上一题基础上,假如已经按学号升序排列,写出插入一个新教师的结点的函数Insert。
第9章习题答案一、选择题1-5 B D D A C 6-10 B C A D C二、填空题1.struct DATA d={2006,10,1};2.sizeof(struct node)3.person[i].sex4.134315.(1)struct node* (2)*s (3)p三、编程题1. 定义一个能正常反映教师情况的结构体teacher,包含教师姓名、性别、年龄、所在部门和薪水;定义一个能存放两人数据的结构体数组tea,并用如下数据初始化:{{“Mary “, ‘W’,40, ‘Computer’ , 1234 },{“Andy“, ‘M’,55, ‘English’ , 1834}};要求:分别用结构体数组tea和指针p输出各位教师的信息,写出完整定义、初始化、输出过程。
#include<stdio.h>struct teacher{ char name[8];char sex;int age;char department[20];float salary;} ;struct teacher tea[2]= {{"Mary ", 'W',40, "Computer" , 1234 },{"Andy ", 'M',55, "English" , 1834}} ;main(){ int i;struct teacher *p;for( i=0;i<2;i++)printf("%s,\t%c,\t%d,\t%s,\t%f",tea[i].name,tea[i].sex,tea[i].age,tea[i].department,tea[i].salary);for(p=tea;p<tea+2;p++)printf("%s,\t%c,\t%d,\t%s,\t%f", p->name, p->sex, p->age, p->department, p->salary);}2. 定义一个结构体变量(包括年、月、日)。
