矢量分析 各种坐标系下梯度算符、拉普拉斯算符形式
在球和柱坐标系下作用于矢量函数的拉普拉斯算子

dP=dx2+dy2'-\-dz2=h\dx \-\rh2dx2+h^dx^ 〇
根据电动力学教材[2~3]可 知 ,假 设 ^ 和文分别表示标量函数和矢量函数(其中I d 心 +4212+ 4 313),可以列
第 36卷 第 1期
苏 州 科 技 大 学 学 报 (自 然 科 学 版 )
2019年 3 月
Journal of Suzhou University of Science and Technology (Natural Science)
doi :10.12084/jassn.2096-3289.2019.01.007
子和作用于矢量函数的拉普拉斯算子,包括它们相互之间存在的关系,以及在不同坐标系下作用于标量函数 和矢量函数的拉普拉斯算子的具体表达式。但 是 ,在许多电磁学和电动力学教材及其附录里,通常只介绍作 用 于 标 量 函 数 的 拉 普 拉 斯 算 子 。对 于 作 用 于 矢 量 函 数 的 拉 普 拉 斯 算 子 只 是 一 笔 带 过 或 者 基 本 不 提 及 ,这让 人们较难理解、不易掌握和灵活运用。在研究某些具体问题时,人们发现作用于矢量函数的拉普拉斯算子也 是相当重要的,值得进一步去研究和讨论。通 常 ,在三维直角坐标系下,作用于矢量函数的拉普拉斯算子的 表 达 形 式 是 比 较 简 单 的 。而 在 球 坐 标 和 柱 坐 标 系 下 ,作 用 于 矢 量 函 数 的 拉 普 拉 斯 算 子 则 需 要 经 过 特 殊 的 坐 标转换,这样一来计算就会变得比较复杂,往往不知从何人手,而这恰恰又是必须要解决的一个难题。例 如 , 在球坐标和柱坐标系下,求 解 多 层 球 颗 粒 和 柱 颗 粒 散 射 截 面 和 解 决 微 波 在 各 种 波 导 管 中 T E 波 和 T M 波 的传输问题[6,14]。如果在球坐标和柱坐标系下,利用作用于标量函数和矢量函数的拉普拉斯算子能够解出比 较 简 单 的 形 式 和 关 系 ,那 么 就 可 以 简 化 分 析 过 程 ,规 避 复 杂 而 又 冗 长 的 理 论 推 导 ,较 为 轻 松 地 求 解 上 述 问 题 在球坐标系和柱坐标系下的波动方程及其他相关结果,甚至可以直接给出简洁明了的结论。
第一章矢量分析

第一章 矢量分析(说明:本章为07电本英语讲义的中译本)电磁场是矢量场,矢量分析是学习电磁场性质的基本数学工具之一。
本章中,我们主要介绍矢量场理论基本知识:矢量运算,标量场的梯度,矢量场的散度和旋度,以及对于矢量场运算有重要作用的称为戴尔(或那布拉)算符∇的运算规则。
稍后,将介绍狄拉克δ函数及一些重要的矢量场定理,它对我们今后学习电磁场理论有重要作用。
1-1 矢量运算我们在电磁场中遇到的大多数量可分为两类:标量和矢量。
仅有大小的量称为标量。
具有大小和方向的量称为矢量。
一矢量A 可写成A A =A e其中A 是矢量A 的大小,e A 是与A 同方向上的单位矢量。
矢量的大小称为矢量的模,单位矢量的模为1。
矢量A 方向上的单位矢量可以这样表示:A A=Ae 矢量将用黑斜体字母表示,单位矢量用e 来表示。
作图时,我们用一有长度和方向的箭头表示矢量,如图1-1-1所示。
如果两矢量A 和B 具有同样的大小和方向,它们是相等的。
如果两矢量A 和B 具有同样的物理的或几何的意义,则它们具有同样的量纲,我们可以对矢量进行比较。
如果一个矢量的大小为零,我们称为零矢量或空矢量。
这是唯一一个不能用箭头表示的矢量。
我们也可以定义面积矢量。
如果有一面积为s 的平面,则面积矢量s 的大小为s ,它的方向按右手螺旋规则确定,如图1-1-2所示。
1-1-1 矢量加和减两矢量A 和B 可彼此相加,其结果给出另一矢量C ,C = A + B 。
矢量三角形或矢量四边形给出了两矢量A 和B 相加的规则,如图1-1-3所示。
由此我们可得出:矢量加法服从加法交换律和加法结合律。
交换律: A + B = B + A (1-1-1) 结合律:(A + B ) + C = A + (B + C ) (1-1-2)由C = A + B ,其也意味着一个矢量C 可以由两个矢量A 和B 来表示,即矢量C 可分解为两个分矢量A 和B (分量)。
也可说,一个矢量可以分解为几个分矢量。
第1章 - 1 矢量坐标系梯度

12
第一章 矢 量 分 析
1 .2 .1 正交坐标系
任意矢量A:
A A
Au21 Au22 Au23
任意矢量B:
(1-22) (1-23) (1-24)
(1-25) (1-26)
13
第一章 矢 量 分 析
e e e u1
u2
u3
A B Au1 Au2 Au3
B B B u1
u2
u3
(1-27)
d , d, dz
拉梅系数:
r
h1 1, h2 , h3 1 (1-58)
位置矢量为: r = e + ez z
线元微分元为: dr = d (e + ez z)
e d de ezdz zdez e d e de ezdz
(1-59) (1-60)
26
第一章 矢 量 分 析
第一章 矢 量 分 析
1 .2 .3 圆柱坐标系
ez
e
e
(u1,u2,u3 ) (,, z)
(1-48)
ez P(ρ0 ,φ0 , z0 )
e e
0 0 2
z
e e ez
e ez e
(1-49)
图 1 -6 柱坐标系
ez e e
21
第一章 矢 量 分 析
ez ez
ex e cos e sin , ey e sin e cos , ez ez
(1-51-2)
22
第一章 矢 量 分 析
园柱坐标系中矢量:
A e A e A ez Az
直角坐标系中:
A ex Ax ey Ay ez Az
坐标变换矩阵为:
Ax cos
矢量分析报告

第一章 矢量分析
静电场的基本方程是
(1-52) 对于各向同性的媒质, 电通量密度和电场强度的关系为
D=εE, 因而式(1-52)可改写为
假设在无限空间中有两个矢量函数F和G,它们具有相同的散 度和旋度。但这两个矢量函数不等,可令
第一章 矢量分析
由于矢量F和矢量G具有相同的散度和旋度, 根据矢量场由其 散度和旋度唯一确定, 那么矢量g应该为零矢量, 也就是矢量 F 与矢量G是同一个矢量。
因为▽·F= ▽ ·G, 所 以
同样由于▽ ×G= ▽ ×F, 所 以
拉普拉斯微分算子▽ 2的表示式为
第一章 矢量分析
例1-14 在一对相距为l的点电荷+q和-q的静电场中, 当距 r>>l离时, 其空间电位的表达式 为
求其电场强度E(r, θ, φ)。 解: 在球面坐标系中,哈密顿微分算子▽的表达式为
第一章 矢量分析
因为
第一章 矢量分析
1.6 亥姆霍兹定理
亥姆霍兹定理的简单表达是: 若矢量场F在无限空间中处处单 值,且其导数连续有界,而源分布在有限空间区域中,则矢量场 由其散度和旋度唯一确定,并且可以表示为一个标量函数的梯度 和一个矢量函数的旋度之和, 即
图 1-6 例 1-11 图
第一章 矢量分析
解: 由于在曲线l上z=0,所以dz=0。
第一章 矢量分析
例1-12 求矢量场A=x(z-y) ex+y(x-z)ey+z(y-x)ez在点 M(1,0 1)处的旋度以及沿n=2ex+6ey+3ez方向的环量面密度。
解: 矢量场A的旋度
各种坐标系下拉普拉斯算符统一解法

有不少问题,由于边界的形状,不宜采用直角坐标系,而应采用球坐标系或柱坐标系等正交曲线坐标系。
在许多数学物理方程中,都用到拉普拉斯算符222222x y z∂∂∂∆=++∂∂∂。
采用正交曲线坐标系的时候,当然需要把拉普拉斯算符用正交曲线坐标表示出来。
“正交曲线坐标系中的拉普拉斯算符”在物理系高等数学教材中是有的。
但为了方便读者这里还是给出简单论述。
1、拉普拉斯算符作用于标量函数以123,,q q q 表示正交曲线坐标,则直角坐标与正交曲线坐标具有下列关系:()()()112233,,,,,,q q x y z q q x y z q q x y z ⎧=⎪=⎨⎪=⎩ ()()()123123123,,,,,,x x q q q y y q q q z z q q q ⎧=⎪=⎨⎪=⎩若两点具有相同的2q 和3q 而1q 相差微量1dq ,则两点间的距离为()()()()22221dz dy dx ds ++=()22221111x y z dq q q q ⎡⎤⎛⎫⎛⎫⎛⎫∂∂∂⎢⎥=++ ⎪ ⎪ ⎪∂∂∂⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦,这可改写为111dq H ds =,1H (1)同理,若两点具有相同的3q 和1q 而2q 相差微量2dq ,则两点间的距离为222ds H dq =,2H (2)若两点具有相同的21,q q 而3q 相差微量3dq ,则两点间的距离为331dq H ds =,3H = (3)321,,H H H 叫做度规系数。
这样,标量函数()321,,q q q u 的梯度u ∇在1q 增长方向的分量为()11111q u H s u u ∂∂=∂∂=∇,从而()1111q u H u ∂∂=∇、()2221q u H u ∂∂=∇、()3331uu H q ∂∇=∂ (4) 再看矢量函数()321,,q q q A 。
取一个微小六面体,它由333222111,;,;,dq q q dq q q dq q q +++六个曲面围成(图1)。
0-2 矢量 算符 张量

∴ ∇ × ( A × Bc ) = (∇ ⋅ Bc ) A − B (∇ ⋅Α) = (Β ⋅ ∇) A − B (∇ ⋅ A)
上两式代入( ),即得证: ),即得证 上两式代入(1),即得证:
五、正交曲线坐标系中
∇ 运算的表达式
Expression of ∇ Operation on Orthogonal Curvilinear CoCoOrdinates System
∂ ∂ ∂ ˆx ⋅ fAc ) + (ey ⋅ fAc ) + (ez ⋅ fAc ) ˆ ˆ ∇ ⋅ ( fAc ) = (e ∂x ∂y ∂z ∂f ∂f ∂f ˆx + A ⋅ ey + A ⋅ ez = A ⋅∇f ˆ ˆ = A⋅ e ∂x ∂y ∂z
例2:证明
∇ × ( A × B) = A(∇ ⋅ B) − ( A ⋅ ∇) B + ( B ⋅ ∇) A − B(∇ ⋅ A)
v v v ex = er cosθ − eθ sinθ v y v v ey = er sinθ + eθ cosθ θ = arctan x
r = x2 + y2
y r f
θ θ
θ
x
∂ v ∂ v ∇ = ex + ey ∂x ∂y
∂ ∂r ∂ ∂θ ∂ = + ∂x ∂x ∂r ∂x ∂θ ∂ ∂r ∂ ∂θ ∂ = + ∂y ∂y ∂r ∂y ∂θ
2 标量场的梯度
v 标量场 ϕ(r )
dφ ˆ gradφ = el dl ∂φ ∂φ ∂φ ˆ ˆ ˆ = ex + ey + ez ∂x ∂y ∂z
即沿某一方向的方向导数就是梯度在该方向上的投影。 即沿某一方向的方向导数就是梯度在该方向上的投影。 梯度表征标量场在空间各点沿不同方向变化快慢的程度 梯度表征标量场在空间各点沿不同方向变化快慢的程度
矢量运算(梯度、散度、旋度)与拉普拉斯算符公式整理
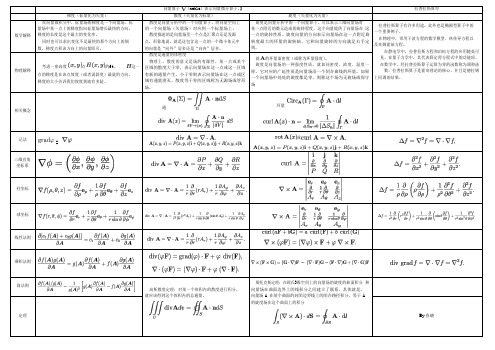
向量算子 (nabla )表示向量微分算子。
】拉普拉斯算符梯度(标量化为矢量)散度(矢量化为标量)旋度(矢量化为矢量)数学解释在向量微积分中,标量场的梯度是一个向量场。
标量场中某一点上的梯度指向标量场增长最快的方向,梯度的长度是这个最大的变化率。
同时也可以求出变化不是最快的那个方向上的倒数,梯度点积该方向上的向量即可。
散度是向量分析中的一个向量算子,将向量空间上的一个向量场(矢量场)对应到一个标量场上。
散度描述的是向量场里一个点是汇聚点还是发源 点,形象地说,就是这包含这一点的一个微小体元中 的向量是“向外”居多还是“向内”居多。
旋度是向量分析中的一个向量算子,可以表示三维向量场对 某一点附近的微元造成的旋转程度。
这个向量提供了向量场在 这一点的旋转性质。
旋度向量的方向表示向量场在这一点附近旋转度最大的环量的旋转轴,它和向量旋转的方向满足右手定则。
拉普拉斯算子有许多用途,此外也是椭圆型算子中的 一个重要例子。
在物理中,常用于波方程的数学模型、热传导方程以 及亥姆霍兹方程。
在静电学中,拉普拉斯方程和泊松方程的应用随处可见。
在量子力学中,其代表薛定谔方程式中的动能项。
在数学中,经拉普拉斯算子运算为零的函数称为调和函 数;拉普拉斯算子是霍奇理论的核心,并且是德拉姆 上同调的结果。
物理解释考虑一座高度 点 的ft 。
这一 点的梯度是在该点坡度(或者说斜度)最陡的方向。
梯度的大小告诉我们坡度到底有多陡。
散度是通量的体密度物理上,散度的意义是场的有源性。
某一点或某个区域的散度大于零,表示向量场在这一点或这一区域有新的通量产生,小于零则表示向量场在这一点或区域有通量湮灭。
散度等于零的区域称为无源场或管形场。
就 的环量面密度(或称为环量强度)。
旋度是向量场的一种强度性质,就如同密度、浓度、温度一 样,它对应的广延性质是向量场沿一个闭合曲线的环量。
如果一个向量场中处处的旋度都是零,则称这个场为无旋场或保守场相关概念通环量记法=或三维直角坐标系柱坐标球坐标线性法则乘积法则商法则高斯散度定理:对某一个体积内的散度进行积分, 就应该得到这个体积内的总通量。
电磁场课件第一章_矢量分析7

(2 2 )dV ( ) dS
V
S
(2 2 )dV ( )dS
V
S n
n
上两式称为标量第二格林定理。
格林定理说明了区域 V 中的场与边界 S 上的场之间的关系。 因此,利用格林定理可以将区域中场的求解问题转变为边界上 场的求解问题。
此外,格林定理反映了两种标量场之间满足的关系。因此, 如果已知其中一种场的分布,即可利用格林定理求解另一种场 的分布。
导数,那么,可以证明该两个标量场 及 满足下列等式:
S
,
V
en
V (
2 )dV
S
n
dS
式中S 为包围V 的闭合曲面, 为标
量场 在 S 表面的外法线 en方n向上
的偏导数。
根据方向导数与梯度的关系,上式又可写成
V ( 2 )dV S ( ) dS
以上两式称为标量第一格林定理。
46
基于上式还可获得下列两式:
格林定理广泛地用于电磁理论。
1. 拉普拉斯运算
• 标量拉普拉斯运算2u
概念: (u) 2u
2 —— 拉普拉斯算符
计算公式: 直角坐标系
2u 2u 2u 2u x2 y2 z2
圆柱坐标系
2u
1
(
u
)
1
2
2u
2
2u z 2
球坐标系
2u
1 r2
r
(r2Leabharlann u ) rr21
sin
(sin
u )
r2
1
sin2
2u
2
44
• 矢量拉普拉斯运算 2F
概念: 2F ( F ) ( F )
直角坐标系中: 2 F
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(27)
2
h
2
dc dc − f (c , c , c )h h dc dc
1
2
31Biblioteka 231 2
1
∂ (h2 h3 f 1 ) 1 2 3 ∂ (h3 h1 f 2 ) 2 1 3 ∂ (h1 h2 f 3 ) 3 1 2 dc dc dc + dc dc dc + dc dc dc ∂c1 ∂c2 ∂c3
• Scales. We use hp as the scales in the p direction in general coordinates. (see below)
Scales
• Definition of unit vectors for general coordinates. The directions of unit vectors equal the direction of gradient of corresponding coordinate; The length of unit vectors should be 1. • Thus we introduce Scales denoted as hp :
∇f ≡
p
(22)
The scales in orthogonal coordinates can be calculated use the method in the former section. • Examples. – In Spherical coordinates we have eq.(20) Thus the Gradient Operation in Spherical coordinates is: ∇f =
(8)
= np i np i
chain rule
q
=
eq. (7)
q
=
q
q ∂x np i ni ∂cq hq
change the order of summation
=
q
∂x δpq ∂cq hq 1 ∂x hp ∂cp
eq. (2)
=
summation with δ f unction
• Through the deduction, eq.(8), we have: ∂x p ˆ = hp e ∂cp (9)
3
• Einstein summation convention ONLY for subscripts. Superscripts is free. e.g. ai bi = ap bp =ap · bp , p = 1, 2, 3.
i=1
ai · bi , however,
• For convenience, in Cartesian coordinate, we also use xi as the coordinates of x, namely, x = (x, y, z ) = (x1 , x2 , x3 ). • Similarly as above, we also will use x ˆi denote unit vectors in Cartesian coordinate, namely, x ˆ1 = e ˆ x, x ˆ2 = e ˆ ˆ3 = e ˆ y, x z . Thus we have: x ˆi = ∂x ∂xi (1)
p is the general coordinates unit vector along ˆ the Spherical coordinates unit vector along the r direction, e
p direction. p = 1, 2, 3 in a 3-D problem. • cp is the coordinate of a point in general coordinates. e.g. coordinate of P in Cartesian is (x, y, z ), in spherical Coordinate is (r, θ, φ), in general orthogonal coordinates is (c1 , c2 , c3 ).
Thus, (h1 )2 = ( ∂x 2 ∂y ∂z ) + ( 1 )2 + ( 1 )2 1 ∂c ∂c ∂c (18)
• Take spherical coordinates as an example. We have: x = r sin θ cos φ y = r sin θ sin φ (19) z = r cos θ c1 = r After calculation, one can easily find that: hr = 1 hθ = r hφ = r sin θ (20) c2 = θ c3 = φ
∆V ∆V →0
∆V
(25)
use Gauss Theorem: ∇ · f dV =
∆V ∂ ∆V
f · dS
(26)
• Calculate the closed surface integral. Let surface units pointing outside in the figure ˆ 1 + on the right, decompose f into f = f 1 e ˆ ˆ 2 + f 3e 3 , we have: f 2e f · dS = f 1 (c1 + dc1 , c2 , c3 )h2 h3 dc2 dc3 − f 1 (c1 , c2 , c3 )h2 h3 dc2 dc3
p = hp · ∇cp ˆ e
(4)
• Use Cartesian coordinates solve the gradient. (∇f =
∂ ∂ ∂ e ˆ e ˆ e ˆ x+ y + z ): ∂x ∂y ∂z ∂cp x ˆi ∂xi (5)
p = hp ˆ e
p in Cartesian coordinates: ˆ • Decompose e p = np x ˆ e i ˆi
q
(
∂x q dc ) · ∂cq
(
p
∂x p dc ) ∂cp
(chain rule)
(10)
Use eq.(9) in the above equation: (dl)2 =
q q dcq ) · ˆ (hq e p p dcp ) ˆ (hp e
(11)
Remember we have the orthogonal condition, eq.(2), we have : (dl)2 =
Gradient
• Consider a scalar function f (x, y, z ). Use chain rule on the gradient: ∇f =
p
∂f ∇cp ∂cp
(21)
And we have eq.(4), so the gradient in general coordinates is: 1 ∂f p ˆ e hp ∂cp
(6)
• Compare equation (5) and (6) we have:
np ∂cp i = p ∂xi h
(7)
• Pure mathematic deduction:
p = ˆ e
np ˆi ix ∂x ∂cq ∂cq ∂xi ∂x nq i ∂cq hq
= np i
∂x ∂xi
eq. (1) & (6)
p
1 ∂f p ∂f 1 ∂f 1 ∂f ˆ = e e ˆ e ˆ e ˆ r+ θ+ φ p p h ∂c ∂r r ∂θ r sin θ ∂φ
(23)
Namely, in spherical coordinates: ∂ 1 ∂ 1 ∂ e ˆ e ˆ e ˆ r+ θ+ φ ∂r r ∂θ r sin θ ∂φ
p
(hp dcp )2 = (h1 dc1 )2 + (h2 dc2 )2 + (h3 dc3 )2
(12)
• Thus we come to a very very important equation, eq.(12). – if the path is along one coordinates axis, its length is: dl1 = h1 dc1 (13)
• The Divergence in general coordinates. – combine with eq.(15), we have: 1 h1 h2 h3 ∂ (h2 h3 f 1 ) ∂ (h3 h1 f 2 ) ∂ (h1 h2 f 3 ) + + ∂c1 ∂c2 ∂c3
Denotation and Convention
We will use the following denotation in the discussion. • e with a hat for unit vector. e.g. e ˆ ˆ x is the Cartesian coordinates unit vector along the x direction, e r is
dc2 =0 dc3 =0
– which means the area of surface element is: dS = dl1 · dl2 = h1 h2 dc1 dc2 (14)
– and the volume of volume element is: dV = dl1 · dl2 · dl3 = h1 h2 h3 dc1 dc2 dc3 (15)
Orthogonal Coordinates
