关于Meta分析中的森林图解析
【最新】森林图

【最新】森林图在Meta分析汇总的结果中,最常见的两个图形就是森林图和漏斗图,但是笔者发现在实际的运用中,经常有人误读和误用这两个图形,从今天起,我讲具体介绍一下这两个图形的解读。
1.森林图的定义:森林图是以统计指标和统计分析方法为基础,用数值运算结果绘制出的图型。
它在平面直角坐标系中,以一条垂直的无效线(横坐标刻度为1或0)为中心,用平行于横轴的多条线段描述了每个被纳入研究的效应量和可信区间,用一个棱形(或其它图形)描述了多个研究合并的效应量及可信区间。
它非常简单和直观地描述了Meta分析的统计结果,是Meta分析中最常用的结果表达形式。
2.分类变量中的森林图当某研究RR(OR,RD)的95%CI包含了1,即在森林图中其95%CI的横线与无效竖线相交时,可认为试验组发生率与对照组发生率相等,试验因素无效。
当某研究RR(OR,RD)的95%CI上下限均_gt;1,即在森林图中,其95%CI 横线不与无效竖线相交,且该横线落在无效线右侧时,可认为试验组的发生率大于对照组的发生率,若研究者所研究的事件是不利事件(如发病、患病、死亡等)时,试验组的试验因素会增加该不利事件的发生,试验因素为有害因素(危险因素);若研究者所研究的事件是有益事件(如有效、缓解、生存等)时,试验因素会增加该有益事件的发生,试验因素为有益因素。
当某研究的95%CI上下限均小于1,即在森林图中,其95%CI横线不与无效竖线相交,且该横线落在无效线左侧时,可认为试验组的发生率小于对照组的发生率,若研究者所研究的事件是不利事件(如发病、患病、死亡等)时,试验组的试验因素会减少该不利事件的发生,试验因素为有益因素(保护因素);若研究者所研究的事件是有益事件(如有效、缓解、生存等)时,试验因素会减少该有益事件的发生,试验因素为有害因素。
2 连续性变量的森林图当某研究的95%CI包含了0,即在森林图中其95%CI横线与无效竖线(横坐标刻度为0)相交时,可认为试验组某指标的均数与对照组相等,试验因素无效。
META分析:手把手教你使用RevMan软件绘制森林图

META分析:手把手教你使用RevMan软件绘制森林图要做好一篇meta分析至少要掌握一些基本的技能,绘制一幅清晰明了、美观直接的森林图就是一项必备技能。
笔者在这里不打算探讨什么高深的统计学理论,本文将以图示的形式展示如何用RevMan 5.3软件做一幅符合SCI杂志投稿要求的森林图。
下图是一篇正式发表的森林图,下面我们将采用RevMan软件做出一幅一样的图形。
第一步,准备工作分为安装Revman软件和数据提取。
首先是安装RevMan5.3软件,这是一个完全免费的软件,管你什么Windows,Mac OS X或者Linux统统可以搞定。
这个软件完全视窗操作,简便易学,适合初学者,关键是虽然简单但是基本可解决大部分的meta 分析的统计学处理,其实很强大。
(需要软件的朋友,可以向解螺旋微信助手索要,助手微信号:helixlife0。
)其次就是数据的准备工作了,采用Excel管理数据足矣。
RevMan最新版本软件是支持直接复制粘贴数据的,我们按要求整理好数据,直接从Excel复制上去就好了。
我们首先看看RevMan来处理二分类数据(所谓二分类数据,就是取值只有是或否两种可能)。
So,在Excel上我们就如上图这样录入数据就好了。
其中r1 、r2分别代表的是干预组和对照组的事件发生数,n1、n2则是它们各自的总人数。
这里可能会碰到一组或者两组的事件发生数为零,不要紧,软件会帮我们处理的,不需要我们去校正这个零。
第二步,添加研究在打开我们的软件之后,我们新建一个文件,点击“create a new review”(新建),接下来创建一个最普通的“Intervention review”(勾选),我们进行相关项目的填写(如果仅仅是使用该软件的统计分析功能,可以不填),选择制作“Full Review” 然后点击Finish就ok了。
如果我们的目标仅仅是画纳入研究的质量评估图或者是流程图,我们可以选择Protocol而不去使用软件的计算功能,Protocol状态下不能使用其统计计算功能。
Meta分析的森林图及临床意义

Meta分析的森林图及临床意义Meta分析是一种用于评估和研究多个独立研究结果的统计方法,通过整合具有共同目标的研究,对其进行系统评价,从而得出更为准确和全面的结论。
在Meta分析过程中,森林图是一种常用的可视化工具,它能够以图形方式展示分析结果,为研究者提供直观的理解和评估。
森林图是以图形方式展示Meta分析结果的工具,通过将多个研究的结果以数值和统计学的方式表达在同一张图中,可以更直观地展示研究间的异质性和不确定性。
森林图的横轴通常表示研究设计或治疗方案,纵轴则表示效应大小,而图中的气泡则代表各个研究的结果。
收集相关研究:进行Meta分析的首要步骤是收集符合纳入标准的研究。
这些研究通常涉及同一主题、具有可比性和可合并性。
提取数据:从每篇研究中提取所需的数据,如样本量、组间差异、效应大小等。
统计分析:利用适当的统计方法对提取的数据进行合成和分析。
常见的统计方法包括加权平均数、标准化的均值差异等。
绘制森林图:将分析结果以数值和图形的方式展示在森林图中。
通常使用统计软件如Stata、R或Excel等来绘制图形。
森林图在临床研究中的应用具有重要意义。
它能够直观地展示多个研究的合并结果,帮助临床医生全面了解治疗效果。
森林图可以揭示研究间的异质性,这有助于解释结果的不确定性。
森林图还可以用于评估某些干预措施的效果,为临床决策提供依据。
例如,在评价某种新药的疗效时,可以收集多个临床试验数据,通过Meta分析得出该药物相对于对照组的疗效差异。
然后,利用森林图展示合并后的结果,帮助医生全面了解该药物的疗效,从而制定更为准确的诊疗方案。
同时,通过观察森林图中的气泡分布,还可以了解到各研究之间的异质性,进一步探讨其潜在影响因素。
Meta分析的森林图是一种有效的可视化工具,用于展示和评估多个独立研究结果的合并统计量。
在制作和分析森林图的过程中,需要经过数据收集、提取、统计分析和图形绘制等步骤。
森林图在临床研究中的应用具有重要意义,它能够直观地展示治疗效果,揭示研究间的异质性,并为临床决策提供依据。
图说meta十:森林图简介
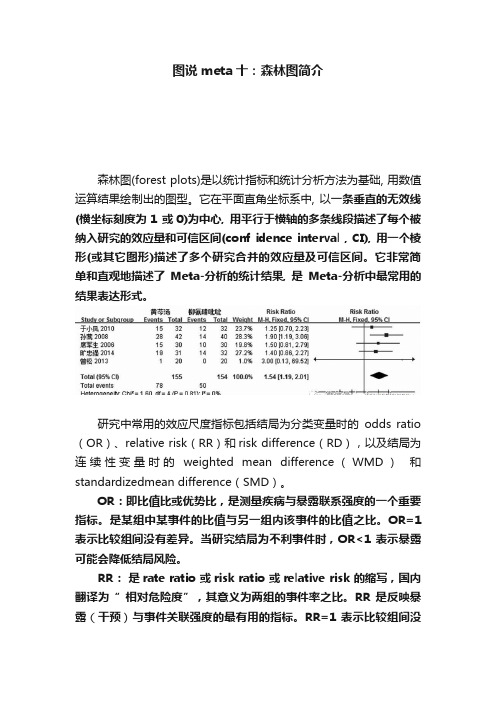
图说meta十:森林图简介森林图(forest plots)是以统计指标和统计分析方法为基础, 用数值运算结果绘制出的图型。
它在平面直角坐标系中, 以一条垂直的无效线(横坐标刻度为1 或0)为中心, 用平行于横轴的多条线段描述了每个被纳入研究的效应量和可信区间(conf idence interval , CI), 用一个棱形(或其它图形)描述了多个研究合并的效应量及可信区间。
它非常简单和直观地描述了Meta-分析的统计结果, 是Meta-分析中最常用的结果表达形式。
研究中常用的效应尺度指标包括结局为分类变量时的odds ratio (OR)、relative risk(RR)和risk difference(RD),以及结局为连续性变量时的weighted mean difference(WMD)和standardizedmean difference(SMD)。
OR:即比值比或优势比,是测量疾病与暴露联系强度的一个重要指标。
是某组中某事件的比值与另一组内该事件的比值之比。
OR=1 表示比较组间没有差异。
当研究结局为不利事件时,OR<1 表示暴露可能会降低结局风险。
RR:是rate ratio 或risk ratio 或relative risk 的缩写,国内翻译为“ 相对危险度”,其意义为两组的事件率之比。
RR 是反映暴露(干预)与事件关联强度的最有用的指标。
RR=1 表示比较组间没有差异。
当研究结局为不利事件时,RR<1 表示干预可降低结局风险。
需要注意的是,只有队列研究和随机对照试验结果可以直接获得相对危险度。
RD(risk difference):即危险差,也被称为归因危险度(attributable risk,AR)、绝对风险差(absoluterisk difference)和绝对风险降低率(absolute riskreduction, ARR),是指干预(暴露)组和对照组结局事件发生概率的绝对差值。
mate分析森林图快速的解读知识分享

m a t e分析森林图快速的解读何瑶全科医学 201530130606题目一:请解读如下森林图。
要求:500字左右。
这张森林图,我们又可以叫它meta分析,它是对研究设计相同或者相似且具有相同目的的,但是又相互独立的多个研究结果(证据)进行系统的综合定量分析,计算其合并效应量,并作出结果解释。
如上图,gao2014的实验中实验组(experimental total)样本量为293,而其中有31个问题样本(experimental events),对照组(control total)样本量为289,问题样本(control events)为40,权重(weight)为16.0%,比值比(OR)为0.74,95%可信区间(95%CI)为(0.45,1.21),其横线与OR=1相交,表示无统计学意义;由此类推,我们不难分析出hu2001的实验结果、li2009年的实验结果和wang2009的实验结果,他们的实验中横线都与OR=1相交,表示无统计学意义。
zang2011的实验中实验组(experimental total)样本量为812,而其中有84个问题样本(experimental events),对照组(control total)样本量为815,问题样本(control events)为152,权重(weight)为60.3%,比值比(OR)为0.5,95%可信区间(95%CI)为(0.38,0.67),其横线与OR=1不相交,表示有统计学意义。
有分析图可见,li2009的实验样本量最小,权重最小,zang2011的实验样本量最大,权重最大,结果较其他组准确。
实验组(experimental total)样本数为1693,对照组(control total)样本数为1358,问题样本数中,实验组(experimental events)为180,对照组(control events)为249,权重(weight)100%,比值比OR=0.57,95%可信区间(95%CI)为(0.46,0.70),其可信区间表现为菱形,位于图中竖线左侧,与竖线不相交,有统计学意义。
meta分析及森林图PPT幻灯片课件

12
Meta分析与系统评价
在系统评价(systematic review)中,当数据资料适合 使用Meta分析时,用Meta分析可以克服传统文献综述的 两大问题,其分析结果的可靠性更高;当数据资料不适合 做Meta分析时,系统评价只能解决文献评价的问题,不能 解决样本含量的问题,因此,对其分析结论应慎重。 没有按系统评价标准操作规范实施,或未经严格文献评 价的研究,即使用了Meta分析也不一定是系统评价的研究, 更难说是高质量的研究。
13
Meta分析数据图怎么解读?
14
此图叫什么? 森林图
15
森林图解析
森林图是以统计指标和统计分析方法为基础,用数值运 算结果绘制出的图型。它在平面直角坐标系中,以一条垂直的 无效线(横坐标刻度1或0)为中心,用平行于横轴的多条线 段描述了每个被纳入研究的效应量和可信区间(CI),用一个 棱形( 或其它图形)描述了多个研究合并的效应量及可信区 间。它非常简单和直观地描述了Meta分析的统计结果,是 Meta分析中最常用的结果表达形式。
《The Cochrane Library》第3页的定义。
9
Meta分析的统计目的 处理同一 问题的多个结果报道时,通常是平等(等权重方 法)对待每个研究结果而得出结论。这种文献综 述一般不进行文献评价,也不考虑文献的质量,
主要是以某类文献数量的多少得出结论。
的影响,以原有的单位真实地反映了试验效应, WMD是试验组的均数 X1 减去 对照组均数 X 2 的差,即WMD= X1 - X 2 。
meta分析森林图解读

meta分析森林图解读Meta分析森林图是一种用于展示不同研究结果之间差异的可视化工具。
它可以帮助读者快速了解不同研究结果的整体趋势,并揭示其中的异质性。
本文将介绍如何读取和解释Meta分析森林图。
首先,森林图的横轴表示每个研究的效应大小(通常使用加权平均数),垂直线表示每个研究的置信区间。
置信区间是指我们对真实效应大小的估计范围。
如果置信区间越窄,我们就越有信心这个结果是准确的。
森林图中每个研究的点大小代表该研究所占的比重。
在元分析中,研究通常被赋予更高的权重,如果样本量越大或研究设计更为合理。
图中每个点都用一条垂直线连接,这条线被称为置信区间。
如果置信区间有重叠,则表明不同研究得出的效应大小没有显著的差异。
在森林图中,所有研究的效应大小线都在一个垂直线上,这个垂直线代表的是元分析的效应大小,也称为固定效应模型的效应大小。
固定效应模型假设所有研究的真实效应大小是相同的,其差异仅仅来源于随机误差。
当所有的研究得出的效应大小都在置信区间内,则此时固定效应模型成立,表示元分析所得结果可靠。
然而,在某些情况下,固定效应模型的假设并不成立,因为不同研究的真实效应大小可能不同。
这时候就需要采用随机效应模型。
随机效应模型假设不同研究的真实效应大小是随机变量,它们之间的差异来源于难以归因于随机误差的因素,如研究人员的实践技巧、受试者的特征、使用不同的方法等。
当元分析结果表现出显著的异质性时,即研究结果存在显著的差异,此时应当检查随机效应模型。
如果随机效应模型成立,则每个研究得出的效应大小都在不同的位置上,形成了一个散点分布。
除了研究的效应大小和置信区间外,森林图还提供了每个研究的名称,高亮显示的点和水平线。
高亮显示的点代表整个元分析的总效应大小,水平线代表元分析的置信区间。
当元分析的总效应大小落在任何一项研究的置信区间之内时,该研究的效应大小被视为显著。
总之,Meta分析森林图是一个十分有用的可视化工具,可以帮助读者更好地了解不同研究结果之间的差异,揭示研究结果的异质性。
森林图

森林图的临床意义
合并结果:THP对比MMC膀胱 刺激症发生率相似
Meta-分析的森林图及临床意义
刘关键 吴泰相 四川大学华西医院中国循证医学中心
中国循证医学杂志.2004,4(3):198-201
什么是森林图
• 森林图是以统计指标和统计分析方法为基础,用数值运算结果绘
制出的图型。它在平面直角坐标系中,以一条垂直的无效线(横坐 标刻度为1或0)为中心,用平行于横轴的多ห้องสมุดไป่ตู้线段描述了每个被纳
入研究的效应量和可信区间(confidence interval,CI),用一个棱形
(或其它图形)描述了多个研究合并的效应量及可信区间。它非常 简单和直观地描述了Meta分析的统计结果,是Meta分析中最常用
的结果表达形式。
• (以唐良友的一篇META分析文献里的图为例)
中间方块大小反 映权重大小 无效线
森林图的临床意义
• 当总体RR=1(某个研究RR的95%CI包含了1)时,或在森林图中, 当某个研究RR 的95%CI横线与无效竖线(横坐标刻度为1)相交时, 表示试验组发生率与对照组发生率差异无统计学意义。
森林图的临床意义
• 当总体RR>1(或某研究RR 的95%CI上下限均>1)时,在森林图中, 某个研究的95%CI的横线不与无效竖线相交,且该横线落在无效 线右侧时,可认为试验组某事件的发生率大于对照组的发生率。
THP对比MMC增加膀胱刺激症 发生率
森林图的临床意义
• 当总体RR<1(或某研究RR的95%CI下限均<1)时,在森林图中,某
个研究的95%CI的横线不与无效竖线相交,且该横线落在无效线 左侧时,可认为试验组某事件的发生率小于对照组的发生率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
关于Meta分析中的森林图解析:
1、OR在统计学中是指比值比、优势比,英文全称是(odds ratio).它的具体意思是在病例-对照研究中,描述疾病与危险因素关联的指标。
OR通常适用于病例对照研究。
由于在病例对照研究中无法获得病例组与对照组的确切发病率,只能获得病例组和对照组的暴露频率,因此不能直接用相对危险度描述疾病与危险因素的关系。
如:
病例组暴露某一事件的优势(odds)=a/b
对照组暴露某一事件的优势(odds)=c/d
病例组和对照组暴露某一事件的优势比为OR=(a/b)/(c/d)=ad/bc
a表示在病例组中暴露某一事件后得病得人,b表示在病例组中没有得病的人
c表示在对照组中暴露某一事件后得病得人,d表示在病例组中没有得病的人
>1 暴露与疾病的危险度增加正相关
<1 暴露与疾病的危险度减少负相关
=1 暴露与疾病的危险度无关无相关
2、OR,即比值比(odds ratio),是病例对照研究中表示疾病与暴露之间联系强度的指标,又称为比数比,优势比,交叉乘积比。
楼上说描述疾病与危险因素关联的指标是不准确的,因为这个暴露不一定是危险因素,也可能是保护因素或者既不是保护因素也不是危险因素。
暴露史病例对照合计
有a b a+b=n1
无c d c+d=n0
合计a+c=m1 b+d-m0 a+b+c+d=T
从表可见,病例对照研究对比的是病例组的曾暴露率即a/(a+c)和对照组的曾暴露率b/(b+d),如a/(a+c)>b/(b+d),并经统计学检验证实差异有统计学意义,则暴露与疾病有联系(为危险因素);如a/(a+c)<b/(b+d),并经统计学检验证实差异有统计学意义,则暴露与疾病有联系(为保护因素);如果经过统计学检验没有统计学意义,则该暴露与该疾病没有联系。
所谓比值就是指某事物发生的可能性与不发生的可能性之比。
据上表病例组的暴露比值为
a/(a+c)/c/(a+c)=a/c;对照组的暴露比值为b/(b+d)/d/(b+d)=b/d;而比值比(OR)=病例组的暴露比值(a/c)/对照组的暴露比值(b/d)即ad/bc。
当OR>1时,说明病例组的暴露频率大于非病例组的,即暴露有较高的发病危险性,暴露与疾病之间为正关联;反之,当OR<1时,说明病例组的暴露概率低于非病例组的,即暴露有保护作用,暴露与疾病之间为负关联。
疾病与暴露联系愈密切,比值比的数值愈大
3、RR也叫危险比(risk ratio)或率比(rate ratio),或相对危险度。
是反映暴露与发病(死亡)关联强度的最有用的指标。
RR适用于队列研究或随机对照试验。
RR表明暴露组发病
或死亡的危险是非暴露组的多少倍。
RR值越大,表明暴露的效应越大,暴露与结局关联的强度越大。
即暴露组发病率或死亡率与非暴露组发病率或死亡率之比。
当它有统计学意义时:
RR=1,说明暴露因素与疾病之间无关联。
RR>1,说明暴露因素是疾病的危险因素(正相关)。
认为暴露与疾病呈"正"关联,即暴露因素是疾病的危险因素。
RR<1,说明暴露因素是疾病的保护因素(负相关)。
认为暴露与疾病呈"负"关联,即暴露因素是保护因素。
4、归因危险度(AR)又叫特异危险度、率差(rate difference, RD)和超额危险度(excess risk),是暴露组发病率与对照组发病率相差的绝对值,它表示危险特异地归因于暴露因素的程度。
1、eight %表示各个试验的权重。
一般来说,对于技术资料使用样本量作为权重的衡量依据,样本量越大,权重越大;计量资料则采用标准差作为权重的衡量依据,标准差越小,权重越大。
2、分类变量:RR和OR的森林图
RR和OR的森林图(forest plots) ,无效线竖线的横轴尺度为1,每条横线为该研究的95%可信区间上下限的连线,其线条长短直观地表示了可信区间范围的大小,线条中央的小方块为RR或OR值的位置,其方块大小为该研究权重大小。
若某个研究95%可信区间的线条横跨为无效竖线,即该研究无统计学意义,反之,若该横线落在无效竖线的左侧或右侧,该研究有统计学意义。
3、数值变量:MD和SMD的森林图
MD和SMD的森林图,无效线竖线的横轴尺度为0,每条横线为该研究的95%可信区间上下限的连线,其线条长短直观地表示了可信区间范围的大小,线条中央的小方块为MD或SMD值的位置,其方块大小为该研究权重大小。
若某个研究95%可信区间的线条横跨为无效竖线,即该研究无统计学意义,反之,若该横线落在无效竖线的左侧或右侧,该研究有统计学意义。
4、。
