一元二次方程全章复习与巩固—知识讲解

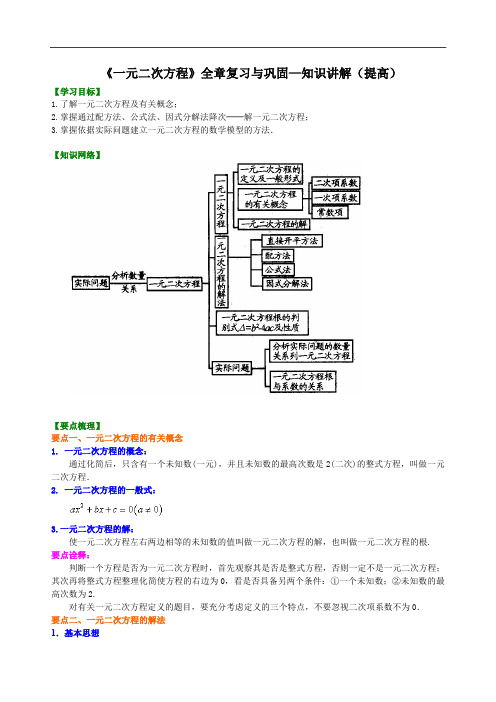
《一元二次方程》全章复习与巩固—知识讲解（提高）【学习目标】

1.了解一元二次方程及有关概念；

2.掌握通过配方法、公式法、因式分解法降次──解一元二次方程；

3.掌握依据实际问题建立一元二次方程的数学模型的方法．

【知识网络】

【要点梳理】

要点一、一元二次方程的有关概念1.一元二次方程的概念：

通过化简后，只含有一个未知数(一元)，并且未知数的最高次数是2(二次)的整式方程，叫做一元二次方程．

2.一元二次方程的一般式：

3.一元二次方程的解：

使一元二次方程左右两边相等的未知数的值叫做一元二次方程的解，也叫做一元二次方程的根.

要点诠释：

判断一个方程是否为一元二次方程时，首先观察其是否是整式方程，否则一定不是一元二次方程；其次再将整式方程整理化简使方程的右边为0，看是否具备另两个条件：①一个未知数；②未知数的最高次数为2.

对有关一元二次方程定义的题目，要充分考虑定义的三个特点，不要忽视二次项系数不为0．

要点二、一元二次方程的解法

1．基本思想

一元二次方程???→

降次一元一次方程

2．基本解法

直接开平方法、配方法、公式法、因式分解法． 要点诠释：

解一元二次方程时，根据方程特点，灵活选择解题方法，先考虑能否用直接开平方法和因式分解

法，再考虑用公式法．

要点三、一元二次方程根的判别式及根与系数的关系 1.一元二次方程根的判别式

一元二次方程)0(02≠=++a c bx ax 中，ac b 42-叫做一元二次方程

)0(02

≠=++a c bx ax 的根的判别式，通常用“?”来表示，即ac b 42

-=?.

（1）当△>0时，一元二次方程有2个不相等的实数根；

（2）当△=0时，一元二次方程有2个相等的实数根；

（3）当△<0时，一元二次方程没有实数根.

2.一元二次方程的根与系数的关系

如果一元二次方程)0(02≠=++a c bx ax 的两个实数根是21x x ，，

那么a b x x -=+21，a

c x x =21.

注意它的使用条件为a ≠0， Δ≥0. 要点诠释：

1.一元二次方程 的根的判别式正反都成立．利用其可以解

决以下问题：

(1)不解方程判定方程根的情况； (2)根据参系数的性质确定根的范围； (3)解与根有关的证明题．

2. 一元二次方程根与系数的应用很多：

(1)已知方程的一根，不解方程求另一根及参数系数；

(2)已知方程，求含有两根对称式的代数式的值及有关未知数系数；

(3)已知方程两根，求作以方程两根或其代数式为根的一元二次方程．

要点四、列一元二次方程解应用题

1.列方程解实际问题的三个重要环节： 一是整体地、系统地审题； 二是把握问题中的等量关系；

三是正确求解方程并检验解的合理性.

2.利用方程解决实际问题的关键是寻找等量关系.

3.解决应用题的一般步骤：

审 (审题目，分清已知量、未知量、等量关系等)；

设 (设未知数，有时会用未知数表示相关的量)；

列 (根据题目中的等量关系，列出方程)；

解 (解方程，注意分式方程需检验，将所求量表示清晰)；

验 (检验方程的解能否保证实际问题有意义）；

答 (写出答案，切忌答非所问).

4.常见应用题型

数字问题、平均变化率问题、利息问题、利润(销售)问题、形积问题等.

要点诠释：

列方程解应用题就是先把实际问题抽象为数学问题（列方程），然后由数学问题的解决而获得对实际问题的解决.【典型例题】

类型一、一元二次方程的有关概念

1．已知（m－1）x|m|+1+3x－2＝0是关于x的一元二次方程，求m的值.

【答案与解析】

依题意得|m|+1＝2，即|m|＝1，

解得m＝±1，

又∵m－1≠0，∴m≠1，

故m＝－1.

【总结升华】依题意可知m－1≠0与|m|+1＝2必须同时成立，因此求出满足上述两个条件的m的值即可.

特别是二次项系数应为非零数这一隐含条件要注意.

举一反三：

【变式】若方程2

(2)310

m

m x mx

---=是关于x的一元二次方程，求m的值．

【答案】根据题意得

22,

20,

m

m

?=

?

?

-≠

??

解得

所以当方程2

(2)310

m

m x mx

--=是关于x的一元二次方程时，2

m=-．

类型二、一元二次方程的解法

2．解下列一元二次方程．

(1)22

4(3)25(2)0

x x

---=； (2)22

5(3)9

x x

-=-； (3)2

(21)4(21)40

x x

++++=．【答案与解析】

(1)原方程可化为：22

[2(3)][5(2)]0

x x

---=，

即(2x-6)2-(5x-10)2＝0，

∴ (2x-6+5x-10)(2x-6-5x+10)＝0，

即(7x-16)(-3x+4)＝0，

∴ 7x-16＝0或-3x+4＝0，∴

116 7

x=，24 3

x=． (2)2

5(3)(3)(3)

x x x

-=+-，

2

5(3)(3)(3)0

x x x

--+-=，

∴ (x-3)[5(x-3)-(x+3)]＝0，

即(x-3)(4x-18)＝0，∴ x-3＝0或4x-18＝0，

∴

13

x=，29

2

x=．(3)2

(21)4(21)40

x x

++++=，

∴2

(212)0

x++=．即2

(23)0

x+=，

∴

12

3

2

x x

==-．

【总结升华】 (1)方程左边可变形为22

[2(3)][5(2)]

x x

---，因此可用平方差公式分解因式；

(2)中方程右边分解后为(x-3)(x+3)，与左边中的(x-3)2有公共的因式，

可移项后提取公因式(x-3)后解题；

(3)的左边具有完全平方公式的特点，可用公式变为(2x+1+2)2＝0再求解．举一反三：

【变式】解方程： (1)3x+15＝-2x2-10x； (2)x2-3x＝(2-x)(x-3)．

【答案】

(1)移项，得3x+15+(2x2+10x)＝0，∴ 3(x+5)+2x(x+5)＝0，

即(x+5)(3+2x)＝0，∴ x+5＝0或3+2x＝0，

∴

1

5

x=-，23

2

x=-．

(2)原方程可化为x(x-3)＝(2-x)(x-3)，移项，x(x-3)-(2-x)(x-3)＝0，

∴ (x-3)(2x-2)＝0，∴ x-3＝0或2x-2＝0，

∴

1

3

x=，21

x=．

类型三、一元二次方程根的判别式的应用

3．关于x 的方程2(5)410a x x ---=有实数根．则a 满足（ ）

A ．a ≥1

B ．a ＞1且a ≠5

C ．a ≥1且a ≠5

D ．a ≠5

【答案】A ；

【解析】①当50a -=，即5a =时，有410x --=，1

4

x =-，有实数根；

②当50a -≠时，由△≥0得2(4)4(5)(1)0a --?-?-≥，解得1a ≥且5a ≠． 综上所述，使关于x 的方程2

(5)410a x x ---=有实数根的a 的取值范围是

1a ≥．

答案：A

【总结升华】注意“关于x 的方程”与“关于x 的一元二次方程”的区别，前者既

可以是一元一次方程，也可以是一元二次方程，所以必须分类讨论，而后者隐含着二次项系数不能为0．

4． k 为何值时，关于x 的二次方程2

690kx x -+=

（1）k 满足 时,方程有两个不等的实数根； （2）k 满足 时,方程有两个相等的实数根；

（3）k 满足 时,方程无实数根. 【答案】（1）10k k ≠＜，且；

（2）1k =；（3）1k ＞. 【解析】求判别式，注意二次项系数的取值范围. 【总结升华】根据判别式ac b 42-=?及k ≠0求解.

类型四、一元二次方程的根与系数的关系

5．已知关于x 的方程222(2)0x m x m --+=，试探求：是否存在实数m 使方程的两个实数根的平方和等于56，若存在，求出m 的值；若不存在，请说明理由．

【答案与解析】

存在．

设方程两根为x 1、x 2，根据题意，得122(2)x x m +=-，212x x m =，221256x x +=， 而222121212()2x x x x x x +=+-，于是有[]2

22(2)256m m --=，整理得28200m m --=， 解这个方程得110m =， 22m =-，

当10m =时，△＝ 2224[2(2)]41440b ac m m -=---=-<， 当2m =-时，△＝2224[2(2)]4480b ac m m -=---=>， 所以符合条件的m 的值为-2．

【总结升华】由两个实数根的平方和等于56，列出关系式，再由根与系数关系求出m的值，通过判别式去验证m值是否符合题意，从而得出结论.

举一反三：

【变式】已知关于x的方程2

(1)(23)10

k x k x k

-+-++=有两个不相等的实数根1x、2x．

(1)求k的取值范围；

(2)是否存在实数k，使方程的两实数根互为相反数如果存在，求出k的值；如果不存在，

请说明理由．

【答案】(1)根据题意，得△＝(2k-3)2-4(k-1)(k+1)＝22

4129412130

k k k k

-+-=-+>，

所以13

12

k<．由k-1≠0，得k≠1.

当13

12

k<且k≠1时，方程有两个不相等的实数根；

(2) 不存在．如果方程的两个实数根互为相反数，则

1223

1

k

x x

k -

+=-=

-，解得3

2

k=．

当3

2

k=时，判别式△＝-5＜0，方程没有实数根．

所以不存在实数k，使方程的两个实数根互为相反数．类型五、一元二次方程的应用

6．甲、乙两人分别骑车从A、B两地相向而行，甲先行1小时后，乙才出发，又经过4小时两人在途中的C地相遇，相遇后两人按原来的方向继续前进.乙在由C 地到达A地的途中因故停了20分钟，结果乙由C地到达A地时比甲由C地到达B 地还提前了40分钟，已知乙比甲每小时多行驶4千米，求甲、乙两人骑车的速度.

【答案与解析】

设甲的速度为x千米/时，则乙的速度为（x+4）千米/时.

根据题意，得54(4)2040

460

x x

x x

++

=-

+

解之,得x1=16，x2=－2.

经检验：x1=16，x2=－2都是原方程的根，但x2=－2不合题意，舍去.

∴当x=16时，x+4=20.

答：甲每小时行驶16千米，乙每小时行驶20千米.

【总结升华】注意解题的格式，解分式方程应用题要双检验，即验根、符合题意.举一反三：

【变式】某工程队在我市实施棚户区改造过程中承包了一项拆迁工程。原计划每天拆迁1250m2，因为准备工作不足，第一天少拆迁了20％。从第二天开始，该工程队加快了拆迁速度，第三天拆迁了1440m2.

求：(1)该工程队第一天拆迁的面积；

(2)若该工程队第二天、第三天每天的拆迁面积比前一天增加的百分数相

同，求这个百分数.

【答案】（1）1000m 2

；（2）20%. 【巩固练习】 一、选择题

1. 关于x 的一元二次方程（a －1）x 2＋x ＋|a|－1＝0的一个根是0，则实数a 的值为（ ）

A.－1 D.－1或1 2．已知a 是方程x 2+x ﹣1=0的一个根，则

2221

1a a a

-

--的值为（ ） A.15

2

-+ B.

15

2

-± C.﹣1

3．若方程式（3x ﹣c ）2﹣60=0的两根均为正数，其中c 为整数，则c 的最小值为何（ ）

4．已知关于x 的方程2(2)230m x mx m -+++=有实根，则m 的取值范围是（ ）

A ．2m ≠

B ．6m ≤且2m ≠

C ．6m <

D ．6m ≤ 5．如果是α、β是方程2234x x +=的两个根，则22αβ+的值为（ ）

A ．1

B ．17

C ．

D ．

6．在一幅长80 cm,宽50 cm 的矩形风景画的四周镶上一条金色纸边,制成一幅矩形挂图,如图所示.如果要使整个挂图的面积是5 400 cm 2,设金色纸边的宽为x cm,那么x 满足的方程是( )

+130x －1 400=0 +65x －350=0 －130x －1 400=0 －65x －350=0

7. 方程x 2+ax+1=0和x 2

-x-a=0有一个公共根，则a 的值是( ) A ．0 B ．1 C ．2 D ．3 8. 若关于x 的一元二次方程

的两个实数根分别是，且满足

．

则k 的值为（ ）

A.－1或

B.－1

C.

D.不存在

二、填空题

9．关于x 的方程2()0a x m b ++=的解是x 1=－2，x 2=1（a ，m ，b 均为常数，a ≠0），则方程2(2)0a x m b +++=的解是 .

10．已知关于x 的方程x 2+2(a+1)x+(3a 2+4ab+4b 2+2)＝0有实根，则a 、b 的值分别

为 ．

11．已知α、β是一元二次方程2430

x x

--=的两实数根，则(α-3)(β-3)＝________．12．当m_________时，关于x 的方程是一元二次方程；当m_________时，此方程是一元一次方程.

13．把一元二次方程3x2-2x-3=0化成3(x+m)2=n的形式是____________；若多项式x2-ax+2a-3是一个完全平方式，则a=_________.

14．已知，则的值等于_________.

15．已知，那么代数式的值为________.

16．当x=_________时，既是最简二次根式，被开方数又相同.

三、解答题

17. 设m为整数，且4＜m＜40，方程有两个不相等的整数根，

求m的值及方程的根.

18．设(a，b)是一次函数y＝(k-2)x+m与反比例函数n

y

x

=的图象的交点，且a、b 是关于x的一元二次方程22(3)(3)0

kx k x k

+-+-=的两个不相等的实数根，其中k 为非负整数，m、n为常数．

（1）求k的值；

（2）求一次函数与反比例函数的解析式．

19. 长沙市某楼盘准备以每平方米5000元的均价对外销售，由于国务院有关房地产

的新政策出台后，购房者持币观望．为了加快资金周转，房地产开发商对价格经过两次下调后，决定以每平方米4050元的均价开盘销售．

(1)求平均每次下调的百分率；

(2)某人准备以开盘均价购买一套100平方米的房子，开发商还给予以下两种优惠方案以供选择：

①打折销售；

②不打折，送两年物业管理费，物业管理费是每平方米每月元，请问哪种方案更优惠

20．已知某项工程由甲、乙两队合做12天可以完成，共需工程费用13 800元，乙队单独完成这项工程所需时间是甲队单独完成这项工程所需时间的2倍少10天，且甲队每天的工程费用比乙队多150元.

(1)甲、乙两队单独完成这项工程分别需要多少天

(2)若工程管理部门决定从这两个队中选一个队单独完成此项工程，从节约资

金的角度考虑，应该选择哪个工程队请说明理由.

【答案与解析】

一、选择题

1．【答案】A ；

【解析】先把x ＝0代入方程求出a 的值，然后根据二次项系数不能为0，把a ＝1舍去．

2．【答案】D ； 【解析】先化简22211a a a

-

--，由a 是方程x 2+x ﹣1=0的一个根，得a 2

+a ﹣1=0，则a 2+a=1，

再整体代入即可．

解：原式=

2(1)(1)(1)a a a a a -++-=1

(1)

a a +，

∵a 是方程x 2

+x ﹣1=0的一个根，

∴a 2

+a ﹣1=0， 即a 2+a=1，

∴原式=

1

(1)

a a +=1．

故选D ．

3．【答案】B ；

【解析】利用平方根观念求出x ，再根据一元二次方程的两根都为正数，求出c

的最小值即可．

解：（3x ﹣c ）2﹣60=0 （3x ﹣c ）2=60

3x ﹣c=± 3x=c± x=

又两根均为正数，且

＞7．

所以整数c 的最小值为8 故选B ．

4.【答案】D ；

【解析】△≥0得6m ≤，方程有实根可能是一元二次方程有实根，也可能是一元一次方程有实根.

5．【答案】C ；

【解析】22+=+-=6.25αβαβαβ2

（）

2. 6．【答案】B ；

【解析】上、下两条金色纸边的面积一样,左、右两条金色纸边的面积一样,

∴2(80+x)·x+2(50+x)·x+80×50=5 400. 整理得x 2+65x －350=0.

7．【答案】C ；

【解析】提示：先求公共根m=-1,再把这个公共根m=-1代入原来任意一个方程可求出a=2. 8．【答案】C ；

【解析】由题意，得：

22

121211=1k k k k k x x x x k ????=-=-??

+=??=-??4

≤≥0435 当时，不符合≤，舍去，故3

54或4

. 二、填空题

9．【答案】x 1=﹣4，x 2=﹣1．

【解析】解：∵关于x 的方程a （x +m ）2+b =0的解是x 1=﹣2，x 2=1，（a ，m ，b 均为

常数，a ≠0），

∴则方程a （x+m +2）2+b =0的解是x 1=﹣2﹣2=﹣4，x 2=1﹣2=﹣1． 故答案为：x 1=﹣4，x 2=﹣1．

10.【答案】a ＝1，1

2

b =-．

【解析】 判别式△＝[2(a+1)]2-4(3a 2+4ab+4b 2+2) ＝4(a 2+2a+1)-(12a 2+16ab+16b 2+8)

＝-8a 2-16ab-16b 2+8a-4 ＝-4(2a 2+4ab+4b 2-2a+1)

＝-4[(a 2+4ab+4b 2)+(a 2-2a+1)]． ＝-4[(a+2b)2+(a-1)2]．

因为原方程有实根，所以-4[(a+2b)2+(a-1)2]≥0，

(a+2b)2+(a-1)2≤0，

又∵ (a+2b)2≥0，(a-1)2≥0，

∴ a-1＝0且a+2b ＝0， ∴ a ＝1，1

2

b =-． 11．【答案】-6；

【解析】∵ α、β是一元二次方程2430x x --=的两实数根，

∴ α+β＝4，αβ＝-3．

∴ (3)(3)3()933496αβαβαβ--=-++=--?+=-． 12．【答案】-3；

．

13．【答案】；2或6.

【解析】即2(-)232

a

a =-.a=2或6. 14.【答案】4；

【解析】原方程化简为：（x 2+y 2）2-2(x 2+y 2)-8=0,解得x 2+y 2=-2或4，-2不符题意舍去.

15.【答案】-2；

【解析】原方程化为：

.

16.【答案】-5；

【解析】由x 2

+3x=x+15解出x=-5或x=3,

当x=3时，

不是最简二次根式，x=3舍去.故x=-5.

三、解答题

17. 【答案与解析】 解方程，

得

，

∵原方程有两个不相等的整数根，∴2m+1为完全平方数，

又∵m 为整数，且4＜m ＜40， ∴m=12或24. ∴当m=12时，，

；

当m=24时，

.

18. 【答案与解析】

(1)因为关于x 的方程22(3)(3)0kx k x k +-+-=有两个不相等的实数根，

所以2

2

0,

44(3)4(3)0,

k b ac k k k ≠??

=-=--->?△ 解得k ＜3且k ≠0，

又因为一次函数y ＝(k-2)x+m 存在，且k 为非负整数，所以k ＝1． (2)因为k ＝1，所以原方程可变形为2420x x --=，于是由根与系数的关系知a+b ＝4，ab ＝-2，

又当k ＝1时，一次函数y x m =-+过点(a ，b)，所以a+b ＝m ，于是m ＝4，

同理可得n ＝-2，

故所求的一次函数与反比例函数的解析式分别为4y x =-+与2y x

=-．

19. 【答案与解析】

(1)设平均每次下调的百分率是x ．

依题意得5000(1-x)2＝4050．

解得x 1＝10%，x 2＝

19

10

(不合题意，舍去)． 答：平均每次下调的百分率为10%．

(2)方案①优惠：4050×100×＝8100(元)；

方案②优惠：×100×12×2＝3600(元) ∵ 8100＞3600．∴ 选方案①更优惠.

20. 【答案与解析】

(1) 设甲队单独完成需x 天，则乙队单独完成需要(2x －10)天. 根据题意,有111

21012

x

x +

=-，

解得x 1=3，x 2=20. 经检验均是原方程的根，x 1=3不符题意舍去.故x=20. ∴乙队单独完成需要 2x －10=30(天).

答：甲、乙两队单独完成这项工程分别需要20天、30天. (2) 设甲队每天的费用为y 元，则由题意有 12y+12(y －150)=138 000，解得y=650 .

∴ 选甲队时需工程费用650×20=13 000，选乙队时需工程费用500×30=15 000.

∵ 13 000 <15 000，

∴ 从节约资金的角度考虑，应该选择甲工程队.