初中数学几何经典模型范文
初中数学几何模型的应用案例分析

初中数学几何模型的应用案例分析数学作为一门基础学科,对于学生的发展具有重要的作用。
在初中阶段,数学的学习内容涉及到各个方面,其中几何模型的应用尤为重要。
几何模型是一种将数学概念与实际问题相结合的方法,通过几何图形的建立和分析,可以帮助学生更好地理解和应用数学知识。
本文将通过几个具体的案例来分析初中数学几何模型的应用。
案例一:计算机图形的绘制在计算机图形学中,几何模型的应用非常广泛。
以绘制一个简单的矩形为例,我们可以通过确定矩形的四个顶点坐标来构建几何模型。
假设矩形的长为5个单位,宽为3个单位,我们可以通过计算每个顶点的坐标来绘制矩形。
通过这个案例,学生可以学习到坐标系的概念和使用方法,进一步理解几何模型在计算机图形中的应用。
案例二:建筑设计中的几何模型几何模型在建筑设计中也有着重要的应用。
以设计一个房间的地板为例,我们可以通过绘制一个矩形来表示房间的平面图。
假设房间的长为6米,宽为4米,我们可以通过计算每个角的坐标来确定矩形的形状。
进一步,我们可以通过在矩形内部添加其他几何图形来表示房间中的家具和装饰物。
通过这个案例,学生可以学习到几何模型在建筑设计中的应用,培养他们的空间想象力和创造力。
案例三:地理测量中的几何模型地理测量中也广泛应用了几何模型。
以测量一块土地面积为例,我们可以通过将土地划分为多个几何图形,然后计算每个几何图形的面积,最后将它们相加得到整个土地的面积。
通过这个案例,学生可以学习到几何模型在地理测量中的应用,培养他们的测量和计算能力。
案例四:物体运动的分析物体运动的分析也经常使用几何模型。
以一个自由落体物体的运动为例,我们可以通过绘制一个高度-时间图来表示物体的运动轨迹。
通过计算物体在不同时间点的高度,我们可以得到一个几何图形,进一步分析物体的运动规律。
通过这个案例,学生可以学习到几何模型在物理运动中的应用,培养他们的观察和分析能力。
通过以上几个案例的分析,我们可以看到初中数学几何模型的应用具有广泛的领域。
中考数学几何模型专题专题十—经典模型
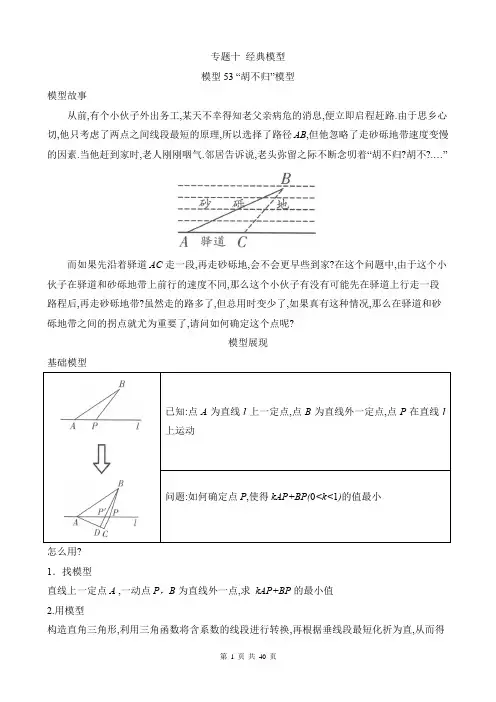
专题十经典模型模型53 “胡不归”模型模型故事从前,有个小伙子外出务工,某天不幸得知老父亲病危的消息,便立即启程赶路.由于思乡心切,他只考虑了两点之间线段最短的原理,所以选择了路径AB,但他忽略了走砂砾地带速度变慢的因素.当他赶到家时,老人刚刚咽气.邻居告诉说,老头弥留之际不断念叨着“胡不归?胡不?.…”而如果先沿着驿道AC走一段,再走砂砾地,会不会更早些到家?在这个问题中,由于这个小伙子在驿道和砂砾地带上前行的速度不同,那么这个小伙子有没有可能先在驿道上行走一段路程后,再走砂砾地带?虽然走的路多了,但总用时变少了,如果真有这种情况,那么在驿道和砂砾地带之间的拐点就尤为重要了,请问如何确定这个点呢?模型展现基础模型怎么用?1.找模型直线上一定点A ,一动点P,B为直线外一点,求kAP+BP的最小值2.用模型构造直角三角形,利用三角函数将含系数的线段进行转换,再根据垂线段最短化折为直,从而得到线段和最小值,最后运用锐角三角函数求解即可 模型分析如图,求这类带有系数的折线最值问题,通常我们都是将折线转化成为线段,再利用两点之间线段最短或垂线段最短求解,该模型就是利用了垂线段最短的性质,具体解题步骤如下: 一找:找带有系数k 的线段kAP ;二构:在点B 异侧,构造以线段AP 为斜边的直角三角形; ①以定点A 为顶点作①CAP ,使得sin ①P AC =h ; ①过动点P 作垂线构造Rt ①P AC ; 三转化:化折为直,将kAP 转化为PC ;四求解:使得hAP +BP =PC +BP ,利用“垂线段最短”转化为求BD 的长度.拓展延伸熟记特殊角的锐角三角函数值,kAP +BP 中系数k 发生变化时,所构造的直角三角形也会发生变化,同学们需要牢记特殊角度的正弦值:01sin 30 =2,0sin 60,0sin 45 =2,03sin 375,04sin 53 5例1如图, 在①ABC 中,AC =6,①A =30°,点D 是AB 边上一动点,(点拨:两定点A 、C ,动点D ,含特殊角30°)则12AD CD 的最小值为_________(点拨:线段数量关系的最小值,考虑“胡不归”)考什么?直角三角形的性质,30°,60°角的锐角三角函数值,垂线段最短.思路点拨哪条线段带有系数,就以它为斜边构造直角三角形,使得其中一锐角的正弦值恰好与系数相等.例2如图, 在平行四边形ABCD中,①DAB=45°,(点拨:特殊角)AB=6,BC=2,P为CD边上的一动点,则22PB PD(点拨:线段数量关系出现,且0<k<1,模型出现)的最小值为_____________考什么?平行四边形的性质,直角三角形的性质,45°角的锐角三角函数值,垂线段最短。
初二上数学几何模型及典型例题

数学几何作为初中数学的重要组成部分,不仅是学习数学的基础,更是培养学生逻辑思维和空间想象能力的重要途径。
在初二数学教学中,数学几何模型及典型例题的学习尤为重要,既能帮助学生更好地理解数学知识,又能提高学生解决实际问题的能力。
本文将围绕初二上数学几何模型及典型例题展开讨论,帮助学生更好地掌握相关知识。
一、数学几何模型的基本概念数学几何模型是指利用几何图形或几何形式来描述和解决数学问题的一种方法。
在初二数学几何模型学习中,主要包括以下几个方面的内容:1. 几何图形的性质:对于常见的几何图形,如三角形、四边形、圆等,需要了解它们的基本性质,如内角和为多少度,各边之间的关系等。
2. 几何变换:包括平移、旋转、翻折等几何变换,这些变换不仅能帮助学生理解几何图形的性质,还能培养学生的空间想象能力。
3. 几何三视图:通过俯视图、前视图和侧视图等三个视图的表示,能够更直观地描述立体图形的形状和结构。
4. 几何模型的应用:将数学几何模型应用到实际问题中,如建筑、工程、地图等领域,能够培养学生的实际应用能力。
二、数学几何典型例题解析除了理论知识的学习外,初二数学几何模型及典型例题的学习也非常重要。
下面我们分别对几种典型的数学几何例题进行解析,帮助学生更好地掌握解题方法和技巧。
1. 三角形的面积计算例题:已知三角形的底边长为5cm,高为8cm,求其面积。
解析:根据三角形的面积公式 S=1/2*底边*高,代入已知数值进行计算,可得三角形的面积为20平方厘米。
2. 圆的周长和面积计算例题:已知圆的半径为3cm,求其周长和面积。
解析:圆的周长计算公式为C=2*π*r,圆的面积计算公式为S=π*r^2。
代入已知半径进行计算,可得圆的周长为6π厘米,面积为9π平方厘米。
3. 直角三角形的性质运用例题:已知直角三角形两直角边分别为3cm和4cm,求斜边长。
解析:根据勾股定理,直角三角形斜边长为 a^2+b^2 的平方根,即5cm。
完整版)初中数学几何模型大全+经典题型(含答案)

完整版)初中数学几何模型大全+经典题型(含答案)通过将倍长中点相关线段进行旋转变换,可以构造出旋转全等模型。
这种模型的特点是,将相邻等线段所成角的一半旋转后拼接在一起,形成对称全等。
同时,也可以通过将两个等腰三角形或正多边形的夹角进行变化,来构造出模型变形。
如果遇到复杂图形找不到旋转全等,可以先找到两个正多边形或等腰三角形的公共极点,然后围绕公共极点找到两组相邻等线段,分组组成三角形证全等。
幂定理可以用等线段、等比值、等乘积进行代换,从而将两个数之间的比值转换成乘积。
在相似证明中,常用的辅助线是平行线,根据题目条件来确定比值并做出相应的平行线。
题目一:在半圆中,圆心为O,圆上有点C、E,CD垂直于AB,EF垂直于AB,EG垂直于CO。
证明CD等于GF。
题目二:在正方形ABCD内部,点P满足∠PAD=∠PDA=15度。
证明△PBC是正三角形。
题目三:在图中,ABCD、A1B1C1D1都是正方形,A2、B2、C2、D2分别是AA1、BB1、CC1、DD1的中点。
证明A2B2C2D2是正方形。
题目四:在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN于E、F。
证明∠DEN=∠F。
题目五:在△ABC中,H为垂心,O为外心,且OM垂直于BC于M。
1)证明AH等于2OM;2)如果∠BAC等于60度,证明AH等于AO。
1.设P为正三角形ABC内任意一点,连接PA,PB,PC,由三角形不等式可得PA+PB>AB。
PB+PC>BC。
PC+PA>CA。
将三式相加得到2PA+2PB+2PC>AB+BC+CA=3,即PA+PB+PC>3/2.又由于P到三角形三边的距离不超过1,所以PA+PB+PC<3,综上可得1.5≤PA+PB+PC<3,即所求不等式成立。
2.设P为正方形ABCD内任意一点,连接PA,PB,PC,PD。
由于正方形四边相等,所以PA+PC=2,PB+PD=2.又由于P到四边的距离不超过1,所以PA+PB+PC+PD<4.将前两式相加得到PA+PB+PC+PD=2(PA+PB)/2+2(PC+PD)/2≥2√(PA·PB)+2√(PC·P D)。
初中几何八大经典模型(一)

初中几何八大经典模型(一)几何对于中考数学来说非常重要,从某种意义上来说中考数学中几何部分做的怎么样直接决定了中考数学是否能够拿到高分,是否能够拉开差距!所以初中数学的江湖中一直流传着这么一句话:得数学者得天下,得几何者得数学!从分值来看,120分题目,几何每次考试都占50%左右,正可谓占着中考的半壁江山。
从得分率来看,填空和选择比较简单,属于送分题,难度不大。
大题难度很大,得分率很低,是孩子们中考拉开差距的关键所在。
中考数学要想取得高分,并且让数学成为自己的优势学科,必须克服几何难题!巧学数学在这里为大家总结了初中几何的八大几何模型,掌握了这些模型,应对考试中的难题将轻而易举。
也希望大家学习后,能够多加练习,掌握其中的奥妙,这对今后的学习大有益处!初中几何八大经典模型(一)旋转模型类型一旋转特殊角度1、旋60°,造等边例:已知:△ABC是正三角形,P是三角形内一点,PA=3,PB=4,PC=5.求:∠APB的度数.考点:[等边三角形的性质, 直角三角形的性质, 勾股定理的逆定理, 旋转的性质]分析:先把△ABP旋转60°得到△BCQ,连接PQ,根据旋转性质可知△BCQ≌△BAP,由于∠PBQ=60°,BP=BQ,易知△BPQ是等边三角形,从而有PQ=PB=4,而PC=5,CQ=3,根据勾股定理逆定理易证△PQC是直角三角形,即∠PQC=90°,进而可求∠APB.2、旋90°,造垂直例1、如图,P为正方形ABCD内一点,若PA=a,PB=2a,PC=3a(a>0)。
(1)求∠APB的度数;(2)求正方形ABCD的面积。
考点:[旋转的性质, 全等三角形的性质, 全等三角形的判定, 勾股定理, 正方形的性质]分析(1)已知PA=a,PB=2a,PC=3a,并不在同一个三角形中,因为AB=BC,可将△ABP 绕点B顺时针方向旋转90°得△CBQ,连接PQ,构成两个特殊三角形,可求∠APB的度数;(2)用(1)的结论,证明∠APQ=180°,得出△AQC是直角三角形,根据AQ,QC 的长及勾股定理求AC,从而可求正方形ABCD的面积.今天练习这两道经典题目,之后我会为大家接着发送其他类型的经典练习,欢迎大家评论和转发!!!。
(完整word版)初中数学经典几何模型.docx
...初中数学经典几何模型(模型即套路)...【应用上面模型解决如下问题】初中数学里的几何证明问题有一个顺口溜是什么呀?分享举报浏览507次4个回答热点话题付费时代,你会花钱买会员,还是等待75 秒广告?最佳答案youlan17122012-06-01人人都说几何难,难就难在辅助线。
辅助线,如何添?把握定理和概念。
还要刻苦加钻研,找出规律凭经验。
图中有角平分线,可向两边作垂线。
角平分线平行线,等腰三角形来添。
角平分线加垂线,三线合一试试看。
线段垂直平分线,常向两端把线连。
三角形中两中点,连接则成中位线。
三角形中有中线,延长中线等中线。
平行四边形出现,对称中心等分点。
梯形里面作高线,平移一腰试试看。
平行移动对角线,补成三角形常见。
证相似,比线段,添线平行成习惯。
等积式子比例换,寻找线段很关键。
直接证明有困难,等量代换少麻烦。
斜边上面作高线,比例中项一大片。
半径与弦长计算,弦心距来中间站。
圆上若有一切线,切点圆心半径连。
切线长度的计算,勾股定理最方便。
要想证明是切线,半径垂线仔细辨。
是直径,成半圆,想成直角径连弦。
弧有中点圆心连,垂径定理要记全。
圆周角边两条弦,直径和弦端点连。
弦切角边切线弦,同弧对角等找完。
如果遇到相交圆,不要忘作公共弦。
内外相切的两圆,经过切点公切线。
若是添上连心线,切点肯定在上面。
辅助线,是虚线,画图注意勿改变。
基本作图很关键,平时掌握要熟练。
解题还要多心眼,经常总结方法显。
切勿盲目乱添线,方法灵活应多变。
分析综合方法选,困难再多也会减。
虚心勤学加苦练,成绩上升成直线。
本回答由提问者推荐4评论分享举报收起wxn10445498832012-06-02展开全部人说几何很困难,难点就在辅助线。
辅助线,如何添?把握定理和概念。
还要刻苦加钻研,找出规律凭经验。
图中有角平分线,可向两边作垂线。
也可将图对折看,对称以后关系现。
角平分线平行线,等腰三角形来添。
角平分线加垂线,三线合一试试看。
初中数学几何经典模型—基本模型法
初中数学常见几何模型—基本模型法前言个人对数学基本模型法的定义是,从一些复杂的图形中,找出部分简单常见图形的过程,所以后面总结的模型,不一定是题目中完整的图,只是题中部分图形而已。
部分模型的一般情况,在这份讲义没有做练习的整理,另外还有最短路径模型、二倍角模型、补全法等部分模型没有整理,如果全部放在一起内容太多,另外因为部分模型应用较广,可能涉及到初二下和初三的内容,如果是在初二上期中复习用的话,请老师们自行筛选。
一、双垂直模型(角相等)如图:则有:∠ACD=∠B 则有:∠2=∠3练习1、如图所示,AB⊥BC,CD⊥BC,垂足分别为B、C,AB=BC,E为BC的中点,且AE⊥BD于F,若CD=4cm,则AB的长度为()练习2、已知:AB⊥BC于B,EF⊥AC于G, DF⊥BC于D,BC=DF,AC等于EF吗?,说明理由。
二、三垂直模型(弦图模型、一线三等角特殊情况)练习:1、在直线L上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1、3、3.5,正放置的四个正方形的面积依次是S1、S2、S3、S4,则S1+2S2+2S3+S4=()A.7.5 B.6.5 C.4.5 D.4 2.如图,△ABC是等腰直角三角形,DE过直角顶点A,∠D=∠E=90°,则下列结论正确的个数有()①CD=AE;②∠1=∠2;③∠3=∠4;④AD=BE.A.1个B.2个C.3个D.4个3.如图所示,AB⊥BC,CD⊥BC,垂足分别为B、C,AB=BC,E为BC的中点,且AE⊥BD于F,若CD=4cm,则AB的长度为()A.4cm B.8cm C.9cm D.10cm 4、如图①所示,在△ABC中,∠C=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于点M,BN⊥MN于点N.(1)求证:MN=AM+BN.(2)如图②.若过点C直线MN与线段AB相交,AM⊥MN于点M,BN⊥M N于N,(1)中的结论是否仍然成立?说明理由.图①图②5、如图,已知∠B=∠C=90°,M是BC的中点,DM平分∠ADC.(1)求证:AM平分∠DAB(2)试说明线段DM与AM有怎样的位置关系?(3)线段CD、AB、AD间有怎样的关系?直接写出结果。
初中数学几何模型之相似三角形模型
数学模型-----相似三角形模型相似三角形是初中几何中的重要的内容,常常与其它知识点结合以综合题的形式呈现,其变化很多,是中考中的常考题型,如果我们注重解题方法或基本解题模型,相信再遇到相似三角形的问题就迎刃而解了.下面就介绍一下相似三角形模型. 一、模型类别二、相关结论的运用 (一)模型1:A 字型图1平行A 字型条件://DE BC ,图1结论:~ADE ABC ; 图2斜交A 字型条件:C AED ∠=∠,图2结论:~ADE ABC ;典例精讲:如图,在Rt ABC 中,90,4cm,3cm C AC BC ∠=︒==.动点,M N 从点C 同时出发,均以每秒1cm 的速度分别沿CA CB 、向终点,A B 移动,同时动点P 从点B 出发,以每秒2cm 的速度沿BA 向终点A 移动,连接,PM PN ,设移动时间为t (单位:秒,025t <<.).(1)当t 为何值时,以,,A P M 为顶点的三角形与ABC 相似?(2)是否存在某一时刻t ,使四边形APNC 的面积S 有最小值?若存在,求S 的最小值;若不存在,请说明理由. 【思路点拨】根据勾股定理求得5cm AB =.(1)根据模型1:平行A 字型的结论得出APM ABC ∽,和模型1:斜交A 字型模型的结论得出AMP ABC ∽两种情况讨论:利用相似三角形的对应边成比例来求t 的值. (2)过点P 作PH BC ⊥于点H ,构造平行线//PH AC ,根据模型1:平行A 字型的结论得出PBH ABC ∽,从而求得以t 表示的PH 的值;然后根据“ABCBPHSSS=-”列出S 与t 的关系式24321(0 2.5)525S t t ⎛⎫=-+<< ⎪⎝⎭,则由二次函数最值的求法即可得到S的最小值. 【详解】解:∵如图,在Rt ABC 中,90,4cm,3cm C AC BC ∠=︒==.∴根据勾股定理,得5cm AB ==.(1)以,,A P M 为顶点的三角形与ABC 相似,分两种情况: ①当APM ABC ∽时,AM AP AC AB =,即45245t t--=,解得0t =(不合题意,舍去).②当AMP ABC ∽时,AP AM AC AB =,即52445t t --=,解得32t =;综上所述,当32t =时,以A P M 、、为顶点三角形与ABC 相似.(2)存在某一时刻t ,使四边形APNC 的面积S 有最小值.理由如下: 假设存在某一时刻t ,使四边形APNC 的面积S 有最小值. 如图,过点P 作PH BC ⊥于点H .则//PH AC , ∴PBH ABC ∽∴PH BPAC BA =, 即245PH t=. ∴85tPH =. ∴ABC BPN S S S =-△△()118343225t t =⨯⨯-⨯-⋅ ()24321=0 2.5525t t ⎛⎫-+<< ⎪⎝⎭. ∵405>, ∴S 有最小值. 当32t =时,215S =最小值.答:当32t =时,四边形A P NC 的面积S 有最小值,其最小值是215. 【解题技法】作平行线构造A 字型相似,是解题中常用的一种作辅助线的方法实战演练:1. 如图,AD经过ABC的重心,点E是AC的中点,过点E作//EG BC交AD 于点G,若12BC=,则线段GE的长为()A. 6B. 4C. 5D. 3【答案】D【解析】【分析】根据重心的概念得到点D为BC中点,即CD的长,再根据平行证明△AGE∽△ADC,结合点E是AC中点,得到12AE GEAC CD==,从而求出GE.【详解】解:∵AD经过ABC的重心,∴点D是BC中点,∵BC=12,∴CD=BD=6,∵GE∥BC,∴△AGE∽△ADC,∵点E是AC中点,∴12AE GEAC CD==,即162GE=,解得:GE=3,故选D.【点睛】本题考查的是重心的概念和性质、相似三角形的判定和性质,掌握三角形的重心是三角形三条中线的交点是解题的关键.2. 如图,在ABC 中,//DE BC ,//EF AB ,则下列结论正确的是( )A.AD DEDB BC= B.BF EFBC AD= C.EF BFAB BC= D.AE DEEC FC= 【答案】D 【解析】【分析】由两直线平行,得到两对同位角相等,证明△ADE ∽△ABC ,△CEF ∽△CAB ;由等代换可证明△ADE ~△EFC ,最后由相似三角形的性质判断四个答案的正误. 【详解】解:∵DE ∥BC , ∴∠ADE=∠B ,∠AED=∠C , ∴△ADE ∽△ABC ,DE AD ADBC AB DB∴=≠ ∴答案A 错舍去; 又∵EF ∥AB ,∴∠CEF=∠A ,∠CFE=∠B , ∴△CEF ∽△CAB ,EF CE FC BFAB AC BC BC∴==≠ ∴答案C 错舍去; ∵//DE BC ,//EF AB , ∴四边形BDEF 是平行四边形,∴DE=BF∵∠ADE=∠B ,∠CFE=∠B , ∴∠ADE=∠CFE , 又∵∠AED=∠C , ∴△ADE ~△EFC ,EF BF BFAD FC D B E FC C∴==≠ ∴答案B 舍去 ∵△ADE ~△EFC ,AE DEEC FC∴= ∴答案D 正确; 故选:D .【点睛】本题考查了平行线的性质,相似三角形的判定与性质,平行四边形的判定与性质等知识点,重点掌握三角形相似的判定与性质,易错点学生不会找两个相似三角形对应边的比相等.3. 如图,在ABC 中,D 、E 分别在AB 边和AC 边上,//DE BC ,M 为BC 边上一点(不与B 、C 重合),连结AM 交DE 于点N ,则( )A.ADANAN AEB.BD MNMN CEC.DN NEBM MCD.DN NEMC BM【答案】C 【解析】【分析】根据平行线的性质和相似三角形的判定可得△ADN ∽△ABM ,△ANE ∽△AMC ,再根据相似三角形的性质即可得到答案.【详解】∵//DE BC ,∴△ADN ∽△ABM ,△ANE ∽△AMC ,∴,DN AN ANNE DN NEBMAM AM MC BM MC,故选C.【点睛】本题考查平行线的性质、相似三角形的判定和性质,解题的关键是熟练掌握平行线的性质、相似三角形的判定和性质.(二)模型2:8字型图1平行8字型条件://AB CD , 图1结论:AOB DOC ∽△△; 图2斜交8字型条件:A D ∠=∠,,图2结论:AOB DOC ∽△△;典例精讲:如图1,在矩形ABCO 中,8,6,,OA OC D E ==分别是,AB BC 上一点,2,3,AD CE OE ==与CD 相交于点F .(1)求证:OE CD ⊥;(2)如图2,点G 是CD 的中点,延长OG 交BC 于H ,求CH 的长. 【思路点拨】(1)根据四边形ABCO 是矩形,可得8,6OA BC OC AB ====,根据模型1中的图1结论得出ADP OCP ∽,从而求出PA 和PO ,再根据模型2中的图1结论得出OPF ECF ∽,求出EF 和CF 的长,再根据勾股定理的逆定理即可得OE CD ⊥;(2)在Rt CBD △中,8,624CB BD AB AD ==-=-=,根据勾股定理可得CD =G 是CD 的中点,可得CG DG ==G 是CP 的三等分点,根据模型2中的图1结论得出OPG HCG ∽即可求出CH 的长. 【详解】(1)∵四边形ABCO 是矩形, ∴8,6OA BC OC AB ====, 在Rt OCE 中,3CE =,∴OE ===∵//AB OC ,即//AD OC ,且2AD =, ∴ADP OCP ∽ ∴AD PAOC PO =, ∴268PA PA =+, ∴4PA =,∴12PO PA OA =+=, ∴在Rt OPC △中,6OC =,∴CP ===,∵//OA BC ,即//OP CE , ∴OPF ECF ∽ ∴CE EF CFOP OF PF ==, ∴31124EF CF OF PF ===,∴15EF OE ==155CF CP ==∵22936955+=+=⎝⎭⎝⎭, ∴222EF CF CE +=, ∴CEF △是直角三角形, ∴90CFE ∠=︒, ∴OE CD ⊥;(2)在Rt CBD △中,8,624CB BD AB AD ==-=-=,根据勾股定理,得CD ===,∵点G 是CD 的中点,∴CGDG ==由(1)知:CP =,∴DP CP CD =-=∴点G 是CP 的三等分点, ∵//OA BC ,即//OP CH , ∴APG HCG ∽ ∴CH CGOP GP=, ∴1122CH =, ∴6CH =. 答:CH 的长为6.【解题技法】利用A 字型和8字型混合模型得出三角形相似,再利用相似三角形的对应边成比例得出线段的长或比值,解决本题的关键实战演练:4. 已知,如图,在平行四边形ABCD 中,M 是BC 边的中点,E 是边BA 延长线上的一点,连接EM ,分别交线段AD 于点F 、AC 于点G .(1)证明:AFG ∆∽CMG ∆ (2)求证:GF EFGM EM=; 【答案】(1)详见解析;(2)详见解析. 【解析】【分析】(1)利用平行线的性质及对顶角相等即可证明AFG ∆∽CMG ∆;(2)由相似三角形的性质可知GF AF GM CM=,由AD∽BC 可知AF EFBM EM =,通过等量代换即可证明结论. 【详解】(1)证明:AD ∥BCFAG MCG ∴∠=∠ AGF CGM ∠=∠ AFG ∴∆∽CMG ∆(2)证明:∵AFG ∆∽CMG ∆GF AFGM CM∴= ∽AD∽BC , ∽AF EFBM EM= 又∵CM =BM ,AF EFCM EM∴=GF EFGM EM∴=【点睛】本题主要考查相似三角形的判定及性质,掌握相似三角形的判定方法及性质是解题的关键.5. 如图,在平行四边形ABCD中,点E在边BC上,连结AE并延长,交对角线BD于点F、DC的延长线于点G.如果23CEBE=,求FEEG的值.【答案】916 FEEG=【解析】【分析】由四边形ABCD是平行四边形,可得AD=BC,AD∥BC,即可证得△ADF∽△EBF,△GEC∽△GAD,然后由相似三角形的对应边成比例,求得答案.【详解】∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,∴△ADF∽△EBF,△GEC∽△GAD,∴EF BE EG ECAF AD AG AD=,=,∵23 CEBE=,∴3255 BE CEAD AD=,=,∴3255FE EGAF AG==,,∴3283FE EGAE AE==,,∴916FEEG=.【点睛】此题考查相似三角形的判定与性质以及平行四边形的性质.解题关键在于注意掌握数形结合思想的应用.6. 如图, ,BD AC 相交于点P ,连结,,,,AB BC CD DA DAP CBP ∠=∠. (1)求证: ADP BCP ∽;(2)直接回答ADP △与BCP 是不是位似图形? (3)若8,4,3AB CD DP ===,求AP 的长.【答案】(1)详见解析;(2)不是;(3)6AP = 【解析】【分析】(1)根据已知条件可知DAP CBP ∠=∠,根据对顶角相等可知DPA CPB ∠=∠,由此可证明ADP BCP ∽;(2)根据位似图形的定义(如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心.)(3)由△ADP ∽△BCP ,可得AP BPDP CP=,而∠APB 与∠DPC 为对顶角,则可证△APB ∽△DPC ,从而得AP ABDP DC=,再根据8,4,3AB CD DP ===即可求得AP 的长.【详解】(1)证明:∵,DAP CBP DPA CPB ∠=∠∠=∠, ∴ADP BCP ∽;(2)点A 、D 、P 的对应点依次为点B 、C 、P ,对应点的连线不相交于一点,故ADP △与BCP 不是位似图形;(3)解:∵ADP BCP ∽ ∴=AP BP DP CP∵APB DPC ∠=∠,∴APB DPC ∽,AP ABDP DC∴= ∴8=43AP ∴6AP =.【点睛】本题考查相似三角形的性质和判定,位似图形的定义.熟练掌握相似三角形的判定定理是解决此题的关键.7. 在△ABC 中,90ACB ∠=,BE 是AC 边上的中线,点D 在射线BC 上.(1)如图1,点D 在BC 边上,:1:2CD BD =,AD 与BE 相交于点P ,过点A 作AFBC ,交BE 的延长线于点F ,易得APPD的值为 ; (2)如图2,在△ABC 中,90ACB ∠=,点D 在BC 的延长线上,AD 与AC 边上的中线BE 的延长线交于点P ,:1:2DC BC =,求APPD的值; (3)在(2)的条件下,若CD=2,AC=6,则BP= . 【答案】(1)32;(2)23;(3)6【解析】【分析】(1)易证△AEF ≌△CEB ,则有AF=BC .设CD=k ,则DB=2k ,AF=BC=3k ,由AF ∥BC 可得△APF ∽△DPB ,然后根据相似三角形的性质就可求出APPD的值;(2)过点A 作AF ∥DB ,交BE 的延长线于点F ,设DC=k ,由DC :BC=1:2得BC=2k,DB=DC+BC=3k.易证△AEF≌△CEB,则有EF=BE,AF=BC=2k.易证△AFP∽△DBP,然后根据相似三角形的性质就可求出APPD的值;(3)当CD=2时,可依次求出BC、AC、EC、EB、EF、BF的值,然后根据FP BP的值求出BFBP的值,就可求出BP的值.【详解】解:(1)如图1中,∵AF∥BC,∴∠F=∠EBC,∵∠AEF=∠BEC,AE=EC,∴△AEF≌△CEB(AAS),∴AF=BC.设CD=k,则DB=2k,AF=BC=3k,∵AF∥BC,∴△APF∽△DPB,∴32 PA AFPD BD==,故答案是:32;(2)如图2,过点A作AF∥DB,交BE的延长线于点F,设DC=k ,由DC :BC=1:2得BC=2k ,DB=DC+BC=3k . ∵E 是AC 中点, ∴AE=CE . ∵AF ∥DB , ∴∠F=∠1.在△AEF 和△CEB 中,123F AE CE ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△AEF ≌△CEB , ∴EF=BE ,AF=BC=2k . ∵AF ∥DB , ∴△AFP ∽△DBP , ∴2233PA FP AF k PD BP BD k ====; (3)当CD=2时,BC=4, ∵AC=6, ∴EC=AE=3, ∴EB=5=∴EF=BE=5,BF=10. ∵23FP BP =, 53BF BP ∴=, ∴BP=35BF=35×10=6.故答案为6.【点睛】本题主要考查了相似三角形的判定与性质、全等三角形的判定与性质、勾股定理等知识,结合中点,作平行线构造全等三角形是解决本题的关键.(三)模型3:k 字型图1一线三垂直条件:,,AB BD DE BD AC CE ⊥⊥⊥,图1结论:ABC CDE ∽△△; 图2一线三等角条件:B ACE D ∠=∠=∠,图2结论:ABC CDE ∽△△;典例精讲:如图,点P 是线段BD 上一个动点,90,6,4,B D AB CD BD a ∠=∠=︒===. (1)当90,14APC a ∠=︒=时,求BP 的长度;(2)若90APC ∠=︒时,点P 有两个符合要求即12,P P ,且122PP =,求a 的值; (3)若120APC ∠=︒时,点P 有且只有一个点符合要求,求a 的值.【思路点拨】(1)根据模型3:k 字型一线三垂直,证得ABP PDC △∽△,根据相似三角形的性质即可求得;(2)设BP x =,则PD a x =-,根据模型3:k 字型的一线三垂直证得ABP PDC △∽△,由相似三角形的性质得到2240x ax -+=,设方程的两个根为12,x x ,根据根与系数的关系可知1212,24x x a x x +=⋅=,根据题意即可得到()2121244x x x x =+-=,即可得到24244a -⨯=,解得即可;(3)作120AEP CFP ∠=∠=︒,解直角三角形求得33BE DF AE CF ====,根据模型3:k 字型的一线三等角证得EPA FCP ∽,由相似三角形的性质得到2320x a x ⎛--+= ⎝⎭,根据题意241320a ⎛∆=--⨯⨯= ⎝⎭,即可即可.【详解】解:(1)∵90,90B D APC ∠=∠=︒∠=︒, ∴90A APB CPD APB ∠+∠=∠+∠=︒, ∴A CPD ∠=∠, ∴ABP PDC △∽△, ∴BP AB CD PD =,即6414BP BP=-, 解得2BP =或12;(2)设BP x =,则PD a x =-, 由(1)可知ABP PDC △∽△, ∴AB BP PD DC=,即64xa x =-, ∴2240x ax -+=,设方程的两个根为12,x x ,根据根与系数的关系可知1212,24x x a x x +=⋅=,∵122PP =, ∴122x x -=,∴()()2212121244x x x x x x -=+-=,∴24244a -⨯=, 解得10a =±(负数舍去), ∴10a =;(3)作120AEP CFP ∠=∠=︒, ∴60AEB CFD ∠=∠=︒, ∵6,4AB CD ==,∴BE AB DF ====∴223AE BE CF DF ====∵120AEP CFP APC ∠=∠=∠=︒, ∴EAP CPF ∠=∠, ∴EPA FCP ∽, ∴AE EPPF FC=, 设EP x =,则3PF a x =--,=,∴2320x a x ⎛--+= ⎝⎭,∵0=,∴2413203a ⎛--⨯⨯= ⎝⎭, ∵0a >,∴3a =+【解题技法】通过运用模型3:k 字型中从特殊到一般的方法,证明出两组对应角相等,从而得出相似三角形,利用对应边成比例是解题的关键.实战演练:8. 如图1和图2,在ABC ∆中,AB AC =,8BC =,3tan 4C =.点K 在AC 边上,点M ,N 分别在AB ,BC 上,且2AM CN ==.点P 从点M 出发沿折线MB BN -匀速移动,到达点N 时停止;而点Q 在AC 边上随P 移动,且始终保持APQ B ∠=∠.(1)当点P 在BC 上时,求点P 与点A 的最短距离;(2)若点P 在MB 上,且PQ 将ABC ∆的面积分成上下4:5两部分时,求MP 的长;(3)设点P 移动的路程为x ,当03x ≤≤及39x ≤≤时,分别求点P 到直线AC 的距离(用含x 的式子表示);(4)在点P 处设计并安装一扫描器,按定角APQ ∠扫描APQ ∆区域(含边界),扫描器随点P 从M 到B 再到N 共用时36秒.若94AK =,请直接..写出点K 被扫描到的总时长.【答案】(1)3;(2)43MP =;(3)当03x ≤≤时,24482525d x =+;当39x ≤≤时,33355d x =-+;(4)23t s =【解析】【分析】(1)根据当点P 在BC 上时,PA ⊥BC 时PA 最小,即可求出答案; (2)过A 点向BC 边作垂线,交BC 于点E ,证明△APQ ∽△ABC ,可得2APQ ABCS AP S AB ∆∆⎛⎫= ⎪⎝⎭,根据S S 上下=45可得 24=9APQ ABC S AP S AB ∆∆⎛⎫= ⎪⎝⎭,可得23AP AB =,求出AB=5,即可解出MP ;(3)先讨论当0≤x≤3时,P 在BM 上运动,P 到AC 的距离:d=PQ ·sinC ,求解即可,再讨论当3≤x≤9时,P 在BN 上运动,BP=x-3,CP=8-(x-3)=11-x ,根据d=CP·sinC 即可得出答案; (4)先求出移动的速度=936=14,然后先求出从Q 平移到K 耗时,再求出不能被扫描的时间段即可求出时间.【详解】(1)当点P 在BC 上时,PA ⊥BC 时PA 最小, ∵AB=AC ,△ABC 为等腰三角形, ∴PA min =tanC·2BC =34×4=3; (2)过A 点向BC 边作垂线,交BC 于点E ,S 上=S △APQ , S 下=S 四边形BPQC , ∵APQ B ∠=∠, ∴PQ ∥BC , ∴△APQ ∽△ABC ,∴APAQPQAB AC BC ==, ∴2APQ ABCS AP S AB ∆∆⎛⎫= ⎪⎝⎭, 当S S 上下=45时,24=9APQ ABC S AP S AB ∆∆⎛⎫= ⎪⎝⎭, ∴23APAB =, AE=2BC·tan 3C =,根据勾股定理可得AB=5, ∴2253APMP AB +==,解得MP=43;(3)当0≤x≤3时,P 在BM 上运动,P 到AC 的距离:d=PQ·sinC ,由(2)可知sinC=35,∴d=35PQ ,∵AP=x+2, ∴25APx PQAB BC +==,∴PQ=285x +⨯,∴d=23855x +⨯⨯=24482525x +,当3≤x≤9时,P 在BN 上运动,BP=x-3,CP=8-(x-3)=11-x , d=CP·sinC=35(11-x )=-35x+335,综上()()24480325253333955x x d x x ⎧+≤≤⎪⎪=⎨⎪-+≤≤⎪⎩; (4)AM=2<AQ=94, 移动的速度=936=14, ①从Q 平移到K ,耗时:92414-=1秒, ②P 在BC 上时,K 与Q 重合时 CQ=CK=5-94=114, ∵∠APQ+∠QPC=∠B+∠BAP ,APQ B ∠=∠∴∠QPC=∠BAP ,又∵∠B=∠C ,∴△ABP ∽△PCQ ,设BP=y ,CP=8-y ,AB BP PC CQ =,即51184y y =-, 整理得y 2-8y=554-, (y-4)2=94, 解得y 1=52,y 2=112, 52÷14=10秒, 112÷14=22秒, ∴点K 被扫描到的总时长36-(22-10)-1=23秒.【点睛】本题考查了相似三角形的判定和性质,锐角三角函数,一次函数的应用,结合知识点灵活运用是解题关键.9. 如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y=1 x 的图象上.若点B在反比例函数y=kx的图象上,则k的值为_____.【答案】-4【解析】【分析】要求函数的解析式只要求出B点的坐标就可以,过点A,B作AC⊥x轴,BD⊥x轴,分别于C,D.根据条件得到△ACO∽△ODB,得到:BD OD OB OC AC OA===2,然后用待定系数法求解即可.【详解】过点A,B作AC⊥x轴,BD⊥x轴,分别于C,D,设点A的坐标是(m,n),则AC=n,OC=m.∵∠AOB=90°,∴∠AOC+∠BOD=90°,∵∠DBO+∠BOD=90°,∴∠DBO=∠AOC,∵∠BDO=∠ACO=90°,∴△BDO∽△OCA.∴BD OD OB OC AC OA==,∵OB =2OA ,∴BD =2m ,OD =2n ,因为点A 在反比例函数y =1x 的图象上, ∴mn =1,∵点B 在反比例函数y =k x的图象上, ∴B 点的坐标是(﹣2n ,2m),∴k =﹣2n •2m =﹣4mn =﹣4,故答案为﹣4.【点睛】本题考查了反比例函数图象上点的坐标特征,相似三角形的判定和性质,利用相似三角形的性质求得点B 的坐标(用含n 的式子表示)是解题的关键. 10. 如图,在ABC 中,点D E 、分别在边BC AC 、上,连接AD DE 、,且B ADE C ∠=∠=∠.(1)证明:BDA CED △∽△;(2)若45,2B BC ∠=︒=,当点D 在BC 上运动时(点D 不与B C 、重合),且ADE 是等腰三角形,求此时BD 的长.【答案】(1)理由见详解;(2)2BD =-1,理由见详解.【解析】【分析】∽1∽根据题目已知条件易得:180ADE ADB EDC ∠+∠+∠=︒,180B ADB DAB ∠+∠+∠=︒,所以得到DAB EDC ∠=∠,问题得证.∽2∽由题意易得ABC 是等腰直角三角形,所以90BAC ∠=︒,当ADE 是等腰三角形时,根据分类讨论有三种情况:①AD=AE ,②AD=DE ,③AE=DE ;因为点D 不与B C 、重合,所以第一种情况不符合,其他两种情况根据等腰三角形的性质“等边对等角”及45B ADE ∠=∠=︒,求出问题即可.【详解】(1)如图可知:180ADE ADB EDC ∠+∠+∠=︒在ABD △中,∴ 180B ADB DAB ∠+∠+∠=︒ 又B ADE C ∠=∠=∠∴EDC DAB ∠=∠∴BDA CED △∽△.(2)B ADE C ∠=∠=∠,45B ∠=︒∴ABC 是等腰直角三角形∴90BAC ∠=︒BC=2,∴AB=AC=2 ①当AD=AE 时,∴ADE AED ∠=∠45B ∠=︒,∴=45B ADE AED ∠=∠∠=︒∴90DAE ∠=︒∴90DAE BAC ∠=∠=︒点D 在BC 上运动时(点D 不与B C 、重合),点E 在AC 上∴此情况不符合题意.②当AD=DE 时,∴DAE DEA ∠=∠∴由(1)结论可知:BDA CED ≌∴∴2BD =③当AE=DE 时,45ADE DAE ∠=∠=︒∴AED 是等腰直角三角形45B ∠=︒,∴==45B C DAE ∠∠∠=︒∴90ADC ∠=︒,即AD BC ⊥ ∴1=12BD BC =.综上所诉:2BD =1.【点睛】本题主要考查相似三角形的判定及等腰三角形的存在性问题,关键是利用“K ”型相似模型及根据“等边对等角”、等腰直角三角形的性质得到线段的等量关系,进而求解问题.11. 感知:如图①,在四边形ABCD 中,AB ∥CD ,∠B =90°,点P 在BC 边上,当∠APD=90°时,可知△ABP∽△PCD.(不要求证明)探究:如图②,在四边形ABCD中,点P在BC边上,当∠B=∠C=∠APD时,求证:△ABP∽△PCD.拓展:如图③,在△ABC中,点P是边BC的中点,点D、E分别在边AB、AC上.若∠B=∠C=∠DPE=45°,BC=,BD=4,则DE的长为.【答案】探究:见解析;拓展:52.【解析】【分析】感知:先判断出∠BAP=∠DPC,进而得出结论;探究:根据两角相等,两三角形相似,进而得出结论;拓展:利用△BDP∽△CPE得出比例式求出CE,结合三角形内角和定理证得AC⊥AB且AC=AB;最后在直角△ADE中利用勾股定理来求DE的长度.【详解】解:感知:∵∠APD=90°,∴∠APB+∠DPC=90°,∵∠B=90°,∴∠APB+∠BAP=90°,∴∠BAP=∠DPC,∵AB∥CD,∠B=90°,∴∠C=∠B=90°,∴△ABP∽△PCD;探究:∵∠APC=∠BAP+∠B,∠APC=∠APD+∠CPD,∴∠BAP+∠B=∠APD+∠CPD.∵∠B=∠APD,∴∠BAP=∠CPD.∵∠B=∠C,∴△ABP∽△PCD;拓展:同探究的方法得出,△BDP ∽△CPE , ∴BD BP CP CE=, ∵点P 是边BC 的中点,∴BP =CP =,∵BD =4,CE=, ∴CE =92, ∵∠B =∠C =45°,∴∠A =180°﹣∠B ﹣∠C =90°,即AC ⊥AB 且AC =AB =6,∴AE =AC ﹣CE =6﹣92=32,AD =AB ﹣BD =6﹣4=2,在Rt △ADE 中,DE 52. 故答案是:52. 【点睛】此题是相似综合题.主要考查了相似三角形的判定与性质、勾股定理、三角形内角和定理以及三角形外角的性质.解本题的关键是判断出△ABP ∽△PCD .(四)模型4:母子型图1垂直母子型条件:,AC BC AB CD ⊥⊥,图1结论:ABC ACD CBD ∽∽; 图2斜交母子字型条件:C ABD ∠=∠,图2结论:ABC ABD ∽;典例精讲:1、在Rt ABC 中,90,ACB CD AB ∠=︒⊥,垂足为,8,2D AD DB ==,求CD 的长【思路点拨】根据垂直母子型模型4证得ADC CDB ∽△△,再根据对应边成比例,即可求出CD 的值.【详解】∵CD AB ⊥,∴90ADC CDB ∠=∠=︒,∴90ACD A ∠+∠=︒,∵90ACB ∠=︒,∴90ACD BCD ∠+∠=︒,∴A BCD ∠=∠,∴ADC CDB ∽△△, ∴CD AD BD CD=, ∴28216CD AD BD =⋅=⨯=,∴4CD =.2、如图,在ABC 中,AB AC =,点P 、D 分别是BC AC 、边上的点,且APD B ∠=∠.(1)求证:AC CD CP BP ⋅=⋅;(2)若10,12AB BC ==,当//PD AB 时,求BP 的长.【思路点拨】(1)根据已知得出APD B C ∠=∠=∠,再根据斜交母子型模型4得出ABP PCD ∽,根据相似三角形的性质得到AB CD CP BP ⋅=⋅,由AB AC =即可得到AC CD CP BP ⋅=⋅;(2)由//PD AB 根据斜交母子型模型4得出BAP BCA ∽,然后运用相似三角形的性质即可求出BP 的长.【详解】(1)∵AB AC =,∴B C ∠=∠.∵APD B ∠=∠,∴APD B C ∠=∠=∠.∵,APC BAP B APC APD DPC ∠=∠+∠∠=∠+∠,∴BAP DPC ∠=∠,∴ABP PCD ∽, ∴BP AB CD CP=, ∴AB CD CP BP ⋅=⋅.∵AB AC =,∴AC CD CP BP ⋅=⋅;(2)如图,∵//PD AB ,∴APD BAP ∠=∠.∵APD C ∠=∠,∴BAP C ∠=∠.∵B B ∠=∠,∴BAP BCA ∽, ∴BA BP BC BA=. ∵10,12AB BC ==, ∴101210BP =, ∴253BP =.【解题技法】利用母子型模型4中有一组隐含的等角,此时需要通过已知得出判定三角形相似的条件,把证明AC CD CP BP ⋅=⋅转化为证明AB CD CP BP ⋅=⋅是解题的关键. 实战演练:12. 如图,已知BC 是O 的直径,AC 切O 于点C ,AB 交O 于点D ,E 为AC 的中点,连接CD ,DE .(1)求证:DE 是O 的切线;(2)若4BD =,3CD =,求AC 的长.【答案】(1)见解析;(2)154=AC . 【解析】 【分析】(1)连接OD ,根据切线的性质和直角三角形斜边的中线以及等腰三角形的性质得出,EDC ECD ∠=∠,ODC OCD ∠=∠,然后利用等量代换即可得出DE OD ⊥,从而证明结论;(2)首先根据勾股定理求出BC 的长度,然后证明BCD BAC ∽△△,最后利用CD BD AC BC=求解即可. 【详解】(1)证明:连接OD ,如图,∵BC 是O 的直径,∴90BDC ∠=︒,∴90ADC ∠=︒,∵E 为AC 的中点, ∴12DE EC AC ==, ∴EDC ECD ∠=∠,∵OD OC = ,∴ODC OCD ∠=∠,∵AC 切O 于点C ,∴AC OC ⊥.∴90EDC ODC ECD OCD ∠+∠=∠+∠=︒,∴DE OD ⊥,∴DE 是O 的切线;(2)解:在Rt BCD 中,∵4BD =,3CD =,∴5BC ==∵90BDC BCA ∠=∠=︒,B B ∠=∠.∴BCD BAC ∽△△, ∴CD BD AC BC=, 即345AC =, ∴154=AC .【点睛】本题主要考查圆的综合问题,掌握切线的判定及性质,相似三角形的判定及性质是解题的关键.13. 如图,在ABC ∆中,2AC =,4BC =,D 为BC 边上的一点,且CAD B ∠=∠.若ADC ∆的面积为a ,则ABD ∆的面积为( )A. 2aB. 52aC. 3aD. 72a 【答案】C【解析】 【分析】根据相似三角形的判定定理得到ACDBCA ∆∆,再由相似三角形的性质得到答案.【详解】∵CAD B ∠=∠,ACD BCA ∠=∠,∴ACD BCA ∆∆, ∴2ACD BCA S AC S AB ∆∆⎛⎫= ⎪⎝⎭,即14BCAa S ∆=,解得,BCA ∆的面积为4a ,∴ABD ∆的面积为:43a a a -=,故选C .【点睛】本题考查相似三角形的判定定理和性质,解题的关键是熟练掌握相似三角形的判定定理和性质.14. 如图,点D 是△ABC 的边BC 的中点,且∠CAD =∠B ,若△ABC 的周长为10,则△ACD 的周长是( )A. 5 C. 52 D. 【答案】B【解析】 【分析】先根据已知证明△ACD ∽△BCA ,再根据相似三角形的性质得到AC 2=CD•CB ,设BD=CD=x ,得到x ,根据相似三角形的性质计算即可.【详解】解:∵∠CAD=∠B ,∠C=∠C ,∴△ACD ∽△BCA , ∴AC CD BC AC=,即AC 2=CD•CB , 设BD=CD=x ,∵点D 是△ABC 的边BC 的中点,∴BC=2x∴x ,∴=ABC 22ACD AC BC ==的周长的周长,即102ACD =的周长;∴△ACD 的周长故选B .【点睛】本题考查的是相似三角形的判定和性质,掌握相似三角形的周长比等于相似比是解题的关键.。
初中数学几何模型在实际问题中的应用
初中数学几何模型在实际问题中的应用数学是一门抽象而又实用的学科,而几何是数学中的一支重要分支。
几何模型是数学几何知识在实际问题中的具体应用,它在日常生活中扮演着重要的角色。
本文将探讨初中数学几何模型在实际问题中的应用,带领读者了解几何模型的实际意义。
首先,让我们来看一个简单的例子。
假设小明要修建一个花坛,他想要在花坛中央修建一个圆形的喷泉。
小明需要知道喷泉的直径,以便购买合适大小的喷泉装置。
这时,几何模型就派上了用场。
小明可以使用圆的几何模型来计算喷泉的直径。
他只需要测量花坛的直径,然后将其除以2,就可以得到喷泉的直径。
通过几何模型,小明能够轻松解决这个实际问题。
几何模型在建筑设计中也发挥着重要的作用。
假设有一座建筑物需要修建一个圆形的天窗,以增加自然光线的进入。
建筑师需要确定天窗的直径,以便购买适当大小的玻璃。
通过几何模型,建筑师可以计算出天窗的直径,并且可以根据需要调整天窗的大小。
几何模型不仅帮助建筑师设计出美观实用的建筑物,还能提高建筑物的能源利用效率。
除了在建筑设计中的应用,几何模型还在工程领域发挥着重要作用。
假设有一座桥需要修建,工程师需要确定桥梁的弧度,以便确保桥梁的稳定性和安全性。
通过几何模型,工程师可以计算出桥梁的弧度,并且可以根据需要调整桥梁的设计。
几何模型在工程领域的应用,不仅能够保证工程的质量和安全,还能够提高工程的效率和可持续性。
几何模型还可以应用于地理学中。
假设有一座城市需要修建一个园区,规划师需要确定园区的形状和面积,以便合理利用土地资源。
通过几何模型,规划师可以计算出园区的形状和面积,并且可以根据需要调整园区的规划。
几何模型在地理学中的应用,不仅能够促进城市的可持续发展,还能够提高城市的生活质量。
总结起来,初中数学几何模型在实际问题中的应用是多样且广泛的。
它们可以帮助我们解决日常生活中的实际问题,如花坛的修建、建筑物的设计、桥梁的建设和园区的规划。
几何模型不仅能够提高问题的解决效率,还能够提高解决方案的质量和可持续性。
完整版)初中数学经典几何模型
完整版)初中数学经典几何模型初中数学经典几何模型(模型即套路),是初中数学里的重要部分。
在解决几何证明问题时,我们可以运用这些模型,从而更加高效地解决问题。
人们常说几何很困难,其中一个难点就在于辅助线的运用。
为了更好地运用辅助线,我们需要把握定理和概念,并且刻苦加钻研,找出规律凭经验。
在绘制图形时,我们可以利用角平分线向两边作垂线,或者将图形对折来寻找对称关系。
利用角平分线的平行线,我们可以构造等腰三角形。
同时,我们也可以尝试将角平分线加上垂线,从而将三条线合为一条。
线段垂直平分线时,我们可以将线段向两端延长或缩短来验证线段的倍数与半数关系。
在三角形中,连接两中点可以构造出中位线,同时延长中线也可以等于中线。
对于平行四边形,我们可以找到对称中心等分点。
在梯形中,我们可以利用高线平移一腰来解决问题。
同时,平行移动对角线,补成三角形也是常见的方法。
当证明相似时,我们可以通过比线段,添加平行线来构造相似三角形。
在等积式子比例换时,寻找线段也是很关键的。
直接证明有困难时,我们可以通过等量代换来简化问题。
在计算圆的相关问题时,我们可以利用半径与弦长计算,或者利用勾股定理来计算切线长度。
同时,在判断是否为切线时,我们可以通过半径垂线来进行辨别。
在解决相交圆的问题时,我们需要注意作公共弦。
对于内外相切的两个圆,我们可以通过切点来构造公切线。
同时,我们也可以利用连心线来确定切点。
在绘制图形时,我们需要注意勿改变虚线的位置。
基本作图也是很关键的,我们需要熟练掌握。
在解题时,我们需要多动脑筋,经常总结方法。
同时,我们也需要注意方法的灵活性,不要盲目乱添线。
在选用分析综合方法时,我们需要根据具体情况进行选择。
最重要的是,我们需要虚心勤学,加以苦练,才能在数学上取得更好的成绩。
斜边上作高线,比例中项一大片。
--。
在斜边上作高线,可以得到比例中项一大片。
半径与弦长计算,弦心距来中间站。
--。
通过计算半径和弦长,可以得到弦心距。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中数学几何经典模型
范文
集团标准化工作小组 [Q8QX9QT-X8QQB8Q8-NQ8QJ8-M8QMN]
如图,正方形ABCD DE=2CE,过点C作CF 如图,ABC中,∠如图,在边长为6
,连接EG,
中,AB=AD,
H G
F C
B D A E H G F B C
A D E 点E 旋转,旋转过程中,线段DE 与线段A
B 相交于点P ,射线EF 与线段AB 相交于点G ,与射线CA 相交于点Q .若AQ =12,BP =3,则PG =.
【例12】如图,在菱形ABCD 中,AB =BD ,点E 、F 分别在AB 、AD 上,且AE =DF .连接
BF 与DE 交于点G ,连接CG 与BD 交于点H ,若CG =1,则BCDG S =四边形.
一线三等角模型【条件】EDF B C DE DF ∠=∠=∠=,且【结论】BDE CFD ≅ 【例13】如图,正方形ABCD 中,点E 、F 、G 分别为AB 、BC 、CD 边上的点,EB =3,GC =4,连接EF 、FG 、GE 恰好构成一个等边三角形,则正方形的边长为 . 最短路径模型【两点之间线段最短】
1、将军饮马
2、费马点【垂线段最短】
【两边之差小于第三边】
【例16】如图,矩形ABCD 是一个长为1000米,宽为600米的货场,A 、D 是入
口.现拟在货场内建一个收费站P ,在铁路线BC 段上建一个发货站台H ,设铺设公路l .求l 的最小值.
AP 、DP 以及PH 之长度和为【例17】如图,E 、F 是正方形ABCD 的边AD 上两个动点,满足AE =DF ,连接CF 交BD 于G ,连接
BE 交AG 于点H ,若正方形的边
长为2,则线段DH 长度的最小值是. 中,4,42AB AD ==,E 是线【例18】如图所示,在矩形ABCD
段AB 的中点,F 是线段BC 上的动点,BEF ∆沿直线EF 翻折到'B EF ∆,连接'DB ,'DB 最短为 .
《三垂直模型》
课后练习题
【练习1】
问题1:如图1,在等腰梯形ABCD 中,AD ∥BC ,AB =BC =CD ,点M ,N 分别在AD ,CD
上,∠MBN =12
∠ABC ,试探究线段MN ,AM ,CN 有怎样的数量关系请直接写出你的猜想;
问题2:如图2,在四边形ABCD 中,AB =BC ,∠ABC +∠ADC =180°,点M ,N 分别在
DA ,CD 的延长线上,若∠MBN =12
∠ABC 仍然成立,请你进一步探究线段MN ,AM ,CN 又有怎样的数量关系写出你的猜想,并给予证明.
【练习2】已知:如图1,正方形ABCD 中,E 为对角线BD 上一点,过E 点作EF ⊥BD 交BC 于F ,连接DF ,G 为DF 中点,连接EG ,CG .。
