长方体和正方体统一公式
长方体正方体所有公式

长方体正方体所有公式长方体和正方体是我们学习过的基本几何体形,它们在日常生活和各个领域都有着广泛的应用,如建筑、制造、工程等。
为了更好地理解和运用长方体和正方体,我们需要掌握它们的一些基本公式,本文将介绍长方体和正方体的基本公式和应用。
一、长方体公式长方体是由长方体的面围成的几何体形。
它有3个不同的面,每个面都是由2个长方形组成的。
长方体的6个面分别是底面、顶面、前面、后面、左面和右面。
下面是长方体的一些重要公式:1. 面积公式长方体的表面积等于2倍长与宽的和再加上2倍长与高的和再加上2倍高与宽的和。
根据这个公式,我们可以得到长方体的表面积公式:S = 2(LW + LH + WH)其中S为长方体的表面积,L为长方体的长度,W为宽度,H为高度。
2. 体积公式长方体的体积可以通过将长、宽和高相乘得出,即:V = LWH其中V为长方体的体积。
3. 对角线长公式长方体的对角线(斜面对角线)长可以使用勾股定理来计算。
假设对角线长为d,则:d² = L² + W² + H²二、正方体公式正方体是长方体的特殊情况,长、宽和高相等。
正方体是最简单的立方体,它有6个正方形面。
下面是正方体一些重要的公式:1. 面积公式正方体的表面积等于6倍其边长的平方。
因此,正方体的表面积公式为:S = 6a²其中S为正方体的表面积,a为其边长。
2. 体积公式正方体的体积等于其边长的立方。
因此,正方体的体积公式为:V = a³其中V为正方体的体积。
3. 对角线长公式正方体的对角线长同样可以使用勾股定理来计算。
对角线长为d,则:d² = 3a²正方体是一种广泛应用于各个领域的几何形体,学习其公式非常重要。
在计算正方体或长方体的体积或表面积时,我们需要牢记上述公式,以便更好地理解并在实际应用中运用。
另外,这些公式也为我们解决一些实际问题提供了有力的工具。
《长方体和正方体》_概念和公式归纳

《长方体和正方体》概念和公式归纳一、概念:1、长方体是由6个长方形(特殊情况有两个相对的面是正方形)围成的立体图形。
在一个长方体中,相对的面完全相同,相对的棱长度相等。
2、正方体是由6个完全相同的正方形围成的立体图形。
(正方体也叫立方体)。
正方体有12条棱,它们的长度都相等,所有的面都完全相同。
3、两个面相交的边叫做棱。
三条棱相交的点叫做顶点。
相交于一个顶点的三条棱的长度分别叫做长方体的长、宽、高。
4、长方体和正方体的面、棱和顶点的数目都一样,只是正方体的棱长都相等,正方体可以说是长、宽、高都相等的长方体,它是一种特殊的长方体。
5、长方体或正方体6个面和总面积叫做它的表面积。
6、物体所占空间的大小叫做物体的体积。
计量体积要用体积单位,常用的体积单位有立方厘米、立方分米、立方米。
规定:棱长是1cm的正方体,体积是1cm³. 棱长是1dm的正方体,体积是1dm³.棱长是1m的正方体,体积是1m³.7、容器所能容纳物体的体积通常叫做它们的容积。
8、3a读作“a的立方”表示3个a相乘,(即a·a ·a)9、至少用(8 )个小正方体能拼成一个大正方体。
10、箱子、油桶、仓库等所能容物体的体积,通常叫做它们的容积。
计量容积,一般就用体积单位。
11、计量液体的体积,如水、油等,常用容积单位升和毫升,也可以写成L和ml 。
12高。
13、计量不规则物体的体积可以用排水法。
(水面上升的那部分水的体积就是不规则物体的体积。
)二、公式:长方体公式:棱长和=(长+宽+高)×4底面积(占地面积、、上面积)=长×宽左面、右面=宽×高前(后)面积=长×高表面积=(长×宽+长×高+宽×高)×2没盖的表面积=长×宽+(长×高+宽×高)×2或=(长×宽+长×高+宽×高)×2-长×宽体积(容积)=长×宽×高长=体积÷宽÷高 宽=体积÷长÷高 高=体积÷长÷宽 体积(容积)=底面积×高 = 横截面积×长底面积=体积÷高 高=体积÷底面积 横截面积=体积÷长 长=体积÷横截面积正方体公式:棱长和=棱长×12 棱长=棱长和÷12 表面积=棱长×棱长×6 (任意一个面积×6) 没盖的表面积=棱长×棱长×5体积(容积)=棱长×棱长×棱长=底面积×棱长 三、体积单位换算:进率: 1L =1000ml 1L=1dm ³ 1ml=1 cm ³ 1立方米=1000立方分米=1000000立方厘米 1立方分米=1000立方厘米=1升=1000毫升1立方厘米=1毫升长度单位: 毫米厘米分米 米 千米 面积单位:平方毫米 平方厘米 平方分米 平方米 公顷 平方千米 体积单位: 立方厘米 立方分米 立方米 容积单位: (毫升) (升)10 10 100 100 100 10000 100 1000 1000 1000 10 1000。
体积公式长方体和正方体

体积公式长方体和正方体长方体和正方体是两种常见的几何体,在日常生活中经常可以见到它们的身影。
它们的体积可以通过相应的公式计算得出。
本文将分别介绍长方体和正方体的体积公式,以及它们的应用。
一、长方体的体积公式长方体是一种具有三个不同边长的立体,其形状类似于一个长方形的立体延伸而成。
长方体的体积可以通过以下公式计算得出:体积 = 长× 宽× 高其中,长、宽、高分别代表长方体的三个不同边长。
这个公式的推导可以通过将长方体切割成若干个立方体来理解。
每个立方体的体积都可以表示为边长的乘积,而长方体的体积就是这些立方体体积的总和。
长方体的体积公式的应用非常广泛。
例如,在建筑工程中,我们常常需要计算房间的体积,以确定需要购买的建筑材料的数量。
在货运业中,我们也需要计算货物的体积,以确定运输车辆的大小和数量。
通过应用长方体的体积公式,我们可以更加准确地进行计算和规划。
二、正方体的体积公式正方体是一种具有六个相等边长的立体,其形状类似于一个立方体。
正方体的体积可以通过以下公式计算得出:体积 = 边长× 边长× 边长其中,边长代表正方体的边长。
这个公式的推导也可以通过将正方体切割成若干个立方体来理解。
每个立方体的体积仍然可以表示为边长的乘积,而正方体的体积就是这些立方体体积的总和。
正方体的体积公式同样具有广泛的应用。
在几何学中,我们常常需要计算正方体的体积,以确定其容量或空间大小。
在三维建模和计算机图形学中,正方体也是常用的基本元素之一,通过计算正方体的体积,我们可以更好地进行模型设计和渲染。
三、长方体和正方体的比较长方体和正方体在形状和性质上有一些相似之处,但也存在一些明显的区别。
首先,长方体的三个边长可以不相等,而正方体的边长必须相等。
其次,长方体的面积可以不相等,而正方体的面积必定相等。
因此,长方体和正方体的体积计算公式也有所不同。
长方体和正方体在应用中也有一些区别。
由于正方体具有均匀的边长和面积,因此在一些几何学问题中更容易使用。
长方体和正方体的统一体积公式

2、一块木料,横截面的面积是24平方分米, 长4米,35根这样的木料一共是多少立方分米?
3、一个正方体的底面积是25平方厘米,高是5厘米。 它的体积是多少立方米?
盘活教材 有效教学
人教版五年级数学下册教材
说教材流程
数学教学的总体目标 本教材的教学内容
本册教学目标 本教材的编写特点
(1)看完这段叙述,你想到什么?
(2)这段文字中描述的长方体有什么特征? 底面积指的是哪一个面的面积?
2、认识底面
你们知道什么是底面吗?
棱
高
底面 长
底面
宽
棱长
长
棱长
结论:底面一般指长方体、正方体的下面
3、认识底面积
什么是底面积? 底面积:长方体和正方体底面的面积叫做它
们的底面积
1 长方体的底面积如何计算?
本册教材具有下面几特点:。
一、改进因数与倍数教学内容的编排,体现数学 教学改革的新理念,培养学生的数学素养
0.09平方米
V=Sh =0.09×3 =0.27(立方米)
小结:今天我们学到了什么?
课堂练习
1,课本45页第8题 2,一个棱长是200cm的正方体的底面 积是45.8平方米,它的体积是多少立方 米?
家庭作业
(一)完成练习册相应的内容 (二)作业本的作业: 1、一段方钢,长3米,它的横截面是边长为0.2米
8、认识复式折线统计图,能根据需要选择适当的统计图表示数据。 9、经历从实际生活中发现问题、提出问题、解决问题的过程,体会数学在
日常生活中的作用,初步形成综合运用数学知识解决问题的能力。 10、体会解决问题策略的多样性及运用优化的数学思想方法解决问题的有效
长方体正方体所有公式

1、长方体的棱长和=长×4+宽×4+高×42、长方体的棱长和=(长+宽+高)×43、长方体的长=棱长和÷4—宽—高4、长方体的宽=棱长和÷4—长—高5、长方体的高=棱长和÷4—长—宽6、长方体的表面积=长×宽×2+长×高×2+宽×高×27、长方体的表面积=(长×宽+长×高+宽×高)×28、长方体的体积=长×宽×高9、正方体的棱长和=棱长×1210、正方体的棱长=棱长和÷1211、正方体的表面积=棱长×棱长×612、正方体的体积=棱长×棱长×棱长13、长(正)方体的体积=底面积×高14、长(正)方体的体积=横截面面积×长1、长方体的棱长和=长×4+宽×4+高×42、长方体的棱长和=(长+宽+高)×43、长方体的长=棱长和÷4—宽—高4、长方体的宽=棱长和÷4—长—高5、长方体的高=棱长和÷4—长—宽6、长方体的表面积=长×宽×2+长×高×2+宽×高×27、长方体的表面积=(长×宽+长×高+宽×高)×28、长方体的体积=长×宽×高9、正方体的棱长和=棱长×1210、正方体的棱长=棱长和÷1211、正方体的表面积=棱长×棱长×612、正方体的体积=棱长×棱长×棱长13、长(正)方体的体积=底面积×高14、长(正)方体的体积=横截面面积×长。
数学人教版五年级下册长、正方体公式集合
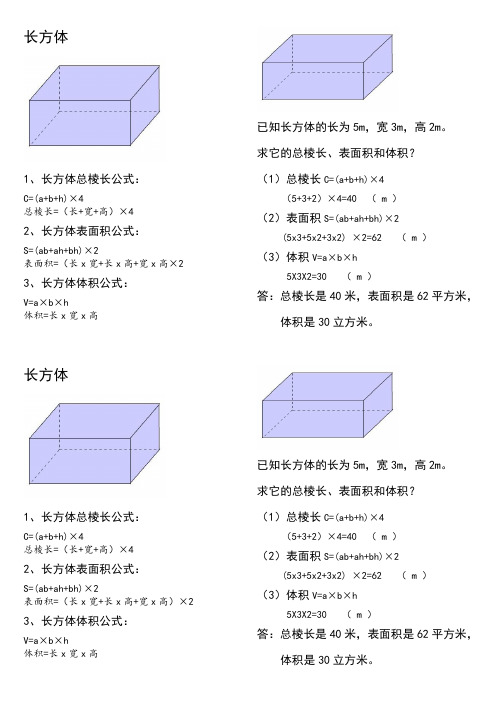
1、长方体总棱长公式:C=(a+b+h)×4总棱长=(长+宽+高)×42、长方体表面积公式:S=(ab+ah+bh)×2表面积=(长x宽+长x高+宽x高×2 3、长方体体积公式:V=a×b×h体积=长x宽x高长方体1、长方体总棱长公式:C=(a+b+h)×4总棱长=(长+宽+高)×42、长方体表面积公式:S=(ab+ah+bh)×2表面积=(长x宽+长x高+宽x高)×2 3、长方体体积公式:V=a×b×h体积=长x宽x高已知长方体的长为5m,宽3m,高2m。
求它的总棱长、表面积和体积?(1)总棱长C=(a+b+h)×4(5+3+2)×4=40 ( m )(2)表面积S=(ab+ah+bh)×2(5x3+5x2+3x2) ×2=62 ( m )(3)体积V=a×b×h5X3X2=30 ( m )答:总棱长是40米,表面积是62平方米,体积是30立方米。
已知长方体的长为5m,宽3m,高2m。
求它的总棱长、表面积和体积?(1)总棱长C=(a+b+h)×4(5+3+2)×4=40 ( m )(2)表面积S=(ab+ah+bh)×2(5x3+5x2+3x2) ×2=62 ( m )(3)体积V=a×b×h5X3X2=30 ( m )答:总棱长是40米,表面积是62平方米,体积是30立方米。
1、正方体总棱长公式:C=a×12总棱长=棱长×122、正方体表面积公式:S=a×a×6表面积=棱长×棱长×6 3、正方体体积公式:V=a×a×a体积=棱长x棱长x棱长正方体1、正方体总棱长公式:C=a×12总棱长=棱长×122、正方体表面积公式:S=a×a×6表面积=棱长×棱长×6 3、正方体体积公式:V=a×a×a体积=棱长x棱长x棱长已知正方体的棱长为5m。
长方体和正方体的周长面积和体积计算公式大全

长方体和正方体的周长面积和体积计算公式大全周长:长方形周长公式=(长+宽)X2正方形周长公式=边长X4直径=半径×2 半径=直径÷2圆的周长=×直径,或=圆周率×半径×2面积:长方形面积=长X宽正方形面积公式=边长X边长三角形的面积=底×高÷2面积=底×高的面积=(上底+下底)×高÷2圆的面积=圆周率×半径×半径容积:容器若能容纳的物体的体积:表面积:长方体或正方体六个面的总面积。
正方体的表面积:S=6a×a(棱长×棱长×6)正方体体积公式:V=a×a×a(棱长×棱长×棱长)长方体的表面积:S=2×(ab+bc+ac)((长×宽+长×高+宽×高)×2)长方体体积公式:长X宽X高长方体棱长总和公式:(长+宽+高)X4正方体体积:Va×b×c(长×宽×高)正方体棱长总:棱长X12体的侧面积=底面圆的周长×高圆柱体表面积=上下底面面积+侧面积,[或S=2π*r*r+2π*r*h(2×π×半径×半径+2×π×半径×高)]圆柱体的体积=底面积×高,[或V=π *r*r*h(π×半径×半径×高)]圆锥体积:V=S底×h÷3(底面积×高÷3)正方体体积公式:棱长X棱长X棱长通用体积公式:底面积X高截面积X长表面积的变化要会人折。
长方体或正方体被锯开后,一次会增加两个面;反之,两个相同,体或长方体拼在一起,一次会减少两个面。
长方体和正方体的特征,相同点和不同点要牢记。
名称符号周长C和面积S正方形 a—边长 C=4aS=a2长方形 a和b-边长 C=2(a+b) S=ab三角形 a,b,c-三边长h-a边上的高s-周长的一半A,B,C-内角其中s=(a+b+c)/2 S=ah/2=ab/2·sinC=[s(s-a)(s-b)(s-c)]1/2=a2sinBsinC/(2sinA)四边形 d,D-对角线长α-对角线夹角 S=dD/2·sinα平行四边形 a,b-边长h-a边的高α-两边夹角 S=ah=absinαa-边长α-夹角D-长对角线长d-短对角线长 S=Dd/2=a2sinα梯形 a和b-上、下底长h-高m-长 S=(a+b)h/2=mh圆 r-半径d-直径 C=πd=2πrS=πr2=πd2/4扇形 r—扇形半径a—度数C=2r+2πr×(a/360)S=πr2×(a/360)弓形 l-弧长b-弦长h-矢高r-半径α-圆心角的度数 S=r2/2·(πα/180-sinα) =r2arccos[(r-h)/r] - (r-h)(2rh-h2)1/2=παr2/360 - b/2·[r2-(b/2)2]1/2=r(l-b)/2 + bh/2≈2bh/3圆环 R-外圆半径r-内圆半径D-外圆直径d-内圆直径 S=π(R2-r2)=π(D2-d2)/4D-长轴d-短轴 S=πDd/4立方图形名称符号面积S和体积V正方体 a-边长 S=6a2V=a3长方体 a-长b-宽c-高 S=2(ab+ac+bc)V=abcS-底面积h-高 V=ShS-底面积h-高 V=Sh/3S1和S2-上、下底面积h-高 V=h[S1+S2+(S1S1)1/2]/3拟 S1-上底面积S2-下底面积S0-中截面积h-高 V=h(S1+S2+4S0)/6圆柱 r-底半径h-高C—底面周长S底—底面积S侧—侧面积S表—表面积 C=2πrS底=πr2S侧=ChS表=Ch+2S底V=S底h=πr2h空心圆柱 R-外圆半径r-内圆半径h-高 V=πh(R2-r2)直圆锥 r-底半径h-高 V=πr2h/3r-上底半径R-下底半径h-高 V=πh(R2+Rr+r2)/3球 r-半径d-直径 V=4/3πr3=πd2/6h-球缺高r-球半径a-球缺底半径 V=πh(3a2+h2)/6 =πh2(3r-h)/3a2=h(2r-h)球台 r1和r2-球台上、下底半径h-高 V=πh[3(r12+r22)+h2]/6 圆环体 R-环体半径D-环体直径r-环体截面半径d-环体截面直径 V=2π2Rr2=π2Dd2/4桶状体 D-桶腹直径d-桶底直径h-桶高 V=πh(2D2+d2)/12 (是圆弧形,圆心是桶的中心)V=πh(2D2+Dd+3d2/4)/15长方体和正方体的特征,相同点和不同点要牢记。
六年级长方体正方体(公式)整理

长方体正方体(公式)整理长方体正方体单位棱长求棱长总和长方体棱长总和=(长+宽+高)×4L长=4(a+b+h)正方体棱长总和=棱长×12L正=12a长度单位cm、dm、m 逆运用长+宽+高=长方体棱长总和÷4a+b+h=L长÷4棱长=正方体棱长总和÷12a=L正÷12表面积求表面积长方体的表面积=(长×高+宽×高+长×宽)×2S表=2(a h+b h+a b)长方体的表面积=2×长×高+2×宽×高+2×长×宽S表=2a h+2b h+2a b正方体的表面积=一个面的面积×6=棱长×棱长×6S表=62a面积单位cm2、dm2、m2体积(容积)求体积长方体的体积=长×宽×高V长=a b h正方体的体积=棱长×棱长×棱长V正=3a体积(容积)单位cm3、dm3、m3(L或mL)长方体正方体体积通用公式:V=S底h逆运用高=长方体的体积÷长÷宽h=V长÷a÷b长=长方体的体积÷宽÷高a=V长÷b÷h宽=长方体的体积÷长÷高b=V长÷a÷h长度单位cm、dm、m或面积单位cm2、dm2、m2底面积=体积÷高S底=V÷h高=体积÷底面积h=V÷S底。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
教学重难 长方体、正方体体积的统一计算公式及其拓展。 点
教学准备 长方体、正方体模型
课型
新授课
主备教师
冯卫星
教学过程
集体备课部分
自主备课部分
一、交流前置 1.口算汇报。 2.长方体、正方体的体积怎样求? 3.激趣:古代数学家求长方体体积的方法。 课件展示:西汉末年《九章算术》,有关体积
计算的问题。书中是这样叙述有两个面是正方形的 长方体体积的计算方法的:“方自乘,以高乘之即 积尺。” 教师持模型,让学生带上自己的模型解读本句话。 (先用边长乘边长得底面积,再乘高就得到长方体 的体积。) 二、探究新知
长方体体积”。 四、全课小结
这节课我们学习了什么知识,你受到了那些启 发? 五、作业
课堂作业:练习四第5、6、7、8题。
板书设计 教后反思
长方体、正方体统一公式
长方体体积=长×宽×高 ↓
=底面积×高 正方体体积=棱长×棱长×棱长
↓↓ = 底面积 × 高
V=Sh
1.长方体体积统一公式 (1)摸摸自己模型的底பைடு நூலகம்积,说说长方体、正方 体的底面积怎样求? (2)师:你觉得,长方体和正方体的体积公式还 可以怎样表示?
(3)达成共识,推出长方体体积的另一种计算方 法,追问道理。
长方体体积=底面积×高,为什么可以这样表 示?
交流中,得出古人和今人计算长方体体积的方 法是一致的,两个公式可以写成如下形式:
备课时间:2014年8月29日 时
单元章节 第一单元第八课
总备课第(8)课 课题名称 统一公式
教学目标
1.通过实物模型,掌握长方体和正方体的统一体积计 算公式,并能做进一步拓展发现其它计算方法。 2.会应用长方体、正方体体积的统一计算公式解决一 些简单的实际问题。 3.在解决问题的过程中,培养学生分析问题,解决问 题的能力。
独立完成,解答讲评。
4、 练习四第5、6、7、8题。 (1) 独立研究课本四题,只列式、不计算。 (2)组内交流,说清对题目的理解,和解答
思路。 (3)申报讲解,互动点评。 第五题:重点理解占地0.84平方米指什么? 第六题:理解要求问题“多少吨”,就得求什
么? 第七题:怎样利用公式列出方程。 第八题:理解题目情景中的含义。“求薄薄的
长方体体积=长×宽×高 ↓
=底面积×高 2.正方体公式统一。 师:这个公式对正方体适用吗?试着用自己的模型 交流说明。 正方体体积=棱长×棱长×棱长
↓↓ = 底面积 × 高 3.字母通一公式:如果用S表示底面积,上面的 公式可以写成:
V=Sh 4.拓展体积统一公式。 教师手持模型,抚摸底面积和高,提问:由统一公 式中的“底面积×高”你还能想到,体积公式的其 它表达吗? 同座讨论,集体交流,汇报梳理,如:侧面积× 长;前面积×宽。
三、巩固练习 1.做书上“练一练”第1、2题。 学生独立作业,提醒学生正确书写体积单
位“立方厘米”,申报板演,集体评讲。 2.练一练,第三题。 呈现题目,诵读题目,说说知道什么信息,谁
懂新名词:“横截面”?(利用模型) (用一个平行于底面的平面去截一个长方体,
所得的截面叫横截面,这个横截面的形状大小与底 面是相同的。)
