材料力学B试题7应力状态_强度理论.
材料力学考试题

2010—2011材料力学试题及答案A一、单选题(每小题2分,共10小题,20分)1、工程构件要正常安全的工作,必须满足一定的条件。
下列除()项,其他各项是必须满足的条件。
A、强度条件B、刚度条件C、稳定性条件D、硬度条件2、内力和应力的关系是()A、内力大于应力B、内力等于应力的代数和C、内力是矢量,应力是标量D、应力是分布内力的集度3、根据圆轴扭转时的平面假设,可以认为圆轴扭转时横截面()。
A、形状尺寸不变,直径线仍为直线。
B、形状尺寸改变,直径线仍为直线。
C、形状尺寸不变,直径线不保持直线。
D、形状尺寸改变,直径线不保持直线。
4、建立平面弯曲正应力公式zIMy=σ,需要考虑的关系有()。
A、平衡关系,物理关系,变形几何关系;B、变形几何关系,物理关系,静力关系;C、变形几何关系,平衡关系,静力关系;D、平衡关系, 物理关系,静力关系;5、利用积分法求梁的变形,不需要用到下面那类条件()来确定积分常数。
A、平衡条件。
B、边界条件。
C、连续性条件。
D、光滑性条件。
6、图示交变应力的循环特征r、平均应力mσ、应力幅度aσ分别为()。
A -10、20、10;B 30、10、20;C 31-、20、10;D 31-、10、20 。
7、一点的应力状态如下图所示,则其主应力1σ、2σ、3σ分别为()。
A 30MPa、100 MPa、50 MPa B 50 MPa、30MPa、-50MPa C 50 MPa、0、-50Mpa、 D -50 MPa、30MPa、50MPa8、对于突加载的情形,系统的动荷系数为()。
A、2B、3C、4D、59、压杆临界力的大小,()。
A与压杆所承受的轴向压力大小有关; B 与压杆的柔度大小有关; C 与压杆材料无关; D 与压杆的柔度大小无关。
10、利用图乘法计算弹性梁或者刚架的位移,要求结构满足三个条件。
以下那个条件不是必须的()A、EI为常量B、结构轴线必须为直线。
C、M图必须是直线。
材料力学第七章应力状态和强度理论

x y 2 a 0 2
x y x y 2
x y
2
) x
2
2
例题1: 已知:单元体各侧面应力 x=60MPa,
求: (1) = - 450斜截面上的应力,(2)主应力和主平面
dA
y
x y
2
sin 2 xy cos2
y
yx
应力圆
y
1 R 2
x
y
2
4 2 xy
x
yx xy x
y
R c
x y
2
2
x
xy
x´
dA
yx
y´
y
x y 1 2 2 2
40
x y
2 0.431MPa
sin( 80 ) xy cos(80 )
C
C
C
例题3:已知梁上的M、Q,试用单元体表示截面上1、2、
3、4点的应力状态。
1
2 0
2
1点 2点
1 2 0 3
3Q = 2A
M x Wz
2 xy
x y
2 20.6 0.69 60 0
17.2
x y
2 (
6.4MPa
2 34.4
max(min)
x
17.20
x y
2
) xy
2
2
x
66.4MPa
60 0 60 0 2 ( ) 20.6 2 2 2 66.4(6.4) MPa
材料力学B试题7应力状态_强度理论.docx

40 MPa.word 可编辑 .应力状态强度理论1. 图示单元体,试求60100 MPa(1)指定斜截面上的应力;(2)主应力大小及主平面位置,并将主平面标在单元体上。
解: (1)x y xy cos 2x sin 276.6 MPa22xy sin 2x cos232.7 MPa231 (2)max xy( x y) 2xy281.98MPa39.35min22121.98181.98MPa,2,3121.98MPa12xy12000arctan()arctan39.352x y24020060602. 某点应力状态如图示。
试求该点的主应力。
129.9129.9解:取合适坐标轴令x25 MPa,x由120xy sin 2xy cos20 得y2所以m axx y( xy ) 2xy 2m in 22129.9 MPa2525(MPa)125MPa50752( 129.9)250 150100 MPa2001 100MPa,20 ,3200MPa3. 一点处两个互成45 平面上的应力如图所示,其中未知,求该点主应力。
解:y150 MPa,x120 MPa.word 可编辑 .由得45xy sin 2xy cos 2x 15080 22x10MPa所以max xy(x y)2222xy min yx454545214.22 MPa 74.221214.22 MPa,20 ,45374.22MPa4.图示封闭薄壁圆筒,内径 d 100 mm,壁厚 t 2 mm,承受内压 p 4 MPa,外力偶矩 M e 0.192 kN·m。
求靠圆筒内壁任一点处的主应力。
0.19210 3解:xπ(0.10440.14)0.05 5.75MPat32x y pd MPa504tpd MPa1002tM e p M emax x y(x y ) 2xy2min22100.7 MPa 49.351100.7MPa,249.35 MPa,3 4 MPa5.受力体某点平面上的应力如图示,求其主应力大小。
材料力学习题应力状态和强度理论
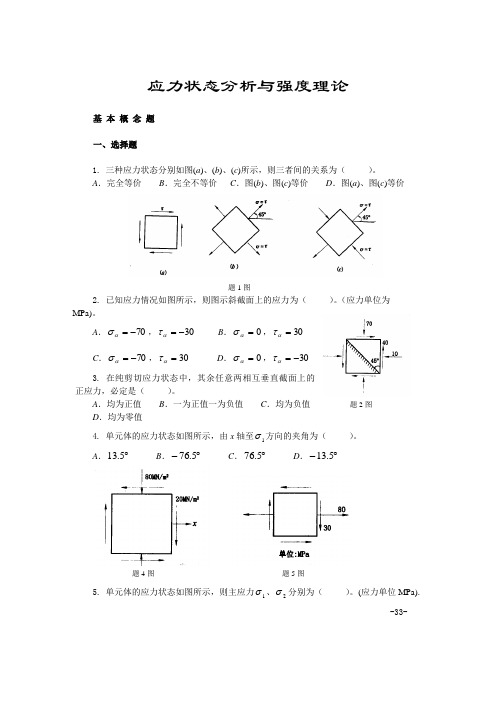
应力状态分析与强度理论基 本 概 念 题一、选择题1. 三种应力状态分别如图(a )、(b )、(c )所示,则三者间的关系为( )。
A .完全等价B .完全不等价C .图(b )、图(c )等价D .图(a )、图(c )等价题1图2. 已知应力情况如图所示,则图示斜截面上的应力为( )。
(应力单位为 MPa)。
A .70-=ασ,30-=ατB .0=ασ,30=ατC .70-=ασ,30=ατD .0=ασ,30-=ατ3. 在纯剪切应力状态中,其余任意两相互垂直截面上的 正应力,必定是( )。
A .均为正值B .一为正值一为负值C .均为负值 题2图D .均为零值4. 单元体的应力状态如图所示,由x 轴至1σ方向的夹角为( )。
A .︒5.13 B .︒-5.76 C .︒5.76 D .︒-5.13题4图 题5图5. 单元体的应力状态如图所示,则主应力1σ、2σ分别为( )。
(应力单位MPa). -33-A .901=σ,102-=σB .1001=σ,102-=σC .901=σ,02=σD .1001=σ,02=σ 6. 如图6所示单元体最大剪应力m ax τ为( )。
A .100 MPaB .50 MPaC .25 MPaD .0题6图 题7图7. 单元体如图所示,关于其主应力有下列四种答案,正确的是( )。
A .1σ>2σ,03=σ B .3σ<2σ<0,03=σ01=σ C .1σ>0,2σ= 0,3σ<0,1σ<3σ D .1σ>0,2σ= 0,3σ<0,1σ>3σ8. 已知应力圆如图7-22所示,图(a )、(b )、(c )、(d )分别表示单元体的应力状态和A 截面的应力,则与应力圆所对应的单元体为( )。
A .图(a )B .图(b )C .图(c )D .图(d )题8图9. 在图示四种应力状态中,其应力圆具有相同的圆心和相同的半径是( )。
-34-题9图A .图(a )、图(d )B .图(b )、图(c )C .图(a )、图(b )、图(c ) 、图(d )D .图(a )、图(d )、图(b )、图(c )10. 如图所示,较大体积的钢块上开有一贯穿的槽,槽内嵌入一铝质立方体,铝块受到均布压力P 作用,假设钢块不变形,铝块处于( )。
材料力学 第07章 应力状态分析与强度理论

sin2a t xy cos2a
18/95
7.2 平面应力状态分析 主应力 7.2.3 主平面的方位及极值正应力 s x s y s x s y sa cos2a t xy sin2a 2 2 s x s y ds a 上式对a 求导 2 sin2a t xy cos2a da 2 s x s y 若a a0时,导数为 0 sin2a 0 t xy cos2a 0 0 2 2t xy tan2a 0 s x s y
7.2.5 应力圆
t
sx
tyx
sy
sx txy sy
D(sx,txy) 1. 确定点 D (s ,t ) x xy
O
D'(sy,tyx)
C
s
2. 确定点D' (sy,tyx) tyx= -txy 3. 连接DD'与s 轴交于点C 4. 以 C 为圆心,CD(CD') 为半径画圆。
26/95
7.2 平面应力状态分析 主应力 7.2.5 应力圆
sx sy sz
sxs1 100 MPas 2
0 MPas 3 120 MPa
11/95
7.1 一点的应力状态的概念 单向、二向(平面)、三向(空间)应力状态 三个主应力中仅有一个主应力不为零 单向应力状态
s1
s1
F
A
F
12/95
7.1 一点的应力状态的概念 单向、二向(平面)、三向(空间)应力状态
O
D'(sy,tyx)
C sx- sx sy/2
s
27/95
7.2 平面应力状态分析 主应力 7.2.5 应力圆 利用应力圆确定角a 斜截面上的正应力和切应力
工程力学c材料力学部分第七章 应力状态和强度理论

无论是强度分析还是刚度分析,都需要求出应力的极值, 无论是强度分析还是刚度分析,都需要求出应力的极值,为了找 到构件内最大应力的位置和方向 需要对各点的应力情况做出分析。 最大应力的位置和方向, 到构件内最大应力的位置和方向,需要对各点的应力情况做出分析。
受力构件内一点处所有方位截面上应力的集合,称为一点的 受力构件内一点处所有方位截面上应力的集合,称为一点的 研究一点的应力状态时, 应力状态 。研究一点的应力状态时,往往围绕该点取一个无限小 的正六面体—单元体来研究。 单元体来研究 的正六面体 单元体来研究。
σ2
σ2
σ1
σ1
σ
σ
σ3
三向应力状态
双向应力状态
单向应力状态 简单应力状态
复杂应力状态 主应力符号按代数值的大小规定: 主应力符号按代数值的大小规定:
σ1 ≥ σ 2 ≥ σ 3
平面应力状态的应力分析—解析法 §7−2 平面应力状态的应力分析 解析法
图(a)所示平面应力单元体常用平面图形(b)来表示。现欲求 )所示平面应力单元体常用平面图形( )来表示。现欲求 垂直于平面xy的任意斜截面 上的应力 垂直于平面 的任意斜截面ef上的应力。 的任意斜截面 上的应力。
二、最大正应力和最大剪应力
σα =
σ x +σ y
2
+
σ x −σ y
2
cos 2α − τ x sin 2α
τα =
令
σ x −σ y
2
sin 2α + τ x cos 2α
dσ α =0 dα
σ x −σ y
2
sin 2α +τ x cos2α = 0
可见在 τ α
=0
材料力学习题参考答案2011年7月-第22章应力状态和强度理论

22-6 图示受力板件,试证明A 点处各截面的正应力、剪应力均为零证明:若在尖点A 处沿自由边界取三角形单元体如图所示,设单元体 、面上的应力分量为、和、,自由边界上的应力分量为,则有由于、,因此,必有、、。
这时,代表A 点应力状态的应力圆缩为 坐标的原点,所以A 点为零应力状态。
22-7 图示槽形刚体,在槽内放置一边长为10mm 、的立方钢块,钢块顶面受到合力为P=8kN 的均布压力作用,试求钢块的三个主应力和最大剪应力。
已知材料的弹性模量GPa E 200=,泊松比3.0=μ。
解: 选取坐标轴x 、y 、z 如图。
x σ=0, σz =-10101083⨯⨯=-80MPa ,εy =1E 〔σy -μ(σz +σx )〕=1E〔σy -μσz 〕=0 由此得 σy =μσz =0.3×(-80)=-24 MPa 。
Pxzyo将x σ、y σ、z σ按代数值大小排列,得三个主应力为 σ1=0 、σ2 =-24 MPa 、σ3=-80 MPa 。
最大剪应力 τm a x =σσ132-=280=40 MPa 。
22-12 试比较图示正方形棱柱体在下列两种情况下的相当应力3xd σ:(a )棱柱体自由受压:(b )棱柱体在刚性方模内受压。
弹性常数E 、μ均为已知.解:对于图(a )中的情况,应力状态如图(c )对于图(b )中的情况,应力状态如图(d )所以,,22-20 N O.28a普通热轧工字钢简支梁如图所示。
今由贴在中性层上某点K处、与轴线夹45º角方向上的应变片测得ε45º=-260×10-6。
已知钢材的E=210GPa,μ=0.28。
求作用在梁上的载荷F P。
《材料力学》第7章-应力状态和强度理论-习题解

支座反力: (↑)
=
(1)梁内最大正应力发生在跨中截面的上、下边缘
超过 的5。3%,在工程上是允许的。
(2)梁内最大剪应力发生在支承截面的中性轴处
(3)在集中力作用处偏外侧横截面上校核点a的强度
超过 的3.53%,在工程上是允许的。
解:坐标面应力:X(—0。05,0);Y(-0.2,0)
。根据以上数据作出如图所示的应
力圆。图中比例尺为 代表 。
按比例尺量得斜面的应力为:
按习题7—5得到的公式计算如下:
作图法(应力圆法)与解析法(公式法)的结果一致。
[习题7-7]试用应力圆的几何关系求图示悬臂梁距离自由端为 的截面上,在顶面以下 的一点处的最大及最小主应力,并求最大主应力与 轴之间的夹角。
解:
…………(1)
…………(2)
(1)、(2)联立,可解得 和 。
至此,三个面的应力均为已知:X( ,0),Y( ,0)( , 均为负值);
( )。由X,Y面的应力就可以作出应力圆。
[习题7-12]一焊接钢板梁的尺寸及受力情况如图所示,梁的自重略去不计。试示 上 三点处的主应力。
解:(1)求 点的主应力
解:坐标面应力:X(15,15),Y(0,-15)
第一强度理论:
因为 , ,即 ,
所以 符合第一强度理论的强度条件,构件不会破坏,即安全.
第二强度理论:
因为 ,
,即 ,
所以 符合第二强度理论的强度条件,构件不会破坏,即安全。
[习题7—25]一简支钢板梁承受荷载如图a所示,其截面尺寸见图b。已知钢材的许用应力为 , .试校核梁内的最大正应力和最大切应力。并按第四强度理论校核危险截面上的a点的强度。注:通常在计算a点处的应力时,近似地按 点的位置计算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
应力状态 强度理论1. 图示单元体,试求(1) 指定斜截面上的应力;(2) 主应力大小及主平面位置,并将主平面标在单元体上。
解:(1)MPa 6.762sin 2cos 22=--++=ατασσσσσαx yx yxM P a7.322cos 2sin 2-=+-=ατασσταx yx (2)22min max )2(2xy y x y x τσσσσσσ+-±+=98.12198.81-=MPa 98.811=σMPa ,02=σ,98.1213-=σ35.3940200arctan 21)2arctan(210==--=y x xy σστα2.解:取合适坐标轴令25=x σ MPa ,9.129-=x τ 由02cos 2sin 2120=+-=ατασστxy yx得125-=yσMPa所以22min max )2(2xy y x y x τσσσσσσ+-±+=20010015050)9.129(755022-=±-=-+±-= MPa1001=σMPa ,02=σ,2003-=σ MPa3. 一点处两个互成 45平面上的应力如图所示,其中σ未知,求该点主应力。
解:150=y σ MPa ,120-=x τ MPaMPa由 ατασστ2cos 2sin 245xy yx +-=802150-=-=x σ得 10-=x σ MPa 所以22min max )2(2xyy x y x τσσσσσσ+-±+=22.7422.214-= MPa22.2141=σ MPa ,02=σ,22.743-=σ4. 图示封闭薄壁圆筒,内径100=d mm ,壁厚2=t mm ,承受内压4=p MPa ,外力偶矩192.0=e M kN ·m 。
求靠圆筒内壁任一点处的主应力。
解:75.505.032)1.0104.0(π10192.0443=⨯-⨯=x τMPa504==t pd x σ MPa1002==tpd y σ MPa35.497.100)2(222min max =+-±+=xy y x y xτσσσσσσ MPa7.1001=σ MPa ,35.492=σ MPa ,43-=σ MPa5. 受力体某点平面上的应力如图示,求其主应力大小。
解:取坐标轴使100=x σMPa ,20=x τατασσσσσα2sin 2cos 22x yx yx --++='45-M e40120sin 20120cos 21002100=--++=yyσσ得1.43=yσMPa22min max )2(2xy y x y x τσσσσσσ+-±+=77.3633.106=MPa 33.1061=σMPa ,77.362=σMPa ,03=σ6.解:22min max )2(2xyy x y x τσσσσσσ+-±+=16.4216.5216.47540252203022-=±=+±-=所以2.521=σMPa ,102=σMPa ,16.423-=σMPa2.47231max =-=σστMPa7. 图示工字形截面梁AB ,截面的惯性矩61056.72-⨯=z I m 4,求固定端截面翼缘和腹板交界处点a 的主应力和主方向。
解:17.361056.7207.075.0105063=⨯⨯⨯⨯=-σ MPa (压应力)8.81056.7203.01085301501050693=⨯⨯⨯⨯⨯⨯⨯=--τMPa22min max )2(2xy y x y x τσσσσσσ+-±+=2.3803.2-= MPa03.21=σ MPa ,02=σ,2.383-=σ MPa05.7717.368.82arctan 21)2arctan(210=⨯-=--=y x xy σστα50kN AB0.75mσ305.77τaσaσ18. 图示矩形截面拉杆受轴向拉力F ,若截面尺寸b 、h 和材料的弹性模量E ,泊松比ν均已知,试求杆表面 45方向线段AB 的改变量=∆AB L ? 解:bhFx=σ,0=y σ,0=xy τ bh F2=ασ,bh F 22=+απσ( 45=α所以)1(2)22(145v EbhFbh F bh F E -=-=νεEbF Ebh Fh AB L AB 2)1(2)1(2245ννε-=-⨯==∆ 9. 一边长为50 mm 的正方形硬铝板处于纯剪切状态,若切应力80=τ MPa ,并已知材料的弹性模量72=E GPa ,泊松比34.0=ν。
试求对角线AC 的伸长量。
解:8045=σMPa ,80135-= σMPa39451048.1)8034.080(10721-⨯=⨯+⨯=ε 25=AC L00105.01048.1253=⨯⨯=∆-AC Lmm10. 一变形体A 四周和底边均与刚性边界光滑接触,上边受均布压力0σ。
已知材料的的弹性模量E ,水平方向上的应变和应力。
解:0σσ-=y,z x σσ=,0==z x εε0)]([1=+-=z y x x E σσνσε,得到10-==ννσσσz x )121()]12([1)]([12000ννσννσνσσσνσε---=---=+-=E E E z x y y11. 设地层由石灰岩组成,其密度3105.2⨯=ρ kg/m 3,泊松比2.0=ν。
计算离地面200m 深处的地压应力。
解: 9.42008.9105.23-=⨯⨯⨯-=y σ MPaz x σσ=,0==zx εε0)]9.4(2.0[1=+-⨯-=z x x Eσσε得到22.1-==zx σσ MPa12. 一体积为101010⨯⨯ mm 3的立方铝块,将其放入宽为10 mm 的刚性槽中。
已知铝的泊松比ν33.0=解: 6001.001.010633-=⨯⨯-=σMPa,01=σ由0)6033.0(122=⨯+=σεE得8.192-=σ13. 直径为D 的实心圆轴,受外力偶e M 作用如图。
测得轴表面点A 与轴线成 45方向的线应变为ε,试导出用e M 、D 、ε表示的切变弹性模量G 的表达式。
解:τσ=-45,τσ-=45τνε)1(145+=E,所以ετG 2=又316D M e πτ=,所以ED M G e 38π=14. 直径100=d mm 的圆轴,受轴向拉力F 和力偶矩e M 作用。
材料的弹性模量200=E GPa ,泊松比3.0=ν。
现测得圆轴表面200mσxσzσy的轴向线应变6010500-⨯=ε,45方向的线应变64510400-⨯=ε,求F 和e M 。
解:7850=⋅=A E F ε kN 设力偶矩引起的切应力为ττσ+=-5045,τσ-=5045)(1454545 νσσε-=-E ]10)50(3.010)50[(102001669⨯-⨯-⨯+⨯=ττ610400-⨯=6.34=τ MPa ,又3)1.0(π16⨯=M τ8.6=e MkN ·m15. 直径100=d mm 的实心钢球,受静水压力42=p MPa 作用。
求直径和体积的缩减量。
设钢球的弹性模量210=E GPa ,泊松比3.0=ν。
解:因为42321-=-===q σσσ MPa所以333211024.042310210)3.021()(21-⨯-=⨯⨯⨯⨯--=++-=σσσνθE 533211108102108.16)]([1-⨯-=⨯-=+-=σσνσεE 得23310257.1100)6(1024.0--⨯-=⨯⨯⨯-==∆πθV Vmm 3351108100108--⨯-=⨯⨯-==∆d d εmm16. 边长10=a 0 mm 的立方体,已知弹性模量200=E GPa ,泊松比3.0=ν。
如将立方体沉入100 m 深的水中,求其体积变化。
解:因为1321-=-===gh ρσσσMPa)(21321σσσνθ++-=E 63106)3(102006.01-⨯-=-⨯⨯-=61.01.01.01066-=⨯⨯⨯⨯--==∆-V V θmm 3ττ17. 图示拉杆,F ,b ,h 及材料的弹性常数E 、ν均为已知。
试求线段AB 的正应变和转角。
解:bhF x =σ,bhF 213545==σσ所以)1(2)(!13545ννσσε-=-=bhEF E AB 又因为bhE F x =ε,bhEFv y -=ε所以bhEv F bhE vF bhE F AB )1()(45+-=+-== γϕ18. 图示曲拐ABC 在水平面内,悬臂端C 处作用铅垂集中力F 。
在上表面E 处,沿与母线成 45方向贴一应变片,已测得线应变45ε,求载荷F 值。
已知长度l 、a 、直径d 及材料的常数E 、v 。
解:应力状态如图示,332d Fl πσ=,316d Fa πτ=τσσ+=245,τσσ-=-245所以)(!454545--=σσεv E所以)1(16)1(16345v a v l dE F ++-=πε19. 三个弹性常数之间的关系:)]1(2/[ν+=E G 适用于 (A)任何材料在任何变形阶段; (B)各向同性材料在任何变形阶段;(C)各向同性材料应力在比例极限范围内; (D)任何材料在弹性变形范围内。
答:C20. 一实心均质钢球,当其外表面处迅速均匀加热,则球心O 点处的应力状态。
(A)单向拉伸应力状态; (B)二向拉伸应力状态; (C)三向等值拉伸应力状态; (D)三向压缩应力状态。
答:C/2στσ/2σ21. 混凝土立方体试样作单向压缩试验时,若在其上、下压板面上涂有润滑剂,则试样破坏时将沿纵向剖面裂开的主要原因。
(A)最大压应力; (B)最大切应力; (C)最大伸长线应变; (D)存在横向拉应力。
答:C22. 已知单元体的主应力为1σ,2σ,推证两相互垂直的截面上的正应力之和为常数 。
证:ασσσσσα2cos 222121-++=)90(2cos 222121︒+-++=ασσσσσβ=+=+21σσσσβα常数 得证。
23. 受内压的薄壁圆筒,已知内压为p ,平均直径为D ,壁厚为t ,弹性常数为E 、ν。
试确定圆筒薄壁上任一点的主应力、主应变及第三、第四强度理论的相当应力。
解:tpD 21=σ,tpD 42=σ,03=σ)2(4)42(1)(1211νννσσε-=-=-=tE pD t pD t pD E E)21(4)24(1)(1122νννσσε-=-=-=tE pD t pD t pD E EtEpD t pD E E 43]430[1)](0[1213ννσσνε-=-=+-=tpD231r3=-=σσσ])()()[(21213232221r4σσσσσσσ-+-+-=t pD 43=24. 图示正方形截面棱柱体,弹性常数E 、ν均为已知。
