2021-2022年高中力学竞赛决赛试题
2021年国际工程力学竞赛试题
2021年国际工程力学竞赛试题简介：工程力学是研究物体受力的学科，它是现代工程科学和技术的基础。
国际工程力学竞赛是一个全球性学术竞赛，吸引了许多热爱工程力学的青年学子参与。
以下是2021年国际工程力学竞赛的试题。
试题：1.某建筑设备使用时出现故障，需要将其吊装到2米高的平台上进行维修。
设备的质量为500千克，绳索的最大拉力为10000牛顿。
请计算需要多少根绳索来保证安全吊装？2.一辆汽车在高速行驶时发生制动失效，撞上了前方的墙壁。
墙壁的抗力为50000牛顿，汽车的质量为1500千克。
请计算汽车撞上墙壁的速度。
3.在一个建筑工地上，一根长为10米的钢梁被用作悬挂重物的支撑。
假设重物的质量为1000千克，钢梁的质量为500千克，重物与钢梁的中心距离为2米。
请计算钢梁受力的情况，并判断其是否安全。
4.一座高楼的电梯被坏人炸毁，导致人们被困在楼层中。
假设电梯口离地面的高度为50米，电梯内有10人，每人的平均质量为70千克。
请计算救援人员需要提供多大的力才能将电梯拉升至安全位置？5.一辆载重货车在斜坡上行驶，坡度角为30度。
车辆的质量为3000千克，货物的质量为2000千克。
请计算货车是否能够成功上坡，并计算所需的最小推力。
6.一根长10米的悬臂梁在中点受到垂直向下的力，力的大小为1000牛顿。
请计算悬臂梁的反弯矩和最大挠度。
7.某工地上正在施工的桥梁跨度为50米，桥面宽度为10米。
桥面的最大荷载为50000牛顿/米²，假设桥梁的质量均匀分布在桥面上。
请计算桥梁可能承受的最大总质量。
8.在一个物体受力的问题中，已知一个力的大小为100牛顿，另一个力的大小为200牛顿，两个力之间的夹角为60度。
请计算这两个力的合力。
9.现有一根长为5米的钢杆，两端分别悬挂了一个质量相等的重物。
重物与钢杆的距离分别为1米和2米。
请计算钢杆的受力情况。
10.一辆汽车以10米/秒的速度行驶，在0.1秒内发生急刹车，停下来所需的加速度为8米/秒²。
高中物理力学竞赛试卷
高中物理力学竞赛试卷一、不定项选择题（共50分）1．做匀加速直线运动的质点,连续过A 、B 、C 三点,已知AB 和BC 两段长度相等,质点在AB 段的平均速度为3m/s ,在BC 段的平均速度为6m/s ,则质点经过A 点、C 点时的速度之比为( )A ．1：2B ．2：5C ．1：5D ．1：72．将4个可视为质点的物体分别沿光滑轨道AB 、AC 、AD 、AE ,由A 点同时从静止开始下滑,如图所示。
则在到达底端前,某一时刻物体在各自轨道上的位置连线如图中粗实线所示,期中正确的是（ ）A B C D3．小木块放在倾角为α的斜面上,受到一个水平方向不为零的力F 作用处于静止状态,如图所示,则小木块受到斜面的支持力和摩擦力的合力的方向与竖直向上的方向的夹角β可能是（ ）A ．β等于零B ．左上方,αβ<C ．右上方,αβ>D ．左上方,αβ>4．已知1F 、2F 的合力方向竖直向下,若保持1F 的大小、方向,2F 的大小都不变,而将2F 的方向在竖直平面内转过060角,仍保持1F 、2F 合力方向竖直向下,下列判断正确的是（ ）A ．1F 一定大于2FB ．1F 可能小于2FC ．2F 方向与水平面成030角D ．1F 方向与2F 方向成060角5． “套圈”是一项老少皆宜的体育运动项目．如图所示,水平地面上固定着3根直杆1、2、3,直杆的粗细不计,高度均为0.1m,相邻两直杆之间的距离为0.3m ．比赛时,运动员将内圆直径为0.2m 的环沿水平方向抛出,刚抛出时环平面距地面的高度为1.35m,环的中心与直杆1的水平距离为1m ．假设直杆与环的中心位于同一竖直面,且运动中环心始终在该平面上,环面在空中保持水平,忽略空气阻力的影响,g 取10m/s 2．以下说法正确的是（ ）A ．如果能够套中直杆,环抛出时的水平初速度不能小于1.9m/sB ．能够套中第2根直杆的初速度范围在2.4m/s 到2.8m/s 之间C ．如以2m/s 的水平初速度将环抛出,就可以套中第1根直杆D ．如环抛出的水平速度大于2.6m/s,就一定不能套中第2根直杆6．1F 方程式赛车的变速系统非常强劲。
第27届北京市高中力学竞赛决赛试题答案
（2）
联立（1） （2）得 8. 解：
rs
R 6.4 10 6 1.6 10 6 m 4 4
假设汽车刹车，车受力如图所示
ac
C f2 mg N2 l f1 N1
h
L
则有：
N1 N 2 mg 0 f1 f 2 mac N1l N 2 ( L l ) f1 f 2 h 0
1 2 1 1 1 1 2 2 2 mV12 mu0 （7） mv1 mu0 = mv1 2 2 2 2 2
解（5） 、 （6）两式，得
0 v1
（8） （9）
V1 = v1 2 gh
碰撞后， 平板从其平衡位置以 V1 为初速度开始作简谐振动． 取固定 坐标，其原点 O 与平板处于平衡位置时板的上表面中点重合，x 轴 的方向竖直向下，若以小球和平板发生碰撞的时刻作为 t 0 ，则平 板在 t 时刻离开平衡位置的位移
FN maM sin mg cos
对 M ： FN sin MaM 由 600 ，可解得 a 所以 t1
2l a
2 3( M m) g 4 M 3m
(4 M 3m)l 3( M m) g
下到底端时，滑块因转弯和物体发生一个比较猛烈的作用，此过程 中水平动量守恒．设转弯结束后滑块和物体的速度分别为 和 ，那么
小球从穿出小孔到相遇的时间
第 27 届北京市高中力学竞赛决赛试题
第 3 页 共 8页
tR
c o t
R
0
2 s2 i n c o t
管道在平面上移动的路程
2 1 sin 2 cot s ut 2 R
第26届北京市高中力学竞赛决赛试题
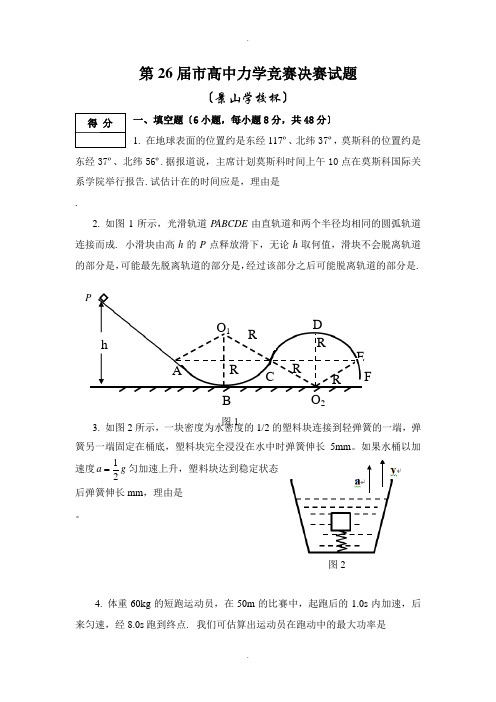
第26届市高中力学竞赛决赛试题〔景山学校杯〕一、填空题〔6小题，每小题8分，共48分〕1. 在地球表面的位置约是东经117º、北纬37º，莫斯科的位置约是东经37º、北纬56º.据报道说，主席计划莫斯科时间上午10点在莫斯科国际关系学院举行报告.试估计在的时间应是，理由是 .2. 如图1所示，光滑轨道P ABCDE 由直轨道和两个半径均相同的圆弧轨道连接而成. 小滑块由高h 的P 点释放滑下，无论h 取何值，滑块不会脱离轨道的部分是，可能最先脱离轨道的部分是，经过该部分之后可能脱离轨道的部分是.3. 如图2所示，一块密度为水密度的1/2的塑料块连接到轻弹簧的一端，弹簧另一端固定在桶底，塑料块完全浸没在水中时弹簧伸长5mm 。
如果水桶以加速度g a 21匀加速上升，塑料块达到稳定状态后弹簧伸长mm ，理由是 。
4. 体重60kg 的短跑运动员，在50m 的比赛中，起跑后的1.0s 内加速，后来匀速，经8.0s 跑到终点. 我们可估算出运动员在跑动中的最大功率是得 分hABCD E F O 1O 2R R RRR图1P 图2AB C Dv 1v 1xW .〔保留两位有效数字〕5. 有一种绳系卫星，母星在确定的轨道上运动，母星上用细绳悬吊一个子星，如图3所示. 稳定时母星和子星间的细绳方向应指向地心，但有时子星会发生摆动，子星上无动力装置，为消除摆动使细绳方向指向地心，可采取的措施是， 理由是 .6. 如图4所示，一鼓轮放在粗糙地面上，右边紧靠光滑的竖直墙壁，鼓轮重量不计，其上由绳索悬吊一重物G ，已知r =R /3，鼓轮与地面间的摩擦因数为μ，鼓轮处于静止平衡状态. 如果增大r ，其他条件不变，鼓轮是否能处于平衡状态？答：， 理由是.二、计算题〔共102分〕7.〔16分〕如图5所示，球与台阶相碰图4图3母星子星地心得 分的恢复系数为e )(接近速度分离速度e =，每级台阶的宽度和高度相同，均等于l ，该球在台阶上弹跳，每次均弹起同样高度且在水平部分的同一位置，即AB =CD ，求球的水平速度和每次弹起的高度，球与台阶间无摩擦.8．〔16分〕特警战士距墙S 0，以速度0υ起跳，如图6所示，再用脚蹬墙面一次，身体变为竖直向上的运动以继续升高，墙与鞋底之间的静摩擦因数为μ．求能使人体重心有最大总升高的起跳角θ.9．〔20分〕如图7所示，A 、B 、C 、D 、E 五个杂技演员在连续靠近放置的跳板上表演杂技．他们各自的质量分别为m 1，m 2，m 3，m 4和m 5.A 演员从h 1高度跳到第一个跳板上. B 、C 、D 接着一个个被竖直向上弹起后又竖直落下到相邻的跳板上．跳板的质量可以忽略，试求E 演员被弹起的高度h 5是多少？图6S 0得 分得 分10.〔25分〕如图8所示，一根质量可以忽略的细杆，长为2l ，两端和中心处分别固连着质量为m 的小球B 、D 和C ，开始时静止在光滑的水平桌面上. 桌面上另有一质量为M 的小球A ，以一给定速度v 0沿垂直于杆DB 的方向与右端小球B 作弹性碰撞. 求刚碰后小球A 、B 、C 、D 的速度，并详细讨论以后可能发生的运动情况.11.〔25分〕如图9所示，一均匀圆盘，质量为M ，半径为R ，静止放在一光滑水平地面上，中心不固定. 质量为m 的人，初始静止站在圆盘边缘上〔人可看作质点〕，当人以相对速率u 沿圆盘边缘走动后，盘的转动角速度大小为)(32RuM m m +=ω，求盘心O 的速度大小. 图7图8得 分得 分第26届市高中力学竞赛决赛试题答案〔景山学校杯〕一、填空题1．下午3点多〔2分〕.地球由西向东自转，24小时转一周，经度为360º，每隔15º差1小时，117º-37º=80º，约5个多小时〔6分〕.2．A →B →C 〔2分〕.C →D 〔3分〕. E →F 〔3分〕.3．7.5 〔2分〕. 水和塑料块都超重，F 弹=F 浮-m 塑〔g +a 〕=〔ρ水-ρ塑〕V 塑〔g +a 〕〔6分〕.4．2.7103〔8分〕a=P m =mav =W 3107.232032060⨯=⨯⨯5．子星摆动最低处放绳，最高处收绳 ，放绳时绳拉力对子星做负功，收绳时做正功，半个周期内负功绝对值大于正功，拉力总功为负，子星机械能减小.〔8分〕OR A.m 图9T 2T 1T 1>T 26. 能，不能〔2分〕. 平衡方程为fR =Gr ，，平衡时〔6分〕二、计算题7、解：球每次弹起的速度v 1都相同，每次落地的速度v 2也相同，由能量守恒：22212121mv mgl mv =+①gl v v v v gl v v y x y x 2,2212122222122=--+=- 〔2分〕 由牛顿碰撞公式：②yy ev v 21=- 〔2分〕在水平方向动量守恒：③x x x x v v mv mv 2121,==由①②③可求得：)2(12 )2(,122221分分e glv e gl ev yy -=--= 平抛公式：⑥⑤④，221111,gt t v y t v l gt v v y x y y +==+= 令v y =v 2y ，由④可求得球从弹起到落地的时间：)1()1(2112212e g e l g e e gl gv v t yy -+=+⋅-=-=)2(分 代入⑤中即可求得球的水平速度：)1(2)1()1(2)1()1()1(2)1()1(2/1e e gl e l le g e g e l e g e l l t l v x +-=+-⋅-+=-+==)2(分令v y =0，由④可求得球达最大高度所需时间：)1(2112221e g le g e gl egv t y -=⋅-=-= 代入⑥中即可求得球所能达到的最大高度：l ee g e g l ge e g l e e gl e y 2222221)1(221)1(212-=-+-⋅--=)4(分 AB C Dv 1v 1 v 2xy8、分析和解：在解答本题时，注意摩擦力的冲量远大于人体重力的冲量，抓住主要因素忽略次要因素，是经常用到的手段.人以角θ起跳，水平初速度和竖直初速度分别为00cos x υυθ=，00sin y υυθ= 从起跳到蹬墙时空中飞行的时间为0cos s t υθ=则人蹬墙前竖直方向的速度为000sin cos y y s gt g υυυθυθ=-=-人重心升高：2220001000000111sin ()tan ()2cos 2cos 2cos y s s s h t gt g s g υυθθυθυθυθ=-=-=-〔6分〕设人蹬墙的时间为△t ，因△t 很小，则静摩擦力的冲量远大于人体重力的冲量，即f G I I >>，由动量定理得：f y I N t m μυ=∆=∆而在水平方向同样由动量定理可知：cos x x o N t m m m υυυθ∆=∆==〔3分〕人蹬墙后获得竖直向上的速度：0000sin cos cos y y y gs υυυυθμυθυθ'=+∆=-+人蹬墙后再上升的高度20022202002000(sin cos )cos (sin cos )1tan ()2222cos y gs s h s s g g g g υθμθυυθυθμθθμυθ⎡⎤+-⎢⎥'+⎣⎦===--+人体重心上升的总高度：220120(sin cos )2H h h s gυθμθμ+=+=-令tan φ=μ，则对0υ、s 0一定时，当2πθϕ+=时H 最大．即1arctanθμ=时，人体的重心总升高最大．〔7分〕9、解：首先我们注意一下图中的翘板，中间是一个无限重的支柱．A 演员跳到翘板的一端，同时把B 演员弹到空中，我们可以看作是演员间“通过〞翘板的碰撞．假定碰撞的持续时间很短，由此我们可以不考虑重力对碰撞本身的影响，因为在碰撞的时间△t 里，每一个演员和重力相关的冲量矩〔对翘板中心计算〕与△t 成正比，是非常小的．碰撞时翘板支点是不动的，我们可以采用角动量守恒定律来研究．又由于翘板非常轻，我们可以认为翘板的转动惯量为零.根据题中后面的说明和上面的假设．我们可以认为碰撞时机械能是守恒的，也就是说是弹性碰撞.令1υ'表示A 演员碰撞后的速度.1υ'与图上的1υ指向同一个方向.由系统的角动量和机械能守恒，可以写出111122m r m r m r υυυ'=+〔4分〕222111122111222m m m υυυ'=+〔4分〕 解这个方程组，我们得到两组解1〕1υυ'=，20υ= 2〕12112m m m m υυ-'=+，121122m m m υυ=+〔2分〕第一组解相当于碰撞之前；而第二组解相当于碰撞之后.B 演员跳到相邻的翘板上，在碰撞的瞬间速度是2υ. 相继而来的过程和第一次完全相似. 因此以后的演员弹起的速度相应地为MDBCAV 0222220A B C D 11111+22222M M m m =++v v mv v v 232232m m m υυ=+，343342m m m υυ=+，454452m m m υυ=+〔5分〕将前面的计算结果代人，可得E 演员弹起的速度为123451223344516()()()()m m m m m m m m m m m m υ=++++〔3分〕所求的高度h 5可以利用下式计算1υ5υ=于是得到21234511223344516()()()()m m m m h h m m m m m m m m ⎡⎤=⎢⎥++++⎣⎦〔2分〕10、解析 ①小球A 、B 碰撞瞬间，球A 挤压B ，其作用力方向垂直于杆，使球B 获得沿0v 方向的速度B v .从而在碰撞瞬间使小球C 、D 的速度也沿0v 方向.对质点组B 、C 、D 与A 组成的系统，碰撞前后动量守恒。
2021年国际工程力学竞赛试题
2021年国际工程力学竞赛试题第一部分：选择题（共30题，每题2分，共60分）1.以下哪个选项最准确地描述了力学？A.研究物体的运动和力的科学B.研究自然界中的能量转化过程的科学C.研究物体的形变和应力分布的科学D.研究热力学过程的科学2.下列哪个选项不是力学的主要分支？A.静力学B.动力学C.统计力学D.流体力学3.下列哪个物理量不是力学中常用的基本物理量？B.加速度C.力D.温度4.力是一个矢量量，它有大小和方向。
力的大小用什么单位来表示？A.米B.秒C.千克D.牛顿5.以下哪个物理量与力不是成正比关系？A.加速度B.质量C.位移6.以下哪个公式描述了牛顿第二定律？A. F = maB. F = mvC. a = mvD. a = F/m7.弹性力是指在一个物体上产生变形时所产生的力。
下列哪个公式可以用来计算弹性力？A. F = kxB. F = mvC. F = maD. F = µN8.在接触面上的压强等于单位面积上承受的力的大小。
下列哪个公式描述了压强？A. P = F/AB. P = F/dC. P = F/mD. P = F/v9.功是力对物体作用时所做的功。
下列哪个公式可以用来计算功？A. W = FvB. W = FdC. W = F/AD. W = mv10.若两个物体相互作用的力的大小相等方向相反，则它们产生的效果是？A.加速度为零B.加速度为正C.加速度为负D.加速度无法确定11.勾股定理是力学中常用的定理，它用来计算什么？A.初速度B.加速度C.位移D.力12.力矩是描述物体绕轴旋转的能力的物理量。
下列哪个公式可以用来计算力矩？A. M = F/dB. M = F/AC. M = FvD. M = F/f13.弹性势能是指物体由于变形而具有的能量。
下列哪个公式可以用来计算弹性势能？A. PE = 1/2mv²B. PE = mghC. PE = kx²D. PE = Fd14.动能是指物体由于运动而具有的能量。
第25届北京市高中力学竞赛决赛试卷
第25届北京市高中力学竞赛决赛试卷（北京四中杯）（全卷满分 分） 年 月 日题 号一 （填空）二（计算题）总 分分 数 阅卷人 复查人一、填空题（ 小题，每小题 分，共 分）一跳远运动员在地球表面跳远，起跳时速度为 ，能跳出 远 已知月球表面的重力加速度是地球表面重力加速度的 ，如果他在月球表面跳远，起跳速度大小也是 ，他跳远的记录将是一举重运动员能举起 的重物，他对一根羽毛能施加 的力吗？答： ，理由是嫦娥飞船绕月球做匀速圆周运动，测出其周期为 ，则飞船距月球表面的距离为 ，可否不计地球引力而近似表述为2324GMTh R π=-，其中 是月球的质量， 是月球半径 答： ，理由是得分据北京晚报 年 月 日和参考消息 月 日报道，奥地利勇士鲍姆加持纳从 万米高空的氦气球吊篮中跃下，下落的最高速度到 下落约 分 秒，距地面 高处打开伞，整个下落到地面的时间持续 分 秒 试根据报纸报道和你的分析，在图 中比较准确地画出奥地利勇士下落到地面过程的 图线下雨天，假设无风，雨滴以速度 竖直下落，雨滴在空中的分布是均匀的，单位体积的雨量是ρ 如图 所示，一个人要从 处运动到 处，他没有带伞， 、 的距离为 ，人的运动速度为 把人简化为长方体模型，头和肩的水平面积为 ，身体前方正面的竖直面积为 则人从 到 过程中，打到面积 上的雨量为 ，打到面积 上的雨量为三个质量均为 的小球 、 、 ，用轻杆连接，如图 所示 、 与 、的距离相等， 、 、 与地球中心在一条直线上 三个小 球在高空绕地球做匀速圆周运动，如果轻杆收到扰动而偏离直线一小角度 ，则轻杆与直线的偏角 将 （增大、减小、不变），理由是图图（本题说明控制卫星天线总指向地球的基本原理）二、计算题（共 分）（ 分）两个相同的半球，半径都是 ，质量为 ，放在静摩擦因数为 的水平面上 在两个半球上放一个半径为 ，质量为 的光滑球，如图 所示 求在平衡状态下两球球心之间的最大距离地球图图．（ 分）两个质量分别为1m 和2m 的小球，它们之间的相互作用表现为斥力（斥力大小表达式为221rm m k，k 是常数，r 为两球之间距离） 现已知1m 以速度0v 接近2m ，瞄准距离为 ，即2m 到1m 速度方向的垂直距离为 ，如图 所示 求1m 小球接近2m 小球的最近距离 设21m m <<，小球2m 可近似看作静止．（ 分）如图 所示，质量为 的小球，用不可伸长的线悬于固定点 ，线长为 ，初始线与铅垂线有一个夹角，初速为在小球开始运动后，线碰到铁钉 铁钉的方向与小球运动的平面垂直 ，且已知 与铅垂线夹角为 ，设l 与铅垂线夹角为α 假设图2m碰后小球恰能做圆周运动 求线与铁钉碰前瞬时与碰后瞬时张力的变化分 如图 所示，理想滑轮（轻质，无摩擦）两端悬挂两个质量均为 的砝码盘 用轻线拴住劲度系数很大的轻弹簧（弹簧劲度系数为 ）两端使它压缩的长度为 ，将此弹簧竖直放在左侧砝码盘上，弹簧上放一质量为 的砝码 右侧砝码盘上也放置质量为 的砝码，使两盘静止 燃断轻线，轻弹簧达到自由伸展状态即与砝码脱离 求（ ）此系统（包括两个盘、两个砝码、弹簧和细绳）中哪些量守恒？（ ）使用守恒定律求砝码脱离弹簧后升起的高度得 分图．（ 分）三个质量为 的小球用两根长为 的不可伸长细绳相连 初始时刻，三个小球在一条线上，静止放在光滑水平面上，标号分别为 、 、 ，如图 所示 给标号为 的小球以初速度0v ，则这三个小球运动起来，求 、 两球相遇时的速度为多大？第 届北京市高中力学竞赛决赛试题答案（北京四中杯） 一、填空题 ． ．（ 分）． 不能 分 ．一根羽毛不能对运动员施加 的力，根据牛顿第三定律，运动员也不能对羽毛施加 的力．（ 分）．可以（ 分）．在地球引力所用下，月球（携带飞船）绕地球做匀速圆周运动，可认为月球飞船处于失重状态，可只考虑月球对飞船的引力作用（ 分）．．得 分 0v图．211v l v S ρ；（ 分） lS 2ρ．（ 分）减少（ 分）， 球受地球引力与惯性离心力平衡， 球受引力大于惯性离心力，合力指向地球， 球受引力小于惯性离心力，合力背向地球， 、 球受力的力矩使 角减少（ 分）．二、计算题解：设最大距离时摩擦力为 ， 球心连线 与竖直夹角 ．对 球 方向：mg N =θcos 2（ 分） θ=cos 2mg N对 球 方向：0cos 21=θ--N mg N B （ 分）mg mg mg N B =+=2121对 球 方向：0sin max =θ-N f （ 分） mg N f B 21max =μ= （ 分）0sin cos 221=θθ-mgmg 1tan =θ地球21θ1)2()2(tan2max2max=-=θbrb （ 分）4443max23maxbrb-= 22m ax8rb= rb22max= （ 分） ．解：1m小球受力始终指向2m小球中心，1m小球在一平面内运动．如图所示．设 轴垂直于此平面且通过2m小球中心，则1m小球所受力对 轴的力矩为零，即对 轴角动量守恒．1m小球以速度运动，对 轴角动量是，但，故，1m小球最接近2m小球（距离为）时，即无继续向2m小球运动的速度，又无远离2m小球的速度，此刻的速度应与1m小球至2m小球的连线垂直，角动量是vdm1．于是11vbmvdm= （ ） （ 分）得dbvv0=在散射过程中，只有斥力作用，故能量守恒。
第28届北京市高中力学竞赛决赛试题答案
(1)
另外，在此过程中，只有保守内力（绳的弹力）做功，因而能 量守恒，
1 2
mv0 1 k (r d ) 2 1 mv 2 2 2
2
(2)
为求解方便，将(1)(2)化简，并代入已知数据可得：
v0 4v (1)'
v0 1.6 v 2
2
(2)'
解此方程组，求得：v0 ≈1.3 m/s
第 28 届北京市高中力学竞赛决赛试题答案 （景山学校杯）
一、 填空题 1．甲拉绳做的功是乙拉绳做的功的 2 倍. 2．有功夫的人能根据鸟对手掌的轻微作用调节手掌的起伏，使鸟腿不 能蹬手，无力起飞. 3．起跳到离开高台的阶段，人蹲高台使人体质心加速上升；加速下蹲 阶段和离开高台上升到下降落水阶段，下蹲过程人体质心加速下降，离 开高台后加速度为重力加速度. 4.
方向沿 y 轴。
或联立(1) (2/)(3)(5)(6)方程求解得，
3 v2 v0 7
或联立(1) (2)(3)(5)(6)方程求解得，
第 28 届北京市高中力学竞赛决赛试题
方向沿 y 轴。
第 6 页 共 8页
3 v2 v0 7
解法二： 设绳张紧瞬间速度如图 4 所示:
方向沿 y 轴。
60 0
讨论：
l sin 2 l sin 2 （1） 1 x 1 ； 2 sin 2 2 sin 2
（2） 若 ，或 90 0 - ，任何情况都平衡。
11.解法一：设绳拉紧的瞬时，A 的速度为 v1 ，B 的速度为 v2 ，取如图 3 所示的坐标系，在 y 方向系统不受外力，动量守恒：
v1x v ' s i n
2022年 新高中物理力学竞赛第29届决赛模拟练习与解答配套精选
第29届北京市高中力学竞赛决赛试题〔景山学校杯〕一、填空题1。
理由 ___________________________________ 。
2．2021年4月6日我国成功发射首颗微重力科学实验卫星—“实践10号〞，微重力水平可达10-6g 〔空间站为l0-3g〕。
卫星整体为柱锥组合体形状，分为返回舱和仪器舱，要进行19项实验。
卫星总质量约3600kg，运3．汽车沿水平直路以速度v1匀速行驶，无风，下雨，雨点竖直下落速度为v2。
汽车水平顶面的面积为S1，4．如图1所示，在光滑水平面上有两物块A、B，中间用不计质量的弹簧相连接，物块A的质量m A=100m B，A受水平向右的恒力，大小为F1，B受水平向左的恒力，大小为F2，F1 > F2。
两物块加速度相同5．水平传送带以稳定的速度v1运行，质量为m的小物块以水平速度v2进入传送带，v2与v1方向垂直，物块与传送带之间的滑动摩擦因数为，当物块在传送带上静止时，物块沿传送带运行方向走过的距离6．小船B被水流冲走，用一长绳连结小船，长绳另一端固定在岸边A点。
将小船看成质点，河水流速为v1，设水流速度沿河面宽度方向不变。
河岸上收绳的速度为v2，某一时刻AB与河岸的夹角为，如图2所示，二、计算题7．质点以初速v0自倾角为β的斜面底端抛出。
v0与水平夹角为α〔β<α〕，求质点在斜面上的最大射程〔不计空气阻力〕8．如图4所示，斜面质量为M，放在光滑水平面上，滑块质量为m，m与M之间无摩擦力，斜面高h，长l，求当m从斜面顶端由静止滑到底端时，支持力对m所做的功。
9．如图5所示卢瑟福等人发现用带正电且带电荷量为2e的α粒子轰击金铂时有些入射粒子散射偏转角很大，甚至超过90°。
卢瑟福于1911年提出原子必有一带正电的核心，即原子核；此即原子结构的行星模型。
α粒子与原子核之间的相互作用力表现为斥力〔斥力大小的表达式为是常数，r为α粒子与原子核之间的距离，q1为α粒子的电荷量，q2为原子核的电荷量；方向在粒子与核的连线上。
全国高中物理力学竞赛试题卷(部分)百度文库整理
全国高中物理力学竞赛试题卷(部分)考生须知：时间150分钟，ｇ取10ｍ／ｓ2(, 题号带△的题普通中学做)一． 单选题（每题5分）△1.如图所示，一物体以一定的初速度沿水平面由A 点滑到B 点，摩擦力做功为W 1；若该物体从M 点沿两斜面滑到N ，摩擦力做的总功为W 2。
已知物体与各接触面的动摩擦因数均相同，则：A ．W 1＝W 2B ．W 1＜W 2C ．W 1＞W 2D ．无法确定△2.下面是一位科学家的墓志铭： 爵士安葬在这里。
他以超乎常人的智力第一个证明了行星的运动与形状、彗星的轨道和海洋的潮汐。
他孜孜不倦地研究光线的各种不同的折射角，颜色所产生的种种性质。
对于自然、历史和圣经，他是一个勤勉、敏锐的诠释者。
让人类欢呼，曾经存在过这样一位伟大的人类之光。
这位科学家是：A ．开普勒B ．牛顿C ．伽利略D ．卡文迪许3.2002年3月25日，北京时间22时15分，我国在酒泉卫星发射中心成功发射了一艘正样无人飞船，除航天员没有上之外，飞船技术状态与载人状态完全一致。
它标志着我国载人航天工程取得了新的重要进展，为不久的将来把中国航天员送上太空打下了坚实的基础。
这飞船是A ．北斗导航卫星B ．海洋一号C ．风云一号D 星 D ．神舟三号4.如图所示，有一箱装得很满的土豆，以一定的初速度在动摩擦因数为μ的水平地面上做匀减速运动，不计其它外力及空气阻力，则中间一质量为ｍ的土豆A 受到其它土豆对它的总作用力大小应是：A ．μmgB ．mg 21μ+C ．mg 21μ-D ．mg 12-μB 、C 、D 、E 、F 五个球并排放置在光滑的水平面上，B 、C 、D 、E 四个球质量相同，均为m=2kg ，A 球质量等于F 球质量，均为m=1kg ，现在A 球以速度v 0向B 球运动，所发生的碰撞均为弹性碰撞，则碰撞之后：A ．五个球静止，一个球运动 B. 四个球静止，二个球运动 C ．三个球静止，三个球运动 D ．六个球都运动6．一物体原来静置于光滑的水平面上。
第22届北京市高一物理竞赛决赛试题参考答案(印刷版)
第22届北京市高一物理（力学）竞赛决赛试题参考答案（北京四中杯）2009年5月24日一、填空题（共30分.每小题5分）1、1000)(1000210)90110(J xF W2、能滑动摩擦力做功只与水平位移有关，B A的水平位移相同。
mgxmgl cos3、3.13s1100360121t tt 1为加速时间13.31t s 舍去不合理的负值由于计算过程中有近似，故t=3.0s~3.4s 均可4、21212222gh gh t h h g x112gh v ，222gh v ，221122t v t v x ，t t t 21，解出：21212222gh gh h h g x5、233232241火地T T 3232322火地飞火火地地r r T rT rT2332322332328121火地火地T T T T T2332322412火地飞T T T t6、mg51竖直向下lv m l v m l mg l mg B A 3233233l v A ，l v B32，g l 59g a A53，g a B 56，质心C ：ga C109gmFmg10922mgF51二、计算题（共70分）7、法一：ma vv v t v v s62212121112sm a s v v a /4.1'2)(12122m a v v v t v v s144221212111222222233/45.1'2sm s a va v a 8、当0→2时任一时刻t 物体受的作用力为t F F 012，利用冲量定理：tF mV 1121mt F V 201。
当2时任一时刻t 物体受的作用力为：tF F 022利用冲量定理：220222121F tF F mV 2202242ttm F V 当t时速率：mF V20冲击力对物体所做总功为mF mVW8212229、对于球竖直方向：cosN mg (1)对于三角木块：1sin N N （2）以B 为支点：5.01N hN （3）以A 为支点：11N hN （4）由（1）（2）（3）得33minh 。
2021年周培源力学竞赛试题
2021年周培源力学竞赛试题2021年周培源力学竞赛试题共包括三个部分：力学知识运用、问题分析与解决、创新设计实践。
本文将为各位参赛选手详细介绍并提供解析。
【第一部分：力学知识运用】1. 在平面上有一木板，长为2m，宽为0.3m，质量为5kg。
一名体重为60kg的人静止站在木板的一端，使其与地面成60°角。
若木板与地面之间的静摩擦系数为0.2，则此人所站木板的重心距离木板底端的距离是多少？解析：首先计算木板受到的重力，即木板的质量乘以重力加速度。
然后计算该重力对应的力矩，即重力大小乘以重心距离木板底端的距离。
由于木板保持平衡，重力所产生的力矩必须等于静摩擦力对应的力矩。
通过解方程即可得到结果。
2. 一个质量为4kg的物体以速度3m/s沿斜面上滑，斜面的倾角为30°，无摩擦。
物体到达斜面上一点时，它的速度是多少？解析：根据题目所给条件，可以使用平行四边形法则来解决该问题。
将物体的速度分解为平行于斜面和垂直于斜面的两个分量。
然后，根据三角函数的关系计算出物体到达斜面上一点时的速度。
【第二部分：问题分析与解决】问题一：在一台电梯中，一个人物体的质量为60kg。
在电梯上升过程中，当电梯加速度为1.5 m/s²时，人物感受到的重力是多少？解析：根据牛顿第二定律，物体所受合力等于质量乘以加速度。
在这个问题中，合力即为人物所感受到的重力，而加速度等于电梯的加速度。
根据题目条件进行计算即可得到结果。
问题二：一个1000N的力施加在一个质量为200kg的物体上，物体受到的加速度是多少？解析：根据牛顿第二定律，物体所受合力等于质量乘以加速度。
在这个问题中，合力即为施加在物体上的力，质量为200kg。
代入公式进行计算即可得到结果。
【第三部分：创新设计实践】本部分主要涉及力学实践问题，如设计一个弹射器、建造一个简易桥梁等。
由于篇幅限制，无法在此详细展开。
参赛选手可根据具体试题要求进行设计，并需提供详细图纸或步骤说明。
2021年北京市高中力学竞赛预赛试卷及答案
北京市高中力学竞赛初赛试卷一、选取题（共44分，每小题4分）下列每小题均有四个备选答案，至少有一种答案是对的，请把所选答案前字母填在下面答案表内.每小题全选对得4分，选对但不全得2分，错选或不答均得0分.1、质点做匀变速直线运动，在这个运动过程中，如下说法对的是A.速度一定跟运动时间成正比B.位移一定跟运动时间平方成正比C.相等时间间隔内速度增量为定值D.相邻相等时间间隔内位移增量为定值2、从空中某高处将a球以v0初速度水平抛出，与此同步让另一球b开始自由落下，不计空气阻力。
如下说法中对的是A.以b球为参照系，a球做平抛运动B.以b球为参照系，a球做自由落体运动C.运动过程中，a球相对于b球速度为v0D.运动过程中，a球相对于b球加速度为03、在下列运动中，哪些物体处在失重状态A.汽车通过凸桥B.汽车通过凹桥C.处在减速下降电梯中物体D.处在人造地球卫星中物体4、小轿车在行驶过程中，乘客必要系安全带。
在下列哪些状况下安全带可以发挥安全保障作用A.小轿车高速行驶B.遇到紧急状况，小轿车急刹车C.遇到紧急状况，小轿车为躲闪其她车辆而拐弯D.小轿车迅速起动5、一均质球上A点与一细线连接，挂靠在竖直墙壁上，球处在平衡状态，如图1所示。
关于球对墙壁摩擦力下列论述，对的是A.球对墙壁摩擦力方向竖直向下B.球对墙壁摩擦力方向竖直向上C.球对墙壁无摩擦力D.无法拟定6、三角形滑块钉子O上悬挂一种单摆，如图2所示。
用O点正下方竖直线到单摆摆线所张角∠O l OP来拟定摆球位置，并规定逆时针旋转为正角，顺时针为负角。
当滑块沿倾角为α粗糙斜面滑下，达到稳定后，滑块沿斜面匀加速下滑，此时∠O l OP大小也许是A.∠O1OP≤0B.0<∠O1OP<αC.∠O l OP≥αD.无法拟定7、如图3所示，在一端固定轻弹簧下通过足够长细线吊一种小球处在静止。
然后将小球竖直拉下一段距离后由静止放手，讨论小球放手后始终向上运动至最高点过程中，小球上升速度和加速度变化状况是 A.加速度大小始终减小B.加速度大小先减小，再增大，最后也许恒定C.速度大小始终减小到零D.速度先增大，再减小到零8、（能量）在距地面高h处，将一种小球沿水平方向抛出，不计空气阻力，取地面为零重力势能面。
力学竞赛-第27届北京市高中力学竞赛预赛试卷参考答案
2/3
F
Fb
O
Ａ
PＢ
0
FbＢ Fa
O
P
F
90 127 Ａ Ａ
F P
O
Ｂ Fc
180 233
Fb P
Ｂ O
Ａ F Fa
0 90
Ｂ Fa
O
P
F
127 180 Ａ Ａ
F
P
O
Ｂ Fb Fc
233 270
O 90
Ｂ Fb Fa
P F
Ａ
F
O
ＢP
Ａ
180
Ａ
F
Fc
O
270
（8 分）
（4 分） （6 分）
23.（24 分）物块在 α 角的不同值时，物块的受力图如图 3 所示。（6 分） 设平台转动的角速度为 ，物块质量为 m，OP=R。物块固定在平台上做匀速 圆周运动，当 AB 与 OP 垂直时，即 90 ，弹簧对物块的压力等于盒 b 侧的压力， 则弹簧的压力 F=6N。（2 分） 当 AB 与 OP 方向一致时，物块做匀速圆周运动，受弹簧的压力和盒 b 侧的压 力 F1（16N），有 F1 F m2R =10N（2 分）；而侧壁 a、c 的压力均为 0。
127 ～ 233 范围内 Fb 都为 0；此后，α 角再增大，Fb 由 0 开始逐渐增大，直到 360 时，Fb 又达到 16N。 （5 分）
压力传感器 a、c 的示数 Fa 和 Fc：随角 α 由 0 开始增大，Fc=0，Fa m2R sin 逐渐增大，当 90 时 Fa m2Rsin m2R =6N；α 角继续增大时，Ｆa 开始减 小直到 180 时 Fa 减到 0，α 角在 0 ～180 范围内 Fc 都为 0；此后，α 角继续增 大 时 ， Fa 变 为 0 ， Fc m2Rsin ， Fc 由 0 开 始 增 加 ， 当 270 时 Fc m2Rsin m2R =6N；α 角继续增大时，Ｆc 开始减小直到 360 时 Fc 减 为 0，α 角在180 ～ 360 范围内 Fa 都为 0。（5 分）
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2021年高中力学竞赛决赛试题
（全卷满分150分） 2012年5月20日9:30~11:30
题 号
一 （填空）
二（计算题）
总 分
7
8 9 10 11 分 数 阅卷人 复查人
一、填空题（6小题，每小题8分，共48分）
1. 一跳远运动员在地球表面跳远，起跳时速度为10m/s ，能跳出7.5m 远. 已知月球表面的重力加速度是地球表面重力加速度的1/6，如果他在月球表面跳远，起跳速度大小也是10m/s ，他跳远的记录将是 m.
2. 一举重运动员能举起100kg 的重物，他对一根羽毛能施加1000N 的力吗？答： ，理由是 .
3. 嫦娥飞船绕月球做匀速圆周运动，测出其周期为T ，则飞船距月球表面的距离为h ，可否不计地球引力而近似表述为，其中M 是月球的质量，R 是月球半径. 答： ，理由是 .
4. 据北京晚报2012年3月17日和参考消息3月18日报道，奥地利勇士鲍姆加持纳从2.18万米高空的氦气球吊篮中跃下，下落的最高速度到163m/s.下落约3分43秒，距地面2400m 高处打开伞，整个下落到地面的时间持续8分8秒. 试根据报纸报道和你的分析，在图1中比较准确地画出奥地利勇士下落到地面过程的v-t 图线.
5. 下雨天，假设无风，雨滴以速度υ1竖直下落，雨滴在空中的分布是均匀的，单位体积的雨量是ρ. 如图2所示，一个人要
从A 处运动到B 处，他没有带伞，A 、B 的距离为l ，人的运动速度为υ2. 把人简化为长方体模型，头和肩的水平面积为S 1，身体前方正面的竖直面积为S 2. 则人从A 到B 过程中，打到面积S 1上的雨量为 ，打到面积S 2上的雨量为 .
得 分
v/m•s -1
t/s
图1
υ1
υ2
S 1
S 2
6. 三个质量均为m 的小球A 、B 、C ，用轻杆连接，如图3所示. A 、B 与B 、C 的距离相等，A 、B 、C 与地球中心O 在一条直线上. 三个小
球在高空绕地球做匀速圆周运动，如果轻杆收到扰动而偏离直线一小角度θ，则轻杆与直线的偏角θ将 （增大、减小、不变），理由是
.（本题说明控制卫星天线总指向地球的基本原理）
二、计算题（共102分）
7.（16分）两个相同的半球，半径都是r ，质量为0.5m ，放在静摩擦因数为μ = 0.5的水平面上. 在两个半球上放一个半径为r ，质量为m 的光滑球，如图4所示. 求在平衡状态下两球球心之间的最大距离b .
8．（16分）两个质量分别为和的小球，它们之间的相互作用表现为斥力（斥力大小表达式为，是常数，为两球之
间距离）. 现已知以速度接近，瞄准距离为b ，即到速度方向的垂直距离为b ，如图5所示. 求小球接近小球的最近距离d . 设，小球可近似看作静止.
图3
图4
9．（20分）如图6所示，质量为m 的小球，用不可伸长的线悬于固定点O ，线长为l ，初始线与铅垂线有一个夹角，初速为0. 在小球开始运动后，线碰到铁钉O 1. 铁钉的方向与小球运动的平面垂直. OO 1=h <l ，且已知OO 1与铅垂线
夹角为β，设与铅垂线夹角为. 假设碰后小球恰能做圆周运动. 求线与铁钉碰前瞬时与碰后瞬时张力的变化.
10. (25分) 如图7所示，理想滑轮（轻质，无摩擦）两端悬挂两个质量均为m 的砝码盘. 用轻线拴住劲度系数很大的轻弹簧（弹簧劲度系数为k ）两端使它压缩的长度为l ，将此弹簧竖直放在左侧砝码盘上，弹簧上放一质量为m
的砝码. 右侧砝码盘上也放置质量为m 的砝码，使两盘静止. 燃断轻线，轻弹簧达到自由伸展状态即与砝码脱离. 求（1）此系统（包括两个盘、两个砝码、弹簧和细绳）中哪些量守恒？（2）使用守恒定律求砝码脱离弹簧后升起的高度.
b
v d
得 分
得 分
图5
v
图6
O 1
β
l
O
11．（25分）三个质量为m 的小球用两根长为l 的不可伸长细绳相连. 初始时刻，三个小球在一条线上，静止放在光滑水平面上，标号分别为1、2、3，如图8所示. 给标号为3的小球以初速度，则这三个小球运动起来，求1、2
两球相遇时的速度为多大？
第25届北京市高中力学竞赛决赛试题答案
（北京四中杯）
一、填空题
1． 45 ．（8 分）
2． 不能 (2分)．一根羽毛不能对运动员施加1000N 的力，根据牛顿第三定律，运动员也不能对羽毛施加1000N 的力．（6
1 3 2
图8
分）
3．可以（2分）．在地球引力所用下，月球（携带飞船）绕地球做匀速圆周运动，可认为月球飞船处于失重状态，可只考虑月球对飞船的引力作用（6分）．
4．
5．；（4分） ．（4分）
6. 减少（2分），B 球受地球引力与惯性离心力平衡，A 球受引力大于惯性离心力，合力指向地球，C 球受引力小于惯性离心力，合力背向地球，A 、C 球受力的力矩使θ角减少（6分）．
二、计算题
7. 解：设最大距离时摩擦力为f max ，AB 球心连线 与竖直夹角θ．
对A 球y 方向： （3分）
对B 球y 方向： （3分）
对B 球x 方向： （3分） （1分） （3分）
（3分）
8．解：小球受力始终指向小球中心，小球在一平面内运
动．如图所示．设z 轴垂直于此平面且通过小球中心，则小球所受力对z 轴的力矩为零，即对z 轴角动量守恒．小球以速度v 0运动，对z 轴角动量是，但，故，小球最接近小球（距离为d ）时，即无继续向小球运动的速度，又无远离小球的速度，此刻的速度v 应与小球至小球的连线垂直，角动量是．于是 （1） （5分）
v
r
163
233
488
v/m•s -1
A
B C
O 地球
θ
mg
N B f max
y
x
N
得
在散射过程中，只有斥力作用，故能量守恒。
最初，其能量为动能，到达离小球最近时，其总能量为
，
后一项为斥力势能，k为一常数．因此，
（2）（5分）
有（1）（2）得
（4分）
d只能为正，故式中负号无物理意义，舍去．
（2分）
9．解：假设碰后小球能作圆周运动，运动到最高点的速度可由
（3分）
得出
设初始夹角为α
由机械能守恒得到：（5分）
假设碰前瞬时速度为v1
则：（2分）
碰前：（3分）
（3分）
（4分）
10.解：（1）该质点系能量守恒（3分），对滑轮轴的角动量守恒（2分）。
（2）设滑轮半径为R，弹簧释放后，弹簧上边的砝码获得的速度为v，方向向上，左边砝码盘及右边砝码盘及砝码获得的速度大小是v'。
该质点系对滑轮轴的角动量守恒，有：
- mvR+mv’R+2mv’R = 0，（6分）即v = 3 v' （1）（3分）
能量守恒（因为弹簧弹性系数很大，所以忽略重力势能的微小变化），有：（6分）
即（2）
左盘中的砝码脱离弹簧获得速度v后做竖直上抛运动
（3）（3分）
由⑴⑵可求得v2=3kl2/4m，代入⑶中得：
h = 3 k l2/8mg （2分）
11．解：设运动起来后三小球竖直方向速度大小为，1、2球相遇时速度大小为．由于是光滑水平面，所以运动起来前后动量守恒、能量守恒，有
（1）（10分）
（2）（10分）
解得（5分）。