部分析因(精)
析因设计与分析

合计
Tg (ΣX)
4.81
5.38
4.58
4.29
5.17 5.52
5.12
4.20 39.07
ΣX2 2.9403 3.6764 2.6768 2.3257 3.3729 3.8540 3.2914 2.2410 24.3785
A1
A2
B1
A1 B1
A2 B1
B2
A1 B2
A2 B2
2×2=4种处理
2019年10月22日
2×3析因设计
各因素各水平全面组合的设计
A
B
B1
B2
B3
A1
A1B1
A1B2
A1B3
A2
A2B1
A2B2
A2B3
2×3=6种处理
2019年10月22日
2×2×2析因设计
B1 A
C1
C2
B2
C1
C2
A1
A1B1C1 A1B1C2
A1B2C1 A1B2C2
A2
A2B1C1 A2B1C2
A2B2C1 A2B2C2
2×2×2 =8种处理
2019年10月22日
3×3析因试验举例
考察不同剂量考的松和党参对ATP酶活 力的作用。
A因素(考的松)
不用 低剂量 高剂量
不用 O B因素 低剂量 B1
高剂量 B2
A1 A1 B1 A1 B2
AB=[( a2b2- a1b2)-(a2b1- a1b1)]/2= (16-4)/2=6
AB=[( a2b2- a2b1)-(a1b2- a1b1)]/2=(22-10)/2=6
2019年10月22日
B
B1 (未用药) B2 (用药)
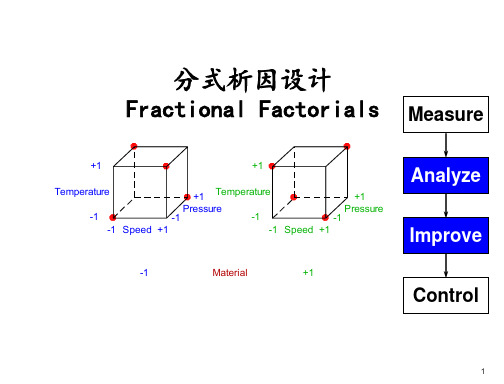
分式析因设计资料
1
1
1 P -1 1
11
T
1
-1 -1 S
2
1
1
P -1
1
-1
M
1
9
符号
分式析因设计的符号表示如下:
2
k R
p
• 2 --每个因素的水平数
• k --因素个数
• 2-p --分式大小 (p=1 1/2 分式,
分式, etc.)
p=2 1/4
• 2k-p --试验次数
• R -24-IV分1 辨度(resolution)
并估计这一变量关系. 注意:这一未知的真实方程式中, ST和PM 都很重要. ST和PM 呈别名关系. 该别名关系影响对过程模型的推导和解释?
15
线性组合
如用Minitab运行1/2方式析因设计, 将显示如下结 果(不包括误差)
Y 505 S 2.5T 1.9 S T 2.1 P M 真实模型
Term Constant S T P M S*T S*P S*M
Effect
10.000 5.000
-0.000 0.000
-8.000 -0.000
0.000
Coef 50.000
5.000 2.500 -0.000 0.000 -4.000 -0.000 0.000
Alias Structure
分式析因设计主要用于因素筛选:实验包含的因素相 对较多而试验次数相对较少
因素筛选实验通常在过程改进项目的初期实施
3
如何分配实验资源$$?
k=#
# main # 2 # 3 # 4 # 5 #6 #7
factors # runs effects ways ways ways ways ways ways
Design-Expert专题讲座-(-4-19)教学文案

3
优化 工艺
1.画三维效应面和二维等高线图; (Minitab和Origin ) 2.选取最优工艺,进行工艺验证
星点设计由二水平的析因设计加上中心点和星点组成。 (1) 析因设计部分:2k或2k×1/2,k是因素数 (2) 星点部分:star point, axial point 为各因素的极值水平
二项式拟合结果:
Y=-0.817+0.0229X1+ 0.585X2-0.00203X1X2-0.0467X22,R=0.9382
工艺验证
因素
X1/min X2/mL
26
5.7
预测值 /%
1.296
实测值 /%
1.160
偏差/% 10.49
参考文献及著作
1. 邱颖, 朱玲, 孙晓英. 星点设计-效应面优化法与正交设计和均 匀设计的比较及其在药剂研究中的应用 [J]. 海峡药学, 2011, 23(2): 18-19.
实验
1
设计 1. 筛选:单因素考察、正交设计或均匀设计;
2.设计: CCD法(Central Composite Design)或
BBD法(Box-Behnken Design)
模型
2 拟合 对模型进行多元线性和多项式拟合, 通过复相关系(R2)和P进行评判。 (SAS、SPSS、Statistica和Design Expert)
各因素实际值转变为编码制
各因素的编码制
按照实验设计进行试验,记录 每组因素组合的实验结果,填 在对应的Response列
点击Analysis下的R1:提取率
1.Tronsform选项卡,取 默认值
2.点击Fit Summary选项卡
Fit Summary选项卡,是 将数据模拟、建模、比 对,最终选择试验最佳 数学模型,再点击Model 选项卡
星点设计-效应面优化法(3)资料

OD 0.4825 0.2076 0.4430 0.2655 0.4938 0.4388 0.5193 0.5118 0 0 0.4284 0.4761 0 0.5054 0.4106
OD值的计算 Overall Desirability
总评“归一值”?
步骤:
(1)各效应分别求“归一值”(desirability)
MD 26.63 12.42 78.12 16.91 51.26 12.75 76.15 19.78 99.31 11.40 14.37 28.60 21.55 30.23 24.66
Span P1 t85 1.37 4.53 132.36 1.74 15.57 25.10 0.97 2.09 156.61 2.19 9.61 50.96 1.62 2.72 113.35 1.83 6.54 61.58 1.17 2.44 164.01 1.26 3.27 127.83 0.94 2.12 287.42 1.00 12.01 43.06 1.64 10.58 37.48 1.70 3.35 145.66 2.58 7.45 47.98 2.02 2.94 131.69 1.98 23.17 63.29
0.1134 6.95 61.23 0.1134 3.06 26.96 0.1134 7.64 67.37 0.1134 3.72 32.76 0.2866 20.24 70.61 0.2866 12.81 44.68 0.2866 23.41 81.66 0.2866 14.42 50.30 0.2000 16.90 84.50 0.2000 4.54 22.72 0.2000 9.18 45.89 0.2000 11.36 56.80 0.0500 1.75 34.92 0.3500 23.45 67.01 0.2000 10.89 54.46
析因设计 (2)

析因设计什么是析因设计?析因设计(也称为因果推断设计)是一种研究方法,旨在评估行为、政策、干预或其他变量对特定结果的因果关系。
该设计试图控制可能对结果产生影响的所有其他因素,以确定自变量对因变量的影响。
析因设计广泛应用于社会科学、医学和其他领域的实证研究中。
在析因设计中,研究者会通过引入特定的独立变量来干预研究对象,并仔细观察引发的结果变化。
这种设计允许研究者推断自变量和因变量之间的因果关系,并排除其他可能的解释因素。
析因设计的要素对于有效的析因设计,需要考虑以下几个要素:1. 分组研究对象通常被随机分成实验组和对照组。
实验组接受研究者的干预或处理,而对照组不接受干预。
分组是为了确保结果的可比性,并排除其他因素对结果的影响。
2. 随机化随机化是分组的关键部分。
随机分配实验对象可以降低个体差异对结果的影响,增加因果推断的有效性。
通过随机分组,研究者可以保证实验组和对照组在实验开始前具有相似的特征。
这有助于控制潜在的混淆变量。
3. 对照组对照组是未接受干预的组,用于与实验组进行比较。
对照组的存在有助于确定干预的真实效果,因为它提供了一个基准来评估实验组的变化。
4. 干预干预是研究者对实验组进行的操作或处理。
这可能是一种新的行为、政策、药物等。
干预应有明确的定义和操作程序,以便进行准确的评估。
5. 结果评估在析因设计中,研究者需要准确测量和评估结果。
结果评估应与研究问题和假设相关,并且应具有可重复性和客观性。
析因设计的优势和局限性析因设计具有以下几个优势:•因果推断:通过控制其他可能影响结果的因素,析因设计允许研究者进行因果推断,确定自变量对因变量的实际效果。
•可靠性和有效性:随机分组和对照组的设计使得研究结果更加可靠和有效,减少了外界因素的干扰。
适用性广泛:析因设计可以适用于各种研究领域和问题,包括社会科学、医学、心理学等。
,析因设计也存在一些局限性:•可行性限制:有时候,出于伦理或其他原因,不可能对自变量进行操纵或进行随机分组。
投石器实验报告数据处理部分

1.1运用doe部分析因设计生成实验表格进行实验并记录数据。
数据如下:1.2我们运用响应曲面回归分析:-------------------------------------------------------------------------- 距离(cm)与 A, B, C 。
其中,响应曲面回归:距离(cm)与A, B, C .其中,不能估计B*B ,C*C并且已经删除。
分析是使用已编码单位进行的。
我们得到如下回归方程:距离(cm)的估计回归系数系数标项系数准误T P常量233.67 21.03 11.112 0.000A 109.00 18.21 5.985 0.000B 45.25 18.21 2.485 0.035C 44.25 18.21 2.430 0.038A*A -32.17 27.82 -1.156 0.277S = 51.5109 PRESS = 93039.8R-Sq = 84.55% R-Sq(预测)= 39.79% R-Sq(调整)= 77.68%距离(cm)的方差分析来源自由度Seq SS Adj SS Adj MS F P回归 4 130641 130641 32660.1 12.31 0.001线性 3 127093 127093 42364.3 15.97 0.001A 1 95048 95048 95048.0 35.82 0.000B 1 16380 16380 16380.5 6.17 0.035C 1 15665 15665 15664.5 5.90 0.038平方 1 3548 3548 3547.5 1.34 0.277A*A 1 3548 3548 3547.5 1.34 0.277残差误差9 23880 23880 2653.4失拟 4 22911 22911 5727.7 29.54 0.001纯误差 5 969 969 193.9合计13 154521距离(cm)的异常观测值拟合值标准化观测值标准序距离(cm)拟合值标准误残差残差2 2 89.000 182.000 36.424 -93.000 -2.55 R14 14 490.000 400.000 36.424 90.000 2.47 R R 表示此观测值含有大的标准化残差距离(cm)的估计回归系数,使用未编码单位的数据项系数常量233.667A 109.000B 45.2500C 44.2500A*A -32.1667其中残差图如下:-------------------------------------------------------------------------------------------------------------------------------- 结论:响应曲面分析得到的结果非常不理想! 首先拟合方程的系数只有84.55%,说明这个拟合方程本身就非常不准确;其次,B*B 、C*C的交互影响不知道什么原因估计不了。
部分析因
实验的目的是确定以上因素中哪些是潜在关键‘少数’因素。 5个因素中每个因素的级别如下图所示。
因素
1.
填充速度
2.
催化剂
3.
搅拌
4.
温度
5.
浓度
低
高
10
15
1
1
1
B
1
1
-1
-1
1
A
22=4次实验
Factorial Design
1 1
B 1
-1 -1
1 1
A
1 1
1 -1
1
1 1
C
23=8次实验
1 1
1 1 1
Factorial Design
1
1
1
1
1 1
1 1
E
-1 1
1
B 1
-1 -1
1
1
1
1 1
1
1
1
1
1
C
1
-1
1 A
-1
D
1
25=32次实验
1 1
在实际操作中,由于实验顺序是随机的, ‘StdOrder’号会打乱。如果不在课堂上,始终随机 进行实验!
6.20
GE Appliances Copyright 1999
部分析因实验
将数据制图
创建主要影响图、交互作用图和立方图: Stat>DOE>
Factorial Plots...
选择和设置所有 图形
1 5 10 10 5 1 32次实验
观众在选择电影过程中的行为分析与建模
观众在选择电影过程中的行为分析与建模哈尔滨理工大学陈金凯、刘宇、杨航摘要随着国民收入及其生活质量的提高,精神娱乐生活的质量已经越来越受到人们的重视。
而观看电影已成为大部分人们精神生活中的重要组成部分。
近年来,我国电影票房呈现跨越式增长,票房的增幅使电影业吸收了大量的投资,为我国经济发展做出了巨大贡献。
而观众在选择电影过程中的行为影响着票房,所以我们有必要对观众行为进行准确深入的了解。
本文选取哈尔滨地区的普通电影观众作为研究对象.通过抽样调查问卷对观众选择行为进行测量、分析与建模.在对观众行为进行分析时,根据对所获得的调查问卷的统计分析,提出影响观众选择电影过程中的几个重要因素:上映档期、电影产地、演员与导演、以及电影题材,然后对以上几个因素进行建模分析。
本文首先根据实际调查研究的情况,用联合分析的方法构建起本文的观众从电影中获得的总效益模型;然后将实际调查研究的数据输入适于联合分析方法建模的专业统计软件(本文运用SPSS17。
0)进行建模和实际数据的分析,并结合聚类分析;最后通过最小二乘法进行参数估计,得出本文中上映档期、电影产地、演员与导演、电影题材等因素之间的关系以及影响效果。
通过本文的研究,对电影投资方正确进行自身定位、满足观众的需求以及提高票房收益具有指导意义。
关键词:电影联合分析聚类分析市场细分最小二乘法回归模型目录一、绪论 (1)(一)研究的目的与意义 (1)(二)研究对象及调查样本描述 (1)1.研究对象 (1)2.样本描述 (1)二、研究理论方法的简单介绍 (2)(一).联合分析的基本理论 (2)(二)联合分析常用的数据收集方法 (3)(三)聚类分析的基本理论 (3)三、研究框架和模型构建 (4)(一)研究框架 (4)(二)模型构建 (5)四、数据处理与模型分析过程 (6)(一)研究设计和数据收集 (6)1。
属性及属性水平的确定 (6)2。
电影组合的确定. (7)3.通过调查收集数据 (7)(二)数据分析结果 (8)1.个人层面效用系数分析及模型拟合优度的检验 (8)2.总体层面效用系数分析及模型拟合优度的检验 (12)3.男女分组的效用分析 (16)4。
部分析因设计法优化分散聚合制备单分散种子微球
其缺点是某些效应可能混杂,这可 以补做少量实验加以区分 。本文 即利用此法 ,获得粒径
为 1p 0a n的单分散 ( S =1 6 微球。 G D .) 0
・ 收 稿 日期 :20 05年 月 日 作 者简 介 :于 英豪(9 0 ) 18 一,男,山东 省人 ,硕士研 究生 .
验以微球的平均粒径为主要考察指标, G D为次要考察指标, 以 S 通过部分析因 设计, 获得 了
粒径为 1 1 的单分散 ( D t1 6 0ma GS . )微球 。 0
关键词:灌注色谱;分散 聚合;单分散;正丁醇;析因设计
中图分类号 :T 2 . 文献标识码 : Q4 53
维普资讯
离子交换与吸附, 0 6 2 ()2 4—2 0 2 0 , 23: 5 6
I ON EXCHANGE AND ADS 0RPr ON I
文章编号 :10 .4 32 0 )30 5-7 0 15 9 (0 60 .2 40
部分析 因设计 法优 化分散 聚合制备单分散种子微 球术
东理工大 学华 昌公司 ,用 前减 压蒸馏 后低 温保存 :偶 氮二异 丁腈 ( B :化学 纯 ,上海 AIN) 试 四赫维化 工 有 限公 司 ,用前无 水 乙醇进 行重 结晶 。 22 主要仪 器 . MP2 0 型 电子天 平 ,上海 天平 仪器 厂 ;K .0DE型 数控超 声波 发生 器 ,昆山市超 一0A Q 10 声仪器 有限 公司 ;Z . KJ1型循环 水 真空 泵 ,上海 嘉鹏 科技 有 限公司 ;D H .0 S Z 30型水 浴恒 温 振荡器 ,江 苏太 仓 实验 设备 厂 ;J 2 0 X.00型 显微 图像仪 ,成都精 新 粉体测 试 设备有 限公
析因设计与分析PPT课件
析因设计方法的提出(意义)
例:在评价药物疗效时,除需知道A药和B 药各剂量的疗效外(主效应),还需知道 两种药同时使用的交互效应。 析因设计及相应的方差分析能分析 药物的单独效应、主效应和交互效应。
2019年8月6日
2×2析因设计
2因素2水平全面组合
AB=[( a2b2- a2b1)-(a1b2- a1b1)]/2=(22-10)/2=6
2019年8月6日BB1ຫໍສະໝຸດ (未用药) B2 (用药)A
A1(未用药)
A2 (用药)
A1B1
A2B1
A1B2
A2B2
0 , a , b , ab 表示4个处理组A1B1,A2B1 ,A1B2,A2B2对应的总体均值
2019年8月6日
45
43
b1
b2
41
39
37
35
33
31
29
27
25
a1
a2
协同作用
2019年8月6日
45 43 41 39 37 35 33 31 29 27 25
a1
b1 b2
a2
拮抗作用
2019年8月6日
一级交互效应: 两个因素间 二级交互效应:三个因素间 设计特点:在一个实验设计里,既可分析 因素的单独效应,又可分析其交互效应。
B因素
A因素
A1
A2
B1
A1 B1
A2 B1
B2
A1 B2
A2 B2
2×2=4种处理
2019年8月6日
2×3析因设计
各因素各水平全面组合的设计
A
B
B1
B2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6.7
GE Appliances Copyright 1999
部分析因实验
修订版 10 1999年2月12日
部分析因设计的正交性
全析因实验 (23)“ 平衡” 且为正交。
注意: • 对于因素“ A” ,有4个 “-1’”和4
个 “1’” • 当“ A” 为“-1”,“B” 和 “C”有两
1
1 120
Factorial Design
1 1
1 1
Agitation
100
1
1 180
T em perature
140 1
1 Catalyst
6 1 C3oncentratio 2
10
Feedrate
1
1 15
2 1
1 1
OR
1
1 120
Factorial Design
1 1
1 1
Agitation
部分析因实验
修订版 10 1999年2月12日
会话窗口输出结果
在会话窗口中,Minitab将提供设计信息,包 括:
• 因素数量 • 区段数量 • 重复次数 • 混合因素信息
– 分辨率 – 别名结构
– 以后会有更多内容 (6.34-6.40页)。
1 1 1
1 1
B
1
1 1
C
1 -1
1 -1
-1
1
A
23=8次实验
Factorial Design
1 1 1
1 1
B
1 -1
-1
1 A
1 -1
1
1 1
C
23-1=4次实验
在全析因实验中,我们试验因 素的所有可能组合。
在部分析因中,我们选择部分 因素设置。
我们这样做的关键考虑因素是 如何选择检测哪个组合。
为何使用它?
用较少次数的实验检测大量的潜在X。
何时使用它?
• 筛选关键少数X时。 • 当由于经济原因而进行全析因实验较困难时。
部分析因是一种进行具有大量X实验的强大方法。
6.5
GE Appliances Copyright 1999
部分析因实验
修订版 10 1999年2月12日
部分析因设计
Factorial Design
但是,在实验早期, 选择不止 两三个候选变量是很正常的。
Factorial Design
1
1
1
B
1
1
-1
-1
1
A
22=4次实验
Factorial Design
1 1
B 1
-1 -1
1 1
A
1 1
1 -1
1
1 1
C
23=8次实验
1 1
1 1 1
Factorial Design
1
1
1
1
1 1
1 1
E
-1 1
100
1
1 180
T em perature
140 1
1 Catalyst
6 1 C3oncentratio 2
10
Feedrate
1
1 15
2 1
1 1
6.13
GE Appliances Copyright 1999
部分析因实验
修订版 10 1999年2月12日
部分析因设计标记
在全析因实验中:
基数 指数
个水平。
这是平衡的。矩阵图为正交,因为任何两栏的点积和都等于0。例如:
A
B
Product
-1
-1
1
1
-1
-1
-1
1
-1
1
1
1
-1
-1
1
1
-1
-1
-1
1
-1
1
1
1
Dot Product
0
如果我们将每个水平代码(1 & -1)的数相 乘,就得出一个点积值。如果将任何两栏 的点积值垂直相加,和将会是0。
在部分析因中,我们必须仔细选择实验来保持这种正交性。
GE Appliances Copyright 1999
部分析因实验
在Minitab中创建析因设计
修订版 10 1999年2月12日
在主对话框中,点击 ‘ Options...’ 调出子对话框。 仅对于课堂举例的一种情况,不点击‘ Randomize runs’ ! 点击两次‘ OK’
6.18
GE Appliances Copyright 1999
如果您思考22实验的设计阵列,将如 此图所示。
Run X1 X2 X1*X2
1 -1 -1 +1 2 +1 -1 -1 3 -1 +1 -1 4 +1 +1 +1 X1 和 X2 是因素。 X1*X2 是因素交互作用。
在实验中增加第三个因素情况会怎 样?如果对于整个实验运行 ½ 次的 实验,设置应怎样?
GE Appliances Copyright 1999
部分析因实验
修订版 10 1999年2月12日
在Minitab中创建和分析 部分析因设计
用创建全析因设计的同一个对话框。
Minitab确保设计的“ 正交性” -- 包括分区因素。
Minitab要求您确制定因素、实验次数和区段的数量。
在生成这些析因设计时,Minitab遵照Box, Hunter, and Hunter book, “Statistics for Experimenters”, 410页的内容。
部分析因实验
修订版 10 1999年2月12日
第6部分:
部分析因
6.1
GE Appliances Copyright 1999
部分析因实验
修订版 10 1999年2月12日
第 6部分: 部分析因
目的:
探求部分析因实验设计的概念,包括何时运用以及此方法的局 限性。
目标:
1. 解释为何使用部分析因实验,以及其用途的分支。 2. 描述部分析因DOE的术语。 3. 介绍部分析因DOE所用的术语 (混合、设计分辨率、别
+
*15
-
16
+
*17
-
18
+
19
-
*20
+
21
-
*22
+
*23
-
24
+
25
-
*26
+
*27
-
28
+
*29
-
30
+
31
-
*32
+
VARIABLE
2
3
4
-
-
-
-
-
-
+
-
-
+
-
-
-
+
-
-
+
-
+
+
-
+
+
-
-
-
+
-
-
+
+
-
+
+
-
+
-
+
+
-
+
+
+
+
+
+
+
+
-
-
-
-
-
-
+
-
-
+
---+ Nhomakorabea-
-
+
-
+
+
-
+
+
-
-
-
+
2 140
1
1 Cataly st
1 6
1 Concentratio 3
2
10
Feedrate
1 1
1 1
15
2 1
1 1
1 1
1 1
6.10
GE Appliances Copyright 1999
部分析因实验
修订版 10 1999年2月12日
设立模型方程式时,未知参数的估计为系数(‘b’s):
Y = b0 + b1X1 + b2X2 + b12X12 + . . .+ 误差 ‘参数估计值’
-
-
+
+
-
+
+
-
+
-
+
+
-
+
+
+
+
+
+
+
+
RESPONSE
(% reacted)
5
y
Product
-
61
-
-
53
+
-
63
+
-
61
-
-
53
+
-
56
-
-
54
-
-
61
+
-
69
+
-
61
-
-
94
-
-
93
+
-
66
-
-
60
