材料力学绪论
材料力学各章重点内容总结

材料力学各章重点内容总结第一章 绪论一、材料力学中工程构件应满足的3方面要求是:强度要求、刚度要求和稳定性要求。
二、强度要求是指构件应有足够的抵抗破坏的能力;刚度要求是指构件应有足够的抵抗变形的能力;稳定性要求是指构件应有足够的保持原有平衡形态的能力。
三、材料力学中对可变形固体进行的3个的基本假设是:连续性假设、均匀性假设和各向同性假设。
第二章 轴向拉压一、轴力图:注意要标明轴力的大小、单位和正负号。
二、轴力正负号的规定:拉伸时的轴力为正,压缩时的轴力为负。
注意此规定只适用于轴力,轴力是内力,不适用于外力。
三、轴向拉压时横截面上正应力的计算公式:N FAσ= 注意正应力有正负号,拉伸时的正应力为正,压缩时的正应力为负。
四、斜截面上的正应力及切应力的计算公式:2cos ασσα=,sin 22αστα=注意角度α是指斜截面与横截面的夹角。
五、轴向拉压时横截面上正应力的强度条件[],maxmax N F Aσσ=≤六、利用正应力强度条件可解决的三种问题:1.强度校核[],maxmax N F Aσσ=≤一定要有结论 2.设计截面[],maxN F A σ≥3.确定许可荷载[],maxN F A σ≤七、线应变ll ε∆=没有量纲、泊松比'εμε=没有量纲且只与材料有关、 胡克定律的两种表达形式:E σε=,N F ll EA∆=注意当杆件伸长时l ∆为正,缩短时l ∆为负。
八、低碳钢的轴向拉伸实验:会画过程的应力-应变曲线,知道四个阶段及相应的四个极限应力:弹性阶段(比例极限p σ,弹性极限e σ)、屈服阶段(屈服极限s σ)、强化阶段(强度极限b σ)和局部变形阶段。
会画低碳钢轴向压缩、铸铁轴向拉伸和压缩时的应力-应变曲线。
九、衡量材料塑性的两个指标:伸长率1100l llδ-︒=⨯︒及断面收缩率1100A A Aϕ-︒=⨯︒,工程上把5δ︒≥︒的材料称为塑性材料。
十、卸载定律及冷作硬化:课本第23页。
材料力学课件第一章绪论

§1.3 外力及其分类 3 一、外力 周围物体对构件的作用。 周围物体对构件的作用。 二、外力分类 按作用方式划分: 1.按作用方式划分: 集中力 表面力 外力 线分布力 面分布力 体积力( 重力,惯性力) 体积力(如:重力,惯性力)
2.按作用趋势划分: .按作用趋势划分: 静载荷 主动力, 主动力,又称为载荷 动载荷 外力 约束力
∑ 由:
Fy = 0, F − FN = 0
o
∑M
= 0, Fa− M = 0
FN = F 得:
M = Fa
三、应力(stress) 应力 1 . 定义 截面内某一点处分布内力的集度称为该点的应力。 定义: 截面内某一点处分布内力的集度称为该点的应力。 2 . 定义式: 定义式:
∆F 平均应力: 平均应力: pm = ∆A
§1.6 杆件变形的基本形式
一、杆件(bar)的概念 杆件 的概念 1. 构件类型: 构件类型: 杆: 板: 壳: 块:
2. 杆件的两个要素: 杆件的两个要素: 轴线 3. 杆件分类: 杆件分类: 横截面 等截面直杆,变截面直杆,等截面曲杆,变截面曲杆。 等截面直杆,变截面直杆,等截面曲杆,变截面曲杆。 吊车图
MN → 0
M ′N ′ − MN ∆s = lim MN MN → 0 ∆ x
ቤተ መጻሕፍቲ ባይዱ
γ = lim
ML →0
π − ∠L′M ′N ′ MN →0 2
三、小变形问题的计算 1. 特点: 特点: 位移、变形和应变都是微小量。 位移、变形和应变都是微小量。 2. 采用简化计算: 采用简化计算: 原始尺寸法。 如:原始尺寸法。
∆F lim lim 应力: 应力: p = ∆A→0 pm = ∆A→0 ∆A
材料力学_江晓禹_第一章绪论
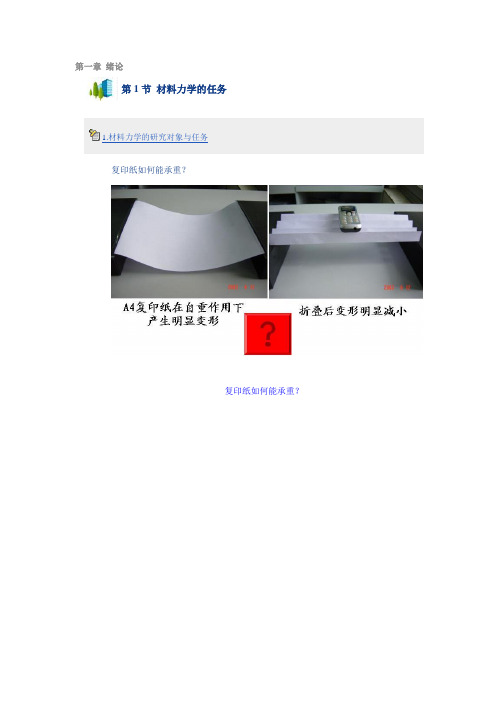
第一章绪论第1节材料力学的任务1.材料力学的研究对象与任务复印纸如何能承重?复印纸如何能承重?高层建筑如何确定其立柱和横梁机车转向架为何要用这样的刚材跨海大桥为何要用这样的结构形式高水平公路建设中桥梁的立柱该如何设计材料力学的研究对象构件大致分为杆、板、壳、块体材料力学的研究内容就是杆件的强度、刚度与稳定性。
•强度:材料抵抗破坏的能力。
而破坏可分为:1 )断裂2 )明显的塑性变形当出现这样的破坏,我们大家都知道,是不能继续使用了。
•刚度:抵抗变形的能力。
下图桥梁在小车经过时不会发生过大的变形,因此,我们知道它是可以正常使用的。
桥梁在小车经过时不会发生过大的变形下图桥梁在小车经过时发生了过大的变形,它还能正常使用吗?明显的塑性变形•稳定性:保持稳定的平衡状态的能力。
很高的桥墩如单从强度上考虑,并不需要建造的这么粗,但实际上对受轴向压缩的杆件,还需要考虑稳定性要求。
很高的桥墩还需要考虑稳定性要求第2节材料力学的基本假设1.材料力学的几个重要基本假设(1) 均匀连续性假设材料是均匀连续分布的。
(2) 各向同性假设材料在各个方向的力学性能相同。
(3) 小变形假设材料力学要研究变形、计算变形;变形与构件的原始尺寸相比很小;受力分析按照构件的原始尺寸计算。
如下图,在杆件变形后,应是虚线构成的位置,但材料力学实际计算时,根据小变形假设,仍取原始位置(实线)来计算,因此,可得:小变形第3节杆件变形的基本形式1.杆件变形的基本形式分类材料力学中,根据杆件发生的变形主要可分为以下四类:1. 轴向拉伸或压缩——主要出现在:拉(压)杆轴向拉伸或压缩2. 剪切——一般与其它形式混合出现剪切3. 扭转——主要出现在:轴扭转4. 弯曲——主要出现在:梁弯曲杆件变形的基本形式分类第4节课程的主要内容1.需学习的课程主要理论内容和实验内容1 .理论学习:( 1 )基本部分:•绪论;•轴向拉伸和压缩;•扭转;•弯曲内力;•弯曲应力;•梁弯曲时的位移。
材料力学(单辉祖)第一章绪论

F1
F2
力集
中
42
3. 作用范围:集中力、分布力 桥面 板作 用在 钢梁 的力
分 布 力
43
4. 时间特性:静载载荷、运动载荷
箱梁:静载试验 活塞连杆受力:运动载荷
44
二、内力与截面法
1. 内力 当物体受到外力作用而变形时,物体内部 各质点的相对位置将发生变化,从而导致 构件内部相邻两部分之间产生附加作用力 构件承载能力与内力大小及其分布有关
22
4. 材料力学的任务
材料力学是固体力学的一个分支,主要 研究构件在外力作用下的变形、受力、 破坏规律,为合理设计构件提供有关强 度、刚度与稳定性分析的理论依据。 近代新问题 疲劳问题 断裂问题
23
疲劳破坏
24
弥散型核燃料棒
核燃料颗粒在基体中的分布
核燃料构件的肿胀破坏 核燃料构件的裂纹生长
物理量连续函数表示; 极限分析的应用
注1:点的概念
数学:没大没小 物理:有大小;物质点---物质微团
微观足够大、宏观足够小
微团大小:微米级---纳米级
32
注2: 连续性保证变形前连续的构件在变形后仍然是连续的
物质不灭
哥伦比亚号左翼上两条裂纹
33
2. 物性假设(个性)
一定的力 一定的变形 Hooke’s Law 1676以拉丁字谜形式发表
45
2. 如何研究内力
由于内力是物体内部的力,只有将物体 假想地截开,并将其显示地表现出来, 才能确定内力的大小及其方向
截面m-m
46
截
m F1 F3 ቤተ መጻሕፍቲ ባይዱn
杆件上有外力F1,F2,Fn 截面m-m将杆件假想截开
材料力学课件第一章绪论1-2

也记为εx 。 (重点掌握)
同理可定义εy , εz 。 线应变,即单位长度上的变形量, 为无量纲量,其物理意义是构件上一点 沿某一方向(相对)变形量的大小。
正交线段MN和ML经变形后,分别是 M' N'和M' L' 。变形前后其角度的变化是:
L' L
N'
弹性体—内力特点 内力是变形引起的物体内部附加 力,内力不能是任意的,与外力引起 的变形有关,还必须满足平衡条件。
(3)分布内力系向截面的形心简化得 截面的合内力主矢FR与主矩MC。
m
z
x
C m
y
内力主矢FR与内力主矩MC按一定的坐标系 (空间)分解成内力分量FN( MX矢量表示)与 截面垂直,FSy, FSz ( My , Mz矢量表示)与截 面相切。
应力量纲 1 Pa = 1 N/m2
[力] / [长度]2
单位— Pa (帕) ( Pascal帕斯卡) 1KPa = 103 Pa 1MPa = 106Pa 1GPa = 109 Pa
材料力学
常用单位
重点掌握
5
变形与应变的概念
对于构件上任“一点” 材料的变形, 只有线变形(线段伸长,缩短)和角变 形(两线段夹角的改变)两种基本变形, 它们分别由线应变和角应变来度量。
平面表示 L Δy L′
N′ Δx
M
N
M′
Δx+ Δu
变形前
变形后
L'
Δy+Δv
MN的绝对变形 M ' N ' MN u
L N'
Δy
M'
Δx
材料力学第1章 绪论

F F Fy 0, F FN 0
MON 0, Fa M 0
பைடு நூலகம்M Fa
应力
截面上,微小面积ΔA上分布内力的合力为ΔF,则平均应力为
pm
F A
当ΔA逐渐缩小,pm的大小和方向都将逐渐变化。 当ΔA趋近于零时,pm的大小和方向都将趋近于某极限值。
lim lim p
pm
A0
A0
F A
(用截面法:一截二取三平衡)
•解(1)沿m-m假想地将钻床分成 两部分。
•研究m-m截面以上部分(如图 1.2b),并以截面的形心O为原点, 选取坐标系如图所示。
•(2)外力F将使m-m见面以上部分
沿y轴方向位移,并绕O点转动,m- (3)由平衡方程
m截面以下部分必然以内力FN及M 作用于截面上,以保持上部的平衡。
建立力学模型:
轴向拉伸
轴向拉伸
轴向压缩
轴向压缩 弯曲
认 销 C处为钉的B重、螺量C栓W理连位想接于化,构为其架光约A滑B束C销既平钉不面。像内光,滑因销此钉可可作自为由平转面动力,系也问不题像来固定端那 处 样理毫。无转动的可能,而是介于两者之间,并与螺栓的紧固程度有关。
构件的强度、刚度和稳定性( C )。
构件 结构
——组成结构物和机械的单个组成部分(建筑物的 梁和柱,机床的轴)。 ——建筑物或构筑物中承受外部作用的骨架称为结构.
构件正常工作的条件:
足够的强度 足够的刚度 足足够够的的稳稳定定性性
强度:构件抵抗破坏的能力
不因发生断裂 或塑性变形而失效
刚度:构件抵抗弹性变形的能力
不因发生过大的弹性变形而失效
稳定性:构件保持原有平衡形式的能力
不因发生因平衡形式的突然转变而失效
力学课件材料力学第一章 绪论.doc

第一章绪论在理论力学中,主要研究了物体在载荷作用下的平衡和运动规律。
但对物体是否能承受载荷,或者说在载荷作用下物体是否会失效这个问题并没有回答,而这是物体平衡和运动的前提。
这个问题正是材料力学所要研究和试图解决的。
在本章则主要讨论材料力学的研究对象和任务,初步建立起变形固体的…些基本概念,为后面的学习打下基础。
第一节变形固体及其理想化由于理论力学主要研究的是物体的平衡和运动规律,因此将研究对象抽象为刚体。
而实际上,任何物体受载荷(外力)作用后其内部质点都将产生相对运动,从而导致物体的形状和尺寸发生变化,称为变形。
例如,橡皮筋在两端受拉后就发生伸长变形;工厂车间中吊车梁在吊车工作时,梁轴线由直变弯,发生弯曲变形。
可变形的物体统称为变形固体。
物体的变形可分为两种:一种是当载荷去除后能恢复原状的弹性变形;另一种是当载荷去除后不能恢复原状的塑性变形。
工程中绝大多数物体的变形是弹性变形,相应的物体称为弹性体。
如果物体的弹性变形大小与载荷成线性关系,则称为线弹性变形,相应的物体材料称为线弹性材料。
大多数金属材料当载荷在一定范围内产生的是线弹性变形。
变形固体的组织构造及其物理性质是十分复杂的,在载荷作用下产生的物理现象也是各式各样的,每门课程根据自身特定的目的研究的也仅仅是某…方面的问题。
为了研究方便,常常需要舍弃那些与所研究的问题无关或关系不大的属性,而保留主要的属性,即将研究对象抽象成•种理想的模型,如在理论力学中将物体看成刚体。
在材料力学中则对变形固体作如下假设:1.连续性假设。
假设物质毫无空隙地充满了整个固体。
而实际的固体是由许多晶粒所组成, 具有不同程度空隙,而且随着载荷或其它外部条件的变化,这些空隙的大小会发生变化。
但这些空隙的大小与物体的尺寸相比极为微小,可以忽略不计,于是就认为固体在其整个体积内是连续的。
这样,就可把某些力学量用坐标的连续函数来表示。
2.均匀性假设。
假设固体内各处的力学性能完全相同。
材料力学-绪论

A
B
d
l 题2图
-1-
第一章 绪论
班级学号Βιβλιοθήκη 姓名3 图示三角形薄板因受外力作用而变形,角点 B 铅垂向上的位移为 0.03mm,但 AB 和 BC 仍保持为直线。试求沿 OB 的平均应变,并求 AB 与 BC 两边在 B 点的角度改变。
题3图
4 圆形薄板的半径为 R,变形后 R 的增量为Δ R。若 R=80mm,Δ R=3×10-3mm,试 求沿半径方向和外圆圆周方向的平均应变。
第一章 绪论
班级
学号
姓名
1 在图示简易吊车的横梁上,F 力可以左右移动。试求截面1-1和2-2上的内力及 其最大值。
题1图
2 拉伸试样上 A、B 两点的距离 l 称为标距。受拉力作用后,用变形仪量出两点距离的增
量 l 5102 mm 。若 l 的原长为 100mm,试求 A 与 B 两点间的平均应变 m 。
题4图
-2-
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2. 剪切 P
P
33
3. 扭转
4. 弯曲 若同时发生几种基本变形,则称为组合变形。
34
刚度:构件抵抗弹性(可恢复)变形的能力
不因发生过大的弹性变形而失效,例如机床主轴不应变形过 大,否则影响加工精度。
足够的稳定性 稳定性:构件保持原有平衡形式的能力
不因发生因平衡形式的突然转变而失效,例如柱子不能弯等。
11
工程构件的强度、 刚度和稳定问题
强度问题
12
工程构件的强度、刚度和稳定问题
垮塌后的彩虹桥 强 度 问 题
材料力学
上海海事大学
2020年10月16日
1
第一章 绪 论
本章内容: 1 材料力学的任务与研究对象 2 材料力学的基本假设 3 外力与内力 4 应力 5 应变 6 胡克定律
2
§1. 1 材料力学的任务与研究对象
本节内容: 1 基本概念 2 材料力学的任务 3 材料力学与工程问题 4 材料力学的研究方法
13
工程构件的强度、刚度和稳定问题
刚 度 问 题
14
压杆的弹性稳定性 分析与稳定性设计
工程背景
压杆
15
压杆的弹性稳定性分 析试验
工程背景
16
2 材料力学的任务 1)研究构件的强度、刚度和稳定性; 2)研究材料的力学性能; 3)为合理解决工程构件设计中安全性与经济性
之间的矛盾提供力学方面的依据。 3 材料力学与工程问题
24
大型桥梁
25
大型水利工程设施
长 江 三 峡 工 程
26
海洋石油钻井平台
27
4 材料力学的研究方法 理论分析方法 探索新理论、新设计、新结构。 实验方法 新理论、新设计、新结构的实验研究或验证。 实验方法在材料力学中占有重要地位。 计算机方法 用计算机和现代计算技术研究材料力学问题。
28
§1. 2 材料力学的基本假设
8
材料力学中,主要研究杆件。
轴线为直线的杆: 直杆;
轴线为曲线的杆: 曲杆;
横截面的大小形状 不变的杆:等截面杆; 否则: 变截面杆。 等截面直杆 等直杆。
9
工程中多为梁、杆结构
构件正常工作的条件:
足够的强度
强度:构件抵抗破坏的能力
不因发生断裂 或塑性变形而失效,例如储气罐不应爆破。
足够的刚度
在材料力学中,对变形固体作如下假设: 1. 连续性假设铸铁的显微组织
29
普通钢材的显微组织 优质钢材的显微组织
2. 均匀性假设: 认为物体内的任何部分,其
力学性能相同、均匀分布。
3. 各向同性假设:认为物体在各个不同方向上
各向异性
3
真正解决问题,还是材料力学形成以后
达.芬奇(Leonardo da Vinci, 1452-1519) 开始着手解决构件的强度计算问题
伽利略(Galilei, 1564-1642) 两种新的科学(Two New Science) 尝试用解析法求解构件的安全尺寸 从那时起,材料力学在奠基
长期的积累、发展,逐渐完善形成 材料力学
6
1 基本概念 理论力学 研究刚体,研究力与运动的关系。 材料力学 研究变形体,研究力与变形的关系。
材料力学:是研究工程构件在载荷作用下的内效 应,确定构件在正常工作条件下承载能力的科学
构件: 构成结构物和机械的 单个组成部分
7
1 基本概念 构件: 组成结构物和机械的单个组成部分。 构件的分类:杆;板、壳体;块体。
大量的工程问题需要用到材料力学的理论和方 法。
17
航 空 航 天 工 程
Space Shuttle Discovery 18
飞行器
19
前起落架锁连杆安装螺栓(销子)发生断裂。
20
高层建筑
21
大型桥梁
江阴长江大桥
缆索
拉杆
承力柱
桥面
22
江阴长江大桥
缆索
长度可调的拉杆 防撞护栏
23
江阴长江大桥的缆索
的力学性能相同。
30
3. 各向同性假设:认为物体内在各个不同方向 上的力学性能相同。
4.小变形假设: 认为构件的变形极其微小, 比构件本身尺寸要小得多。
31
小变形的要点: 1 在列平衡方程求力时,可忽略变形,仍用
变形前的形状和尺寸。 原始尺寸原理 2 在变形分析时,可以直线代曲线。
32
在工程结构中,杆件的基本变形有四种形式。 1. 拉伸或压缩
