五年级奥数几何专项二十三 表面涂色与三视图(2)
2018五年级奥数.几何.长方体与正方体表面涂色与三视图(B级).学生版
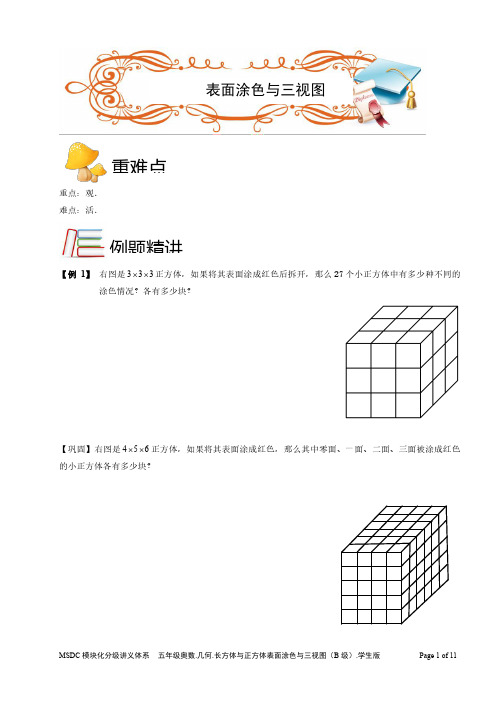
重难点重点:观.难点:活.例题精讲【例1】右图是333⨯⨯正方体,如果将其表面涂成红色后拆开,那么27个小正方体中有多少种不同的涂色情况?各有多少块?【巩固】右图是456⨯⨯正方体,如果将其表面涂成红色,那么其中零面、一面、二面、三面被涂成红色的小正方体各有多少块?表面涂色与三视图【例2】将一个表面积涂有红色的长方体分割成若干个棱长为1厘米的小正方体,其中一面都没有红色的小正方形只有3个,求原来长方体的表面积是多少平方厘米?【巩固】一个长方体,六个面均涂有红色,沿着长边等距离切5刀,沿着宽边等距离切4刀,沿着高边等距离切_______次后,要使各面上均没有红色的小方块为24块.欢迎关注:奥数轻松学余老师薇芯:69039270【例3】将长为5,宽为3,高为1的长方体木块的表面涂上漆,再切成15块棱长为1的小正方体。
则三个面涂漆的小正方体有________块。
【巩固】将8个相同的小正方体拼成一个体积为8立方厘米的长方体,表面涂上漆,然后分开,则3个面涂漆的小正方体最多有_________个,最少有________个。
【例4】将16个相同的小正方体拼成一个体积为16平方厘米的长方体,将表面涂漆,然后分开,结果,其中2面涂漆的小正方体有8个,那么3面涂漆的小正方体有__________个,4面涂漆的小正方体有__________个。
【巩固】把一个大长方体木块表面上涂满红色后,分割成若干个同样大小的小正方体,其中恰好有两个面涂上红色的小正方体恰好是100块,那么至少要把这个大长方体分割成多少个小正方体?欢迎关注:奥数轻松学余老师薇芯:69039270【例5】有一个3×4×5的长方体,先把其中相邻的两个面染红,再把它切成60个1×1×1的小正方体,请问:这些小正方体中最多有多少个是恰有一个面被染红的?【巩固】有6个相同的棱长分别是3厘米、4厘米、5厘米的长方体,把它们的某些面染上红色,使得有的长方体只有1个面是红色的,有的长方体恰有2个面是红色的,有的长方体恰有3个面是红色的,有的长方体恰有4个面是红色的,有的长方体恰有5个面是红色的,还有一个长方体6个面都是红色的,染色后把所有长方体分割成棱长为1厘米的小正方体.分割完毕后,恰有一面是红色的小正方体最多有多少个?【例6】有64个边长为1厘米的同样大小的小正方体,其中34个为白色的,30个为黑色的.现将它们拼成一个444⨯⨯的大正方体,在大正方体的表面上白色部分最多可以是多少平方厘米?欢迎关注:奥数轻松学余老师薇芯:69039270【巩固】有l25个同样大小的正方体木块,木块的每个面的面积均为1平方厘米,其中63个表面涂上白色,还有62个表面涂上蓝色。
(完整版)五年级立体几何拓展----三视图专属奥数讲义

学科教师辅导讲义班级:年 级: 五年级 辅导科目:小学思维学科教师:上课时间授课主题 立体几何拓展----三视图一.三视图在观察物体的时候,我们往往可以从不同的角度进行观察.角度不同,看到的风景就会不同.比如:我们可以从正面看,上面看,左面看,看到的图形分别称为正视图,俯视图和左视图.并且容易发现:正面看和后面看,上面看和下面看,左面看和右面看得到的图形是知识图谱错题回顾三视图知识精讲相同的.对于较复杂的立体图形,通过三视图法往往可以很方便地计算出表面积. 二.正方体的展开图我们采用不同的剪开方法,共可以得到下面11种展开图.三.长方体的展开图观察上图可以发现,长方体的展开图由6个长方形组成,相对面的面积相等,即上面=下面=长×宽,左面=右面=宽×高,前面=后面=长×高. 四.判断图形折叠后能否围成长方体或正方体的方法.判断一个图形折叠后能否围成正方体或长方体,首先,要依据它们各自展开图的特点判断;其次,可以运用空间想象或实际操作进一步判断.重难点:展开图、三视图及三视图求个数和表面积.上 后 前右左下 展开后由上、下、左、右、前、后六个正方形面组成,这六个正方形面的面积都相等.高宽长右面左面 后面下面 前面 上面三点剖析题模精选题模一:展开图与对立面例1.1.1 一个正方体的六个面上分别写着A ,B ,C ,D ,E ,F 六个字母.请你根据图中的三种摆放情况,判断每个字母的对面是______________,______________,______________【答案】 B 与D 相对,E 与A 相对,C 与F 相对 【解析】 由于正方体的6个面上写了6个不同的字母,那么每个字母在正方体的面上只能出现1次,如果2个字母在相邻的面上出现,那么它们一定不能相对.第一步,先看前2种摆放情况:在这2种摆放情况中,只有字母B 出现了2次,那么由第一种摆放可知,B 不与A 相对,也不与F 相对;由第二种摆放可知,B 不与C 相对,也不与E 相对.那么在所有的字母中,B 只能与D 相对.第二步,再看后2种摆放情况:在这2种摆放情况中,只有字母E 出现了2次,那么由第二种摆放可知,E 不与B 相对,也不与C 相对;由第三种摆放可知,E 不与D 相对,也不与F 相对.那么在所有的字母中,E 只能与A 相对.正方体有三个对面,因B 与D 相对,E 与A 相对,那么第三组对面上一定是C 与F 相对.例1.1.2 图中的四个正方体标字母的方式是完全相同的,请你利用图中已知的信息,判断A 、B 、C 的对面分别标的是哪个字母?【答案】 A 的对面标有D ,B 的对面标有F ,C 的对面标有E【解析】 由已知条件,标有C ,D 的两个面不能相对,那么或A 的对面标有D ,或B 的对面标有D .如果标有D ,A 的两个面相对,那么“标有C ,D 的两个面不能相对”,“标有E ,A 的两个面也不能相对”这两个条件都可以满足.注意到当D 在朝右的面,E 在朝上的面时,F 在朝前的面上,那么只能是标有E ,C 的两个面相对,而标有F ,B 的两个面相对.经检验,这种情况满足题目要求.如果标有D ,B 的两个面相对,那么由于标有E ,A 的两个面也不能相对,于是标有A 的对面就是标有F 的面,而标有C 的对面就是标有E 的面.此时D 在朝后的面上,E 在朝左的面上,F 在朝下的面上.我们把六面体旋转,把D 转到朝右的面,并把E 转到朝上的面,BFA EBC FED A BCD CCEAEF D此时朝前的面上标的是A ,而朝后的面上标的是F ,与题意不符.综上所述,满足题意的答案只有一个:A 的对面标有D ,B 的对面标有F ,C 的对面标有E .例1.1.3 如图,第1个方格内放着一个正方体木块,木块六个面上分别写着ABCDEF 六个字母.其中A 与D 相对,B 与E 相对,C 与F 相对.现在将木块标有字母A 的那个面朝上,标有字母D 的那个面朝下放在第1个方格内,然后让木块按照箭头指向,沿着图中方格滚动,当木块滚到21格时,木块向上的面上写的是哪个字母?【答案】 字母A【解析】 发现木块向左滚4格后,各个面上标的字母与初始时的情况完全一致.那么木块朝其它方向滚时也有类似的情况,即木块向任意方向连滚4格,它的各个面上标的字母不变. 所以木块向左滚4格到第5格时,各个面上标的字母与在第1格时的情况完全一致.再向下滚4格到第9格,再向右滚4格到第13格,再向下滚4格到第17格,最后向左滚4格到第21格,每次都是朝同一方向滚4格,因此在第5格,第9格,第13格,第17格,第21格木块向上的面上总是写的字母A .例1.1.4 如图,在一个正方体的表面上写着1~6这6个自然数,并且1对着4,2对着5,3对着6.现在将正方体的一些棱剪开,使它的表面展开图如图所示.如果只知道1和2所在的面,那么6应该在哪个面上(写出字母代号)?【答案】 A【解析】 对于立方体展开图,我们可以把任一个面当作底面,把它还原成立方体的表面.如图1,观察虚线圈住的部分,可以发现写有1,A ,B 的三个面两两相邻;再观察图2的虚线圈住的部分,发现写有A ,B ,C 的三个面也两两相邻.此时,写有1的面与A 面,B 面都相邻,C 面也与A 面,B 面都相邻,因此写有1的面与C 面相对,即C 面上写的是4.1 AB C 2D 3 121A B C 2D1A B C 2D1与C 相对,C 面上写的是421 5920 19观察图3中的虚线圈住的部分,容易看出写有2的面与B 面相对,因此B 面上写的是5.则立方体展开图就如图4所示.还剩下A 面与D 面上的数字没有确定,这两个面上分别写有3和6.由于写有1的面,写有5的面与A 面两两相邻,把这三个面还原到立方体中.在图2所示的立方体中,5与2相对,在立方体朝左的侧面上;1在朝前的侧面上.在展开图中以写有1的面为朝前的侧面,A 面为下底面,则写有5的面恰好在朝左的侧面上.此时写有1的面,写有5的面都对齐了,而原立方体中下底面写有数字6,因此A 面上就是6.例1.1.5 下图是正方体,四边形APQC 是表示用平面截正方体的截面,截面的线表现在展开图的哪里呢?把大致的图形在右面展开图里画出来.【答案】 见解析【解析】 截线在展开图中如图所示:例1.1.6 右图是一个立体图形的平面展开图,图中的每个小方格都是边长为1的正方形.现在将其沿实线...折叠,还原成原来的立体图形,那么立体图形的体积等于_________. 图3 1A B 4 2D2与B 相对, B 面上写的是5图41 A 54 2DBPEAD CB GHQFAEDCB HGFA . 3B . 4C . 5D . 6 【答案】B【解析】 根据实线还原,体积为4. 题模二:三视图求表面积例1.2.1 下图是由5个相同的正方体木块搭成的,从上面看到的图形是( ).A . A 图B . B 图C . C 图D . D 图【答案】C【解析】 5个在原图均已看到,易知C 符合要求.例1.2.2 右图是由18个棱长为1cm 的小正方形拼成的立体图形,它的表面积是( )平方厘米.A . 44B . 46C . 48D . 50【答案】C【解析】 从正面、左面、上面分别可看见8、7、9块,故表面积为()21879248cm ⨯++⨯=.例1.2.3 右图中的一些积木是由16块棱长为2cm 的正方体堆成的,它的表面积是________2cm .【答案】 200D .B .C .A .【解析】 从前到后的3面依次有2块、5块、7块,因此还剩162572---=块,为可看见的1块与其下方的1块.由此易知正视图、俯视图、左视图分别能看到7块、9块、8块,此外离我们最近的2块有两个面从6个方向均无法看到,综上共可看到()7982250++⨯+=个面,表面积为22250200cm ⨯=.例 1.2.4 图中的立体是由大小相同的若干单位正方体积木搭成的.这样的积木一共有多少【答案】 37;三视图如下图所示;102【解析】 将此图分为从左到右的5层,分别有16、9、5、6、1块,故共有16956137++++=块.三视图见答案,分别可看见17、15、16块,其中左视图有3块“被遮挡”,因此表面积为()17151632102+++⨯=⎡⎤⎣⎦.例1.2.5 图中的立体图形由11个棱长为1的立方块搭成,这个立体图形的表面积为_______.【答案】34【解析】 按一定的顺序,从不同的角度来看这个立体图形的表面的面积. 题模三:已知三视图反推个数例1.3.1 这个图形最少是由( )个正方体整齐堆放而成的.正视图 俯视图 左视图A.12B.13C.14D.15【答案】B【解析】从上面看下去,最少需要:122412113++++++=.例1.3.2此图是某几何体从正面和左面看到的图形.若该几何体是由若干个棱长为1的正方体垒成的,则这个几何体的体积最小是________.【答案】6【解析】根据正视图,理论上最少需要6块.而6块可以构造出来,例如,其俯视图如下图所示.因此,体积最小为3166⨯=.例 1.3.3一个立体图形,从前面,上面,右边三个方向看到的图形都如图所示,是一个样的,那么该立体图形最多由__________块小立方体组成.【答案】23【解析】按由上到下逐层分析,各层的小立方体数目分别不超过1个、4个、8个、10个,所以该立体图形最多由23个小立方体组成.例 1.3.4有一些大小相同的正方形木块堆成一堆,从上往下看是图3-1,从前往后看是图3-2,从左往右看是图3-3,那么这堆木块最多有多少块?最少有多少块?1412212从正面看从左面看【答案】16,13【解析】43416+⨯=块,424113+⨯+=块.这堆木块最多有16块,最少有13块.例1.3.5地上有一堆小立方体,从上面看时如图1所示,从前面看时如图2所示,从左边看时如图3所示.这一堆立方体一共有几个?如果每个小立方体的棱长为1厘米,那么这堆立方体所堆成的立体图形表面积为多少平方厘米?【答案】10个;42平方厘米【解析】采用在俯视图上标数的方法来求解,只要知道俯视图上的每格有几块小立方体,就可以很轻松的得到这堆立方体所形成的立体图形的样子.首先从俯视图很容易看出,有3个格子里是没有小立方体的,而其他6个格子里至少有一个小立方体.如下图,将所得信息填入俯视图中.结合俯视图和主视图,不难看出,有两格只有1块小立方体.将所得信息填入俯视图中.同样的,结合俯视图和左视图,又可以知道有一格只有1块小立方体.将所得信息填入俯视图中.图1 图2 图3从前面看1001我们来继续考虑,左视图中最左边一排有2块小立方体,所以俯视图左上角处有2块小立方体.将所得信息填入俯视图中.同理,主视图最右边一排有2块小立方体,所以俯视图最右边中间处有2块小立方体.将所得信息填入俯视图中.不难看出,俯视图中最后剩下的那块有3个小立方体,所以俯视图中每格的小立方体数如下:于是这一堆立方体一共有21321110+++++=个. 接着很容易得到这个立体图形的样子,如下图.上下各能看到6个面,前后各能看到6个面,左右各能看到6个面,同时注意到立体图形的中间共有6个会互相遮挡的面,所以表面积是()2666642⨯+++=平方厘米.从左边看1 0 0 012 1 0 0 012 1 0 0 2 0 112 1 03 0 2 011随练1.1将一正方体纸盒沿右图所示的粗实线剪开,展开成平面图,其展开图的形状为().A.A图B.B图C.C图D.D图【答案】B【解析】竖向只剪了1刀,故前、后、左、右四个面应在一条线上,排除A、D.易知上、下两面不在一条线上,排除C,故选B.随练1.2水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示.如下图,是一个正方体的平面展开图,若图中的“似”表示正方体的前面,“锦”表示右面,“程”表示下面.则“祝”、“你”、“前”分别表示正方体的________________________.【答案】后面、上面、左面【解析】易知你、程相对,前、锦相对,祝、似相对,因此“祝”、“你”、“前”分别表示正方体的后面、上面、左面.随练1.3小明把五颗完全相同的骰子拼摆成一排(如图),那么这五颗骰子底面上的点数之和是__________.【答案】16【解析】根据已知推出(4,5)(1,3)(2,6)互为对立面,所以这五颗骰子底面上的点数之和是6152216++++=.随练1.4右图是由八个相同的小正方体组成而成的几何体,则从正面观察,得到的平面图随堂练习形是__________.序号)【答案】 ②【解析】 从正面看到图②,从上面看到图①,从右面看到图③.所以正确答案是图②.随练1.5 由棱长为1的正方体搭成如图所示的图形,共有__________个正方体,它的表面积是__________.【答案】 10;34【解析】 第一层有8个,第二层有2个,共10个.其三视图分别能看到4、5、8个,故表面积为()11458234⨯⨯++⨯=.随练1.6 如图,有9个边长为1米的正方体,如图所示堆成一个立体图形.该立体图形的表面积等于__________平方米.【答案】 38【解析】 利用三视图.从前面、右面、上面看依次如图所示.所以该立体图形的表面积是()26672138++⨯⨯=平方米.随练1.7 如图6,用若干个棱长为1的小正方体堆成一个大的几何体,这个几何体的表面积(含底面积)是__________.① ② ③ ④【答案】90【解析】根据三视图,大的几何体的表面积等于正视图面积+俯视图面积+右视图面积的2倍,所以是()2++⨯⨯=.1415162190随练 1.8用棱长是1厘米的小立方体拼成如图所示的立体图形,这个图形的表面积是__________平方厘米.【答案】46平方厘米【解析】如图1,从立体图形上方和下方看去,看到的都是9块小正方形.面积是9平方厘米.图1图2从四个侧面看去,看到的是图2形式的7块小正方形,面积是7平方厘米.所以立体图形的表面积为927446⨯+⨯=平方厘米.随练1.9把若干个棱长为1厘米的小正方体木块搭成一个图形,从上面和前面看到的都是如图所示的情形,这个图形最多需要__________个这样的小正方体,最少需要__________个这样的小正方体.【答案】9;7【解析】由从上方看到的结果可知第一层必有5个,且第二层至多5个;由从前面看到的结果可知共有2层,且第二层至少2个.再结合两个视图可知第二层至多4个.综上,最多9个,最少7个.作业1一个数学玩具的包装盒是正方体,其表面展开图如下.现在每方格内都填上相应的数字.已知将这个表面展开图沿虚线折成正方体后,相对面的两数之和为“3”,则填在A、B、C内的三个数字依次是_____________.【答案】3,1,2【解析】正方体的平面展开图中,相对面之间一定隔着一个正方形,所以在此正方体上与“A”相对的面上的数是“0”.与“B”相对的面上的数是“2”.与“C”相对的面上的数是“1”.所以A、B、C内的三个数字依次是3,1,2.作业2把1至6各一个分别写在正方形的六个面上,每个面只写一个数字,且1与4相对,2与5相对,3与6相对,从某个角度看到的三个面上的数字如图(a)所示,从另一个角度看到的三个面如图(b)所示,那么图(b)中的“?”代表的数字是___________.A.2B.3C.4D.5【答案】A【解析】如图,4对面是1,所以在图a中把4翻到底面,顶部变成了1,如图b,而5C 2B 0A 1自我总结课后作业对面是2,所以当6转到正面时,5在左侧,右侧自然是2了,故答案是2..作业3下图由一个正五边形,五个长方形,五个等边三角形组成,它是一个立体图形的平面展开图,那么这个立体图形有__________条棱.【答案】20【解析】此立体图形,示意图如上:共20条棱.作业4用若干个棱长为1cm的小正方体码放成如图所示的立体,则这个立体的表面积(含下底面面积)等于___________2cm.【答案】60【解析】根据三视图,我们可知,此立体图形的前面与后面,左面与右面,上面与下面的表面积分别相等.所以我们只要知道前面有11个正方形,右面有8个正方形,上面有11个面,就可求出它露在外面的面共计()11811260++⨯=个正方形,所以它的表面积是2260160cm⨯=.作业5如图,把19个边长为1厘米正方体重叠起来堆成如图所示的立方体,这个立方体的表面积是______平方厘米.【答案】54【解析】从上下左右前后六个方向看,分别可以看到9、9、8、8、10、10个小正方形面,所以总的表面积为54平方厘米.作业6图中的立体是由大小相同的若干单位正方体积木搭成的.这样的积木一共有多少块?画出它的三视图,表面积是多少?【答案】30;三视图如下图所示;76【解析】将此图分为从左到右的4层,分别有11、7、5、7块,故共有1175730+++=块.三视图见答案,分别可看见13、12、11块,其中左视图有2块“被遮挡”,因此表面积为()1312112276+++⨯=⎡⎤⎣⎦.作业7由若干个相同的正方体木块搭成的立体,从正面和左面看到的图形都是右图,搭这样的立体,最少用()个这样的木块.A.4B.5C.6D.8【答案】A【解析】按如图方式摆放即可.正视图俯视图左视图作业8由若干个棱长为1的正方体堆成的立体图形,其正视图、俯视图和左视图如下所示,请问这个立体图形体积是________.正视图俯视图左视图【答案】5【解析】由正视图和左视图可知共两层,且顶层只有1块,由俯视图可知底层有4块,故共有5块,体积为5.作业9一仓库里堆放着若干个完全相同的正方体货箱,这堆货箱的三视图如图所示,这堆真方体货箱共有______________个.【答案】9【解析】俯视图确定基座,分析每块上的高度.。
五年级奥数几何专项二十三 表面涂色与三视图(2)

一、表面涂色问题:对于棱长大于2的长方体和正方体,表面涂色后切成小正方体:三面涂红色的在顶点处 两面涂红色的在棱长处 一面涂红的表面中间部分每面都没涂色的只有正方体体内。
重点:熟练掌握表面涂色问题的基本类型. 难点:复杂三视图问题.2.右图是333⨯⨯正方体,如果将其表面涂成红色,那么其中二面、三面被涂成红色的小正方体各有多少块?知识框架重难点例题精讲专项二十三 表面涂色与三视图(2)⨯⨯正方体,如果将其表面涂成红色,那么其中二面、三面被涂成红色的小正方【巩固】右图是456体各有多少块?⨯⨯正方体,如果将其表面涂成红色,那么其中一面被涂成红色和未被涂色的3.右图是333小正方体各有多少块?⨯⨯正方体,如果将其表面涂成红色,那么其中一面、二面、三面被涂成红色的【巩固】右图是456小正方体各有多少块?4.将一个表面积涂有红色的长方体分割成若干个棱长为1厘米的小正方体,其中一面都没有红色的小正方形只有3个,求原来长方体的表面积是多少平方厘米?【巩固】一个长方体,六个面均涂有红色,沿着长边等距离切5刀,沿着宽边等距离切4刀,沿着高边等距离切_______次后,要使各面上均没有红色的小方块为24块.⨯⨯长方体,如果将其表面涂成红色,再切成5个小正方体,那么各个正方体有5.右图是115几面被涂成红色?⨯⨯长方体,如果将其表面涂成红色,再切成20个小正方体,共有几种不同的【巩固】右图是225涂色情况?⨯⨯长方体,如果将其表面涂成红色,再切成10个小正方体,共有几种不同的6.右图是125涂色情况?【巩固】将长为5,宽为3,高为1的长方体木块的表面涂上漆,再切成15块棱长为1的小正方体。
则三个面涂漆的小正方体有________块。
7.小华用相同的若干个小正方体摆成一个立体(如图2)。
从上体上面看这个立方体,看到的图形是图①~③中的 。
(填序号)【巩固】小华用相同的若干个小正方体摆成一个立体(如图2)。
从右侧面看这个立方体,看到的图形是图 。
五年级数学长方体与正方体涂色与三视图

表面涂色与三视图知识框架一、表面涂色问题:对于棱长大于2的长方体和正方体,表面涂色后切成小正方体:三面涂红色的在顶点处两面涂红色的在棱长处一面涂红的表面中间部分每面都没涂色的只有正方体体内。
重难点重点:熟练掌握表面涂色问题的基本类型.难点:复杂三视图问题.例题精讲【例 1】右图是333⨯⨯正方体,如果将其表面涂成红色,那么其中二面、三面被涂成红色的小正方体各有多少块?【考点】长方体与正方体【难度】☆☆【题型】解答【解析】三面涂红色的只有8个顶点处的8个立方体;两面涂红色的在棱长处,共(32)4(32)4(32)412-⨯+-⨯+-⨯=块;【答案】8,12【巩固】右图是456⨯⨯正方体,如果将其表面涂成红色,那么其中二面、三面被涂成红色的小正方体各有多少块?【考点】长方体与正方体【难度】☆☆【题型】解答【解析】三面涂红色的只有8个顶点处的8个立方体;两面涂红色的在棱长处,共(42)4(52)4(62)436-⨯+-⨯+-⨯=块;【答案】8,36【例 2】右图是333⨯⨯正方体,如果将其表面涂成红色,那么其中一面被涂成红色和未被涂色的小正方体各有多少块?【考点】长方体与正方体【难度】☆☆【题型】解答一面涂红的表面中间部分:(32)(32)2(32)(32)2(32)(32)26-⨯-⨯+-⨯-⨯+-⨯-⨯=块.-⨯-⨯-=块六面都没涂色的只有正方体内的小方块:(32)(32(32)1【答案】6,1【巩固】右图是456⨯⨯正方体,如果将其表面涂成红色,那么其中一面、二面、三面被涂成红色的小正方体各有多少块?【考点】长方体与正方体【难度】☆☆【题型】解答【解析】一面涂红的表面中间部分:(42)(52)2(42)(62)2(52)(62)252-⨯-⨯+-⨯-⨯+-⨯-⨯=块.-⨯-⨯-=块六面都没涂色的只有正方体内的小方块:(42)(52)(62)1【答案】52【例 3】将一个表面积涂有红色的长方体分割成若干个棱长为1厘米的小正方体,其中一面都没有红色的小正方形只有3个,求原来长方体的表面积是多少平方厘米?【考点】长方体与正方体【难度】☆☆【题型】解答【解析】长:3+1+1=5厘米;宽:1+1+1=3厘米;高:1+1+1=3厘米;所以原长方体的表面积是:(3⨯5+3⨯5+3⨯3)3⨯2=78平方厘米.【答案】78【巩固】一个长方体,六个面均涂有红色,沿着长边等距离切5刀,沿着宽边等距离切4刀,沿着高边等距离切_______次后,要使各面上均没有红色的小方块为24块.【考点】长方体与正方体【难度】☆☆【题型】填空【解析】沿着长边等距离切5刀,可切为516+=块;沿着宽边等距离切4刀,可切为415+=块;沿着高边等距离切n刀,可切为1n+块.由题意可知,长方体每一个面的外层是涂有1面(或2面、或3面)的小方块,所以,各面均没有红色的小方块共(62)(52)(12)12(1)-⨯-⨯+-=-个,因各面n n 均没有红色的小方块为24块,所以,12(1)24n=.n-=,解得3【答案】3【例 4】右图是115⨯⨯长方体,如果将其表面涂成红色,再切成5个小正方体,那么各个正方体有几面被涂成红色?【考点】长方体与正方体【难度】☆☆【题型】解答【解析】两端的正方体有5面,中间的正方体有4面;【答案】两端的正方体有5面,中间的正方体有4面;【巩固】右图是225⨯⨯长方体,如果将其表面涂成红色,再切成20个小正方体,共有几种不同的涂色情况?【考点】长方体与正方体【难度】☆☆【题型】解答【解析】共有两种不同的染色情况:顶角上的8个正方体有3面,棱上的12个正方体有2面;【解析】共有两种不同的染色情况:顶角上的8个正方体有3面,棱上的12个正方体有2面【例 5】右图是125⨯⨯长方体,如果将其表面涂成红色,再切成10个小正方体,共有几种不同的涂色情况?【考点】长方体与正方体【难度】☆☆【题型】解答【解析】共有两种不同的染色情况:两端的4个正方体有4面,中间的6个正方体有3面;【解析】共有两种不同的染色情况:两端的4个正方体有4面,中间的6个正方体有3面;【巩固】将长为5,宽为3,高为1的长方体木块的表面涂上漆,再切成15块棱长为1的小正方体。
小学奥数 长方体正方体染色问题、三视图 知识点+例题+练习 (分类全面)

教学内容长方体正方体染色问题、沉浸问题、三视图教学目标掌握长方体正方体染色问题、沉浸问题、三视图重点染色问题、沉浸问题、三视图难点染色问题、沉浸问题、三视图教学过程一、染色问题一个棱长1分米的正方体木块,表面涂满了红色,把它切成棱长1厘米的小正方体。
在这些小正方体中:(1)三个面涂有红色的有多少个?(2)两个面涂有红色的有多少个?(3)一个面涂有红色的有多少个?(4)六个面都没有涂色的有多少个?下面我们结合图示,分别来看看这几个问题。
(1)三个面涂有红色的小正方体在大正方体的顶点处,正方体有8个顶点,所以三个面涂有红色的有8个。
(2)两个面涂有红色的小正方体在大正方体的棱上,每条棱上有8个,正方体有12条棱,所以两个面涂有红色的有8×12=96个。
(3)一个面涂有红色的小正方体在大正方体的面上,每个面上有8×8=64个,正方体有6个面,所以一个面涂有红色的有8×8×6=384个。
(4)六个面都没有涂色的在大正方体的中间,有两种算法:算法1: 1000-8-96-384=512(个);算法2: 8×8×8=512(个)。
公式:(1)正方体有8个顶点、12条棱、6个面假设把棱n等分(n≥3),那么:N的三次方个小立方体组成的立方体的表面图涂上颜色,则未被涂色的小立方体有(n-2)3个.一面被涂色的小立方体为(n-2)2*6个.两面被涂色的小立方体有(n-2)*12个.三面被涂色的有8个.(2)长方体, 有a*b*c个立方体组成的长方体表面涂上颜色.则未被涂色的小立方体有(a-2)*(b-2)*(c-2)个一面被涂色的小立方体有(a-2)* (b-2)*2+(b-2)* (c-2)*2+(c-2)* (a-2)*2两面被涂色的小立方体有(a-2)*4+(b-2)*4+(c-2)*4三面被涂色的有8个【例 1】下图是333⨯⨯正方体,如果将其表面涂成红色,那么其中一面、两面、三面被涂成红色的小正方体及未被涂色的小正方体各有多少块?0面:1; 1面:6;两面:2;三面:8【巩固】下图是456⨯⨯长方体,如果将其表面涂成红色,那么其中一面、两面、三面被涂成红色的小正方体及未被涂色的小正方体各有多少块?0面:24; 1面:52;两面:36;三面:8图1图2【巩固】小明用若干个大小相同的正方体木块堆成一个几何体,这个几何体从正面看如图2所示,从上面看如图3所示,那么这个几何体至少用了块木块.26图2图3课堂作业:1.一个长方体,六个面均涂有红色,沿着长边等距离切5刀,沿着宽边等距离切3刀,沿着高边等距离切_______次后,要使各面上均没有红色的小方块为40块.5.用一些棱长是1的小正方体码放成一个立体,从上、从右看这个立体都如下图,则这个形体最少由________个小正方体构成,6.小明用若干个大小相同的正方体木块堆成一个几何体,这个几何体从正面看如图2所示,从上面看如图3所示,那么这个几何体至少用了块木块.。
三视图知识点五年级

三视图知识点五年级三视图是一种常见的图形表达方式,它包括主视图、侧视图和俯视图。
在小学五年级的数学课程中,学生开始接触和学习三视图的基本概念和应用。
通过学习三视图,学生们能够更好地理解物体在不同方向上的投影,从而培养他们的空间想象能力和几何直观。
三视图的基本概念:- 主视图:通常指物体正面的视图,即从物体的正面看去所得到的图形。
- 侧视图:指的是物体侧面的视图,通常是从物体的左侧或右侧看去所得到的图形。
- 俯视图:指的是从物体上方看下去的视图,即从物体的顶部看去所得到的图形。
学习三视图的重要性:- 空间观念的培养:通过三视图的学习,学生可以更直观地理解物体在空间中的位置和形状。
- 几何知识的应用:三视图是解决几何问题的重要工具,它帮助学生在解决实际问题时,能够从不同角度考虑问题。
- 数学思维的锻炼:三视图的学习要求学生进行空间想象,这有助于培养学生的数学思维和逻辑推理能力。
三视图的绘制方法:- 确定观察点:在绘制三视图之前,需要确定观察者的位置,即从哪个方向观察物体。
- 绘制轮廓线:根据观察点,绘制物体的轮廓线,确保线条清晰,能够反映出物体的基本形状。
- 标注尺寸:在绘制完轮廓线后,需要对物体的各个部分进行尺寸标注,以确保三视图的准确性。
三视图的应用实例:- 在建筑学中,设计师会使用三视图来展示建筑物的各个面,以便于施工和理解。
- 在工程设计中,三视图是展示机械零件和产品结构的重要方式。
- 在艺术创作中,三视图可以帮助艺术家从不同角度捕捉物体的形态,创造出立体的视觉效果。
总结:通过学习三视图,五年级的学生们不仅能够掌握一项基本的数学技能,还能够提高他们对空间和形状的认识,为将来更复杂的数学和科学学习打下坚实的基础。
此外,三视图的学习也有助于培养学生的创新思维和解决问题的能力。
希望学生们能够在学习过程中,不断探索和实践,从而更好地理解和掌握三视图。
五年级下册数学扩展专题练习长方体与正方体涂色与三视图(a级).学生版全国通用(无答案)

一、表面涂色问题:对于棱长大于的长方体和正方体,表面涂色后切成小正方体:三面涂红色的在顶点处 两面涂红色的在棱长处 一面涂红的表面中间部分 每面都没涂色的只有正方体体内。
重点:熟练掌握表面涂色问题的基本类型. 难点:复杂三视图问题.【例 1】右图是333⨯⨯正方体,如果将其表面涂成红色,那么其中二面、三面被涂成红色的小正方体各有多少块?例题精讲知识框架重难点表面涂色与三视图【巩固】右图是456⨯⨯正方体,如果将其表面涂成红色,那么其中二面、三面被涂成红色的小正方体各有多少块?【例2】右图是333⨯⨯正方体,如果将其表面涂成红色,那么其中一面被涂成红色和未被涂色的小正方体各有多少块?【巩固】右图是456⨯⨯正方体,如果将其表面涂成红色,那么其中一面、二面、三面被涂成红色的小正方体各有多少块?【例3】将一个表面积涂有红色的长方体分割成若干个棱长为1厘米的小正方体,其中一面都没有红色的小正方形只有个,求原来长方体的表面积是多少平方厘米?【巩固】一个长方体,六个面均涂有红色,沿着长边等距离切刀,沿着宽边等距离切刀,沿着高边等距离切次后,要使各面上均没有红色的小方块为块.【例4】右图是115⨯⨯长方体,如果将其表面涂成红色,再切成个小正方体,那么各个正方体有几面被涂成红色?【巩固】右图是225⨯⨯长方体,如果将其表面涂成红色,再切成个小正方体,共有几种不同的涂色情况?【例5】右图是125⨯⨯长方体,如果将其表面涂成红色,再切成个小正方体,共有几种不同的涂色情况?【巩固】将长为,宽为,高为的长方体木块的表面涂上漆,再切成块棱长为的小正方体。
则三个面涂漆的小正方体有块。
【例6】小华用相同的若干个小正方体摆成一个立体(如图)。
从上体上面看这个立方体,看到的图形是图①~③中的。
(填序号)。
立方体魔方涂色问题探索图形五年级下册数学ppt课件

27 64 125 … 888… 12 24 36 … 6 24 54 … 1 8 27 …
n×n×n
8
(n-2) ×12 (n-2)2×6 (n-2) 3
整理版课件
22
感谢亲观看此幻灯片,此课件部分内容来源于网络, 如有侵权请及时联系我们删除,谢谢配合!
分割块数27三面有色二面有色12一面有色整理版课件10整理版课件11整理版课件12分割块数64三面有色二面有色24一面有色24没有颜色整理版课件13整理版课件14整理版课件15整理版课件16整理版课件17分割块数125三面有色二面有色36一面有色54没有颜色27整理版课件18整理版课件19整理版课件20整理版课件21整理版课件22分割块数27三面有色二面有色12一面有色2424365427n212n2感谢亲观看此幻灯片此课件部分内容来源于网络如有侵权请及时联系我们删除谢谢配合
64 8 24 24 8 12
整理版课件
13
整理版课件
14
整理版课件
15
整理版课件
16
整理版课件
分割块数 125 三面有色 8 二面有色 36 一面有色 54 没有颜色 27 17
整理版课件
18
整理版课件
19
整理版课件
20
整理版课件
21
分割块数 三面有色 二面有色 一面有色 没有颜色
立方体涂色问题
整理版课件
1
ห้องสมุดไป่ตู้
整理版课件
2
整理版课件
3
整理版课件
4
整理版课件
5
整理版课件
6
整理版课件
分割块数 三面有色 二面有色 一面有色 没有颜色
27 8 12 6 17
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、表面涂色问题:
对于棱长大于2的长方体和正方体,表面涂色后切成小正方体:
三面涂红色的在顶点处 两面涂红色的在棱长处 一面涂红的表面中间部分
每面都没涂色的只有正方体体内。
重点:熟练掌握表面涂色问题的基本类型. 难点:复杂三视图问题.
2.
右图是333⨯⨯正方体,如果将其表面涂成红色,那么其中二面、三面被涂成红色的小正方体各有多少块?
知识框架
重难点
例题精讲
专项二十三 表面涂色与三视图(2)
⨯⨯正方体,如果将其表面涂成红色,那么其中二面、三面被涂成红色的小正方【巩固】右图是456
体各有多少块?
⨯⨯正方体,如果将其表面涂成红色,那么其中一面被涂成红色和未被涂色的3.右图是333
小正方体各有多少块?
⨯⨯正方体,如果将其表面涂成红色,那么其中一面、二面、三面被涂成红色的【巩固】右图是456
小正方体各有多少块?
4.将一个表面积涂有红色的长方体分割成若干个棱长为1厘米的小正方体,其中一面都没有
红色的小正方形只有3个,求原来长方体的表面积是多少平方厘米?
【巩固】一个长方体,六个面均涂有红色,沿着长边等距离切5刀,沿着宽边等距离切4刀,沿着高边等距离切_______次后,要使各面上均没有红色的小方块为24块.
⨯⨯长方体,如果将其表面涂成红色,再切成5个小正方体,那么各个正方体有5.右图是115
几面被涂成红色?
⨯⨯长方体,如果将其表面涂成红色,再切成20个小正方体,共有几种不同的【巩固】右图是225
涂色情况?
⨯⨯长方体,如果将其表面涂成红色,再切成10个小正方体,共有几种不同的6.右图是125
涂色情况?
【巩固】将长为5,宽为3,高为1的长方体木块的表面涂上漆,再切成15块棱长为1的小正方体。
则三个面涂漆的小正方体有________块。
7.
小华用相同的若干个小正方体摆成一个立体(如图2)。
从上体上面看这个立方体,看到的图形是图①~③中的 。
(填序号)
【巩固】小华用相同的若干个小正方体摆成一个立体(如图2)。
从右侧面看这个立方体,看到的图形是图 。
A
B
C
D
①
②
③
8.用一些棱长是1的小正方体码放成一个立体如下图,请画出从正面、上面和右面看到的图
形
【巩固】用一些棱长是1的小正方体码放成一个立体如下图,请画出从上面和正面看到的图形
9.
用一些棱长是1的小正方体码放成一个立体,从上向下看这个立体,如下图a ,从正面看这个立体,如下图b ,则这个形体最多由_______个小正方体构成。
v
【巩固】用一些棱长是1的小正方体码放成一个立体,从上向下看这个立体,如下图a ,从正面看这个立体,如下图b ,则这个形体最少由________个小正方体构成。
图a
(从上向下看)图b
(从正面看)
图a
(从上向下看)图b (从正面看)
10.小明在桌面上摆了一些大小一样的正方体木块,摆完后从正面看如左下图,从侧面看如右
下图,那么他最多用了________块木块.
【巩固】小明在桌面上摆了一些大小一样的正方体木块,摆完后从正面看如左下图,从侧面看如右下图,那么他最少用了____ __块木块。
11.小明用若干个大小相同的正方体木块堆成一个几何体,这个几何体从正面看如图1所示,
从上面看如图2,那么这个几何体至少用了块木块.
图1图2
【巩固】小明用若干个大小相同的正方体木块堆成一个几何体,这个几何体从正面看如图2所示,从上面看如图3
所示,那么这个几何体至少用了 块木块.
1. 一个长方体,六个面均涂有红色,沿着长边等距离切5刀,沿着宽边等距离切3刀,沿着高边
等距离切_______次后,要使各面上均没有红色的小方块为40块.
图2图3
课堂检测
2.将8个相同的小正方体拼成一个体积为8立方厘米的长方体,表面涂上漆,然后分开,则3个
面涂漆的小正方体最多有_________个,最少有________个。
3.用一些棱长是1的小正方体码放成一个立体如下图,请画出从正面、上面和右面看到的图形。
4.用一些棱长是1的小正方体码放成一个立体,从上、从右看这个立体都如下图,则这个形体最
多由________个小正方体构成。
1.
右图是61012⨯⨯块小长方体堆叠而成,如果将其表面涂成红色,那么其中一面、二面、三面被涂成红色的小长方体各有多少块?
家庭作业
1.一个长方体的长是12厘米,宽8厘米,高也是整厘米数,在它的表面涂满颜色后,截成棱长是
1厘米的小正方体,其中一面有色的小正方体有280个.求原来长方体的体积。
2.将长为6,宽为5,高为1的长方体木块的表面涂上漆,再切成15块棱长为1的小正方体。
则
三个面涂漆的小正方体有________块。
3.用一些棱长是1的小正方体码放成一个立体如下图,请画出从正面、上面和右面看到的图形
4.用一些棱长是1的小正方体码放成一个立体,从上、从右看这个立体都如下图,则这个形体最
少由________个小正方体构成,
5.小明用若干个大小相同的正方体木块堆成一个几何体,这个几何体从正面看如图2所示,从上
面看如图3所示,那么这个几何体至少用了块木块.。
