实验6_nbsp_调制定理
高频调制实验报告

一、实验目的1. 理解高频调制的基本原理和过程。
2. 掌握振幅调制(AM)和解调(AM-D)的基本方法。
3. 学习使用实验仪器进行高频信号的调制和解调。
4. 分析调制信号的频谱特性,验证调制和解调效果。
二、实验原理高频调制是将低频信号(信息信号)与高频载波信号进行混合,使信息信号以某种方式影响载波信号的幅度、频率或相位,从而实现信号的传输。
本实验主要研究振幅调制(AM)。
1. 振幅调制(AM)振幅调制是指载波信号的振幅随信息信号的变化而变化。
AM信号可以表示为:\[ s(t) = c(t) \cdot [1 + m \cdot x(t)] \]其中,\( c(t) \) 是载波信号,\( x(t) \) 是信息信号,\( m \) 是调制指数。
2. 振幅解调(AM-D)振幅解调是指从调幅信号中恢复出原始信息信号。
常见的解调方法有包络检波法和同步检波法。
三、实验仪器1. 双踪示波器2. 高频信号发生器3. 低频信号发生器4. 调制器5. 解调器6. 万用表四、实验步骤1. 调制过程(1)设置高频信号发生器,产生一个频率为 \( f_c \) 的正弦波作为载波信号。
(2)设置低频信号发生器,产生一个频率为 \( f_m \) 的正弦波作为信息信号。
(3)将载波信号和信息信号输入调制器,进行振幅调制。
(4)观察调制器的输出波形,验证调制效果。
2. 解调过程(1)将调制信号输入解调器,进行振幅解调。
(2)观察解调器的输出波形,验证解调效果。
3. 频谱分析(1)使用频谱分析仪对调制信号进行频谱分析。
(2)观察调制信号的频谱特性,验证调制效果。
4. 性能测试(1)测试调制信号的调制指数 \( m \)。
(2)测试解调信号的解调指数 \( D \)。
五、实验结果与分析1. 调制过程通过实验,成功实现了振幅调制。
调制信号的波形如图1所示。
图1 振幅调制信号波形2. 解调过程通过实验,成功实现了振幅解调。
解调信号的波形如图2所示。
通信原理实验六 PSK系统综合实验

通信原理实验报告学院:信息工程学院专业班级:通信工程4班姓名:学号:实验六 PSK系统综合实验一. 实验目的1.掌握二相BPSK(DPSK)调制解调的工作原理及电路组成。
2.了解载频信号的产生方法。
3.掌握二相绝对码与相对码的码变换方法。
4.掌握数字基带信号的传输过程。
5.学会观察眼图及其分析方法。
二. 实验电路工作原理(一)调制实验:在本实验中,绝对移相键控(PSK)是采用直接调相法来实现的,也就是用输入的基带信号直接控制已输入载波相位的变化来实现相移键控。
图6-1 PSK/DPSK调制原理框图本实验中PSK调制二相PSK(DPSK)的载波为1.024MHz,数字基带信号有32Kbit/s 伪随机码、2KHz方波、CVSD编码信号等。
模拟信号1.024MHz载波输入到载波倒相器的反相输入端,在输出端即可得到一个反相的载波信号,即π相载波信号。
调节电位器VR801和VR802可使0相载波与π相载波的幅度相等。
对载波的相移键控是用模拟开关电路实现的。
0相载波与π相载波分别加到两个模拟开关的输入端,在数字基带信号的信码中,它的正极性加到模拟开关1的输入控制端,它反极性加到模拟开关2的输入控制端,用来控制两个同频反相载波的通断。
当信码为“1”码时,模拟开关1的输入控制端为高电平,开关1导通,输出0相载波;而模拟开关2的输入控制端为低电平,开关2截止。
反之,当信码为“0”码时,模拟开关1的输入控制端为低电平,开关1截止;而模拟开关2的输入控制端却为高电平,开关2导通,输出π相载波。
两个模拟开关的输出通过载波输出开关J801合路叠加后输出为二相PSK调制信号。
图6-2 模拟开关相乘器工作波形DPSK是利用前后相邻码元对应的载波相对相移来表示数字信息的一种相移键控方式。
绝对码是以基带信号码元的电平直接表示数字信息的,如规定高电平代表“1”,低电平代表“0”。
相对码是用基带信号码元的电平与前一码元的电平有无变化来表示数字信息的,如规定:相对码中有跳变表示1,无跳变表示0。
普通调制解调实验报告(3篇)

第1篇一、实验目的1. 了解普通调制解调的基本原理和过程。
2. 掌握模拟调制和解调的基本方法。
3. 学习调制解调设备的使用和调试方法。
4. 培养实际操作能力和分析问题的能力。
二、实验原理调制解调是一种将数字信号转换为模拟信号,或将模拟信号转换为数字信号的通信技术。
调制是将数字信号转换为模拟信号的过程,解调是将模拟信号转换为数字信号的过程。
调制解调的基本原理如下:1. 模拟调制:将数字信号转换为模拟信号的过程称为模拟调制。
模拟调制分为调幅(AM)、调频(FM)和调相(PM)三种。
2. 数字调制:将模拟信号转换为数字信号的过程称为数字调制。
数字调制分为调幅键控(ASK)、调频键控(FSK)和调相键控(PSK)三种。
3. 解调:将模拟信号转换为数字信号的过程称为解调。
解调分为模拟解调和数字解调。
三、实验器材1. 模拟调制解调设备:调幅(AM)、调频(FM)、调相(PM)调制器和解调器。
2. 数字调制解调设备:调幅键控(ASK)、调频键控(FSK)、调相键控(PSK)调制器和解调器。
3. 信号发生器:产生模拟信号和数字信号。
4. 示波器:观察调制解调信号波形。
5. 连接线:连接实验器材。
四、实验步骤1. 调制实验(1)调幅(AM)调制实验1)将信号发生器产生的模拟信号接入AM调制器。
2)调整调制器的调制频率和调制指数。
3)观察示波器上的调制信号波形,记录波形数据。
(2)调频(FM)调制实验1)将信号发生器产生的模拟信号接入FM调制器。
2)调整调制器的调制频率和调制指数。
3)观察示波器上的调制信号波形,记录波形数据。
(3)调相(PM)调制实验1)将信号发生器产生的模拟信号接入PM调制器。
2)调整调制器的调制频率和调制指数。
3)观察示波器上的调制信号波形,记录波形数据。
2. 解调实验(1)调幅(AM)解调实验1)将调制信号接入AM解调器。
2)调整解调器的解调频率和解调指数。
3)观察示波器上的解调信号波形,记录波形数据。
实验6 PAM调制与解调实验报告

PAM调制输出:
波形:PAM音频输入为4.5K正弦波,PAM时钟输入为8K方波(即抽样频率为8K)时的波形
PAM音频输入:PAM解调输出:
3、满足抽样定理临界点时的波形:给出临界点的音频输入频率,抽样频率
PAM音频输入:(写出频率)PAM解调输出:(写出抽样频率)
八、实验思考题
1,抽样频率为8K,而音频频率的临界点为3.915K(写你自己得出的临界点频率),并不是精确满足fs= 2fH,为什么?
九、调试中遇到的问题及解决方法
现代通信原理实验报告
实验室名称:通信原理实验室实验日期:年月日
学院
班级、组号
姓名
实验项目名称
脉冲幅度调制与解调实验
指导
教师
一、实验目的
二、实验内容
三、实验仪器
四、实验原理
五、实验步骤
六、实验思考题解答
1、简述抽样定理
七、实验结果及分析
1、满足抽样定理时的波形:PAM音频输入为2K正弦波,PAM时钟输入为32K/64K方波(即抽样频率为32K)时的波形
《高频实验》实验六 频率调制与解调
实验六频率调制与解调一、实验目的1.掌握变容二极管调频器电路的原理。
2.掌握集成电路频率解调器的基本原理。
3.了解调频器调制特性及测量方法。
4.掌握MC3361用于频率解调的调试方法。
5.掌握调频与解调系统的联测方法二、实验内容:1.测试变容二极管的静态调制特性2.观察调频波波形3.观察调制信号振幅对频偏的影响4、观察寄生调幅现象三、基本原理:调频即为载波的瞬时频率受调制信号的控制。
其频率的变化量与调制信号成线性关系,常采用变容二极管实现调频。
该调频电路即为实验三所做振荡器电路,将S2置于“1”为Lc振荡电路,从J1处加入调制信号,改变变容二极管反向电压即改变变容二极管的结电容,从而改变振荡器频率。
R1,R 3和VR1为变容二极管提供静态时的反向直流偏置电压。
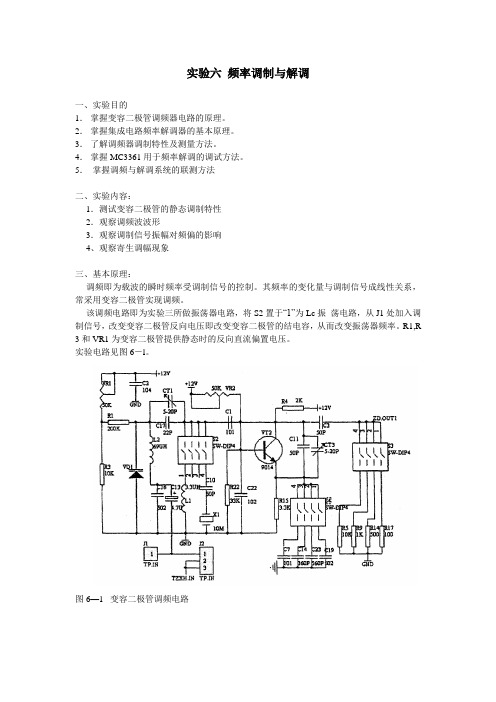
实验电路见图6-l。
图6—1 变容二极管调频电路图6—2 MC3361构成鉴频电路解调电路如图6-2所示,它主要完成二次混频和鉴频。
MC3361广泛用于通信机中完成接收功能,用于解调窄带调频信号,功耗低。
它的内部包含振荡、混频、相移、鉴频、有源滤波、噪声抑制、静噪等功能电路。
该电路工作电压为十5V。
通常输入信号频率为10.7MHZ,内部振荡信号为10.245MHZ。
本实验电路中根据前端电路信号频率,将输入信号频率定为6.455MHZ,内部振荡频率为6MHZ,二次混频信号仍为455KHZ。
集成块16脚为高频6.455MHZ信号输入端。
通过内部混频电路与6MHZ本振信号差拍出455KHZ中频信号由3脚输出,该信号经过FLI陶瓷滤波器(455KHZ)输出455KHZ中频信号并经5脚送到集成电路内部限幅、鉴频、滤波。
MC3361的鉴频采用如图6-3所示的乘积型相位鉴频器,其中的相移网络部份由MC3361的8脚引出在组件外部(由CP4移相器)完成。
图6—3 乘积型相位鉴频器C54、R62、C58、R63、R58与集成电路内的运算放大器组成有源滤波器。
模拟调制与解调实验报告

模拟调制与解调实验报告
一、实验目的:理解调制原理;
掌握通信原理实验箱和示波器的使用方法;
二、实验器材:通信原理实验箱,示波器,连接线若干
三、实验原理:幅度调制是由调制信号去控制高频载波幅度,使之随调制信号作线性变化的过程。
正弦波为:c(t)=A )cos(ϕωτ+
调制信号为:s m ()t =A ()t t m c ωcos
则已调信号:
()()()[]
c c m M M A s ωωωωω-++=2 在波形上已调信号的幅度随基带信号的规律呈正比变化,在频率上,完全是基带频率的简单搬移。
因此,幅度调制又称线性调制。
相干解调也是同步检波,即把在载频位置的已调信号搬回原始基带位置,为了无失真的恢复原基带信号,接收端必须提供一个与接收的已调载波严格同步的本地载波,与已调信号相乘后,经低通滤波器取出低频分量,即可得到原始的基带调制信号。
实验步骤:将实验箱对应的开关打开,将正弦信号借入示波器,调出对应波形,调节幅度,频率旋钮观察波形变化,将正弦信号改为方波信号重复上述步骤;将正弦波借入到实验箱模拟调制区的基带信号处,调制信号接入调制信号处,将输出接入示波器,调出图像,调节幅度频率旋钮观察波形变化。
将调制信号输入到解调端口,观察示波器的正弦波形,并与原始
信号波形相比较。
实验结果:
正弦载波:
调制载波:
调制后的波形:
解调后的波形:。
调制解调实验报告
调制解调实验报告一、实验目的本次调制解调实验的主要目的是深入理解调制解调的基本原理和技术,通过实际操作和观察实验现象,掌握常见调制解调方式的性能特点,并能够对实验结果进行分析和总结。
二、实验原理1、调制的概念调制是将原始信号(基带信号)的某些特征按照一定的规则变换到另一个信号(已调信号)的过程。
其目的是为了使信号能够在特定的信道中有效传输,例如增加信号的抗干扰能力、实现频谱搬移等。
2、常见的调制方式(1)幅度调制(AM):使载波的幅度随基带信号的变化而变化。
(2)频率调制(FM):使载波的频率随基带信号的变化而变化。
(3)相位调制(PM):使载波的相位随基带信号的变化而变化。
3、解调的概念解调是调制的逆过程,从已调信号中恢复出原始基带信号。
三、实验设备与器材1、信号发生器用于产生不同频率和幅度的基带信号。
2、调制器模块实现对基带信号的调制功能。
3、解调器模块用于对已调信号进行解调,恢复出原始基带信号。
4、示波器用于观察输入输出信号的波形。
5、频谱分析仪用于分析信号的频谱特性。
四、实验步骤1、连接实验设备按照实验电路图,将信号发生器、调制器、解调器、示波器和频谱分析仪等设备正确连接。
2、产生基带信号使用信号发生器产生一定频率和幅度的正弦波作为基带信号。
3、幅度调制实验(1)设置调制器的参数,如载波频率、调制深度等。
(2)观察示波器上已调信号的幅度变化,并与基带信号进行对比。
(3)使用频谱分析仪观察已调信号的频谱分布。
4、频率调制实验(1)调整调制器的参数,实现频率调制。
(2)在示波器上观察已调信号的频率变化。
(3)通过频谱分析仪分析频率调制信号的频谱。
5、相位调制实验(1)设置调制器进行相位调制。
(2)观察已调信号的相位变化情况。
(3)用频谱分析仪查看相位调制信号的频谱特征。
6、解调实验(1)将已调信号输入解调器。
(2)调整解调器的参数,使解调输出尽可能接近原始基带信号。
(3)在示波器上比较解调输出信号与原始基带信号。
实验六PSK调制与解调
实验六2PSK调制与解调一、实验目的1、理解二进制移相键控(Phase Shift Keying,PSK)调制和解调的基本原理;2、了解2PSK调制和解调的实现方法。
二、实验原理一个正弦载波。
如果它被一个双极性比特流按照图6-1所示的方案调制,它的极性将在每一次比特流极性改变时跟着改变。
图6-1对正弦波来说,极性的翻转就等价于反相。
因此,乘法器的输出就是BPSK(2PSK)信号。
二进制移相键控的解调可分两个步骤来考虑。
1、限带信号波形的恢复,使其转化到基带信号;2、从基带的限带波形里重建二进制消息比特流。
在本实验中,实现第一步依靠的是一个“窃取”的本地同步载波。
第二步的抽样判决由定标模块实现,最后还应线性解码,重建原始单极性基带信号。
解调原理如图6-2所示。
图6-2三、实验设备1、主机TIMS-301F2、TIMS基本插入模块(1)TIMS-148音频振荡器(Audio Oscillator)(2)TIMS-150乘法器(Multiplier)或TIMS-425正交模块(Quadrature Utilities),此模块集成了2个乘法器和1个加法器(3)TIMS-151移相器(Phase Shifer)(4)TIMS-153序列产生器(Sequence Generator)(5)TIMS-154可调低通滤波(Tuneable LPF)(6)TIMS-402定标模块(decision-maker module)(7)TIMS-406线性编码器(Line Code Encoder)(8)TIMS-407线性译码器(Line Code Decoder)3、计算机4、Pico虚拟仪器四、实验步骤1、将Tims系统中音频振荡(Audio Oscillator)、移相器(Phase Shifter)、序列码产生器(Sequence Generator)、线性编码器(Line-code Encode)、乘法器(Multiplier)按图6-3连接。
频率调制实验报告
频率调制实验报告一、实验目的:通过本次实验,掌握频率调制的原理和方法,了解频率调制在通信系统中的应用。
二、实验原理:频率调制是指在信号调制过程中,改变信号的频率以实现信号的传输和调制。
频率调制可以将模拟信号转换为远距离传输的载波信号,常见的应用包括调频广播、调频电视、无线电通信等领域。
频率调制的主要实现方式包括调频调制(FM)和相移键控调制(PM)。
三、实验仪器与材料:1. 示波器2. 音频信号发生器3. 频率调制解调实验箱4. 连接线5. 电源线四、实验步骤:1. 将音频信号发生器与调频解调实验箱相连,并接通电源;2. 在音频信号发生器上输入一个正弦波载频率的模拟信号;3. 在频率调制解调实验箱上进行频率调制的调节,观察调制后的信号波形;4. 调节调频解调实验箱的解调部分,观察解调后的信号波形;5. 分析实验结果,并记录数据。
五、实验结果与分析:在实验中,我们成功实现了对模拟信号的频率调制,并通过示波器观察到了调制前后的信号波形变化。
实验结果表明,频率调制可以改变信号的频率特性,从而实现信号的传输和调制。
通过观察解调后的信号波形,我们可以验证频率调制的有效性,并进一步了解频率调制在通信系统中的应用。
六、实验总结:本次实验通过频率调制的实际操作,使我们更深入地理解了频率调制的原理和方法。
实验结果也验证了频率调制在通信系统中的重要作用。
在今后的学习和研究中,将深入探讨频率调制的相关知识,并将其应用于实际工程中。
七、实验心得:通过本次实验,我们感受到了实验操作的乐趣和挑战,同时也认识到了频率调制在通信领域的广泛应用。
在未来的学习和工作中,我们将不断深化对频率调制的理解,努力创新和应用,为通信技术的发展贡献自己的力量。
以上就是关于频率调制实验的报告,希望对你有所帮助。
频率调制电路实验报告
一、实验目的1. 理解频率调制(FM)的基本原理和过程。
2. 掌握变容二极管调频电路的设计和调试方法。
3. 熟悉高频电子线路实验系统的操作和常用仪器。
4. 通过实验验证频率调制电路的性能指标。
二、实验原理频率调制(Frequency Modulation,FM)是一种通过改变载波频率来传输信息的调制方式。
在FM调制过程中,载波的频率会根据调制信号的幅度而变化,而载波的幅度保持不变。
常用的调频电路有变容二极管调频电路、电压控制振荡器(VCO)调频电路等。
本实验采用变容二极管调频电路,其基本原理如下:1. 调制信号与本振信号经过调制器进行调制,得到调频信号。
2. 调频信号通过变容二极管,其电容值随调制信号的变化而变化,从而改变谐振频率。
3. 调频信号通过滤波器滤波,得到稳定的调频信号。
三、实验仪器与设备1. 高频电子线路实验系统2. 双踪示波器3. 频率计4. 变容二极管5. 滤波器6. 调制信号发生器7. 本振信号发生器四、实验步骤1. 按照实验原理图搭建变容二极管调频电路。
2. 将调制信号发生器输出信号接入调制器,调节调制信号幅度和频率。
3. 将本振信号发生器输出信号接入变容二极管,调节本振信号频率。
4. 使用示波器观察调制器输出信号波形,分析调频效果。
5. 使用频率计测量调频信号的频率变化范围,计算调频指数。
6. 使用滤波器对调频信号进行滤波,观察滤波效果。
7. 改变调制信号幅度和频率,观察调频效果的变化。
五、实验结果与分析1. 调制信号幅度为1Vpp,频率为1kHz时,调频信号波形如图1所示。
可以看出,调频效果较好,调频指数约为10。
图1 调频信号波形2. 本振信号频率为10MHz时,调频信号频率变化范围为9.9MHz至10.1MHz,调频指数约为0.2。
图2 调频信号频率变化范围3. 使用滤波器对调频信号进行滤波,滤波后信号波形如图3所示。
可以看出,滤波效果较好,信号较为稳定。
图3 滤波后信号波形六、实验结论1. 通过实验验证了变容二极管调频电路的基本原理和性能指标。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1) 在调用函数fourier( )及ifourier( )之前, 要用syms命令对所有需要用到的变量 (如t,u,v,w) 等进行说明,即要将这些变量说明成符号变量。对fourier( )中的f及ifourier( )中的F也要用符 号定义符sym将其说明为符号表达式。 (2) 采用fourier( )及fourier( )得到的返回函数, 仍然为符号表达式。 在对其作图时要用ezplot( ) 函数,而不能用plot()函数。 (3)fourier( )及fourier( )函数的应用有很多局限性,如果在返回函数中含有δ(ω)等函数,则 ezplot( )函数也无法作出图来。另外,在用fourier( )函数对某些信号进行变换时,其返回函数 如果包含一些不能直接表达的式子,则此时当然也就无法作图了。这是fourier( )函数的一个 局限。另一个局限是在很多场合,尽管原时间信号f(t)是连续的,但却不能表示成符号表达 式,此时只能应用下面介绍的数值计算法来进行傅氏变换了,当然,大多数情况下,用数值 计算法所求的频谱函数只是一种近似值。 例 求门函数 f (t ) = ε (t + 1) − ε (t − 1) 的傅里叶变换,并画出幅度频谱图
调制器 调制波 已调波
所示
f (t )
载 波
y ( t ) = f ( t ) cos ω 0 t
cos ω 0 t
从频域上看,已调制信号y(t )的频谱为原调制信号f (t)的频谱搬移到 ±w0 处,幅 度降为原F( jw)的 1/2,即
1 f (t ) cos ω0t ↔ [ F (ω + ω0 ) + F (ω − ω0 )] 2
(2)、傅里叶变换的数值计算实现法 严格说来,如果不使用 symbolic 工具箱,是不能分析连续时间信号的。采用数值计算 方法实现连续时间信号的傅里叶变换,实质上只是借助于 MATLAB 的强大数值计算功能, 特别是其强大的矩阵运算能力而进行的一种近似计算。 傅里叶变换的数值计算实现法的原理 如下: 对于连续时间信号 f(t),其傅里叶变换为:
1 2π
∫
∞
−∞
F ( jω )e jωt d ω 。
在这一部分的学习中,大家都体会到了这种数学运算的麻烦。在 MATLAB 语言中有专 门对信号进行正反傅里叶变换的语句,使得傅里叶变换很容易在 MATLAB 中实现。在 MATLAB 中实现傅里叶变换的方法有两种,一种是利用 MATLAB 中的 Symbolic Math Toolbox 提供的专用函数直接求解函数的傅里叶变换和傅里叶反变换, 另一种是傅里叶变换 的数值计算实现法。下面分别介绍这两种实现方法的原理。 (1.)直接调用专用函数法 ①在 MATLAB 中实现傅里叶变换的函数为: F=fourier( f ) 对f(t)进行傅里叶变换,其结果为F(w) F=fourier(f,v) 对f(t)进行傅里叶变换,其结果为F(v) F=fourier( f,u,v ) 对f(u)进行傅里叶变换,其结果为F(v) ②傅里叶反变换 f=ifourier( F ) 对F(w)进行傅里叶反变换,其结果为f(x) f=ifourier(F,U) 对 F(w)进行傅里叶反变换,其结果为 f(u) f=ifourier( F,v,u ) 对 F(v)进行傅里叶反变换,其结果为 f(u) 由于MATLAB中函数类型非常丰富,要想了解函数的意义和用法,可以用mhelp命令。 如在命令窗口键入:mhelp fourier回车,则会得到fourier的意义和用法。 注意:
F ( jω ) = ∫
∞
−∞
f (t )e− jωt dt
f (t ) 的傅里叶变换存在的充分条件是 f (t ) 在无限区间内绝对可积,即 f (t ) 满足下式:
∫
∞
−∞
f (t ) dt < ∞
在引入广义函数概念之后, 使一些不满足绝对可积 但上式并非傅里叶变换存在的必要条件。 条件的函数也能进行傅里叶变换。 傅里叶反变换的定义为: f (t ) =
-80
-60
-40
-20
0 W
20
40
60
80
100
图
3.1.3 解调信号的时域和频域图
信号原型 1
0.5 f(t) 0 -0.5 -20
-15
-10
0 5 t 信号的振幅频谱图
-5
10
15
20
1.5
1 F(W) 0.5 0 -100
-80
-60
-40
-20
0 W
20
40
60
80
100
图 3.1.4 通过低通滤波后恢复的原信号时域和频谱图
信号原型 1
0.5 f(t)
0
-0.5 -10
-8
-6
-4
0 2 t 信号的振幅频谱图
-2
4
6
8
10
1.5
1 F (W ) 0.5 0 -100
-80
-60
-40
-20
0 W
20
40
60
80
100
图 3.1.1 调制信号时域和频域图
信号原型
1 0.5 f(t) 0 -0.5 -1 -10
-8
-6
-4
F ( jω ) = ∫
∞
−∞
f (t )e − jωt dt = lim
τ →0
n =−∞
∑
∞
f ( nτ )e − jω nτ τ
其中 τ 为取样间隔,如果 f(t)是时限信号,或者当|t|大于某个给定值时,f(t)的值已经衰 减得很厉害,可以近似地看成是时限信号,则上式中的 n 取值就是有限的,假定为 N,有:
3 多路复用
频分多路系统是将频分复用就是在发送端利用不同频率的载波将多路信号的频 谱调制到不同的频段, 以实现多路复用。 频分复用的多路信号在频率上不会重叠,
合并在一起通过一条信道传输,到达接收端后,可以通过中心频率不同的带通滤 波器将它们彼此分离开来,解调还原出基带信号。 三、 实验内容
1. 给定调制信号 f (t ) = Sa(t ) ,载波为cos(10πt),用matlab画出调制信号和已调信号在时
2 给定调制信号 f1 (t ) = Sa 2 (t ) ,载波为cos(20πt),用matlab画出调制信号和已调信号在时域 和频域的图形, (提示: 用sinc () 函数产生信号 f1 (t ) , 具体函数使用参见 可以调用fuliye(ft, t, R)函数求出信号幅度谱, 频谱图的W取值范围可以通过修改fuliye () 函数里面的参数 W1 得到, 每次调用fuliye(ft, t, R)函数前先调用figure 函数) , 保存两张实验波形图。 (图3.2.1 和 图3.2.2)。采用同步解调方法解调, 既用已调信号和相干载波相乘, 实现解调. (频谱搬移) 如图3.2.3 。再通过低通滤波器取出有用的低频分量,如图3.2.4所示。
域和频域的图形, (提示:用sinc()函数产生抽样信号,具体函数使用参见 可以调用 fuliye(ft,t,R)函数求出信号幅度谱,每次调用fuliye(ft,t,R)函数前先调用figure 函数) , 保存两张实验波形图(图3.1.1 和图3.1.2)。 采用同步解调方法解调, 既用已调信号和相干载波 相乘, 实现解调. 如图3.1.3 。再通过低通滤波器取出有用的低频分量,如图3.1.4所示。
MATLAB 程序如下: syms t w %定义两个符号变量t,w Gt=sym('Heaviside(t+1)-Heaviside(t-1)'); %产生门宽为 2 的门函数 Fw=fourier(Gt,t,w); %对门函数作傅氏变换求F(jw) FFw=maple('convert',Fw,'piecewise'); %数据类型转换 FFP=abs(FFw); %求振幅频谱| F(jw)| ezplot(FFP,[-10*pi 10*pi]);grid; %绘制函数图形,并加网格 axis([-10*pi 10*pi 0 2.2]) %限定坐标轴范围 运行结果:Fw= exp(i*w)*(pi*Dirac(w)-i/w)-exp(-i*w)*(pi*Dirac(w)-i/w) % Dirac(w)为 δ(ω),即傅立叶变换结果中含有奇异函数,故绘图前需作函数类型 转换 FFw= -i*exp(i*w)/w+i*exp(-i*w)/w % FFw为复数 FFP= abs(-i*exp(i*w)/w+i*exp(-i*w)/w) %求FFw的模值
-2
0 t
2
4
6
8
10
信号的振幅频谱图
0.8 0.6 F(W ) 0.4 0.2 0 -100
-80
-60
-40
-20
0 W
20
40
60
80
100
图 3.1.2 已调信号的时域和频域图
信号原型 1
0.5 f(t) 0 -0.5 -10
-8
-6
-4
0 2 t 信号的振幅频谱图
-2
4
6
8
10
0.8 0.6 F(W) 0.4 0.2 0 -100
F ( jω ) = τ ∑ f ( nτ )e − jω nτ
n=0
N −1
若对频率变量 ω 进行取样,得:
F (k ) = F ( jωk ) = τ ∑ f (nτ )e − jωk nτ
n=0
N −1
0< k <M
通常取: ωk =
ω0
M
k=
2π 其中 ω0 是要取的频率范围, 或信号的频带宽度。 采用MATLAB k, Mτ
