[工学]热工基础 第3讲
合集下载
003工程热力学第三讲(录像)

对于无耗散准静态过程(可逆过程),
Q dU pdV
2
Q12
(U2
U1)
pdV
1
q du pdv
2
q12
(u2
u1)
pdv
1
10
11
※
※※Βιβλιοθήκη ※1213
e
u
ek
ep
u
1 2
cf2
gz
4. Cyclic Processes (热力循环)
(1) definition(定义)
A system is said to have undergone a cycle if it returns to its initial state at the end of the process.
Q W E 0
E 0
Q W
q w
8
§2-2 closed system energy equation (闭口系统能量方程)
Q
W
dU
对于微元过程, Q dU W
对于热力过程1-2, Q12 (U2 U1) W12
对于单位质量工质, q du w
q12 (u2 u1) w12 9
复习
1.功量的计算
δW pdV
2
2
W12
W
1
1
pdV
δw pdv
2
2
w12
w
1
1
pdv
2.热量的计算
Q TdS
2
Q12
TdS
1
q Tds
2
q12
Tds
1
1
Chapter Two
The First Law of Thermodynamics
热工基础第三节-(1)

A=常数旳物体称为灰体
4、辐射力
辐射力(E )( 本身辐射):单位时间、单位物体表面上向半球 空间全部方向发射全部波长范围内旳辐射能。(W/m2 )。
黑体旳辐射力则用E0表达,
单色辐射力(Eλ ):单位时间、单位物体表面上向半球空间全部 方向发射单位波长段dλ范围内旳辐射能(W/m2 )。
E 与 Eλ 旳关系
所以,在工业上常根据物体加热后旳亮度变化来近似判断 其加热温度。
3、斯蒂芬—玻尔兹曼定律(四次方定律)
反应黑体表面对半球空间全部方向发射全部波长旳总辐射能.
由普朗克定律
E 0
c15
ec2 / T 1
积分:
E0
E 0d
0
c1
0
5d
ec2 / T 1
T 4
C0
(T 100
)4
W/m2
该式表白黑体旳辐射力与温度旳四次方成正比
(一)角系数旳概念 1、定义:
如图:1、2为黑体
φ
φ2
1
Q12
称表为面表F面1F发1对射表旳面辐F射2旳能角到系达数表φ面F122旳份额,F1, Eb1
12
Q12 E10 F1
同理:表面F2发射旳辐射能到达表面F1旳份额,称为表面F2 对表面F1旳角系数φ 21
21
Q21 E20 F2
2、角系数旳性质
φ12+φ13=1 φ21+φ23=1 φ31+φ32=1 分别乘以F1、F2和F3,得: φ12F1+φ13F1=F1 φ21F2+φ23F2=F2 φ31F3+φ32F3=F3 再根据角系数旳互换性
F2 F3 F1
φ12F1=φ21F2 φ13F1=φ31F3 φ23F2=φ32F3 联立以上6式求解可得
4、辐射力
辐射力(E )( 本身辐射):单位时间、单位物体表面上向半球 空间全部方向发射全部波长范围内旳辐射能。(W/m2 )。
黑体旳辐射力则用E0表达,
单色辐射力(Eλ ):单位时间、单位物体表面上向半球空间全部 方向发射单位波长段dλ范围内旳辐射能(W/m2 )。
E 与 Eλ 旳关系
所以,在工业上常根据物体加热后旳亮度变化来近似判断 其加热温度。
3、斯蒂芬—玻尔兹曼定律(四次方定律)
反应黑体表面对半球空间全部方向发射全部波长旳总辐射能.
由普朗克定律
E 0
c15
ec2 / T 1
积分:
E0
E 0d
0
c1
0
5d
ec2 / T 1
T 4
C0
(T 100
)4
W/m2
该式表白黑体旳辐射力与温度旳四次方成正比
(一)角系数旳概念 1、定义:
如图:1、2为黑体
φ
φ2
1
Q12
称表为面表F面1F发1对射表旳面辐F射2旳能角到系达数表φ面F122旳份额,F1, Eb1
12
Q12 E10 F1
同理:表面F2发射旳辐射能到达表面F1旳份额,称为表面F2 对表面F1旳角系数φ 21
21
Q21 E20 F2
2、角系数旳性质
φ12+φ13=1 φ21+φ23=1 φ31+φ32=1 分别乘以F1、F2和F3,得: φ12F1+φ13F1=F1 φ21F2+φ23F2=F2 φ31F3+φ32F3=F3 再根据角系数旳互换性
F2 F3 F1
φ12F1=φ21F2 φ13F1=φ31F3 φ23F2=φ32F3 联立以上6式求解可得
热工基础3_答案_
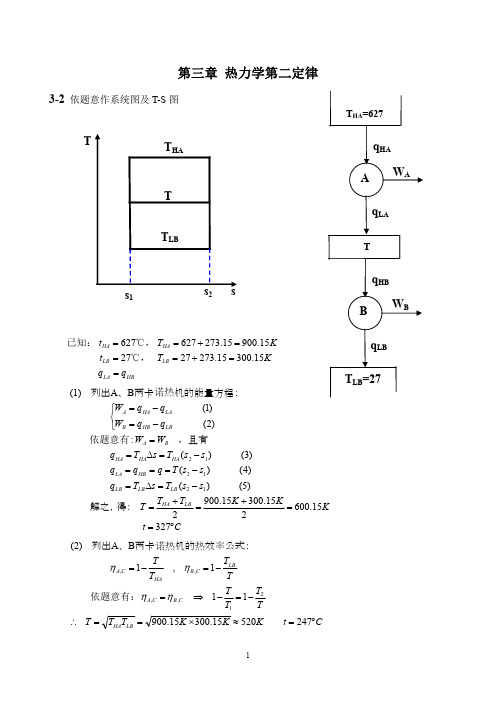
(1) QH 1500 J , QL 800 J S iso QH QL 0 TH TL 1500 J 800 J 0 1.93( J / K ) 0 2000 K 300 K
QL TL = 300K
根据孤立系熵增原理判定:该循环可行,且不可 逆。 (2) QH 2000 J , W0 1800 J , QL QH W0 2000 J 1800 J 200 J S iso QH QL 0 TH TL
Tav
Q
5
1) 当冷源0℃的冰变的0℃的水时,可将冷、热源视为恒温
3-17
依题意有:TH 298K (t H 25℃) , TL 273K (t L 0℃) QL mrice 其中:m 1000kg , rice 333kJ / kg 且为可逆热机,故有 t C 1 QH TH T QL H mrice TL TL QL T 1 L QH TH
TH TH mrice mrice mrice 1 TL TL 298K 1000kg 333kJ / kg 1 30 103 kJ 273K 2) 当冷源0℃的水变为25℃的水时,可将热源视为恒温, 冷源为变温 W1 QH QL 热机工作循环视为无数个微元卡诺循环 故有
4
I
Sg
3-16
依题意有:mt 50℃ 8kg , t m 8kg 50℃ , Tm 8 kg 323.15 K mt 100℃ 5kg , t m5kg 100℃ , Tm 5 kg 373.15 K cw 4.187 kJ /(kg K ) 设8kg 50℃的水与5kg100℃的水混合后的混合水质量为m,温度为Tav m mt 50℃ mt 100℃ 则有 cw mt 50℃ (Tav 323.15 K ) cw mt 100℃ (373.15 K Tav ) 解得 Tav 373.15 Kmt 100℃ 323.15 Kmt 50℃ mt 50℃ mt 100℃
热工基础--水蒸气图表及热力过程(精品课件)

15、一个人炫耀什么,说明他内心缺 少什么 。。202 0年10 月下午4 时16分 20.10.6 16:16O ctober 6, 2020
16、业余生活要有意义,不要越轨。2 020年1 0月6日 星期二 4时16 分14秒1 6:16:14 6 October 2020
17、一个人即使已登上顶峰,也仍要 自强不 息。下 午4时16 分14秒 下午4 时16分1 6:16:14 20.10.6
初、终状态参数。若初状态是湿蒸汽或过热蒸汽,则可在h-s图 上确定过程的初、终态点,并得到其他状态参数,如下图所示:
水蒸气的定熵过程
17
2)绝热过程的参数坐标图
水蒸气绝热过程在参数坐标图上的表示如图5-12、如图5-13 所示。
18
3)工质与外界交换的功量
根据查得的初、终态点的各参数,结合过程特点,利用能量 方程式得到:wt=- △h=h1-h2(定熵过程的技术功等于焓降)。
3
②未饱和水与过热蒸汽表:根据不同温度和不同压力,相应地 列出未饱和水和过热蒸汽的v、h、s。用粗黑线分隔,粗线 上方为未饱和水的参数,粗线下方为过热蒸汽的参数。 4
2)几点说明 ①:u=h-pv(工程使用较少,未列); ②:对于湿蒸汽的状态参数,要根据干度以及该压力下
的饱和水与干蒸汽计算,如hx = (1-x)h '+xh ''. ③:表中没有列出的中间温度和中间压力,要用内插法。
t = ts ,饱和状态,需用干度再确定状态。
t > ts , 过热蒸汽状态。
6
3)、水蒸气状态的确定
①、已知p(或t)和某一参数如v、h、s,查饱和水与饱和蒸
汽表,得已知p(或t)下的v‘和v '' 。
热工基础-3-完整-第三章 理想气体ppt课件

始压力p1=7×105Pa,温度t1=20℃。因泄漏,后 压力降至p2=4.9×105Pa ,温度未变。问漏去多少
氧气?
解:取钢瓶的容积为系统(控制容积),泄漏过 程看成是一个缓慢的过程。初终态均已知。假定 瓶内氧气为理想气体。根据状态方程:
精选ppt
8
二. 理想气体的比热容
物体温度升高1K所吸收的热量称为热容; 一单位质量的物体温度升高(或降低)1℃所吸 收(或放出)的热量称为(质量)比热容。
2) 理想气体: pvRgT cpcv Rg
uf(T) hf(T)
kcp cv
ucv T; hcp T
s c vln T T 1 2 R lnv v 1 2; s cpln T T 1 2 R lnp p 1 2
3)可逆过程:
w pdv 精选ppt
w t vdp
q
Tds
37
分析热力过程的步骤:
讨论:
1、比较教材P75例3-4的解法,上面是利用基本 定义来解的,显然要容易得多,不需记忆相关换算公 式;
2、若本题不要求折合摩尔质量,仅要求折合气 体常数,则也可用:
Rg,eq wiRg,i
i
精选ppt
34
作业:P103-104
3-10 3-15
思考题: P102
10
精选ppt
35
五. 理想气体的基本热力过程
1.热力学能的变化量: u cvdT
若比热容取定值或平均值,有: u cvT
2.焓的变化量: hcpdT
u cV
T T2
T1
若比热容取定值或平均值,有: h cpT
h cp
T2 T1
T
精选ppt
21
3. 理想气体熵变化量的计算:
氧气?
解:取钢瓶的容积为系统(控制容积),泄漏过 程看成是一个缓慢的过程。初终态均已知。假定 瓶内氧气为理想气体。根据状态方程:
精选ppt
8
二. 理想气体的比热容
物体温度升高1K所吸收的热量称为热容; 一单位质量的物体温度升高(或降低)1℃所吸 收(或放出)的热量称为(质量)比热容。
2) 理想气体: pvRgT cpcv Rg
uf(T) hf(T)
kcp cv
ucv T; hcp T
s c vln T T 1 2 R lnv v 1 2; s cpln T T 1 2 R lnp p 1 2
3)可逆过程:
w pdv 精选ppt
w t vdp
q
Tds
37
分析热力过程的步骤:
讨论:
1、比较教材P75例3-4的解法,上面是利用基本 定义来解的,显然要容易得多,不需记忆相关换算公 式;
2、若本题不要求折合摩尔质量,仅要求折合气 体常数,则也可用:
Rg,eq wiRg,i
i
精选ppt
34
作业:P103-104
3-10 3-15
思考题: P102
10
精选ppt
35
五. 理想气体的基本热力过程
1.热力学能的变化量: u cvdT
若比热容取定值或平均值,有: u cvT
2.焓的变化量: hcpdT
u cV
T T2
T1
若比热容取定值或平均值,有: h cpT
h cp
T2 T1
T
精选ppt
21
3. 理想气体熵变化量的计算:
热工基础第三章2
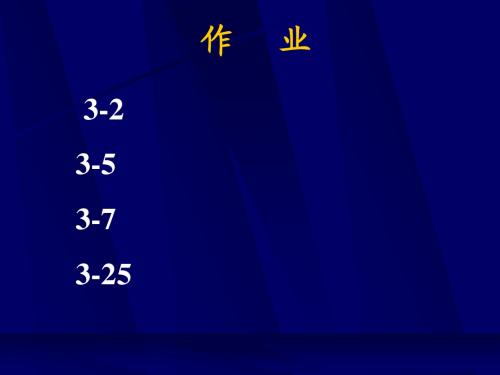
可逆
ds =
δ qR
T
绝热
ds = 0
说明: 说明
s
adiabatic isentropic (1) 不能说绝热过程就是等熵过程 不能说绝热过程就是等熵过程, 绝热过程就是等熵过程 可逆绝热过程才是等熵过程 必须是可逆绝热过程才是等熵过程。 必须是可逆绝热过程才是等熵过程。 Reversible adiabatic (2) 不仅 s = 0 , ds = 0 s 处处相等
对象 1) 参数 ( p, T, v, u, h, s ) 变化 2) 能量转换关系, q , w, wt 能量转换关系 方法 1) 抽象分类
p v T
s
n
基本过程 2) 可逆过程 (不可逆再修正 不可逆再修正) 不可逆再修正
研究热力学过程的依据
1) 热一律 稳流 2) 理想气体
δ q = du + δ w = dh + δ wt
理想气体 s 的过程方程
ds = 0
理想气体
γ=
cp cv
dp dv ds = cv + cp =0 p v dp dv +γ =0 p v
当 γ = const
γ
ln p + γ ln v = Const
绝热指数 κ 三个条件: 三个条件 (1)理想气体 (2)可逆过程 (3) γ = const 理想气体 可逆过程
dT dv dT dp dv dp ds = cv + Rg = cp Rg = cp + cv T v T p v p
适用于理想气体任何过程 1、若定比热 、
cv , cp = const
T2 v2 s = cv ln + Rg ln T1 v1 T2 p2 v2 p2 = cp ln Rg ln = cp ln + cv ln T1 p1 v1 p1
ds =
δ qR
T
绝热
ds = 0
说明: 说明
s
adiabatic isentropic (1) 不能说绝热过程就是等熵过程 不能说绝热过程就是等熵过程, 绝热过程就是等熵过程 可逆绝热过程才是等熵过程 必须是可逆绝热过程才是等熵过程。 必须是可逆绝热过程才是等熵过程。 Reversible adiabatic (2) 不仅 s = 0 , ds = 0 s 处处相等
对象 1) 参数 ( p, T, v, u, h, s ) 变化 2) 能量转换关系, q , w, wt 能量转换关系 方法 1) 抽象分类
p v T
s
n
基本过程 2) 可逆过程 (不可逆再修正 不可逆再修正) 不可逆再修正
研究热力学过程的依据
1) 热一律 稳流 2) 理想气体
δ q = du + δ w = dh + δ wt
理想气体 s 的过程方程
ds = 0
理想气体
γ=
cp cv
dp dv ds = cv + cp =0 p v dp dv +γ =0 p v
当 γ = const
γ
ln p + γ ln v = Const
绝热指数 κ 三个条件: 三个条件 (1)理想气体 (2)可逆过程 (3) γ = const 理想气体 可逆过程
dT dv dT dp dv dp ds = cv + Rg = cp Rg = cp + cv T v T p v p
适用于理想气体任何过程 1、若定比热 、
cv , cp = const
T2 v2 s = cv ln + Rg ln T1 v1 T2 p2 v2 p2 = cp ln Rg ln = cp ln + cv ln T1 p1 v1 p1
西安交大热工基础课件
热与流体研究中心
28
4. 状态参数熵
定义ds
( q
T
)r
为状态参数熵的微分
p ab A
用一组可逆绝热线,把它分
割成无限多种微元循环,每个微 元循环都是可逆旳。
1 dc
O
2
B
v
热与流体研究中心
29
pA
q1 b
• a•
• 1
对任意微元循环abcda:
2 •
•c •d q2 q2
B v
吸热:q1,温度为T1
理想气体等温膨胀
T
Q
W
多种说法等效
热与流体研究中心
9
热力学第二定律多种表述旳等效性:
QL QL
QH
热源:失去 QH QL QH QL QO WOt
外界:得到 WO
QL
冷源:失去 QL QL 0
TH WO QL TL
总效果:从单一热源吸热 Q1 Q2 Qnet
பைடு நூலகம்
全部转变为功
Wnet
Ex,Q
Q(1
T0 T
)
En,Q
Q T0 T
热与流体研究中心
25
3. 多热源旳可逆循环
1. 热源多于两个旳可逆循环
任意可逆循环,如左图之1H2L1。
T
H
•
•2 1•
L• s
吸热过程: 1H2,工质温度变化,为可逆,
需热源温度时时与工质相等,这么就 要有无限多种热源。
放热过程: 2L1,无限多种冷源。
第三节 热力学第二定律
热与流体研究中心
1
一、热力过程旳方向性
温差传热
A
QA
B
热工基础yse3
此时, 此时,肋片顶端的温度可表 示为
h, t ∞
θH =
θ0
cosh m ) ( H
0
x
四、肋片效率
肋片效率: 肋片效率 : 肋片的实际散热 量 Φ 与假定整个肋片表面都 处在肋基温度t 处在肋基温度 0时的理想散热 的比值。 量 Φ0 的比值。 对于等截面直肋片其肋效 率可表示为
t0 t∞
Φ Φ ηf = = Φ hPH(t0 −t∞) 0
[W]
式中
R = λ
1 2 l πλ
ln r2 / r ) ( 1
为通过圆筒壁导热的热阻
2.通过多层圆筒壁的导热 2.通过多层圆筒壁的导热 采用热阻的概念进行分析。 采用热阻的概念进行分析。在 稳态、无内热源的情况下, 稳态、无内热源的情况下,通过 各层的热流量相等。 各层的热流量相等。
Φ= t −t t −t t1 −t2 = 2 3 = 3 4 r r r 1 1 1 ln 2 ln 4 ln 3 2 1l r 2 2l r 2 3l r πλ πλ πλ 1 3 2
h,t∞ δ
dx
H x
t t0 t∞ 0
t x→∞ =t∞
t∞ 0 H
x
t∞ 0 H
x
H
x
采用第二种情况, 采用第二种情况,顶端绝热
dt dθ x = H = 0, , =0 dx dx
用两个边界条件, 用两个边界条件,可以得到两个未知的常数 C1和 C2, 最后,肋片中的温度分布可表示为 最后,
t b>0 t1 t2 b<0
0 x
dt Φ= −λA dx
δ
热流密度计算式为 :
t t1 t2
b t1 −t2 q = λ0 + (t2 +t1) 1 2 δ
h, t ∞
θH =
θ0
cosh m ) ( H
0
x
四、肋片效率
肋片效率: 肋片效率 : 肋片的实际散热 量 Φ 与假定整个肋片表面都 处在肋基温度t 处在肋基温度 0时的理想散热 的比值。 量 Φ0 的比值。 对于等截面直肋片其肋效 率可表示为
t0 t∞
Φ Φ ηf = = Φ hPH(t0 −t∞) 0
[W]
式中
R = λ
1 2 l πλ
ln r2 / r ) ( 1
为通过圆筒壁导热的热阻
2.通过多层圆筒壁的导热 2.通过多层圆筒壁的导热 采用热阻的概念进行分析。 采用热阻的概念进行分析。在 稳态、无内热源的情况下, 稳态、无内热源的情况下,通过 各层的热流量相等。 各层的热流量相等。
Φ= t −t t −t t1 −t2 = 2 3 = 3 4 r r r 1 1 1 ln 2 ln 4 ln 3 2 1l r 2 2l r 2 3l r πλ πλ πλ 1 3 2
h,t∞ δ
dx
H x
t t0 t∞ 0
t x→∞ =t∞
t∞ 0 H
x
t∞ 0 H
x
H
x
采用第二种情况, 采用第二种情况,顶端绝热
dt dθ x = H = 0, , =0 dx dx
用两个边界条件, 用两个边界条件,可以得到两个未知的常数 C1和 C2, 最后,肋片中的温度分布可表示为 最后,
t b>0 t1 t2 b<0
0 x
dt Φ= −λA dx
δ
热流密度计算式为 :
t t1 t2
b t1 −t2 q = λ0 + (t2 +t1) 1 2 δ
热工基础热工基础 (3)
第1章 热力学第一定律和第二定律主要内容☐基本概念☐热力学第一定律☐热力学第二定律定义:从燃料燃烧中得到热能,并利用热能得到动力的设备。
热能机械能化学能分类燃气动力装置蒸汽动力装置内燃机燃气轮机喷气动力装置热力设备工作物质: 燃气燃气热能机械能燃料化学能排入大气3. 燃烧、膨胀; 4. 排气1. 吸气;2. 压缩;工作过程:能量转换:内燃机☐膨胀做功☐ 排气☐压缩☐燃烧、吸热工作过程:燃气轮机蒸汽动力装置不同点:构造和工作特性不同。
结论:各种形式的热机都存在以下几个相同的热力过程: 吸热、膨胀作功、放热两种热机的异同相同点:☐存在某一种媒介物质以获得能量;(如内燃机中混合气,蒸汽机中的水)☐存在能提供热能的能量源;☐余下的热能排向环境介质。
名词定义工质: 实现热能和机械能相互转化的媒介物质。
热源温度高低温度变化高温热源低温热源(冷源)恒温热源 变温热源热源: 工质从中吸取或向之排放热能的物质系统。
膨胀性; 流动性; 热容量; 稳定性、安全性;环保性能;价格。
常见工质:蒸汽、燃气、空气等。
制冷装置:实现热量从低温物体向高温物体的转移。
放热耗功吸热蒸气压缩制冷循环装置示意图热动装置原理E'T 1T 2Q 1Q 2W 0E'T 1T 2Q 1Q 2W 0制冷装置原理热力设备工作(能量转换)原理。
热工基础A第三章(理想气体的热力性质及过程)西南交大载运
xi M i x M = i i Σxi M i M eq
ϕi = xi
, xi =
ω i R gi ω i R gi = ∑ ω i R gi R g , eq
(三)、分压力的确定 )、分压力的确定 对任一组分: 对任一组分 PiV=NiRT PVi=NiRT ∴ 或 或
=miRgT =miRgT
w= wt
2. 定熵过程 s 定熵过程:
( 等熵 = 绝热 + 可逆 )
(1) 过程方程式 过程条件 : s = const 即 ds = 0 ds = Cp dv/v + Cv dP/P = 0 推导 由 k = Cp/Cv 积分: 积分 k lnv + lnP = lnPvk = C 可得: 可得:
二、理想气体状态方程式 { PV=RgT (m kg 理想气体)
1. 方程式: 方程式 Pv = RgT
PVm=RT ( 1 kmol 理想气体)
PV=NRT ( N kmol 理想气体) 称通用气体常数。 式中 R=8314.5 J/(kmol·k),称通用气体常数。 称通用气体常数
R 8314.3 Rg= = J/kg·k,称气体常数。(N = m/M 千摩尔数 称气体常数。 千摩尔数) 称气体常数 M M
二、学习目标 熟练掌握并灵活应用理想气体状态方程式;正确利用定值比热容和平 均比热容计算过程的热量以及理想气体热力学能、焓、熵等参数的计算; 掌握理想气体混合物的热力学计算;能正确对理想气体4种基本热力过 程以及多变过程进行分析计算。
理想气体及其状态方程式: 第一节 理想气体及其状态方程式:
一、理想气体
∴ du = cv dT , △u = cv△T
3. 理想气体cp、cυ关系式 理想气体 ∵ h = u + pv = CvT + RgT = CP T ∴
ϕi = xi
, xi =
ω i R gi ω i R gi = ∑ ω i R gi R g , eq
(三)、分压力的确定 )、分压力的确定 对任一组分: 对任一组分 PiV=NiRT PVi=NiRT ∴ 或 或
=miRgT =miRgT
w= wt
2. 定熵过程 s 定熵过程:
( 等熵 = 绝热 + 可逆 )
(1) 过程方程式 过程条件 : s = const 即 ds = 0 ds = Cp dv/v + Cv dP/P = 0 推导 由 k = Cp/Cv 积分: 积分 k lnv + lnP = lnPvk = C 可得: 可得:
二、理想气体状态方程式 { PV=RgT (m kg 理想气体)
1. 方程式: 方程式 Pv = RgT
PVm=RT ( 1 kmol 理想气体)
PV=NRT ( N kmol 理想气体) 称通用气体常数。 式中 R=8314.5 J/(kmol·k),称通用气体常数。 称通用气体常数
R 8314.3 Rg= = J/kg·k,称气体常数。(N = m/M 千摩尔数 称气体常数。 千摩尔数) 称气体常数 M M
二、学习目标 熟练掌握并灵活应用理想气体状态方程式;正确利用定值比热容和平 均比热容计算过程的热量以及理想气体热力学能、焓、熵等参数的计算; 掌握理想气体混合物的热力学计算;能正确对理想气体4种基本热力过 程以及多变过程进行分析计算。
理想气体及其状态方程式: 第一节 理想气体及其状态方程式:
一、理想气体
∴ du = cv dT , △u = cv△T
3. 理想气体cp、cυ关系式 理想气体 ∵ h = u + pv = CvT + RgT = CP T ∴
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
体a和b的分子量。 • 因为 Va V ' ,所以气体的质量之比也可 写成 • 比较上述两式,得
m a m a / Va Pa Va mb mb / Vb Pb Vb
•
或
a Vb b Va
a Vb b Va
• 说明在同温同压下,各种完全气体的摩尔 体积相等。
P0 101325 R 287J / kg K 0T0 1.293 2735
• 例 容积为20L的空气瓶,压力表上指压力 为55bar,温度为20°C,求气瓶的空气质 量。如果在起动发动机时,用去了2/5(按 质量计),而其温度不变,则瓶中的空气绝 对压力为多少? • 解 已知 6 • P≈55+1=56bar=56×10 Pa • T ≈273十20=293K 20 V 0.02 m 3 R 287J / kg K 1000
完全气体与实际气体 状态方程式 通用气体常数
介绍完全气体与实际气体的区别 完全气体状态方程式的应用 完全气体状态方程式的推导
完全气体状态方程式的应用 通用气体常数的意义
2/6
§1—6 完全气体与实际气体
• • • • 一、实际气体 日常所见到的气体就是实际气体。 二、完全气体 气体分子设想只有质量而没有体积,分子 间完全没有作用力的气体,叫做完全气体。 • 航空发动机所用的工质——空气和燃气, 一般在压力不太大,温度不太低的条件下 工作,基本上符合完全气体的两个假定, 所以可把空气和燃气当作完全气体。
M
• lmol气体所占的体积,叫做1摩尔体积。 • 在标准状态下,1mol气体占有的体积叫 做标准摩尔体积,任何完全气体在标准状 态下的摩尔体积约为22.4升(精确值应为 22.41383升)。在已知各气体的分子量μ 以后,则很容易求得在标准状态下该气体 的比容 v0 和密度 0 。
• 三、通用气体常数 • 从阿佛加德罗定律可知,各种气体的 1mol的气体常数( R )都相等。 • 由此有: P V URT • 对于第一种气体a得
PV 56 105 0.02 m 1.332kg RT 287 293
• 二、阿佛加德罗定律 • 阿佛加德罗定律表述为:在同温同压下,同 体积的各种完全气体具有相同的分子数。 2N • 因为 P CT 3V • • 那么,对于两种不同的气体a和b有
2 Na Pa CTa 3 Va
• 故 N m N ,又由于 V mv ,得
• 则 •
N V v
PV 2 N C T 3
N 为一定值,而 C是比 • 对于给定的气体, 例系数,所以上式的右边乃是一个常数。由 此可见。此常数不随气体状态而变化,而只 决定于气体的性质。现在称此常数为气体常 数,以符号R表示之,即
•
在SI制中,压力单位为帕(Pa),即牛顿每 平方米,比容的单位为立方米每千克,绝对 温度的单位为(k),因此,可得出气体常数 3 m 的单位是 / kg
Pv (N / m ) m / kg PV R N m / kg K T K T Pv J / kg K T
2 3
• 其中牛顿米( N m )是功的单位,又叫做焦 耳,以符号J表示之。
• 在工程制中,压力的单位为千克/每平方 2 kg / m 米( ),比容的单位为立方米每 3 ( m / kg ),绝对温度的单位为开(K),故 气体常数的单位为千克米每千克开尔文,即 •
kg m /(kg k )
§1——7 完全气体状态方程式 通用气体常数
• 一、完全气体状态方程式 • 根据气体分子运动的基本方程来推导完全 气体状态方程式。
2 m0 w 2 P nCT 3 3 3 • 式中 n—分子浓度,即单位容积的分子数, 若容积V内的分子数为N,则 N n V
2
N N ,即1kg气体的分子数, • 令 m
•
2 R N C 3
• 由于是1kg气体的分子数,所以这时的R就 叫做1千克气体的气体常数。得 • Pv RT
• 或 P RT • r • 或 P RT g • • 这就是完全气体的状态方程式或特性方程 式,它是对1千克气体而言。
• 根据状态方程式可以由任意状态的两个已知 参数去计算第三个参数。对于mkg气体, 则完全气体的状态方程式为 pmv mRT 或 PV mR •
2 Nb Pb CTb 3 Vb
• 当 Pa Pb、 Ta Tb、 Va Vb 时,由上述两式 • 即可得 N a Nb • • 可以推知:在同温同压下,同容积的各种气 体的质量之比,等于其分子量之比。由于气 体的质量与分子数和分子量的乘积成正比, 所以
ma N a a a mb N b b b
• 完全气体的状态方程式也可以用微分形式 表示: dP dv dT • P v T • 或 dP d dT • P T • 上式说明了完全气体的状态参数相对变 化之间的关系式。 例 在标准状态下(压力为latm,温度为0℃ 时的状态),测出空气的密度为 3 kg / m 1.293 ,求空气的气体常数。
• 空气是氧、氮等气体的混合物,它具有单一气体 的性质,也是符合完全气体状态方程的。 • 解 因为气体常数R与气体所处的状态无关, 所以可以用任意状态下的参数求气体常数R的数 值。根据题意,空气在标准状态下的参数 P0 = 1.01325bar = 101325Pa • • T0 =273.15K 0 1.293 kg / m3
• 1摩尔补充说明:摩尔是物质的量的单 位。热力学中把气体中所包含的分子 数与0.012kg碳—12的原子数目相等时 气体的量,叫做1摩尔。当物质的克数 等于该物质的分子量时,就叫做1摩尔。 例如,氧气的分子量是32,那么32g 的氧气便是lmol的氧,64g的氧气便是 2mol的氧,气体的摩尔数以M表示, 则 m( g )
m a m a / Va Pa Va mb mb / Vb Pb Vb
•
或
a Vb b Va
a Vb b Va
• 说明在同温同压下,各种完全气体的摩尔 体积相等。
P0 101325 R 287J / kg K 0T0 1.293 2735
• 例 容积为20L的空气瓶,压力表上指压力 为55bar,温度为20°C,求气瓶的空气质 量。如果在起动发动机时,用去了2/5(按 质量计),而其温度不变,则瓶中的空气绝 对压力为多少? • 解 已知 6 • P≈55+1=56bar=56×10 Pa • T ≈273十20=293K 20 V 0.02 m 3 R 287J / kg K 1000
完全气体与实际气体 状态方程式 通用气体常数
介绍完全气体与实际气体的区别 完全气体状态方程式的应用 完全气体状态方程式的推导
完全气体状态方程式的应用 通用气体常数的意义
2/6
§1—6 完全气体与实际气体
• • • • 一、实际气体 日常所见到的气体就是实际气体。 二、完全气体 气体分子设想只有质量而没有体积,分子 间完全没有作用力的气体,叫做完全气体。 • 航空发动机所用的工质——空气和燃气, 一般在压力不太大,温度不太低的条件下 工作,基本上符合完全气体的两个假定, 所以可把空气和燃气当作完全气体。
M
• lmol气体所占的体积,叫做1摩尔体积。 • 在标准状态下,1mol气体占有的体积叫 做标准摩尔体积,任何完全气体在标准状 态下的摩尔体积约为22.4升(精确值应为 22.41383升)。在已知各气体的分子量μ 以后,则很容易求得在标准状态下该气体 的比容 v0 和密度 0 。
• 三、通用气体常数 • 从阿佛加德罗定律可知,各种气体的 1mol的气体常数( R )都相等。 • 由此有: P V URT • 对于第一种气体a得
PV 56 105 0.02 m 1.332kg RT 287 293
• 二、阿佛加德罗定律 • 阿佛加德罗定律表述为:在同温同压下,同 体积的各种完全气体具有相同的分子数。 2N • 因为 P CT 3V • • 那么,对于两种不同的气体a和b有
2 Na Pa CTa 3 Va
• 故 N m N ,又由于 V mv ,得
• 则 •
N V v
PV 2 N C T 3
N 为一定值,而 C是比 • 对于给定的气体, 例系数,所以上式的右边乃是一个常数。由 此可见。此常数不随气体状态而变化,而只 决定于气体的性质。现在称此常数为气体常 数,以符号R表示之,即
•
在SI制中,压力单位为帕(Pa),即牛顿每 平方米,比容的单位为立方米每千克,绝对 温度的单位为(k),因此,可得出气体常数 3 m 的单位是 / kg
Pv (N / m ) m / kg PV R N m / kg K T K T Pv J / kg K T
2 3
• 其中牛顿米( N m )是功的单位,又叫做焦 耳,以符号J表示之。
• 在工程制中,压力的单位为千克/每平方 2 kg / m 米( ),比容的单位为立方米每 3 ( m / kg ),绝对温度的单位为开(K),故 气体常数的单位为千克米每千克开尔文,即 •
kg m /(kg k )
§1——7 完全气体状态方程式 通用气体常数
• 一、完全气体状态方程式 • 根据气体分子运动的基本方程来推导完全 气体状态方程式。
2 m0 w 2 P nCT 3 3 3 • 式中 n—分子浓度,即单位容积的分子数, 若容积V内的分子数为N,则 N n V
2
N N ,即1kg气体的分子数, • 令 m
•
2 R N C 3
• 由于是1kg气体的分子数,所以这时的R就 叫做1千克气体的气体常数。得 • Pv RT
• 或 P RT • r • 或 P RT g • • 这就是完全气体的状态方程式或特性方程 式,它是对1千克气体而言。
• 根据状态方程式可以由任意状态的两个已知 参数去计算第三个参数。对于mkg气体, 则完全气体的状态方程式为 pmv mRT 或 PV mR •
2 Nb Pb CTb 3 Vb
• 当 Pa Pb、 Ta Tb、 Va Vb 时,由上述两式 • 即可得 N a Nb • • 可以推知:在同温同压下,同容积的各种气 体的质量之比,等于其分子量之比。由于气 体的质量与分子数和分子量的乘积成正比, 所以
ma N a a a mb N b b b
• 完全气体的状态方程式也可以用微分形式 表示: dP dv dT • P v T • 或 dP d dT • P T • 上式说明了完全气体的状态参数相对变 化之间的关系式。 例 在标准状态下(压力为latm,温度为0℃ 时的状态),测出空气的密度为 3 kg / m 1.293 ,求空气的气体常数。
• 空气是氧、氮等气体的混合物,它具有单一气体 的性质,也是符合完全气体状态方程的。 • 解 因为气体常数R与气体所处的状态无关, 所以可以用任意状态下的参数求气体常数R的数 值。根据题意,空气在标准状态下的参数 P0 = 1.01325bar = 101325Pa • • T0 =273.15K 0 1.293 kg / m3
• 1摩尔补充说明:摩尔是物质的量的单 位。热力学中把气体中所包含的分子 数与0.012kg碳—12的原子数目相等时 气体的量,叫做1摩尔。当物质的克数 等于该物质的分子量时,就叫做1摩尔。 例如,氧气的分子量是32,那么32g 的氧气便是lmol的氧,64g的氧气便是 2mol的氧,气体的摩尔数以M表示, 则 m( g )
