山科大材料力学复习9章后
材料力学(第四版)第九章

Pl M z max 4 43.3MPa Wz Wz
它比α=150时的斜弯曲最大正应力151.5Mpa小很多。可见, 当 Wy Wz 时,尽管荷载偏离y轴一个不大的角度,也会使梁的 正应显著增加,所以,在工程中应尽量避免发生斜弯曲.
例 :矩形截面木檩条如图,跨长L=3.3m,受集度为 q=800N/m 的均布力作用, []=12MPa,容许挠度为:L/200 ,E=9GPa, q 试校核此梁的强度和刚度。
Mz My
z
中性轴
y
6.最大正应力及强度条件 在危险截面上作与中性轴平行且与截面只有一个交点的直 线,则这些交点距离中性轴最远。由斜弯曲正应力计算公式可 知,这些交点就是最大正应力作用点。 本例中的矩形截面悬臂梁的最大正应力发生在固定端截面 的a点(最大拉应力)和c点(最大压应力),强度条件为:
max
M z ,max y max Iz M y ,max Wy
M y ,max z max Iy
Mz My
M z ,max Wz
P y
z
中性轴
7.变形计算 斜弯曲的变形计算也可用叠加法。 Py引起的自由端的挠度 Py l 3 P cos l 3
fy 3EI z 3EI z
2.查型钢表得: No.32a工字钢的 Wz 692.2cm3
Wy 70.758cm3
A
C
B x Pz z
P a Py y l P
3.校核梁的正应力强度
max
M z max M y max 151.5MPa 160MPa Wz Wy
所以,梁的正应力强度足够。 附:本题中,若α=00,则梁发生平面弯曲,此时
材料力学答案第9章

通解为
w1 = A1sinkx1 + B1coskx1 +
w2 = A2 sinkx 2 + B2 coskx 2 +
当 x1 = 0,w1 = 0 → B1 = 0 当 x 2 = 0,w2 = 0 → B2 = 0 当 x1 = x2 = 或写成
l F ′ = − w2 ′ ,w1 = w2 = c ,w1 2 c
式中,
k12 =
以上二微分方程的通解为
F F 2 ,k 2 = EI 1 EI 2
w1 = A1sink1 x1 + B1cosk1 x1 + δ w2 = A2 sink 2 x 2 + B2 cosk 2 x 2 + δ
定未知常数的条件为
8
′=0 x1 = 0,w1 = 0,w1 x1 = l ′ = w2 ′ ,w1 = w2,w1 x2 = 0 x2 = l,w2 = δ
3
的扭力矩为
M B = Fϕa
而
ϕ=
注意到 T = M B ,于是得
Tl GI p
F=
即
GI p al
πGd 4 Fcr = = al 32al
由此得(题中给出 F= 42kN )
GI p
d=
4
32alFcr = πG
4
32 × 0.500 × 0.300 × 42 ×103 m = 0.030m = 30mm π × 79 ×10 9
题 9-10 图 解:该细长压杆的微弯状态如图 9-10 所示。
按图中所取坐标,有
M ( x1 ) =
Fc F x1 − Fw1,M ( x 2 ) = c x 2 − Fw2 2 2
【智慧树知到】《工程力学(山东科技大学)》章节测试题及答案

【智慧树知到】《工程力学(山东科技大学)》章节测试题及答案第一章测试1、凡是受二力作用的直杆就是二力杆。
()正确答案:2、力的可传性()。
A、适用于同一刚体B、适用于刚体和变形体C、适用于刚体系统D、既适用于单个刚体,又适用于刚体系正确答案:3、在力的作用下不变形的物体称为()。
A、固体B、刚体C、永久体D、半固体易正确答案:4、光滑面和柔性体约束力FN、T的方向分别为( )。
A、FN背离物体、T指向物B、FN背离物体、T背离物体C、FN指向物体、T指向物体D、FN指向物体、T背离物体正确答案:5、力对刚体的作用效果决定于()。
A、力的大小和力的方向B、力的方向和力的作用点C、力的大小、力的方向、力的作用点D、力的大小、力的作用点正确答案:第二章测试1、无论平面汇交力系所含汇交力的数目是多少,都可用力多边形法则求其合力。
()正确答案:2、用解析法求解平面汇交力系的平衡问题时,所取两投影轴必须相互垂直。
()正确答案:3、力在轴上投影是()。
A、矢量B、代数量C、零D、不一定是矢量正确答案:4、平面汇交力系平衡的几何条件是()。
A、力多边形自行封闭B、力多边形成圆形C、力多边形成正方形D、力多边形成三角形正确答案:5、已知、、、、为作用于刚体上的平面共点力系,其力矢关系如图所示为平行四边形,由此可知()。
A、力系可合成为一个力偶B、力系可合成为一个力C、力系简化为一个力和一个力偶D、力系的合力为零,力系平衡正确答案:第三章测试1、力偶中二力对其中作用面内任意一点的力矩之和等于此力偶的力偶矩。
()正确答案:2、力偶只能使刚体转动,而不能使刚体移动。
()正确答案:3、作用于物体上同一点的两个力,可以合成为一个()。
A、合力B、力偶C、一个力和一个力偶D、力矩正确答案:4、图示半径为r的鼓轮,作用力偶m,与鼓轮左边重P的重物使鼓轮处于平衡,轮的状态表明()。
A、力偶可以与一个力平衡B、力偶不能与力偶平衡C、力偶只能与力偶平衡D、一定条件下,力偶可以与一个力平衡正确答案:5、互成平衡的两个力对同一点之矩的代数和为()。
山东科技大学材料力学2004--2006 2008,2013--2014,2016--2019年考研真题
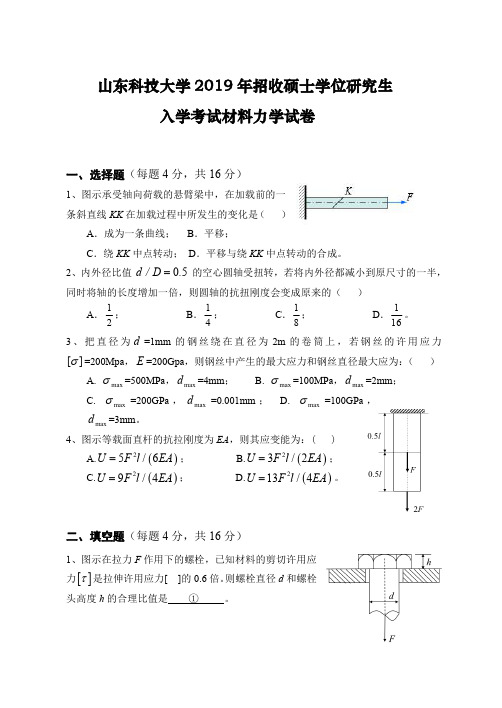
山东科技大学2019年招收硕士学位研究生入学考试材料力学试卷一、选择题(每题4分,共16分)1、图示承受轴向荷载的悬臂梁中,在加载前的一条斜直线KK 在加载过程中所发生的变化是()A .成为一条曲线;B .平移;C .绕KK 中点转动;D .平移与绕KK 中点转动的合成。
2、内外径比值05d /D .=的空心圆轴受扭转,若将内外径都减小到原尺寸的一半,同时将轴的长度增加一倍,则圆轴的抗扭刚度会变成原来的()A .21;B .41;C .81;D .161。
3、把直径为d =1mm 的钢丝绕在直径为2m 的卷筒上,若钢丝的许用应力][σ=200Mpa ,E =200Gpa ,则钢丝中产生的最大应力和钢丝直径最大应为:()A.max σ=500MPa ,max d =4mm ; B.max σ=100MPa ,max d =2mm ;C.max σ=200GPa ,max d =0.001mm ;D.max σ=100GPa ,max d =3mm 。
4、图示等载面直杆的抗拉刚度为EA ,则其应变能为:()A.()25/6U F l EA =; B.()23/2U F l EA =;C.()29/4U F l EA =;D.()213/4U F l EA =。
二、填空题(每题4分,共16分)1、图示在拉力F 作用下的螺栓,已知材料的剪切许用应力[]τ是拉伸许用应力[]的0.6倍。
则螺栓直径d 和螺栓头高度h 的合理比值是①。
2、螺栓受轴向的最大拉力F max =6kN ,最小拉力F min =5kN 作用;螺栓直径d =12mm ,则其交变应力的循环特征r =②,应力幅值a σ=③MPa ,平均应力m σ=④MPa 。
3、已知图(a )所示梁C 截面的转角()2/8c Fl EI θ=,则图(b )所示梁B 截面的挠度为⑤。
4、图示梁的A、B、C、D 四点中,单向应力状态的点是⑥,纯剪应力状态的点是⑦,在任何截面上应力均为零的点是⑧。
材料力学知到章节答案智慧树2023年山东科技大学

材料力学知到章节测试答案智慧树2023年最新山东科技大学第一章测试1.材料力学的研究方法与理论力学的研究方法完全相同。
参考答案:错2.内力只作用在杆件截面的形心处。
参考答案:错3.杆件某截面上的内力是该截面上应力的代数和。
参考答案:错4.确定截面内力的截面法,适用于不论等截面或变截面、直杆或曲杆、基本变形或组合变形、横截面或任意截面的普遍情况。
参考答案:对5.根据各向同性假设,可认为材料的弹性常数在各方向都相同。
参考答案:对6.根据均匀性假设,可认为构件的弹性常数在各点处都相同。
参考答案:对7.若物体各部分均无变形,则物体内各点的应变均为零。
参考答案:对8.外力就是构件所承受的载荷。
参考答案:错9.构件的强度、刚度和稳定性问题均与材料的力学性能有关。
参考答案:对10.可变形固体的变形必须满足几何相容条件,即变形后的固体既不可以引起“空隙”,也不产生“挤入”现象。
参考答案:对11.材料力学的研究对象为杆件。
参考答案:对12.题图所示直杆初始位置为ABC,作用力P后移至AB’C’,但右半段BCDE的形状不发生变化。
试分析哪一种答案正确。
参考答案:AB、BC两段都产生位移;13.根据各向同性假设,可认为构件的()沿各个方向相同。
参考答案:材料的弹性常数14.关于确定截面内力的截面法的适用范围,有下列说法正确的是()。
参考答案:不论等截面或变截面、直杆或曲杆、基本变形或组合变形、横截面或任意截面的普遍情况15.下列结论中是正确的是()。
参考答案:若物体各点均无位移,则该物体必定无变形16.以下结论中正确的是()。
参考答案:应力是内力的集度17.根据均匀性假设,可认为构件的下列各量中的哪个量在各点处都相同。
参考答案:材料的弹性常数18.材料力学的四个基本假设是()参考答案:连续性;各向同性;均匀性;小变形19.工程构件的基本类型是()参考答案:壳;板;杆件;块体20.下列描述正确的是()参考答案:应力是构件破坏的决定因素;应力是指内力的分布集度;应变是描述构件变形程度的量第二章测试1.因为轴力要按平衡条件求出,所以轴力的正负与坐标轴的指向一致。
完整版材料力学各章重点内容总结

完整版材料力学各章重点内容总结材料力学各章重点内容总结第一章绪论一、材料力学中工程构件应满足的3方面要求是:强度要求、刚度要求和稳定性要求。
二、强度要求是指构件应有足够的抵抗破坏的能力;刚度要求是指构件应有足够的抵抗变形的能力;稳定性要求是指构件应有足够的保持原有平衡形态的能力。
三、材料力学中对可变形固体进行的3个的基本假设是:连续性假设、均匀性假设和各向同性假设。
第二章轴向拉压、轴力图:注意要标明轴力的大小、单位和正负号。
、轴力正负号的规定:拉伸时的轴力为正,压缩时的轴力为负。
注意此规定只适用于轴力,轴力是内力,不适用于外力。
、轴向拉压时横截面上正应力的计算公式: F N注意正应力有正负号,A拉伸时的正应力为正,压缩时的正应力为负。
四、斜截面上的正应力及切应力的计算公式:注意角度是指斜截面与横截面的夹角七、线应变一-没有量纲、泊松比一没有量纲且只与材料有关、l胡克定律的两种表达形式: E , I 出注意当杆件伸长时I 为正,EA缩短时I 为负。
八、低碳钢的轴向拉伸实验:会画过程的应力一应变曲线,知道四个阶段及相应的四个极限应力:弹性阶段(比例极限p,弹性极限e )、屈服阶段(屈服极限s )、强化阶段(强度极限 b )和局部变形阶段会画低碳钢轴向压缩、铸铁轴向拉伸和压缩时的应力一应变曲线cos 2 ,sin2五、轴向拉压时横截面上正应力的强度条件F N,maxmaxA六、利用正应力强度条件可解决的三种问题: 1?强度校核maxF N ,maxA定要有结论 2.设计截面A F N,max3.确定许可荷载F^max A180八、圆轴在扭转时的刚度条件maxT maxGI p(注意单位:给出的许用单九、衡量材料塑性的两个指标:伸长率耳100 及断面收缩率 A-A 1100,工程上把 5 的材料称为塑性材料。
十、卸载定律及冷作硬化:课本第23页。
对没有明显屈服极限的塑性材料,如何来确定其屈服指标?见课本第24页。
材料力学9-知识归纳整理
求知若饥,虚心若愚。 第 8 页/共 148 页
千里之行,始于足下。 第 9 页/共 148 页
求知若饥,虚心若愚。 第 10 页/共 148 页
千里之行,始于足下。 第 11 页/共 148 页
求知若饥,虚心若愚。 第 12 页/共 148 页
千里之行,始于足下。 第 13 页/共 148 页
求知若饥,虚心若愚。 第 20 页/共 148 页
千里之行,始于足下。 第 21 页/共 148 页
求知若饥,虚心若愚。 第 22 页/共 148 页
千里之行,始于足下。 第 23 页/共 148 页
求知若饥,虚心若愚。 第 24 页/共 148 页
千里之行,始于足下。 第 25 页/共 148 页
求知若饥,虚心若愚。 第 62 页/共 148 页
千里之行,始于足下。 第 63 页/共 148 页
求知若饥,虚心若愚。 第 64 页/共 148 页
千里之行,始于足下。 第 65 页/共 148 页
求知若饥,虚心若愚。 第 66 页/共 148 页
千里之行,始于足下。 第 67 页/共 148 页
求知若饥,虚心若愚。 第 14 页/共 148 页
千里之行,始于足下。 第 15 页/共 148 页
求知若饥,虚心若愚。 第 16 页/共 148 页
千里之行,始于足下。 第 17 页/共 148 页
求知若饥,虚心若愚。 第 18 页/共 148 页
千里之行,始于足下。 第 19 页/共 148 页
知识归纳整理 第 1 页/共 148 页
求知若饥,虚心若愚。 第 2 页/共 148 页
千里之行,始于足下。 第 3 页/共 148 页
求知若饥,虚心若愚。 第 4 页/共 148 页
材料力学全部习题解答讲解
1 2 R2
3
2
(b)
yc =
ydA
A
=
A
b 0
y ayndy b ayndy
=
n n
1 2
b
0
26
Iz =
y2dA
A
Iy =
z2dA
A
解: 边长为a的正方截面可视为由图示截面和一个半 径为R的圆截面组成,则
Iz
=I(za)
I(zR)=
a4 12
2R 4
0
FN A
10103 N 1000 106 m2
10MPa
由于斜截面的方位角 450
得该截面上的正应力和切应力分别为
45
0 cos2 10106 cos2 450 pa 5MPa
0 sin 2 1 10106 sin 900 pa 5MPa
2
18
解:1.求预紧力 由公式l FNl 和叠加原理,故有
EA
l
l1
l2
l3
Fl1 EA1
Fl2 EA2
Fl3 EA3
4F
E
l1 d12
l2 d22
l3 d32
由此得 F
El
18.65kN
4
l1
d
2 1
l2
d
2 2
l3
根据式
tan 2 2I y0z0
I z0 I y0
解得主形心轴 y 的方位角为 a =
3.计算主形心惯性矩
材料力学-单祖辉-第三版课后答案-(第九章—第十九章)
σr2 σ1 μ(σ2 σ3)[σ] 将上述各主应力值代入上式,得
σr2 [100.25(42.7)] MPa20.7 MPa[σ] 可见,该铸铁构件满足强度要求。
9-12 图示圆球形薄壁容器,其内径为 D,壁厚为 ,承受压强为 p 之内压。试证明
r3 2 4 2 154.52 414.962 MPa 157.4MPa [ ] b 点处的正应力和切应力分别为
3
σ
M yb Iz
7.80104 (0.140 0.0137)N 7.07105 m2
1.393108
Pa 139.3
MPa
τ
FS S z ( b ) Izδ
130103 2.23104 N 7.07105 0.0085m2
(α1
α2
)ΔT
FN1 E1 A1
FN2 E2 A2
σ1t E1
σ2t E2
(d)
由式(a)可知,
σ1t
A1
σ2t
A2,
σ1t σ2t
A2 A1
δ2 δ1
即
σ1t
δ2 δ1
σ2t
(e)
将方程(e)与方程(d)联立求解,得铜环和钢环内的周向正应力依次为
σ1t
(α1 α2 )E1E2δ2 E1δ1 E2δ2
4.82107
Pa 48.2
MPa
该点也处于单向与纯剪切组合应力状态,其相当应力为
r3 139.32 448.22 MPa169.4MPa[ ] c 点处于纯剪切应力状态,其切应力为
τ
FS S z ,max Izδ
材料力学各章节知识点
◆第一部分:辅导班授课思路(大工名师授课)材料力学相对知识点多而杂。
但各知识点相对独立,相应章节出大题多是“拼盘”式的组合,但要求对每个知识点深刻理解,搞懂搞透!!各章节知识点:材力一:第一章:了解,没什么重要知识点。
第二章:轴向拉伸压缩。
轴力,轴力图。
与后面超静定一起出题。
年年考。
正应力,切应力,低碳钢拉伸试验,弹性变形,塑性变形,变形四阶段,塑性指标,轴向拉伸应变,变形。
第三章:扭转。
比较简单,考扭转超静定。
圆轴扭转切应力,扭转角,最大切应力,扭转强度刚度验算。
第四章:弯曲应力。
重点!!!每年考2~3道大题。
详细见讲义和讲课。
弯矩剪力图,年年考,送分题,每年10分,考专业基本功。
梁的正应力,正应力强度验算。
梁的切应力,切应力强度验算。
第五章:梁弯曲位移挠度,转角,挠曲线大致形状,叠加法求梁的挠度,积分法求梁的挠度。
每年一题。
第六章:超静定问题。
出综合大题。
拉伸超静定,弯曲超静定,扭转超静定。
每年一题。
难度较大。
第七章:应力状态和强度理论。
重点!!!每年30分左右。
详细见讲义和讲课。
任意截面正应力,切应力。
主应力。
主平面。
应力圆。
应力应变关系,应变能,应变能密度。
四大强度理论。
双剪强度理论,莫尔强度理论。
第八章:组合变形。
年年考拉伸,弯曲,扭转组合变形。
难度大。
但深刻理解后,比较简单。
第九章:压杆稳定。
冲击荷载。
临界压力,临界压力图,稳定性计算。
材力二:第一章:5个问题1.两个公式,正应力,角2.两种材料。
重点3.弯曲中心。
4.约束扭转5.曲杆计算第二章:塑性。
重点详细见讲课内容。
第三章:能量法应变能,余能计算。
第四章:了解第五章:应变状态分析,重点.详细见讲课内容。
第六章:动荷载年年考第七章:不是重点,看看。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
① 90 ②
CL13TU16
解:由静力平衡条件可解得两杆的压力分别为:
N1 P cos , N2 P sin
两杆的临界压力分别为:
2E I
Pcr1 l12
,
2E I
Pcr 2 l22
要使P最大,只有N1、N 2 都达
到临界压力,即
P cos
2E l12
I
(1)
①
90
②
P sin
2E
l2 2
200 106 100
所以,只有压杆的长细比λ≥100时,才能应用 欧拉公式计算其临界压力。
当压杆的长细比λ<λp时,欧拉公式已不 适用。在工程上,一般采用经验公式。 在 我国的设计手册和规范中给出的是直线公式和 抛物线公式。
直线公式 cr a b
式中 a、b是与材料性质有关的系数。
下面考虑经验公式的适用范围:
2EI 2EI 2EI
Pcr l 2
(2l )2 (0.7l )2
2EI
(0.5l )2
附:求二阶常系数齐次微分方程y p y q 0 的通解
特征方程为 r 2 pr q 0 ①两个不相等的实根 r1、r2 通解
y C1er1 x C2er2 x ②两个相等的实根 r1 r2 通解
CL13TU10
解:图(a)中,AD杆受压
N AD
2EI
2 P1
2
2a
P1
1 22
2EI
a2
图(b)中,AB杆受压
2EI
N AB P2 a 2
2EI
P2 a 2
例:圆截面的细长压杆,材料、杆长和杆端 约束保持不变,若将压杆的直径缩小一半,则 其临界力为原压杆的_____;若将压杆的 横截面改变为面积相同的正方形截面,则其临 界力为原压杆的_____。
正方形
等边角钢
槽钢
CL13TU12
例:五根直径都为 d的细长圆杆铰接构成 平面正方形杆系ABCD,如各杆材料相同,弹 性模量为E。求图 (a)、(b)所示两种载荷作用下 杆系所能承受的最大载荷。
CL13TU15
解:(a) 杆BD受压,其余杆受拉
BD杆的临界压力:
2EI 2EI
Pcr
2 2a
解:(1)
2EI Pcr ( l)2
2E d4
64
( l)2
1 16
2E I正
(2)
Pcr 正 Pcr 圆
( l)2 2E I圆
( l)2
d2 2
a4 4
I正 I圆
12
d4
12
d4
3
64
64
例:三种不同截面形状的细长压杆如图所 示。试标出压杆失稳时各截面将绕哪根形心主 惯性轴转动。
分方程
E I v M(x)
在推导该方程时,应用了胡克定律。因此,欧拉 公式也只有在满足胡克定律时才能适用:
cr
2E 2
p
或写成
2E p
记
p
2E p
则 欧拉公式的适用范围:
p
满足该条件的杆称为细长杆或大柔度杆
对A3钢,当取E=206GPa,σp=200MPa,则
p
2E p
2 206 109
k n P
l EI
P
n
2
k
l
2
2
2
E
IP
EI
§13-3 压杆的临界应力及临界应力总图
一、压杆的临界应力
2EI Pcr (l )2
cr
Pc r A
2EI (l )2 A
2 E (i 2 A) (l )2 A
2E l 2
i
令 l
i
则
cr
2E 2
二、欧拉公式的适用范围 经验公式
在推导欧拉公式时,使用了挠曲线的近似微
二、其它杆端约束条件下细长压杆的临界压力
2EI Pcr (l )2 称为长度系数
l
i
crΒιβλιοθήκη 2E 2压杆的长细比 压杆的柔度
计算压杆的临界 应力的欧拉公式
2EI
Pcr l 2
1
2EI
Pcr (2 l)2
2
2EI
Pcr (0.7 l)2
0.7
2EI
Pcr (0.5l)2
0.5
y (C1 C2 x)er1 x
③一对共轭复根 r1,2 i 通解 y e x (C1 cos x C2 sin x)
通解: v Asin kx B cos kx
边界条件:x 0时:v 0 B 0
x l 时:v 0 Asin kl 0
sin kl 0 kl n (n 0,1,2,)
对于塑性材料:
cr a b s
即
as
b
记
s
a
s
b
则 s p 经验公式的适用范围
对于 λ<λs的杆,不存在失稳问题,应考虑强
度问题
cr s
经验公式中,抛物线公式的表达式为
cr a1 b12
式中 a1、b1 也是与材料性质有关的系数,可
在有关的设计手册和规范中查到。
I
(2)
将式(2)除以式(1), 便得
tg
l1 l2
2
ctg 2
由此得 arc tg(ctg2)
① 90 ②
第十章 动载荷(Dynamic loading)
§10-1 概述 §10-2 动静法的应用 §10-3 构件受冲击时的应力和变形 §10-4 冲击韧性
l
i
CL13TU20
§13-4 压杆的稳定性计算
稳定性条件:
Pmax
Pc r [nst ]
式中 Pmax ------压杆所受最大工作载荷 Pcr ------压杆的临界压力 [nst ] ------压杆的规定稳定安全系数
稳定性条件也可以表示成: nst
Pc r Pmax
[nst ]
式中 nst 为压杆实际的工作稳定安全系数。
三、临界应力总图
1. 细长杆( p ), 用欧拉公式
cr
2E 2
2. 中长杆( s p ), 用经验公式
cr a b
3. 粗短杆( s ), 用强度条件
cr s
cr s cr s
p
cr a b
cr
2E 2
小柔度杆 中柔度杆 大柔度杆
O
s
a
s
b
p
2E p
例:非细长杆如果误用了欧拉公式计算临 界力,其结果比实际_大_,_危_险__;横截面上 的正应力有可能__超_过_比_例_极_限__。
例:图示两桁架中各杆的材料和截面均相 同,设P1和P2分别为这两个桁架稳定的最大载 荷,则
(A) P1=P2 (C) P1>P2
(B) P1<P2 (D) 不能断定P1和P2的关系
2a 2
故杆系所能承受的最大载荷
Pmax
Pcr
2EI
2a 2
3Ed4
128a 2
(b) 杆BD受拉,其余杆受压 四根受压杆的临界压力:
2EI
Pcr a 2 故杆系所能承受的最大载荷:
2 3Ed4
Pmax 2 Pcr 64a 2
例:图示结构,①、②两杆截面和材料相 同,为细长压杆。确定使载荷 P 为最大值时的 θ角(设0<θ<π/2)。
