2015年全国卷2高考文科数学试题附答案
2015年全国新课标2卷高考文科数学答案
2015年全国新课标2卷高考文科数学答案2015普通高等学校招生全国统一考试?卷文科数学第一卷一、选择题:本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。
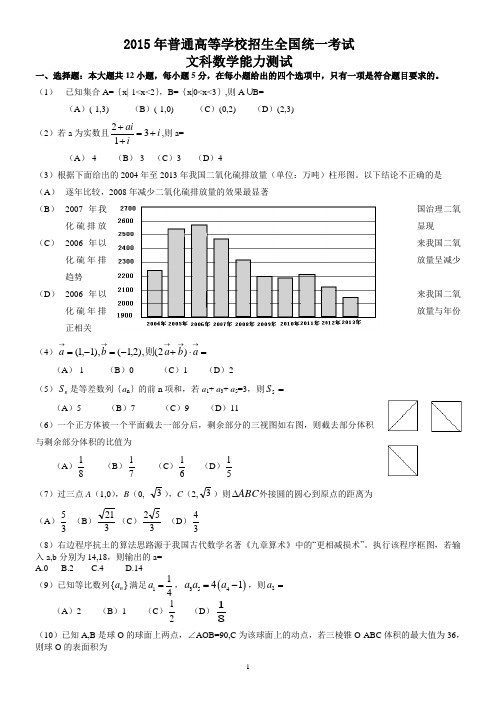
(1)已知集合A= ,,,,x,1,x,2,B,x0,x,3,则A:B,A.(-1，3)B.(-1，0 )C.(0，2)D.(2，3)1、选A2，ai(2)若a实数，且,3，i,则a, 1，iA.-4B. -3C. 3D. 4 2、解:因为故选D 2，ai,(3，i)(1，i),2，4i,所以a,4.(3)根据下面给出的2004年至2013年我国二氧化碳年排放量(单位:万吨)柱形图，以下结论中不正确的是27002600250024002300220021002000 1900A.逐年比较，2008年减少二氧化碳排放量的效果最显著;2013(年)B.2007年我国治理二氧化碳排放显现成效;C.2006年以来我国二氧化碳排放量呈减少趋势;D.2006年以来我国二氧化碳年排放量与年份正相关。
3、选D(4)已知向量 a,(0,,1),b,(,1,2),则(2a，b),a,A. -1B. 0C. 1D. 2 、选B 4,,S是等差数列a的前n项和，a，a，a,3,则S,(5)设若 nn1355A. 5B. 7C. 9D. 11 5、解:在等差数列中，因为(a，a)，515a，a，a,3,所以a,1,S,,5a,5,故选A. 1353532(6)一个正方体被一个平面截去一部分后，剩余部分的三视图如右图，则截去部分体积与剩余部分体积的比值为- 1 -1111A. B. C. D. 87656、解:如图所示，选D.,ABC(7)已知三点,则外接圆的A(1，0),B(0，3)，C(2，3)圆心到原点的距离为542125A. B. C. D. 33337、解:根据题意，三角形ABC是等边三角形，设外接圆的23圆心为D，则D(1，)所以， 34721OD,1，,,.故选B. 333(8)右边程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”。
2015年全国新课标2卷高考文科数学及答案详解
2015年普通高等学校招生全国统一考试(新课标Ⅱ卷)数学(文科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，共150分，考试时间120分钟．第Ⅰ卷一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．已知集合{}{}30|,21|<<=<<-=x x B x x A ，则=⋃B A ( )A ．(－1,3)B ．(－1,0)C ．(0,2)D ．(2,3)2．若a 为实数，且i iai +=++312，则=a ( ) A ．－4 B ．－3 C ．3 D ．43．根据下面给出的2004年至2013年我国二氧化硫年排放量(单位：万吨)柱形图，以下结论中不正确的是( )A ．逐年比较，2008年减少二氧化硫排放量的效果最显著B ．2007年我国治理二氧化硫排放显现成效C ．2006年以来我国二氧化硫年排放量呈减少趋势D ．2006年以来我国二氧化硫年排放量与年份正相关4．向量()1,1-=a ，()2,1-=b ，则()=⋅+a b a 2 ( )A ．－1B ．0C ．1D ．25．设n S 是等差数列{}n a 的前n 项和，若3531=++a a a ，则=5S ( )A ．5B ．7C ．9D ．11 6.第6题图一个正方体被一个平面截去一部分后，剩余部分的三视图如右图，则截去部分体积与剩余部分体积的比值为( ) A.18 B.17 C.16 D.157．已知三点()01，A ()30，B ，()32，C ，则ABC ∆外接圆的圆心到原点的距离为( )A.53B.213C.253D.438.第8题图右边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”．执行该程序框图，若输入的a ，b 分别为14,18，则输出的=a ( )A ．0B ．2C ．4D ．149．已知等比数列{}n a 满足411=a ，()14453-=a a a ，则=2a ( ) A ．2 B ．1 C.12 D.1810．已知A ，B 是球O 的球面上两点，∠AOB ＝90°，C 为该球面上的动点．若三棱锥O ABC 体积的最大值为36，则球O 的表面积为( ) A ．36π B ．64π C．144π D．256π11.如图，长方形ABCD 的边AB ＝2，BC ＝1，O 是AB 的中点．点P 沿着边BC ，CD 与DA 运动，记∠BOP ＝x ，将动点P 到A ，B 两点距离之和表示为x 的函数f (x )，则y ＝f (x )的图象大致为( )12.设函数()()2111ln x x x f +-+=，则使得()()12->x f x f 成立的x 的取值范围是( )A.⎝ ⎛⎭⎪⎫13，1B.()∞+⋃⎪⎭⎫ ⎝⎛∞，，131- C.⎝ ⎛⎭⎪⎫－13，13 D.⎪⎭⎫ ⎝⎛∞+⋃⎪⎭⎫ ⎝⎛∞，，3131-- 第Ⅱ卷二、填空题(本大题共4小题，每小题5分，共20分．把答案填在题中横线上)13．已知函数()x ax x f 23-=的图象过点()4,1-，则=a ________.14．若x ，y 满足约束条件⎩⎨⎧ x ＋y －5≤0，2x －y －1≥0，x －2y ＋1≤0，则y x z +=2的最大值为________． 15．已知双曲线过点()34，，且渐近线方程为x y 21±=，则该双曲线的标准方程为________．16．已知曲线x x y ln +=在点()1,1处的切线与曲线()122+++=x a ax y 相切，则=a ________. 三、解答题(解答应写出文字说明，证明过程或演算步骤)17．(本小题满分12分) ABC ∆中，D 是BC 上的点，AD 平分BAC ∠，DC BD 2=(1)求CB sin sin (2)若︒=∠60BAC ，求B ∠18.(本小题满分12分)某公司为了解用户对其产品的满意度，从A ，B 两地区分别随机调查了40个用户，根据用户对产品的满意度评分，得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频数分布表．图①B地区用户满意度评分的频数分布表满意度评分[50,60)[60,70)[70,80)[80,90)[90,100] 分组频数281410 6 2015·新课标Ⅱ卷第4页(1)在图②中作出B地区用户满意度评分的频率分布直方图，并通过直方图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值，给出结论即可)．图②(2)根据用户满意度评分，将用户的满意度分为三个等级：满意度评分 低于70分 70分到89分 不低于90分满意度等级 不满意 满意 非常满意估计哪个地区用户的满意度等级为不满意的概率大？说明理由．19.(本小题满分12分)如图，长方体1111D C B A ABCD -中，16=AB ，10=BC ,81=AA ，点E ,F 分别在11B A ,11C D 上，411==F D E A .过点E ,F 的平面α与此长方体的面相交，交线围成一个正方形．(1)在图中画出这个正方形(不必说明画法和理由)；(2)求平面α把该长方体分成的两部分体积的比值．20.(本小题满分12分)已知椭圆C ：12222=+by a x ()0.>>b a 的离心率为22，点()22，在C 上．(1)求C 的方程；(2)直线l 不过原点O 且不平行于坐标轴，l 与C 有两个交点A ,B ，线段AB 的中点为M .证明：直线OM 的斜率与直线l 的斜率的乘积为定值．21.(本小题满分12分)已知函数()()x a x x f -+=1ln ．(1)讨论()x f 的单调性；(2)当()x f 有最大值，且最大值大于22-a 时，求a 的取值范围．请考生在第22、23、24题中任选一题作答，如果多做，则按所做的第一题计分．作答时请写清题号．22. （本小题满分10分）选修4-1：几何证明选讲如图O 是等腰三角形AB C 内一点, ⊙O 与△ABC 的底边BC 交于M ,N 两点,与底边上的高交于点G ,且与AB ,AC 分别相切于E ,F 两点.（I ）证明EF ∥BC .（II ）若AG 等于⊙O 的半径,且23AE MN == ,求四边形EDCF 的面积23.（本小题满分10分）选修4-4：坐标系与参数方程在直角坐标系xOy 中,曲线1cos ,:sin ,x t C y t αα=⎧⎨=⎩ （t 为参数,且0t ≠ ）,其中0απ≤<,在以O 为极点,x 轴正半轴为极轴的极坐标系中,曲线23:2sin ,:23cos .C C ρθρθ== （I ）求2C 与3C 交点的直角坐标；（II ）若1C 与 2C 相交于点A ,1C 与3C 相交于点B ,求AB 最大值24.(本小题满分10分)选修4－5：不等式选讲设a ，b ，c ，d 均为正数，且a ＋b ＝c ＋d .证明：(1)若ab >cd ，则a ＋b >c ＋d ；N M G OFE D C B A(2)a＋b>c＋d是|a－b|<|c－d|的充要条件．2015·新课标Ⅱ卷第8页1、选A2、故选D3、选D4、选B5、解：在等差数列中，因为.,5525)(,1,335153531A a a a S a a a a 故选所以==⨯+===++6、解：如图所示，选D.7、选B.8、故选B.9、解：因为{}),1(4,414531-==a a a a a n 满足所以， .21241,2,2),1(4123144424=⨯=====-=q a a q q a a a a a 所以，所以又解得故选C.10、解：因为A,B 都在球面上，又为该球面上动点，C AOB ,90︒=∠所以 三棱锥的体积的最大值为3661213132==⨯⨯R R R ，所以R=6，所以球的表面积为 S=14442=R ππ，故选C.11、解：如图，当点P 在BC 上时， ,tan 4tan ,tan 4,tan ,22x x PB PA x PA x PB x BOP ++=+∴+===∠ 当4π=x 时取得最大值51+，以A,B 为焦点C,D 为椭圆上两定点作椭圆，显然，当点P 在C,D 之间移动时PA+PB<51+. 又函数)(x f 不是一次函数，故选B.xP O DC B A12、解：因为函数时函数是增函数是偶函数，),0[,11)1ln()(2+∞∈+-+=x x x x f .131,)12(,12)12()(22<<->∴->∴->x x x x x x f x f 解得 故选A.第二卷一、填空题：本大题共4个小题，每小题5分 13、答：a=-214、解：当x=3,y=2时，z=2x+y 取得最大值8.15、解：设双曲线的方程为.43,4),0(422=≠=-k k k y x ）代入方程，解得，点（1422=-∴y x 双曲线的标准方程为16、解：.122,11'-=∴+=x y xy ，切线方程为切线的斜率为 .8120.08,08,021)2(12222=+=====-=∆=+++++=-=a x y a a a a a ax ax x a ax y x y 所以与切线平行，不符。
2015年普通高等学校招生全国统一考试数学文试题(新课标2卷,含答案)
2015年普通高等学校招生全国统一考试文科数学注意事项：1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。
答卷前，考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上。
2．回答第Ⅰ卷时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号框涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号框。
写在本试卷上无效。
3．答第Ⅱ卷时，将答案写在答题卡上，写在本试卷上无效。
4．考试结束，将试题卷和答题卡一并交回。
第Ⅰ卷一、 选择题：本大题共12小题。
每小题5分，在每个小题给出的四个选项中，只有一项是符合要求的。
1.已知集合}21|{<<-=x x A ，}30|{<<=x x B ，则A ∪B=A. )3,1(-B. )0,1(-C. )2,0(D. )3,2( 2.若a 为实数，且i iai+=++312，则=a A. 4- B. 3- C. 3 D. 43. 根据下面给出的2004年至2013年我国二氧化碳年排放量（单位：万吨）柱形图，以下结论中不正确的是A.逐年比较，2008年减少二氧化碳排放量的效果显著B.2007年我国治理二氧化碳排放显现成效C.2006年以来我国二氧化碳年排放量呈逐渐减少趋势D.2006年以来我国二氧化碳年排放量与年份正相关 4.向量a=(1，-1) b=(-1，2)，则（2a +b ）.a=A. 1-B. 0C. 1D.2 5. 设n S 是数列}{n a 的前n 项和，若3531=++a a a ，则=5S A. 5 B. 7 C. 9 D. 116. 一个正方体被一个平面截取一部分后，剩余部分的三视图如图，则截去部分体积与剩余部分体积的比值为 A.81 B. 71 C. 61 D. 517.已知三点)0,1(A ，)3,0(B ，)3,2(C ，则ABC ∆外接圆的圆心到原点的距离为 A.35 B. 321 C. 352 D. 34 8.右边程序框图的算法思路源于我国古代数学名著《九章算术》中“更相减损术”.执行该程序框图，若输入的a 、b 分别为14、18，则输出的=aA. 0B. 2C. 4D. 149.已知等比数列}{n a 满足411=a ，)1(4453-=a a a ，则=2a A. 2 B. 1 C.21 D. 8110.已知A 、B 是球O 的球面上两点，90=∠AOB ，C 为该球面上的动点.若三棱锥ABC O -体积的最大值为36，则球O 的表面积为A. π36B. π64C. π144D. π25611.如图，长方形ABCD 的边2=AB ，1=BC ，O 是AB 的中点，点P 沿着BC 、CD 与DA 运动，记x BOP =∠.将动点P 到A 、B 两点距离之和表示为x 的函数)(x f ，则)(x f y =的图象大致为12. 设函数211|)|1ln()(xx x f +-+=，则使得)12()(->x f x f 成立的x 的取值范围是 A. )1,31( B. ),1()31,(+∞-∞U C. )31,31(- D. ),31()31,(+∞--∞U 二．填空题：共4小题，每小题5分.13. 已知函数x ax x f 2)(3-=的图象过点)4,1(-，则=a .14.若x 、y 满足约束条件⎪⎩⎪⎨⎧≤+-≥--≤-+01201205y x y x y x ，则y x z +=2的最大值为 .15.已知双曲线过点)3,4(，且渐近线方程为x y 21±=，则该双曲线的标准方程为 . 16.已知曲线x x y ln +=在点)1,1(处的切线与曲线1)2(2+++=x a ax y 相切，则=a .三、解答题：解答应写出文字说明，证明过程或演算步骤． 17、（本小题满分12分）ΔABC 中，D 是BC 上的点，AD 平分∠BAC ，BD=2DC.（I）求sinsinBC∠∠；（II）若∠BAC=60°,求∠B.18、（本小题满分12分）某公司为了解用户对其产品的满意度，从A，B两地区分别随机调查了40个用户，根据用户对产品的满意度评分，得分A地区用户满意评分的频率分布直方图和B地区用户满意度评分的频数分布表.B地区用户满意度评分的频数分布表度评分的平均值及分散程度（不要求计算出具体值，给出结论即可）(II)根据用户满意度评分，将用户的满意度分为三个等级；19、（本小题满分12分）如图，长方体ABCD﹣A1B1C1D1中，AB=16，BC=10，AA1=8,点E，分别在A1B1, D1C1上，A1E= D1F=4.过点E,F的平面α与此长方体的面相交，交线围成一个正方形.（I ） 在图中画出这个正方形（不必说明画法和理由） （II ）求平面α把该长方体分成的两部分体积的比值.20、（本小题满分12分）已知椭圆C ：22221x y a b +=（a >b >0）的离心率为2，点（2C 上.（I ） 求C 的方程.（II ）直线l 不过原点O 且不平行于坐标轴，l 与C 有两个交点A ，B ，线段AB 的中点为M.直线OM 的斜率与直线l 的斜率的乘积为定值. 21、（本小题满分12分） 已知函数f （x ）=ln x +a （1- x ） （I ） 讨论f （x ）的单调性；（II ） 当f （x ）有最大值，且最大值大于2a-2时，求a 的取值范围.请考生在第22、23、24题中任选一题作答，如果多做，则按所做的第一题记分，作答时请写清题号。
(完整word版)2015年全国新课标2高考数学文科试题及答案,推荐文档
2015年普通高等学校招生全国统一考试文科数学能力测试一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。
（1） 已知集合A=｛x|-1<x<2｝，B=｛x|0<x<3｝,则A ∪B=（A ）(-1,3) （B ）(-1,0) （C ）(0,2) （D ）(2,3)（2）若a 为实数且231aii i+=++,则a= （A ）-4 （B ）-3 （C ）3 （D ）4（3）根据下面给出的2004年至2013年我国二氧化硫排放量（单位：万吨）柱形图。
以下结论不正确的是 （A ） 逐年比较，2008年减少二氧化硫排放量的效果最显著 （B ） 2007年我国治理二氧化硫排放显现 （C ） 2006年以来我国二氧化硫年排放量呈减少趋势（D ） 2006年以来我国二氧化硫年排放量与年份正相关（4）=⋅+-=-=→→→→→a b a b a )2(),2,1(),1,1(则（A ）-1 （B ）0 （C ）1 （D ）2（5）n S 是等差数列｛a n ｝的前n 项和，若a 1+ a 3+ a 5=3，则=5S（A ）5 （B ）7 （C ）9 （D ）11（6）一个正方体被一个平面截去一部分后，剩余部分的三视图如右图，则截去部分体积与剩余部分体积的比值为（A ）81 （B ）71 （C ）61（D ）51 （7）过三点A （1,0），B （0, 3），C （2,3）则ABC ∆外接圆的圆心到原点的距离为（A ）35 （B ）321（C ）352 （D ）34（8）右边程序抗土的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”。
执行该程序框图，若输入a,b 分别为14,18，则输出的a= A.0 B.2 C.4 D.14 （9）已知等比数列{}n a 满足114a =，()35441a a a =-，则2a = （A ）2 （B ）1 （C ）21 （D ）81（10）已知A,B 是球O 的球面上两点，∠AOB=90,C 为该球面上的动点，若三棱锥O-ABC 体积的最大值为36，则球O 的表面积为A ．36π B.64π C.144π D.256π（11）.如图，长方形ABCD 的边AB=2，BC=1，O 是AB 的中点，点P 沿着边BC ，CD 与DA 运动，∠BOP=x 。
2015年普通高等学校招生全国统一考试(全国新课标II卷)数学试题 (文科)解析版
2015年普通高等学校招生全国统一考试全国新课标 II 卷文 科 数 学一、选择题：本大题共12道小题,每小题5分,共60分. 1．已知集合{}|12A x x =-<<,{}|03B x x =<<,则A B =（ ）A ．()1,3-B ．()1,0-C ．()0,2D ．()2,3【答案】A考点：集合运算.2. 若为a 实数,且2i3i 1ia +=++,则a =( ) A ．4- B ．3- C ．3 D ．4【答案】D【解析】试题分析：由题意可得()()2i 1i 3i 24i 4a a +=++=+⇒= ,故选D.考点：复数运算.3. 根据下面给出的2004年至2013年我国二氧化碳年排放量（单位：万吨）柱形图,以下结论中不正确的是（ ）A ．逐年比较,2008年减少二氧化碳排放量的效果最显著B ．2007年我国治理二氧化碳排放显现成效C ．2006年以来我国二氧化碳年排放量呈减少趋势D ．2006年以来我国二氧化碳年排放量与年份正相关 【答案】 D考点：柱形图4. 已知()1,1=-a ,()1,2=-b ,则(2)+⋅=a b a （ ）A ．1-B ．0C ．1D ．2【答案】C 【解析】试题分析：由题意可得22=a ,3,⋅=-a b 所以()222431+⋅=+⋅=-=a b a a a b .故选C.考点：向量数量积.5. 设n S 是等差数列{}n a 的前n 项和,若1353a a a ++=,则5S =（ ） A ．5 B ．7 C ．9 D ．11【答案】A 【解析】试题解析：13533331a a a a a ++==⇒=,()15535552a a S a +===.故选A. 考点：等差数列6. 一个正方体被一个平面截去一部分后,剩余部分的三视图如下图,则截去部分体积与剩余部分体积的比值为（ ）1A.8 1B.7 1C.6D.15【答案】D【解析】试题分析：截去部分是正方体的一个角,其体积是正方体体积的16,所以截去部分体积与剩余部分体积的比值为15 ,故选D.考点：三视图7. 已知三点(1,0),A B C ,则△ABC 外接圆的圆心到原点的距离为（ ）5A.3 3 4D.3【答案】B考点：直线与圆的方程.8. 右边程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的,a b 分别为14,18,则输出的a 为（ ）A.0B. 2C.4D.14【答案】B 【解析】试题分析：由题意输出的a 是18,14的最大公约数2,故选B. 考点：1. 更相减损术；2.程序框图.9．已知等比数列{}n a 满足114a =,()35441a a a =-,则2a =（ ）A.2B.1C.12 1D.8【答案】C【解析】试题分析：由题意可得()235444412a a a a a ==-⇒=,所以34182a q q a ==⇒= ,故2112a a q ==,选C.考点：等比数列.10. 已知B A ,是球O 的球面上两点,︒=∠90AOB ,C 为该球面上的动点.若三棱锥ABC O -体积的最大值为36,则球O 的表面积为（ ）A.π36B. π64C.π144D. π256【答案】C考点：球与几何体的切接.11. 如图,长方形的边AB =2,BC =1,O 是AB 的中点,点P 沿着边BC ,CD 与DA 运动,记BOP x ∠= ,将动点P 到A ,B 两点距离之和表示为x 的函数()f x ,则的图像大致为（ ）A ．B ．C ．D ．【答案】B考点：函数图像12. 设函数21()ln(1||)1f x x x =+-+,则使得()(21)f x f x >-成立的x 的取值范围是（ ）A ．1,13⎛⎫ ⎪⎝⎭B ．()1,1,3⎛⎫-∞+∞ ⎪⎝⎭C ．11,33⎛⎫-⎪⎝⎭ D ．11,,33⎛⎫⎛⎫-∞-+∞ ⎪ ⎪⎝⎭⎝⎭【答案】A 【解析】试题分析：由21()ln(1||)1f x x x=+-+可知()f x 是偶函数,且在[)0,+∞是增函数,所以 ()()()()121212113f x f x f x f x x x x >-⇔>-⇔>-⇔<< .故选A.考点：函数性质二、填空题：本大题共4小题,每小题5分,共20分13. 已知函数()32f x ax x =-的图像过点（-1,4）,则a = ．【答案】-2 【解析】试题分析：由()32f x ax x =-可得()1242f a a -=-+=⇒=- .考点：函数解析式14. 若x ,y 满足约束条件50210210x y x y x y +-≤⎧⎪--≥⎨⎪-+≤⎩,则z =2x +y 的最大值为 ．【答案】8考点：线性规划15. 已知双曲线过点(,且渐近线方程为12y x =±,则该双曲线的标准方程为 ．【答案】2214x y -=考点：双曲线几何性质16. 已知曲线ln y x x =+在点()1,1 处的切线与曲线()221y ax a x =+++ 相切,则a = ． 【答案】8 【解析】试题分析：由11y x'=+可得曲线ln y x x =+在点()1,1处的切线斜率为2,故切线方程为21y x =-,与()221y ax a x =+++ 联立得220ax ax ++=,显然0a ≠,所以由2808a a a ∆=-=⇒=.考点：导数的几何意义.三、解答题17（本小题满分12分）△ABC 中D 是BC 上的点,AD 平分∠BAC ,BD =2DC .（I ）求sin sin BC∠∠ ；（II ）若60BAC ∠=,求B ∠.【答案】（I ）12；30.考点：解三角形试题解析：（I ）由正弦定理得,,sin sin sin sin AD BD AD DCB BADC CAD==∠∠∠∠ 因为AD 平分∠BAC ,BD =2DC ,所以sin 1.sin 2B DC C BD ∠==∠.（II ）因为()180,60,C BAC B BAC ∠=-∠+∠∠=所以()1sin sin sin .2C BAC B B B ∠=∠+∠=∠+∠ 由（I ）知2sin sin B C ∠=∠,所以tan 30.B B ∠=∠= 考点：解三角形18. （本小题满分12分）某公司为了了解用户对其产品的满意度,从A ,B 两地区分别随机调查了40个用户,根据用户对其产品的满意度的评分,得到A 地区用户满意度评分的频率分布直方图和B 地区用户满意度评分的频率分布表.A 地区用户满意度评分的频率分布直方图（I ）在答题卡上作出B 地区用户满意度评分的频率分布直方图,并通过此图比较两地区满意度评分的平均值及分散程度.（不要求计算出具体值,给出结论即可）B 地区用户满意度评分的频率分布直方图（II）根据用户满意度评分,将用户的满意度评分分为三个等级：估计那个地区的用户的满意度等级为不满意的概率大,说明理由.【答案】（I）见试题解析（II）A地区的用户的满意度等级为不满意的概率大.考点：1.频率分布直方图；2.概率估计.19. （本小题满分12分）如图,长方体1111ABCD A B C D -中AB =16,BC =10,18AA =,点E ,F 分别在1111,A B D C 上,11 4.A E D F ==过点E ,F 的平面α与此长方体的面相交,交线围成一个正方形.（I ）在图中画出这个正方形（不必说明画法与理由）； （II ）求平面α把该长方体分成的两部分体积的比值. 【答案】（I ）见试题解析（II ）97 或79考点：1.几何体中的截面问题；2.几何体的体积20. （本小题满分12分）已知椭圆()2222:10x y C a b a b +=>> ,点(在C 上.（I ）求C 的方程； （II ）直线l 不经过原点O ,且不平行于坐标轴,l 与C 有两个交点A ,B ,线段AB 中点为M ,证明：直线OM 的斜率与直线l 的斜率乘积为定值.【答案】（I ）2222184x y +=（II ）见试题解析考点：直线与椭圆21. （本小题满分12分）已知()()ln 1f x x a x =+-. （I ）讨论()f x 的单调性；（II ）当()f x 有最大值,且最大值大于22a -时,求a 的取值范围. 【答案】（I ）0a ≤,()f x 在()0,+∞是单调递增；0a >,()f x 在10,a ⎛⎫⎪⎝⎭单调递增,在1,a ⎛⎫+∞ ⎪⎝⎭单调递减；（II ）()0,1. 【解析】考点：导数的应用.请考生在22、23、24题中任选一题作答,如果多做,则按所做的第一题计分,作答时请写清题号22. （本小题满分10分）选修4-1：几何证明选讲如图O是等腰三角形AB C内一点,圆O与△ABC的底边BC交于M,N两点,与底边上的高交于点G,且与AB,AC分别相切于E,F两点.（I）证明EF BC；（II）若AG等于圆O半径,且AE MN【答案】（I）见试题解析；（II考点：1.几何证明；2.四边形面积的计算.23. （本小题满分10分）选修4-4：坐标系与参数方程 在直角坐标系xOy 中,曲线1cos ,:sin ,x t C y t αα=⎧⎨=⎩ （t 为参数,且0t ≠ ）,其中0απ≤<,在以O为极点,x 轴正半轴为极轴的极坐标系中,曲线23:2sin ,:.C C ρθρθ== （I ）求2C 与3C 交点的直角坐标；（II ）若1C 与 2C 相交于点A ,1C 与3C 相交于点B ,求AB 最大值.【答案】（I ）()30,0,2⎫⎪⎪⎭；（II ）4. 【解析】试题分析：（I ）把2C 与3C 的方程化为直角坐标方程分别为2220x y y +-=,220x y +-=,联立解考点：参数方程、直角坐标及极坐标方程的互化.24. （本小题满分10分）选修4-5：不等式证明选讲 设,,,a b c d 均为正数,且a b c d +=+.证明：（I ）若ab cd > ,+>；（II ）>是a b c d -<-的充要条件. 【答案】【解析】试题分析：（I ）由a b c d +=+及ab cd >,可证明22>,开方即得>（II ）本小题可借助第一问的结论来证明,但要分必要性与充分性来证明. 试题解析：解：（I ）因为22a b c d =++=++考点：不等式证明.。
2015年全国新课标2卷高考文科数学试题及答案
2015年全国新课标2卷高考文科数学试题及答案2015普通高等学校招生全国统一考试II卷文科数学第一卷一、选择题：本大题共12小题，每小题5分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
1.已知集合 $A=x-1<x<2$，$B=x<x<3$，则 $A\cup B=$A。
$(-1,3)$ B。
$(-1,0)$ C。
$(0,2)$ D。
$(2,3)$2.若 $a$ 是实数，且 $\frac{2+ai}{1+i}=3+i$，则 $a=$A。
$-4$ B。
$-3$ C。
$3$ D。
$4$3.根据下面给出的2004年至2013年我国二氧化碳年排放量（单位：万吨）柱形图，以下结论中不正确的是此处删除明显有问题的段落）4.已知向量 $a=(1,-1)$，$b=(-1,2)$，则 $(2a+b)\cdot a=$A。
$-1$ B。
$0$ C。
$1$ D。
$2$5.设 $S_n$ 是等差数列 $\{a_n\}$ 的前 $n$ 项和。
若$a_1+a_3+a_5=3$，则 $S_5=$A。
$5$ B。
$7$ C。
$9$ D。
$11$6.一个正方体被一个平面截去一部分后，剩余部分的三视图如右图，则截去部分体积与剩余部分体积的比值为A。
$\frac{1}{1111}$ B。
$\frac{1}{8576}$ C。
$\frac{2}{1254}$ D。
$\frac{1}{333}$7.已知三点 $A(1,-1)$，$B(2,3)$，$C(2,3)$，则 $\triangle ABC$ 外接圆的圆心到原点的距离为A。
$\sqrt{5}$ B。
$3$ C。
$2\sqrt{5}$ D。
$3\sqrt{2}$8.右边程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”。
执行该程序框图，若输入的$a,b$ 分别为14,18，则输出的 $a$ 为开始输入a,ba>b是a≠b 否输出a是否结束a=a-b b=b-aA。
2015年高考新课标Ⅱ卷文数试题+解析
2015年普通高等学校招生全国统一考试（全国卷2）文科数学一、 选择题：本大题共12小题。
每小题5分，在每个小题给出的四个选项中，只有一项是符合要求的。
1.已知集合}21|{<<-=x x A ，}30|{<<=x x B ，则A ∪B=（ ）A. )3,1(-B. )0,1(-C. )2,0(D. )3,2(2.若a 为实数，且i iai+=++312，则=a （ ） A. 4- B. 3- C. 3 D. 43. 根据下面给出的2004年至2013年我国二氧化碳年排放量（单位：万吨）柱形图，以下结论中不正确的是（ ）A.逐年比较，2008年减少二氧化碳排放量的效果显著B.2007年我国治理二氧化碳排放显现成效C.2006年以来我国二氧化碳年排放量呈逐渐减少趋势D.2006年以来我国二氧化碳年排放量与年份正相关 4.向量a =(1，-1) b =(-1，2)，则（2a +b ）.a = （ ） A. 1- B. 0 C. 1 D.2 5. 设n S 是数列}{n a 的前n 项和，若3531=++a a a ，则=5S （ ）A. 5B. 7C. 9D. 116. 一个正方体被一个平面截取一部分后，剩余部分的三视图如图，则截去部分体积与剩余部分体积的比值为（ ） A.81 B. 71 C. 61 D. 51 7.已知三点)0,1(A ，)3,0(B ，)3,2(C ，则ABC ∆外接圆的圆心到原点的距离为（ ） A.35 B. 321 C. 352 D. 348.右边程序框图的算法思路源于我国古代数学名著《九章算术》中“更相减损术”.执行该程序框图，若输入的a 、b 分别为14、18，则输出的=a （ ）A. 0B. 2C. 4D. 149.已知等比数列}{n a 满足411=a ，)1(4453-=a a a ，则=2a （ ） A. 2 B. 1 C. 21 D. 8110.已知A 、B 是球O 的球面上两点， 90=∠AOB ，C 为该球面上的动点.若三棱锥ABC O -体积的最大值为36，则球O 的表面积为（ ）A. π36B. π64C. π144D. π256 11.如图，长方形ABCD 的边2=AB ，1=BC ，O 是AB 的中点，点P 沿着BC 、CD 与DA 运动，记x BOP =∠.将动点P 到A 、B 两点距离之和表示为x 的函数)(x f ，则)(x f y =的图象大致为（ ）12. 设函数211|)|1ln()(xx x f +-+=，则使得)12()(->x f x f 成立的x 的取值范围是（ ） A. )1,31( B. ),1()31,(+∞-∞U C. )31,31(- D. ),31()31,(+∞--∞U二．填空题：共4小题，每小题5分.13. 已知函数x ax x f 2)(3-=的图象过点)4,1(-，则=a .14.若x 、y 满足约束条件⎪⎩⎪⎨⎧≤+-≥--≤-+01201205y x y x y x ，则y x z +=2的最大值为 .15.已知双曲线过点)3,4(，且渐近线方程为x y 21±=，则该双曲线的标准方程为 . 16.已知曲线x x y ln +=在点)1,1(处的切线与曲线1)2(2+++=x a ax y 相切，则=a .三、解答题：解答应写出文字说明，证明过程或演算步骤．17、（本小题满分12分）ΔABC中，D是BC上的点，AD平分∠BAC，BD=2DC.（1）求sinsinBC∠∠；（2）若∠BAC=60°,求∠B.18、（本小题满分12分）某公司为了解用户对其产品的满意度，从A，B两地区分别随机调查了40个用户，根据用户对产品的满意度评分，得分A地区用户满意评分的频率分布直方图和B地区用户满意度评分的频数分布表.B地区用户满意度评分的频数分布表（1）在答题卡上作出B地区用户满意度评分的频数分布直方图，并通过直方图比较两地区满意度评分的平均值及分散程度（不要求计算出具体值，给出结论即可）19、（本小题满分12分）如图，长方体ABCD ﹣A 1B 1C 1D 1中，AB=16，BC=10，AA 1=8,点E ，分别在A 1B 1, D 1C 1上，A 1E= D 1F=4.过点E,F 的平面α与此长方体的面相交，交线围成一个正方形.（1）在图中画出这个正方形（不必说明画法和理由） （2）求平面α把该长方体分成的两部分体积的比值. 20、（本小题满分12分）已知椭圆C ：22221x y a b+=（a >b >0，点（2）在C 上.（1）求C 的方程.（2）直线l 不过原点O 且不平行于坐标轴，l 与C 有两个交点A ，B ，线段AB 的中点为M.直线OM 的斜率与直线l 的斜率的乘积为定值.21、（本小题满分12分）已知函数f （x ）=ln x +a （1- x ） （1）讨论f （x ）的单调性；（2）当f （x ）有最大值，且最大值大于2a -2时，求a 的取值范围. 22、（本小题满分10分）选修4-4：坐标系与参数方程在直线坐标系xOy 中，曲线C 1：cos sin x t y t ==αα｛（t 为参数，t ≠0）其中0≤α≤π.在以O 为极点，x 轴正半轴为极轴的极坐标系中，曲线C 2：p=2sin θ，C 3：cos θ。
【推荐】2015年全国新课标2卷高考文科数学真题及答案
2015普通高等学校招生全国统一考试Ⅱ卷文科数学第Ⅰ卷一选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。
（1）已知集合A={}{}=<<=<<-B A x x B x x 则,30,21 A.(-1，3) B.(-1，0 ) C.(0，2) D.(2，3) 1．选A (2)若a 实数，且=+=++a i iai则,312 A.-4 B. -3 C. 3 D. 42．解：因为.4,42)1)(3(2=+=++=+a i i i ai 所以故选D(3)根据下面给出的2004年至2013年我国二氧化碳年排放量（单位：万吨）柱形图，以下 结论中不正确的是2700260025002400210020001900)A.逐年比较，2008年减少二氧化碳排放量的效果最显著；B.2007年我国治理二氧化碳排放显现成效；C.2006年以来我国二氧化碳排放量呈减少趋势；D.2006年以来我国二氧化碳年排放量与年份正相关。
3．选DA. -1B. 0C. 1D. 24．选B(5)设{}项和，的前是等差数列n a S n n 若==++5531,3S a a a 则A. 5B. 7C. 9D. 115．解：在等差数列中，因为1353,a a a ++=所以15353()51,55,2a a a S a +⨯====故选A (6)一个正方体被一个平面截去一部分后，剩余部分的三视图如右图，则截去部分体积与剩余部分体积的比值为A.81B.71C. 61D. 51 6．解：如图所示，选D.(7)已知三点)32()30(),01(，，，，C B A ,则ABC ∆外接圆的圆心到原点的距离为A.35B. 321C. 352D. 34 7．解：根据题意，三角形ABC 是等边三角形，设外接圆的圆心为D ，则(1,3D 所以，.32137341==+=OD 故选B. (8)右边程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”。
2015年(全国卷II)(含答案)高考文科数学
2015年普通高等学校招生全国统一考试（2全国Ⅱ卷）数学(文）试题一、选择题 ( 本大题 共 12 题， 共计 60 分）1.已知集合A={}{}=<<=<<-B A x x B x x 则,30,21（ ） A.( −1,3) B 。
( −1,0 ) C.(0，2) D.(2,3） 2。
若a 实数,且=+=++a i iai则,312( ） A 。
—4 B. -3 C 。
3 D. 43.根据下面给出的2004年至2013年我国二氧化碳年排放量（单位：万吨）柱形图，以下结论中不正确的是（ ）2700260025002400210020001900)A.逐年比较,2008年减少二氧化碳排放量的效果最显著； B 。
2007年我国治理二氧化碳排放显现成效； C.2006年以来我国二氧化碳排放量呈减少趋势； D 。
2006年以来我国二氧化碳年排放量与年份正相关。
4。
已知向量=•+-=-=a b a b a ）则（2),2,1(),1,0(（ ） A. -1 B 。
0 C 。
1 D. 25。
设{}项和，的前是等差数列n a S n n 若==++5531,3S a a a 则（ ）A 。
5B 。
7 C. 9 D. 116.一个正方体被一个平面截去一部分后,剩余部分的三视图如右图,则截去部分体积与剩余部分体积的比值为 ( ）A 。
81 B 。
71 C. 61 D. 51 7。
已知三点)32()30(),01(，，，，C B A ,则ABC 外接圆的圆心到原点的距离为( ）A 。
35B 。
321C 。
352D 。
348。
右边程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”。
执行该程序框图,若输入的a,b分别为14，18，则输出的a为（)否否A。
0 B. 2 C。
4 D。
149。
已知等比数列{}=-==24531),1(4,41aaaaaan则满足（)A. 2B. 1C.21D.8110.已知A,B是球O的球面上两点,为该球面上动点，CAOB,90︒=∠若三棱锥O-ABC体积的最大值为36，则球O的表面积为（）A. 36πB. 64πC。
2015全国卷2数学试卷及答案
绝密★启封并使用完毕前2015年普通高等学校招生全国统一考试文科数学（全国卷Ⅱ）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。
第Ⅰ卷1至3页，第Ⅱ卷4至6页。
第Ⅰ卷一、选择题：本大题共12小题，每小题5分，共60分1．已知集合{}|12A x x =-<<，{}|03B x x =<<，则A B =A ．()1,3-B ．()1,0-C ．()0,2D ．()2,32．若为a 实数，且231aii i +=++，则a =A ．4-B ．3-C ．3D ．43．根据下面给出的2004年至2013年我国二氧化碳年排放量（单位：万吨）柱形图，以下结论中不正确的是A ．逐年比较，2008年减少二氧化碳排放量的效果最显着 B ．2007年我国治理二氧化碳排放显现成效C ．2006年以来我国二氧化碳年排放量呈减少趋势D ．2006年以来我国二氧化碳年排放量与年份正相关4．已知()0,1a =-，()1,2b =-，则(2)a b a +=A ．1-B ．0C ．1D ．25．设n S 是等差数列{}n a 的前n 项和，若1353a a a ++=，则5S =A ．5B ．7C ．9D ．116．一个正方体被一个平面截去一部分后，剩余部分的三视图如右图，则截去部分体积与剩余部分体积的比值为7．已知三点(1,0),A B C ,则ABC ∆外接圆的圆心到原点的距离为8．右边程序框图的算法思路来源于我国古代数学名着《九章算术》中的“更相减损术”，执行该程序框图，若输入的,a b 分别为14,18,则输出的a 为（ ）9．已知等比数列{}n a 满足114a =，()35441a a a =-，则2a =10．已知B A ,是球O 的球面上两点，︒=∠90AOB ,C 为该球面上的动点。
若三棱锥ABC O -体积的最大值为36，则球O 的表面积为 A 、π36 B 、 π64 C 、π144 D 、 π25611．如图，长方形ABCD 的边AB=2，BC=1，O 是AB 的中点，点P 沿着边BC ，CD 与DA 运动，∠BOP=x。
2015年高考全国2卷文科数学考试试题(含解析)
2015年高考全国2卷文科数学考试试题(含解析)1 / 15绝密★启用前2015年高考全国2卷文科数学试题（含解析）注意事项：1．答题前填写好自己的姓名、班级、考号等信息 2．请将答案正确填写在答题卡上第I 卷（选择题）请点击修改第I 卷的文字说明一、选择题（题型注释）1．已知集合{}|12A x x =-<<,{}|03B x x =<<,则A B =（ ）A ．()1,3- B ．()1,0- C ．()0,2 D ．()2,32．若为a 实数,且2i3i 1ia +=++,则a =（ ） A ．4- B ．3- C ．3 D ．43．根据下面给出的2004年至2013年我国二氧化碳年排放量（单位：万吨）柱形图,以下结论中不正确的是（ ）A ．逐年比较,2008年减少二氧化碳排放量的效果最显著B ．2007年我国治理二氧化碳排放显现成效C ．2006年以来我国二氧化碳年排放量呈减少趋势D ．2006年以来我国二氧化碳年排放量与年份正相关4．已知()1,1=-a ,()1,2=-b ,则(2)+⋅=a b a （ ）A ．1-B ．0C ．1D ．25．设n S 是等差数列{}n a 的前n 项和,若1353a a a ++=,则5S =（ ） A ．5 B ．7 C ．9 D ．116．一个正方体被一个平面截去一部分后,剩余部分的三视图如下图,则截去部分体积与剩余部分体积的比值为（ ）1A.8 1B.7 1C.6 1D.5第3页 共8页 ◎ 第4页 共8页……订…………○…………线…………○线※※内※※答※※题※※……订…………○…………线…………○7．已知三点(1,0),A B C ,则△ABC 外接圆的圆心到原点的距离为（ ）5A.3 4D.38．下边程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的,a b 分别为14,18,则输出的a 为（ ）A.0B.2C.4D.149．已知等比数列{}n a 满足114a =,()35441a a a =-,则2a =（ ）A.2B.1 1C.2 1D.810．已知B A ,是球O 的球面上两点,︒=∠90AOB ,C 为该球面上的动点.若三棱锥ABC O -体积的最大值为36,则球O 的表面积为（ ） A.36π B. 64π C.144π D. 256π11．如图,长方形的边AB=2,BC=1,O 是AB 的中点,点P 沿着边BC,CD 与DA 运动,记BOP x ∠= ,将动点P 到A,B 两点距离之和表示为x 的函数()f x ,则的图像大致为（ ）12．设函数21()ln(1||)1f x x x =+-+,则使得()(21)f x f x >-成立的x 的取值范围是（ ） A ．1,13⎛⎫ ⎪⎝⎭ B ．()1,1,3⎛⎫-∞+∞ ⎪⎝⎭C ．11,33⎛⎫-⎪⎝⎭D ．11,,33⎛⎫⎛⎫-∞-+∞ ⎪ ⎪⎝⎭⎝⎭2015年高考全国2卷文科数学考试试题(含解析)3 / 15第II 卷（非选择题）请点击修改第II 卷的文字说明二、填空题（题型注释）13．已知函数()32f x ax x=-的图像过点（-1,4）,则a= ．14．若x,y 满足约束条件50210210x yx y x y +-≤⎧⎪--≥⎨⎪-+≤⎩,则z=2x+y 的最大值为 ．15．已知双曲线过点(,且渐近线方程为12y x =±,则该双曲线的标准方程为 ． 16．已知曲线ln y x x =+在点()1,1 处的切线与曲线()221y ax a x =+++ 相切,则a= ．三、解答题（题型注释）17．（本小题满分12分）△ABC 中D 是BC 上的点,AD 平分∠BAC,BD=2DC. （Ⅰ）求sin sin BC∠∠ ；（Ⅱ）若60BAC ∠=,求B ∠.18．（本小题满分12分）某公司为了了解用户对其产品的满意度,从A,B 两地区分别随机调查了40个用户,根据用户对其产品的满意度的评分,得到A 地区用户满意度评分的频率分布直方图和B 地区用户满意度评分的频率分布表.A 地区用户满意度评分的频率分布直方图B 地区用户满意度评分的频率分布表 满意度评分分组[50,60)[50,60)[50,60)[50,60)[50,60)频数 2814106（Ⅰ）在答题卡上作出B 地区用户满意度评分的频率分布直方图,并通过此图比较两地区满意度评分的平均值及分散程度.（不要求计算出具体值,给出结论即可）B 地区用户满意度评分的频率分布直方图（Ⅱ）根据用户满意度评分,将用户的满意度评分分为三个等级：满意度评分 低于70分70分到89分 不低于90分…○…………线………题※※…○…………线………满意度等级不满意满意非常满意估计那个地区的用户的满意度等级为不满意的概率大,说明理由.19．（本小题满分12分）如图,长方体1111ABCD A B C D-中AB=16,BC=10,18AA=,点E,F分别在1111,A B D C上,114.A E D F==过点E,F的平面α与此长方体的面相交,交线围成一个正方形.（Ⅰ）在图中画出这个正方形（不必说明画法与理由）；（Ⅱ）求平面α把该长方体分成的两部分体积的比值.20．（本小题满分12分）已知椭圆()2222:10x yC a ba b+=>>,点(在C上.（Ⅰ）求C的方程；（Ⅱ）直线l不经过原点O,且不平行于坐标轴,l与C有两个交点A,B,线段AB中点为M,证明：直线OM的斜率与直线l的斜率乘积为定值.21．（本小题满分12分）已知()()ln1f x x a x=+-.（Ⅰ）讨论()f x的单调性；（Ⅱ）当()f x有最大值,且最大值大于22a-时,求a的取值范围.22．（本小题满分10分）选修4-1：几何证明选讲如图O是等腰三角形ABC内一点,圆O与△ABC的底边BC交于M,N两点,与底边上的高交于点G,且与AB,AC分别相切于E,F两点.（Ⅰ）证明EF BC；（Ⅱ）若AG等于圆O半径,且AE MN==求四边形EBCF的面积.23．（本小题满分10分）选修4-4：坐标系与参数方程在直角坐标系xOy中,曲线1cos,:sin,x tCy tαα=⎧⎨=⎩（t为参数,且0t≠）,其中0απ≤<,在以O为极点,x轴正半轴为极轴的极坐标系中,曲线23:2sin,:.C Cρθρθ==（Ⅰ）求2C与3C交点的直角坐标；（Ⅱ）若1C与2C相交于点A,1C与3C相交于点B,求AB最大值.24．（本小题满分10分）选修4-5：不等式证明选讲设,,,a b c d均为正数,且a b c d+=+.证明：（Ⅰ）若ab cd> ,>>a b c d-<-的充要条件.第7页共8页◎第8页共8页2015年高考全国2卷文科数学考试试题(含解析)1 / 15参考答案1．A 【解析】因为{}|12A x x =-<<,{}|03B x x =<<,所以{}|13.A B x x =-<<故选A.考点：本题主要考查不等式基础知识及集合的交集运算. 2．D【解析】由题意可得()()2i 1i 3i 24i 4a a +=++=+⇒= ,故选D.考点：本题主要考查复数的乘除运算,及复数相等的概念. 3． D【解析】由柱形图可知2006年以来,我国二氧化碳排放量基本成递减趋势,所以二氧化碳排放量与年份负相关,故选D.考点：本题主要考查统计知识及对学生柱形图的理解 4．C 【解析】试题分析：由题意可得2112=+=a ,123,⋅=--=-a b 所以()222431+⋅=+⋅=-=a ba a ab .故选C.考点：本题主要考查向量数量积的坐标运算. 5．A 【解析】试题解析：由13533331a a a a a ++==⇒=,所有()15535552a a S a +===.故选A. 考点：本题主要考查等差数列的性质及前n 项和公式的应用. 6．D 【解析】本卷由系统自动生成，请仔细校对后使用，答案仅供参考。
2015年普通高等学校招生全国统一考试(全国新课标II卷)数学试题 (文科)解析版
2015年普通高等学校招生全国统一考试全国新课标 II 卷文 科 数 学一、选择题：本大题共12道小题,每小题5分,共60分. 1．已知集合{}|12A x x =-<<,{}|03B x x =<<,则A B =（ ）A ．()1,3-B ．()1,0-C ．()0,2D ．()2,3【答案】A考点：集合运算.2. 若为a 实数,且2i3i 1ia +=++,则a =( ) A ．4- B ．3- C ．3 D ．4【答案】D【解析】试题分析：由题意可得()()2i 1i 3i 24i 4a a +=++=+⇒= ,故选D.考点：复数运算.3. 根据下面给出的2004年至2013年我国二氧化碳年排放量（单位：万吨）柱形图,以下结论中不正确的是（ ）A ．逐年比较,2008年减少二氧化碳排放量的效果最显著B ．2007年我国治理二氧化碳排放显现成效C ．2006年以来我国二氧化碳年排放量呈减少趋势D ．2006年以来我国二氧化碳年排放量与年份正相关 【答案】 D考点：柱形图4. 已知()1,1=-a ,()1,2=-b ,则(2)+⋅=a b a （ ）A ．1-B ．0C ．1D ．2【答案】C 【解析】试题分析：由题意可得22=a ,3,⋅=-a b 所以()222431+⋅=+⋅=-=a b a a a b .故选C.考点：向量数量积.5. 设n S 是等差数列{}n a 的前n 项和,若1353a a a ++=,则5S =（ ） A ．5 B ．7 C ．9 D ．11【答案】A 【解析】试题解析：13533331a a a a a ++==⇒=,()15535552a a S a +===.故选A. 考点：等差数列6. 一个正方体被一个平面截去一部分后,剩余部分的三视图如下图,则截去部分体积与剩余部分体积的比值为（ ）1A.8 1B.7 1C.6D.15【答案】D【解析】试题分析：截去部分是正方体的一个角,其体积是正方体体积的16,所以截去部分体积与剩余部分体积的比值为15 ,故选D.考点：三视图7. 已知三点(1,0),A B C ,则△ABC 外接圆的圆心到原点的距离为（ ）5A.3 4D.3 【答案】B考点：直线与圆的方程.8. 右边程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的,a b 分别为14,18,则输出的a 为（ ）A.0B. 2C.4D.14【答案】B 【解析】试题分析：由题意输出的a 是18,14的最大公约数2,故选B. 考点：1. 更相减损术；2.程序框图.9．已知等比数列{}n a 满足114a =,()35441a a a =-,则2a =（ ）A.2B.1C.12 1D.8【答案】C【解析】试题分析：由题意可得()235444412a a a a a ==-⇒=,所以34182a q q a ==⇒= ,故2112a a q ==,选C.考点：等比数列.10. 已知B A ,是球O 的球面上两点,︒=∠90AOB ,C 为该球面上的动点.若三棱锥ABC O -体积的最大值为36,则球O 的表面积为（ ）A.π36B. π64C.π144D. π256【答案】C考点：球与几何体的切接.11. 如图,长方形的边AB =2,BC =1,O 是AB 的中点,点P 沿着边BC ,CD 与DA 运动,记BOP x ∠= ,将动点P 到A ,B 两点距离之和表示为x 的函数()f x ,则的图像大致为（ ）A ．B ．C ．D ．【答案】B考点：函数图像12. 设函数21()ln(1||)1f x x x =+-+,则使得()(21)f x f x >-成立的x 的取值范围是（ ）A ．1,13⎛⎫ ⎪⎝⎭B ．()1,1,3⎛⎫-∞+∞ ⎪⎝⎭C ．11,33⎛⎫-⎪⎝⎭ D ．11,,33⎛⎫⎛⎫-∞-+∞ ⎪ ⎪⎝⎭⎝⎭【答案】A 【解析】试题分析：由21()ln(1||)1f x x x=+-+可知()f x 是偶函数,且在[)0,+∞是增函数,所以 ()()()()121212113f x f x f x f x x x x >-⇔>-⇔>-⇔<< .故选A.考点：函数性质二、填空题：本大题共4小题,每小题5分,共20分13. 已知函数()32f x ax x =-的图像过点（-1,4）,则a = ．【答案】-2 【解析】试题分析：由()32f x ax x =-可得()1242f a a -=-+=⇒=- .考点：函数解析式14. 若x ,y 满足约束条件50210210x y x y x y +-≤⎧⎪--≥⎨⎪-+≤⎩,则z =2x +y 的最大值为 ．【答案】8考点：线性规划15. 已知双曲线过点(,且渐近线方程为12y x =±,则该双曲线的标准方程为 ．【答案】2214x y -=考点：双曲线几何性质16. 已知曲线ln y x x =+在点()1,1 处的切线与曲线()221y ax a x =+++ 相切,则a = ． 【答案】8 【解析】试题分析：由11y x'=+可得曲线ln y x x =+在点()1,1处的切线斜率为2,故切线方程为21y x =-,与()221y ax a x =+++ 联立得220ax ax ++=,显然0a ≠,所以由2808a a a ∆=-=⇒=.考点：导数的几何意义.三、解答题17（本小题满分12分）△ABC 中D 是BC 上的点,AD 平分∠BAC ,BD =2DC .（I ）求sin sin BC∠∠ ；（II ）若60BAC ∠=,求B ∠.【答案】（I ）12；30.考点：解三角形试题解析：（I ）由正弦定理得,,sin sin sin sin AD BD AD DCB BADC CAD==∠∠∠∠ 因为AD 平分∠BAC ,BD =2DC ,所以sin 1.sin 2B DC C BD ∠==∠.（II ）因为()180,60,C BAC B BAC ∠=-∠+∠∠=所以()1sin sin sin .2C BAC B B B ∠=∠+∠=∠+∠ 由（I ）知2sin sin B C ∠=∠,所以tan 30.B B ∠=∠= 考点：解三角形18. （本小题满分12分）某公司为了了解用户对其产品的满意度,从A ,B 两地区分别随机调查了40个用户,根据用户对其产品的满意度的评分,得到A 地区用户满意度评分的频率分布直方图和B 地区用户满意度评分的频率分布表.A 地区用户满意度评分的频率分布直方图（I ）在答题卡上作出B 地区用户满意度评分的频率分布直方图,并通过此图比较两地区满意度评分的平均值及分散程度.（不要求计算出具体值,给出结论即可）B 地区用户满意度评分的频率分布直方图（II）根据用户满意度评分,将用户的满意度评分分为三个等级：估计那个地区的用户的满意度等级为不满意的概率大,说明理由.【答案】（I）见试题解析（II）A地区的用户的满意度等级为不满意的概率大.考点：1.频率分布直方图；2.概率估计.19. （本小题满分12分）如图,长方体1111ABCD A B C D -中AB =16,BC =10,18AA =,点E ,F 分别在1111,A B D C 上,11 4.A E D F ==过点E ,F 的平面α与此长方体的面相交,交线围成一个正方形.（I ）在图中画出这个正方形（不必说明画法与理由）； （II ）求平面α把该长方体分成的两部分体积的比值. 【答案】（I ）见试题解析（II ）97 或79考点：1.几何体中的截面问题；2.几何体的体积20. （本小题满分12分）已知椭圆()2222:10x y C a b a b +=>> ,点(在C 上.（I ）求C 的方程； （II ）直线l 不经过原点O ,且不平行于坐标轴,l 与C 有两个交点A ,B ,线段AB 中点为M ,证明：直线OM 的斜率与直线l 的斜率乘积为定值.【答案】（I ）2222184x y +=（II ）见试题解析考点：直线与椭圆21. （本小题满分12分）已知()()ln 1f x x a x =+-. （I ）讨论()f x 的单调性；（II ）当()f x 有最大值,且最大值大于22a -时,求a 的取值范围. 【答案】（I ）0a ≤,()f x 在()0,+∞是单调递增；0a >,()f x 在10,a ⎛⎫⎪⎝⎭单调递增,在1,a ⎛⎫+∞ ⎪⎝⎭单调递减；（II ）()0,1. 【解析】考点：导数的应用.请考生在22、23、24题中任选一题作答,如果多做,则按所做的第一题计分,作答时请写清题号22. （本小题满分10分）选修4-1：几何证明选讲如图O是等腰三角形AB C内一点,圆O与△ABC的底边BC交于M,N两点,与底边上的高交于点G,且与AB,AC分别相切于E,F两点.（I）证明EF BC；（II）若AG等于圆O半径,且AE MN【答案】（I）见试题解析；（II考点：1.几何证明；2.四边形面积的计算.23. （本小题满分10分）选修4-4：坐标系与参数方程在直角坐标系xOy 中,曲线1cos ,:sin ,x t C y t αα=⎧⎨=⎩ （t 为参数,且0t ≠ ）,其中0απ≤<,在以O为极点,x 轴正半轴为极轴的极坐标系中,曲线23:2sin ,:.C C ρθρθ== （I ）求2C 与3C 交点的直角坐标；（II ）若1C 与 2C 相交于点A ,1C 与3C 相交于点B ,求AB 最大值.【答案】（I ）()30,0,2⎫⎪⎪⎭；（II ）4. 【解析】试题分析：（I ）把2C 与3C 的方程化为直角坐标方程分别为2220x y y +-=,220x y +-=,联立解考点：参数方程、直角坐标及极坐标方程的互化.24. （本小题满分10分）选修4-5：不等式证明选讲设,,,a b c d 均为正数,且a b c d +=+.证明：（I ）若ab cd > ,+>；（II ）>是a b c d -<-的充要条件. 【答案】【解析】试题分析：（I ）由a b c d +=+及ab cd >,可证明22>,开方即得>（II ）本小题可借助第一问的结论来证明,但要分必要性与充分性来证明. 试题解析：解：（I ）因为22a b c d =++=++考点：不等式证明.。
2015年全国新课标2卷高考文科数学试题及答案
2015 普通高等学校招生全国统一考试Ⅱ卷文科数学第一卷选择题：本大题共12 小题，每小题 5 分，在每小题给出的四个选项中，只有一项是符合题目要求的。
x 1 x 2 ,B x0x 3 ,则A B（1）已知集合A=A.(-1 ，3)B.(-1，0 )C.(0，2)D.(2 ，3)(2)若a 实数，且21a ii3 ,i则aA.-4B. -3C. 3D. 4(3)根据下面给出的2004 年至2013 年我国二氧化碳年排放量（单位：万吨）柱形图，以下结论中不正确的是2700260025002400230022002100200019002004 2005 2006 2007 2008 2009 2010 2011 2012 2013( 年)A.逐年比较，2008 年减少二氧化碳排放量的效果最显著；B.2007 年我国治理二氧化碳排放显现成效；C.2006 年以来我国二氧化碳排放量呈减少趋势；D.2006 年以来我国二氧化碳年排放量与年份正相关。
（4）已知向量a (0, 1), b ( 1,2),则（2a b）aA. -1B. 0C. 1D. 2(5)设S n是等差数列a n n的前项和，S n是等差数列a nn若a1 a3 a5 3,则S5A. 5B. 7C. 9D. 11(6)一个正方体被一个平面截去一部分后，剩余部分的三视图如右图，则截去部分体积与剩余部分体积的比值为1 1 1 1A. 8B. 7C. 6D. 5(7)已知三点A(1，0), B(0，3)，C(2，3) ,则ABC 外接圆的圆心到原点的距离为- 1 -5 21 2 5 4A. 3B. 3C. 3D. 3(8)右边程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”。
执行该程序框图，若输入的a,b 分别为14,18，则输出的 a 为开始输入a,b输出 a是否a>ba b是否结束a=a-b b=b-aA. 0B. 2C. 4D.14(9)已知等比数列1a n 满足a1 ,a a 4(a 1),则3 5 44a2 C1 1A. 2B. 1C. 2D. 8（10）已知A,B 是球O 的球面上两点，AOB 90 ,C为该球面上动点，若三棱锥O-ABC 体积的最大值为36，则球O 的表面积为A. 36 πB. 64πC. 144πD.256π(11)如图，长方形的边AB=2 ，BC=1,O 是AB 的中点，点P 沿着边BC,CD, 与DA 运动，记BOP x, 将动点P A, B f (x), f (x)到两点距离之和表示为函数则的图像大致为D CPxA O B- 2 -。
【数学】2015年高考真题——新课标Ⅱ卷(文)(word版含解析)
2015年普通高等学校招生全国统一考试文科数学注意事项：1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。
答卷前，考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上。
2．回答第Ⅰ卷时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号框涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号框。
写在本试卷上无效。
3．答第Ⅱ卷时，将答案写在答题卡上，写在本试卷上无效。
4．考试结束，将试题卷和答题卡一并交回。
第Ⅰ卷一、 选择题：本大题共12小题。
每小题5分，在每个小题给出的四个选项中，只有一项是符合要求的。
1.已知集合}21|{<<-=x x A ，}30|{<<=x x B ，则A ∪B=（ ）A. )3,1(-B. )0,1(-C. )2,0(D. )3,2( 2.若a 为实数，且i iai+=++312，则=a （ ） A. 4- B. 3- C. 3 D. 43. 根据下面给出的2004年至2013年我国二氧化碳年排放量（单位：万吨）柱形图，以下结论中不正确的是（ ）A.逐年比较，2008年减少二氧化碳排放量的效果显著B.2007年我国治理二氧化碳排放显现成效C.2006年以来我国二氧化碳年排放量呈逐渐减少趋势D.2006年以来我国二氧化碳年排放量与年份正相关 4.向量a =(1，-1) b =(-1，2)，则（2a +b ）⋅a = （ ）A. 1-B. 0C. 1D.2 5. 设n S 是数列}{n a 的前n 项和，若3531=++a a a ，则=5S （ ） A. 5 B. 7 C. 9 D. 116. 一个正方体被一个平面截取一部分后，剩余部分的三视图如图，则截去部分体积与剩余部分体积的比值为（ ） A.81 B. 71 C. 61 D. 517.已知三点)0,1(A ，)3,0(B ，)3,2(C ，则ABC ∆外接圆的圆心到原点的距离为（ ）A.35B. 321C. 352 D. 348.右边程序框图的算法思路源于我国古代数学名著《九章算术》中“更相减损术”.执行该程序框图，若输入的a 、b 分别为14、18，则输出的=a （ ）A. 0B. 2C. 4D. 149.已知等比数列}{n a 满足411=a ，)1(4453-=a a a ，则=2a （ ） A. 2 B. 1 C. 21 D. 8110.已知A 、B 是球O 的球面上两点， 90=∠AOB ，C 为该球面上的动点.若三棱锥ABC O -体积的最大值为36，则球O 的表面积为（ ）A. π36B. π64C. π144D. π25611.如图，长方形ABCD 的边2=AB ，1=BC ，O 是AB 的中点，点P 沿着BC 、CD 与DA 运动，记x BOP =∠.将动点P 到A 、B 两点距离之和表示为x 的函数)(x f ，则)(x f y =的图象大致为（ ）12. 设函数211|)|1ln()(x x x f +-+=，则使得)12()(->x f x f 成立的x 的取值范围是（ ）A. )1,31( B. ),1()31,(+∞-∞U C. )31,31(- D. ),31()31,(+∞--∞U 二．填空题：共4小题，每小题5分.13. 已知函数x ax x f 2)(3-=的图象过点)4,1(-，则=a .14.若x 、y 满足约束条件⎪⎩⎪⎨⎧≤+-≥--≤-+01201205y x y x y x ，则y x z +=2的最大值为 .15.已知双曲线过点)3,4(，且渐近线方程为x y 21±=，则该双曲线的标准方程为 . 16.已知曲线x x y ln +=在点)1,1(处的切线与曲线1)2(2+++=x a ax y 相切，则=a .三、解答题：解答应写出文字说明，证明过程或演算步骤． 17、（本小题满分12分）ΔABC 中，D 是BC 上的点，AD 平分∠BAC ，BD=2DC. （Ⅰ）求sin sin BC∠∠；（Ⅱ）若∠BAC=60°,求∠B.18、（本小题满分12分）某公司为了解用户对其产品的满意度，从A ，B 两地区分别随机调查了40个用户，根据用户对产品的满意度评分，得分A 地区用户满意评分的频率分布直方图和B 地区用户满意度评分的频数分布表.B 地区用户满意度评分的频数分布表（Ⅰ）在答题卡上作出B 地区用户满意度评分的频数分布直方图，并通过直方图比较两地区满意度评分的平均值及分散程度（不要求计算出具体值，给出结论即可）（Ⅱ）根据用户满意度评分，将用户的满意度分为三个等级；估计哪个地区用户的满意度等级为不满意的概率大？说明理由.19、（本小题满分12分）如图，长方体ABCD﹣A1B1C1D1中，AB=16，BC=10，AA1=8,点E，分别在A1B1, D1C1上，A1E= D1F=4.过点E,F的平面α与此长方体的面相交，交线围成一个正方形.（Ⅰ）在图中画出这个正方形（不必说明画法和理由）（Ⅱ）求平面α把该长方体分成的两部分体积的比值.20、（本小题满分12分）已知椭圆C ：22221x y a b +=（a >b >0）的离心率为2，点（2C 上.（Ⅰ）求C 的方程.（Ⅱ）直线l 不过原点O 且不平行于坐标轴，l 与C 有两个交点A ，B ，线段AB 的中点为M.直线OM 的斜率与直线l 的斜率的乘积为定值.21、（本小题满分12分） 已知函数f （x ）=ln x +a （1- x ） （Ⅰ）讨论f （x ）的单调性；（Ⅱ）当f （x ）有最大值，且最大值大于2a -2时，求a 的取值范围.请考生在第22、23、24题中任选一题作答，如果多做，则按所做的第一题记分，作答时请写清题号。
2015年普通高等学校招生全国统一考试 全国卷2 数学试卷含答案(文科)
2015年普通高等学校招生全国统一考试(课标全国卷Ⅱ)文数本卷满分150分,考试时间120分钟.第Ⅰ卷(选择题,共60分)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合A={x|-1<x<2},B={x|0<x<3},则A∪B=()A.(-1,3)B.(-1,0)C.(0,2)D.(2,3)2.若a为实数,且=3+i,则a=( )A.-4B.-3C.3D.43.根据下面给出的2004年至2013年我国二氧化硫年排放量(单位:万吨)柱形图,以下结论中不正确的是( )A.逐年比较,2008年减少二氧化硫排放量的效果最显著B.2007年我国治理二氧化硫排放显现成效C.2006年以来我国二氧化硫年排放量呈减少趋势D.2006年以来我国二氧化硫年排放量与年份正相关4.向量a=(1,-1),b=(-1,2),则(2a+b)·a=()A.-1B.0C.1D.25.设S n是等差数列{a n}的前n项和.若a1+a3+a5=3,则S5=( )A.5B.7C.9D.116.一个正方体被一个平面截去一部分后,剩余部分的三视图如下图,则截去部分体积与剩余部分体积的比值为( )A. B. C. D.7.已知三点A(1,0),B(0,),C(2,),则△ABC外接圆的圆心到原点的距离为( )A. B. C. D.8.下边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为14,18,则输出的a=( )A.0B.2C.4D.149.已知等比数列{a n}满足a1=,a3a5=4(a4-1),则a2=( )A.2B.1C.D.10.已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点.若三棱锥O-ABC体积的最大值为36,则球O的表面积为( )A.36πB.64πC.144πD.256π11.如图,长方形ABCD的边AB=2,BC=1,O是AB的中点.点P沿着边BC,CD与DA运动,记∠BOP=x.将动点P到A,B两点距离之和表示为x的函数f(x),则y=f(x)的图象大致为( )12.设函数f(x)=ln(1+|x|)-,则使得f(x)>f(2x-1)成立的x的取值范围是( )A.,B.- ,∪(1,+ )C.-,D.- ,-∪,第Ⅱ卷(非选择题,共90分)本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须作答.第22题~第24题为选考题,考生根据要求作答.二、填空题:本大题共4小题,每小题5分.13.已知函数f(x)=ax3-2x的图象过点(-1,4),则a= .14.若x,y满足约束条件-,--,-,则z=2x+y的最大值为.15.已知双曲线过点(4,),且渐近线方程为y=±x,则该双曲线的标准方程为.16.已知曲线y=x+ln x在点(1,1)处的切线与曲线y=ax2+(a+2)x+1相切,则a= .三、解答题:解答应写出文字说明、证明过程或演算步骤.17.(本小题满分12分)△ABC中,D是BC上的点,AD平分∠BAC,BD=2DC.(Ⅰ)求;(Ⅱ)若∠BAC=60°,求∠B.某公司为了解用户对其产品的满意度,从A,B两地区分别随机调查了40个用户,根据用户对产品的满意度评分,得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频数分布表.B地区用户满意度评分的频数分布表(Ⅰ)作出B地区用户满意度评分的频率分布直方图,并通过直方图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可);(Ⅱ)根据用户满意度评分,将用户的满意度分为三个等级:估计哪个地区用户的满意度等级为不满意的概率大?说明理由.如图,长方体ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4.过点E,F的平面α与此长方体的面相交,交线围成一个正方形.(Ⅰ)在图中画出这个正方形(不必说明画法和理由);(Ⅱ)求平面α把该长方体分成的两部分体积的比值.20.(本小题满分12分)已知椭圆C:+=1(a>b>0)的离心率为,点(2,在C上.(Ⅰ)求C的方程;(Ⅱ)直线l不过原点O且不平行于坐标轴,l与C有两个交点A,B,线段AB的中点为M.证明:直线OM的斜率与直线l的斜率的乘积为定值.21.(本小题满分12分)已知函数f(x)=ln x+a(1-x).(Ⅰ)讨论f(x)的单调性;(Ⅱ)当f(x)有最大值,且最大值大于2a-2时,求a的取值范围.请从下面所给的22、23、24三题中选定一题作答,多答按所答第一题评分.22.(本小题满分10分)选修4—1:几何证明选讲如图,O为等腰三角形ABC内一点,☉O与△ABC的底边BC交于M,N两点,与底边上的高AD交于点G,且与AB,AC分别相切于E,F两点.(Ⅰ)证明:EF∥BC;(Ⅱ)若AG等于☉O的半径,且AE=MN=2求四边形EBCF的面积.23.(本小题满分10分)选修4—4:坐标系与参数方程在直角坐标系xOy中,曲线C1:,(t为参数,t≠0),其中0≤α<π.在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=2sin θ,C3:ρ=2cos θ. (Ⅰ)求C2与C3交点的直角坐标;(Ⅱ)若C1与C2相交于点A,C1与C3相交于点B,求|AB|的最大值.24.(本小题满分10分)选修4—5:不等式选讲设a,b,c,d均为正数,且a+b=c+d.证明:(Ⅰ)若ab>cd,则++(Ⅱ)+>+是|a-b|<|c-d|的充要条件.2015年普通高等学校招生全国统一考试(课标全国卷Ⅱ)一、选择题1.A 因为A=(-1,2),B=(0,3),所以A∪B=(-1,3),故选A.2.D 由已知得2+ai=(1+i)(3+i)=2+4i,所以a=4,故选D.3.D 由已知柱形图可知A、B、C均正确,2006年以来我国二氧化硫年排放量呈减少趋势,所以排放量与年份负相关,∴D不正确.4.C 因为2a+b=2(1,-1)+(-1,2)=(2,-2)+(-1,2)=(1,0),所以(2a+b)·a=(1,0)·(1,-1)=1×1+0×(-1)=1.故选C.5.A ∵{a n}为等差数列,∴a1+a5=2a3,得3a3=3,则a3=1,∴S5=()=5a3=5,故选A.6.D 如图,由已知条件可知,在正方体ABCD-A1B1C1D1中,截去三棱锥A-A1B1D1后剩余的部分即为题中三视图对应的几何体,设该正方体的棱长为a,则截去部分的体积为a3,剩余部分的体积为a3-a3=a3.它们的体积之比为.故选D.评析本题主要考查三视图和体积的计算;考查空间想象能力.7.B 在平面直角坐标系xOy中画出△ABC,易知△ABC是边长为2的正三角形,其外接圆的圆心为D,.因此|OD|===.故选B.8.B 执行程序框图:当a=14,b=18时,a<b,则b=18-14=4;当a=14,b=4时,a>b,则a=14-4=10;当a=10,b=4时,a>b,则a=10-4=6;当a=6,b=4时,a>b,则a=6-4=2;当a=2,b=4时,a<b,则b=4-2=2,此时a=b=2,输出a为2,故选B.评析本题主要考查程序框图,属容易题.9.C 设{a n}的公比为q,由等比数列的性质可知a3a5=,∴=4(a4-1),即(a4-2)2=0,得a4=2,则q3===8,得q=2,则a2=a1q=×2=,故选C.10.C 因为△AOB的面积为定值,当OC垂直于平面AOB时,三棱锥O-ABC的体积取得最大值.由R3=36得R=6.从而球O的表面积S=4πR2=144π.故选C.11.B 当点P与C、D重合时,易求得PA+PB=1+;当点P为DC中点时,PA+PB=2PA=2.显然,1+,故当x=时, f(x)不取最大值,故C、D选项错误.当x∈,时, f(x)=tan x+,不是一次函数,排除A.故选B.评析做选择题可以取特殊位置进行研究.12.A 当x>0时,f(x)=ln(1+x)-,∴f '(x)=+()>0,∴f(x)在(0,+ )上为增函数,∵f(-x)=f(x),∴f(x)为偶函数,由f(x)>f(2x-1)得f(|x|)>f(|2x-1|),∴|x|>|2x-1|,即3x2-4x+1<0,解得<x<1,故选A.二、填空题13.答案-2解析因为函数f(x)=ax3-2x的图象过点(-1,4),所以4=a×(-1)3-2×(-1),故a=-2. 14.答案8解析由约束条件画出可行域(如图所示).解方程组-,-得A(3,2).当动直线2x+y-z=0经过点A(3,2)时,z max=2×3+2=8.评析本题考查了简单的线性规划,考查了数形结合的思想方法.15.答案-y2=1解析根据渐近线方程为x±2y=0,可设双曲线方程为x2-4y2=λ(λ≠0).因为双曲线过点(4,),所以42-4×()2=λ,即λ=4.故双曲线的标准方程为-y2=1.16.答案8解析令f(x)=x+ln x,求导得f '(x)=1+, f '(1)=2,又f(1)=1,所以曲线y=x+ln x在点(1,1)处的切线方程为y-1=2(x-1),即y=2x-1.设直线y=2x-1与曲线y=ax2+(a+2)x+1的切点为P(x0,y0),则y'|=2ax0+a+2=2,得a(2x0+1)=0,∴a=0或x0=-,又a+(a+2)x0+1=2x0-1,即a+ax0+2=0,当a=0时,显然不满足此方程,∴x0=-,此时a=8.评析本题主要考查导数的几何意义,能够利用点斜式求出切线方程是解题关键.三、解答题17.解析(Ⅰ)由正弦定理得=,=.因为AD平分∠BAC,BD=2DC,所以==.(Ⅱ)因为∠C=180°-(∠BAC+∠B),∠BAC=60°,所以sin∠C=sin(∠BAC+∠B)=cos∠B+sin∠B.由(Ⅰ)知2sin∠B=sin∠C,所以tan∠B=,即∠B=30°.评析本题考查了正弦定理;考查了解三角形的能力.属中档题.18.解析(Ⅰ)通过两地区用户满意度评分的频率分布直方图可以看出,B地区用户满意度评分的平均值高于A地区用户满意度评分的平均值;B地区用户满意度评分比较集中,而A地区用户满意度评分比较分散.(Ⅱ)A地区用户的满意度等级为不满意的概率大.记C A表示事件:“A地区用户的满意度等级为不满意”;C B表示事件:“B地区用户的满意度等级为不满意”.由直方图得P(C A)的估计值为(0.01+0.02+0.03)×10=0.6,P(C B)的估计值为(0.005+0.02)×10=0.25.所以A地区用户的满意度等级为不满意的概率大.19.解析(Ⅰ)交线围成的正方形EHGF如图:(Ⅱ)作EM⊥AB,垂足为M,则AM=A1E=4,EB1=12,EM=AA1=8.因为EHGF为正方形,所以EH=EF=BC=10.于是MH=-=6,AH=10,HB=6.因为长方体被平面α分成两个高为10的直棱柱,所以其体积的比值为也正确.20.解析(Ⅰ)由题意有-=,+=1,解得a2=8,b2=4.所以C的方程为+=1.(Ⅱ)设直线l:y=kx+b(k≠0,b≠0),A(x1,y1),B(x2,y2),M(x M,y M).将y=kx+b代入+=1得(2k2+1)x2+4kbx+2b2-8=0.故x M==-,y M=k·x M+b=.于是直线OM的斜率k OM==-,即k OM·k=-.所以直线OM的斜率与直线l的斜率的乘积为定值.评析本题考查了椭圆的方程、直线与椭圆的位置关系;考查了定值问题的解题方法.利用韦达定理解决线段的中点是求解关键.21.解析(Ⅰ)f(x)的定义域为(0,+ ),f '(x)=-a.若a≤0,则f '(x)>0,所以f(x)在(0,+ )上单调递增.若a>0,则当x∈,时,f '(x)>0;当x∈,时,f '(x)<0.所以f(x)在,上单调递增,在,上单调递减.(Ⅱ)由(Ⅰ)知,当a≤0时,f(x)在(0,+ )上无最大值;当a>0时,f(x)在x=处取得最大值,最大值为f=ln+a-=-ln a+a-1.因此f>2a-2等价于ln a+a-1<0.令g(a)=ln a+a-1,则g(a)在(0,+ )上单调递增,g(1)=0.于是,当0<a<1时,g(a)<0;当a>1时,g(a)>0.因此,a的取值范围是(0,1).22.解析(Ⅰ)由于△ABC是等腰三角形,AD⊥BC,所以AD是∠CAB的平分线.又因为☉O分别与AB,AC相切于点E,F,所以AE=AF,故AD⊥EF.从而EF∥BC.(Ⅱ)由(Ⅰ)知,AE=AF,AD⊥EF,故AD是EF的垂直平分线.又EF为☉O的弦,所以O在AD上. 连结OE,OM,则OE⊥AE.由AG等于☉O的半径得AO=2OE,所以∠OAE=30°.因此△ABC和△AEF都是等边三角形.因为AE=2,所以AO=4,OE=2.因为OM=OE=2,DM=MN=,所以OD=1.于是AD=5,AB=.所以四边形EBCF的面积为××-×(2)2×=.评析本题考查了直线和圆的位置关系,考查了圆的初步知识.23.解析(Ⅰ)曲线C 2的直角坐标方程为x2+y2-2y=0,曲线C3的直角坐标方程为x2+y2-2x=0.联立-,-,解得,或,.所以C2与C3交点的直角坐标为(0,0)和,.(Ⅱ)曲线C1的极坐标方程为θ=α(ρ∈R,ρ≠0),其中0≤α<π.因此A的极坐标为(2sin α,α),B的极坐标为(2cos α,α).所以|AB|=|2sin α-2cos α|=4-.当α=时,|AB|取得最大值,最大值为4.评析本题考查了极坐标和参数方程,考查了最值问题.利用极径的几何意义建立关系式是求解关键.24.证明(Ⅰ)因为(+)2=a+b+2,(+)2=c+d+2,由题设a+b=c+d,ab>cd得(+)2>(+)2.因此+>+.(Ⅱ)(i)若|a-b|<|c-d|,则(a-b)2<(c-d)2,即(a+b)2-4ab<(c+d)2-4cd.因为a+b=c+d,所以ab>cd.由(Ⅰ)得++.(ii)若++则(+2>(+)2,即a+b+2因为a+b=c+d,所以ab>cd.于是(a-b)2=(a+b)2-4ab<(c+d)2-4cd=(c-d)2.因此|a-b|<|c-d|.综上,+>+是|a-b|<|c-d|的充要条件.评析本题主要考查不等式证明,对带有根号、绝对值的不等式,平方作差比较是常用的方法.。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
∠AOB = x。将动点 P 到 A，B 两点距离之和表示为 x 的函数 f (x) ，则 y f (x) 的图象大致为
y
y
y
y
2
2
2
2
3 x 42 4
A
3 x 42 4
B
3 x 42 4
C
3 x 42 4
D
12．设函数
f
(x)
ln(1 |
x
|)
1
1 x2
，则使得
f
(x)
C．2006 年以来我国二氧化硫年排放量呈减少年排放量与年份正相关
4．向量 a (1, 1) ， b (1, 2) ，则 (2a b) a
A．-1
B．0
C．1
D．3
5．设 Sn 等差数列{an} 的前 n 项和。若 a1 + a3 + a5 = 3，则 S5 =
2015 年全国卷 2 高考文科数学试题
1．已知集合 A {x | 1 x 2}， B {x | 0 x 3}，则 A B
A． (1,3)
B． (1,0)
2．若 a 为实数，且 2 ai 3 i ，则 a = 1 i
A．-4
B．-3
C． (0, 2)
C．3
D． (2,3)
D．4
3．根据下面给出的 2004 年至 2013 年我国二氧化硫年排放量（单位：万吨）柱形图，以下结论不正确的
O
50 60 70 80 90 100 满意度评分
（2）根据用户满意度评分，将用户的满意度从低到高分为三个等级：
满意度评分
低于 70 分
70 分到 89 分
不低于 90 分
满意度等级
不满意
满意
非常满意
估计哪个地区的满意度等级为不满意的概率大？说明理由
19．（本小题满分 12 分）
D1 F
如图，长方体 ABCD—A1B1C1D1 中，AB = 16，BC = 10，AA1 A1 E
（1）求 sin B ； sin C
（2）若 AD = 1， DC 2 ，求 BD 和 AC 的长。 2
18．（本小题满分 12 分）
某公司为了解用户对其产品的满意度，从 A，B 两地区分别随机调查了 40 个用户，根据用户对产品的
满意度评分，得到 A 地区用户满意度评分的频率分布直方图和 B 地区用户满意度评分的频数分布表。
频数
2
8
14
10
6
（1）在答题卡上作出 B 地区用户满意度评分的频率分布直方图，并通过直方图比较两地区满意度评分
的平均值及分散程度（不要求计算出具体值，给出结论即可）；
B 地区用户满意度评分的频率分布直方图
频率/组距
0.040 0.035 0.030 0.025 0.020 0.015 0.010 0.005
A．5
B．7
C．9
D．11
6．一个正方体被一个平面截去一部分后，剩余部分的三视图如右图，则截去
部分体积与剩余部分体积的比值为
A． 1 8
C． 1 6
B． 1 7
D． 1 5
7．已知三点 A(1, 0) ， B(0, 3) ， C(2, 3) ，则ΔABC 外接圆的圆心到原点的距离为
A． 5 3
B． 21 3
f
(2x
1)
成立的
x
的取值范围是
A． (1 ,1) 3
B． (, 1) (1, ) 3
C． ( 1 , 1) 33
D． (, 1) (1 , ) 33
第 II 卷（非选择题，共 90 分）
本卷包括必考题和选考题两部分。第 13 题 ~ 第 21 题为必考题，每个试题考生都必须作答。第 22
题 ~ 第 24 题为选考题，考生根据要求作答。
a1
1 4
，a3a5
=
4(a4 1) ，则 a2 =
A．2
B．1
C． 1 2
D． 1 8
10．已知 A，B 是球 O 的球面上两点，∠AOB = 90°，C 为
D
P
C
该球面上的动点。若三棱锥 O—ABC 体积的最大值为 36，
则球 O 的表面积为
A
x
O
B
A．36π
B．64π
C．144π
D．256π
11．如图，长方形 ABCD 的边 AB = 2，BC = 1，O 是 AB 的中点，点 P 沿着边 BC，CD 与 DA 运动，记
D
= 8，点 E，F 分别在 A1B1，D1C1 上，A1E = D1F = 4，过点 E，F
A
C1
B1 C
B
的平面α与此长方体的面相交，交线围成一个正方形。
（1）在图中画出这个正方形（不必说明画法和理由）；
8．右边程序框图的算法思路源于我国古代数学名
著《九章算术》中的“更相减损术”。执行该程序框
图，若输入的 a，b 分别为 14，18，则输出的 a =
A．0
B．2
C． 2 5 3
D． 4 3
开始
输入 a，b
是
否
a≠b
是
否
a>b
输出 a
a=a-b
b=b-a
结束
C．4
D．14
9．已知等比数列 {an} 满足
二、填空题：本大题共 4 小题，每小题 5 分。
13．已知函数 f (x) ax3 2x 的图象过点 (1, 4) ，则 a = _________。
x y 5 0 14．若 x，y 满足约束条件 2x y 1 0 ，则 z 2x y 的最大值为__________。
x 2 y 1 0 15．已知双曲线过点 (4, 3) ，且渐近线方程为 y 1 x ，则该双曲线的标准方程为__________。
2
16．已知曲线 y x ln x 在点 (1,1) 处的切线与曲线 y ax2 (a 2)x 1相切，则 a = __________。
三、解答题：解答应写出文字说明、证明过程或演算步骤。
17．（本小题满分 12 分）
ΔABC 中，D 是 BC 上的点，AD 平分∠BAC，ΔABD 面积是ΔADC 面积的 2 倍。
A 地区用户满意度评分的频率分布直方图
频率/组距
0.040 0.035 0.030 0.025 0.020 0.015 0.010 0.005
O
40 50 60 70 80 90 100 满意度评分
B 地区用户满意度评分的频数分布表
满意度评分分组 [50,60) [60,70) [70,80) [80,90) [90,100]
是
2700 2600 2500 2400 2300 2200 2100 2000 1900
2004 年 2005 年 2006 年 2007 年 2008 年 2009 年 2010 年 2011 年 2012 年 2013 年
A．逐年比较，2008 年减少二氧化硫排放量的效果最显著
B．2007 年我国治理二氧化硫排放显现成效