圆正多边形的画法
圆内正多边形的画法
单
Page 5
作图过程如下:
(1)找出圆周与水平中心线的交点2、5,如图2-5(a)所示。 (2)放好丁字尺,用60°三角板短边紧靠丁字尺,60°角放在右边,固定丁 字尺,移动三角板使其斜边通过圆心,与圆周交于点3和点6,如图2-5(b)所 示。 (3)固定丁字尺,用60°三角板短边紧靠丁字尺,60°角放在左边,同样移 动三角板使其斜边通过圆心,与圆周交于点1和点4,如图2-5(c)所示。 (4)如图2-5(d)所示,在圆周上总共得到1、2、3、4、5、6六个点, 用直尺顺次连接各点,即得所求的正六边形。
单击此处编几辑母何版标作题样图式
圆内正多边形的画法
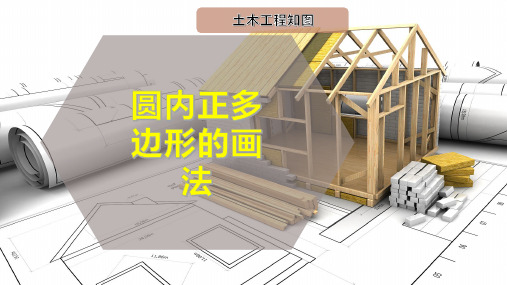
1.1 圆内正五边 形的画法
圆内正五边形的 作图方法和步骤如图 2-4所示。
Page 2
单击此处编几辑母何版标作题样图式
圆内正多边形的画法
Page 3
作图过程如下:
(1)以圆的半径为半径,A点为圆心,画圆弧与圆周相交,得到 交点C、D,连接C点、D点,CD与OA相交于M点,即OA的中点。
(2)以M点为圆心,1M为半径画圆弧,与OE交于N点,以1N为弦 长,从1点开始,在圆周上截取等分点,得到2、3、4、5点,即圆周内 的五个等分点。
(3)用直尺依次连接圆周上的五个等分点,即得圆内接正五边形。
单击此处编几辑母何版标作题样图式
圆内正多边形的画法
1.2 圆内正六边形 的画法
圆内正六边形的作 图方法和步骤如图2-5 所示。
人教版数学九年级上册第二十四章《24.3 正多边形和圆》课件(共19张PPT)

对于一些特殊的正多边形,还可以用圆规和直尺来作图. 再如,用直尺和圆规作两条互相垂直的直径,就可以把圆四等分,从而作 出正方形.
用尺规等分圆: 用尺规作图的方法等分圆周,然后依次连接圆上各分点得到正多边形,这 种方法有局限性,不是任意正多边形都能用此法作图,这种方法从理论上 讲是一种准确方法.
2.如图,正五边形ABCDE的对角线AC和BE相交于点M. 求证:(1) AC//ED;(2) ME=AE.
如图,正五边形ABCDE的对角线AC和BE相交于点M. 求证:(1) AC//ED;(2) ME=AE.
归纳新知
正多边形 的画法
用量角器等分圆 用尺规等分圆
此方法可将圆任意n等分,所以用 该方法可作出任意正多边形,但边 数很大时,容易产生较大的误差.
度量法③:
用圆规在⊙O 上顺次截取6条长度等于半径(2 cm)的弦,连接其中的 AB, BC,CA 即可.
B
O
A
C
对于一些特殊的正多边形,还可以用圆规和直尺来作图. 例如,我们也可以这样来作正六边形.由于正六边形的边长等于半径,所以 在半径为R的圆上依次截取等于R的弦,就可以把圆六等分,顺次连接各分 点即可得到半径为R的正六边形.
课堂练习
1.画一个半径为2 cm的正五边形,再作出这个正五边形的各条对角线,画 出一个五角星.
2.面积相等的正三角形与正六边形的边长之比为
.
中考实题
1.已知⊙O如图所示. (1) 求作⊙O的内接正方形(要求尺规作图,保留作图痕迹,不写作法); (2) 若⊙O的半径为4,求它的内接正方形的边长.
此方法是一种比较准确的等分圆的方 法,但有局限性,不能将圆任意等分.
再见
合作探究
已知⊙O 的半径为 2 cm,画圆的内接正三角形. 度量法①: 用量角器或 30°角的三角板度量,使∠BAO=∠CAO=30°.
正多边形与圆及正多边形的画法

正多边形与圆及正多边形的画法内容:1.正多边形和圆的有关概念:正多边形的外接圆,正多边形的中心,•正多边形的半径,正多边形的中心角,正多边形的边心距.2.在正多边形和圆中,圆的半径、边长、边心距中心角之间的等量关系.3.正多边形的画法.问题:1.什么叫正多边形?2.从你身边举出两三个正多边形的实例,正多边形具有轴对称、•中心对称吗?其对称轴有几条,对称中心是哪一点?1.各边相等,各角也相等的多边形是正多边形.2.实例略.正多边形是轴对称图形,对称轴有无数多条;•正多边形是中心对称图形,其对称中心是正多边形对应顶点的连线交点.探究:如果我们以正多边形对应顶点的交点作为圆心,过点到顶点的连线为半径,能够作一个圆,很明显,这个正多边形的各个顶点都在这个圆上,如图,•正六边形ABCDEF,连结AD、CF交于一点,以O为圆心,OA为半径作圆,那么肯定B、C、•D、E、F都在这个圆上.因此,正多边形和圆的关系十分密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆.我们以圆内接正六边形为例证明.如图所示的圆,把⊙O•分成相等的6•段弧,依次连接各分点得到六边ABCDEF,下面证明,它是正六边形.根据正多边形的定义,各边相等、各角相等、六边形ABCDEF是⊙O的内接正六边形,⊙O是正六边形ABCDEF的外接圆.为了今后学习和应用的方便,•我们把一个正多边形的外接圆的圆心叫做这个多边形的中心.外接圆的半径叫做正多边形的半径.正多边形每一边所对的圆心角叫做正多边形的中心角.中心到正多边形的一边的距离叫做正多边形的边心距.例1.已知正六边形ABCDEF ,如图所示,其外接圆的半径是a ,•求正六边形的周长和面积.例2.利用你手中的工具画一个边长为3cm 的正五边形.例3.在直径为AB 的半圆内,划出一块三角形区域,如图所示,使三角形的一边为AB ,顶点C 在半圆圆周上,其它两边分别为6和8,现要建造一个内接于△ABC•的矩形水池DEFN ,其中D 、E 在AB 上,如图24-94的设计方案是使AC=8,BC=6. (1)求△ABC 的边AB 上的高h .(2)设DN=x ,且h DN NFh AB-=,当x 取何值时,水池DEFN 的面积最大? (3)实际施工时,发现在AB 上距B 点1.85的M 处有一棵大树,问:这棵大树是否位于最大矩形水池的边上?如果在,为了保护大树,请设计出另外的方案,使内接于满足条件的三角形中欲建的最大矩形水池能避开大树.hF DEC BANG课时作业1.如图1所示,正六边形ABCDEF内接于⊙O,则∠ADB的度数是().A.60° B.45° C.30° D.22.5°(1) (2) (3)2.圆内接正五边形ABCDE中,对角线AC和BD相交于点P,则∠APB的度数是(). A.36° B.60° C.72° D.108°3.若半径为5cm的一段弧长等于半径为2cm的圆的周长,•则这段弧所对的圆心角为()A.18° B.36° C.72° D.144°4.已知正六边形边长为a,则它的内切圆面积为_______.5.在△ABC中,∠ACB=90°,∠B=15°,以C为圆心,CA长为半径的圆交AB于D,如图2所示,若AC=6,则AD的长为________.6.四边形ABCD为⊙O的内接梯形,如图3所示,AB∥CD,且CD为直径,•如果⊙O 的半径等于r,∠C=60°,那图中△OAB的边长AB是______;△ODA的周长是_______;∠BOC的度数是________.7.等边△ABC的边长为a,求其内切圆的内接正方形DEFG的面积.8.如图所示,•已知⊙O•的周长等于6 cm,•求以它的半径为边长的正六边形ABCDEF 的面积.9.如图所示,正五边形ABCDE的对角线AC、BE相交于M.(1)求证:四边形CDEM是菱形;(2)设MF2=BE·BM,若AB=4,求BE的长.。
正多边形和圆-ppt课件

“各边相等,各内角相等”是正多边形的两
个基本特征,当边数n>3时,二者必须同时具备,
缺一不可,否则多边形就不是正多边形.
感悟新知
3. 正多边形的有关概念
知1-讲
(1)正多边形的中心: 一个正多边形的外接圆的圆心叫作正
多边形的中心 .
(2)正多边形的半径: 正多边形的外接圆的半径叫作正多边形
的半径 .
心,OA 为半径作⊙ O,直径 FC ∥ AB, AO, BO
的延长线交⊙ O 于点 D, E.
求证:六边形 ABCDEF 为圆内接
正六边形 .
感悟新知
知1-练
思路导引:
感悟新知
知1-练
证明: ∵三角形 AOB 是正三角形,
∴∠ AOB= ∠ OAB= ∠ OBA=60°, OB=OA.
∴点 B 在⊙ O 上 .
(1)作半径为 0.9 cm 的⊙ O;
(2)用量角器画∠ AOB = ∠ BOC=120°,其中 A, B,C
均为圆上的点;
(3)连接 AB, BC, CA,则△ ABC 为
所求作的正三角形 ,如图 24. 3-4所示.
感悟新知
作法二
(1)作半径为 0.9 cm 的⊙ O;
知3-练
(2)作⊙ O 的任一直径 AB;
︵
︵
︵
︵
︵ ︵
∴BDE-CDE=CDA-CDE,即BC=AE.∴BC=AE.
同理可证其余各边都相等,
∴五边形 ABCDE 是正五边形.
感悟新知
知识点 2 正多边形的有关计算
1. 正 n 边形的每个内角都等于
(-)· °
.
2. 正 n 边形的每个中心角都等于
2018_2019学年九年级数学上册第24章圆24.3正多边形和圆课件新版新人教版

24.3 正多边形和圆
学习指南 知识管理 归类探究 当堂测评 分层作业
学习指南
★教学目标★ 使学生经历正多边形的形成过程,了解正多边形的有关概念,掌握用等分 圆周画圆的内接正多边形的方法.
★情景问题引入★ 我国古代数学家刘徽,在公元三世纪用“割圆术”求得 π 的近似值为15507 ≈3.14,祖冲之在公元五世纪又进一步求得 π 的值在 3.141 592 6 与 3.141 592 7 之间,是当时世界上最先进的成就.现代利用电子计算机,已有人把 π 的值算 到小数点后上万亿位.它是从圆内接正六边形开始,逐步计算所得的结果.你 知道正多边形和圆有什么关系吗?给你一个圆,怎样就能作出一个正多边形? 圆中依次出现几段相等的弧?
3 B. 2
C. 2Biblioteka D. 3【解析】 如答图 1,∵OC=2,∴OD=1;
如答图 2,∵OB=2,∴OE= 2;如答图 3,∵OA=2,∴OD= 3;则该
三角形的三边分别为 1, 2, 3.∵12+( 2)2=( 3)2,∴该三角形是直角三角
形,∴该三角形的面积是21×1×
2=
2 2.
7.小刚有一块边长为 a m 的正方形花布,准备做一个形状为正八边形的
第7题答图
∴x+x+ 2x=a,解得 x=2-2 2a,
因此,从四个角上各剪去一个直角边长为2-2
2 a
m
的等腰直角三角形,即
可得到一个面积最大的正八边形风筝.
8.如图 24-3-8 所示,已知正五边形 ABCDE,连接对角 线 AC,BD,设 AC 与 BD 相交于点 O.
(1)写出图中所有的等腰三角形; (2)判断四边形 AODE 的形状,并说明理由. 解:(1)△ABO,△ABC,△BOC, △DOC,△BCD; (2)四边形 AODE 是菱形,理由: ∵AB=BC,∠ABC=108°,
圆内接正五边形画法
椭圆画法:
已知:长轴AB,短轴CD,常用的椭圆画法有: 四心法 (近似画法)见图a, 同心圆法(准确画法)见图b。
( a)
( b)
四心扁圆法画椭圆
已知:椭圆的长轴和短轴. 作图:椭圆.
作题步骤: 1.连接AC,在短轴的延长 线上量OE=OA,在AC上 量CF=CE; 2.作AF的中垂线,交长轴于 O1,交短轴于O2,定出其对 称点O3.O4;
§2-2
等分圆周
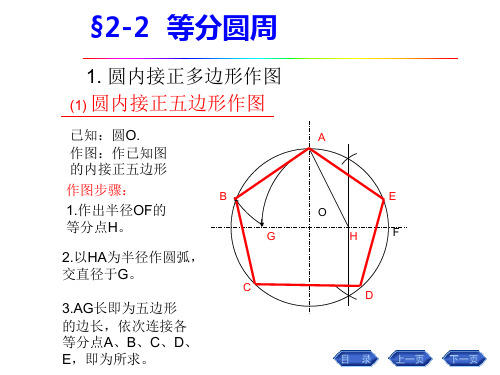
1. 圆内接正多边形作图 (1) 圆内接正五边形作图
已知:圆O. 作图:作已知图 的内接正五边形 作图步骤: 1.作出半径OF的 等分点H。 2.以HA为半径作圆弧, 交直径于G。
C D B O G H F A
E
3.AG长即为五边形 的边长,依次连接各 等分点A、B、C、D、 E,即为所求。
E O4 C F
O A O1
O2 B
3.分别以O3.O4和O1.O2为 圆心,以O4D.O1A为半径 作圆弧,所得图形即所求。
D O3
(2)已知正六边形对角线长度,作正六边形 画图步骤:
1.画水平、垂直对称 中心线,取1、4等 于对角线长。 2.过1、0、4点分别 做同方向的60 ° 斜线。 3.过1、4点做另一方 向的斜线。 4.过2、5点分别做 水平线即为所求。
3
1 o 2
5 4 6
§2-3
圆弧链接
作图要点:根据已知条件,准确地求出连接圆弧的圆心 和切点。
R2
作图原理:a为切点
R1
o
R2
a
o
a
R1
o
a(外切)
相减
(c)圆弧与圆弧连接(内切)
(a)圆弧与直线连接
[例]已知:O1(R1)和O2(R2)两个弧(如 图),用R3弧将它们连接起来(外切)。
人教版九年级数学上册《正多边形和圆形》圆PPT精品课件

正多边形和圆
学习目标
1.理解并掌握正多边形的半径和边长、边心距、中心角
之间的关系.
(重点)
2.会进行特殊的与正多边形有关的计算,会画
某些正多边形.
(难点)
新课导入
知识回顾
圆内接四边形的性质:
1.对角互补; 2.四个内角的和是360°; 3.任一外角与其相邻的内角的对角相等(即外角等于内对角).
新课讲解
证明:如图,把⊙O分成相等的5段弧,依次连接各分点 得到五边形ABCDE. ∵A⌒B=B⌒C=C⌒D=D⌒E=E⌒A,
知识点
∴AB=BC=CD=DE=EA, BC⌒E=3A⌒B=C⌒DA.
∴∠A=∠B. 同理∠B=∠C=∠D=∠E. 又五边形ABCDE的顶点都在⊙O上, ∴五边形ABCDE是⊙O的内接正五边形, ⊙O是正五边形ABCDE的外接圆.
作OP⊥BC,垂足为P.
在Rt△OPC中,OC=4 m,
PC= BC 4 =2(m),利用勾股定理,
22
可得边心距r= 42 22 2 3(m).
亭子地基的面积S=
1 lr 1 24 2 3 41.6(m2 ). 22
新课讲解
正n边形的一个内角的度数是多少?中
心角呢?正多边形的中心角与外角的大小有 什么关系?
新课导入
课时导入
下面这些美丽的图案,都是在日常生活中我们经常能看到的.你 能从这些图案中找出类似的图形吗?
新课讲解
知识点1 圆内接正多边形
正三 角形
三条边相等,三个角 相等(60度).
正方形
四条边相等,四个角 相等(900).
新课讲解
什么叫做正多边形? 各边相等、各角也相等的多边形叫做正多边形.
圆内接正五边形的画法

圆内接正五边形的画法
1、圆内接正五边形五条边长度相等。
(即圆的五条弦长度相等)。
2、圆内接正五边形的五个内角相等,都是108°。
3、圆内接正五边形的五条边在圆内所对的五条优弧长度相等。
4、圆内接正五边形的五条边在圆内所对的五条优弧的弧度数相等。
扩展资料:
圆外切正多边形判定方法
正多边形的判定,正多边形的定义当然是正多边形的判定方法之一,但如同全等三角形的判定一样,用定义来证明两个三角形全等显然不可取,因此需用判定定理来证。
判定定理:把圆几等分(n>2)
①依次连结各分点所得的多边形是这个圆的内接正n边形。
②经过各分点做圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形,也就是说,若要证明一个多边形是圆内接正多边形,只要证明这个多边形的顶点是圆的等分点即可。
如:要证明一个圆内接n边形ABCDEF……是圆内接正n边形,就要证A、B、C、D、E、F……各点是圆的n等分点,就是要证
AB=BC=CD=DE=EF=…….同样,要证明一个圆外切边形是圆外切正n边形,只要证明各切点是圆的等分点即可。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
巩固练习
教科书P108练习题第1题.
布置作业
教科书习题24.3第8,9题.
应用画图
问题3 除了正六边形,用圆规和直尺还能 够作哪些正多边形? 在用圆规和直尺作出正方形和正六边形的基 础上,你还能作出哪些正多边形?
设计图案
问题4 你能用等分圆周的方法画出以下图案 吗?
小结归纳
问题5 通过这节课,你学会了什么? (1)两种等分圆周的方法:
量角器和尺规; (2)用量角器等分圆周的方法能够画任意正多 边形,而用尺规等分圆周只能画一些特殊的正 多边形.
圆正多边形的画法
复习引入
问题1 如何做出一个圆的内接正多边形? • 如何等分圆周? • 通过等分圆心角ቤተ መጻሕፍቲ ባይዱ分圆周,进而做出正多边
形的方法,能够画出任意的正n边形吗?
应用画图
问题2 画一个边长为2cm的正六边形,你有 什么方法? 你能用圆规和直尺作出边长为2cm的正六边 形吗?
应用画图
问题3 除了正六边形,用圆规和直尺还能 够作哪些正多边形?
