磁单极子存在时的Maxwell方程组的初边值问题_王治蓉
如果存在磁单极子,则麦克斯韦方程组中需要改写的式子是 高斯定律 磁场的高斯定律

如果存在磁单极子,则麦克斯韦方程组中需要改写的式子是高斯定律磁场的高斯定律。
如果存在磁单极子,则麦克斯韦方程组中需要改写的式子是高斯定律磁场的高斯定律在物理学领域,磁单极子一直是一个备受关注的研究课题。
传统上,我们所熟悉的磁场是由磁偶极子产生的,它们总是成对出现,并且不可能存在独立的磁单极子。
然而,如果存在磁单极子,那么麦克斯韦方程组中的一些式子就需要做出相应的改写,其中包括高斯定律和磁场的高斯定律。
在本文中,我们将深入探讨这一主题,分析磁单极子对麦克斯韦方程组的影响,并对其中涉及的概念和原理进行全面的评估。
让我们回顾一下麦克斯韦方程组的基本形式。
麦克斯韦方程组描述了电磁场的行为,它由4个方程组成:电场的高斯定律、电场的安培定律、磁场的高斯定律和法拉第电磁感应定律。
在正常情况下,这些方程描述了电磁场的产生、传播和相互作用,然而如果考虑到磁单极子的存在,其中的一些方程就需要做出相应的修改。
具体来说,如果存在磁单极子,那么磁场的高斯定律就需要做出改写。
传统的磁场高斯定律表达了磁场的闭合性,即磁场线既没有起点也没有终点,这是由于磁场总是由磁偶极子所产生的。
然而,如果存在磁单极子,那么磁场线就会出现起点或终点,从而破坏了磁场的闭合性。
在存在磁单极子的情况下,我们需要重新审视磁场的高斯定律,并对其进行修正。
除了磁场的高斯定律之外,麦克斯韦方程组中的高斯定律也需要进行相应的修改。
传统的高斯定律描述了电场或磁场穿过一个闭合曲面的总通量与该曲面所包围的电荷量或磁荷量的比例关系。
然而,如果考虑到磁单极子的存在,那么电场或磁场的通量就会发生改变,从而需要对高斯定律进行修正。
在对麦克斯韦方程组中的式子进行修改时,我们需要考虑到磁单极子对整个理论体系所带来的影响。
除了对高斯定律的修改外,还需要进一步分析磁单极子与其他物理量之间的相互作用,探讨磁单极子的产生机制和性质,并考察它对电磁场的传播和辐射的影响等多方面问题。
研究磁单极子不仅仅是对麦克斯韦方程组的修改,更是对整个电磁理论的深入探讨。
电磁场数值计算边值问题分解课件

电磁场基本理论
02
麦克斯韦方程组
微分形式
描述电磁场在空间中的变化和传播。
积分形式
描述电荷和电流在空间中的分布。
电磁场的边界条件
电场和磁场在边界处的连续性
在两种不同媒质的交界处,电场强度和磁场强度保持连续。
迭代法
定义
应用
迭代法是一种通过不断迭代来逼近问题解 的方法,通常从初始猜测开始,通过逐步 修正猜测来得到最终的解。
在电磁场数值计算中,迭代法可以用于求 解边值问题,例如从初始猜测开始,通过 逐步修正猜测来得到最终的解。
优点
缺点
迭代法可以自动寻找问题的解,不需要人 工干预。
迭代法的收敛速度较慢,需要更多的计算 资源。
特点
有限差分法简单易行,适用于规则的问题域,但难以处理复杂的问题域。
03
应用场景
有限差分法广泛应用于偏微分方程的数值计算中,如热传导方程、波动
方程等。
有限元法
01
定义
有限元法是一种基于变分原理的数值计算方法,通过将 连续的空间离散为有限个单元,用单元的组合来逼近原 函数,从而可以进行数值计算。
02
使结果更接近真实情况。
适用性
扩大数值计算方法的应用范围, 使其能够解决更多种类的电磁
场问题。
高效性
优化算法,提高计算效率,减 少计算时间和资源消耗。
自动化
提高数值计算的自动化程度, 减少人工干预,提高计算过程
的可靠性。
研究挑 战
复杂性问题 高维度问题 不确定性量化 计算资源需求
对于具有复杂形状和结构的电磁场问题,如何设计有效的数值 计算方法是当前面临的一个挑战。
【精品】第八讲:麦克斯韦方程组、电磁场的边界条件
第八讲:麦克斯韦方程组、电磁场的边界条件2.6麦克斯韦方程组2.7电磁场的边值关系1、了解麦克斯韦方程组的建立过程,掌握它的基本性质;2、了解边界上场不连续的原因,能导出电磁场的边值关系;3、掌握电磁场方程微分形式和边界形式的联系与区别。
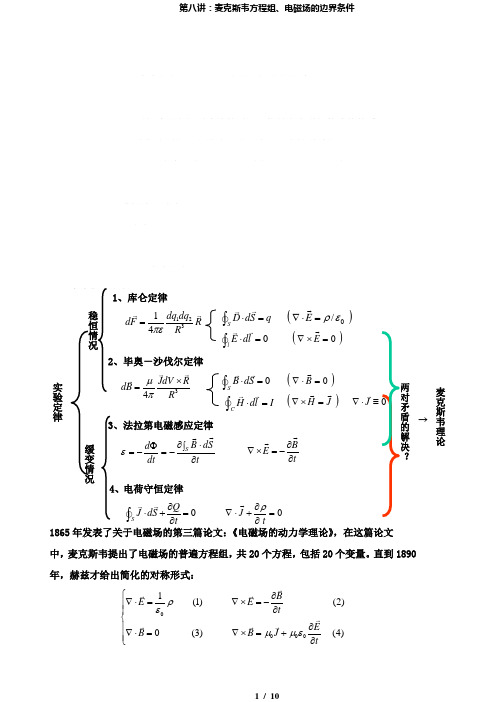
重点:1)麦克斯韦方程组的基本性质;2)电磁场的边值关系 难点:电磁场切向边值关系的推导 讲授法、讨论 2学时2.6麦克斯韦方程组(Maxwell ’sEquations )一、麦克斯韦方程1865年发表了关于电磁场的第三篇论文:《电磁场的动力学理论》,在这篇论文中,麦克斯韦提出了电磁场的普遍方程组,共20个方程,包括20个变量。
直到1890 年,赫兹才给出简化的对称形式:00001(1)(2)0(3)(4)BE E tE B B J tρεμμε⎧∂∇⋅=∇⨯=-⎪∂⎪⎨∂⎪∇⋅=∇⨯=+⎪∂⎩实验定律3、法拉第电磁感应定律4、电荷守恒定律12314dq dq dF RR πε=S D dS q ⋅=⎰0l E dl ⋅=⎰34JdV R dB R μπ⨯=0SB dS ⋅=⎰()0=⋅∇B CH dl I ⋅=⎰()JH =⨯∇tB E ∂∂-=⨯∇ 0=∂∂+⋅∇tJ ρ 0J ∇⋅≡对矛盾的解决麦克斯韦理论稳恒况缓变情况2、毕奥-沙伐尔定律1、库仑定律()/ερ=⋅∇E()=⨯∇E t S d B dt d S ∂⎰⋅∂-=Φ-= ε0S QJ dS t ∂⋅+=∂⎰→上式即为真空中的麦克斯韦方程组,其中(2)(4)含有对时间的偏导数,对应 运动方程,(1)(3)为约束方程。
二、麦克斯韦方程组的基本性质 1、线性性麦克斯韦方程组是一组线性方程,表明场服从迭加原理。
2、自洽性方程组各个方程彼此协调,且与电荷守恒定律协调。
如(2)式和(3)式一致:由(2)式有:()0=∂⋅∂∇-=⨯∇⋅∇tBE⇒C B =⋅∇ ,考虑到静磁时0=⋅∇B,所以取0=C 。
第9讲 电磁场基本规律(5)

第一方程,表明磁场的 环量等于传导电流和位 移电流之和
2.麦克斯韦方程组的微分形式
D H J t E B t B 0 D
第一方程,表明传导电流和变化 的电场都能产生磁场 第二方程,表明变化的 磁场产生电场 第三方程,表明磁场是无源场, 磁力线总是闭合曲线 麦克斯韦第四方程, 表明电荷产生电场
H y k 2 Em ex ex sin(t kz ) z z Hz
D H t
ex Em sin(t kz )
k
2 2
2.电磁场的边界条件
什么是电磁场的边界条件
en
媒质1
为什么要研究边界条件
? 实际电磁场问题都是在一定的物理空 如何讨论边界条件? 间内发生的,该空间中可能是由多种不同
相应的其它场矢量。 B E (ex t Ex e y e y z 对时间 t 积分,得
kEm B ey cos(t kz )
ey ez ) ex Ex x y z E0 cos(t kz ) ey kE0 sin(t kz ) z
是电磁场的基本方程;
是分析研究电磁问题的基本出发点。
3.麦克斯韦方程组
麦克斯韦方程组 —— 宏观电磁现象所遵循的基本规律,是电磁场 的基本方程
1.麦克斯韦方程组的积分形式
D ) dS C H dl S ( J t 第二方程,表明电场的环 B dS C E dl S 量等于磁通变化率的负值 t 第三方程,表明闭合曲面的 S B dS 0 磁通量恒等于0 S D dS V dV 第四方程,表明电位仪 通量等于曲面内的自由 S J dS V t dV 电荷量
1.1 Maxwell方程组

1 电磁场计算中的基本问题1.1 Maxwell 方程组电磁场理论研究的主要问题是场量与场源之间的关系,或者说是场强、位、通量、通量密度、能量等等与电荷或电流等之间的关系。
研究在一定激励源作用下,所产生的响应的分布情况。
反之,根据场量的大小、分布的具体要求来设计合适的场源。
在此基础上,研究电磁场对电荷、电流的作用力,电场与磁场的相互关系,电磁感应的影响,媒质的极化和磁化等重要问题。
1.1.1 场与源赫姆霍兹定理指出:任何一个矢量场),,()(z y x F r F=,只要在有限区域V '所有各点处, )()(r b r F =∙∇和)()(r c r F=⨯∇已知,)(r F在场域边界上的切向或法向分量已知,则矢量场)(r F可以完全地被确定下来。
由定理可知,场的散度和旋度可以确定场的分布,实际上场的散度和旋度表达式正是场与源之间的微分关系式,不同媒质分界面上的衔接条件也由场的散度和旋度唯一的确定。
工程中常遇的电磁场可分为四种类型,设定在各向同性、线性、均匀媒质中: 1. 无散场:在V '空间内,0=⋅∇F,而F⨯∇不一定为零。
选择A为辅助函数,取A F ⨯∇=,由0)(≡⨯∇⋅∇A ,在如图示情况下,应有:⎰⎰''''='⨯∇=V V V Rr c V R F r A d 41d 41)()( ππ由A F ⨯∇=,()r c F'=⨯∇,有)(r c A'=⨯∇⨯∇例如静磁场中:B F =,J B μ=⨯∇, ))((J r cμ=',⎰''=V V d RJ r A μπ41)(⎰''⨯=⨯∇=V RV Re J A r B d 412μπ)( 毕奥-沙阀定律2. 无旋场:V '空间内,0=⨯∇F,0≠⋅∇F 。
=⨯∇F0≡∇⨯∇⇒ϕ,无旋场必然存在一标量位ϕ:ϕ-∇=F ,当)(r b F'=⋅∇时,()ϕ∇-⋅∇=⋅∇F )(r b '-=∇ ϕ2使V Rr b V d RF V V ''='⋅∇=⎰⎰''d 4141)( ππϕ例如静电场:E F =,ερ=⋅∇E ,ερϕ-=∇2()()⎰'''=V V Rr r d 41ερπϕ()⎰''=-∇=V R V Re r r r E d 412ρπεϕ)()(3. 调和场:V '空间中,0=⋅∇F,0=⨯∇F 。
第六章电磁场的边值问题

),因此,
方程数少于未知量,是非定解方式,必须加本构方程才为定解形式, 对于简单媒质,本构方程为
D E
B H
J E
(1-6)
3
3、 材 料 性 质 材料是均匀的 材料是非均匀:
co n st , co n st , co n st x, y, z , x, y, z , x, y, z
2
H t E t
H
2
t
2
2
0
E
2
E t
2
0
取洛伦兹规范 A
t
2
,则位函数满足的波动方程 A t t A
2
A
t
2
2
J
2
t
2
11
1、 静 电 场 方 程 静电场的基本方程 泊松方程 D , x x y y z z E 0
三维方程
若ε 是均匀、各向同性介质,上式为
, B 0, E 0, D 0
, D 0
M Q S 场 求 解 时 ,磁 场 可 以 用 稳 态 磁 场 的 方 法 求 解 ,然 后 用 上 述 公 式 求 电 场 ;E Q S 场求解时,电场可以用静电场的方法求解,然后用上述公式求磁场。
9
(1)扩散方程(抛物型方程) 忽略位移电流,MQS场的方程为
1
— 强加边界条件
12
例 1
铁磁体的磁场和电容器的电场(二维)
电磁场小论文

电磁场理论大作业题目时变电磁场的唯一性姓名王志全学号2140920046专业物理电子学日期2015年1月15日摘要:从麦克斯韦方程组的初边值问题出发,引入子区域边界条件和外边界条件,给出了均匀介质区域中时变电磁场惟一性定理的一般证明及其物理解释,得到了时变电磁场解惟一性的普遍条件,并对时变电磁场惟一性定理作了新的表述。
关键词:麦克斯韦方程组;时变电磁场;初边值问题;惟一性定理1引言我们都知道在静电场和静磁场的情况下,静电场和静磁场都具有唯一性定理:静电场静电场唯一性定理是在一个空间内,导体的带电量或者电势给定以后,空间电场分布恒定,唯一,边界条件可以是各导体电势,各导体电量或部分导体电量与部分导体电势之混合[1];静磁场的唯一性定理:我们假设磁场空间为一封闭曲面S所包围,如果S有限,则给定S面上的法向磁感应强度BSn件,以与高斯定理一致;如果S无限,则要求BS趋于0,其次,设磁介质各向同性,磁导率已知但允许出现非均匀性,以及在不同磁介质界面处出现间断[2]。
静电场、静磁场和时谐电磁场定解问题的唯一性定理可应用微分几何的外微分分析对其进行统一表述和证明.那么在时变电磁场中是不是也具有唯一性定理呢?法拉第电磁感应定律表明时变的磁场能够产生电场,反之,时变的电场也能够产生磁场。
时变的电场和磁场相互激励、相互依存,构成了统一电磁场不可分割的两部分。
自然界中所存在的磁场室友激励源产生的,一旦激励源确定后,电磁场也就随之确定了。
如果考虑范围局限于一个有限区域内,那么这个有限区域内的电磁场,除了由处在这个区域内的激励源产生,还可以由这个区域外的激励源产生,仅知道这个区域内的激励源还不能完全确定这个区域内的电磁场。
为了彻底确定这个区域内的电磁场,还必须知道区域外的激励源的影响。
外部激励源的影响反映在区域边界的边值上。
电磁场的基本问题就是给定所有边界上的边界条件求出满足麦克斯韦方程组描述的电磁场的解。
同一电磁场问题的求解可以采用不同的场量作变量求解,也可以采用不同的方法求解用不同的变量或者是用不同的方法求解得的电磁场定解问题的解答是不是正确的?电磁场定解问题的解是不是独一无二的?这就是电磁场的唯一性问题。
maxwell方程组及边界条件

CQU
0 (静态场) 当 t
D H J t
B E t B 0 D
恒定场是时变电磁场的特殊形式
H J
E 0 B 0 D
变的磁场也能产生电场; • 磁通连续性原理——表明磁场是无散场,磁力线总是 D 高斯定律 闭合曲线; • 高斯定律——表明电荷以发散的方式产生电场。 BH D E J E
性能方程(构成方程)
5.3
电磁场基本方程组 • 分界面上的衔接条件
CQU
积分形式
D 全电流定律 l H dl s J c dS s t dS s v dS B dS 电磁感应定律 l E dl S t 磁通连续性原理 B dS 0
折射定律
tan 1 1 tan 2 2
tan 1 1 tan 2 2
1865年,Maxwell总结了电磁场基本方程组 (Maxwell方程)为
D 全电流定律 H J c v t • 全电流定律——麦克斯韦第一方程, 表明传导电流和时变的 B E 电磁感应定律 电场都能产生磁场;t 磁通连续性原理 B 0 • 电磁感应定律——麦克斯韦第二方程 , 表明除电荷外,时
en B2 B1 0
B1n B2 n
H 2t H1t K
en H 2 H1 K
பைடு நூலகம்
电场:
en E2 E1 0 en D2 D1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
义在 G 上的已知向量函数和数量函数. 方程( 10 ) 等 价于下面的方程组 ·Ψ = 0 , + × = - K, t ψ Φ ·Φ = ρ, t Φ - × ψ = - J.
| x2 | 2 +| x3 | 2 ) 2 . 将 R4 中的元简记为( t, x) , 其中, 4 x = ( x1 , x2 , x3 ) . 称 f: R → Q, f( t, x ) = f0 ( t , x ) e0 + f1 ( t , x ) e1 + f2 ( t , x ) e2 + f3 ( t , x) e3 为拟四元数函数,
i =1
∫
g1 ( x' x' 2, 3) t2 - η2 槡
dV -
η≤ t
∫ dξ ×
0
20
2 2
四川师范大学学报( 自然科学版)
第 37 卷
-2κ -1
(
∫
0, x' x' φ + φ ) ( t - ξ, 2, 3) x1 x2 2 x1 x3 3
2 2 ξ -η 槡
[13 ] 引理 1
方程(
3
x) = 有解 ψ + iΦ, Φ( t, φi = 1 t 1 1 [ 4 π t t
i
φi e i , 其中 ∑ i =1
2 方程 (
e + ) ( ψ + iΦ) = - K + i( ρ - t 0 J) 的初边值问题
x) φ1 ( t,
∫
| ζ -x| = t
2 - △ ) ( ψ + i Φ) = t
2
Φ( 0 , ζ ) ) + ω( x ) , t T3 (
e - ) 得 t 0
( Φ( 0 , ζ) ) = t 1 1 - ) ( Φ( 0 , ( ζ ζ) ) dV ζ , 4π Ω r( ζ, x) t ω( x) = ω1 + ( ω2 e0 + iω3 e1 ) e2 , (
摘要: 磁单极子的概念被狄拉克提出后 , 就一直被关注, 但一直都没有发现其存在的证据 , 最近, 一些物 Maxwell 方程就会发生变 理学家在动量空间及自旋冰材料中找到其存在的确切证据 . 当磁单极子存在时, 化. 用复分析与四元数分析的方法 , 研究了磁单极子存在时的 Maxwell 方程组的初边值问题, 获得了不同情 况下问题的可解条件和通解 . 进一步完善用复分析与四元数分析的方法研究双曲型方程的边值问题的理 论, 并且对物理学中磁单极子存在时的电磁研究有一定的应用价值 . 关键词: 拟四元数代数; 磁单极子; Maxwell 方程组; 初边值问题 中图分类号: O175. 2 文献标志码: A 文章编号: 1001 - 8395 ( 2014 ) 01 - 0018 - 07 doi: 10. 3969 / j. issn. 1001 - 8395. 2014. 01. 004
2 x3 ) ∈ Г = { x2 ( 15 ) ( x2 , 2 + x3 = 1 } , fi , gi ( i = 1, 2, 3) , r ( x2 , x3 ) 均为实值函 其中, τ( x) ,
引入一阶微分算子 D = e0 + e + e + e = e0 + , t x1 1 x2 2 x3 3 t 珚 D = e0 - e - e - e = e0 - . t x1 1 x2 2 x3 3 t 2 2 2 2 2 D珚 D = ( 2 - 2 - 2 - 显然, 2 ) e0 = ( 2 - t x1 x2 x3 t △3 ) e 0 , 而 和 △3 分别为三维梯度算子和 Laplace . 算子 12] 在文献[ 中讨论了某些一阶双曲方程组的 13] 初边值问题, 用类似的方法, 在文献[ 中讨论了 Maxwell 方程组 ( 6 ) 的初边值问题, 12] 而在文献[ Maxwell 方程组 ( 6 ) 可表 中引入了拟四元数空间后, 示为 D( ψ + iΦ) = if2 , ( 8) 而方程组( 7 ) 可表示为 D( ψ + iΦ) = f1 + if2 , ( 9) 而方程组 ( 7 ) 是磁单极子存在时的 Maxwell 方 程 下面就讨论此方程组的初边值问题. 为了简化 组, 计算, 先讨论方程 ( e0 + ) ( ψ + iΦ) = - K + i( ρ - J) t 的初边值问题, 再讨论方程( e0 + ) ( ψ + iΦ) = t g0 - K + i( ρ - J) 的初边值问题.
3
1
( 11 )
x) = 记 ω( t ,
f i ( t, x) e i , 并称其为向量函数. ∑ i =1
x) | | x | < 1 - t, 0 < t < 1} , 记 Ω = { ( t, 即 Ω 是空 4 0, 0, 0) , 间 R 中的一个顶点在 ( 1 , 而底在超平面 t = 0 上的单位球 B3 的锥形区域. 考虑方程 ( 11 ) 的 以下边值问题. 问题 F 求方程( 11 ) 在区域 Ω 上的解 ψ + iΦ, 使 ψ, Φ ∈ C( 珚 Ω) , x ) = f2 e0 + i f3 e1 , ( φ2 e 0 + i φ3 e 1 ) ( 0 , ( φ e + i φ3 e 1 ) ( 0 , x ) = g2 e0 + i g3 e1 , ( 12 ) t 2 0 0, x2 , x3 ) = f1 ( x2 , x3 ) , φ1 ( 0 , 0, x2 , x3 ) = g1 ( x2 , x3 ) , ( 13 ) φ ( 0, t 1 x ) = τ( x ) , x ∈ B3 , ( 14 ) ψ1 ( 0 , κ Re( x2 e0 - ix3 e1 ) [ 0, x2 , x3 ) e0 + ψ2 ( 0 , iψ3 ( 0 , 0, x2 , x3 ) e1] = r( x2 , x3 ) e0 ,
f2 , f3 ∈ C 4 ( B 3 ) , g2 , g3 ∈ C3 ( B3 ) , f1 ∈ C 3 ( B 2 ) , 数, g1 ∈ C2 ( B2 ) , r ( x2 , x3 ) ∈ C α ( Γ ) , 0 τ ∈ C ( B3 ) , < α < 1, κ 是一个整数. κ 称为问题 F 的指标. e + ) ( ψ + iΦ) = 0 在 t 0 上述问题 F 中的初边值条件下的解 1 ) 当 κ ≥ 0 时,
( 2)
( 7)
( 3) ( 4)
方程组( 1) 中第三与第四式在磁荷存在时仍然成立. 因此, 磁单极子存在时, 得到一组新的 Maxwell 方程组为
收稿日期: 2012 - 10 - 28
( ) ( )
( (
) )
基金项目: 国家自然科学基金( 61173121 ) 、 高校博士点基金( 20095134110001 ) 和四川教育厅重点项目( 12ZA136 ) 资助项目 * 通信作者简介: 杨丕文( 1951 —) , E - mail: ypwen1@ sina. com 男, 教授, 主要从事函数论与偏微分方程的研究,
f i ( ζ) dS +
4 设 G 是 R 中的一个区域, 考虑 G 上关于 ( ψ + iΦ) 的方程
, i = 2, 3; ∫ g ( ζ) dS] =- ∫ ( x, x ), φ + φ ) dx + C( t, x x
| ζ -x| = t x1 0 2 3 1 2 3 2 3
Maxwell 方程组是电磁理论的核心, 描述了宏 观电磁现象, 方程组的微分形式为 ·B = 0 , B + × E = 0, t ·D = ρ, D - × H = - J, t
Байду номын сангаас
( 1)
·B = g0 , t B + × E = - K, ( 5) ·D = ρ, t D - × H = - J. E = Φ, H = Ψ, Maxwell 方程组 设 C = 1, ε0 = μ0 = 1 , ( 1 ) 与方程组( 5 ) 即可简化为[10 - 11] ·ψ = 0 , + × = 0, t ψ Φ ·Φ = ρ, t Φ - × ψ = - J; ·ψ = g0 , t ψ + × Φ = - K, ·Φ = ρ, t Φ - × ψ = - J. [12 ] 引入拟四元数空间 , 即记二阶矩阵 1 0 1 0 e0 = , e1 = , 0 1 0 -1 0 1 0 i e2 = , e3 = , 1 0 -i 0 则有
( x2 e0 - i x3 e1 ) dV] ,
η≤ξ 2
∫
B2
x' ω ( 0, 2 + ix' 3) ) x1 1 1 dV + × e0 - ( x' πi 2 e0 + ix' 3 e1 ) ( x2 e0 - i x3 e1 ) (
2 3 2 0
η = ( x' 2 - x2 ) x) = - ψ( t, i T3 ( 其中
t 0
2
+ ( x' 3 - x3 ) ,
2
( x' e ∫ r' ( x' - ix' ) / [
Γ
+ ix' 3 e1 )
-κ
[ ( x' 2 e0 + ( 19 )
