(完整版)圆锥曲线存在性问题
第8章-第11节圆锥曲线中的定点、定值、存在性问题

y-1=k1x, 由 y=-2,
3 x=- , 3 k1 得 ∴M-k ,-2. 1 y =- 2 , 1 x=- , 1 k2 得 ∴N-k ,-2. 2 y =- 2 ,
高三一轮总复习 攻考向·三级提能
定点问题
(2016· 福州模拟)在平面直角坐标系xOy中,A,B两点的坐标分别为 1 (0,1),(0,-1),动点P满足直线AP与直线BP的斜率之积为- 4 ,直线AP,BP与 直线y=-2分别交于点M,N.
(1)求动点P的轨迹方程; (2)求线段MN的最小值; (3)以线段MN为直径的圆是否经过某定点?若经过定点,求出定点的坐 标;若不经过定点,请说明理由.
2 2 x 2 1 2 x1+ 2 +2- 2 =2+ 2 x1,
+
2 6 2 =2+ 2 . 2
∵2|MF|=|PF|+|QF|,
∴2 2+
2 2 =4+ 2 (x1+x2), 2
高三一轮总复习
∴x1+x2=2.
2 2 x1+2y1=4, ①当x1≠x2时,由 2 2 x + 2 y 2 2=4, 2 2 2 x2 - x + 2( y - y 1 2 1 2)=0,
高三一轮总复习
(2)当直线AB的斜率存在时,设直线AB的方程为y=kx+1,A,B的坐标分 别为(x1,y1),(x2,y2). x2 y2 + =1, 联立 4 2 得(2k2+1)x2+4kx-2=0. y=kx+1, 其判别式Δ=(4k)2+8(2k2+1)>0, 4k 2 所以x1+x2=- 2 ,x1x2=- 2 . 2k +1 2k +1
最全总结之圆锥曲线定点问题
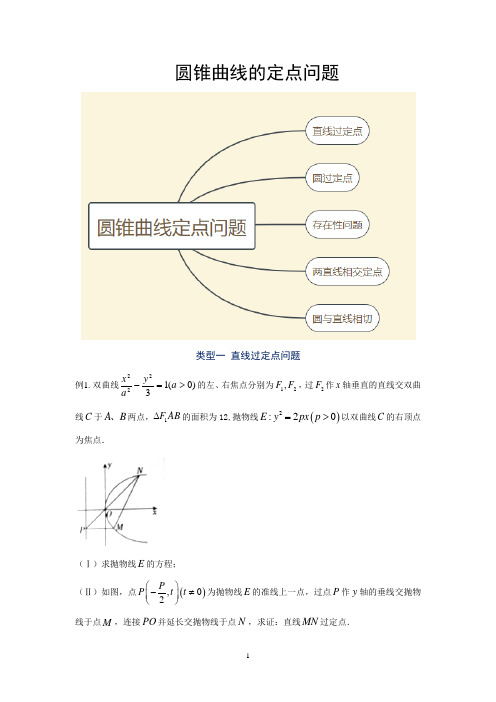
圆锥曲线的定点问题类型一 直线过定点问题例1. 双曲线)0(13222>=-a y ax 的左、右焦点分别为12,F F ,过2F 作x 轴垂直的直线交双曲线C 于A B 、两点,1F AB ∆的面积为12,抛物线()2:20E y px p =>以双曲线C 的右顶点为焦点.(Ⅰ)求抛物线E 的方程; (Ⅱ)如图,点(),02P P t t ⎛⎫-≠ ⎪⎝⎭为抛物线E 的准线上一点,过点P 作y 轴的垂线交抛物线于点M ,连接PO 并延长交抛物线于点N ,求证:直线MN 过定点.解析:(Ⅰ)设()()2,00F c c >,则23c a =+令x c =代入C 的方程有:3A y a= ∴1216322122F ABA a S c y a∆+=⨯⨯== ∴1a =,故12pa ==,即2p = ∴抛物线E 的方称为:24y x =.(Ⅱ)由(Ⅰ)知:()()1,0P t t -≠,则2,4t M t ⎛⎫⎪⎝⎭直线PO 的方称为y tx =-,代入抛物线E 的方程有:244,N tt ⎛⎫-⎪⎝⎭ 当24t ≠时,22244444MNt tt k t t t +==--, ∴直线MN 的方程为:22444t t y t x t ⎛⎫-=- ⎪-⎝⎭,即()2414ty x t =-- ∴此时直线MN 过定点()1,0,当24t =时,直线MN 的方称为:1x =,此时仍过点()1,0 即证直线MN 过定点. 跟踪训练1. (泰安市2019届)已知椭圆的离心率为,抛物线的准线被椭圆截得的线段长为.(1)求椭圆的方程; (2)如图,点分别是椭圆的左顶点、左焦点直线与椭圆交于不同的两点(都在轴上方).且.证明:直线过定点,并求出该定点的坐标.解析:(1)由题意可知,抛物线的准线方程为,又椭圆被准线截得弦长为,∴点在椭圆上,∴,① 又,∴,∴,②,由①②联立,解得,∴椭圆的标准方程为:,(2)设直线,设,把直线代入椭圆方程,整理可得,,即,∴,,∵,∵都在轴上方.且,∴,∴,即,整理可得,∴,即,整理可得,∴直线为,∴直线过定点.【点睛】本题考查椭圆的标准方程,直线与椭圆的位置关系,考查韦达定理,直线的斜率公式的应用,考查计算能力,属于中档题.2.已知抛物线2:2(0)C y px p =>的焦点曲线22:1243x y Γ-=的一个焦点, O 为坐标原点,点M 为抛物线C 上任意一点,过点M 作x 轴的平行线交抛物线的准线于P ,直线OP 交抛物线于点N .(Ⅰ)求抛物线C 的方程;(Ⅱ)求证:直线MN 过定点G ,并求出此定点的坐标.解析:(Ⅰ)由曲线22:1243x y Γ-=,化为标准方程可得2211344x y -=, 所以曲线22:11344x y Γ-=是焦点在x 轴上的双曲线,其中2213,44a b ==,故2221c a b =+=, Γ的焦点坐标分别为()()121,01,0F F -、,因为抛物线的焦点坐标为,0,(0)2p F p ⎛⎫> ⎪⎝⎭,由题意知12p=,所以2p =,即抛物线的方程为24y x =. (Ⅱ)由(Ⅰ)知抛物线24y x =的准线方程为1x =-,设()1,P m -,显然0m ≠.故2,4m M m ⎛⎫ ⎪⎝⎭,从而直线OP 的方程为y mx =-,联立直线与抛物线方程得24{ y x y mx ==-,解得244,N m m ⎛⎫-⎪⎝⎭①当2244m m =,即2m =±时,直线MN 的方程为1x =,②当2244m m ≠,即2m ≠±时,直线MN 的方程为22444m m y m x m ⎛⎫-=- ⎪-⎝⎭,整理得MN的方程为()2414my x m =--,此时直线恒过定点()1,0G , ()1,0Q 也在直线MN 的方程为1x =上,故直线MN 的方程恒过定点()1,0G .3.已知抛物线2:2(0)C y px p =>上一点P 到其焦点F 的距离为32,以P 为圆心且与抛物线准线l 相切的圆恰好过原点O .点A 是l 与x 轴的交点, ,M N 两点在抛物线上且直线MN 过A 点,过M 点及()1,1B -的直线交抛物线于Q 点.(1)求抛物线C 的方程;(2)求证:直线QN 过一定点,并求出该点坐标. 解析:(1)依题意得23||||==PF PO ,则△POF 是等腰三角形,所以点P 的横坐标为x=4p,由抛物线的焦半径公式:223242||=⇒=+=+=p p p p x PF 故抛物线的方程为x y 42=(2)证明:如图所示,设AM 的方程为()1y k x =+,代入抛物线的方程,可得2440ky y k -+=.设()11,M x y , ()22,N x y , ()33,Q x y ,则124y y =,由1313134MQ y y k x x y y -==-+,直线MB 的方程为()13411y x y y +=-+,∴()1113411y x y y +=-+,可得31341y y y +=-+,∴323441y y y +=-+, ∴()2323440y y y y +++=.① 直线QN 的方程为()22234y y x x y y -=-+.可得()232340y y y y y x -++=,②由①②可得1x =, 4y =-,∴直线QN 过定点()1,4-.4.如图,已知()11,0F -, ()21,0F 是椭圆C 的左右焦点, B 为椭圆C 的上顶点,点P 在椭圆C 上,直线1PF 与y 轴的交点为M , O 为坐标原点,且2PM F M =, 34OM =.(1)求椭圆C 的方程;(2)过点B 作两条互相垂直的直线分别与椭圆C 交于S , T 两点(异于点B ),证明:直线ST 过定点,并求该定点的坐标.解析:(1)由题意可得MO 为12F PF ∆的中位线,从而可得2MO PF P ,故212PF F F ⊥,且22322b PF OM a ===,然后根据222a b c =+和1c =可得24a =, 23b =,由此可得椭圆的方程13422=+y x . (2)解法一:设),(),,(2211y x T y x S ,直线BS: 3+=kx y联立方程⎪⎩⎪⎨⎧=++=1343y 22y x kx 整理得038)34(22=++kx x k 解得83kx =或0x =(舍去).∴183kx =,以1k -代替上式中的k ,可得22838343k k x k=-=+ 由题意可得,若直线BS 关于y 轴对称后得到直线''B S , 则得到的直线''S T 与ST 关于x 轴对称,所以若直线ST 经过定点,该定点一定是直线''S T 与ST 的交点,故该点必在y 轴上.设该点坐标()0,t ,则有121121t y y y x x x --=--, ∴121221y x x y t x x -=-(1212211kx x x x k x x ⎛+-- ⎝⎭=-, 将12,x x的值代入上式,化简得t = ∴直线ST经过定点0,7⎛- ⎝⎭. 解法二:化齐次式。
(完整版)解圆锥曲线问题常用的八种方法与七种常规题型

解圆锥曲线问题常用的八种方法与七种常规题型总论:常用的八种方法1、定义法2、韦达定理法3、设而不求点差法4、弦长公式法5、数形结合法6、参数法(点参数、K 参数、角参数)7、代入法8、充分利用曲线系方程法七种常规题型(1)中点弦问题(2)焦点三角形问题(3)直线与圆锥曲线位置关系问题 (4)圆锥曲线的有关最值(范围)问题 (5)求曲线的方程问题1.曲线的形状已知---—-—--这类问题一般可用待定系数法解决. 2.曲线的形状未知-———-求轨迹方程(6) 存在两点关于直线对称问题 (7)两线段垂直问题常用的八种方法1、定义法(1)椭圆有两种定义。
第一定义中,r 1+r 2=2a 。
第二定义中,r 1=ed 1 r 2=ed 2。
(2)双曲线有两种定义。
第一定义中,a r r 221=-,当r 1〉r 2时,注意r 2的最小值为c-a :第二定义中,r 1=ed 1,r 2=ed 2,尤其应注意第二定义的应用,常常将 半径与“点到准线距离”互相转化。
(3)抛物线只有一种定义,而此定义的作用较椭圆、双曲线更大,很多抛物线问题用定义解决更直接简明.2、韦达定理法因直线的方程是一次的,圆锥曲线的方程是二次的,故直线与圆锥曲线的问题常转化为方程组关系问题,最终转化为一元二次方程问题,故用韦达定理及判别式是解决圆锥曲线问题的重点方法之一,尤其是弦中点问题,弦长问题,可用韦达定理直接解决,但应注意不要忽视判别式的作用。
3、设而不求法解析几何的运算中,常设一些量而并不解解出这些量,利用这些量过渡使问题得以解决,这种方法称为“设而不求法”。
设而不求法对于直线与圆锥曲线相交而产生的弦中点问题,常用“点差法",即设弦的两个端点A(x 1,y 1),B(x 2,y 2),弦AB 中点为M (x 0,y 0),将点A 、B 坐标代入圆锥曲线方程,作差后,产生弦中点与弦斜率的关系,这是一种常见的“设而不求”法,具体有:(1))0(12222>>=+b a b y a x 与直线相交于A 、B ,设弦AB 中点为M(x 0,y 0),则有02020=+k b y a x 。
圆锥曲线中的存在性问题

第11讲圆锥曲线中的存在性问题一、考情分析圆锥曲线中的存在性问题、探索问题是高考常考题型之一,它是在题设条件下探索某个数学对象(点、线、数等)是否存在或某个结论是否成立.由于题目多变,解法不一,我们在平时的教学中对这类题目训练较少,因而学生遇到这类题目时,往往感到无从下手,本文针对圆锥曲线中这类问题进行了探讨.二、经验分享探索性问题是一种具有开放性和发散性的问题,此类题目的条件或结论不完备。
要求解答者自己去探索,结合已有条件,进行观察、分析、比较和概括。
它对学生的数学思想、数学意识及综合运用数学方法的能力提出了较高的要求。
它有利于培养学生探索、分析、归纳、判断、讨论与证明等方面的能力,使学生经历一个发现问题、研究问题、解决问题的全过程。
探索性问题一般可分为:条件追溯型,结论探索型、条件重组型,存在判断型,规律探究型,实验操作型。
1、条件追溯型这类问题的基本特征是:针对一个结论,条件未知需探索,或条件增删需确定,或条件正误需判断。
解决这类问题的基本策略是:执果索因,先寻找结论成立的必要条件,再通过检验或认证找到结论成立的充分条件。
在“执果索因”的过程中,常常会犯的一个错误是不考虑推理过程的可逆与否,误将必要条件当作充分条件,应引起注意。
2、结论探索型这类问题的基本特征是:有条件而无结论或结论的正确与否需要确定。
解决这类问题的策略是:先探索结论而后去论证结论。
在探索过程中常可先从特殊情形入手,通过观察、分析、归纳、判断来作一番猜测,得出结论,再就一般情形去认证结论。
3、条件重组型这类问题是指给出了一些相关命题,但需对这些命题进行重新组合构成新的复合命题,或题设的结求的方向,条件和结论都需要去探求的一类问题。
此类问题更难,解题要有更强的基础知识和基本技能,需要要联想等手段。
一般的解题的思路是通过对条件的反复重新组合进行逐一探求。
应该说此类问题是真正意义上的创新思维和创造力。
4、存在判断型这类问题的基本特征是:要判断在某些确定条件下的某一数学对象(数值、图形、函数等)是否存在或某一结论是否成立。
圆锥曲线中的证明与存在性问题

1
1
2
同理,联立直线 BC 与抛物线 W 的方程,并消去 y 得 x + x - x 0- 02
=0,且| BC |= 1 +
= 1+
1 1
2
+ 20 ,
1 2
−
·| x 2- x 0|=
1+
1 2
1
−
·−
− 20
∴| AB |+| BC |= 1 +
−4
−
3+2−6
−2
=
9−6+18 −2 +4 3+2−6
,
−62 +4−8+24
−62 +4−8+24
= 2
= 2
2
9 +8 +6−12−36
9 +72−182 +6−12−36
2 −32 +2−4+12
−62 +4−8+24
|,| |,| |成等差数列,并求该数列的公差.
(2)由题意得 F (1,0).设 P ( x 3, y 3),
则( x 3-1, y 3)+( x 1-1, y 1)+( x 2-1, y 2)=(0,0).
由(1)及题设得 x 3=3-( x 1+ x 2)=1,
y 3=-( y 1+ y 2)=-2 m <0.
圆锥曲线中的证明与存在性问题
考点一
例1
圆锥曲线中的证明问题
(2023·新高考Ⅰ卷)在直角坐标系 xOy 中,点 P 到 x 轴的距离等于点 P
圆锥曲线存在性问题

圆锥曲线中的存在性问题一、基础知识1、在处理圆锥曲线中的存在性问题时,通常先假定所求的要素(点,线,图形或是参数)存在,并用代数形式进行表示。
再结合题目条件进行分析,若能求出相应的要素,则假设成立;否则即判定不存在2、存在性问题常见要素的代数形式:未知要素用字母代替 (1)点:坐标()00,x y(2)直线:斜截式或点斜式(通常以斜率为未知量) (3)曲线:含有未知参数的曲线标准方程 3、解决存在性问题的一些技巧:(1)特殊值(点)法:对于一些复杂的题目,可通过其中的特殊情况,解得所求要素的必要条件,然后再证明求得的要素也使得其它情况均成立。
(2)核心变量的选取:因为解决存在性问题的核心在于求出未知要素,所以通常以该要素作为核心变量,其余变量作为辅助变量,必要的时候消去。
(3)核心变量的求法:①直接法:利用条件与辅助变量直接表示出所求要素,并进行求解②间接法:若无法直接求出要素,则可将核心变量参与到条件中,列出关于该变量与辅助变量的方程(组),运用方程思想求解。
二、典型例题:例1:已知椭圆()2222:10x y C a b a b +=>>F 的直线l 与C 相交于,A B 两点,当l 的斜率为1时,坐标原点O 到l 。
(1)求,a b 的值(2)C 上是否存在点P ,使得当l 绕F 旋转到某一位置时,有OP OA OB =+成立?若存在,求出所有的P 的坐标和l 的方程,若不存在,说明理由解:(1)::3c e a b c a ==⇒=则,a b ==,依题意可得:(),0F c ,当l 的斜率为1时:0l y x c x y c =-⇒--=2O l d -∴==解得:1c =a b ∴== 椭圆方程为:22132x y += (2)设()00,P x y ,()()1122,,,A x y B x y 当l 斜率存在时,设():1l y k x =-OP OA OB =+ 012012x x x y y y =+⎧∴⎨=+⎩ 联立直线与椭圆方程:()221236y k x x y =-⎧⎪⎨+=⎪⎩ 消去y 可得:()2222316x k x +-=,整理可得:()2222326360kx k x k +-+-=2122632k x x k ∴+=+ ()312122264223232k ky y k x x k k k k +=+-=-=-++22264,3232k k P k k ⎛⎫∴- ⎪++⎝⎭因为P 在椭圆上22222642363232k k k k ⎛⎫⎛⎫∴⋅+-= ⎪ ⎪++⎝⎭⎝⎭()()()2242222272486322432632k k k k k k ∴+=+⇒+=+()2224632k k k ∴=+⇒=当k =时,):1l y x =-,3,2P ⎛ ⎝⎭当k =):1l y x =-,3,22P ⎛ ⎝⎭当斜率不存在时,可知:1l x =,1,,1,33A B ⎛⎫⎛- ⎪ ⎝⎭⎝⎭,则()2,0P 不在椭圆上∴综上所述:):1l y x =-,3,2P ⎛ ⎝⎭或):1l y x =-,32P ⎛ ⎝⎭例2:过椭圆()2222:10x y a b a bΓ+=>>的右焦点2F 的直线交椭圆于,A B 两点,1F 为其左焦点,已知1AF B 的周长为8(1)求椭圆Γ的方程(2)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆Γ恒有两个交点,P Q ,且OP OQ ⊥?若存在,求出该圆的方程;若不存在,请说明理由解:(1)由1AF B 的周长可得:482a a =⇒=2c e c a ∴==⇒=2221b a c ∴=-= 椭圆22:14x y Γ+= (2)假设满足条件的圆为222x y r +=,依题意,若切线与椭圆相交,则圆应含在椭圆内01r ∴<<若直线PQ 斜率存在,设:PQ y kx m =+,()()1122,,,P x y Q x yPQ 与圆相切 ()2221O l d r m r k -∴==⇐=+0OP OQ OP OQ ⊥⇒⋅= 即12120x x y y +=联立方程:2244y kx mx y =+⎧⇒⎨+=⎩()222148440k x kmx m +++-=2121222844,4141km m x x x x k k -∴+=-=++()()()2212121212y y kx m kx m k x x km x x m ∴=++=+++()()22121212121x x y y k x x km x x m ∴+=++++()2222244814141m km k km m k k -⎛⎫=⋅++⋅-+ ⎪++⎝⎭22254441m k k --=+ 225440m k ∴--=对任意的,m k 均成立将()2221m r k =+代入可得:()()22251410r k k +-+=()()225410r k ∴-+= 245r ∴=∴存在符合条件的圆,其方程为:2245x y +=当PQ 斜率不存在时,可知切线PQ 为x =若:PQ x =,5555P Q ⎛⎛- ⎝⎭⎝⎭0OP OQ ∴⋅= :PQ x ∴=若:PQ x = 综上所述,圆的方程为:2245x y +=例3:已知椭圆()222210x y a b a b+=>>经过点(,离心率为12,左,右焦点分别为()1,0F c -和()2,0F c(1)求椭圆C 的方程(2)设椭圆C 与x 轴负半轴交点为A ,过点()4,0M -作斜率为()0k k ≠的直线l ,交椭圆C 于,B D 两点(B 在,M D 之间),N 为BD 中点,并设直线ON 的斜率为1k ① 证明:1k k ⋅为定值② 是否存在实数k ,使得1F N AD ⊥?如果存在,求直线l 的方程;如果不存在,请说明理由解:(1)依题意可知:12c e a ==可得:::a b c =∴椭圆方程为:2222143x y c c+=,代入(可得:1c =∴椭圆方程为:22143x y += (2)① 证明:设()()1122,,,B x y D x y ,线段BD 的中点()00,N x y 设直线l 的方程为:()4y k x =+,联立方程:()2243412y k x x y ⎧=+⎪⎨+=⎪⎩ 化为:()2222343264120k x k x k +++-= 由0∆>解得:214k < 且22121222326412,4343k k x x x x k k --+==++ 2120216243x x k x k +∴==-+ ()00212443k y k x k =+=+01034y k x k∴==- 13344k k k k ∴=-⋅=-② 假设存在实数k ,使得1F N AD ⊥,则11F N AD k k ⋅=-12022021243416114134F Nky k k k k x k k +∴===+--++ ()2222422AD k x y k x x +==++ ()1222441142F N AD k x kk k k x +⋅=⋅=--+即()222222224164182282k x k k x k x k +=-+-⇒=--<-因为D 在椭圆上,所以[]22,2x ∈-,矛盾所以不存在符合条件的直线l例4:设F 为椭圆()2222:10x y E a b a b +=>>的右焦点,点31,2P ⎛⎫⎪⎝⎭在椭圆E 上,直线0:34100l x y --=与以原点为圆心,以椭圆E 的长半轴长为半径的圆相切(1)求椭圆E 的方程(2)过点F 的直线l 与椭圆相交于,A B 两点,过点P 且平行于AB 的直线与椭圆交于另一点Q ,问是否存在直线l ,使得四边形PABQ 的对角线互相平分?若存在,求出l 的方程;若不存在,说明理由 解:(1)0l 与圆相切1025O l d r -∴=== 2a ∴= 将31,2P ⎛⎫⎪⎝⎭代入椭圆方程22214x y b +=可得:b =∴椭圆方程为:22143x y += (2)由椭圆方程可得:()1,0F 设直线():1l y k x =-,则()3:12PQ y k x -=- 联立直线l 与椭圆方程:()2213412y k x x y ⎧=-⎪⎨+=⎪⎩消去y 可得:()22224384120k x k x k +-+-= ()()()2222218443412144144k k k k ∴∆=-+-=+()212212143k AB x k +∴=-==+同理:联立直线PQ 与椭圆方程:()223123412y k x x y ⎧=-+⎪⎨⎪+=⎩消去y 可得:()()22224381241230k x k k x k k +--+--= ()()()222222181244123431444k k k k k k k ⎛⎫⎡⎤∆=----+=++ ⎪⎣⎦⎝⎭PQ ∴==因为四边形PABQ 的对角线互相平分∴四边形PABQ 为平行四边形AB PQ ∴= ()2212143k k +∴=+解得:34k =∴存在直线:3430l x y --=时,四边形PABQ 的对角线互相平分例5:椭圆()2222:10x y C a b a b+=>>的左右焦点分别为12,F F ,右顶点为A ,P 为椭圆1C 上任意一点,且12PF PF ⋅的最大值的取值范围是22,3c c ⎡⎤⎣⎦,其中c = (1)求椭圆1C 的离心率e 的取值范围(2)设双曲线2C 以椭圆1C 的焦点为顶点,顶点为焦点,B 是双曲线2C 在第一象限上任意一点,当e 取得最小值时,试问是否存在常数()0λλ>,使得11BAF BF A λ∠=∠恒成立?若存在,求出λ的值;若不存在,请说明理由 解:(1)设()()()12,,,0,,0P x y F c F c -()()12,,,PF c x y PF c x y ∴=---=-- 22212PF PF x y c ∴⋅=+-由22221x y a b +=可得:22222b y b x a=-代入可得: 2222222222212221b c PF PF x y c x b c x b c a a ⎛⎫⋅=+-=-+-=+- ⎪⎝⎭[],x a a ∈- ()212maxPF PF b ∴⋅=222222222222334c ac b c c a c c c a⎧≤⎪∴≤≤⇒≤-≤⇒⎨≥⎪⎩21114222e e ∴≤≤⇒≤≤(2)当12e =时,可得:2,a c b = ∴双曲线方程为222213x y c c-=,()()12,0,,0A c F c -,设()00,B x y ,000,0x y >>当AB x ⊥轴时,002,3x c y c ==13tan 13c BF A c ∴== 14BF A π∴∠= 因为12BAF π∠= 112BAF BF A ∴∠=∠所以2λ=,下面证明2λ=对任意B 点均使得11BAF BF A λ∠=∠成立 考虑1001100tan ,tan 2AB BF y y BAF k BF A k x c x c∠=-=-∠==-+ ()()000101222210000222tan tan 21tan 1y y x c BF Ax cBF A BF Ax c yy x c ⋅+∠+∴∠===-∠+-⎛⎫- ⎪+⎝⎭由双曲线方程222213x y c c-=,可得:2220033y x c =-()()()()2222222000000003322422x c y x c x c x cx c x c c x ∴+-=+-+=-++=+-()()()000110002tan 2tan 222y x c y BF A BAF x c c x c x +∴∠===∠+--112BAF BF A ∴∠=∠结论得证2λ∴=时,11BAF BF A λ∠=∠恒成立例6:如图,椭圆()2222:10x y E a b a b +=>>的离心率是2,过点()0,1P 的动直线l 与椭圆相交于,A B 两点,当直线l 平行于x 轴时,直线l 被椭圆E截得的线段长为(1)求椭圆E 的方程(2)在平面直角坐标系xOy 中,是否存在与点P 不同的定点Q ,使得对于任意直线l ,QA PA QBPB=恒成立?若存在,求出点Q 的坐标;若不存在,请说明理由解:(1)2c e a ==::a b c ∴= ∴椭圆方程为222212x y b b+=由直线l 被椭圆E截得的线段长为点)在椭圆上22221122b b b+=⇒= 24a ∴= ∴椭圆方程为22142x y += (2)当l 与x 轴平行时,由对称性可得:PA PB =1QA PA QBPB∴==即QA QB =Q ∴在AB 的中垂线上,即Q 位于y 轴上,设()00,Q y当l 与x轴垂直时,则((,0,A B1,1PA PB ∴=-=+00QA y QB y ==+QA PA QBPB∴=⇒=可解得01y =或02y = ,P Q 不重合 02y ∴=()0,2Q ∴下面判断()0,2Q 能否对任意直线均成立若直线l 的斜率存在,设:1l y kx =+,()()1122,,,A x y B x y联立方程可得:()222224124201x y k x kx y kx ⎧+=⇒++-=⎨=+⎩由QA PA QBPB=可想到角平分线公式,即只需证明QP 平分BQA ∠∴只需证明0QA QB QA QB k k k k =-⇒+=()()1122,,,A x y B x y ∴121222,QA QB y y k k x x --∴== ()()()21122112121212121222222QA QBx y x y x y x y x x y y k k x x x x x x -+-+-+--∴+=+==① 因为()()1122,,,A x y B x y 在直线1y kx =+上,112211y kx y kx =+⎧∴⎨=+⎩代入①可得:()()()()211212121212121122QA QB x kx x kx x x kx x x x k k x x x x +++-+-+∴+==联立方程可得:()222224124201x y k x kx y kx ⎧+=⇒++-=⎨=+⎩12122242,1212k x x x x k k ∴+=-=-++ 22224212120212QA QBkk k k k k k ⋅-+++∴+==-+ 0QA QB k k ∴+=成立QP ∴平分BQA ∠ ∴由角平分线公式可得:QA PA QBPB=例7:椭圆()2222:10x y C a b a b +=>>的上顶点为A ,4,33b P ⎛⎫⎪⎝⎭是C 上的一点,以AP 为直径的圆经过椭圆C 的右焦点F (1)求椭圆C 的方程(2)动直线l 与椭圆C 有且只有一个公共点,问:在x 轴上是否存在两个定点,它们到直线l 的距离之积等于1?若存在,求出这两个定点的坐标;如果不存在,请说明理由解:由椭圆可知:()()0,,,0A b F cAP 为直径的圆经过F FA FP ∴⊥0FA FP ∴⋅= ()4,,,33b FA c b FP c ⎛⎫=-=- ⎪⎝⎭22244003333b b c c c c ⎛⎫∴--+=⇒-+= ⎪⎝⎭由4,33b P ⎛⎫⎪⎝⎭在椭圆上,代入椭圆方程可得:222211611299b a a b ⋅+⋅=⇒= 22222401332b c c b c b c a ⎧-+=⎪⇒==⎨⎪+==⎩∴椭圆方程为2212x y +=(2)假设存在x 轴上两定点()()1122,0,,0M M λλ,()12λλ< 设直线:l y kx m =+12M l M l d d --∴==所以依题意:()12221212211M l M l k km m d d k λλλλ--+++⋅===+ ①因为直线l 与椭圆相切,∴联立方程:()2222221422022y kx m k x kmx m x y =+⎧⇒+++-=⎨+=⎩ 由直线l 与椭圆相切可知()()()2224421220km k m ∆=-+-=化简可得:2221m k =+,代入①可得:()()221212222121222112111k km k k km k k k λλλλλλλλ++++=⇒++++=++()()2121210k km λλλλ∴+++=,依题意可得:无论,k m 为何值,等式均成立121122121101λλλλλλλλ=-⎧=-⎧⎪∴+=⇒⎨⎨=⎩⎪<⎩所以存在两定点:()()121,0,1,0M M -例8:已知椭圆221:41C x y +=的左右焦点分别为12,F F ,点P 是1C 上任意一点,O 是坐标原点,12OQ PF PF =+,设点Q 的轨迹为2C (1)求点Q 的轨迹2C 的方程(2)若点T 满足:2OT MN OM ON =++,其中,M N 是2C 上的点,且直线,OM ON 的斜率之积等于14-,是否存在两定点,使得TA TB +为定值?若存在,求出定点,A B 的坐标;若不存在,请说明理由(1)设点Q 的坐标为(),x y ,点P 的坐标为()00,x y ,则220041x y +=由椭圆方程可得:12,F F ⎛⎫⎫ ⎪⎪ ⎪⎪⎝⎭⎝⎭12OQ PF PF =+ 且10020033,,,22PF x y PF x y ⎛⎫⎛⎫=---=-- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭()002,2Q x y ∴-- 00002222x x x x y y yy ⎧=-⎪=-⎧⎪∴⇒⎨⎨=-⎩⎪=-⎪⎩代入到220041x y +=可得:2214x y += (2)设点(),T x y ,()()1122,,,M x y N x y2OT MN OM ON =++()()()()12121122,,2,,x y x x y y x y x y ∴=--++212122x x x y y y =+⎧∴⎨=+⎩设直线,OM ON 的斜率分别为,OM ON k k ,由已知可得:212114OM ON y y k k x x ⋅==- 121240x x y y ∴+=考虑()()222221214242x y x x y y +=+++()()222211221212444416x y x y x x y y =+++++,M N 是2C 上的点 221122224444x y x y ⎧+=⎪∴⎨+=⎪⎩ 22444420x y ∴+=+⨯=即T 的轨迹方程为221205x y +=,由定义可知,T 到椭圆221205x y +=焦点的距离和为定值 ,A B ∴为椭圆的焦点()),A B∴所以存在定点,A B例9:椭圆()2222:10x y E a b a b +=>>的焦点到直线30x y -=抛物线()2:20G y px p =>的焦点与椭圆E 的焦点重合,斜率为k 的直线l 过G 的焦点与E 交于,A B ,与G 交于,C D (1)求椭圆E 及抛物线G 的方程 (2)是否存在常数λ,使得1AB CDλ+为常数?若存在,求出λ的值;若不存在,请说明理由解:(1)设,E G 的公共焦点为(),0F c2F l d c -∴==⇒=5c e a a ∴==⇒= 2221b a c ∴=-= 22:15x E y ∴+=28y x ∴=(2)设直线():2l y k x =-,()()()()11223344,,,,,,,A x y B x y C x y D x y与椭圆联立方程:()()22222225120205055y k x k x k x k x y ⎧=-⎪⇒+-+-=⎨+=⎪⎩ 2212122220205,1515k k x x x x k k -∴+==++)22115k AB k+∴==+直线与抛物线联立方程:()()22222248408y k x k x k x k y x⎧=-⎪⇒-++=⎨=⎪⎩ 234248k x x k +∴+= CD 是焦点弦 ()2342814k CD x x k+∴=++=()222222420181kk AB CD k λλ++∴+=+==+ 若1AB CDλ+为常数,则204= 5λ∴=- 例10:如图,在平面直角坐标系xOy 中,椭圆()2222:10x y C a b a b+=>>的离心率为3直线l 与x 轴交于点E ,与椭圆C 交于,A B 两点,当直线l 垂直于x 轴且点E为椭圆C 的右焦点时,弦AB 的长为3(1)求椭圆C 的方程(2)是否存在点E ,使得2211EA EB+为定值?若存在,请求出点E 的坐标,并求出该定值;若不存在,请说明理由解:(1)依题意可得:3c e a ==::a b c ∴=当l 与x 轴垂直且E 为右焦点时,AB 为通径22b AB a ∴==a b ∴=22162x y ∴+= (2)思路:本题若直接用用字母表示,,A E B 坐标并表示,EA EB ,则所求式子较为复杂,不易于计算定值与E 的坐标。
第9节 圆锥曲线中的定值、定点与存在性问题(课件PPT)

12
解:(1)由题意知 A(1,1),B(4,-2),设点 P 的坐标为(xP,yP), 切线 l1:y-1=k(x-1),联立yy-2=1x=k(x-1),由抛物线与直线 l1 相切,解得 k=12, 即 l1:y=12x+12,同理,l2:y=-14x-1.
xP=-2, 联立 l1,l2 的方程,可解得yP=-12, 即点 P 的坐标为-2,-12.
y0),由 k1+k2=2 得y0x-0 1+-yx00-1=2,得 x0=-1. 当直线 AB 的斜率存在时,设直线 AB 的方程为 y=kx+m(m≠1),A(x1,y1),B(x2,
y2). 则x22+y2=1 ,可得(1+2k2)x2+4kmx+2m2-2=0, y=kx+m
栏目导航
17 则 Δ=8(2k2-m2+1)>0,x1+x2=1-+42kkm2,x1·x2=21m+2-2k22 . 由 k1+k2=2,得y1x-1 1+y2x-2 1=2, 即(kx2+m-1)x1x+1x2(kx1+m-1)x2=2,(2-2k)x1x2=(m-1)(x1+x2),(2-2k)(2m2-
点,不妨设 C 为椭圆的左顶点,则 C(- 2,0),x1+x2=-x3= 2,x1=x2= 22,
可取 A 22, 23,B 22,- 23,则 S△ABC=12×
3×3 2
2=3
4
6 .
综上,△ABC 的面积为定值,定值为346.
栏目导航
10
解析几何中的定值问题是指某些几何量(线段的长度、图形的面积、角的度数、直线 的斜率等)的大小或某些代数表达式的值等和题目中的参数无关,不依参数的变化而变 化,始终是一个确定的值.求定值问题常见的方法有两种:①从特殊入手,求出定值, 再证明这个值与变量无关;②直接推理、计算,并在计算推理的过程中消去变量,从而 得到定值.
(完整版)圆锥曲线常见题型及答案

圆锥曲线常见题型归纳一、基础题涉及圆锥曲线的基本概念、几何性质,如求圆锥曲线的标准方程,求准线或渐近线方程,求顶点或焦点坐标,求与有关的值,求与焦半径或长(短)轴或实(虚)轴有关的角和三角形面积。
此类题在考试中最常见,解此类题应注意:(1)熟练掌握圆锥曲线的图形结构,充分利用图形来解题;注意离心率与曲线形状的关系; (2)如未指明焦点位置,应考虑焦点在x 轴和y 轴的两种(或四种)情况;(3)注意2,2,a a a ,2,2,b b b ,2,2,c c c ,2,,2p p p 的区别及其几何背景、出现位置的不同,椭圆中222b a c -=,双曲线中222b a c +=,离心率a c e =,准线方程a x 2±=;例题:(1)已知定点)0,3(),0,3(21F F -,在满足下列条件的平面上动点P 的轨迹中是椭圆的是 ( )A .421=+PF PFB .621=+PF PF C .1021=+PF PF D .122221=+PF PF (答:C );(2)方程8=表示的曲线是_____ (答:双曲线的左支)(3)已知点)0,22(Q 及抛物线42x y =上一动点P (x ,y ),则y+|PQ|的最小值是_____ (答:2)(4)已知方程12322=-++k y k x 表示椭圆,则k 的取值范围为____ (答:11(3,)(,2)22---); (5)双曲线的离心率等于25,且与椭圆14922=+y x 有公共焦点,则该双曲线的方程_______(答:2214x y -=);(6)设中心在坐标原点O ,焦点1F 、2F 在坐标轴上,离心率2=e 的双曲线C 过点)10,4(-P ,则C 的方程为_______(答:226x y -=)二、定义题对圆锥曲线的两个定义的考查,与动点到定点的距离(焦半径)和动点到定直线(准线)的距离有关,有时要用到圆的几何性质。
此类题常用平面几何的方法来解决,需要对圆锥曲线的(两个)定义有深入、细致、全面的理解和掌握。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆锥曲线中的存在性问题、基础知识1、在处理圆锥曲线中的存在性问题时,通常先假定所求的要素(点,线,图形或是参数)存在, 并用代数形式进行表示。
再结合题目条件进行分析,若能求出相应的要素, 则假设成 立;否则即判定不存在2、存在性问题常见要素的代数形式:未知要素用字母代替 1)点:坐标 x 0, y 02)直线:斜截式或点斜式(通常以斜率为未知量)3)曲线:含有未知参数的曲线标准方程 3、解决存在性问题的一些技巧:(1)特殊值(点)法:对于一些复杂的题目,可通过其中的特殊情况,解得所求要素的必 要条件,然后再证明求得的要素也使得其它情况均成立。
(2)核心变量的选取:因为解决存在性问题的核心在于求出未知要素,所以通常以该要素 作为核心变量,其余变量作为辅助变量,必要的时候消去。
(3)核心变量的求法:①直接法:利用条件与辅助变量直接表示出所求要素,并进行求解 ②间接法: 若无法直接求出要素, 则可将核心变量参与到条件中, 列出关于该变量与辅助变 量的方程(组) ,运用方程思想求解。
、典型例题:于 A, B 两点,当 l 的斜率为 1时,坐标原点 O 到l 的距离为 (1)求 a,b 的值uuur uuur uuur(2) C 上是否存在点 P ,使得当 l 绕F 旋转到某一位置时,有 OP OA OB 成立?若存 在,求出所有的 P 的坐标和 l 的方程,若不存在,说明理由 解:(1)e c 3a:b:c 3: 2 :1a322例 1:已知椭圆 C : x 2 y 2 1 a ab0 的离心率为过右焦点 F 的直线 l 与 C 相交2则a3c,b2c ,依题意可得:c,0,当l 的斜率为1时l:y xc xycd O解得:c13,b椭圆方程为:x22)设P x0, y0 ,x1, y1 ,B x2,y2当l 斜率存在时,设l:kxuuur uuur uuur QOP OA OBx0 x1x2联立直线与椭圆方程:3k2 2 x2 6k2 xx16k2x23k226k 2,3k22,6k23k 224272k 448k2y0 y1y2x2 3 y23k260y1y2 ky2消去6x1 x 2y 可得:2x2 3k 22k6k33k22k21 6 ,整理可得:4k3k 224k23k 2 2因为P 在椭圆上3 3k42k226 3k 222224k23k 23k224k 2 6 3k 2当k 2时,l :2x当k 2 时,l :y3,22,2当斜率不存在时,可知l:x,A1,2 3,B3233则P2,0 不在椭圆上1,综上所述: l : y 2 x 1 ,P 3, 2或l:y 2x 1,P 3, 22 2 2 2 22 例 2:过椭圆 : x 2 y 2 1 a a 2 b 2 b 0 的右焦点 F 2的直线交椭圆于 A,B 两点, F 1为其左 焦点,已知 VAF 1B 的周长为 8, 椭圆的离心率为 32 1) 求椭圆 的方程 2) 是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆 恒有两个交点 P,Q ,且 OP OQ ?若存在,求出该圆的方程;若不存在,请说明理由 解:(1)由 VAF 1B 的周长可得: 4a 8 a2 c 3c 3 a2 b 2椭圆 2 x 2 x 4 y 2 1 2) 假设满足条件的圆为 ,依题意,若切线与椭圆相交,则圆应含在椭圆内 r1若直线 PQ 斜率存在,设 PQ: kx m , P x 1, y 1 ,Q x 2,y 2Q PQ 与圆相切 dO m k 21 2k 2OP OQ uuur uuur OP OQ 即 x 1x 2 y 1y 2 0联立方程: y kx m 22x 2 4 y 24 1 4k 2 x 28kmx4m240x 1 x 28km 4k 2 1, x 1x 2 4m 2 4 4k 2 1y 1y 2kx 1 m kx 2 mk 2x 1x 2 km x 1 x 2 x 1x 2 y 1 y 2k 21 x 1x 2km x 1x 2 m 2225m 4k 44k 21若PQ:x 25,则 P 2 5,2 5,Q 2 5,2 55 5 5 5 5uuur uuur 2OP OQ 0 PQ: x 5符合题意52若PQ : x5 ,同理可得也符合条件5综上所述,圆的方程为: 2 24 x 2 y 2 5例 3:22已知椭圆 x2 y2 a 2b2 1 a b 0 经过点 0,,离心率为 1,左,右焦点分别为2F1c,0 和 F 2 c,0(1)求椭圆 C 的方程2)设椭圆 C 与x 轴负半轴交点为 A ,过点 M 4,0 作斜率为 k k 0 的直线 l ,交椭圆C 于B,D 两点( B 在 M,D 之间),N 为 BD 中点,并设直线 ON 的斜率为 k 1 ① 证明: k k 1 为定值② 是否存在实数 k ,使得 F 1N AD ?如果存在,求直线 l 的方程;如果不存在,请说明 理由c1解:(1)依题意可知: e可得: a:b: c 2: 3:1a24m244k 2 1k21km8km 2 2m 4k 21225m 2 4k 2 4 0 对任意的 将m 2 r 2 k 2 1 代入可得: 225r 2 4 k 2 1 0存在符合条件的圆,其方程为: 当 PQ 斜率不存在时,可m,k 均成立5r 2 k 2 1 4 k 2 1 0 24 r5 22xyPQ 为x25 5x 2椭圆方程为:2x 4c 22 y3c21,代入 0, 3 可得: c 122椭圆方程x y14 32)① 证明: 设B x 1,y 1,D x 2,y 2 ,线段 BD 的中点 N x 0, y 0 设直线 l 的方程为:k yx 4 ,联立方程:y 3x 2 4 y 212化为:3 4k2232k 2x 64k 212 00解得: k 2 x 1 x2 32k 232k3,x 1x 2 4k264k 24k 2123 x0 x 1 x 2 216k 2 4k 23 y 0 x 012k 4k 23k1 y0 x0 4k k 1k ② 假设存在实数 k ,使得 F 1 N yx12k 3 4k 2 16k 2 3 4k 2 y2k x 2 44kAD , kF 1Nk AD 14k4k2x2F 1N 4k1 4k 2k x2 x2即 4k 2 x 2 22 16k 2 4k 2 1 x28k2x22 2 8k 2因为 D 在椭圆上,所以 x 2 2,2 ,矛盾所以不存在符合条件的直线22例 4 :设 F 为椭圆 E : x2 y2 1 a bab的右焦点,点3P 1, 在椭圆 E 上,直线2l 0: 3x 4y 10 0与以原点为圆心,以椭圆 E 的长半轴长为半径的圆相切3x 24y 2 32消去 y 可得:124k 2 3 x 28k 2 12k x 4k 2 12k 3 08k 212k 4 4k 2212k 3 4k 23 144 1k k 244k 3 1 k 2144 1k k 24k 2 31)求椭圆 E 的方程2)过点 F 的直线 l 与椭圆相交于 A,B 两点,过点 P 且平行于 AB 的直线与椭圆交于另l ,使得四边形 PABQ 的对角线互相平分?若存在,求出 l 的方程; 若不存在,说明理由 解:(1)Q l 0 与圆相切2x椭圆方程为:4联立直线 l 与椭圆方程:同理:联立直线 PQ 与椭圆方程:点 Q ,问是否存在直线 d O l102 r 53将 P 1, 代入椭圆方程2x 22 yb 21 可得: b 32)由椭圆方程可得:1,0设直线 l : y k x 1,则 PQ:yy3x 2x14y 2消去 y 可得: 4k 2 3 12x 2 8k 2x 4k 2 12 0AB8k 24 4k 23 4k 2122 144k 21441 k2x 1 x 2k 24k 2 13212 k 2 1 4k 2 3PQ因为四边形 PABQ 的对角线互相平分 3解得: k4若存在,求出 的值;若不存在,请说明理由 解:( 1)设 P x, y ,F 1 c,0 ,F 2 c,0uuuuuu PF 1c x, y,PF 2c x, yuuu uuur 222cPF 1 2PF 2 x 2y2 2b 2由 x22y21 可得:2 yb 2 b2x 2代入可得:ab 2a 2uuur uuur 2 2PF 1 PF 2 x 2 y 22 c b 2 2 2 1 2 x b c 2c 2 2 22 x b ca auuur uuur 2Q x a, aPF 1 PF 2 b 2maxc 2b 2 3c 2c 2 a 2 c 2 3c 2222c a 224c a四边形 PABQ 为平行四边形AB PQ12 k 24k 2 311k 2144 1k k 24k 2存在直线 l : 3x 4y0时, 四边形 PABQ 的对角线互相平分2 x例 5:椭圆 C :2 a 22 yb 2ab 0 的左右焦点分别为 F 1, F 2 ,右顶点为 A , P 为椭圆 C 1uuur uuur 上任意一点,且 PF 1 PF 2 的最大值的取值范围是c 2 ,3c 2,其中 c a 2 b 21)求椭圆C 1的离心率 e 的取值范围2)设双曲线 C 2 以椭圆 C 1 的焦点为顶点,顶点为焦点, B 是双曲线 C 2 在第一象限上任意一点,当 e 取得最小值时, 试问是否存在常数0 ,使得 BAF 1 BF 1A 恒成立?2) 当e12时,可得: a 2c, b3c2x双曲线方程为 2c 22y21, A 2c,0 , F 1 c,0 ,设 3c2 B x 0,y 0 , x 00, y 0 0当 AB x 轴时, x0 2c, y 0 3ctanBF 1A 33c c 1 BF 1A因为BAF 1所以 BAF 1 2 BF 1A考虑 tan tan2 2, 面证明 BAF 1 BF 1A 2tan1 tan 2由双曲线方程 2 x 2c 2y3c 2 2对任意 yx 0 2cBF 1A BF 1A1,可得:B 点均使得BAF 1BF 1 A 成立,tanBF 1AkBF 1yx 0 cyx 0 c2 y 0 x 0 c2 y 02 x 0 c 2 y 02 x 03c 2 tan2 BF 1 A 2 y 0 x 0 c 2 x 0 BAF 1 BF 1A 结论得证 2时, BAF 1 例 6:如图, 2椭圆 E: x 2 a 2 yx 0 c3x 023c2x2 y2cx 04c22 x 0 c 2c x 0c 2c x 0 2cBF 1A 恒成立 2b y 2 1 a b 0 圆相交于 A,B 两点,当直线 l 平行于 x 轴时,1)求椭圆 E 的方程xtan BAF 1的离心率是 2,过点 P 0,12的动直线 l 与椭直线 l 被椭圆 E 截得的线段长为 2 22)在平面直角坐标系 xOy 中,是否存在与点 P 不同的定点 Q ,使得对于任意直线 l ,Q Q B A P P B A恒成立?若存在,求出点 Q 的坐标;若不存在,请说明理由22椭圆方程为 2xb 2 b y2 1由直线 l 被椭圆 E 截得的线段长为 2 2 及椭圆的对称性可得: 点 2,1 在椭圆上22xy椭圆方程为42Q 在 AB 的中垂线上,即 Q 位于 y 轴上,设 Q 0,y 0当l 与x 轴垂直时,则 A 0, 2 ,B 0, 2A x 1,y 1 ,B x 2, y 2解:(1) e c 2a2a:b:c 2 :1:12b 2 b2 1 b 2a 2 42)当 l 与 x 轴平行时,由对称性可得: PA PBQA QBP PA B 1即 QA QBPA 2 1, PB 21QAy 02, QB y 0 2QA PA QBPBQ P,Q 不重合Q 0,2面判断 Q 0,2 若直线22 1可解得y 02 2 1y 0y 0 2能否对任意直线均成立 l 的 斜 率 存 在 , 设 l : y kxy 0 1 或 y 0 21,第九章圆锥曲线中的存在性问题解析几何1 2m2 2 00 成立直径的圆经过椭圆 C 的右焦点 F (1)求椭圆 C 的方程(2)动直线 l 与椭圆 C 有且只有一个公共点,问:在 x 轴上是否存在两个定点,它们到直 线 l 的距离之积等于 1?若存在,求出这两个定点的坐标;如果不存在,请说明理由联立方程可得: x 2 2y 24 y kx 1221 2k2 x 2 4kx 2 0QAQBPA可想到角平分线公式,即只需证明QP 平分 BQA只需证明 k QAk QBk QAk QB 0A x 1, y 1 ,B x 2, y 2k QAy 1 x 1y 2 2x 2k QA k QBy 1 2x 1y 2 2x 2x 2 y 1 2 x 1y 2 2 x 2y 1 x 1 y 2 2 x 1 x 2x 1x 2x 1x 2因为 A x 1, y 1 ,B x 2, y 2 在直线kx 1 上,y 1y 2kx1 1代入①可得:kx 2 1 k QA1 2 x 1x 22kx 1x 2 x 1 x 2联立方程可得:x 22y 2 kx 1x 1 x 2k QA4k1 2k2k 22 1 2k 22 1 2k 22 , x 1x 2x 1x 2x 1x 2221 2k2 x 222 1 2k 24k 1 2k 2 0 4kx 20k QAQP 平分 BQA由角平分线公式可得:QAQBP P B A2 x例 7 :椭圆 C :2 a b y2 1 a b 0 的上顶点为 A ,4bP , 是 C 上的一点,以 AP 为33第九章圆锥曲线中的存在性问题解析几何解:由椭圆可知:A 0,b , F c,0uuur uuur uuurQ FA uuur c,b ,FP43bc,3FA FP 04b2024b2c c c c3333Q AP 为直径的圆经过F FA FP代入椭圆方程可得:在椭圆上,316 1b2b2b2 4c32cb232a bcx椭圆方程为22)假设存在x 轴上两定点M1 1,0 , M 22 ,0 ,设直线l: y kx md M1 , d M 212 k2k21所以依题意:d M 1 l 2m k21 2 km 1 k211①因为直线l 与椭圆相切,联立方程:y kx m 2 y x2 k2x y2m22k221 x 4kmx 2m220由直线l 与椭圆相切可知 24km 24 2k 22化简可得:m22k 21,代入①可得:k 1 2 km 1 2k 212k21 1km 1 2 2k2第九章圆锥曲线中的存在性问题解析几何1 2m2 2 0k1 2 1km120 ,依题意可得:无论 k,m 为何值,等式均成立1 2 1 1 2 01 21 112所以存在两定点:M11,0,M 2 1,0例 8:已知椭圆 C 1 :x 24y2 1的左右焦点分别为 F 1, F 2 ,点 P 是C 1上任意一点, O 是坐uuur uuur uuur标原点, OQ PF 1 PF 2 ,设点 Q 的轨迹为 C 21)求点 Q 的轨迹 C 2 的方程uuur uuuur uuuur uuur2)若点T 满足:OT MN 2OM ON ,其中 M , N 是C 2上的点,且直线 OM,ON 的1斜率之积等于 ,是否存在两定点,4标;若不存在,请说明理由y 21uuur uuuu uuuur uuur Q OT MN 2OM ONx,yx1x 2,y 1 y 2 2 x 1, y 1x 2,y 2x 2x 2x1y2y 2 y1设点 T x, y , 2) M x 1, y 1 , Nx 2, y 2使得 TA TB 为定值?若存在, 求出定点 A,B 的坐1)设点 Q 的坐标为x, y , 点 P 的坐标为 x 0, y 0 , 则x 02 4 y 02 1由椭圆方程可得: F 123,0 ,F 2 23,0uuur Q OQ uuu rPF uuu r PFuuur 且 PF 1 x 0,uuur y 0 ,PF 2 32 x 0, y 02x 0 , 2y 02 x 0 2y 0x 0y 0x2 代入到y222x 02 4 y 02 1可得:c 1010y 2 1设直线 OM , ON 的斜率分别为 k OM ,k ON , 由已知可得: k OM kONy 2 y 1x2 x1x 1x 2 4y 1 y 2 考虑 x 2 4 y 22x 2 x 1 2 242y 2y12 x 14y 122 x 24y 224x 1x 2 16y 1 y 2Q M ,N 是 C 2上的点 2x1 2x 2 4y 124y 22x 2 4 y 24 4 4 20 x 2即T 的轨迹方程为 20 1, 由定义可知, T 到椭圆 x 220 1焦点的距离和为定值 A,B 为椭圆的焦点 15,0 , B 15,0 所以存在定点 A, B 2 x 例 9 :椭圆 E : 2 a 22yb 2 b 0 的焦点到直线 x 3y 10 0 的距离为 10,离心率为 5 2 5,抛物线 G : y 522 px p 0 的焦点与椭圆 E 的焦点重合, 斜率为 k 的直线 l 过 G 的 焦点与 E 交于 A,B ,与 G 交于 C,D 1)求椭圆 E 及抛物线 G 的方程 2)是否存在常数 ,使得1 ABCD为常数?若存在,求出 的值;若不存在,请说明理由 解:( 1)设 E, G 的公共焦点为 F c,0dFc225b2 a 2c2 12E:x 25a3y 28x2)设直线 l : y k x 2 , A x 1,y 1 ,B x 2,y 2 ,C x 3, y 3 ,D x 4,y 4与椭圆联立方程: y k x 222x25 y2 55k 2 1 x 2 20k 2x 20k 25 020k 2x 1 x 22, x 1x 21 5k20k 251 5k 2AB 1 k 2x 12x24x1x21 5k 2直线与抛物线联立方程: kx 8x 2 2 2 k 2x24k 228 x 4k 2 0x 3 x 4 4k 28 k 2Q CD 是焦点弦 CDx3x 4 48 k 2 1k 21 AB 5k 2CD 2 5 k 2 1 k 2 8 k 2 1 4 20k 28 5 k 2120 5 k 2 8 5 k 2 1若 A 1B为常数,则 20 CD54 16 5 5例 10 :如图, 在平面直角坐标系 xOy 中,2 x 椭圆 C : 2 a b 21a的离心率为直线 l 与 x 轴交于点 E ,与椭圆 C 交于 A,B 两点,当直线 右焦点时,弦AB 的长为 2 63 1)求椭圆 C 的方程 2)是否存在点 E ,使得 12 EA 2 1 EB2请求出点 E 的坐标,并求出该定值; 若不存在, 请说明理 l 垂直于 x 轴且点 E 为椭圆 C的为定值?若存在, 解:( 1)依题意可得:c6 ea:b:c 3 :1: 21 EA23y 2当l与x轴垂直且E为右焦点时,AB 为通径AB2b 2 2 6a3a 6,b 222x2y21622)思路:本题若直接用用字母表示A, E, B坐标并表示EA ,EB ,则所求式子较为复杂,不易于计算定值与E 的坐标。
