常微分方程作业欧拉法与改进欧拉法
微分方程的数值解法

微分方程的数值解法微分方程是自然科学和现代技术领域中一种最基本的数学描述工具,它可以描述物理世界中的各种现象。
微分方程的解析解往往很难求出,因此数值解法成为解决微分方程问题的主要手段之一。
本文将介绍几种常见的微分方程的数值解法。
一、欧拉法欧拉法是微分方程初值问题的最简单的数值方法之一,它是由欧拉提出的。
考虑一阶常微分方程:$y'=f(t,y),y(t_0)=y_0$其中,$f(t,y)$表示$y$对$t$的导数,则$y(t_{i+1})=y(t_i)+hf(t_i,y_i)$其中,$h$为步长,$t_i=t_0+ih$,$y_i$是$y(t_i)$的近似值。
欧拉法的精度较低,误差随着步长的增加而增大,因此不适用于求解精度要求较高的问题。
二、改进欧拉法改进欧拉法又称为Heun方法,它是由Heun提出的。
改进欧拉法是在欧拉法的基础上进行的改进,它在每个步长内提高求解精度。
改进欧拉法的步骤如下:1. 根据当前$t_i$和$y_i$估算$y_{i+1}$:$y^*=y_i+hf(t_i,y_i),t^*=t_i+h$2. 利用$y^*$和$t^*$估算$f(t^*,y^*)$:$f^*=f(t^*,y^*)$3. 利用$y_i$、$f(t_i,y_i)$和$f^*$估算$y_{i+1}$:$y_{i+1}=y_i+\frac{h}{2}(f(t_i,y_i)+f^*)$改进欧拉法具有比欧拉法更高的精度,但是相较于其他更高精度的数值方法,它的精度仍然较低。
三、龙格-库塔法龙格-库塔法是一种广泛使用的高精度数值方法,它不仅能够求解一阶和二阶常微分方程,还能够求解高阶常微分方程和偏微分方程。
其中,经典的四阶龙格-库塔法是最常用的数值方法之一。
四阶龙格-库塔法的步骤如下:1. 根据当前$t_i$和$y_i$估算$k_1$:$k_1=f(t_i,y_i)$2. 根据$k_1$和$y_i$估算$k_2$:$k_2=f(t_i+\frac{h}{2},y_i+\frac{h}{2}k_1)$3. 根据$k_2$和$y_i$估算$k_3$:$k_3=f(t_i+\frac{h}{2},y_i+\frac{h}{2}k_2)$4. 根据$k_3$和$y_i$估算$k_4$:$k_4=f(t_i+h,y_i+hk_3)$5. 根据$k_1$、$k_2$、$k_3$和$k_4$计算$y_{i+1}$:$y_{i+1}=y_i+\frac{h}{6}(k_1+2k_2+2k_3+k_4)$龙格-库塔法的精度较高,在求解一些对精度要求较高的问题时,龙格-库塔法是一个比较好的选择。
分别利用欧拉法和改进欧拉法求解微分方程组的数值解

分别利用欧拉法和改进欧拉法求解微分方程组的数值解欧拉法(Euler’s Method)和改进欧拉法(Improved Euler’s Method),是求解常微分方程数值解的两种常用方法。
它们都属于一阶精度的显式迭代算法。
首先,我们来介绍一下欧拉法。
欧拉法是一种简单的数值求解算法,它基于微分方程的定义,将微分方程转化为差分方程。
考虑一个一阶常微分方程 dy/dx = f(x, y),并给定初始条件 y(x0)= y0,我们希望求解在给定区间 [x0, xn] 上方程的数值解。
首先,我们将区间 [x0, xn] 平均分成 N 个小区间,每个小区间的长度为 h = (xn - x0) / N。
然后,我们可以使用以下的欧拉迭代公式计算数值解:y[i+1] = y[i] + h * f(x[i], y[i])其中,x[i] = x0 + i * h,y[i] 是在点 x[i] 处的数值解。
通过不断迭代上述公式,我们可以获得[x0, xn] 上微分方程的数值解。
欧拉法的优点在于简单易懂,计算速度较快。
然而,欧拉法的缺点是精度较低,误差随着步长h 的增大而增大。
为了提高精度,我们可以使用改进欧拉法。
改进欧拉法,也称为龙格–库塔算法(Runge-Kutta Method)或四阶龙格–库塔方法,是一种基于欧拉法的改进算法。
改进欧拉法使用了更多的近似取值,以减小误差。
与欧拉法类似,我们将区间 [x0, xn] 平均分成 N 个小区间,每个小区间的长度为 h = (xn - x0) / N。
然后,我们可以使用以下的公式计算数值解:k1 = h * f(x[i], y[i])k2 = h * f(x[i] + h/2, y[i] + k1/2)y[i+1] = y[i] + k2其中,k1 和 k2 是计算过程中的辅助变量。
通过不断迭代上述公式,我们可以获得 [x0, xn] 上微分方程的数值解。
改进欧拉法相对于欧拉法而言,计算精度更高。
第8章 常微分方程数值解法 本章主要内容: 1.欧拉法、改进欧拉法 2

第8章 常微分方程数值解法本章主要内容:1.欧拉法、改进欧拉法. 2.龙格-库塔法。
3.单步法的收敛性与稳定性。
重点、难点一、微分方程的数值解法在工程技术或自然科学中,我们会遇到的许多微分方程的问题,而我们只能对其中具有较简单形式的微分方程才能够求出它们的精确解。
对于大量的微分方程问题我们需要考虑求它们的满足一定精度要求的近似解的方法,称为微分方程的数值解法。
本章我们主要讨论常微分方程初值问题⎪⎩⎪⎨⎧==00)(),(yx y y x f dx dy的数值解法。
数值解法的基本思想是:在常微分方程初值问题解的存在区间[a,b]内,取n+1个节点a=x 0<x 1<…<x N =b (其中差h n = x n –x n-1称为步长,一般取h 为常数,即等步长),在这些节点上把常微分方程的初值问题离散化为差分方程的相应问题,再求出这些点的上的差分方程值作为相应的微分方程的近似值(满足精度要求)。
二、欧拉法与改进欧拉法欧拉法与改进欧拉法是用数值积分方法对微分方程进行离散化的一种方法。
将常微分方程),(y x f y ='变为()*+=⎰++11))(,()()(n xn x n n dtt y t f x y x y1.欧拉法(欧拉折线法)欧拉法是求解常微分方程初值问题的一种最简单的数值解法。
欧拉法的基本思想:用左矩阵公式计算(*)式右端积分,则得欧拉法的计算公式为:Nab h N n y x hf y y n n n n -=-=+=+)1,...,1,0(),(1 欧拉法局部截断误差11121)(2++++≤≤''=n n n n n x x y h R ξξ或简记为O (h 2)。
我们在计算时应注意欧拉法是一阶方法,计算误差较大。
欧拉法的几何意义:过点A 0(x 0,y 0),A 1(x 1,y 1),…,A n (x n ,y n ),斜率分别为f (x 0,y 0),f (x 1,y 1),…,f (x n ,y n )所连接的一条折线,所以欧拉法亦称为欧拉折线法。
求常微分方程的数值解

求常微分方程的数值解一、背景介绍常微分方程(Ordinary Differential Equation,ODE)是描述自然界中变化的数学模型。
常微分方程的解析解往往难以求得,因此需要寻找数值解来近似地描述其行为。
求解常微分方程的数值方法主要有欧拉法、改进欧拉法、龙格-库塔法等。
二、数值方法1. 欧拉法欧拉法是最简单的求解常微分方程的数值方法之一。
它基于导数的定义,将微分方程转化为差分方程,通过迭代计算得到近似解。
欧拉法的公式如下:$$y_{n+1}=y_n+f(t_n,y_n)\Delta t$$其中,$y_n$表示第$n$个时间步长处的函数值,$f(t_n,y_n)$表示在$(t_n,y_n)$处的导数,$\Delta t$表示时间步长。
欧拉法具有易于实现和理解的优点,但精度较低。
2. 改进欧拉法(Heun方法)改进欧拉法又称Heun方法或两步龙格-库塔方法,是对欧拉法进行了精度上提升后得到的一种方法。
它利用两个斜率来近似函数值,并通过加权平均来计算下一个时间步长处的函数值。
改进欧拉法的公式如下:$$k_1=f(t_n,y_n)$$$$k_2=f(t_n+\Delta t,y_n+k_1\Delta t)$$$$y_{n+1}=y_n+\frac{1}{2}(k_1+k_2)\Delta t$$改进欧拉法比欧拉法精度更高,但计算量也更大。
3. 龙格-库塔法(RK4方法)龙格-库塔法是求解常微分方程中最常用的数值方法之一。
它通过计算多个斜率来近似函数值,并通过加权平均来计算下一个时间步长处的函数值。
RK4方法是龙格-库塔法中最常用的一种方法,其公式如下:$$k_1=f(t_n,y_n)$$$$k_2=f(t_n+\frac{\Delta t}{2},y_n+\frac{k_1\Delta t}{2})$$ $$k_3=f(t_n+\frac{\Delta t}{2},y_n+\frac{k_2\Delta t}{2})$$ $$k_4=f(t_n+\Delta t,y_n+k_3\Delta t)$$$$y_{n+1}=y_n+\frac{1}{6}(k_1+2k_2+2k_3+k_4)\Delta t$$三、数值求解步骤对于给定的常微分方程,可以通过以下步骤求解其数值解:1. 确定初值条件:确定$t=0$时刻的函数值$y(0)$。
常微分方程的数值解法(欧拉法、改进欧拉法、泰勒方法和龙格库塔法)
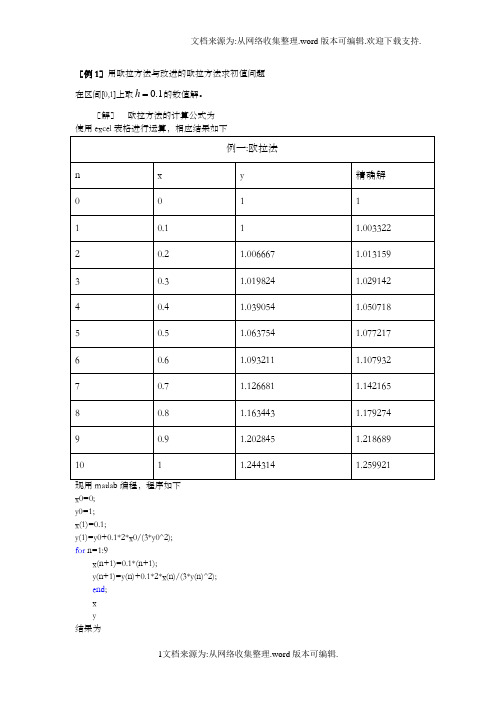
[例1]用欧拉方法与改进的欧拉方法求初值问题h 的数值解。
在区间[0,1]上取0.1[解]欧拉方法的计算公式为x0=0;y0=1;x(1)=0.1;y(1)=y0+0.1*2*x0/(3*y0^2);for n=1:9x(n+1)=0.1*(n+1);y(n+1)=y(n)+0.1*2*x(n)/(3*y(n)^2);end;xy结果为x =Columns 1 through 80.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000 0.8000 Columns 9 through 100.9000 1.0000y =Columns 1 through 81.0000 1.0067 1.0198 1.0391 1.0638 1.0932 1.1267 1.1634 Columns 9 through 101.2028 1.2443改进的欧拉方法其计算公式为本题的精确解为()y x=x0=0;y0=1;ya(1)=y0+0.1*2*x0/(3*y0^2);y(1)=y0+0.05*(2*x0/(3*y0^2)+2*x0/(3*ya^2));for n=1:9x(n+1)=0.1*(n+1);ya(n+1)=ya(n)+0.1*2*x(n)/(3*ya(n)^2);y(n+1)=y(n)+0.05*(2*x(n)/(3*y(n)^2)+2*x(n+1)/(3*ya(n+1)^2));end;xy结果为x =Columns 1 through 80.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000 0.8000 Columns 9 through 100.9000 1.0000y =Columns 1 through 81.0000 1.0099 1.0261 1.0479 1.0748 1.1059 1.1407 1.1783 Columns 9 through 101.2183 1.2600[例2]用泰勒方法解x=0.1, 0.2, …, 1.0处的数值解,并与精确解进行比较。
Euler法与修正的Euler法局部截断误差Range-Kutta公式

Comparison with exact results
Temperature, θ(K)
1500
1000
500
0 0
-500
-1000
-1500
Exact solution
h=120 h=240
100
200
300
400
500
Tim e, t (sec)
h=480
Figure 4. Comparison of Euler’s method with exact solution for different step sizes 5
考虑形如
k
ynk ynk 1 h i fni i0
的 k步法,称为阿当姆斯(Adams)方法. k为显0式方法, 为隐k 式0方法,通常称为阿
当姆斯显式与隐式公式,也称Adams-Bashforth公式与Adam -Monlton公式.
22
阿当姆斯显式公式
kp
公式
c p1
1 1 yn1 yn h fn
y( xn ) f ( xn , yn )
y( xn )
d dx
f
( xn ,
yn )
0.5h[f(xn,yn)+f(xn+1, yn+hf(xn, yn))]
=hy’(xn)+0.5h2y”(xn)+0.5h2y'(xn) [fy’]n+
O局 故(h部修y3n)截正+1断 的= 误Eyun差l+er:h法yy(’具xddyn(x有y+(x1x)20n–))阶+fy精0n(+.xy15度0,=hy。2y)y(,”xxn)(–xnxy)n0+=OO((hh33))
向前欧拉法,向后欧拉法与改进欧拉法求解微分方程

向前欧拉法,向后欧拉法与改进欧拉法求解微分方程
向前欧拉法、向后欧拉法和改进欧拉法是求解微分方程的常用数值方法。
这些方法都是基于欧拉公式,即将微分方程中的导数用差分代替,从而将微分方程转化为差分方程,进而用数值方法求解。
向前欧拉法是一种简单的数值方法,它利用当前时刻的导数来估计下一时刻的解。
具体来说,假设微分方程为dy/dt=f(y,t),则向前欧拉法的迭代公式为:y_n+1=y_n+hf(y_n,t_n),其中h为时间步长。
这个公式可以看作是在当前时刻上做一个切线,然后用这个切线的斜率来估计下一时刻的解。
向后欧拉法是一种更加精确的数值方法,它利用下一时刻的导数来估计当前时刻的解。
具体来说,向后欧拉法的迭代公式为:
y_n+1=y_n+hf(y_n+1,t_n+1),其中h为时间步长。
这个公式可以看作是在下一时刻上做一个切线,然后用这个切线的斜率来估计当前时刻的解。
由于向后欧拉法需要解一个非线性方程,因此比向前欧拉法更加复杂。
改进欧拉法是向前欧拉法和向后欧拉法的结合,它利用当前时刻和下一时刻的导数来估计当前时刻的解。
具体来说,改进欧拉法的迭代公式为:y_n+1=y_n+(h/2)(f(y_n,t_n)+f(y_n+1,t_n+1)),其中h 为时间步长。
这个公式可以看作是在当前时刻和下一时刻上各做一个切线,然后将这两个切线的斜率取平均值来估计当前时刻的解。
改进欧拉法相对于向前欧拉法和向后欧拉法更加精确。
总的来说,向前欧拉法、向后欧拉法和改进欧拉法都是求解微分
方程的有力工具,使用时需要根据具体问题选择合适的方法。
常微分方程的数值求解

常微分方程的数值求解在数学中,常微分方程是一类重要的数学模型,通常用来描述物理、化学、生物等自然现象中的变化规律。
对于一些复杂的微分方程,无法通过解析方法进行求解,这时候就需要借助数值方法来近似求解。
本文将介绍常微分方程的数值求解方法及其应用。
一、数值求解方法常微分方程的数值求解方法主要包括欧拉法、改进的欧拉法、龙格-库塔法等。
欧拉法是最简单也是最常用的数值求解方法,其基本思想是根据微分方程的导数近似求解下一个时间步上的解,并通过逐步迭代来得到整个解的数值近似。
改进的欧拉法在欧拉法的基础上做出了一定的修正,提高了数值求解的精度。
而龙格-库塔法则是一种更加精确的数值求解方法,通过考虑多个点的斜率来进行求解,从而减小误差。
二、应用领域常微分方程的数值求解方法在科学研究和工程实践中有着广泛的应用。
在物理学中,通过数值求解微分方程可以模拟天体运动、粒子运动等现象;在生物学领域,可以模拟生物种群的增长和变化规律;在工程领域,可以通过数值求解微分方程来设计控制系统、优化结构等。
三、实例分析以一个简单的一阶常微分方程为例:dy/dx = -y,初始条件为y(0) = 1。
我们可以用欧拉法来进行数值求解。
将时间间隔取为0.1,通过迭代计算可以得到y(1)的近似值为0.367。
而利用改进的欧拉法或者龙格-库塔法可以得到更加精确的数值近似。
这个例子展示了数值方法在解决微分方程问题上的有效性。
四、总结常微分方程是求解自然界中变化规律的重要数学工具,而数值方法则是解决一些难以解析求解的微分方程的有效途径。
通过本文的介绍,读者可以了解常微分方程的数值求解方法及其应用,希望可以对相关领域的研究和实践有所帮助。
至此,关于常微分方程的数值求解的文章正文部分结束。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y(i+1)=y(i)+1/2*h*(fun(t(i),y(i))+ fun(t(i+1),y1(i+1)))
end
plot(t,y,'*r')
function y=fun(t,y);
y=y+1;
调用:Euler(0,3,[0,2],
得到解析解:hold on;
y=dsolve('Dy=y+1','(y(0)=3)','t');
t=t0;
x(1)=int(1);
y(1)=int(2);
for i=1:n
x1(i+1)=x(i)+h*xfun(t(i),x(i),y(i));
y1(i+1)=y(i)+h*yfun(t(i),x(i),y(i));
t(i+1)=t(i)+h;
x(i+1)=x(i)+1/2*h*(xfun(t(i),x(i),y(i))+xfun(t(i+1),x1(i+1),y1(i+1)));
y(i+1)=y(i)+1/2*h*(yfun(t(i),x(i),y(i))+yfun(t(i+1),x1(i+1),y1(i+1)));
end
plot(t,x,'o-r')
hold on
plot(t,y,'*-g&#
function x=xfun(t,x,y);
x=y+y^2;
ezplot(y,[0,2])
图像:
代码:
function Euler1(t0,y0,inv,h)
n=round(inv(2)-inv(1))/h;
t(1)=t0;
y(1)=y0;
for i=1:n
y1(i+1)=y(i)+h*fun(t(i),y(i));
t(i+1)=t(i)+h;
y(i+1)=y(i)+1/2*h*(fun(t(i),y(i))+ fun(t(i+1),y1(i+1)))
hold on
plot(t,y,'*-g')
hold on
plot(x,y)
function x=xfun(t,x,y);
x=y;
function y=yfun(t,x,y);
y=-2*x-3*y;
调用函数:Euler4(0,[1,1],5,
图像:
(2)代码:function Euler5(t0,int,n,h)
end
plot(t,y,'*r')
function y=fun(t,y);
y=y^2-4*t;
调用:
Euler1(0,,[0,2],
图像:
代码:
function Euler2(t0,y0,inv,h)
n=round(inv(2)-inv(1))/h;
t(1)=t0;
y(1)=y0;
for i=1:n
y1(i+1)=y(i)+h*fun(t(i),y(i));
t(i+1)=t(i)+h;
y(i+1)=y(i)+1/2*h*(fun(t(i),y(i))+ fun(t(i+1),y1(i+1)))
end
plot(t,y,'*r')
function y=fun(t,y);
y=(3-y)*(y+1);
function y=yfun(t,x,y);
y=-x+*y-x*y+*y^2;
调用函数:Euler5(0,[1,1],5,
图像:
调用:
Euler2(0,4,[0,5],1)
得到解析解:
hold on;
y=dsolve('Dy=(3-y)*(y+1)','y(0)=4','t');
ezplot(y)
图像:
代码:
function Euler2(t0,y0,inv,h)
n=round(inv(2)-inv(1))/h;
t(1)=t0;
(1)代码:
function Euler4(t0,int,n,h)
t=t0;
x(1)=int(1);
y(1)=int(2);
for i=1:n
x1(i+1)=x(i)+h*xfun(t(i),x(i),y(i));
y1(i+1)=y(i)+h*yfun(t(i),x(i),y(i));
t(i+1)=t(i)+h;
y=(3-y)*(y+1);
调用:
Euler2(0,4,[0,5],
得到解析解:
hold on;
y=dsolve('Dy=(3-y)*(y+1)','y(0)=4','t');
ezplot(y)
图像:
14.考虑满足初始条件(x(0),y(0))=(1,1)的下列方程组:
选定时间步长 t=,n=5.用改进欧拉方法求两个方程组的近似解;
P77 31.利用改进欧拉方法计算下列初值问题,并画出近似解的草图:
代码:
%改进欧拉法
function Euler(t0,y0,inv,h)
n=round(inv(2)-inv(1))/h;
t(1)=t0;
y(1)=y0;
for i=1:n
y1(i+1)=y(i)+h*fun(t(i),y(i));
y(1)=y0;
for i=1:n
y1(i+1)=y(i)+h*fun(t(i),y(i));
t(i+1)=t(i)+h;
y(i+1)=y(i)+1/2*h*(fun(t(i),y(i))+ fun(t(i+1),y1(i+1)))
end
plot(t,y,'*r')
function y=fun(t,y);
x(i+1)=x(i)+1/2*h*(xfun(t(i),x(i),y(i))+xfun(t(i+1),x1(i+1),y1(i+1)));
y(i+1)=y(i)+1/2*h*(yfun(t(i),x(i),y(i))+yfun(t(i+1),x1(i+1),y1(i+1)));
end
plot(t,x,'o-r')
