2019-2020年高考数学小题综合训练3

合集下载

2019年高考数学(理)模拟试题(三)含答案及解析

2019年高考数学(理)模拟试题(三)含答案及解析2019年高考数学（理）模拟试题（三）注意事项：1、本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

答题前，考生务必将自己的姓名、考生号填写在答题卡上。

2、回答第Ⅰ卷时，选出每小题的答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号。

写在试卷上无效。

3、回答第Ⅱ卷时，将答案填写在答题卡上，写在试卷上无效。

4、考试结束，将本试卷和答题卡一并交回。

第Ⅰ卷选择题共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的。

1.已知复数z满足(1-i)z=2+i，则z的共轭复数在复平面内对应的点在（）A。

第一象限B。

第二象限C。

第三象限D。

第四象限2.设集合M={x|x<36}，N={2,4,6,8}，则M∩N=（）A。

{2,4}B。

{2,4,6}C。

{2,6}D。

{2,4,6,8}3.下图中的图案是我国古代建筑中的一种装饰图案，形若铜钱，寓意富贵吉祥．在圆内随机取一点，则该点取自阴影区域内（阴影部分由四条四分之一圆弧围成）的概率是（）A。

1/4B。

1/3C。

1/2D。

2/34.将5个人从左至右排成一行，最左端只能排甲或乙，最右端不能排甲，则不同的排法共有（）A。

42种B。

48种C。

54种D。

60种5.如图所示是一个几何体的三视图，则这个几何体外接球的体积为（）A。

32π/3B。

64π/3C。

32πD。

64π/26.数学家欧拉在1765年提出定理：三角形的外心、重心、垂心依次位于同一直线上，且重心到外心的距离是重心到垂心距离的一半，这条直线被后入称之为三角形的欧拉线．已知△ABC的顶点A(2,0)，B(0,4)，AC=BC，则△ABC的欧拉线方程为（）A。

2x+y-3=0B。

2x-y+3=0C。

x-2y-3=0D。

x-2y+3=07.执行如图所示的程序框图，则输出S的值为（）A。

2019-2020年高考数学二轮复习小题综合限时练三

2n
解析
设圆的半径为 r ，则 P＝n＝
πr 2
，得
π＝
. m
故选
B.
答案 B x2 y2
5. 已知直线 y＝ 3x 与双曲线 C： a2－ b2＝ 1( a＞ 0， b＞0) 有两个不同的交点，则双曲线 C
的离心率的取值范围是 ( )
A.(1 ， 3)
B.(1 ， 2)
C.( 3，＋∞ )
D.(2 ，＋∞）
D.4 3π＋ 8 3
解析由三视图可知该几何体是一个半圆锥和一个三棱锥组合而成的，其体积为：
1 2π＋ 4
4 3π＋ 8 3
V＝ 3Sh＝ 3 ×２ 3＝
3
.
答案 A 1
9. 已知△ ABC的三个内角 A、 B、 C所对的边分别为 a、 b、 c. 若 a＝ 2， cos A＝ 3，则△ ABC
面积的最大值为 ( )
ωｘ( ω＞ 0) 在区间
0， 3
上单调递增，得
3
≤2ω ?
ω≤
. 4
2π
5π
5π π
3
3
3
由f
3 ＞f
6
，得
6
＞
2ω，ω＞
，所以 5
＜ 5
ω
≤. 4
故选
C.
答案 C
8. 一个空间几何体的三视图如图所示，则该几何体的体积为
()
4 3π＋ 8 3
A.
3
4 3π B. 3 ＋ 8 3
83 C.4 3π＋ 3
1
22 343
4 12 12 4
5 48 a 48 5
……
解析数表的规律是每行从第二个数起一个数等于它肩上的两个数的乘积，所以

2019-2020年高考数学试卷题含答案

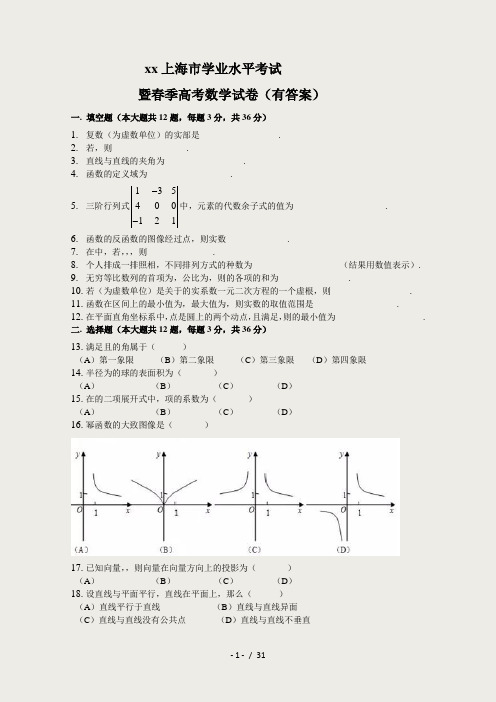
xx 上海市学业水平考试暨春季高考数学试卷（有答案）一. 填空题（本大题共12题，每题3分，共36分）1.复数（为虚数单位）的实部是__________________. 2.若，则_________________. 3.直线与直线的夹角为__________________. 4. 函数的定义域为___________________.5. 三阶行列式135400121--中，元素的代数余子式的值为_____________________. 6. 函数的反函数的图像经过点，则实数______________.7. 在中，若，，，则_______________.8. 个人排成一排照相，不同排列方式的种数为____________________（结果用数值表示）. 9. 无穷等比数列的首项为，公比为，则的各项的和为________________.10. 若（为虚数单位）是关于的实系数一元二次方程的一个虚根，则__________________. 11. 函数在区间上的最小值为，最大值为，则实数的取值范围是___________________. 12. 在平面直角坐标系中，点是圆上的两个动点，且满足，则的最小值为____________________.二. 选择题（本大题共12题，每题3分，共36分）13. 满足且的角属于（）（A ）第一象限（B ）第二象限（C ）第三象限（D ）第四象限 14. 半径为的球的表面积为（）（A ）（B ）（C ）（D ）15. 在的二项展开式中，项的系数为（）（A ）（B ）（C ）（D ）16. 幂函数的大致图像是（）17. 已知向量，，则向量在向量方向上的投影为（）（A ）（B ）（C ）（D ）18. 设直线与平面平行，直线在平面上，那么（）（A ）直线平行于直线（B ）直线与直线异面（C ）直线与直线没有公共点（D ）直线与直线不垂直19. 在用数学归纳法证明等式212322n n n ++++=+ 的第步中，假设时原等式成立，那么在时需要证明的等式为（）（A ）2212322(1)22(1)(1)k k k k k k ++++++=+++++ （B ）212322(1)2(1)(1)k k k k ++++++=+++ （C ）221232212(1)22(1)(1)k k k k k k k ++++++++=+++++ （D ）21232212(1)2(1)(1)k k k k k ++++++++=+++20. 关于双曲线与的焦距和渐近线，下列说法正确的是（）（A ）焦距相等，渐近线相同（B ）焦距相等，渐近线不相同（C ）焦距不相等，渐近线相同（D ）焦距不相等，渐近线不相同21. 设函数的定义域为，则“”是“为奇函数”的（）（A ）充分不必要条件（B ）必要不充分条件（C ）充要条件（D ）既不充分也不必要条件22. 下列关于实数的不等式中，不恒成立的是（）（A ）（B ）（C ）（D ）23. 设单位向量与既不平行也不垂直，对非零向量、有结论：○1若，则；○2若，则. 关于以上两个结论，正确的判断是（）（A ）○1成立，○2不成立（B ）○1不成立，○2成立（C ）○1成立，○2成立（D ）○1不成立，○2不成立24. 对于椭圆22(,)22: 1 (,0,)a b x y C a b a b a b+=>≠. 若点满足. 则称该点在椭圆内，在平面直角坐标系中，若点在过点的任意椭圆内或椭圆上，则满足条件的点构成的图形为（）（A ）三角形及其内部（B ）矩形及其内部（C ）圆及其内部（D ）椭圆及其内部三. 解答题（本大题共5题，共8+8+8+12+12=48分）25. （本题满分8分）如图，已知正三棱柱的体积为，底面边长为，求异面直线与所成的角的大小.26.（本题满分8分）已知函数，求的最小正周期及最大值，并指出取得最大值时的值.27.（本题满分8分）如图，汽车前灯反射镜与轴截面的交线是抛物线的一部分，灯口所在的圆面与反射镜的轴垂直，灯泡位于抛物线的焦点处. 已知灯口直径是，灯深，求灯泡与反射镜的顶点的距离.28.（本题满分12分）本题共有2个小题，第1小题满分4分，第2小题满分8分.已知数列是公差为的等差数列.（1）若成等比数列，求的值；（2）设，数列的前项和为. 数列满足，记，求数列的最小项（即对任意成立）.29.（本题满分12分）本题共有2个小题，第1小题满分5分，第2小题满分7分.对于函数，记集合.（1）设，，求；（2）设，，，如果.求实数的取值范围.2019-2020年高考数学试卷题含答案一. 选择题:(9分)1.若函数是偶函数,则的一个值是 ( )(A) (B) (C) (D)2.在复平面上,满足的复数的所对应的轨迹是( )(A) 两个点 (B)一条线段 (C)两条直线 (D) 一个圆3.已知函数的图像是折线,如图,其中(1,2),(2,1),(3,2),(4,1),(5,2)A B C D E ,若直线与的图像恰有四个不同的公共点,则的取值范围是( )(A) (B) (C) (D)二. 填空题:(9分)4.椭圆的长半轴的长为_________________5.已知圆锥的母线长为10,母线与轴的夹角为,则该圆锥的侧面积为__________________6.小明用数列记录某地区xx12月份31天中每天是否下过雨,方法为:当第天下过雨时,记,当第天没下过雨时,记,他用数列记录该地区该月每天气象台预报是否有雨,方法为:当预报第天有雨时,记,当预报第天没有雨时,记记录完毕后,小明计算出112233313125a b a b a b a b ++++=,那么该月气象台预报准确的总天数为______________________三. 解答题:(12分)对于数列与,若对数列的每一项,均有或,则称数列是与的一个“并数列”。

2019-2020年高考数学二轮复习小题综合限时练八(I)

1 D. －∞， 7 ∩[5 ，＋∞）
解析依题意知，直线 (2 ＋λ) x－ (3 ＋ λ) y＋(1 － 2λ) ＝ 0( λ∈R) 可以转化为 2x－3y＋ 1
2x－ 3y＋ 1＝ 0，＋ λ( x－ y－ 2) ＝ 0，联立
x－ y－ 2＝ 0，
x＝ 7，
y－ 5
解得
y＝
∴ 5，
z＝
x－
7，作出二元一次不等式组所表示的平面
区域如图阴影部分所示，点
18 16 B － 5 ，－ 5 ，点 C(6 ， 0) ，点
y－5 D(0 ， 4) ，观察可知 z＝ x－ 7表示阴影区域内的点与 A(7 ， 5) 两
y－ 5
1
y－ 5
y－ y0
1
点连线的斜率，∴
kAD≤ z＝
x－
7≤
k
AC，即
7≤
z＝
解析依题意，该几何体是一个直四棱柱，其中底面是一个上底长为
1、下底长为 2、高
1 为 2 的梯形，侧棱长为 2，因此其表面积等于 2× 2×(1 ＋2) ×2＋ (1 ＋ 2＋ 2＋ 5) ×2＝ 16
＋ 2 5. 故选 C.
答案 C
5. 在 6 道题中有 3 道理综题和 3 道文综题，如果不放回地依次抽取
x－
7≤
5.
∴
z＝
x－
x
的取值范围为
0
7， 5 .
故选 B.
答案 B
Hale Waihona Puke 8. 已知函数 f ( x) ＝ 2ax3＋ 3， g( x) ＝ 3x2＋ 2，若关于 x 的方程 f ( x) ＝ g( x) 有唯一解 x0，且
x0∈(0 ，＋∞ ) ，则实数 a 的取值范围为 (

2019年度-2020年度高考数学小题集训平面向量(含解析)

,.2019-2020年高考数学小题集训——平面向量（一）一、选择题uuur uuur(uuur uuur uuur0, n 0) ，若 m n[1,2] ，则1.已知向量OA(3,1) ， OB1,3) ， OC mOA nOB (muuur| OC | 的取值范围是（）A．[ 5, 25] B ．[5, 210) C ．(5, 10) D ．[ 5,210]r r r r rr r r r a2.已知a，b为平面向量，若a b 与 a 的夹角为， a b 与 b 的夹角为，则 r（）34bA ．3B ．6C ．5D ．6 3433 r r r r rr r3.设a(1,2) ， b(1,1) ， c a kb .若 b c，则实数k的值等于（）A ．5B ．5C ．3D ．3 33224.已知△ABC 中， AB2， AC 4 ，BAC 60ouuur uuur ，P 为线段 AC 上随意一点，则PB PC的范围是（）A ．[1,4]B ．[0,4]C．[－2,4]9D ．[ ,4]45.在实数集R 中，我们定义的大小关系“”为全体实数排了一个“序”，近似的，我们这D r r(x, y), x R, y R 上也能够定义一个称为“序”的关系，记为平面向量会合 a | aur uur ur uur“＞” ．定义以下：对于任意两个向量 a1( x1 , y1) ， a2( x2 , y2 ) ， a1a2当且仅当“ x1x2”或“ x1x2且 y1y2”，按上述定义的关系“ ”，给出以下四个命题：ur uur r ur uur r①若 e1(1,0)， e2(0,1) ，0(0,0) ，则e1e20 ；ur uur uur uur ur uur②若 a1a2， a2a3，则 a1a3；,.ur uur r ur r uur r③若 a1a2，则对于随意的a D ，a1 a a2 a ；r r r ur uur r ur r uur④对于随意的向量 a 0 ，此中 0 (0,0) ，若a1a2，则 a a1 a a2．此中正确的命题的个数为（）A ．4B．3C． 2 D ．16.如图，在OMN 中，A、B 分别是 OM 、ONuuur uuur uuur的中点，若OP xOA yOB （ x ，y R ），且点P落在四边形ABNM内（含界限），则y1的取值范围是（）x y2A．1,2B．1,3C．1,3D．1,2 333444437. 在△ABC中，BAC 60， AB3， ACuuur uuur uuur uuur uuurR ），且2 .若BD2DC ， AE AC AB （uuur uuur的值为（）AD AE4，则A ．3B．4C.5D ．6 111111118.设 P 是△ABC 内随意一点， S△ABC表示△ABC 的面积，λ1＝SPBC，λ2＝SPCA，λ3＝SABC SABCS S PABABC,定义f（）=（1,2,3） ,若 G 是△ABC 的重心，（Q）＝（1，1，1），则（P f236）A ．点 Q 在△GAB 内B．点 Q 在△GBC 内C．点 Q 在△GCA 内D．点 Q 与点 G 重合9.在直角梯形 ABCD中，AB2AD4，同一平面内的两个动点P，M知足,.|CP | 1,PMMA，则| BM |的取值范围为（）A ．[ 10 1,10 1]B ．[10 1 , 101]2 2C. [ 1,3]D ． [21 37 ]2,2ABC uuur uuur uuur uuur uuuruuur2，且 B , 2uuur uuur10. 在△ 中， BC CA CA AB ， BABC 33 ，则 BA BC 的取值范围是（）A ．[－2,1)B ．2,1C ． 2,2D ． 2,23 33r rr r r r11. 已知向量 a 与 b 的夹角为 120 °，a1,0 ， b 2 ，则 2a b （）A ． 3B ．2C ．2 3D ．42 2PA PB12. 在直角三角形 ABC 中,点 D 是斜边 AB 的中点 ,点 P 为线段 CD 的中点 ,A ．2B ．4C ．5D ．102（）PC13. 在平面直角坐标系 xOy 中，已知点 A ，B 分别为 x 轴， y 轴上一点，且 AB 1，若点uuur uuur uuurP 1, 3 ，则 AP BP OP 的取值范围是（）A ．[5,6]B ．[6,7] C.[6,9]D ．[5,7]uuuruuur uuur10 ，则△ABC 是钝角三角形的概率是（14. 已知 k R, AB k,1 , AC2,4 ，若 AB）A ．1B ．1C.2D ．56 3 3 6,.15.生于瑞士的数学巨星欧拉在1765 年发布的《三角形的几何学》一书中有这样一个定理：“三角形的外心、垂心和重心都在同向来线上。

(完整)2019-2020年高考数学小题综合训练3

2019-2020年高考数学小题综合训练 311 .已知 U = {y|y = log 2x , x>1}, P = y y = x ，x >2 ，则?U P 等于( )1 r 1A. 2，+mB. 0, 21 ,C . (0,+s )D . ( — a, 0)U 2，答案 A解析由集合U 中的函数y = log 2x , x>1，解得y>0,所以全集U = (0, + a ),1 1同样 P = 0, 2，得到?U P = ?,+ a .2.“ a>0”是“函数f(x)= x 3 + ax 在区间(0,+a )上是增函数”的( )A .必要不充分条件B .充分不必要条件C .充要条件D .既不充分也不必要条件答案 B解析当a>0时，f ' (x) = 3x 2 + a>0在区间(0, + a )上恒成立，即f(x)在(0,+a )上是增函数，充分性成立；当f(x)在区间(0,+a )上是增函数时，f ' (x)= 3x 2 + a > 0在(0 , + a )上恒成立，即要性不成立，故“a>0 ”是“函数f(x) = x 3 + ax 在区间(0 ,+a )上是增函数”的充分不必要条件.sin x n 0< x < 1, 3 .已知函数f(x)= lOg 2 010x , x>1 , b , c 互不相等，且 f(a)= f(b) = f(c),的取值范围是( ) A . (1,2 010) C . (2,2 011)答案 C则 0<a<b<1<c ,由f(a)= f(b)知，a , b 关于直线x = *对称,所以a + b = 1.解析因为a , b , c 互不相等，不妨设 a<b<c ,a > 0，必右a ,a +b +c B . (1,2 011)D . [2,2 011]4由 0<log 2 oio c<1，知 1<c<2 010 , 所以 2<a + b + c<2 011.4.设S n 是等差数列｛a n ｝的前n 项和，若畫=£则S 等于（）7 35A.3B.~ C . 4 D . 5答案 D 解析在等差数列｛a n ｝中，设首项为a 1,公差为d , 5.如图，在△ ABC 中，AN = TNC , P 是直线BN 上的一点，若 AP = mAB + ZAC ，则实数 m 的 4 5值为（）A 4B 1C . 1D . 4答案 B解析由题意，设BP = nBN ,则 AP = AB + EB P=AB + nBN=A B + n （AN —AB ）T1 T T=AB + n NC — AB 解得a 1 7 a 1+ 4d3，得 E= 73,d S 5= 2， S 3 3 a 1 + a 3 2別一.2 5d--2 3 3=AB + n 1AC — AB 5~» n ~>=(1 — n)AB + 5AC ,-> -> 2 ~又•/ AP = mAB +匸AC ,5解得 n = 2, m =— 1. 6 .在四棱锥 P — ABCD 中，PA 丄底面 ABCD ，底面ABCD 为正方形，PA = AB ，该四棱锥被一平面截去一部分后，剩余部分的三视图如图，则截去部分体积与剩余部分体积的比值为1111 A. B. C. D" 2 34 5答案 B /• m = 1 —n , 2 5.解析根据几何体的三视图，得该几何体是过BD 且平行于PA 的平面截四棱锥 P - ABCD 所得的几何体. 设AB = 1，则截去的部分为三棱锥 E - BCD ，它的体积为1 1 1V 三棱锥 E -BCD =3X 2X 1 x 1X 2= 剩余部分的体积为V 剩余部分=V 四棱锥P - ABCD — V 三棱锥E - BCD所以截去部分的体积与剩余部分的体积比为1 112: 4 =1 : 3.7.秦九韶是我国南宋时期著名的数学家，普州（现四川省安岳县）人，他在所著的《数书九章》中提出的多项式求值的秦九韶算法，至今仍是比较先进的算法•如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例，若输入x 的值为3,每次输入a 的值均为4,输出 s 的值为484，则输入n 的值为（） A . 6 B . 5 C . 4 D . 3答案 C解析模拟程序的运行，可得x = 3, k = 0, s = 0, a = 4, s = 4, k = 1; 不满足条件 k>n , 执行循环体， a = 4, s = 16, k = 2; 不满足条件 k>n, 执行循环体， a = 4, s = 52, k = 3; 不满足条件 k>n, 执行循环体， a = 4, s = 160, k = 4; 不满足条件 k>n, 执行循环体， a = 4, s = 484, k = 5.由题意，此时应该满足条件 k>n ，退出循环，输出s 的值为484,_1 12,=1X 12 x 1 -丄 3 12 1 4.可得5>n》4,所以输入n的值为4.18. (2x+ 1)1 —X 6的展开式中的常数项是()A. —5B. 7C. —11 D . 13答案C1 1111解析•/1—x 6的展开式的通项公式是c k —- k，其中含丄的项是C6 —x S常数项为C6 —-x x x x x1°= 1,故(2x+ 1) 1 —1 6的展开式中的常数项是x2x X C e — 1 1+ 1X 1 = —12+ 1 = —11.x9. 把正方形ABCD沿对角线AC折起，当以A, B, C, D四点为顶点棱锥体积最大时，直线BD和平面ABC所成角的大小为()A. 90 °B. 60 °C. 45 °D. 30 °答案C解析如图，当DO丄平面ABC时，三棱锥 D —ABC的体积最大.•••/ DBO为直线BD和平面ABC所成的角,•/在Rt△ DOB 中，OD = OB,•直线BD和平面ABC所成角的大小为45°10 . 在区间［—1,1］上任取两数s和t，则关于x的方程X2+ 2sx+ t= 0的两根都是正数的概率为（)1 A.2 41 1B* C.41答案B—1 < s< 1, 解由题意可得, 其区域是边长为2的正方形，面积为4,—1 < t< 1,由二次方程x2+ 2sx+ t= 0有两正根，可得4s2—4t> 0,—2s>0,t>0,s2> t,即s<0 , 其区域如图阴影部分所示，t>0,1 1面积 S = ?^i s 2ds = §s 3 -1= 3, 3 1所求概率P =4= ~.P(m , n)在直线y =— x 的左下方，则该椭圆离心率的取值范围为 ( )2 1 2 1A. —, 1B. 2，1C. 0, "2D. 0，2答案 A解析方法一如图所示，右顶点 B(1,0)，上顶点A(0, b),左焦点F( — 1 — b 2,0),线段1 —寸 1 — b2 1 bFB 的垂直平分线为x = 三 •线段AB 的中点坐标为2，2 .=1(0<b<1)的左焦点为 F ，上顶点为 A ,右顶点为 B , 若厶FAB 的外接圆圆心11 •椭圆x 2 +k AB =— b , •••线段AB 的垂直平分线的斜率 k =1, b •线段AB 的垂直平分线方程为 b 1 1^1 — V 1 — b 2 y —b =b x —2，把 x = ' 代入上述方程，可得 y =『—门：—"=n. 2b 由P(m , n)在直线y =— x 的左下方，可得 m + n<0,由P(m , n)在直线y =— x 的左下方，可知 m + n<0 ,—c + a b 2— ac__2+ 2b <0，整理得 1 — c + b — b<°, • b — c + 宁<°,• b — c<0 ,又椭圆的离心率 e =c = c , a• c 2>b 2 ,即 c 2>a 2— c 2,2c 2>a 2,2e 2>1, 由 0<e<1,解得丁<e<1 ,•椭圆离心率的取值范围为 ~2, 1 .1 + z12. 已知正数 x , y , z 满足x 2+ y 2 +m , <0, 化简得b< 1— b 2, 又0<b<1，解得0<b 晋. • e = C = c = 1 — b 2 € -, 1 , a 2 •椭圆离心率的取值范围为亠2, 1 2 方法二设 A(0, b), B(a,O), F( — c,0), 设厶FAB 的外接圆的方程为 x 2 + y 2 + Dx + Ey + F = 0 , 将A , B , F 代入外接圆方程，解得m = —c + a b 2— ac 2bb 2—二 1 — b 2 2bA . 3 C . 4 答案 C解析由题意可得0<z<1,0<1 — z<1 ,••• z(1 — z) < 也三 2 = 1,v 7 2 4' 当且仅当z = 1 — Z ,即z = 2时取等号.又 x 2 + y 2+ z 2= 1, ••• 1 — z 2= x 2 + y 2> 2xy ,1 一 z 2当且仅当x = y 时取等号，• > 1, 2xy.1 + z 1 — z 1 + z 、 1… 卩I ，… 卩 ",2xy 2xy 1 — z当且仅当x = y=¥且z = 1时取等号,4 + 3i = 4+ 3i = 4+ 3i — 2 — i1 + 2i i = — 2+ i = — 2+ i —2 — i•复数z 在复平面内对应的点的坐标为（一1, — 2），在第三象限.x + y + 4>0,14•若直线y = 3x 上存在点（x , y ）满足约束条件 2x — y + 8> 0,贝U 实数 m 的取值范围是 x w m ,B.D . 2( 2+ 1)2xyz1—zz 》41 + z茹的最小值为 4.13. 已知复数z 满足iz =帀，则复数z 在复平面内对应的点在第答案三___________ 象限. 解析 iz = 4+ 3i1 + 2i—5 — 10i 5=—1 — 2i ,答案（—1 ,+^ ）解析由题意作出其平面区域,y = 3x , 由解得 A(— 1,— 3) •故 m>— 1.y =- x — 4, 115.已知△ ABC 的内角 A , B , C 的对边分别为 a , b , c ,若 cos B = 4, b = 4, sin A = 2sin C , 则厶ABC 的面积为 ________ .答案 15解析根据余弦定理的推论1 = a 2+ c 2-424 2ac化简得 2a 2+ 2c 2— 32 = ac.(*)即a = 2c ,代入(*)式得2 (2c)2 + 2c 2 — 32= 2c c,化简得c 2= 4,所以c = 2,又 B € (0, n ,则 sin B = 1 — CO W B U 」5,4cos B = a 2 + c 2- b 22ac ，可得又由正弦定理 a sin A csin C ,可得c = sin A sin C 21’S SBC = ^acsin B= 丁x 4X 2X^= 15, 即厶ABC的面积为.15.2 2I6.已知双曲线拿一器一i(a>0, b>0)上一点C,过双曲线中心的直线交双曲线于A, B两点,2记直线AC,BC的斜率分别为k i ,k2,当蕊+ In|k i |+ In|k2|最小时，双曲线的离心率为答案空解析设A(X i, y i), C(X2, y2),由题意知，点A, B为过原点的直线与双曲线f-b2=1的交点,•••由双曲线的对称性，得A, B关于原点对称,…B(—x i,—y i),• —y2—y i y2+ y i=y?…k i k2—• 2 2，X2—x i x2+ x i x2—x i•••点A, C都在双曲线上,• x! y i= i xi y i= i•-a2—b2= i,a2—b2= i，b2两式相减，可得k i k2 —~2>0,a2 2对于尿+ ln |k i 1+ In |k2|= k；k；+ ln |k i k2|,2设函数y=-+ In x, x>0,x 2 1由y' =—7+1=0得x=2,当x>2 时，y' >0，当0<x<2 时，y' <0,•••当x= 2时，函数y= x+ln x，x>0取得最小值,2 b?•当kik + In(尿2)最小时，k i k2= /= 2,+ ¥=3。

2019-2020年高考数学二轮复习小题综合限时练十一理

2019-2020年高考数学二轮复习小题综合限时练十一理一、选择题(本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.)1.若集合A ＝{x |3＋2x －x 2＞0}，集合B ＝{x |2x＜2}，则A ∩B 等于( ) A.(1，3) B.(－∞，－1) C.(－1，1)D.(－3，1)解析 ∵A ＝(－1，3)，B ＝(－∞，1)，∴A ∩B ＝(－1，1). 答案 C 2.若复数z ＝a ＋3ii＋a 在复平面上对应的点在第二象限，则实数a 可以是( )A.－4B.－3C.1D.2解析若z ＝a ＋3ii＋a ＝(3＋a )－a i 在复平面上对应的点在第二象限，则a ＜－3，选A. 答案 A3.已知sin ⎝ ⎛⎭⎪⎫x －9π14cos π7＋cos ⎝ ⎛⎭⎪⎫x －9π14sin π7＝13，则cos x 等于( )A.13 B.－13C.223D.±223解析 sin ⎝ ⎛⎭⎪⎫x －9π14cos π7＋cos ⎝ ⎛⎭⎪⎫x －9π14sin π7＝sin ⎝ ⎛⎭⎪⎫x －π2＝－cos x ＝13，即cos x ＝－13.答案 B4.我国古代数学著作《九章算术》有如下问题：“今有金箠，长五尺.斩本一尺，重四斤.斩末一尺，重二斤.问次一尺各重几何？”意思是：“现有一根金杖，一头粗，一头细.在粗的一端截下1尺，重4斤；在细的一端截下1尺，重2斤；问依次每一尺各重多少斤？”根据上题的已知条件，若金杖由粗到细是均匀变化的，问中间3尺的重量为( ) A.6斤 B.9斤 C.9.5斤D.12斤解析这是一个等差数列问题，设首项为2，则第5项为4，所以中间3尺的重量为32×(2＋4)＝9斤. 答案 B5.已知双曲线x 2a 2－y 2b2＝1(a ＞0，b ＞0)的右焦点为F ，直线x ＝a 与双曲线的渐近线在第一象限的交点为A ，且直线AF 与双曲线的一条渐近线关于直线y ＝b 对称，则双曲线的离心率为( ) A. 5 B.3 C.2D. 2解析易得点A 坐标为(a ，b )，∵直线AF 与双曲线的一条渐近线关于直线y ＝b 对称，∴直线AF 的斜率为－b a，即ba －c＝－b a ⇒c a＝2.答案 C6.袋子中装有大小相同的6个小球，2红1黑3白.现从中有放回的随机摸球2次，每次摸出1个小球，则2次摸球颜色不同的概率为( ) A.59 B.23 C.1118D.1318解析每次摸到红球、黑球和白球的概率分别为13、16和12，则所求概率为1－⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫132＋⎝ ⎛⎭⎪⎫162＋⎝ ⎛⎭⎪⎫122＝1118. 答案 C7.如图是一个程序框图，若输出i 的值为5，则实数m 的值可以是 ( ) A.3 B.4 C.5D.6解析 S ＝2，i ＝2，2≤2m ；S ＝6，i ＝3，6≤3m ；S ＝13，i ＝4，13≤4m ；S ＝23，i ＝5，23＞5m ，此时程序结束，则134≤m ＜235，故选B. 答案 B8.如图是一个几何体的三视图，在该几何体的各个面中，面积最小的面的面积为( )A.4B.4 2C.4 3D.8解析由三视图可知，该几何体的直观图如图所示，面积最小的面为面VAB ，S △VAB ＝12×2×42＝4 2.答案 B9.将函数f (x )＝sin(2x ＋φ)⎝⎛⎭⎪⎫|φ|＜π2的图象向左平移π6个单位后的图形关于原点对称，则函数f (x )在⎣⎢⎡⎦⎥⎤0，π2上的最小值为( )A.32B.12C.－12D.－32解析 f (x )＝sin(2x ＋φ)的图象向左平移π6个单位得g (x )＝sin ⎝ ⎛⎭⎪⎫2x ＋π3＋φ，它的图象关于原点对称，∴π3＋φ＝k π(k ∈Z )，即φ＝k π－π3，又|φ|＜π2，∴φ＝－π3，∴f (x )＝sin ⎝⎛⎭⎪⎫2x －π3，∵x ∈⎣⎢⎡⎦⎥⎤0，π2，∴2x －π3∈⎣⎢⎡⎦⎥⎤－π3，2π3，∴f (x )在⎣⎢⎡⎦⎥⎤0，π2上的最小值为f (0)＝－32.答案 D10.对定义在[0，1]上，并且同时满足以下两个条件的函数f (x )称为M 函数： (ⅰ)对任意的x ∈[0，1]，恒有f (x )≥0；(ⅱ)当x 1≥0，x 2≥0，x 1＋x 2≤1时，总有f (x 1＋x 2)≥f (x 1)＋f (x 2)成立. 则下列四个函数中不是M 函数的个数是( ) ①f (x )＝x 2，②f (x )＝x 2＋1，③f (x )＝ln(x 2＋1)， ④f (x )＝2x －1 A.1 B.2 C.3D.4解析 (ⅰ)在[0，1]上，四个函数都满足；(ⅱ)x 1≥0，x 2≥0，x 1＋x 2≤1；对于①，f (x 1＋x 2)－[f (x 1)＋f (x 2)]＝(x 1＋x 2)2－(x 21＋x 22)＝2x 1x 2≥0，满足；对于②，f (x 1＋x 2)－[f (x 1)＋f (x 2)]＝[x 1＋x 2)2＋1]－[(x 21＋1)＋(x 22＋1)]＝2x 1x 2－1＜0，不满足；对于③，f (x 1＋x 2)－[f (x 1)＋f (x 2)]＝ln[(x 1＋x 2)2＋1]－[ln(x 21＋1)＋ln(x 22＋1)] ＝ln[(x 1＋x 2)2＋1]－ln[(x 21＋1)(x 22＋1)] ＝ln （x 1＋x 2）2＋1（x 21＋1）（x 22＋1）＝ln x 21＋x 22＋2x 1x 2＋1x 21x 22＋x 21＋x 22＋1，而x 1≥0，x 2≥0，∴1≥x 1＋x 2≥2x 1x 2，∴x 1x 2≤14，∴x 21x 22≤14x 1x 2≤2x 1x 2，∴x 21＋x 22＋2x 1x 2＋1x 21x 22＋x 21＋x 22＋1≥1，∴ln x 21＋x 22＋2x 1x 2＋1x 21x 22＋x 21＋x 22＋1≥0，满足；对于④，f (x 1＋x 2)－[f (x 1)＋f (x 2)]＝(2x 1＋x 2－1)－(2x 1－1＋2x 2－1)＝2x 12x 2－2x 1－2x 2＋1＝(2x 1－1)(2x 2－1)≥0，满足. 答案 A11.双曲线C ：x 2a 2－y 2b2＝1(a ＞0，b ＞0)的一条渐近线与直线x ＋2y ＋1＝0垂直，F 1，F 2为C的焦点，A 为双曲线上一点，若又|F 1A |＝2|F 2A |，则cos∠AF 2F 1＝( ) A.32 B.54C.55D.14解析因为双曲线的一条渐近线与直线x ＋2y ＋1＝0垂直，所以b ＝2a ，又|F 1A |＝2|F 2A |，且|F 1A |－|F 2A |＝2a ，所以|F 2A |＝2a ，|F 1A |＝4a ，而c 2＝5a 2⇒2c ＝25a ，所以cos∠AF 2F 1＝|F 1F 2|2＋|AF 2|2－|AF 1|22|F 1F 2||AF 2|＝20a 2＋4a 2－16a 22×25a ×2a ＝55.答案 C12.若对∀x ，y ∈[0，＋∞)，不等式4ax ≤e x ＋y －2＋ex －y －2＋2恒成立，则实数a 的最大值是( ) A.14 B.1 C.2 D.12解析因为e x ＋y －2＋ex －y －2＋2＝ex －2(e y ＋e －y )＋2≥2(ex －2＋1)，再由2(ex －2＋1)≥4ax ，可有2a ≤1＋ex －2x，令g (x )＝1＋ex －2x，则g ′(x )＝ex －2（x －1）－1x2，可得g ′(2)＝0，且在(2，＋∞)上g ′(x )＞0，在[0，2)上g ′(x )＜0，故g (x )的最小值为g (2)＝1，于是2a ≤1，即a ≤12.答案 D二、填空题(本大题共4个小题，每小题5分，共20分.请把正确的答案填写在答题中的横线上.)13.⎝⎛⎭⎪⎫2x －15x 25的展开式中常数项为________. 解析由通项公式得展开式中的常数项为(2)4C 15⎝ ⎛⎭⎪⎫－15＝－4.答案－414.已知向量e 1，e 2不共线，a ＝2e 1＋m e 2，b ＝n e 1－3e 2，若a ∥b ，则mn ＝________.解析 ∵a ∥b ，∴a ＝λb ，即2e 1＋m e 2＝λ(n e 1－3e 2)⇒⎩⎪⎨⎪⎧λn ＝2，m ＝－3λ，得mn ＝－6. 答案－615.如果实数x ，y 满足条件⎩⎪⎨⎪⎧x ＋y －2≥0，x －1≤0，y －2≤0，则z ＝y x ＋a 的最小值为12，则正数a 的值为________.解析根据约束条件画出可行域，可判断当x ＝1，y ＝1时，z 取最小值为12，即11＋a ＝12⇒a＝1. 答案 116.在数列{a n }中，a 1＝13，1a n ＋1＝3a n （a n ＋3），n ∈N *，且b n ＝13＋a n.记P n ＝b 1·b 2·b 3·…·b n ，S n ＝b 1＋b 2＋…＋b n ，则3n ＋1P n ＋S n ＝________.解析 ∵1a n ＋1＝3a n （a n ＋3），b n ＝13＋a n ，∴b n ＝a n 3a n ＋1，1a n ＋1＝1a n －1a n ＋3＝1a n－b n ，∴P n ＝a 13a 2·a 23a 3·…·a n 3a n ＋1＝13n ＋1·a n ＋1，S n ＝1a 1－1a 2＋1a 2－1a 3＋…＋1a n －1a n ＋1＝3－1a n ＋1，则3n ＋1·P n ＋S n ＝1a n ＋1＋3－1a n ＋1＝3.答案 3。

2019-2020年高考数学大题专题练习——立体几何(三)

2019-2020年高考数学大题专题练习——立体几何（三）53.如图，在四棱锥E ﹣ABCD 中，平面CDE ⊥平面ABCD ，∠DAB =∠ABC =90°，AB =BC =1，AD =ED =3，EC =2．（1）证明：AB ⊥平面BCE ；（2）求直线AE 与平面CDE 所成角的正弦值．54.如图1，2，已知ABCD 是矩形，M ，N 分别为边AD ，BC 的中点，MN 与AC 交于点O ，沿MN 将矩形MNCD 折起，设AB =2，BC =4，二面角B ﹣MN ﹣C 的大小为θ．（1）当θ=90°时，求cos ∠AOC 的值；（2）点θ=60°时，点P 是线段MD 上一点，直线AP 与平面AOC 所成角为α．若sin α=，求714线段MP 的长．55.在四棱锥P ﹣ABCD 中，PA ⊥平面ABCD ，底面ABCD 为直角梯形，∠CDA =∠BAD =90°，AD =DC =，AB =PA =2，且E 为线段PB 上的一动点．22（1）若E 为线段PB 的中点，求证：CE ∥平面PAD ；（2）当直线CE 与平面PAC 所成角小于，求PE 长度的3π取值范围．56.如图，在几何体中，平面底面，四边形是正方111ABC A B C -11A ACC ⊥ABC 11A ACC 形，，是的中点，且11B C BC ∥Q 1A B 112AC BC B C ==，． 2π3ACB ∠=(Ⅰ) 证明：平面；1B Q ∥11A ACC (Ⅱ) 求直线与平面所成角的正弦值．AB 11A BB57.如图，已知和所在平面互相垂直，且，ABC V BCD V 090BAC BCD ∠=∠=，点分别在线段,AB AC =CB CD =,E F ,BD CD上，沿直线将向上翻折使得与重EF EFD V D A 合（Ⅰ）求证：；AB CF ⊥（Ⅱ）求直线与平面所成角。

AE ABC 58.如图，四边形是圆台的轴截面，，点在底面圆周上，且ABCD 1OO 24AB CD ==M ，．2π=∠AOM DM AC ⊥（Ⅰ）求圆台的体积；1OO （Ⅱ）求二面角的平面角的余弦值．A DMO--59.如图，已知菱形与等腰所在平面相互垂直..ABCD PAB ∆120PAB BAD ∠=∠=为PB 中点．E （Ⅰ）求证：平面ACE ；//PD （Ⅱ）求二面角的余弦值B CE D --60.如图，在四面体中，平面⊥平面，，，ABCD ACD BCD 90BCA ∠=︒1AC =，为等边三角形.2AB =BCD ∆（Ⅰ）求证：⊥平面AC BCD（Ⅱ）求直线与平面所成角的正弦值.CDABD61.已知：平行四边形ABCD 中，∠DAB =45°，AB =AD =2，平面AED ⊥平面ABCD ，△22AED 为等边三角形，EF ∥AB ，EF =，M 为线段BC 的中点。

(完整)2019-2020年高考数学大题综合练习(三)

2019-2020年高考数学大题综合练习( 三)ABC 的内角A , B , C 的对边分别为a , b , c ,已知bcosA (1) 求 cosB ; (2) 如图，D ABC 外一点，若在平面四边形 ABCD中,D 2 B ，且 AD 1 , CD 3 , BC .6，求 AB 的长.【解析】解：(1)在ABC 中，由正弦定理得 sin BcosA3sin A sin C 3 又C(AB)，所以 sin B cos A巧i A sinA 3 sin (A B),故 sin B cos A 又A(0,)，所以 sin A 0 , 故 cos B.33(2)Q D 2B ,cosD22cos B1 13又在ACD 中， AD 1, CD > 3•由余弦定理可得 AC 2AD 2 CD 2 2AD CD cosD 1 9 2 3 (丄)12 ,所以 sin A cos B3••• AC 2 3 ,在 ABC 中，BC . 6 , AC 2 ■3, cosB•由余弦定理可得AC 2 AB 2 BC 2 2AB BCcosB ,即12 AB 26 2 AB ，化简得 AB 222AB 6 0 ,解得ABsin AcosB cos AsinB ,負inA , 3故AB的长为3 2 .2•已知四棱锥P-ABCD，底面ABCD为正方形，且PA丄底面ABCD，过AB的平面与侧面PCD的交线为EF，且满足S PEF：S四边形CDEF 1：3（S PEF表示PEF的面积）.AB时，二面角C AF D的余弦值为乜，求的值.(2)当PA5【解析】（1）证明：由题知四边形ABCD为正方形••• AB//CD，又CD 平面PCD, AB 平面PCD••• AB// 平面PCD又AB 平面ABFE ,平面ABFE 平面PCD EF•EF //AB,又AB//CD•EF //CD ,由S PEF :S四边形CDEF 1： 3知E,F分别为PC, PD的中点连接BD交AC与G，则G为BD中点，在PBD中FG为中位线，• EG//FB••• EG//FB,EG 平面ACE , PB 平面ACE•- PB//平面ACE.7KI J \/ \沐II '9^L J H I I. a, . 丁* †Ql±.......（2）•••底面ABCD为正方形，且PA 底面ABCD.†PA, AB, AD两两垂直，建立如图所示空间直角坐标系 A xyz.设AB AD 2a,AP 2b，贝U A 0,0,0 ,D 0,2a,0 ,C2a,2a,0 ,G a,a,0 , P 0,0,2 b , F a, a,b ，••• PA底面 ABCD ,DG 底面 ABCD ,.・.DG PA ,••• DG 平面 CAF ,3. 在数列｛a n ｝中，a i(1) 证明数列a n 1 a n 是等比数列，并求数列｛a n ｝的通项公式；a 13 2 n(2) 设 b n 2log 2 a n 1 1, c nn，求数列｛c n ｝的前 n 项和S n .t n ?b n 1【解析】•••四边形ABCD 为正方形二AC BD ,即 DGAC,AC PA A•平面CAF 的一个法向量为 DGa, a,0 .设平面AFD 的一个法向量为 m x, y, z ，而 uur uurAD 0,2a,0 , AF a, a,bir uur 出 mAD 田 ir uur m AFn 0 x 2 ay 00 得 ax ay bz 0 a 可得b,0, 为平面AED 的一个法向量,设二面角AF D 的大小为则cosab又PA2b, AB 2a.a 2a 2 a 2b 2•••当二面D 的余弦值为乜时53a n 1 2 a n, nuur urDG m又a1 1 , a23，所以a2a12,所以an 1a In是首项为2，公比为2的等比数列.，所以a n 1 a n 2n，所以ana1a2a iL a n a n 1121 2 n 1 n 丄2 L 2 2 1(2)Q a n 2n 1, 0 2log2 2n1 1 1 2n 1，C n2n3 2n 2n 1 2n 1 '又C n2n 3 2n2* 2* 1 2n 1 2n 1 2n 1 2n 1(〔)由a n 2 3a n 1 2a n，得a n 2a n 12 a n 1 a n ,2n2n 1 2* i 2n 12* i 2n 12* i 2n 14. 在创建全国文明卫生城”过程中，某市创城办”为了调查市民对创城工作的了解情况，进行了一次创城知识问卷调查（一位市民只能参加一次） •通过随机抽样，得到参加问卷调查的100人的得分（满分100分）统计结果如下表所示：（1）由频数分布表可以大致认为，此次问卷调查的得分 Z 服从正态分布N ,198，近似为这100人得分的平均值（同一组中的数据用该组区间的中点值作代表），利用该正态分布，求 P（37 Z 79 ；（2）在（1）的条件下，创城办”为此次参加问卷调查的市民制定如下奖励方案： ① 得分不低于的可以获赠2次随机话费，得分低于的可以获赠1次随机话费；② 每次获赠的随机话费和对应的概率为：现有市民甲参加此次问卷调查，记（单位：元）为该市民参加问卷调查获赠的话费，求的分布列与数学期望•附：参考数据与公式：.198 14. 若 X : N, 2，贝U P （X ） 0.6826，P （ 2 X 2 ） 0.9544，P （ 3X 3） 0.9974 .【解析】(1) EZ 35 0.02 45 0.15 55 0.2 65 0.25 75 0.24 85 0.1 95 0.04 65, 故 65，^.198 14 ••• P(65 14 Z 65 14) P(51 Z 79) 0.6826，P(65 2 14 Z 65 2 14) P(37 Z 93) 0.9544 .P(37 Z9可 PQ Z79)0.13592所以数列 c n 的前n 项和为22n 2n 1•- P(37 Z 51)3综上，P(37 Z 79) P(37 Z 51) P(51 Z 79)0.1359 0.6826 0.8185.(2)易知 P(Z ) P Z60 803 1 31 E20 - 40 -60 — 808 3163221(a b 0)的右焦点F ，点B 为此抛物线与 b5 椭圆C 在第一象限的交点，且BF -. 3(1)求椭圆C 的方程；11，12，直线11与椭圆C 交于P ，Q 两点，直线12与直线【解析】(1)由已知，可得 y 3 设 B(x o ,y o )(x °0, y g解得x 0 —，所以y 035. 已知抛物线y 4x 的焦点为椭圆C :笃a4x 的焦点坐标为F(1,0)，0)，则 BF5 x 13， ,2 84 -3 3 .4交于点T ，求的取值范围.获赠话费的可能取值为20 ,40, 60 , 80 .20 401113 313321632(2)过点F 作两条互相垂直的直线2 21, 即冷由点B在椭圆C上，得爲ay。

2019-2020年高考数学三模试卷文(含解析)

2019-2020年高考数学三模试卷文（含解析）一、选择题（本大题共10个小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的）1．（5分）已知复数z=（1﹣i）（1+2i），其中i为虚数单位，则的虚部为（）A．﹣i B．1 C．﹣1 D．i2．（5分）设全集U=R，A={x∈N|y=ln（2﹣x）}，B={x|2x（x﹣2）≤1}，A∩B=（）A．{x|x≥1}B．{x|1≤x＜2} C．{1} D．{0，1}3．（5分）若点P（3，﹣1）为圆（x﹣2）2+y2=25的弦AB的中点，则直线AB的方程为（）A．x+y﹣2=0 B．2x﹣y﹣7=0 C．2x+y﹣5=0 D．x﹣y﹣4=04．（5分）设向量，=（2，sinα），若，则tan（α﹣）等于（）A．﹣B．C．﹣3 D．35．（5分）设直线l：kx﹣y+1=0与圆C：x2+y2=4相较于A、B两点，=+，且点M在圆C上，则实数k等于（）A．1 B．2 C．﹣1 D．06．（5分）已知点P（a，b）与点Q（1，0）在直线2x+3y﹣1=0的两侧，且a＞0，b＞0，则w=a﹣2b的取值范围是（）A．[﹣，] B．（﹣，0）C．（0，）D．（﹣，）7．（5分）在等差数列{a n}中，满足3a4=7a7，且a1＞0，S n是数列{a n}的前n项的和，若S n取得最大值，则n取值为（）A．7 B．8 C．9 D．108．（5分）设a=，b=，c=，则a，b，c的大小关系为（）A．a＞b＞c B．b＞a＞c C．c＞b＞a D．c＞a＞b9．（5分）已知双曲线﹣=1（a＞0，b＞0）的实轴长为4，虚轴的一个端点与抛物线x2=2py（p ＞0）的焦点重合，直线y=kx﹣1与抛物线相切且与双曲线的一条渐进线平行，则p=（）A．4 B．3 C．2 D．110．（5分）已知函数f（x）=ax3﹣3x2+1，若f（x）存在唯一的零点x0，且x0＞0，则a的取值范围是（）A．（2，+∞）B．（1，+∞）C．（﹣∞，﹣2）D．（﹣∞，﹣1）二、填空题：本大题共5小题，每小题5分，共25分，把答案填在答题卷的横线上．. 11．（5分）已知等差数列{a n}中，a3=6，a6=3，则a9=．12．（5分）直线过点（2，﹣3），且在两个坐标轴上的截距互为相反数，则这样的直线方程是．13．（5分）已知x，y满足，则|x+y+1|的最大值为．14．（5分）某班级54名学生第一次考试的数学成绩为x1，x2，…，x54，其均值和标准差分别为90分和4分，若第二次考试每位学生的数学成绩都增加5分，则这54位学生第二次考试数学成绩的均值与标准差的和为分．15．（5分）椭圆满足这样的光学性质：从椭圆的一个交点发射的光线，经椭圆反射后，反射光先经过椭圆的另一个交点，现设有一个水平放置的椭圆形台球盘，满足方程+=1，点A和B 是它们的两个交点，当静止的小球放在点A处，从点A沿直线出发，经椭圆壁反弹后，再回到点A时，小球经过的路程是．三、解答题：本大题共6小题，满分75分，解答应写出文字说明、证明过程或演算步骤16．（12分）已知向量=（cosA，﹣sinA），=（cosB，sinB），•=cos2C，其中A，B，C是△ABC 的内角（1）求角C的大小；（2）求sinA+2sinB的取值范围．17．（12分）在如图所示的几何体中，四边形CDEF为正方形，四边形ABCD为等腰梯形，A B∥CD，AC=，AB=2BC=2，AC⊥FB．（1）求三棱锥A﹣BCF的体积．（2）线段AC上是否存在点M，使得EA∥平面FDM？证明你的结论．18．（12分）一个袋中有4个大小质地相同的小球，其中红球1个，白球2个（分别标号为1，2），黑球1个，现从袋中有放回的取球，每次随机取1个．（1）求连续取两次都没取到白球的概率；（2）若取1个红球记2分，取1个白球记1分，取1个回球记0分，连续取两次球，求分数之和为2或3的概率．19．（12分）设数列{a n}的前n项和为S n．已知a1=a，a n+1=S n+3n，n∈N*．由（Ⅰ）设b n=S n﹣3n，求数列{b n}的通项公式；（Ⅱ）若a n+1≥a n，n∈N*，求a的取值范围．20．（13分）已知点B是椭圆C：+=1（a＞b＞0）的上顶点，F1，F2分别是椭圆的左右焦点，直线BF1，BF2与椭圆分别交于E，F两点，△BEF为等边三角形．（1）求椭圆C的离心率；（2）已知点（1，）在椭圆C上，且直线l：y=kx+m与椭圆C交于M、N两点，若直线F1M，F2N 的倾斜角分别为α，β，且α+β=，求证：直线l过定点，并求该定点的坐标．21．（14分）已知函数f（x）=a x+x2﹣xlna（a＞0，a≠1）．（1）求函数f（x）在点（0，f（0））处的切线方程；（2）求函数f（x）单调增区间；（3）若存在x1，x2∈[﹣1，1]，使得|f（x1）﹣f（x2）|≥e﹣1（e是自然对数的底数），求实数a的取值范围．山东省淄博市实验中学xx高考数学三模试卷（文科）参考答案与试题解析一、选择题（本大题共10个小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的）1．（5分）已知复数z=（1﹣i）（1+2i），其中i为虚数单位，则的虚部为（）A．﹣i B．1 C．﹣1 D．i考点：复数代数形式的乘除运算．专题：数系的扩充和复数．分析：利用复数的运算法则、虚部的定义即可得出．解答：解：∵复数z=（1﹣i）（1+2i）=3+i，∴=3﹣i的虚部为﹣1．故选：C．点评：本题考查了复数的运算法则、虚部的定义，属于基础题．2．（5分）设全集U=R，A={x∈N|y=ln（2﹣x）}，B={x|2x（x﹣2）≤1}，A∩B=（）A．{x|x≥1}B．{x|1≤x＜2} C．{1} D．{0，1}考点：交集及其运算．专题：集合．分析：求出A与B中x的范围，确定出A与B，找出两集合的交集即可．解答：解：由A中x∈N，y=ln（2﹣x），得到2﹣x＞0，即x＜2，∴A={0，1}，由B中不等式变形得：2x（x﹣2）≤1=20，即x（x﹣2）≤0，解得：0≤x≤2，即B=[0，2]，则A∩B={0，1}．故选：D．点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．3．（5分）若点P（3，﹣1）为圆（x﹣2）2+y2=25的弦AB的中点，则直线AB的方程为（）A．x+y﹣2=0 B．2x﹣y﹣7=0 C．2x+y﹣5=0 D．x﹣y﹣4=0考点：直线与圆的位置关系．专题：计算题．分析：设圆心C（2，0），连接PC，由P（3，﹣1）为圆的弦的中点可得AB⊥PC，由可求K AB=1，从而可求直线AB的方程．解答：解：设圆心C（2，0），连接PC由P（3，﹣1）为圆的弦的中点可得AB⊥PC∵∴K AB=1直线AB的方程为x﹣y﹣4=0故选D．点评：本题主要考查了利用直线垂直关系求解直线的斜率，主要应用了圆的性质：垂直于（平分）弦的直径平分（垂直于）弦4．（5分）设向量，=（2，sinα），若，则tan（α﹣）等于（）A．﹣B．C．﹣3 D．3考点：数量积判断两个平面向量的垂直关系；两角和与差的正切函数．专题：平面向量及应用．分析：利用⇔，即可得出tanα，再利用两角差的正切公式即可得出．解答：解：∵，∴2cosα﹣sinα=0，即tanα=2．∴=，故选B．点评：熟练掌握⇔、两角差的正切公式是解题的关键．5．（5分）设直线l：kx﹣y+1=0与圆C：x2+y2=4相较于A、B两点，=+，且点M在圆C上，则实数k等于（）A．1 B．2 C．﹣1 D．0考点：直线与圆的位置关系．专题：直线与圆．分析：由已知得四边形OAMB为菱形，弦AB的长为2，又直线过定点N（0，1），且过N的弦的弦长最小值为2，由此能求出结果．解答：解：由题意可得，四边形OAMB为平行四边形，∴四边形OAMB为菱形，∴△OAM为等边三角形，且边长为2，解得弦AB的长为2，又直线过定点N（0，1），且过N的弦的弦长最小值为2，此时此弦平行x轴，即k=0，故选：D．点评：本题考查满足条件的实数值的求法，是中档题，解题时要认真审题，注意圆的性质的合理运用，属于基础题．6．（5分）已知点P（a，b）与点Q（1，0）在直线2x+3y﹣1=0的两侧，且a＞0，b＞0，则w=a﹣2b的取值范围是（）A．[﹣，] B．（﹣，0）C．（0，）D．（﹣，）考点：简单线性规划的应用；二元一次不等式的几何意义；直线的斜率．专题：不等式的解法及应用．分析：点P（a，b）与点Q（1，0）在直线2x+3y﹣1=0的两侧，那么把这两个点代入2x+3y ﹣1，它们的符号相反，结合a＞0，b＞0，画出可行域，则w=a﹣2b的取值范围．解答：解：点P（a，b）与点Q（1，0）在直线2x+3y﹣1=0的两侧，且a＞0，b＞0，可得：，可行域如图：w=a﹣2b经过可行域的A与B时分别取得最大值与最小值．∵A（），B（），∴w A=，w B=，∴w∈（﹣，）．故选：D．点评：本题考查了线性规划问题、直线的斜率计算公式及其单调性，考查了问题的转化能力和推理能力，属于中档题．7．（5分）在等差数列{a n}中，满足3a4=7a7，且a1＞0，S n是数列{a n}的前n项的和，若S n取得最大值，则n取值为（）A．7 B．8 C．9 D．10考点：等差数列的性质．专题：计算题．分析：把a1和d代入3a4=7a7，求得a1=﹣d，进而可判断a9＞0，a10＜0，故可知数列前9项均为正数，进而可知答案．解答：解：∵3a4=7a7，且a1＞0，∴数列的公差d＜0∵3a4=7a7∴3（a1+3d）=7（a1+6d）整理得a1=﹣d∴a9=a1+8d＞0，a10=a1+9d＜0∴前9项和S n最大．故选C．点评：本题主要考查了等差数列的性质．数列的单调性．属基础题．8．（5分）设a=，b=，c=，则a，b，c的大小关系为（）A．a＞b＞c B．b＞a＞c C．c＞b＞a D．c＞a＞b考点：不等式比较大小．专题：不等式的解法及应用．分析：化为a==，b==，c=，即可比较出大小．解答：解：∵a==，b==，c=，36e2＞49e＞64，∴a＜b＜c．故选：C．点评：本题考查了不等式的性质，属于基础题．9．（5分）已知双曲线﹣=1（a＞0，b＞0）的实轴长为4，虚轴的一个端点与抛物线x2=2py（p ＞0）的焦点重合，直线y=kx﹣1与抛物线相切且与双曲线的一条渐进线平行，则p=（）A．4 B．3 C．2 D．1考点：圆锥曲线的综合；双曲线的简单性质．专题：圆锥曲线的定义、性质与方程．分析：求出抛物线的焦点坐标，推出双曲线的渐近线方程，利用直线与抛物线相切求解即可．解答：解：抛物线x2=2py（p＞0）的焦点（0，），可得b=，a=2，双曲线方程为：，它的渐近线方程为：，即：，直线y=kx﹣1与抛物线相切且与双曲线的一条渐进线平行，不妨：k=，，可得=．△=，解得p=±4．∵p＞0，∴p=4．故选：A．点评：本题考查抛物线与双曲线以及直线方程的综合应用，考查分析问题解决问题的能力．10．（5分）已知函数f（x）=ax3﹣3x2+1，若f（x）存在唯一的零点x0，且x0＞0，则a的取值范围是（）A．（2，+∞）B．（1，+∞）C．（﹣∞，﹣2）D．（﹣∞，﹣1）考点：函数零点的判定定理．专题：综合题；导数的概念及应用．分析：分类讨论：当a≥0时，容易判断出不符合题意；当a＜0时，由于而f（0）=1＞0，x→+∞时，f（x）→﹣∞，可知：存在x0＞0，使得f（x0）=0，要使满足条件f（x）存在唯一的零点x0，且x0＞0，则必须极小值f（）＞0，解出即可．解答：解：当a=0时，f（x）=﹣3x2+1=0，解得x=±，函数f（x）有两个零点，不符合题意，应舍去；当a＞0时，令f′（x）=3ax2﹣6x=3ax（x﹣）=0，解得x=0或x=＞0，列表如下：x （﹣∞，0） 0 （0，）（，+∞）f′（x）+ 0 ﹣ 0 +f（x）单调递增极大值单调递减极小值单调递增∵x→﹣∞，f（x）→﹣∞，而f（0）=1＞0，∴存在x＜0，使得f（x）=0，不符合条件：f（x）存在唯一的零点x0，且x0＞0，应舍去．当a＜0时，f′（x）=3ax2﹣6x=3ax（x﹣）=0，解得x=0或x=＜0，列表如下：x （﹣∞，）（，0）0 （0，+∞）f′（x）﹣ 0 + 0 ﹣f（x）单调递减极小值单调递增极大值单调递减而f（0）=1＞0，x→+∞时，f（x）→﹣∞，∴存在x0＞0，使得f（x0）=0，∵f（x）存在唯一的零点x0，且x0＞0，∴极小值f（）＞0，化为a2＞4，∵a＜0，∴a＜﹣2．综上可知：a的取值范围是（﹣∞，﹣2）．故选：C．点评：本题考查了利用导数研究函数的单调性极值与最值、分类讨论的思想方法，考查了推理能力和计算能力，属于难题．二、填空题：本大题共5小题，每小题5分，共25分，把答案填在答题卷的横线上．. 11．（5分）已知等差数列{a n}中，a3=6，a6=3，则a9=0．考点：等差数列的通项公式．专题：计算题；等差数列与等比数列．分析：在等差数列{a n}中，设出公差为d，根据a3=6，a6=3，求出公差和首项，然后求出等差数列的通项公式，从而求解．解答：解：在等差数列{a n}中，a3=6，a6=3，a1+2d=6①，a1+5d=3②，联立①②可得，3d=﹣3，d=﹣1；a1=8，∴a n=a1+（n﹣1）d=8+（n﹣1）×（﹣1）=9﹣n；∴a9=0，故答案为：0．点评：本题主要考查等差数列的通项公式及其应用，考查解方程的运算求解能力，属于基础题．12．（5分）直线过点（2，﹣3），且在两个坐标轴上的截距互为相反数，则这样的直线方程是3x+2y=0或x﹣y﹣5=0．考点：直线的截距式方程．专题：直线与圆．分析：当直线经过原点时满足条件，直接得出；当直线不经过原点时，设，把点（2，﹣3）代入即可得出．解答：解：当直线经过原点时满足条件，此时直线方程为，化为3x+2y=0；当直线不经过原点时，设，把点（2，﹣3）代入可得：=1，解得a=5．∴直线方程为x﹣y﹣5=0．综上可得：直线方程为3x+2y=0或x﹣y﹣5=0．故答案为：3x+2y=0或x﹣y﹣5=0．点评：本题考查了直线的截距式、分类讨论方法，考查了推理能力与计算能力，属于基础题．13．（5分）已知x，y满足，则|x+y+1|的最大值为6．考点：简单线性规划．专题：不等式的解法及应用．分析：作出不等式组对应的平面区域，利用目标函数的几何意义，进行求解即可．解答：解：作出不等式组对应的平面区域如图：（阴影部分ABC）．设z=x+y+1得y=﹣x+z﹣1，平移直线y=﹣x+z﹣1，由图象可知当直线y=﹣x+z﹣1经过点A（1，0）时，直线y=﹣x+z﹣1的截距最小，此时z最小．此时z=1+1=2，当直线经过点B时，直线截距最大，由，解得，即B（2，3），代入目标函数z=x+y+1得z=2+3+1=6．即2≤z≤6，则2≤|x+y+1|≤6，故|x+y+1|的最大值为6．故答案为：6．点评：本题主要考查线性规划的应用，利用目标函数的几何意义，结合数形结合的数学思想是解决此类问题的基本方法．14．（5分）某班级54名学生第一次考试的数学成绩为x1，x2，…，x54，其均值和标准差分别为90分和4分，若第二次考试每位学生的数学成绩都增加5分，则这54位学生第二次考试数学成绩的均值与标准差的和为99 分．考点：极差、方差与标准差．专题：概率与统计．分析：利用标准差、均值的性质即得结论．解答：解：当每位学生的数学成绩都增加5分时，由标准差的性质可知：标准差不变，但均值增加5，即均值与标准差的和增加了5，故答案为：99．点评：本题考查标准差、均值的性质，注意解题方法的积累，属于基础题．15．（5分）椭圆满足这样的光学性质：从椭圆的一个交点发射的光线，经椭圆反射后，反射光先经过椭圆的另一个交点，现设有一个水平放置的椭圆形台球盘，满足方程+=1，点A和B 是它们的两个交点，当静止的小球放在点A处，从点A沿直线出发，经椭圆壁反弹后，再回到点A时，小球经过的路程是2或18或20．考点：椭圆的简单性质．专题：计算题；圆锥曲线的定义、性质与方程．分析：根据椭圆的光学性质可知，当静止的小球放在点A处，从点A沿直线出发，射到左顶点，经椭圆壁反弹后，再回到点A时，小球经过的路程是2；射到右顶点，经椭圆壁反弹后，再回到点A时，小球经过的路程是18；小球从点A沿直线出发，经椭圆壁反弹到B点继续前行碰椭圆壁后回到A点，所走的轨迹正好是两次椭圆上的点到两焦点距离之和，进而根据椭圆的定义可求得答案．解答：解：依题意可知+=1中，a=5，b=3，c=4，设A，B分别为左、右焦点，则当静止的小球放在点A处，从点A沿直线出发，射到左顶点，经椭圆壁反弹后，再回到点A 时，小球经过的路程是2；射到右顶点，经椭圆壁反弹后，再回到点A时，小球经过的路程是18；小球经两次椭圆壁后反弹后回到A点，根据椭圆的性质可知所走的路程正好是4a=4×5=20．故答案为：2或18或20．点评：本题主要考查了椭圆的应用．解题的关键是利用了椭圆的第一定义．三、解答题：本大题共6小题，满分75分，解答应写出文字说明、证明过程或演算步骤16．（12分）已知向量=（cosA，﹣sinA），=（cosB，sinB），•=cos2C，其中A，B，C是△ABC 的内角（1）求角C的大小；（2）求sinA+2sinB的取值范围．考点：平面向量数量积的运算；三角函数中的恒等变换应用．专题：不等式的解法及应用；平面向量及应用．分析：（1）由数量积的坐标运算结合两角和的余弦化为关于cosC的一元二次方程求得cosC，从而得到角C的大小；（2）用A表示B，借助于辅助角公式化简，则sinA+2sinB的取值范围可求．解答：解：（1）=cosAcosB﹣sinAsinB=cos（A+B），∵A+B+C=π，∴cos（A+B）=﹣cosC=cos2C，即2cos2C+cosC﹣1=0．故cosC=或cosC=﹣1．又0＜C＜π，∴C=；（2）sinA+2sinB=sinA+2sin（﹣A）=2sinA+cosA=sin（A+θ），其中θ为锐角，且tanθ=．∵0＜A＜，0＜θ＜．∴θ＜A+θ＜+θ．当A+θ=时，sinA+2sin有最大值；又∵A=0时，sinA+2sinB=，A=时，sinA+2sinB=，故sinA+2sin2B的取值范围是．点评：本题考查平面向量的数量积运算，考查三角函数值域的求法，关键是对角范围的讨论，是中档题．17．（12分）在如图所示的几何体中，四边形CDEF为正方形，四边形ABCD为等腰梯形，AB∥CD，AC=，AB=2BC=2，AC⊥FB．（1）求三棱锥A﹣BCF的体积．（2）线段AC上是否存在点M，使得EA∥平面FDM？证明你的结论．考点：棱柱、棱锥、棱台的体积；直线与平面平行的判定．专题：综合题；空间位置关系与距离．分析：（1）根据线面垂直的判定定理证明AC⊥平面FBC，FC⊥平面ABCD，再利用体积公式求解即可；（2）根据线面平行的判定定理即可证明．解答：解：（1）在△ABC中，因为AC=，AB=2，BC=1，所以AC⊥BC，∠ABC=60，∠ADC=120°．在△ADC中，由余弦定理可得DC=1，又因为AC⊥FB，BC∩FB=B，所以AC⊥平面FBC．因为FC⊂平面FBC，所以AC⊥FC，因为CDEF为正方形，所以DC⊥FC，FC=1，因为AC∩DC=C，所以FC⊥平面ABCD，即FC⊥BC，所以V A﹣FBC===；（2）M为线段AC的中点，EA∥平面FDM．连结CE，与DF交于点N，连接MN．因为CDEF为正方形，所以N为CE中点．在△ACE中，EA∥MN．因为MN⊂平面FDM，EA⊄平面FDM，所以EA∥平面FDM．点评：本题主要考查空间直线和平面平行和垂直的判定，考查体积的计算，要求熟练掌握相应的判定定理．18．（12分）一个袋中有4个大小质地相同的小球，其中红球1个，白球2个（分别标号为1，2），黑球1个，现从袋中有放回的取球，每次随机取1个．（1）求连续取两次都没取到白球的概率；（2）若取1个红球记2分，取1个白球记1分，取1个回球记0分，连续取两次球，求分数之和为2或3的概率．考点：列举法计算基本事件数及事件发生的概率．专题：概率与统计．分析：（1）利用列举法写出连续取两次的事件总数情况，共16种，从中算出连续取两次都不是白球的种数，最后求出它们的比值即可；（2）从中数出连续取二次分数之和为2或3的种数，根据互斥事件的概率公式，计算即可．解答：解：（1）连续取两次所包含的基本事件有：（红，红），（红，白1），（红，白2），（红，黑）；（白1，红）（白1，白1）（白1，白2），（白1，黑）；（白2，红），（白2，白1），（白2，白2），（白2，黑）；（黑，红），（黑，白1），（黑，白2），（黑，黑），所以基本事件的总数16个，设事件A：“连续取两次都没有取到白球”，则事件A所包含的基本事件有：（红，红），（黑，红），（红，黑），（黑，黑）4个基本事件，所以P（A）==，（2）设事件B：“连续取两次分数之和为2“，则事件B由（红，黑），（白1，白1），（白1，白2），（白2，白1），（白2，白2），（黑，红），6个基本事件组成，则P（B）==，设事件C：“连续取两次分数之和为3“，则事件C由（红，白1），（红，白2），（白1，红）；（白2，红），4个基本事件组成，则P（C）==，设事件D，“连续取两次分数之和为2或3”，且B与C互斥，则P（D）=P（B）+P（C）=+=．点评：本题考查了古典概型的概率问题，关键是列举基本的事件，属于基础题．19．（12分）设数列{a n}的前n项和为S n．已知a1=a，a n+1=S n+3n，n∈N*．由（Ⅰ）设b n=S n﹣3n，求数列{b n}的通项公式；（Ⅱ）若a n+1≥a n，n∈N*，求a的取值范围．考点：数列递推式；数列的概念及简单表示法．专题：计算题；压轴题．分析：（Ⅰ）依题意得S n+1=2S n+3n，由此可知S n+1﹣3n+1=2（S n﹣3n）．所以b n=S n﹣3n=（a﹣3）2n﹣1，n∈N*．（Ⅱ）由题设条件知S n=3n+（a﹣3）2n﹣1，n∈N*，于是，a n=S n﹣S n﹣1=，由此可以求得a的取值范围是[﹣9，+∞）．解答：解：（Ⅰ）依题意，S n+1﹣S n=a n+1=S n+3n，即S n+1=2S n+3n，由此得S n+1﹣3n+1=2S n+3n﹣3n+1=2（S n﹣3n）．（4分）因此，所求通项公式为b n=S n﹣3n=（a﹣3）2n﹣1，n∈N*．①（6分）（Ⅱ）由①知S n=3n+（a﹣3）2n﹣1，n∈N*，于是，当n≥2时，a n=S n﹣S n﹣1=3n+（a﹣3）×2n﹣1﹣3n﹣1﹣（a﹣3）×2n﹣2=2×3n﹣1+（a﹣3）2n﹣2，a n+1﹣a n=4×3n﹣1+（a﹣3）2n﹣2=，当n≥2时，⇔a≥﹣9．又a2=a1+3＞a1．综上，所求的a的取值范围是[﹣9，+∞）．（12分）点评：本题考查数列的综合运用，解题时要仔细审题，注意挖掘题设中的隐含条件．20．（13分）已知点B是椭圆C：+=1（a＞b＞0）的上顶点，F1，F2分别是椭圆的左右焦点，直线BF1，BF2与椭圆分别交于E，F两点，△BEF为等边三角形．（1）求椭圆C的离心率；（2）已知点（1，）在椭圆C上，且直线l：y=kx+m与椭圆C交于M、N两点，若直线F1M，F2N 的倾斜角分别为α，β，且α+β=，求证：直线l过定点，并求该定点的坐标．考点：直线与圆锥曲线的综合问题．专题：圆锥曲线的定义、性质与方程．分析：（Ⅰ）根据三角形为等边三角形，列式求解离心率．（Ⅱ）先求得椭圆方程，直线l：y=kx+m与椭圆C联立，得所以（k2﹣1）x1x2+（mk+1）（x1+x2）+m2﹣1=0，依条件求解．解答：解：（Ⅰ）B（0，b）F1（﹣c，0），F2（c，0）．又△BEF为等边三角形，所以，△BF1F2为等边三角形．∴2c=，①又a2=b2+c2②由①②解得椭圆C的离心率．…（3分）（Ⅱ）由题意椭圆方程为3x2+4y2=3a2，由于点（1，）在椭圆C上，因此a2=4，b2=3，因此椭圆方程为．…（4分）联立，消去y，得（3+4k2）x2+8mkx+4m2﹣12=0．设M（x1，y1）．N（x2，y2），则，由，得sinα=cosβ，cosα=sinβ，…（7分）因此tanαtanβ=1，即，因此（kx1+m）（kx2+m）=（x1﹣1）（x2﹣1），所以（k2﹣1）x1x2+（mk+1）（x1+x2）+m2﹣1=0，…（9分）因此+m2﹣1=0，整理，得m2+8mk+16k2﹣9=0，即（m+4k）2=3，m=﹣4k±3．…（11分）于是直线方程为y=k（x﹣4）±3，因此直线过定点（4，3）或（4，﹣3）．…（13分）点评：本题主要考查了椭圆离心率的求法和直线和圆锥曲线的综合应用，属于中档题，xx 高考经常涉及．21．（14分）已知函数f（x）=a x+x2﹣xlna（a＞0，a≠1）．（1）求函数f（x）在点（0，f（0））处的切线方程；（2）求函数f（x）单调增区间；（3）若存在x1，x2∈[﹣1，1]，使得|f（x1）﹣f（x2）|≥e﹣1（e是自然对数的底数），求实数a的取值范围．考点：利用导数研究曲线上某点切线方程；利用导数研究函数的单调性；利用导数求闭区间上函数的最值．专题：导数的综合应用．分析：（1）先求函数的导函数f′（x），再求所求切线的斜率即f′（0），由于切点为（0，0），故由点斜式即可得所求切线的方程；（2）先求原函数的导数得：f'（x）=a x lna+2x﹣lna=2x+（a x﹣1）lna，再对a进行讨论，得到f'（x）＞0，从而函数f（x）在（0，+∞）上单调递增．（3）f（x）的最大值减去f（x）的最小值大于或等于e﹣1，由单调性知，f（x）的最大值是f（1）或f（﹣1），最小值f（0）=1，由f（1）﹣f（﹣1）的单调性，判断f（1）与f（﹣1）的大小关系，再由f（x）的最大值减去最小值f（0）大于或等于e﹣1求出a的取值范围．解答：解：（1）∵f（x）=a x+x2﹣xlna，∴f′（x）=a x lna+2x﹣lna，∴f′（0）=0，f（0）=1即函数f（x）图象在点（0，1）处的切线斜率为0，∴图象在点（0，f（0））处的切线方程为y=1；（3分）（2）由于f'（x）=a x lna+2x﹣lna=2x+（a x﹣1）lna＞0①当a＞1，y=2x单调递增，lna＞0，所以y=（a x﹣1）lna单调递增，故y=2x+（a x﹣1）lna 单调递增，∴2x+（a x﹣1）lna＞2×0+（a0﹣1）lna=0，即f'（x）＞f'（0），所以x＞0故函数f（x）在（0，+∞）上单调递增；②当0＜a＜1，y=2x单调递增，lna＜0，所以y=（a x﹣1）lna单调递增，故y=2x+（a x﹣1）lna单调递增，∴2x+（a x﹣1）lna＞2×0+（a0﹣1）lna=0，即f'（x）＞f'（0），所以x＞0故函数f（x）在（0，+∞）上单调递增；综上，函数f（x）单调增区间（0，+∞）；（8分）（3）因为存在x1，x2∈[﹣1，1]，使得|f（x1）﹣f（x2）|≥e﹣1，所以当x∈[﹣1，1]时，|（f（x））max﹣（f（x））min|=（f（x））max﹣（f（x））min≥e﹣1，（12分）由（2）知，f（x）在[﹣1，0]上递减，在[0，1]上递增，所以当x∈[﹣1，1]时，（f（x））min=f（0）=1，（f（x））max=max{f（﹣1），f（1）}，而f（1）﹣f（﹣1）=（a+1﹣lna）﹣（ +1+lna）=a﹣﹣2lna，记g（t）=t﹣﹣2lnt（t＞0），因为g′（t）=1+﹣=（﹣1）2≥0（当t=1时取等号），所以g（t）=t﹣﹣2lnt在t∈（0，+∞）上单调递增，而g（1）=0，所以当t＞1时，g（t）＞0；当0＜t＜1时，g（t）＜0，也就是当a＞1时，f（1）＞f（﹣1）；当0＜a＜1时，f（1）＜f（﹣1）（14分）①当a＞1时，由f（1）﹣f（0）≥e﹣1⇒a﹣lna≥e﹣1⇒a≥e，②当0＜a＜1时，由f（﹣1）﹣f（0）≥e﹣1⇒+lna≥e﹣1⇒0＜a≤，综上知，所求a的取值范围为a∈（0，]∪[e，+∞）．（16分）点评：本题考查了基本函数导数公式，导数的几何意义，利用导数研究函数的单调性及利用导数求闭区间上函数的最值．属于中档题．。

北京市西城区2019-2020学年高考数学仿真第三次备考试题含解析

北京市西城区2019-2020学年高考数学仿真第三次备考试题一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．一小商贩准备用50元钱在一批发市场购买甲、乙两种小商品，甲每件进价4元，乙每件进价7元，甲商品每卖出去1件可赚1元，乙商品每卖出去1件可赚1.8元.该商贩若想获取最大收益，则购买甲、乙两种商品的件数应分别为（） A ．甲7件，乙3件 B ．甲9件，乙2件C ．甲4件，乙5件D ．甲2件，乙6件【答案】D 【解析】【分析】由题意列出约束条件和目标函数，数形结合即可解决. 【详解】设购买甲、乙两种商品的件数应分别x ，y 利润为z 元，由题意*4750,,,x y x y N +≤⎧⎨∈⎩ 1.8z x y =+，画出可行域如图所示，显然当5599y x z =-+经过(2,6)A 时，z 最大. 故选：D. 【点睛】本题考查线性目标函数的线性规划问题，解决此类问题要注意判断x ，y 是否是整数，是否是非负数，并准确的画出可行域，本题是一道基础题.2．已知双曲线22122:1x y C a b -=与双曲线222:14y C x -=没有公共点，则双曲线1C 的离心率的取值范围是( ) A ．(3 B ．)3,⎡+∞⎣C ．(5D ．)5,⎡+∞⎣【答案】C 【解析】【分析】先求得2C 的渐近线方程，根据12,C C 没有公共点，判断出1C 渐近线斜率的取值范围，由此求得1C 离心率的取值范围. 【详解】双曲线222:14y C x -=的渐近线方程为2y x =±，由于双曲线22122:1x y C a b -=与双曲线222:14y C x -=没有公共点，所以双曲线1C 的渐近线的斜率2b a ≤，所以双曲线1C 的离心率(e =.故选：C 【点睛】本小题主要考查双曲线的渐近线，考查双曲线离心率的取值范围的求法，属于基础题.3．公差不为零的等差数列{a n }中，a 1+a 2+a 5=13，且a 1、a 2、a 5成等比数列，则数列{a n }的公差等于( ) A ．1 B ．2C ．3D ．4【答案】B 【解析】【分析】设数列的公差为,0d d ≠.由12513a a a ++=，125,,a a a 成等比数列，列关于1,a d 的方程组，即求公差d . 【详解】设数列的公差为,0d d ≠，125113,3513a a a a d ++=∴+=Q ①.125,,a a a Q 成等比数列，()()21114a d a a d ∴+=+②，解①②可得2d =. 故选：B . 【点睛】本题考查等差数列基本量的计算，属于基础题. 4．已知(,)a bi a b R +∈是11ii +-的共轭复数,则a b +=（） A ．1- B ．12- C ．12D ．1【答案】A 【解析】【分析】先利用复数的除法运算法则求出11ii+-的值，再利用共轭复数的定义求出a+bi ，从而确定a ，b 的值，求出a+b ．【详解】()()21(1)21112i i ii i i ++===-+-i ， ∴a+bi ＝﹣i ， ∴a ＝0，b ＝﹣1， ∴a+b ＝﹣1，故选：A ．【点睛】本题主要考查了复数代数形式的乘除运算，考查了共轭复数的概念，是基础题．5．己知函数()()1,0,ln ,0,kx x f x x x ->⎧=⎨--<⎩若函数()f x 的图象上关于原点对称的点有2对，则实数k 的取值范围是（） A ．(),0-∞ B ．()0,1C ．()0,∞+D ．10,2⎛⎫ ⎪⎝⎭【答案】B 【解析】【分析】考虑当0x >时，1ln kx x -=有两个不同的实数解，令()ln 1h x x kx =-+，则()h x 有两个不同的零点，利用导数和零点存在定理可得实数k 的取值范围. 【详解】因为()f x 的图象上关于原点对称的点有2对，所以0x >时，1ln kx x -=有两个不同的实数解.令()ln 1h x x kx =-+，则()h x 在()0,∞+有两个不同的零点. 又()1kxh x x-'=，当0k ≤时，()0h x '>，故()h x 在()0,∞+上为增函数，()h x 在()0,∞+上至多一个零点，舍.当0k >时，若10,⎛⎫∈ ⎪⎝⎭x k ，则()0h x '>，()h x 在10,k ⎛⎫⎪⎝⎭上为增函数；若1,⎛⎫∈+∞⎪⎝⎭x k ，则()0h x '<，()h x 在1,k ⎛⎫+∞ ⎪⎝⎭上为减函数；故()max 11ln h x h k k ⎛⎫==⎪⎝⎭，因为()h x 有两个不同的零点，所以1ln 0k>，解得01k <<. 又当01k <<时，11e k <且10k h e e ⎛⎫=-< ⎪⎝⎭，故()h x 在10,k ⎛⎫ ⎪⎝⎭上存在一个零点.又22ln +122ln e e e h t et k k k ⎛⎫=-=+-⎪⎝⎭，其中11t k =>. 令()22ln g t t et =+-，则()2etg t t-'=，当1t >时，()0g t '<，故()g t 为()1,+∞减函数，所以()()120g t g e <=-<即20e h k ⎛⎫<⎪⎝⎭. 因为2211e k k k >>，所以()h x 在1,k ⎛⎫+∞ ⎪⎝⎭上也存在一个零点. 综上，当01k <<时，()h x 有两个不同的零点. 故选：B. 【点睛】本题考查函数的零点，一般地，较为复杂的函数的零点，必须先利用导数研究函数的单调性，再结合零点存在定理说明零点的存在性，本题属于难题.6．命题“20,(1)(1)∀>+>-x x x x ”的否定为（） A ．20,(1)(1)∀>+>-x x x x B ．20,(1)(1)∀+>-x x x x „ C ．20,(1)(1)∃>+-x x x x „ D ．20,(1)(1)∃+>-x x x x „【答案】C 【解析】【分析】套用命题的否定形式即可. 【详解】命题“,()x M p x ∀∈”的否定为“,()x M p x ∃∈⌝”，所以命题“20,(1)(1)∀>+>-x x x x ”的否定为“20,(1)(1)x x x x ∃>+≤-”.故选：C 【点睛】本题考查全称命题的否定，属于基础题.7．在直三棱柱111ABC A B C -中，己知AB BC ⊥，2AB BC ==，122CC =，则异面直线1AC 与11A B 所成的角为（） A ．30︒ B ．45︒C ．60︒D ．90︒【答案】C 【解析】【分析】由条件可看出11AB A B P ，则1BAC ∠为异面直线1AC 与11A B 所成的角，可证得三角形1BAC 中，1AB BC ⊥，解得1tan BAC ∠，从而得出异面直线1AC 与11A B 所成的角．【详解】连接1AC ，1BC ，如图：又11AB A B P ，则1BAC ∠为异面直线1AC 与11A B 所成的角.因为AB BC ⊥，且三棱柱为直三棱柱，∴1AB CC ⊥，∴AB ⊥面11BCC B ， ∴1AB BC ⊥，又2AB BC ==，122CC =()22122223BC =+=，∴1tan 3BAC ∠=160BAC ∠=︒. 故选C 【点睛】考查直三棱柱的定义，线面垂直的性质，考查了异面直线所成角的概念及求法，考查了逻辑推理能力，属于基础题．8．若向量(1,5),(2,1)a b ==-vv，则(2)a a b ⋅+=vv v（）A ．30B ．31C ．32D ．33【答案】C 【解析】【分析】先求出2a b +r r ,再与a r相乘即可求出答案.【详解】因为2(1,5)(4,2)(3,7)a b +=+-=-r r ,所以(2)35732a a b ⋅+=-+⨯=r r r.故选:C. 【点睛】本题考查了平面向量的坐标运算,考查了学生的计算能力,属于基础题.9．已知点()11,A x y ，()22,B x y 是函数()2f x bx =的函数图像上的任意两点，且()y f x =在点1212,22x x x x f ⎛++⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭处的切线与直线AB 平行，则( ) A ．0a =，b 为任意非零实数 B ．0b =，a 为任意非零实数 C ．a 、b 均为任意实数 D ．不存在满足条件的实数a ，b【答案】A 【解析】【分析】求得()f x 的导函数，结合两点斜率公式和两直线平行的条件：斜率相等，化简可得0a =，b 为任意非零实数. 【详解】依题意()'2fx bx =+，()y f x =在点1212,22x xx x f ⎛++⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭处的切线与直线AB平行，即有()1221b x x +=()1221ab x x x x =++-=，由于对任意12,x x 上式都成立，可得0a =，b 为非零实数.故选：A 【点睛】本题考查导数的运用，求切线的斜率，考查两点的斜率公式，以及化简运算能力，属于中档题．10．已知椭圆2222:1x y C a b+=的短轴长为2，焦距为12F F 、分别是椭圆的左、右焦点，若点P 为C 上的任意一点，则1211PF PF +的取值范围为（） A ．[]1,2 B． C．⎤⎦D ．[]1,4【答案】D 【解析】【分析】先求出椭圆方程，再利用椭圆的定义得到124PF PF +=，利用二次函数的性质可求1214PF PF ≤≤，从而可得1211PF PF +的取值范围. 【详解】由题设有1,b c ==2a =，故椭圆22:14x C y +=，因为点P 为C 上的任意一点，故124PF PF +=.又()12121212111144=4PF PF PF PF PF PF PF PF PF PF ++==-，因为122PF ≤≤，故()11144PF PF ≤-≤，所以121114PF PF ≤+≤. 故选：D. 【点睛】本题考查椭圆的几何性质，一般地，如果椭圆()2222:10x y C a b a b+=>>的左、右焦点分别是12F F 、，点P 为C 上的任意一点，则有122PF PF a +=，我们常用这个性质来考虑与焦点三角形有关的问题，本题属于基础题.11．已知a r ，b r ，c r 是平面内三个单位向量，若a b ⊥r r，则232a c a b c +++-r r r r r 的最小值（） AB．CD ．5【答案】A 【解析】【分析】由于a b ⊥r r，且为单位向量，所以可令()1,0a =r ，()0,1b =r ，再设出单位向量c r 的坐标，再将坐标代入232a c a b c +++-r r r r r中，利用两点间的距离的几何意义可求出结果．【详解】解：设(),c x y =r ，()1,0a =r ，()0,1b =r ，则221x y +=，从而232+++-=r r r r r a c a b c==≥=故选：A 【点睛】此题考查的是平面向量的坐标、模的运算，利用整体代换，再结合距离公式求解，属于难题．12．已知等比数列{}n a 的前n 项和为n S ，且满足122n n S λ+=+，则λ的值是( )A ．4B ．2C ．2-D ．4-【答案】C 【解析】【分析】利用n S 先求出n a ，然后计算出结果. 【详解】根据题意，当1n =时，11224S a λ==+,142a λ+∴=, 故当2n ≥时，112n n n n a S S --=-=,Q 数列{}n a 是等比数列,则11a =，故412λ+=, 解得2λ=-, 故选C . 【点睛】本题主要考查了等比数列前n 项和n S 的表达形式，只要求出数列中的项即可得到结果，较为基础. 二、填空题：本题共4小题，每小题5分，共20分。

2019江苏高考数学小题强化训练50练(提升版)(含详细解答)

高考数学小题强化训练50篇(提升版)8个填空题+4个解答题 (含详细参考答案)班级 __________ 姓名 __________ 分数 __________小题强化训练一一、填空题：本大题共8小题，每题5分，共40分． 1.给出以下结论：①命题“若x 2－3x －4＝0，则x ＝4”的逆否命题为“若x ≠4，则x 2－3x －4≠0”； ②“x ＝4”是“x 2－3x －4＝0”的充分条件；③命题“若m >0，则方程x 2＋x －m ＝0有实根”的逆命题为真命题；④命题“若m 2＋n 2＝0，则m ＝0且n ＝0”的否命题是“若m 2＋n 2≠0，则m ≠0或n ≠0”．则其中错误的是________．(填序号)2.已知函数f (x )＝⎩⎨⎧sin 5πx 2，x ≤0，16－log 3x ，x ＞0，则f (f (33))＝________．3.连续抛掷两枚骰子分别得到的点数是a ，b ，则函数f (x )＝ax 2－bx 在x ＝1处取得最值的概率是________．4.设S n 为正项等比数列{a n }的前n 项和．若a 4·a 8＝2a 10，则S 3的最小值为________．5.在平面直角坐标系xOy 中，圆C 的方程为x 2＋y 2－4x ＝0，若直线y ＝k (x ＋1)上存在一点P ，使过点P 所作的圆的两条切线相互垂直，则实数k 的取值范围是____________．(第6题)6.如图，在平行四边形ABCD 中，AC ，BD 相交于点O ，E 为线段AO 的中点．若BE →＝λBA →＋μBD →(λ，μ∈R )，则λ＋μ＝________．7.已知a >0，b >0，则a 2a ＋b ＋2b2b ＋a的最大值为________.8.已知函数f (x )＝x 2－2x ＋a (e x －1＋e －x ＋1)有唯一的零点，则a ＝________．二、解答题：本大题共4小题，共60分．解答时应写出必要的文字说明、证明过程或演算步骤． 9.(本小题满分14分)如图，在三棱柱ABCA 1B 1C 1中，已知M ，N 分别为线段BB 1，A 1C 的中点，MN 与AA 1所成角的大小为90°，且MA 1＝MC .求证：(1)平面A 1MC ⊥平面A 1ACC 1； (2)MN ∥平面ABC .10.(本小题满分14分)已知向量m ＝(cos α，－1)，n ＝(2，sin α)，其中α∈(0，π2)，且m ⊥n .(1)求cos2α的值；(2)若sin(α－β)＝1010，且β∈(0，π2)，求角β的值．11.(本小题满分16分)设椭圆C ：x 22＋y 2＝1的右焦点为F ，过点F 的直线l 与C 交于A ，B 两点，点M 的坐标为(2，0)．(1)当l 与x 轴垂直时，求直线AM 的方程； (2)设O 为坐标原点，求证：∠OMA ＝∠OMB .12.(本小题满分16分)已知等差数列{a n }的前n 项和为S n ，且满足S 4＝24，S 7＝63. (1)求数列{a n }的通项公式； (2)若b n ＝2a n ＋(－1)n ·a n ，求数列{b n }的前n 项和T n .班级 __________ 姓名 __________ 分数 __________小题强化训练二一、填空题：本大题共8小题，每题5分，共40分．1.已知复数z 满足(z －2)i ＝1＋i (i 为虚数单位)，则复数z 的共轭复数z 在复平面内对应的点位于第________象限．2.设集合A ＝{x |y ＝ln(x 2－3x )}，B ＝{y |y ＝2x ，x ∈R }，则A ∪B ＝____________．3.若θ∈(0，π4)，且sin2θ＝14，则sin(θ－π4)＝________．4.已知一个正方体的外接球体积为V 1，其内切球体积为V 2，则V 1V 2的值为________.5.记等差数列{a n }的前n 项和为S n .已知a 1＝3，且数列{S n }也为等差数列，则a 11＝________．6.在▱ABCD 中，∠BAD ＝60°，E 是CD 上一点，且AE →＝12AB →＋BC →，|AB →|＝λ|AD →|.若AC →·EB →＝12AD → 2，则λ＝________．7.设函数f (x )＝ln x ＋mx，m ∈R ，若对任意x 2＞x 1＞0，f (x 2)－f (x 1)＜x 2－x 1恒成立，则实数m 的取值范围是__________．8.已知实数x ，y 满足x 2＋y 2＝1，则1（x －y ）2＋1（x ＋y ）2的最小值为________．二、解答题：本大题共4小题，共60分．解答时应写出必要的文字说明、证明过程或演算步骤． 9.(本小题满分14分)在平面四边形ABCD 中，∠ADC ＝90°，∠A ＝45°，AB ＝2，BD ＝5. (1)求cos ∠ADB 的值；(2)若DC ＝22，求BC 的值．10.(本小题满分14分)如图，在三棱锥ABCD中，AB⊥AD，BC⊥BD，平面ABD⊥平面BCD，点E，F(点E与点A，D不重合)分别在棱AD，BD上，且EF⊥AD.求证：(1)EF∥平面ABC；(2)AD⊥AC.11.(本小题满分16分)如图所示的某种容器的体积为90πcm3，它是由圆锥和圆柱两部分连结而成的，圆柱与圆锥的底面圆半径都为rcm.圆锥的高为h1cm，母线与底面所成的角为45°；圆柱的高为h2cm.已知圆柱底面造价为2a元/cm2，圆柱侧面造价为a元/cm2，圆锥侧面造价为2a元/cm2.(1)将圆柱的高h2表示为底面圆半径r的函数，并求出定义域；(2)当容器造价最低时，圆柱的底面圆半径r为多少？12.(本小题满分16分)已知等比数列{a n}的前n项和为S n，且2n＋1，S n，a成等差数列(n∈N*)．(1)求a的值及数列{a n}的通项公式；(2)若b n＝(2n－1)a n，求数列{b n}的前n项和T n.班级 __________ 姓名 __________ 分数 __________小题强化训练三一、填空题：本大题共8小题，每题5分，共40分．1.设集合A ＝⎩⎨⎧⎭⎬⎫x |14≤2x ≤64，x ∈N ，B ＝{x |y ＝ln(x 2－3x )}，则A ∩B 的子集的个数是________．2.设θ∈R ，则“⎪⎪⎪⎪θ－π12＜π12”是“sin θ＜12”的__________条件． 3.已知双曲线C ：x 2a 2－y2b2＝1(a >0，b >0)的离心率为2，焦点到渐近线的距离为3，则双曲线C 的焦距为________．4.已知{a n }，{b n }均为等比数列，其前n 项和分别为S n ，T n .若对任意的n ∈N *，总有S n T n ＝3n＋14，则a 3b 3＝________．5.已知在平行四边形ABCD 中，∠BAD ＝120°，AB ＝1，AD ＝2，P 是线段BC 上的一个动点，则AP →·DP →的取值范围是________．(第7题)6.已知函数f (x )＝sin x (x ∈[0，π])和函数g (x )＝12tan x 的图象交于A ，B ，C 三点，则△ABC 的面积为________．7.如图，在圆柱O 1O 2内有一个球O ，该球与圆柱的上、下底面及母线均相切．记圆柱O 1O 2的体积为V 1，球O 的体积为V 2，则V 1V 2的值是________．8.已知函数f (x )＝⎩⎪⎨⎪⎧x 3＋x 2＋m ，0≤x ≤1，mx ＋2，x >1，若函数f (x )有且只有两个零点，则实数m 的取值范围是________．二、解答题：本大题共4小题，共60分．解答时应写出必要的文字说明、证明过程或演算步骤． 9.(本小题满分14分)已知向量a ＝(cos x ，sin x )，b ＝(3，－3)，x ∈[0，π]． (1)若a ∥b ，求x 的值； (2)记f (x )＝a·b ，求f (x )的最大值和最小值以及对应的x 的值．10.(本小题满分14分)在平面直角坐标系xOy 中，圆O ：x 2＋y 2＝4，直线l ：4x ＋3y －20＝0.A (45，35)为圆O 内一点，弦MN 过点A ，过点O作MN 的垂线交l 于点P .(1)若MN ∥l ，求△PMN 的面积；(2)判断直线PM 与圆O 的位置关系，并证明．11.(本小题满分16分)某农场有一块农田，如图，它的边界由圆O 的一段圆弧MPN (P 为此圆弧的中点)和线段MN 构成．已知圆O 的半径为40米，点P 到MN 的距离为50米．现规划在此农田上修建两个温室大棚，大棚Ⅰ内的地块形状为矩形ABCD ，大棚Ⅱ内的地块形状为△CDP ，要求A ，B 均在线段MN 上，C ，D 均在圆弧上．设OC 与MN 所成的角为θ. (1)用θ分别表示矩形ABCD 和△CDP 的面积，并确定sin θ的取值范围；(2)若大棚Ⅰ内种植甲种蔬菜，大棚Ⅱ内种植乙种蔬菜，且甲、乙两种蔬菜的单位面积年产值之比为4∶3.求当θ为何值时，能使甲、乙两种蔬菜的年总产值最大．12.(本小题满分16分)已知数列{a n }的前n 项和S n ＝3n 2＋8n ，{b n }是等差数列，且a n ＝b n ＋b n ＋1. (1)求数列{b n }的通项公式；(2)令c n ＝（a n ＋1）n ＋1（b n ＋2）n，求数列{c n }的前n 项和T n .班级 __________ 姓名 __________ 分数 __________小题强化训练四一、填空题：本大题共8小题，每题5分，共40分．1.已知集合A ＝{x |2≤x <4}，B ＝{x |x >a }，若A ∩B ＝{x |3<x <4}，则实数a ＝________．2.已知f (x )＝ax 5＋bx 3＋sin x －8，且f (－2)＝10，那么f (2)＝________．3.已知sin θ－cos θ＝43，θ∈(3π4，π)，则sin(π－θ)－cos(π－θ)＝________．4.记函数f (x )＝3－2x －x 2的定义域为D .在区间[－4，5]上随机取一个数x ，则x ∈D 的概率是________．5.在三棱锥ABCD 中，E 是AC 的中点，F 在AD 上，且2AF ＝FD .若三棱锥ABEF 的体积为2，则四棱锥BECDF 的体积为________．6.在平面直角坐标系xOy 中，已知圆C ：x 2＋(y －1)2＝4.若等边三角形P AB 的一边AB 为圆C 的一条弦，则PC 的最大值为________．7.设数列{a n }满足a 1＝1，(1－a n ＋1)(1＋a n )＝1(n ∈N *)，则k ＝1100(a k a k ＋1)的值为________．8.已知函数f (x )＝⎩⎪⎨⎪⎧x 2，0＜x ≤1，|ln （x －1）|，x ＞1.若方程f (x )＝kx －2有两个不相等的实数根，则实数k 的取值范围是________．二、解答题：本大题共4小题，共60分．解答时应写出必要的文字说明、证明过程或演算步骤．9.(本小题满分14分)在△ABC 中，a ＝7，b ＝8，cos B ＝－17.(1)求A 的值；(2)求边AC 上的高．10.(本小题满分14分)如图，在四棱锥P ABCD 中，AB ∥CD ，且∠BAP ＝∠CDP ＝90°. (1)求证：平面P AB ⊥平面P AD ；(2)若P A ＝PD ＝AB ＝DC ，∠APD ＝90°，且四棱锥P ABCD 的体积为83，求该四棱锥的侧面积．11.(本小题满分16分)已知函数f (x )＝1x－x ＋a ln x .(1)讨论f (x )的单调性；(2)若f (x )存在两个极值点x 1，x 2，求证：f （x 1）－f （x 2）x 1－x 2<a －2.12.(本小题满分16分)设数列{a n }的前n 项和为S n ，已知a 1＝1，S n ＋1＝2S n ＋n ＋1(n ∈N *)． (1)求数列{a n }的通项公式；(2)若b n ＝na n ＋1－a n，数列{b n }的前n 项和为T n ，n ∈N *，求证：T n <2.班级 __________ 姓名 __________ 分数 __________小题强化训练五一、填空题：本大题共8小题，每题5分，共40分．1.欧拉公式e xi ＝cos x ＋i sin x (i 为虚数单位)是由瑞士著名数学家欧拉发现的，它将指数函数的定义域扩大到复数，建立了三角函数和指数函数的关系，它在复变函数论里占有非常重要的地位，被誉为“数学中的天桥”，根据欧拉公式可知，e －3i 表示的复数在复平面中位于第________象限．2.某校有三个兴趣小组，甲、乙两名学生每人选择其中一个参加，且每人参加每个兴趣小组的可能性相同，则甲、乙不在同一兴趣小组的概率为________．3.在矩形ABCD 中，AB ＝2BC ＝2，现向矩形ABCD 内随机投掷质点P ，则满足P A →·PB →≥0的概率是________． 4.已知向量a ＝(cos θ，sin θ)，向量b ＝(3，－1)，则|2a －b|的最大值与最小值的和为________．(第5题)5.已知函数y ＝A sin(ωx ＋φ)(A ＞0，ω＞0，|φ|＜π)的图象如图所示，则该函数的解析式是______________．6.若抛物线x 2＝4y 的弦AB 过焦点F ，且AB 的长为6，则弦AB 的中点M 的纵坐标为________．7.已知数列{a n }满足a 1＝0，数列{b n }为等差数列，且a n ＋1＝a n ＋b n ，b 15＋b 16＝15，则a 31＝________．8.已知函数f (x )＝x (a －1ex )，曲线y ＝f (x )上存在两个不同的点，使得曲线在这两点处的切线都与y 轴垂直，则实数a的取值范围是__________．二、解答题：本大题共4小题，共60分．解答时应写出必要的文字说明、证明过程或演算步骤． 9.(本小题满分14分)在△ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c .已知b sin A ＝a cos(B －π6)．(1)求角B 的大小；(2)设a ＝2，c ＝3，求b 和sin(2A －B )的值．10.(本小题满分14分)如图，在直三棱柱ABCA 1B 1C 1中，BC ⊥AC ，D ，E 分别是AB ，AC 的中点．求证： (1)B 1C 1∥平面A 1DE ；(2)平面A 1DE ⊥平面ACC 1A 1.11.(本小题满分16分)某群体的人均通勤时间，是指单日内该群体中成员从居住地到工作地的平均用时．某地上班族S 中的成员仅以自驾或公交方式通勤，分析显示：当S 中x %(0<x <100)的成员自驾时，自驾群体的人均通勤时间为f (x )＝⎩⎪⎨⎪⎧30，0<x ≤30，2x ＋1 800x －90，30<x <100(单位：分钟)，而公交群体的人均通勤时间不受x 影响，恒为40分钟．试根据上述分析结果回答下列问题：(1)当x 在什么范围内时，公交群体的人均通勤时间少于自驾群体的人均通勤时间？(2)求该地上班族S 的人均通勤时间g (x )的表达式；讨论g (x )的单调性，并说明其实际意义．12.(本小题满分16分)如图，在平面直角坐标系xOy 中，椭圆E ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)的左、右焦点分别为F 1，F 2，离心率为12，两准线之间的距离为8.点P 在椭圆E 上，且位于第一象限，过点F 1作直线PF 1的垂线l 1，过点F 2作直线PF 2的垂线l 2. (1)求椭圆E 的标准方程；(2)若直线l 1，l 2的交点Q 在椭圆E 上，求点P 的坐标．班级 __________ 姓名 __________ 分数 __________小题强化训练六一、填空题：本大题共8小题，每题5分，共40分． 1.若A ＝{x ||x |＜3}，B ＝{x |2x ＞1}，则A ∩B ＝________．2.电视台组织的中学生知识竞赛，共设有5个版块的试题，主题分别是“立德树人”“社会主义核心价值观”“依法治国理念”“中国优秀传统文化”“创新能力”．某参赛队从中任选2个主题作答，则“立德树人”主题被该队选中的概率是________．3.将函数y ＝3sin(2x －π6)的图象向左平移π4个单位长度，所得图象对应的函数解析式为____________．4.已知实数x ，y 满足⎩⎪⎨⎪⎧x ＋2y －4≤0，x －y －1≤0，x ≥1，则y ＋1x的取值范围是________．(第5题)5.如图，从热气球A 上测得正前方的河流的两岸B ，C 的俯角分别为75°，30°，此时热气球的高度是60m ，则河流的宽度BC ＝________．6.已知函数f (x )是定义在R 上的偶函数，且在区间[0，＋∞)上单调递增．若实数a 满足f (log 2a )＋f (log 12a )≤2f (1)，则a的取值范围是________．7.已知O 为矩形P 1P 2P 3P 4内的一点，满足OP 1＝4，OP 3＝5，P 1P 3＝7，则OP 2→·OP 4→＝________．8.已知函数f (x )＝⎩⎨⎧1－（x －1）2，0≤x <2，f （x －2），x ≥2.若对于正数k n (n ∈N *)，直线y ＝k n x 与函数y ＝f (x )的图象恰有(2n ＋1)个不同的交点，则数列{k 2n }的前n 项和为________．二、解答题：本大题共4小题，共60分．解答时应写出必要的文字说明、证明过程或演算步骤． 9.(本小题满分14分)如图，在平行六面体ABCDA 1B 1C 1D 1中，AA 1＝AB ，AB 1⊥B 1C 1.求证： (1)AB ∥平面A 1B 1C ；(2)平面ABB 1A 1⊥平面A 1BC .10.(本小题满分14分)已知△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，且c tan C ＝3(a cos B ＋b cos A )． (1)求角C ；(2)若c ＝23，求△ABC 面积的最大值．11.(本小题满分16分)某厂花费2万元设计了某款式的服装．根据经验，每生产1百套该款式服装的成本为1万元，每生产x (百套)的销售额(单位：万元)P (x )＝⎩⎪⎨⎪⎧－0.4x 2＋4.2x －0.8，0<x ≤5，14.7－9x －3，x >5.(1)该厂至少生产多少套此款式服装才可以不亏本？(2)试确定该厂生产多少套此款式服装可使利润最大，并求最大利润． (注：利润＝销售额－成本，其中成本＝设计费＋生产成本)12.(本小题满分16分)已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的离心率为32，且过点A (0，1)．(1)求椭圆C 的方程；(2)不经过点A 的直线l 与椭圆C 交于P ，Q 两点，且AP →·AQ →＝0，求证：直线l 过定点．班级 __________ 姓名 __________ 分数 __________小题强化训练七一、填空题：本大题共8小题，每题5分，共40分．1.已知集合A ＝{x |x 2－x －2≤0}，集合B ＝{x |1＜x ≤3}，则A ∪B ＝____________．2.已知复数z ＝(1＋i )(1＋2i )，其中i 是虚数单位，则z 的模是________．3.已知函数f (x )＝⎩⎪⎨⎪⎧x 2－x ，x ≤1，11－x，x ＞1，则f (f (－2))＝________．4.已知e 1，e 2是不共线向量，a ＝m e 1＋2e 2，b ＝n e 1－e 2，且mn ≠0.若a ∥b ，则mn＝________．5.中国古代数学著作《算法统宗》中有这样一个问题：“三百七十八里关，初行健步不为难，次日脚痛减一半，六朝才得到其关，要见次日行里数，请公仔细算相还．”其意思如下：有一个人走378里路，第一天健步行走，从第二天起脚痛，每天走的路程为前一天的一半，走了6天后到达目的地，请问第二天走了________．6.已知sin α＝3sin(α＋π6)，则tan(α＋π12)＝________．7.已知经过点P (1，32)的两个圆C 1，C 2都与直线l 1：y ＝12x ，l 2：y ＝2x 相切，则这两圆的圆心距C 1C 2等于________.8.已知函数f (x )＝log 2(ax 2＋2x ＋3)，若对于任意实数k ，总存在实数x 0，使得f (x 0)＝k 成立，则实数a 的取值范围是________．二、解答题：本大题共4小题，共60分．解答时应写出必要的文字说明、证明过程或演算步骤． 9.(本小题满分14分)在长方体ABCDA 1B 1C 1D 1中，AB ＝BC ＝EC ＝12AA 1.求证：(1)AC 1∥平面BDE ； (2)A 1E ⊥平面BDE .10.(本小题满分14分)已知数列{a n }是公差不为0的等差数列，a 2＝3，且a 3，a 5，a 8成等比数列． (1)求数列{a n }的通项公式；(2)设b n ＝a n cos a n π2，求数列{b n }的前2018项和．11.(本小题满分16分) 为建设美丽乡村，政府欲将一块长12百米，宽5百米的矩形空地ABCD 建成生态休闲园，园区内有一景观湖EFG (图中阴影部分)．以AB 所在直线为x 轴，AB 的垂直平分线为y 轴，建立平面直角坐标系xOy (如图)．景观湖的边界曲线符合函数y ＝x ＋1x (x >0)模型．园区服务中心P 在x 轴正半轴上，PO ＝43百米．(1)若在点O 和景观湖边界曲线上一点M 之间修建一条休闲长廊OM ，求OM 的最短长度； (2)若在线段DE 上设置一园区出口Q ，试确定Q 的位置，使通道PQ 最短．12.(本小题满分16分)如图，在平面直角坐标系xOy 中，已知F 1，F 2分别为椭圆x 2a 2＋y 2b2＝1(a >b >0)的左、右焦点，且椭圆经过点A (2，0)和点(1，3e )，其中e 为椭圆的离心率． (1)求椭圆的方程；(2)过点A 的直线l 交椭圆于另一点B ，点M 在直线l 上，且OM ＝MA .若MF 1⊥BF 2，求直线l 的斜率．班级 __________ 姓名 __________ 分数 __________小题强化训练八一、填空题：本大题共8小题，每题5分，共40分． 1.若向量a ＝(cos10°，sin10°)，b ＝(cos70°，sin70°)，则|a －2b|＝________．2.在同一平面直角坐标系中，函数y ＝sin(x ＋π3)(x ∈[0，2π))的图象和直线y ＝12的交点的个数是________.3.由命题“存在x 0∈R ，使得e |x 0－1|－m ≤0”是假命题，得m 的取值范围是(－∞，a )，则实数a 的值是________．4.已知圆柱M 的底面圆半径为2，高为6，圆锥N 的底面圆直径和母线长相等，若圆柱M 和圆锥N 的体积相同，则圆锥N 的高为________．5.在平面直角坐标系xOy 中，双曲线x 23－y 2＝1的右准线与它的两条渐近线分别交于点P ，Q ，其焦点是F 1，F 2，则四边形F 1PF 2Q 的面积是________．6.设定义在R 上的偶函数f (x )在区间(－∞，0]上单调递减．若f (1－m )＜f (m )，则实数m 的取值范围是________．7.设S n 为数列{a n }的前n 项和，S n ＝kn 2＋n ，n ∈N *，其中k 是常数．若对于任意的m ∈N *，a m ，a 2m ，a 4m 成等比数列，则k 的值为________．8.已知直线y ＝kx ＋2－2k 与曲线y ＝2x －3x －2交于A ，B 两点，平面上的动点P 满足|P A →＋PB →|≤2，则|PO →|的最大值为________.二、解答题：本大题共4小题，共60分．解答时应写出必要的文字说明、证明过程或演算步骤． 9.(本小题满分14分)如图，在正四棱锥VABCD 中，E ，F 分别为棱VA ，VC 的中点．求证： (1)EF ∥平面ABCD ； (2)平面VBD ⊥平面BEF .10.(本小题满分14分) 如图，某公园有三条观光大道AB ，BC ，AC 围成直角三角形，其中直角边BC ＝200m ，斜边AB ＝400m ．现有甲、乙、丙三位小朋友分别在AB ，BC ，AC 大道上嬉戏，所在位置分别记为点D ，E ，F .(1)若甲、乙都以每分钟100m 的速度从点B 出发在各自的大道上奔走，到大道的另一端时即停，乙比甲迟2分钟出发，当乙出发1分钟后，求此时甲、乙两人之间的距离；(2)设∠CEF ＝θ，乙、丙之间的距离是甲、乙之间距离的2倍，且∠DEF ＝π3，请将甲、乙之间的距离ym 表示为θ的函数，并求甲、乙之间的最小距离．11.(本小题满分16分)如图，在平面直角坐标系xOy 中，设P 为圆O ：x 2＋y 2＝2上的动点，过点P 作x 轴的垂线，垂足为Q ，点M 满足PQ→＝2MQ →.(1)求证：当点P 运动时，点M 始终在一个确定的椭圆上； (2)过点T (－2，t )(t ∈R )作圆O 的两条切线，切点分别为A ，B . ①求证：直线AB 过定点(与t 无关)；②设直线AB 与(1)中的椭圆交于C ，D 两点，求证：ABCD≤ 2.12.(本小题满分16分)已知函数f (x )＝⎩⎪⎨⎪⎧x 2＋4x ＋t ，x ＜0，x ＋ln x ，x ＞0，其中t 是实数．设A ，B 为该函数图象上的两点，横坐标分别为x 1，x 2，且x 1<x 2.(1)求f (x )的单调区间和极值；(2)若x 2<0，函数f (x )的图象在点A ，B 处的切线互相垂直，求x 1－x 2的最大值．班级 __________ 姓名 __________ 分数 __________小题强化训练九一、填空题：本大题共8小题，每题5分，共40分．1.已知向量a ＝(－1，2)，b ＝(m ，1)．若向量a ＋b 与a 垂直，则m ＝________．2.如图，正方形ABCD 内的图形来自中国古代的太极图．正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称．在正方形内随机取一点，则此点取自黑色部分的概率是________．3.如图，在△ABC 中，已知AN →＝12AC →，P 是BN 上一点．若AP →＝mAB →＋14AC →，则实数m 的值是________．(第2题)(第3题)(第4题)4.如图，正方体ABCDA 1B 1C 1D 1的棱长为1，E ，F 分别为线段AA 1，B 1C 上的点，则三棱锥D 1DEF 的体积为________．5.已知实数x ，y 满足不等式组⎩⎪⎨⎪⎧2x －y ≥0，x ＋y －4≥0，x ≤3，则2x 3＋y 3x 2y的取值范围是________．6.若x ＝－2是函数f (x )＝(x 2＋ax －1)e x －1的极值点，则f (x )的极小值为________．7.若数列⎩⎨⎧⎭⎬⎫2n （2n －1）（2n ＋1－1）的前k 项的和不小于2 0182 019，则k 的最小值为________．8.在平面直角坐标系xOy 中，A (－12，0)，B (0，6)，点P 在圆O ：x 2＋y 2＝50上．若P A →·PB →≤20，则点P 的横坐标的取值范围是________．二、解答题：本大题共4小题，共60分．解答时应写出必要的文字说明、证明过程或演算步骤． 9.(本小题满分14分)在△ABC 中，a ，b ，c 分别为内角A ，B ，C 的对边，且b sin2C ＝c sin B . (1)求角C ；(2)若sin(B －π3)＝35，求sin A 的值．10.(本小题满分14分)在一张足够大的纸板上截取一个面积为3600平方厘米的矩形纸板ABCD ，然后在矩形纸板的四个角上切去边长相等的小正方形，再把它的边沿虚线折起，做成一个无盖的长方体纸盒(如图)．设小正方形边长为x 厘米，矩形纸板的两边AB ，BC 的长分别为a 厘米和b 厘米，其中a ≥b . (1)当a ＝90时，求纸盒侧面积的最大值；(2)试确定a ，b ，x 的值，使得纸盒的体积最大，并求出最大值．11.(本小题满分16分)已知斜率为k 的直线l 与椭圆C ：x 24＋y 23＝1交于A ，B 两点，线段AB 的中点为M (1，m )(m >0)．(1)求证：k <－12；(2)设F 为C 的右焦点，P 为C 上一点，且FP →＋F A →＋FB →＝0.求证：|F A →|，|FP →|，|FB →|成等差数列，并求该数列的公差．12.(本小题满分16分)设等差数列{a n }是无穷数列，且各项均为互不相同的正整数．(1)设数列{a n }的前n 项和为S n ，b n ＝S na n－1，n ∈N *.①若a 2＝5，S 5＝40，求b 2的值； ②若数列{b n }为等差数列，求b n .(2)求证：数列{a n }中存在三项(按原来的顺序)成等比数列．班级 __________ 姓名 __________ 分数 __________小题强化训练十一、填空题：本大题共8小题，每题5分，共40分．1.若复数(a －i )(1－i )(a ∈R )的实部与虚部相等，则实数a ＝________．2.在三张奖券中有一、二等奖各一张，另一张无奖，甲、乙两人各抽取一张(不放回)，两人都中奖的概率为________．3.执行下面的流程图，输出的T ＝________．4.已知正项等比数列{a n }的前n 项和为S n ，且4a 2＝a 4，则S 4a 2＋a 5＝________．5.已知点P (1，22)在角θ的终边上，则sin(2θ＋π2)＋sin(2θ＋2π)＝________．6.从x 2m －y2n＝1(其中m ，n ∈{－1，2，3})所表示的圆锥曲线(椭圆、双曲线、抛物线)方程中任取一个，则此方程是焦点在x 轴上的双曲线方程的概率为________．7.在平面直角坐标系xOy 中，若直线l ：x ＋2y ＝0与圆C ：(x －a )2＋(y －b )2＝5相切，且圆心C 在直线l 的上方，则ab 的最大值为________．8.设函数f (x )＝⎩⎪⎨⎪⎧x 2＋2，x ≤0，e x －1，x ＞0，若函数y ＝f (x )－2x ＋t 有两个零点，则实数t 的取值范围是______________．二、解答题：本大题共4小题，共60分．解答时应写出必要的文字说明、证明过程或演算步骤． 9.(本小题满分14分)已知α，β为锐角，tan α＝43，cos(α＋β)＝－55.(1)求cos2α的值； (2)求tan(α－β)的值．10.(本小题满分14分)如图，在一条海防警戒线上的点A ，B ，C 处各有一个水声监测点，B ，C 两点到点A 的距离分别为20km 和50km .某时刻，B 收到发自静止目标P 的一个声波信号，8s 后A ，C 同时接收到该声波信号，已知声波在水中的传播速度是1.5km /s .(1)设A 到P 的距离为xkm ，用x 表示B ，C 到P 的距离，并求x 的值； (2)求P 到海防警戒线AC 的距离．11.(本小题满分16分)如图，在平面直角坐标系xOy 中，已知椭圆C ：x 24＋y 23＝1的左、右顶点分别为A ，B ，过右焦点F 的直线l 与椭圆C交于P ，Q 两点(点P 在x 轴上方)． (1)若QF ＝2FP ，求直线l 的方程；(2)设直线AP ，BQ 的斜率分别为k 1，k 2.是否存在常数λ，使得k 1＝λk 2？若存在，求出λ的值；若不存在，请说明理由．12.(本小题满分16分) 已知函数f (x )＝e x －ax 2.(1)若a ＝1，求证：当x ≥0时，f (x )≥1；(2)若f (x )在(0，＋∞)上只有一个零点，求实数a 的值．班级 __________ 姓名 __________ 分数 __________小题强化训练十一一、填空题：本大题共8小题，每题5分，共40分．1.若集合A ＝{x ∈Z |x 2＋x －12＜0}，B ＝{x |x <sin5π}，则A ∩B 中元素的个数为________．2.根据如图所示的伪代码，可知输出的结果S 是________．i ←1Whilei <6 i ←i ＋2 S ←2i ＋3 EndWhile PrintS3.已知首项为负数的等差数列{a n }中，a 5a 4<－1，若S n 取到最小正数，则此时的n ＝________．4.在平面直角坐标系xOy 中，双曲线x 2－y 24＝1的一条渐近线与准线的交点到另一条渐近线的距离为________．5.已知约束条件⎩⎪⎨⎪⎧x ＋y －3≥0，x －2y ＋3≥0，x ≤a表示的可行域为D ，其中a >1，点(x 0，y 0)∈D ，点(m ，n )∈D .若3x 0－y 0与n ＋1m的最小值相等，则实数a ＝________．6.已知双曲线x 2a 2－y 2b 2＝1(a ＞0，b ＞0)的渐近线l 恰好是曲线y ＝x 3－3x 2＋22x 在原点处的切线，左顶点到一条渐近线的距离为263，则双曲线的标准方程为__________．7.将函数y ＝3sin(π4x )的图象向左平移3个单位长度，得函数y ＝3sin(π4x ＋φ)(|φ|<π)的图象(如图)，点M ，N 分别是函数f (x )图象上y 轴两侧相邻的最高点和最低点．设∠MON ＝θ，则tan(φ－θ)的值为________．8.已知函数f (x )＝x 3－2x ＋e x －1ex ，其中e 是自然对数的底数．若f (a －1)＋f (2a 2)≤0，则实数a 的取值范围是________．二、解答题：本大题共4小题，共60分．解答时应写出必要的文字说明、证明过程或演算步骤． 9.(本小题满分14分)在△ABC 中，AB ＝6，AC ＝32，AB →·AC →＝－18. (1)求BC 的长； (2)求tan2B 的值．10.(本小题满分14分)记S n 为等差数列{a n }的前n 项和，已知a 1＝－7，S 3＝－15. (1)求{a n }的通项公式；(2)求S n ，并求S n 的最小值．11.(本小题满分16分)曲线f (x )＝x 2－a 2ln x 在点(12，f (12))处的切线斜率为0.(1)讨论函数f (x )的单调性；(2)若g (x )＝f (x )＋12mx 在区间(1，＋∞)上没有零点，求实数m 的取值范围．12.(本小题满分16分)如图，圆柱体木材的横截面半径为1dm ，从该木材中截取一段圆柱体，再加工制作成直四棱柱A 1B 1C 1D 1ABCD ，该四棱柱的上、下底面均为等腰梯形，分别内接于圆柱的上、下底面，下底面圆的圆心O 在梯形ABCD 内部，AB ∥CD ，∠DAB ＝60°，AA 1＝AD ，设∠DAO ＝θ. (1)求梯形ABCD 的面积；(2)当sin θ取何值时，四棱柱A 1B 1C 1D 1ABCD 的体积最大？并求出最大值．(注：木材的长度足够长)班级 __________ 姓名 __________ 分数 __________小题强化训练十二一、填空题：本大题共8小题，每题5分，共40分．1.已知集合A ＝{x ∈R |log 12(x －2)≥－1}，B ＝⎩⎨⎧⎭⎬⎫x ∈R |2x ＋63－x ≥1，则A ∩B ＝________． 2.设向量a ＝(2，m )，b ＝(1，－1)，若b ⊥(a ＋2b )，则实数m ＝________．3.已知正五边形ABCDE 的边长为23，则AC →·AE →的值为________．4.正方形铁片的边长为8cm ，以它的一个顶点为圆心，一边长为半径画弧，剪下一个顶角为π4的扇形，用这块扇形铁片围成一个圆锥形容器，则这个圆锥形容器的容积等于________cm 3.5.等比数列{a n }的各项均为实数，其前n 项和为S n ，已知S 3＝74，S 6＝634，则a 8＝________．6.已知sin α＝55，α∈(0，π2)，tan β＝13，则tan(α＋2β)＝________．7.已知a >0，函数f (x )＝x (x －a )2和g (x )＝－x 2＋(a －1)x ＋a 存在相同的极值点，则a ＝________.8.设函数f (x )＝⎩⎪⎨⎪⎧x 3－3x ，x <a ，－2x ，x ≥a ，若关于x 的不等式f (x )>4a 在实数集R 上有解，则实数a 的取值范围是____________.二、解答题：本大题共4小题，共60分．解答时应写出必要的文字说明、证明过程或演算步骤． 9.(本小题满分14分)△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知△ABC 的面积为a 23sin A.(1)求sin B sin C 的值；(2)若6cos B cos C ＝1，a ＝3，求△ABC 的周长．10.(本小题满分14分)如图，在四棱锥P ABCD 中，底面ABCD 为梯形，CD ∥AB ，AB ＝2CD,AC 交BD 于点O ，锐角三角形P AD 所在平面P AD ⊥底面ABCD ，P A ⊥BD ，点Q 在侧棱PC 上，且PQ ＝2QC .求证： (1)P A ∥平面QBD ； (2)BD ⊥AD .11.(本小题满分16分)设椭圆x 2a 2＋y 2b 2＝1(a >b >0)的左焦点为F ，上顶点为B .已知椭圆的离心率为53，点A 的坐标为(b ，0)，且FB ·AB ＝6 2.(1)求椭圆的方程；(2)设直线l ：y ＝kx (k >0)与椭圆在第一象限的交点为P ，且l 与直线AB 交于点Q .若AQ PQ ＝524sin ∠AOQ (O 为原点)，求k 的值．12.(本小题满分16分)如图，半圆AOB 是某爱国主义教育基地一景点的平面示意图，半径OA 的长为1百米．为了保护景点，基地管理部门从道路l 上选取一点C ，修建参观线路CDEF ，且CD ，DE ，EF 均与半圆相切，四边形CDEF 是等腰梯形．设DE＝t 百米，记修建每1百米参观线路的费用为f (t )万元，经测算f (t )＝⎩⎨⎧5，0＜t ≤13，8－1t ，13<t <2.(1)用t 表示线段EF 的长；(2)求修建该参观线路的最低费用．班级 __________ 姓名 __________ 分数 __________小题强化训练十三一、填空题：本大题共8小题，每题5分，共40分．(第3题)1.已知复数z ＝2＋i1－i (i 为虚数单位)，那么z 的共轭复数为________．2.若tan(α－π4)＝16，则tan α＝________．3.执行如图所示的程序框图，若a ＝2018，则输出的S ＝________．4.设等边三角形ABC 的边长为1，t 为任意的实数，则|AB →＋tAC →|的最小值为________．5.已知函数f (x )＝2sin x ＋1(x ∈[0，2π])，设h (x )＝|f (x )|－a ，则当1<a <3时，函数h (x )的零点个数为________．6.已知函数f (x )＝(x 2－2x )sin(x －1)＋x ＋1在x ∈[－1，3]上的最大值为M ，最小值为m ，则M ＋m ＝________．7.已知x ＞y ＞0，且x ＋y ≤2，则4x ＋3y ＋1x －y的最小值为________．8.设椭圆C ：x 2a 2＋y 2b2＝1(a >b >0)的左、右焦点分别为F 1，F 2.若椭圆上恰好有6个不同的点P ，使得△F 1F 2P 为等腰三角形，则椭圆C 的离心率的取值范围是______________．二、解答题：本大题共4小题，共60分．解答时应写出必要的文字说明、证明过程或演算步骤． 9.(本小题满分14分)如图，在四棱锥P ABCD 中，底面ABCD 是矩形，PD ⊥平面ABCD ，过AD 的平面分别与PB ，PC 交于点E ，F .求证： (1)平面PBC ⊥平面PCD ； (2)AD ∥EF .10.(本小题满分14分)已知椭圆C ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)的离心率为32，且点(－3，12)在椭圆C 上．(1)求椭圆C 的标准方程；(2)若直线l 交椭圆C 于P ，Q 两点，线段PQ 的中点为H ，O 为坐标原点，且OH ＝1，求△POQ 面积的最大值．11.(本小题满分16分)如图，圆O 是一块半径为1米的圆形钢板，为生产某部件需要，需从中截取一块多边形ABCDFGE .其中AD 为圆O的直径，点B ，C ，G 在圆O 上，BC ∥AD ，点E ，F 在AD 上，且OE ＝OF ＝12BC ，EG ＝FG .(1)设∠AOB ＝θ，试将多边形ABCDFGE 面积S 表示成θ的函数关系式； (2)求多边形ABCDFGE 面积S 的最大值．12.(本小题满分16分)已知数列{a n }与{b n }的前n 项和分别为A n 和B n ，且对任意n ∈N *，a n ＋1－a n ＝2(b n ＋1－b n )恒成立． (1)若A n ＝n 2，b 1＝2，求B n ；(2)若对任意n ∈N *，都有a n ＝B n 及b 2a 1a 2＋b 3a 2a 3＋b 4a 3a 4＋…＋b n ＋1a n a n ＋1<13恒成立，求正实数b 1的取值范围；(3)若a 1＝2，b n ＝2n ，是否存在两个互不相等的整数s ，t (1<s <t )，使A 1B 1，A s B s ，A tB t成等差数列？若存在，求出s ，t 的值；若不存在，请说明理由．班级 __________ 姓名 __________ 分数 __________小题强化训练十四一、填空题：本大题共8小题，每题5分，共40分．1.设全集U ＝{x |x ≥2，x ∈N }，集合A ＝{x |x 2≥5，x ∈N }，则∁U A ＝________．2.如图所示的茎叶图记录了甲、乙两组各八名学生在一次数学测试中的成绩(单位：分)，规定85分以上(含85分)为优秀，现分别从甲、乙两组中随机选取一名同学的数学成绩，则两人成绩都为优秀的概率是________．错误!(第2题) (第3题) (第5题)3.如图，在一个面积为8的矩形中随机撒一粒黄豆，若黄豆落到阴影部分的概率为14，则阴影部分的面积为________．4.我国古代数学名著《算法统宗》中有如下问题：“远望巍巍塔七层，红光点点倍加增，共灯三百八十一，请问尖头几盏灯？”意思是：一座7层塔共挂了381盏灯，且相邻两层中的下一层灯数是上一层灯数的2倍，则塔的顶层共有灯________盏．5.如图，在四棱锥P ABCD 中，P A ⊥平面ABCD ，底面ABCD 是菱形．若AB ＝2，∠BAD ＝60°，则当四棱锥P ABCD 的体积等于23时，PC ＝________．6.已知双曲线x 2a 2－y 2b2＝1(a ＞0，b ＞0)的左、右端点分别为A ，B ，点C (0，2b )．若线段AC 的垂直平分线过点B ，则双曲线的离心率为________．7.在平行四边形ABCD 中，AB ＝2，AD ＝1，AB →·AD →＝－1，点M 在边CD 上，则MA →·MB →的最大值为________．8.已知函数f (x )＝x (e x －e －x )－(2x －1)(e 2x －1－e 1－2x )，则满足f (x )>0的实数x 的取值范围是________．二、解答题：本大题共4小题，共60分．解答时应写出必要的文字说明、证明过程或演算步骤． 9.(本小题满分14分)已知角α的顶点与原点O 重合，始边与x 轴的非负半轴重合，它的终边过点P (－35，－45)．(1)求sin(α＋π)的值；(2)若角β满足sin(α＋β)＝513，求cos β的值．。

2020年高考数学(理)复习【直线与平面的平行与垂直】小题精练卷附答案解析

2020年高考数学（理）复习【直线与平面的平行与垂直】小题精练卷刷题增分练○28一、选择题1．[2019·湖北省重点中学模拟]设m，n是两条不同的直线，α，β是两个不同的平面，下列命题中正确的是()A．若α⊥β，m⊂α，n⊂β，则m⊥n B．若α∥β，m⊂α，n⊂β，则m∥nC．若m⊥n，m⊂α，n⊂β，则α⊥βD．若m⊥α，m∥n，n∥β，则α⊥β答案：D解析：选项A，若α⊥β，m⊂α，n⊂β，则可能m⊥n，m∥n，或m，n异面，故A错误；选项B，若α∥β，m⊂α，n⊂β，则m∥n，或m，n异面，故B错误；选项C，若m⊥n，m⊂α，n⊂β，则α与β可能相交，平行，或垂直，故C错误；选项D，若m⊥α，m∥n，则n⊥α，再由n∥β可得α⊥β，因此D 正确．故选D.2．有下列命题：①若直线l平行于平面α内的无数条直线，则l∥α；②若直线a在平面α外，则a∥α；③若直线a∥b，b∥α，则a∥α；④若直线a∥b，b∥α，则a平行于平面α内的无数条直线．其中真命题的个数是()A．1B．2C．3D．4答案：A解析：命题①，l可以在平面α内，不正确；命题②，直线a与平面α可以是相交关系，不正确；命题③，a可以在平面α内，不正确；命题④正确．3．[2019·泉州质检]已知直线a，b，平面α，β，a⊂α，b⊂α，则“a∥β，b∥β”是“α∥β”的() A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件答案：B解析：因为直线a，b不一定相交，所以a∥β，b∥β不一定能够得到α∥β；而当α∥β时，a∥β，b∥β一定成立，所以“a∥β，b∥β”是“α∥β”的必要不充分条件．4．已知E，F分别是正方体ABCD－A1B1C1D1的棱AB，AA1的中点，M，N分别是线段D1E与C1F 上的点，则与平面ABCD垂直的直线MN有()A．0条B．1条C．2条D．无数条答案：B解析：连接AC，A1C1，设D1E与平面AA1C1C相交于点M，在平面AA1C1C内过点M作MN∥AA1交C1F于点N，由C1F与D1E为异面直线知MN唯一，且MN⊥平面ABCD，故选B.5．PA垂直于以AB为直径的圆所在的平面，C为圆上异于A，B两点的任一点，则下列关系不正确的是()A．PA⊥BC B．BC⊥平面PAC C．AC⊥PB D．PC⊥BC答案：C解析：由PA⊥平面ABC⇒PA⊥BC，A正确；由BC⊥PA，BC⊥AC，PA∩AC＝A，可得BC⊥平面PAC，BC⊥PC，即B，D正确．6．过三棱柱ABC－A1B1C1的任意两条棱的中点作直线，其中与平面ABB1A1平行的直线共有() A．2条B．4条C．6条D．8条答案：C解析：如图，过三棱柱ABC－A1B1C1的任意两条棱的中点作直线，其中与平面ABB1A1平行的直线只可能落在平面DEFG内(其中D，E，F，G分别为三棱柱棱的中点)，易知经过D，E，F，G中任意两点的直线共有C24＝6条，故选C.7．如图，P为平行四边形ABCD所在平面外一点，E为AD的中点，F为PC上一点，当PA∥平面EBF时，PFFC＝()A.23 B.14 C.13 D.12答案：D解析：连接AC 交BE 于点G ，连接FG ，因为PA ∥平面EBF ，PA ⊂平面PAC ，平面PAC ∩平面EBF＝FG ，所以PA ∥FG ，所以PF FC ＝AG GC .因为AD ∥BC ，AD ＝BC ，E 为AD 的中点，所以AG GC ＝AE BC ＝12，所以PF FC ＝12.8．[2019·四川资阳模拟]在三棱锥P －ABC 中，PA ⊥底面ABC ，∠BAC ＝120°，AB ＝AC ＝1，PA ＝2，则直线PA 与平面PBC 所成角的正弦值为()A.255 B.223 C.55 D.13答案：D解析：如图，∵PA ⊥底面ABC ，∴∠PAB ＝∠PAC ＝90°.又AB ＝AC ＝1，PA ＝2，∴△PAB ≌△PAC (SAS)，∴PB ＝PC .取BC 中点D ，连接AD ，PD ，∴PD ⊥BC ，AD ⊥BC ，∴BC ⊥平面PAD .∴平面PAD ⊥平面PBC .过点A 作AO ⊥PD 于点O ，可得AO ⊥平面PBC ，∴∠APD 就是直线PA 与平面PBC 所成的角．在Rt △PAD 中，AD ＝AB sin30°＝12，PA ＝2，PD ＝PA 2＋AD 2＝32，sin ∠APD ＝AD PD ＝13.故选D.二、非选择题9．[2019·杭州模拟]如图，在正方体ABCD －A 1B 1C 1D 1中，AB ＝2，E 为AD 的中点，点F 在CD 上，若EF ∥平面AB 1C ，则EF ＝________.答案：2解析：根据题意，因为EF∥平面AB1C，所以EF∥AC.又E是AD的中点，所以F是CD的中点．因为在Rt△DEF中，DE＝DF＝1，故EF＝ 2.10．已知α，β表示两个不同的平面，m，n表示两条不同的直线，且m⊥β，α⊥β，给出下列四个结论：①∀n⊂α，n⊥β；②∀n⊂β，m⊥n；③∃n⊂α，m⊥n.则上述结论正确的为________．(写出所有正确结论的序号)答案：②③解析：由于m⊥β，α⊥β，所以m⊂α或m∥α.∀n⊂α，则n⊂β或n∥β或n与β相交，所以①不正确；∀n⊂β，则由直线与平面垂直的性质定理，知m⊥n，②正确；当m⊂α或m∥α时，∃n⊂α，m⊥n，③正确．11．[2019·青岛模拟]如图所示，在四棱锥P－ABCD中，PA⊥底面ABCD，且底面各边都相等，M 是PC上一动点，当点M满足________时，平面MBD⊥平面PCD.(只要填写一个你认为正确的条件即可)答案：DM⊥PC(或BM⊥PC等)(不唯一)解析：如图，连接AC，∵四边形ABCD的各边都相等，∴四边形ABCD为菱形，∴AC⊥BD，又PA⊥平面ABCD，∴PA⊥BD，又AC∩PA＝A，∴BD⊥平面PAC，∴BD⊥PC.∴当DM⊥PC(或BM⊥PC 等)时，有PC⊥平面MBD，而PC⊂平面PCD，∴平面MBD⊥平面PCD.12．[2019·河北定州中学模拟]如图，在正方形ABCD中，E，F分别是BC，CD的中点，G是EF的中点．现在沿AE，AF及EF把这个正方形折成一个空间图形，使B，C，D三点重合，重合后的点记为H.下列说法错误的是________(将符合题意的选项序号填到横线上)．①AG⊥△EFH的在平面；②AH⊥△EFH所在平面；③HF⊥△AEF所在平面；④HG⊥△AEF所在平面．答案：①③④解析：根据条件AH⊥HE，AH⊥HF，所以AH⊥平面EFH，故AG不可能垂直平面EFH，所以①错误；②正确；③若HF⊥△AEF所在平面，则HF⊥AF，显然一个三角形中不能有两个直角，错误；④若HG⊥△AEF所在平面，则△AHG中有两个直角，错误，故填①③④.刷题课时增分练○28一、选择题1．[2019·重庆六校联考]设a，b是两条不同的直线，α，β是两个不同的平面，则α∥β的一个充分条件是()A．存在一条直线a，a∥α，a∥βB．存在一条直线a，a⊂α，a∥βC．存在两条平行直线a，b，a⊂α，b⊂β，a∥β，b∥αD．存在两条异面直线a，b，a⊂α，b⊂β，a∥β，b∥α答案：D解析：对于选项A，若存在一条直线a，a∥α，a∥β，则α∥β或α与β相交，若α∥β，则存在一条直线a，使得a∥α，a∥β，所以选项A的内容是α∥β的一个必要条件；同理，选项B，C的内容也是α∥β的一个必要条件而不是充分条件；对于选项D，可以通过平移把两条异面直线平移到一个平面中，成为相交直线，则有α∥β，所以选项D的内容是α∥β的一个充分条件．故选D.2．[2019·河北武邑月考]如图，在四棱锥P－ABCD中，△PAB与△PBC是正三角形，平面PAB⊥平面PBC，AC⊥BD，则下列结论不一定成立的是()A．PB⊥AC B．PD⊥平面ABCDC．AC⊥PD D．平面PBD⊥平面ABCD答案：B解析：如图，对于选项A，取PB的中点O，连接AO，CO.∵在四棱锥P－ABCD中，△PAB与△PBC是正三角形，∴AO⊥PB，CO⊥PB.∵AO∩CO＝O，∴PB⊥平面AOC.∵AC⊂平面AOC，∴PB⊥AC，故A成立．对于选项B，∵AC⊥BD，AC⊥PB，BD∩PB＝B，∴AC⊥平面PBD.设AC∩BD＝M，连接PM，则PM⊥AC，∴PD与AC不垂直．对于选项C，∵PB⊥平面AOC，AC⊂平面AOC，∴AC⊥PB.∵AC⊥BD，PB∩BD＝B，∴AC⊥平面PBD，∵PD⊂平面PBD，∴AC⊥PD，故C成立．对于选项D，∵AC⊥平面PBD，AC⊂平面ABCD，∴平面PBD⊥平面ABCD，故D成立，故选B.3．[2019·长沙模拟]如图所示，在直角梯形BCEF中，∠CBF＝∠BCE＝90°，A、D分别是BF、CE 上的点，AD∥BC，且AB＝DE＝2BC＝2AF(如图1)．将四边形ADEF沿AD折起，连接AC、CF、BE、BF、CE(如图2)，在折起的过程中，下列说法错误的是()A．AC∥平面BEFB．B、C、E、F四点不可能共面C．若EF⊥CF，则平面ADEF⊥平面ABCDD．平面BCE与平面BEF可能垂直答案：D解析：A选项，连接BD，交AC于点O，取BE的中点M，连接OM，FM，易证四边形AOMF是平行四边形，所以AO∥FM，因为FM⊂平面BEF，AC⊄平面BEF，所以AC∥平面BEF；B选项，若B、C、E、F四点共面，因为BC∥AD，所以BC∥平面ADEF，可推出BC∥EF，又BC∥AD，所以AD∥EF，矛盾；C选项，连接FD，在平面ADEF内，易得EF⊥FD，又EF⊥CF，FD∩CF＝F，所以EF⊥平面CDF，所以EF⊥CD，又CD⊥AD，EF与AD相交，所以CD⊥平面ADEF，所以平面ADEF⊥平面ABCD；D选项，延长AF至G，使AF＝FG，连接BG、EG，易得平面BCE⊥平面ABF，过F作FN⊥BG于N，则FN⊥平面BCE，若平面BCE⊥平面BEF，则过F作直线与平面BCE垂直，其垂足在BE上，矛盾．综上，选D.4．[2019·湖北八校联考]如图所示，在四边形ABCD中，AD∥BC，AD＝AB，∠BCD＝45°，∠BAD ＝90°，将△ABD沿BD折起，使得平面ABD⊥平面BCD，构成四面体A－BCD，则在四面体A－BCD 中，下列说法正确的是()A．平面ABD⊥平面ABC B．平面ACD⊥平面BCDC．平面ABC⊥平面BCD D．平面ACD⊥平面ABD答案：D解析：由题意可知，AD⊥AB，AD＝AB，所以∠ABD＝45°，故∠DBC＝45°，又∠BCD＝45°，所以BD⊥DC.因为平面ABD⊥平面BCD，且平面ABD∩平面BCD＝BD，所以CD⊥平面ABD，所以平面ACD⊥平面ABD.5．[2019·荆州模拟]如图，在三棱柱ABC－A′B′C′中，点E，F，H，K分别为AC′，CB′，A′B′，B′C′的中点，G为△ABC的重心．从K，H，G，B′中取一点作为P，使得该棱柱恰有2条棱与平面PEF平行，则P为()A．K B．H C．G D．B′答案：C解析：取A′C′的中点M，连接EM，MK，KF，EF，则EM綊12CC′綊KF，得四边形EFKM为平行四边形，若P＝K，则AA′∥BB′∥CC′∥KF，故与平面PEF平行的棱超过2条；HB′∥MK⇒HB′∥EF，若P＝H或P＝B′，则平面PEF与平面EFB′A′为同一平面，与平面EFB′A′平行的棱只有AB，不满足条件；连接BC′，则EF∥A′B′∥AB，若P＝G，则AB，A′B′与平面PEF平行．故选C.6．如图，在三棱锥P－ABC中，已知PA⊥底面ABC，AB⊥BC，E，F分别是线段PB，PC上的动点，则下列说法错误的是()A．当AE⊥PB时，△AEF一定是直角三角形B．当AF⊥PC时，△AEF一定是直角三角形C．当EF∥平面ABC时，△AEF一定是直角三角形D．当PC⊥平面AEF时，△AEF一定是直角三角形答案：B解析：由PA ⊥底面ABC ，得PA ⊥BC ，又AB ⊥BC ，所以BC ⊥平面PAB ，BC ⊥AE .又AE ⊥PB ，所以AE ⊥平面PBC ，所以AE ⊥EF ，故A 正确；当EF ∥平面ABC 时，因为EF ⊂平面PBC ，平面PBC ∩平面ABC ＝BC ，所以EF ∥BC ，故EF ⊥平面PAB ，AE ⊥EF ，故C 正确；当PC ⊥平面AEF 时，PC ⊥AE ，又BC ⊥AE ，所以AE ⊥平面PBC ，所以AE ⊥EF ，故D 正确．故选B.7．[2019·广西南宁模拟]已知三棱锥P －ABC 的四个顶点都在球O 的球面上，PA ⊥平面ABC ，△ABC是边长为2的等边三角形，若球O 的体积为823π，则直线PC 与平面PAB 所成角的正切值为()A.31111 B.21111C.31010 D.1010答案：A解析：如图，设△ABC 的中心为E ，M 为AB 的中点，过球心O 作OD ⊥PA ，则D 为PA 的中点．由题意可得CM ⊥平面PAB ，∴∠CPM 是直线PC 与平面PAB 所成的角．∵△ABC 是边长为2的等边三角形，∴OD ＝AE ＝23CM ＝233.∵43π·OP 3＝82π3，∴OP ＝2，∴PA ＝2PD ＝2OP 2－OD 2＝263.∴PM ＝PA 2＋AM 2＝333.∴tan ∠CPM ＝CM PM ＝31111.故选A.8.如图，在以角C 为直角顶点的三角形ABC 中，AC ＝8，BC ＝6，PA ⊥平面ABC ，F 为PB 上的点，在线段AB 上有一点E ，满足BE ＝λAE .若PB ⊥平面CEF ，则实数λ的值为()A.316 B.516 C.916 D.3答案：C解析：∵PB ⊥平面CEF ，CE ⊂平面CEF ，∴PB ⊥CE ，又PA ⊥平面ABC ，CE ⊂平面ABC ，∴PA ⊥CE ，而PA ∩PB ＝P ，∴CE ⊥平面PAB ，∴CE ⊥AB ，∴λ＝EB AE ＝EB ·AB AE ·AB ＝BC 2AC 2＝916.二、非选择题9.如图所示，正方体ABCD －A 1B 1C 1D 1的棱长为a ，M ，N 分别为A 1B 和AC 上的点，且A 1M ＝AN ＝23a ，则MN 与平面BB 1C 1C 的位置关系是________．答案：MN ∥平面BB 1C 1C 解析：如图，连接AM 并延长，交BB 1的延长线于点P ，连接CP ，则由已知可得AA 1∥BB 1，所以A 1M MB＝AM MP ＝12，又AN NC ＝12，所以AM MP ＝AN NC ＝12，所以MN ∥PC ，故有MN ∥平面BB 1C 1C .10．[2019·黄冈质检]如图，PA ⊥圆O 所在的平面，AB 是圆O 的直径，C 是圆O 上一点，E ，F 分别是点A 在PB ，PC 上的射影，给出下列结论：①AF⊥PB；②EF⊥PB；③AF⊥BC；④AE⊥平面PBC.其中正确结论的序号是________．答案：①②③解析：①由于PA⊥平面ABC，因此PA⊥BC，又AC⊥BC，因此BC⊥平面PAC，所以BC⊥AF，由于PC⊥AF，因此AF⊥平面PBC，所以AF⊥PB；②因为AE⊥PB，AF⊥PB，所以PB⊥平面AEF，因此EF⊥PB；③在①中已证明AF⊥BC；④若AE⊥平面PBC，由①知AF⊥平面PBC，由此可得出AF∥AE，这与AF，AE有公共点A矛盾，故AE⊥平面PBC不成立．故正确的结论为①②③.11．如图，在直三棱柱ABC－A1B1C1中，D，E分别为AB，BC的中点，点F在侧棱B1B上，且B1D⊥A1F，A1C1⊥A1B1.求证：(1)直线DE∥平面A1C1F；(2)平面B1DE⊥平面A1C1F.证明：(1)在直三棱柱ABC－A1B1C1中，A1C1∥AC.在△ABC中，因为D，E分别为AB，BC的中点，所以DE∥AC，于是DE∥A1C1.又DE⊄平面A1C1F，A1C1⊂平面A1C1F，所以直线DE∥平面A1C1F.(2)在直三棱柱ABC－A1B1C1中，A1A⊥平面A1B1C1.因为A1C1⊂平面A1B1C1，所以A1A⊥A1C1.又A1C1⊥A1B1，A1A⊂平面ABB1A1，A1B1⊂平面ABB1A1，A1A∩A1B1＝A1，所以A1C1⊥平面ABB1A1.因为B1D⊂平面ABB1A1，所以A1C1⊥B1D.又B1D⊥A1F，A1C1⊂平面A1C1F，A1F⊂平面A1C1F，A1C1∩A1F＝A1，所以B1D⊥平面A1C1F.因为直线B1D⊂平面B1DE，所以平面B1DE⊥平面A1C1F.。

2020年新高考数学小题分类练(三)推理论证类

小题分类练（三）推理论证类一、选择题 1.（2019福州模拟）已知x € R ，则“ x< - 1”是x 2>1 ”的（）A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件0 42.（2019重庆市七校联合考试）设a = 5 . , b = log o.40.5, c = log 50.4，贝U a , b , c 的大小关系是（）A . a<b<cB . c<b<aC . c<a<bD . b<c<a3.已知在四边形 ABCD 中，AB + CD = 0, （A B - AD ） A C = 0,则四边形 ABCD 是（）B .正方形C .菱形4 .若0 v b v a v 1,则下列结论不成立的是（）D . log b a > log a b< r 2”，若p 是q 的必要不充分条件，则实数 r 的取值范围是（B . (0, 1] D . [2 ,+^ )A •矩形D •梯形b 是两条异面直线，直线c 与a , b 都垂直,则下列说法正确的是( )A .若c?平面a,贝9 a 丄aB .若c 丄平面 a,贝 9 a // a, b II aC .存在平面 a ,使得 c 丄 a , a? a , b I aD .存在平面 a ,,使得c I a, a 丄a, b 丄ax , y € R , p : “|x|+ 霽 1 ”，q :“ x 2+ y 25. （2019成都市第二次诊断性检测）已知a ,6. （2019C.A. 0,7.某校有A, B, C, D四件作品参加航模类作品比赛.已知这四件作品中恰有两件获奖，在结果揭晓前，甲、乙、丙、丁四位同学对这四件参赛作品的获奖情况预测如下.甲说：“ A, B同时获奖.”乙说：“ B, D不可能同时获奖.”丙说：“ C获奖.”丁说：“ A , C 至少一件获奖.”如果以上四位同学中有且只有两位同学的预测是正确的，则获奖的作品是A .作品A 与作品Bn D . 2 a + 3=10.已知函数f(x)是定义在区间(0,+^ )上的可导函数，满足f(x)>0且f(x) + f'(x)<0(f'(x)为函数f(x)的导函数)，若0<a<1<b 且ab = 1，则下列不等式一定成立的是( )A . f(a)>(a + 1)f(b) C . af(a)>bf(b)11.(多选)对于实数a , b , c ,下列命题是真命题的是a >b ，贝U acv bcac 2> bc 2，贝U a > b a v b v 0，贝U a 2> ab >b 2 c > a > b > 0,则 ~^>c — a c — b12. 侈选)在厶ABC 中，a , b , c 分别是角A , B , C 的对边，以下四个结论中，正确的若 a >b >c ,贝U sin A >sin B >sin C若 A > B >C ,贝V sin A >sin B >sin C acos B + bcos A = c 若a 2 + b 2>氏则厶ABC 是锐角三角形13.(多选)如图所示，P 为矩形ABCD 所在平面外一点，矩形对角线交点为 0, M 为PB的中点，下列结论正确是()B .作品B 与作品C .作品C 与作品D2 28.设双曲线x 2 — y 2 =a b D .作品A 与作品1(a > 0, b >0)的离心率 e =・.2，右焦点 F(c , 0). 方程 2ax — bx — c=0的两个实数根分别为X 1, X 2,则点P (X 1, X 2)与圆x 2 + y 2= 8的位置关系为A .点P 在圆外B .点P 在圆上C .点P 在圆内D .不确定9. 设 a€ 0,—,B € p , -2，，且 cos 3 = tan a (1 + sin 3 )，则(n2 a — 3=af(b)>bf( a)A . PD // 平面 AMCB . OM // 平面 PCDC . OM // 平面 PDAD . OM // 平面 PBA二、填空题214. ______ 已知点P(1, m)在椭圆X + y 2=1的外部，则直线y = 2mx + . 3与圆x 2 + y 2= 1的位置关系为 ________ .15. 对于使f(x )w M 成立的所有常数 M 中，我们把 M 的最小值叫做f(x)的上确界.若正 1 2数a , b € R 且a + b = 1,则一——2的上确界为2a b16. 有一支队伍长 L 米，以一定的速度匀速前进•排尾的传令兵因传达命令赶赴排头，到达排头后立即返回，且往返速度不变.如果传令兵回到排尾后，整个队伍正好前进了 L 米，则传令兵所走的路程为 _________ .17.对于三次函数f(x)= ax 3 + bx 2 + cx + d(a ^ 0),给出定义：设f'(x )是y = f(x )的导数，f " (x)是y = f'(x)的导数，若f"(x)= 0有实数解x o ,则称x 0是函数y = f(x)的拐点•经过研究发现，任何一个三次函数都有“拐点”，且该“拐点”也为该函数的对称中心•若f(x) = x 3 — |x 2+1小题分类练(三)推理论证类1 .解析：选A.解不等式x 2>1，可得x< — 1或x>1，所以x< — 1是x 2>1的充分不必要条件，故选A.2. 解析：选 B.因为 0 = log o.41<log o.40.5<log 0.40.4= 1,所以 0<b<1, a = 5°.4>5°= 1, c = Iog 50.4<log 51= 0,所以 c<b<a.故选 B.3. 解析：选C.因为AB + CD = 0, 所以AB = — CD = DC ，所以四边形 ABCD 是平行四边形.又(AB — AD) AC = DB AC = 0,所以四边形的对角线互相垂直，所以四边形 ABCD 是菱形.4.解析：选D.对于A ，函数y =1在(0,+^ )上单调递减，所以当 0v b v a v 1时，1 vxaX ,贝y f"(x) =；f 2^ +f 金 +f 金 +…+f f0i =7.解析：选D.若甲预测正确，则乙预测正确，丙预测错误，丁预测正确，与题意不符, 故甲预测错误；若乙预测错误，则依题意丙、丁均预测正确，但若丙、丁预测正确，则获奖作品可能是“ A , C ” “ B , C ” “C , D ”，这几种情况都与乙预测错误相矛盾，故乙预测正确,所以丙、丁中恰有一人预测正确•若丙预测正确，丁预测错误，两者互相矛盾，排除；若丙预测错误，丁预测正确，则获奖作品只能是“ A , D ”，经验证符合题意•故选 D. =2,所以己j =1,&解析：选C.因为e 2= 1 +所以 a=j 所所以方程ax 2 — bx — c = 0可化为x 2— x — 2= 0, 所以 x 1 + X 2= 1, X 1 • X 2=— . 2.所以 x 1 + x 2 =(X 1 + X 2) 2一 2x 1x 2= 1 + 2马 2 v 8,所以点P 在圆内，故选 C.9.解析：选D.由cossin a3 = tan a (1 + sin 3 )，可得 cos 3 =(1 + sin 3 ), cos 3cos a7tcos a 一 sin a sin3 = sin a = cos 2 — a ，即 cos( a+ 3 = 7t0,亍，则 a+n 1 3€ (0, n ), ~― a€ 0, n 丨 n n丁！故 a+ 3= "2 — a,即 2a+ 3=三.故选 D.10.解析:C.构造函数 F(x) = e x f(x), 则 F'(x)= e x (f(x) + f (x))<0，即 F(x)单调递减,所以 F(a)>F(b)，即 e a f(a)>e b f(b)，即 >e b —a = e a - a .选项可变形为: A.S >a + 1 , f (b ) ，1-恒成立；对于B ，函数y = x 在(0,+^ )上单调递增，所以当0v b v a v 1时，.a >. b 恒成立；对于C ,函数y = a x (o v a v 1)单调递减，函数 y = x a (0v a v 1)单调递增，所以当 0v b v a1 1 1v 1 时，a b > a a > b a 恒成立；当 a =㊁，b = 4时，log a b = 2, log b a = 2， log a b > log b a , D 选项不成立，故选D.5.解析：选C.对于A ，直线a 可以在平面a 内，也可以与平面 a 相交；对于B ,直线a 可以在平面 a 内，或者b 在平面a 内；对于D ，如果a 丄a, b 丄a ，则有a // b ，与条件中两直线异面矛盾. 6.解析：选A.由题意，命题p 对应的是菱形及其内部，当x>0 , y>0时，可得菱形的一边所在的直线方程为 x + y = 1，即2x + y — 2= 0,由p 是q 的必要不充分条件，可得圆 x 2+ y 2=r 2的圆心到直线2x + y — 2 = 0的距离d=—=红5> r ，又r>0，所以实数r 的取值范围+ 1 5故选A. 是0,一 a ，又 a€ 0, ~ , 311 1 1对于选项 C ,以下证明-2<e- — a ,即证-一a + 2ln a>0(a € (0, 1))成立，令h(a)= — a + a aa a1 2(a — 1) 2 、、2ln a(0<a < 1)，贝U h'(a)=—亍一1+ =—2----- < 0，所以 h(a)在(0, 1］上单调递减，所以 a aa1h(a)> h(1) = 0，所以当0<a<1时，—a + 2ln a>0成立，则选项 C 正确•若选项 B 成立，则 am a ，即 a -a +ln(1 - a)<0(a € (0，1))成立，取a =e 则e -1+ln 1—； ln(e — 1) — 1>0 ,矛盾，则选项 B 不正确；同理选项 D 不正确.故选 C.11.解析：选BCD.当c = 0时，ac = bc ,故A 错误；当ac 2>bc 2，贝U C M 0, c 2>0,故a >b ,故B 为真命题；若 a v b v 0,贝U a 2>ab 且 ab > b 2, 即卩 a 2>ab > b 2,故 C 为真命题; 若c >a > b > o ,则芋$，则0v宁v宇，则兰〉土，故 D 为真命题.a b c 12.解析：选ABC.对于A ，由于a > b >c ,由正弦定理，而=孑丽=2R ， sin A > sin B > sin C ,故 A 正确;对于B , A > B >C ，由大边对大角定理可知，则a >b > c ，由正弦定理sin A sin B sin C =2R,可得 sin A > sin B >sin C ,故 B 正确;对于 C ,根据正弦定理可得 acos B + bcos A = 2R(sin Acos B + sin Bcos A) = 2Rsin(B + A)=2Rsin( n — C)= 2Rsin C = c ,故 C 正确; 且仅当b = 2a 时取等号，因此— 丄—-的上确界为—-.2a b 29答案：一9B.f (a )f (a) b 1 n 丁孑，D.f (b )f (b ) <匕，C.f (b ) a af (a )<a 2. 必有可得对于D , a 2+ b 2>c 2,由余弦定理可得cos C =孑+£—J >0,2ab由C € (0, n )，可得C 是锐角，故A 或B 可能为钝角，故 D 错误.13.解析：选ABC.矩形ABCD 的对角线 AC 与BD 交于点O , △ PBD 中，M 是PB 的中点，所以 OM 是厶PBD 的中位线，OM //所以O 为BD 的中点.在PD ，贝U PD // 平面 AMC ,OM //平面 PCD ，且OM //平面 PDA.因为 M € PB ,所以OM 与平面 PBA 相交.2314.解析：由点P(1, m)在椭圆4 + y 2= 1的外部，得m 2>4,则圆x 2+ y 2 = 1的圆心(0,0)到直线y — 2mx — .3 = 0的距离d = —引c v 二32v 1，所以直线y = 2mx +・3与圆x 2+ y 2= 1相交.答案：相交1 215.解析：—亦— 9当2，当16. 解析：设传令兵的速度为v',队伍行进速度为v,则传令兵从排尾到排头的时间为—，从排头到排尾的时间为—，则易得丄 + 丄 =L，化简得v2—v2= 2vv，得v =v v v '+ v v v v '+ v v v -.2+ 1,由于队伍与传令兵行进时间相等，故传令兵所走路程为(1 + 一2)L.答案：(1 + 2)L3 3 2 1 2 117. 解析：由f(x)= x3—^x2+ *,得f'(x)= 3x2—3x+ 2，所以f"(x) = 6x—3;由6x— 3 = 0得x= 1,所以f * = 0,所以f(x)的对称中心为1, 0 ,所以f(1—x) + f(x)=0所以f i丄\f i丄\f i丄L...+ f i込Lo0，所以f\2 018 / T\2 018 +也018 / + A2 018/ 0.答案：6x— 3 0。

高考数学第三轮专题复习必考小题专讲专练(3)-命题及充要条件(5年真题)

第- 1 -页高考数学必考小题讲练之专题（3）-《命题与充要条件》【考点综述】充要条件部分是高考必考小题，属容易题。

涉及到与不等式、函数性质、三角函数、平面向量、数列、复数、空间点线面位置关系、圆锥曲线等知识内容关联。

而命题部分内容新高考删除对四种命题间的相互转化和真假判断、复合命题改写。

但还保留含全称量词和特称量词的命题及其真假判断、否定。

【例析考点】题型一：充要条件与空间点线面的位置关系例1.（2019全国Ⅱ理7）设α，β为两个平面，则α∥β的充要条件是（）A ．α内有无数条直线与β平行B ．α内有两条相交直线与β平行C ．α，β平行于同一条直线D ．α，β垂直于同一平面练习1．(2018浙江)已知平面α，直线m ，n 满足m α⊄，n α⊂，则“m ∥n ”是“m ∥α”的（） A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件D ．既不充分也不必要条件题型二：充要条件与平面向量例 2.（2019北京理7）设点A ,B ,C 不共线，则“与的夹角是锐角”是“AB AC BC +>”的（）（A ）充分而不必要条件（B ）必要而不充分条件（C ）充分必要条件（D ）既不充分也不必要条件练习2．(2018北京)设a ，b 均为单位向量，则“33-=+a b a b ”是“a ⊥b ”的（）A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件题型三：充要条件与不等式例3.（2019天津理3）设x ∈R ，则“250x x -<”是“|1|1x -<”的（）A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件练习3．(2018天津)设x ∈R ，则“11||22x -<”是“31x <”的（） A ．充分而不必要条件 B ．必要而不充分条件 C ．充要条件 D ．既不充分也不必要条件题型四：充要条件与三角函数例4．（2017天津）设θ∈R ，则“ππ||1212θ-<”是“1sin 2θ<”的（） A ．充分而不必要条件 B ．必要而不充分条件 C ．充要条件 D ．既不充分也不必要条件练习4．（2015陕西）“sin cos αα=”是“cos20α=”的（）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要题型五：充要条件与数列例5．（2017浙江）已知等差数列{}n a 的公差为d ，前n 项和为n S ，则“0d >”是“465+2S S S >”的（）第- 2 -页A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件练习5．（2016年天津）设{}n a 是首项为正数的等比数列，公比为q ，则“0q <”是“对任意的正整数n ，2120n n a a -+<”的（） A ．充要条件 B ．充分而不必要条件 C ．必要而不充分条件 D ．既不充分也不必要条件题型六：充要条件与函数性质例5．（2013安徽）“0a ≤”是“函数()=(-1)f x ax x 在区间(0,+)∞内单调递增”的（）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件练习6．(2012山东)设0>a 且1≠a ，则“函数()xa x f =在R 上是减函数”是“()()32x a x g -=在R 上是增函数”的（）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件题型七：充要条件与函数性质例7．（2014浙江）已知i 是虚数单位，R b a ∈,,则“1==b a ”是“i bi a 2)(2=+”的（）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件练习7．（2012北京）设,a b ∈R ，“0a =”是“复数i a b +是纯虚数”的（）A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件题型八：命题真假判断例7．（2017新课标Ⅰ）设有下面四个命题1p ：若复数z 满足1z ∈R 错误!未找到引用源。

高考数学一轮总复习练习函数小题综合练

1．函数f (x )＝x 2＋|x |的图象( ) A ．关于原点对称 B ．关于y 轴对称 C ．关于x 轴对称D ．关于y ＝x 对称2．设f (x )＝⎩⎪⎨⎪⎧x ＋3，x <0，f (x －2)，x ≥0，则f (log 23)的值为( )A ．log 23B ．log 26C ．log 23＋3D ．03．已知y ＝f (x ＋1)＋2是定义域为R 的奇函数，则f (e)＋f (2－e)等于( ) A ．－4 B ．2e C ．4 D ．e4．(2019·丽水模拟)已知奇函数f (x )是定义在R 上的减函数，且a ＝－f ⎝⎛⎭⎫log 3110，b ＝f (log 39.1)，c ＝f (20.8)，则a ，b ，c 的大小关系为( ) A ．a >b >cB ．b >a >cC ．c >b >aD ．c >a >b5．函数y ＝a x (a >0且a ≠1)与函数y ＝f (x )的图象关于直线y ＝x 对称，则函数y ＝f (x )与二次函数y ＝(a －1)x 2－x 在同一坐标系内的图象可能是( )6．(2020·金华质检)函数f (x )＝(1－x )|x －3|在(－∞，t ]上取得最小值－1，则实数t 的取值范围是( ) A ．(－∞，2) B ．[2－2，2] C ．[2,2＋ 2 ]D ．[2，＋∞)7．已知函数f (x )＝⎩⎪⎨⎪⎧2x＋1，x ≤0，12log x ，x >0，且f ⎝⎛⎭⎫m －12＝0，则不等式f (x )>m 的解集为( ) A.⎝⎛⎭⎫0，22 B.⎝⎛⎭⎫0，24C.⎝⎛⎭⎫－1，24 D ．(－1，＋∞)8．已知函数f (x )＝2x (x <0)与g (x )＝ln(x ＋a )的图象上存在关于y 轴对称的点，则a 的取值范围是( )A ．(－∞，2)B ．(－∞，e)C ．(2，e)D ．(e ，＋∞)9．(2020·温州四校联考)已知奇函数f (x )＝⎩⎪⎨⎪⎧2x －a ，x ≥0，g (x )，x <0，则f (－2)＝______，g (x )的表达式为________．10．已知a ∈R ，函数f (x )＝⎪⎪⎪⎪x ＋4x －a ＋a 在区间[1,4]上的最大值是5，则a 的取值范围是________．11．函数f (x －1)(x ∈R )是偶函数，且函数f (x )的图象关于点(1,0)成中心对称，当x ∈[－1,1]时，f (x )＝x －1，则f (2 020)等于( ) A ．－2 B ．1 C ．0 D ．212．如果函数y ＝f (x )在区间I 上是增函数，且函数y ＝f (x )x在区间I 上是减函数，那么称函数y ＝f (x )是区间I 上的“缓增函数”，区间I 叫做“缓增区间”．若函数f (x )＝12x 2－x ＋32是区间I 上的“缓增函数”，则“缓增区间”I 为( ) A ．[1，＋∞) B ．[0，3] C ．[0,1]D ．[1，3]13．(2020·温州质检)已知函数f (x )是偶函数且满足f (x ＋2)＝－f (x )，当x ∈[0,2]时，f (x )＝x －1，则不等式xf (x )>0在[－1,3]上解集为( ) A ．(1,3) B ．(－1,1)C ．(－1,0)∪(1,3)D ．(－2，－1)∪(0,1)14．已知函数f (x )＝ax 3－3x 2＋b (1<a <2)只有两个零点，则实数log a 2＋log b 2的最小值是( ) A ．－ 2 B.32－ 2 C ．2 2D.32＋ 2 15．设直线x ＝m 与函数f (x )＝x 2＋1，g (x )＝x ＋ln x 的图象分别交于P ，Q 两点，则|PQ |的最小值为________．16．(2019·杭州月考)已知函数f (x )＝⎩⎪⎨⎪⎧|log 2(x －1)|，1<x ≤3，12x 2－92x ＋10，x >3，若方程f (x )＝m 有四个不同的实根x 1，x 2，x 3，x 4，且满足x 1<x 2<x 3<x 4，则⎝⎛⎭⎫m x 1＋m x 2(x 3＋x 4)的取值范围是________．一、选择题1．(2019·绍兴模拟)已知集合A ＝{x |y ＝(1－x )(x ＋3)}，B ＝{x |log 2x ≤1}，则A ∩B 等于( ) A ．{x |－3≤x ≤1} B ．{x |0<x ≤1} C ．{x |－3≤x ≤2}D ．{x |x ≤2}2．若x ∈R ，则下列所给函数中f (x )与g (x )表示同一个函数的是( ) A ．f (x )＝x ，g (x )＝x 2 B ．f (x )＝2，g (x )＝2x 0 C ．f (x )＝x 2－1x ＋1，g (x )＝x －1D ．f (x )＝(2x )22x ，g (x )＝x(x )23．(2020·宁波月考)函数f (x )＝3x 21－x ＋lg(3x ＋1)的定义域是( )A.⎣⎡⎦⎤－13，1 B.⎝⎛⎭⎫－13，1 C.⎝⎛⎭⎫13，1D.⎣⎡⎦⎤－1，－13 4．若f (x ＋1)＝x ＋2x ，则f (x )的解析式为( ) A ．f (x )＝x 2－x B ．f (x )＝x 2－1(x ≥0) C ．f (x )＝x 2－1(x ≥1)D ．f (x )＝x 2＋x5．已知条件p ：(x －2)2≤1，条件q ：2x －1≥1，则q 是p 的( )A ．充要条件B ．充分不必要条件C ．必要不充分条件D ．既不充分也不必要条件6．(2019·丽水期末)f (x )＝⎩⎪⎨⎪⎧x 2＋1，x ≥0，f (x ＋3)，x <0，则f (－5)等于( )A ．1B ．2C ．26D ．107．下列所给函数中图象关于原点对称且在定义域内单调递增的函数是( ) A ．f (x )＝cos x －1 B ．f (x )＝x 2＋2 C ．f (x )＝－1xD ．f (x )＝x 38．已知奇函数f (x )满足f (x ＋2)＝f (x )，当x ∈(0,1)时，函数f (x )＝2x ，则f (12log 23)等于( )A ．－1623 B.1623 C ．－2316 D.23169．函数f (x )＝e x ·ln|x |的大致图象为( )10．已知函数f (x )是定义在R 上的奇函数，当x <0时，f (x )＝e x (x ＋1)，给出下列命题：①当x >0时，f (x )＝e x (1－x )；②函数f (x )有2个零点；③f (x )>0的解集为(－1,0)∪(1，＋∞)；④任意x 1，x 2∈R ，都有|f (x 1)－f (x 2)|<2.其中真命题的序号是( ) A ．①③ B ．②③ C ．②④ D ．③④ 二、填空题11．已知全集U ＝{1,2,3,4,5}，集合A ＝{1,2,3}，∁U B ＝{2,5}，则集合B ＝________，A ∩B ＝________.12．在平面直角坐标系xOy 中，已知幂函数f (x )＝x α的图象过点(8，2)，则α的值为________，f (64)＝________.13．(2020·温州模拟)已知命题p ：－4<x －a <4，q ：(x －2)(3－x )>0，若q 是p 的充分条件，则实数a 的取值范围是________．14．已知f (x )＝⎩⎪⎨⎪⎧x 2，x <0，2x －2，x ≥0，则f (f (－2))＝________，函数f (x )的零点个数为________．15．(2019·杭州市第二中学期末)已知函数f (x )＝⎩⎪⎨⎪⎧x 2＋x ，－2≤x ≤c ，1x ，c <x ≤3.若c ＝0，则f (x )的值域是________；若f (x )的值域是⎣⎡⎦⎤－14，2，则实数c 的取值范围是______________． 16．已知函数f (x )＝lg ⎝⎛⎭⎫2kx 2－kx ＋38的定义域为R ，则实数k 的取值范围是________． 17．若函数f (x )＝⎩⎪⎨⎪⎧2x ＋2－3，x ≤0，x 3－ax ＋2，x >0有三个不同的零点，则实数a 的取值范围是________．三、解答题18．已知集合A ＝{x |1≤x ≤4}，B ＝{x |log 2x <1}． (1)求A ∪(∁R B )；(2)已知集合C ＝{x |2a －1≤x ≤a ＋1}，若C ⊆A ，求实数a 的取值范围．19．(1)23278-⎛⎫ ⎪⎝⎭－⎝⎛⎭⎫4990.5＋()230.008-×225； (2)2log 32－log 332＋log 38－5log 53.20.(2019·金华质检)已知函数f (x )＝x ＋mx的图象过点P (1,5)．(1)求实数m的值，并证明函数f(x)是奇函数；(2)利用单调性定义证明f(x)在区间[2，＋∞)上是增函数．21．设f(x)是定义在R上的奇函数，且当x>0时，f(x)＝2x＋1.(1)求f(x)的解析式；(2)若x<0时，方程f(x)＝x2＋tx＋2t仅有一实根(若有重根按一个计算)，求实数t的取值范围．22.对于函数f (x )，若在定义域内存在实数x 0，满足f (－x 0)＝－f (x 0)，则称f (x )为“M 类函数”． (1)若函数f (x )＝sin ⎝⎛⎭⎫x ＋π3，试判断f (x )是否为“M 类函数”？并说明理由； (2)若f (x )＝2x ＋m 是定义在[－1,1]上的“M 类函数”，求实数m 的最小值；(3)若f (x )＝⎩⎪⎨⎪⎧log 2(x 2－2mx )，x ≥2，－3，x <2为其定义域上的“M 类函数”，求实数m 的取值范围．答案精析1．B 2.B 3.A 4.C 5.A 6.C 7.C 8．B 9.－3 g (x )＝1－2－x 10.⎝⎛⎦⎤－∞，92 11.B 12．D [因为函数f (x )＝12x 2－x ＋32的对称轴为x ＝1，所以函数y ＝f (x )在区间[1，＋∞)上是增函数，又当x ≥1时，f (x )x ＝12x －1＋32x ，令g (x )＝12x －1＋32x (x ≥1)，则g ′(x )＝12－32x 2＝x 2－32x 2，由g ′(x )≤0得1≤x ≤3，即函数f (x )x ＝12x －1＋32x 在区间[1，3]上单调递减，故“缓增区间”I 为[1，3]．]13．C [设x ∈[0,2]，则f (x ＋2)＝－f (x )＝－x ＋1，即f (x ＋2)＝－x ＋1.设x ＋2＝t ，t ∈[2,4]，x ＝t －2，则f (t )＝－t ＋3.设x ∈[－1,0)，－x ∈(0,1]，f (x )为偶函数； ∴f (－x )＝－x －1＝f (x )． ∴f (x )＝⎩⎪⎨⎪⎧－x －1，x ∈[－1，0)，x －1，x ∈[0，2]，－x ＋3，x ∈(2，3].∴由xf (x )>0得⎩⎪⎨⎪⎧x >0，f (x )>0或⎩⎪⎨⎪⎧x <0，f (x )<0.∴⎩⎪⎨⎪⎧ 0<x ≤2，x －1>0或⎩⎪⎨⎪⎧ 2<x ≤3，－x ＋3>0或⎩⎪⎨⎪⎧－1≤x <0，－x －1<0，解得－1<x <0或1<x <3.∴不等式xf (x )>0在[－1,3]上的解集为(－1,0)∪(1,3)．]14．D [f ′(x )＝3ax 2－6x＝3ax ⎝⎛⎭⎫x －2a ，令f ′(x )＝0，解得x ＝0，x ＝2a，故函数在(－∞，0)和⎝⎛⎭⎫2a ，＋∞上单调递增，在⎝⎛⎭⎫0，2a 上单调递减，所以f (x )极大值＝f (0)，f (x )极小值＝f ⎝⎛⎭⎫2a ，而f (0)＝b >0，因为函数只有两个零点，所以f ⎝⎛⎭⎫2a ＝0，故a 2b ＝4，取对数得2log 2a ＋log 2b ＝2，即log 2a ＋12log 2b ＝1，而log a 2＋log b 2＝⎝⎛⎭⎫1log 2a ＋1log 2b ⎝⎛⎭⎫log 2a ＋12log 2b ＝32＋12log 2b log 2a ＋log 2a log 2b ≥32＋2，当且仅当log 2a ＝2－2，log 2b ＝22－2时等号成立，故最小值为32＋ 2.] 15．116．(0,9)解析作出函数图象如图．根据图象可得m ∈(0,1)，且－log 2(x 1－1)＝log 2(x 2－1)，则(x 1－1)(x 2－1)＝1，即x 1x 2＝x 1＋x 2. 又因为x 3，x 4关于x ＝92对称，所以x 3＋x 4＝9. 化简原式⎝⎛⎭⎫m x 1＋mx 2(x 3＋x 4)＝9m ∈(0,9)．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2019-2020年高考数学小题综合训练31．已知U ＝{y |y ＝log 2x ，x >1}，P ＝⎩⎨⎧⎭⎬⎫y ⎪⎪y ＝1x，x>2，则∁U P 等于( ) A.⎣⎡⎭⎫12，＋∞ B.⎝⎛⎭⎫0，12 C ．(0，＋∞) D ．(－∞，0)∪⎝⎛⎭⎫12，＋∞ 答案 A解析由集合U 中的函数y ＝log 2x ，x >1，解得y >0，所以全集U ＝(0，＋∞)，同样P ＝⎝⎛⎭⎫0，12，得到∁U P ＝⎣⎡⎭⎫12，＋∞. 2．“a >0”是“函数f (x )＝x 3＋ax 在区间(0，＋∞)上是增函数”的( ) A ．必要不充分条件 B ．充分不必要条件 C ．充要条件D ．既不充分也不必要条件答案 B解析当a >0时，f ′(x )＝3x 2＋a >0在区间(0，＋∞)上恒成立，即f (x )在(0，＋∞)上是增函数，充分性成立；当f (x )在区间(0，＋∞)上是增函数时，f ′(x )＝3x 2＋a ≥0在(0，＋∞)上恒成立，即a ≥0，必要性不成立，故“a >0”是“函数f (x )＝x 3＋ax 在区间(0，＋∞)上是增函数”的充分不必要条件． 3．已知函数f (x )＝⎩⎨⎧sin πx ，0≤x≤1，log2 010x ，x>1，若a ，b ，c 互不相等，且f (a )＝f (b )＝f (c )，则a ＋b ＋c 的取值范围是( ) A ．(1,2 010) B ．(1,2 011) C ．(2,2 011) D ．[2,2 011]答案 C解析因为a ，b ，c 互不相等，不妨设a <b <c ，则0<a <b <1<c ，由f (a )＝f (b )知，a ，b 关于直线x ＝12对称，所以a ＋b ＝1.由0<log 2 010c <1，知1<c <2 010，所以2<a ＋b ＋c <2 011.4．设S n 是等差数列{a n }的前n 项和，若a5a3＝73，则S5S3等于( )A.73B.359 C ．4 D ．5 答案 D解析在等差数列{a n }中，设首项为a 1，公差为d ，由于a5a3＝73，得a1＋4d a1＋2d ＝73，解得a 1＝－d 2，S5S3＝5a1＋a523a1＋a32＝5a33a2＝5·3d23·d 2＝5. 5.如图，在△ABC 中，AN →＝14NC →，P 是直线BN 上的一点，若AP →＝m AB →＋25AC →，则实数m 的值为( )A ．－4B ．－1C ．1D ．4 答案 B解析由题意，设BP →＝n BN →，则AP →＝AB →＋BP → ＝AB →＋n BN → ＝AB →＋n (AN →－AB →) ＝AB →＋n ⎝⎛⎭⎫14NC →－AB → ＝AB →＋n ⎝⎛⎭⎫15AC →－AB → ＝(1－n )AB →＋n 5AC →，又∵AP →＝m AB →＋25AC →，∴m ＝1－n ，n 5＝25.解得n ＝2，m ＝－1.6．在四棱锥P －ABCD 中，PA ⊥底面ABCD ，底面ABCD 为正方形，PA ＝AB ，该四棱锥被一平面截去一部分后，剩余部分的三视图如图，则截去部分体积与剩余部分体积的比值为()A.12B.13C.14D.15 答案 B解析根据几何体的三视图，得该几何体是过BD 且平行于PA 的平面截四棱锥P －ABCD 所得的几何体．设AB ＝1，则截去的部分为三棱锥E －BCD ，它的体积为 V 三棱锥E －BCD ＝13×12×1×1×12＝112，剩余部分的体积为V 剩余部分＝V 四棱锥P －ABCD －V 三棱锥E －BCD ＝13×12×1－112＝14. 所以截去部分的体积与剩余部分的体积比为 112∶14＝1∶3. 7．秦九韶是我国南宋时期著名的数学家，普州(现四川省安岳县)人，他在所著的《数书九章》中提出的多项式求值的秦九韶算法，至今仍是比较先进的算法．如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例，若输入x 的值为3，每次输入a 的值均为4，输出s 的值为484，则输入n 的值为( )A ．6B ．5C ．4D ．3 答案 C解析模拟程序的运行，可得x ＝3，k ＝0，s ＝0，a ＝4，s ＝4，k ＝1；不满足条件k >n ，执行循环体，a ＝4，s ＝16，k ＝2；不满足条件k >n ，执行循环体，a ＝4，s ＝52，k ＝3；不满足条件k >n ，执行循环体，a ＝4，s ＝160，k ＝4；不满足条件k >n ，执行循环体，a ＝4，s ＝484，k ＝5.由题意，此时应该满足条件k >n ，退出循环，输出s 的值为484，可得5>n ≥4，所以输入n 的值为4.8．(2x ＋1)⎝⎛⎭⎫1－1x 6的展开式中的常数项是( ) A ．－5 B ．7 C ．－11 D ．13 答案 C解析 ∵⎝⎛⎭⎫1－1x 6的展开式的通项公式是Ck 6⎝⎛⎭⎫－1x k ，其中含1x的项是C16⎝⎛⎭⎫－1x 1，常数项为C06⎝⎛⎭⎫－1x 0＝1，故(2x ＋1)⎝⎛⎭⎫1－1x 6的展开式中的常数项是2x ×⎣⎡⎦⎤C16⎝⎛⎭⎫－1x 1＋1×1＝－12＋1＝－11. 9．把正方形ABCD 沿对角线AC 折起，当以A ，B ，C ，D 四点为顶点棱锥体积最大时，直线B D 和平面ABC 所成角的大小为( ) A ．90° B ．60° C ．45° D ．30°答案 C解析如图，当DO ⊥平面ABC 时，三棱锥D －ABC 的体积最大．∴∠DBO 为直线BD 和平面ABC 所成的角， ∵在Rt △DOB 中，OD ＝OB ，∴直线BD 和平面ABC 所成角的大小为45°. 10．在区间[－1,1]上任取两数s 和t ，则关于x 的方程x 2＋2sx ＋t ＝0的两根都是正数的概率为( ) A.124B.112C.14D.13 答案 B解析由题意可得，⎩⎪⎨⎪⎧－1≤s≤1，－1≤t≤1，其区域是边长为2的正方形，面积为4，由二次方程x 2＋2sx ＋t ＝0有两正根，可得 ⎩⎪⎨⎪⎧4s2－4t≥0，－2s>0，t>0，即⎩⎪⎨⎪⎧s2≥t ，s<0，t>0，其区域如图阴影部分所示，面积S ＝ʃ0－1s 2d s ＝⎪⎪13s30－1＝13，所求概率P ＝134＝112.11．椭圆x 2＋y2b2＝1(0<b <1)的左焦点为F ，上顶点为A ，右顶点为B ，若△FAB 的外接圆圆心P (m ，n )在直线y ＝－x 的左下方，则该椭圆离心率的取值范围为( ) A.⎝⎛⎭⎫22，1 B.⎝⎛⎭⎫12，1 C.⎝⎛⎭⎫0，22 D.⎝⎛⎭⎫0，12 答案 A解析方法一如图所示，右顶点B (1,0)，上顶点A (0，b )，左焦点F (－1－b2，0)，线段FB 的垂直平分线为x ＝1－1－b22.线段AB 的中点坐标为⎝⎛⎭⎫12，b 2.∵k AB ＝－b ，∴线段AB 的垂直平分线的斜率k ＝1b ，∴线段AB 的垂直平分线方程为 y －b 2＝1b ⎝⎛⎭⎫x －12，把x ＝1－1－b22＝m ，代入上述方程，可得y ＝b2－1－b22b＝n .由P (m ，n )在直线y ＝－x 的左下方，可得m ＋n <0， ∴1－1－b22＋b2－1－b22b<0，化简得b <1－b2，又0<b <1，解得0<b <22. ∴e ＝c a ＝c ＝1－b2∈⎝⎛⎭⎫22，1，∴椭圆离心率的取值范围为⎝⎛⎭⎫22，1.方法二设A (0，b )，B (a,0)，F (－c,0)，设△FAB 的外接圆的方程为x 2＋y 2＋Dx ＋Ey ＋F ＝0，将A ，B ，F 代入外接圆方程，解得m ＝－c ＋a 2，n ＝b2－ac2b.由P (m ，n )在直线y ＝－x 的左下方，可知m ＋n <0， ∴－c ＋a 2＋b2－ac2b<0，整理得1－c ＋b －cb <0，∴b －c ＋b －c b <0，∴b －c <0，又椭圆的离心率e ＝ca ＝c ，∴c 2>b 2，即c 2>a 2－c 2,2c 2>a 2,2e 2>1，由0<e <1，解得22<e <1， ∴椭圆离心率的取值范围为⎝⎛⎭⎫22，1.12．已知正数x ，y ，z 满足x 2＋y 2＋z 2＝1，则S ＝1＋z2xyz 的最小值为( )A ．3 B.33＋12C ．4D ．2(2＋1)答案 C解析由题意可得0<z <1,0<1－z <1， ∴z (1－z )≤⎝⎛⎭⎫z ＋1－z 22＝14，当且仅当z ＝1－z ，即z ＝12时取等号．又x 2＋y 2＋z 2＝1，∴1－z 2＝x 2＋y 2≥2xy ，当且仅当x ＝y 时取等号，∴1－z22xy≥1， ∴1＋z1－z2xy≥1，∴1＋z 2xy ≥11－z，∴1＋z 2xyz ≥11－z z≥4，当且仅当x ＝y ＝64且z ＝12时取等号， ∴S ＝1＋z2xyz的最小值为4.13．已知复数z 满足i z ＝4＋3i1＋2i ，则复数z 在复平面内对应的点在第__________象限．答案三解析 ∵i z ＝4＋3i1＋2i，∴z ＝4＋3i 1＋2i i ＝4＋3i －2＋i ＝4＋3i－2－i－2＋i－2－i＝－5－10i5＝－1－2i ， ∴复数z 在复平面内对应的点的坐标为(－1，－2)，在第三象限．14．若直线y ＝3x 上存在点(x ，y )满足约束条件⎩⎪⎨⎪⎧x ＋y ＋4>0，2x －y ＋8≥0，x≤m ，则实数m 的取值范围是__________．答案 (－1，＋∞)解析由题意作出其平面区域，由⎩⎪⎨⎪⎧y ＝3x ，y ＝－x －4，解得A (－1，－3)．故m >－1. 15．已知△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，若cos B ＝14，b ＝4，sin A ＝2sin C ，则△ABC 的面积为________．答案15解析根据余弦定理的推论 cos B ＝a2＋c2－b22ac ，可得14＝a2＋c2－422ac，化简得2a 2＋2c 2－32＝ac .(*) 又由正弦定理a sin A ＝c sin C，可得a c ＝sin A sin C ＝21，即a ＝2c ，代入(*)式得 2·(2c )2＋2c 2－32＝2c ·c ，化简得c 2＝4，所以c ＝2，则a ＝4，又B ∈(0，π)，则sin B ＝1－cos2B ＝154， S △ABC ＝12ac sin B ＝12×4×2×154＝15，即△ABC 的面积为15. 16．已知双曲线x2a2－y2b2＝1(a >0，b >0)上一点C ，过双曲线中心的直线交双曲线于A ，B 两点，记直线AC ，BC 的斜率分别为k 1，k 2，当2k1k2＋ln|k 1|＋ln|k 2|最小时，双曲线的离心率为________．答案3解析设A (x 1，y 1)，C (x 2，y 2)，由题意知，点A ，B 为过原点的直线与双曲线x2a2－y2b2＝1的交点，∴由双曲线的对称性，得A ，B 关于原点对称， ∴B (－x 1，－y 1)，∴k 1k 2＝y2－y1x2－x1·y2＋y1x2＋x1＝y22－y21x22－x21，∵点A ，C 都在双曲线上， ∴x21a2－y21b2＝1，x22a2－y22b2＝1，两式相减，可得k 1k 2＝b2a2>0，对于2k1k2＋ln|k 1|＋ln|k 2|＝2k1k2＋ln|k 1k 2|，设函数y ＝2x ＋ln x ，x >0，由y ′＝－2x2＋1x＝0，得x ＝2，当x >2时，y ′>0，当0<x <2时，y ′<0， ∴当x ＝2时，函数y ＝2x＋ln x ，x >0取得最小值，∴当2k1k2＋ln(k 1k 2)最小时，k 1k 2＝b2a2＝2，∴e ＝1＋b2a2＝ 3.。