多边形面积的计算练习题(2)
五年级数学思维训练《多边形的面积计算(二)》专题训练
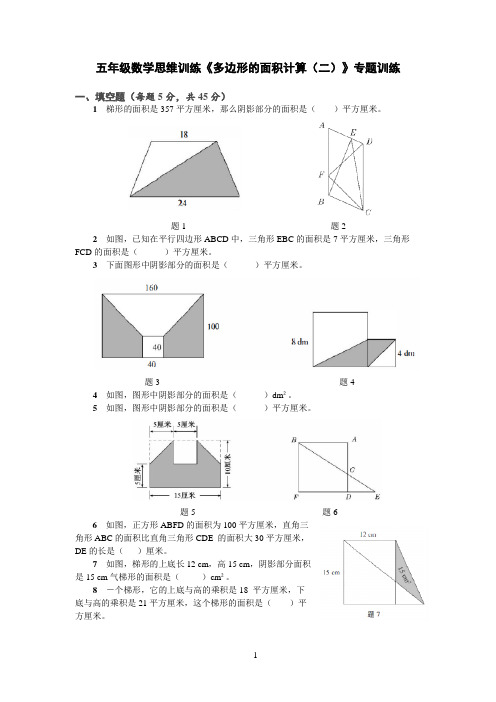
五年级数学思维训练《多边形的面积计算（二）》专题训练一、填空题（每题5分，共45分）1梯形的面积是357平方厘米，那么阴影部分的面积是（）平方厘米。
题1 题2 2如图，已知在平行四边形ABCD中，三角形EBC的面积是7平方厘米，三角形FCD的面积是（）平方厘米。
3下面图形中阴影部分的面积是（）平方厘米。
题3 题4 4如图，图形中阴影部分的面积是（）dm²。
5如图，图形中阴影部分的面积是（）平方厘米。
题5 题66 如图，正方形ABFD的面积为100平方厘米，直角三角形ABC的面积比直角三角形CDE 的面积大30平方厘米，DE的长是（）厘米。
7如图，梯形的上底长12 cm，高15 cm，阴影部分面积是15 cm气梯形的面积是（）cm²。
8－个梯形，它的上底与高的乘积是18 平方厘米，下底与高的乘积是21平方厘米，这个梯形的面积是（）平方厘米。
9－个用四根木条钉成的平行四边形，它的底是18厘米，高是11厘米，把它拉成一个长方形后，面积增加了72平方厘米，这个平行四边形的周长是（）厘米。
二、解答题（笫10题15分，笫ll~13题20分，共75分）10如图所示，三角形ABC的面积是10平方厘米，将AB，BC，CA分别延长一倍到D，E，F，两两连接D，E，F，得到一个新的三角形DEF。
求三角形DEF的面积。
11一个正方形，将它的一边截去15厘米，另一边截去10厘米，剩下的长方形比原来正方形的面积减少1725平方厘米，求剩下的长方形的面积。
12有红、黄、绿三块同样大小的正方形纸片，放在一个正方形盒的底部，它们之间互相叠合（见右图）。
已知露在外面的部分中，红色面积是20，黄色面积是14，绿色面积是10 ，求正方形盒子底部的面积。
13如图中，三角形ABC和DEF是两个完全相同的等腰直角三角形，其中DF长9厘米，CF长3厘米，求阴影部分的面积。
三、选做题（每题15分，共30分）14在图中，五个小正方形的边长都是2厘米，求三角形ABC的面积。
人教版五年级上册数学 第6单元《多边形的面积》单元测试卷2(含答案)
人教版五（上）数学第六单元《多边形的面积》测试卷2姓名：班级：学号：一、填空题。
（1题3分，其余每空2分，共23分）1、用字母表示：平行四边形的面积计算公式（），三角形的面积计算公式（），梯形的面积计算公式（）。
2、一个三角形的面积是12平方分米，底是6分米，高是（）分米．3、一个梯形上底是8cm，下底是14cm，高是5cm，它的面积是（）cm2。
4、一个等腰直角三角形，腰长16cm，面积是（）cm2。
5、一个平行四边形停车位的底是4 m，高是5 m，这个平行四边形停车位的面积是（）平方米。
6、一个平行四边形的面积是18m2，高是3m，与它等底等高的三角形的面积是（）m2。
7、下图中平行四边形ABCD的面积是96 cm2，E是AD的中点，F是BC的中点，平行四边形AFCE的面积是（）cm2。
8、一块直角三角形玻璃被打碎了，剩下一部分(如下图)，原来这块直角三角形玻璃的面积是（）平方厘米。
9、两个完全一样的梯形可以拼成一个平行四边形，平行四边形的高等于梯形的（），平行四边形的底等于梯形（）。
10、如下图，A、B两点是平行四边形底边上的三等分点（即A、B两点把平行四边形的底边平均分成了三份），阴影部分三角形的面积是12 cm2，平行四边形的面积是（）cm2。
二、判断题。
（10分）1、一个梯形的面积是6.3平方米．高是1.5米，上、下底的和是4.2米。
（）2、直角梯形仍然只有两条高。
（）3、平行四边形的面积是三角形面积的2倍。
（）4、两个三角形等底等高，那么这两个三角形的面积相等。
（）5、两个梯形的面积相等，这两个梯形一定能拼成一个平行四边形。
（）三、选择题。
（12分）1、平行四边形的高有（）条。
A．无数B．2C．42、一个直角三角形，三条边分别是3dm、4dm、5dm，这个直角三角形的面积是（）A．6dm2B．12dm2C．10dm23、如图梯形ABCD中，甲乙两块阴影的面积（）A．甲大B．乙大C．一样大D．无法比较大小4、图中梯形的高和下底相等，下面计算梯形面积方法错误的是（）A．（2+4）×4÷2B．2×4×3C．4×4﹣（2×4÷2）5、一个长方形框架拉成平行四边形，拉成后框架的周长与原来长方形周长比较（）。
多边形的面积计算 练习题
多边形的面积计算练习题多边形的面积计算练习题多边形是几何学中的一个重要概念，它由若干条边和顶点组成。
而计算多边形的面积是几何学中的一项基本技能。
在这篇文章中，我们将通过一些练习题来巩固和提高我们对多边形面积计算的理解。
练习题一：正方形的面积计算假设有一个正方形，边长为5cm。
那么这个正方形的面积是多少？解答：正方形的面积可以通过边长的平方来计算。
所以这个正方形的面积为5cm ×5cm = 25cm²。
练习题二：矩形的面积计算现在考虑一个矩形，长为6cm，宽为4cm。
那么这个矩形的面积是多少？解答：矩形的面积可以通过长乘以宽来计算。
所以这个矩形的面积为6cm × 4cm = 24cm²。
练习题三：三角形的面积计算接下来我们来计算一个三角形的面积。
假设有一个底边长为8cm，高为6cm的三角形。
那么这个三角形的面积是多少？解答：三角形的面积可以通过底边乘以高再除以2来计算。
所以这个三角形的面积为(8cm × 6cm) ÷ 2 = 24cm²。
练习题四：梯形的面积计算现在我们来计算一个梯形的面积。
假设有一个上底长为5cm，下底长为8cm，高为4cm的梯形。
那么这个梯形的面积是多少？解答：梯形的面积可以通过上底和下底的平均值乘以高来计算。
所以这个梯形的面积为((5cm + 8cm) ÷ 2) × 4cm = 26cm²。
练习题五：多边形的面积计算最后我们来计算一个不规则多边形的面积。
假设有一个五边形，边长分别为3cm、4cm、5cm、6cm、7cm，且相邻两边之间的夹角分别为90°、120°、100°、80°。
那么这个五边形的面积是多少？解答：我们可以将这个五边形分割成三个三角形，然后分别计算每个三角形的面积，最后将它们相加得到整个五边形的面积。
首先，我们计算第一个三角形的面积。
多边形面积练习题及答案
多边形面积练习题及答案练习题一：矩形的面积计算1. 已知一个矩形的长度为12cm，宽度为8cm，求其面积。
解答：矩形的面积等于长度乘以宽度。
根据题目给出的数据，我们可以计算矩形的面积：面积 = 长度 ×宽度 = 12cm × 8cm = 96cm²练习题二：三角形的面积计算2. 已知一个三角形的底边长为5cm，高为6cm，求其面积。
解答：三角形的面积等于底边乘以高再除以2。
根据题目给出的数据，我们可以计算三角形的面积：面积 = 1/2 ×底边 ×高 = 1/2 × 5cm × 6cm = 15cm²练习题三：平行四边形的面积计算3. 已知一个平行四边形的底边长为9cm，高为4cm，求其面积。
解答：平行四边形的面积等于底边乘以高。
根据题目给出的数据，我们可以计算平行四边形的面积：面积 = 底边 ×高 = 9cm × 4cm = 36cm²练习题四：梯形的面积计算4. 已知一个梯形的上底长为6cm，下底长为10cm，高为8cm，求其面积。
解答：梯形的面积等于上底加下底再乘以高再除以2。
根据题目给出的数据，我们可以计算梯形的面积：面积 = 1/2 × (上底 + 下底) ×高 = 1/2 × (6cm + 10cm) × 8cm = 64cm²练习题五：菱形的面积计算5. 已知一个菱形的对角线1长为7cm，对角线2长为4cm，求其面积。
解答：菱形的面积等于对角线1乘以对角线2再除以2。
根据题目给出的数据，我们可以计算菱形的面积：面积 = 1/2 ×对角线1 ×对角线2 = 1/2 × 7cm × 4cm = 14cm²练习题六：不规则多边形的面积计算6. 已知一个不规则四边形的边长依次为5cm、6cm、8cm和7cm，求其面积。
(必考题)小学数学五年级上册第六单元多边形的面积检测(有答案解析)(2)
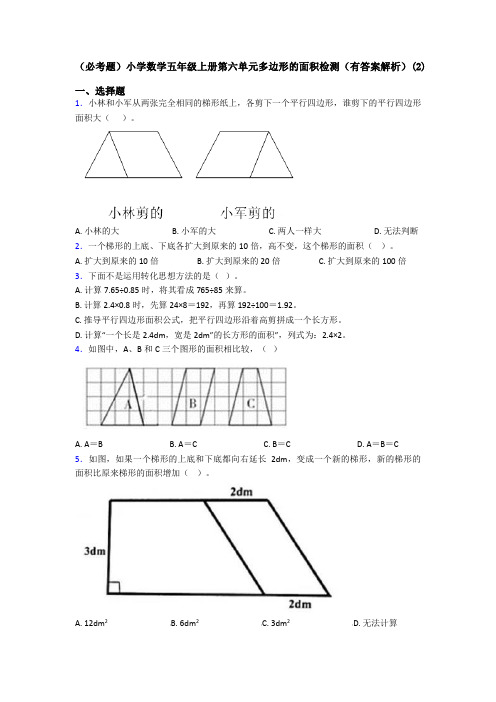
（必考题）小学数学五年级上册第六单元多边形的面积检测（有答案解析）(2)一、选择题1．小林和小军从两张完全相同的梯形纸上，各剪下一个平行四边形，谁剪下的平行四边形面积大（）。
A. 小林的大B. 小军的大C. 两人一样大D. 无法判断2．一个梯形的上底、下底各扩大到原来的10倍，高不变，这个梯形的面积（）。
A. 扩大到原来的10倍B. 扩大到原来的20倍C. 扩大到原来的100倍3．下面不是运用转化思想方法的是（）。
A. 计算7.65÷0.85时，将其看成765÷85来算。
B. 计算2.4×0.8时，先算24×8＝192，再算192÷100＝1.92。
C. 推导平行四边形面积公式，把平行四边形沿着高剪拼成一个长方形。
D. 计算“一个长是2.4dm，宽是2dm”的长方形的面积”，列式为：2.4×2。
4．如图中，A、B和C三个图形的面积相比较，（）A. A＝BB. A＝CC. B＝CD. A＝B＝C5．如图，如果一个梯形的上底和下底都向右延长2dm，变成一个新的梯形，新的梯形的面积比原来梯形的面积增加（）。
A. 12dm2B. 6dm2C. 3dm2D. 无法计算6．一条红领巾的面积是1650平方厘米，它的高是33厘米，则它的底是（）厘米．A. 50B. 100C. 1507．一个三角形和一个平行四边形的面积相等，底边也相等．已知平行四边形的高是0.8dm，三角形的高是（）dm．A. 0.4B. 0.8C. 1.68．三角形的底和高都扩大4倍，它的面积就扩大（）倍A. 4B. 6C. 8D. 169．一个三角形和一个平行四边形面积相等，高相等，三角形的底是40厘米，那么平行四边形的底是（）。
A. 30厘米B. 40厘米C. 60厘米D. 20厘米10．一个梯形的面积是84cm2，上底和下底的长度之和是7cm，它的高是（）。
A. 24cmB. 12cmC. 48cmD. 36cm 11．如图，阴影部分的面积与空白部分的面积相比较，它们（）。
多边形的面积练习题及答案
多边形的面积练习题及答案一、选择题1. 下列哪个图形是不规则多边形？A. 正方形B. 三角形C. 长方形D. 梯形2. 以下哪个公式可用于计算正方形的面积？A. S = a * bB. S = 1/2 * a * bC. S = a^2D. S = (a + b) * h3. 如图所示，一块田地被修建成了如下图形，哪个图形的面积最大？A. 正方形B. 正三角形C. 圆形D. 正五边形二、计算题1. 计算下列多边形的面积：a) 一个正方形的边长为5cm;b) 一个边长为6cm的正三角形;c) 一个边长分别为4cm和6cm，高为3cm的梯形;d) 一个有6个边，每个边长为4cm的正六边形。
2. 计算下述图形的面积，保留两位小数：a) 一个边长为9cm的正方形的周长为36cm;b) 一个边长为6cm的正三角形的外接圆半径为10cm。
三、解答题1. 如图所示，一个边长为6cm的正方形被切割成4个等边三角形和1个小正方形，请计算小正方形的面积。
[示意图]2. 已知一个正方形的面积为36cm²，求其边长。
[解答]四、答案1. 选择题1. B2. C3. C2. 计算题1.a) 正方形的面积为 S = a^2 = 5^2 = 25cm²b) 正三角形的面积为 S = (sqrt(3) / 4) * a^2 = (sqrt(3) / 4) * 6^2 =9sqrt(3) cm² (约为 15.59cm²)c) 梯形的面积为 S = (a + b) * h / 2 = (4 + 6) * 3 / 2 = 15cm²d) 正六边形的面积为 S = (3 * sqrt(3) / 2) * a^2 = (3 * sqrt(3) / 2) * 4^2 = 24sqrt(3) cm² (约为 41.57cm²)2.a) 正方形的边长为 9cm / 4 = 2.25cm，面积为 2.25^2 = 5.06cm²b) 正三角形的外接圆半径为 a / (2sqrt(3)) = 6 / (2sqrt(3)) = 1.73cm，面积为(sqrt(3) / 4) * (2.66)^2 ≈ 6cm²三、解答题1. 小正方形的边长等于等边三角形的边长，即6cm，所以小正方形的面积为 6^2 = 36cm².2. 已知正方形的面积为36cm²，设其边长为 a，则 a^2 = 36，解得 a = 6cm，所以正方形的边长为6cm。
多边形的面积练习题及答案
多边形的面积练习题及答案多边形的面积练习题及答案在几何学中，多边形是由一系列直线段连接而成的封闭图形。
多边形的面积是几何学中的基本概念之一，它描述了一个多边形所占据的平面区域。
计算多边形的面积需要一定的数学技巧和公式，下面将给出一些多边形的面积练习题及其答案，帮助读者加深对多边形面积的理解。
练习题一：计算三角形的面积已知一个三角形的底边长为6cm，高为4cm，求该三角形的面积。
解答：三角形的面积可以通过底边长和高的乘积再除以2来计算。
根据题目中的数据，可以得到：面积 = 底边长× 高÷ 2= 6cm × 4cm ÷ 2= 12cm²所以，该三角形的面积为12平方厘米。
练习题二：计算正方形的面积已知一个正方形的边长为8cm，求该正方形的面积。
解答：正方形的面积可以通过边长的平方来计算。
根据题目中的数据，可以得到：面积 = 边长× 边长= 8cm × 8cm= 64cm²所以，该正方形的面积为64平方厘米。
练习题三：计算矩形的面积已知一个矩形的长为10cm，宽为5cm，求该矩形的面积。
解答：矩形的面积可以通过长和宽的乘积来计算。
根据题目中的数据，可以得到：面积 = 长× 宽= 10cm × 5cm= 50cm²所以，该矩形的面积为50平方厘米。
练习题四：计算梯形的面积已知一个梯形的上底长为6cm，下底长为10cm，高为8cm，求该梯形的面积。
解答：梯形的面积可以通过上底长、下底长和高的乘积再除以2来计算。
根据题目中的数据，可以得到：面积 = (上底长 + 下底长) × 高÷ 2= (6cm + 10cm) × 8cm ÷ 2= 80cm²所以，该梯形的面积为80平方厘米。
练习题五：计算圆的面积已知一个圆的半径为5cm，求该圆的面积（取π≈3.14）。
2023年人教版五年级数学《多边形的面积》同步试题(附答案) (2)
《多边形的面积》同步试题一、填空1．完成下表。
考查目的：平行四边形、三角形和梯形的面积计算及变式练习。
答案：解析：直接利用公式计算这三种图形的面积，对于学生来说完成的难度不大。
对于已知平行四边形的面积和高求底、已知三角形的面积和底求高这两个变式练习，可引导学生进行比较，理解并强化三角形和梯形的类似计算中需要先将“面积×2”这一知识点。
2．下图是一个平行四边形，它包含了三个三角形，其中两个空白三角形的面积分别是15 平方厘米和25平方厘米。
中间涂色三角形的面积是（）。
考查目的：等底等高的三角形和平行四边形的面积之间的关系。
答案：40平方厘米。
解析：引导学生仔细观察图形，得出涂色部分三角形与整个平行四边形存在等底等高的关系，则该三角形的面积应为平行四边形面积的一半，据此进一步推导出涂色三角形的面积和两个空白三角形的面积之和相等这一结论。
3．有一批圆木堆成梯形，最上面一层有3根，最下面一层有8根，相邻两层相差1根，一共堆了6层，这堆圆木共有（）根。
考查目的：运用梯形的面积计算方法解决相关的实际问题。
答案：33。
解析：根据“（顶层根数+底层根数）×层数÷2”进行解答。
在此基础上，可引导学生用不同的方法对结果加以验证，重点分析采用等差数列求和的方法即“（首项+末项）×项数÷2”，这既是解决该题的基本数学模型，也能突出体现“数形结合”的思想。
4．如图的小花瓶中，1个小正方形的面积是1平方厘米，那么整个花瓶的面积是（）平方厘米。
考查目的：组合图形的面积计算。
答案：5。
解析：通过转化，小花瓶左右两侧的部分可以组合成两个小正方形，再加瓶身的部分即可。
也可采用计算的方法，由题意可得一个小正方形的边长为1厘米，则花瓶两边三角形的面积之和为2×1÷2×2=2（平方厘米），整个花瓶的面积为2+3=5（平方厘米）。
5．下图中，已知AB=BC=CD=EF=FG=GH=1 dm。
西师版五年级上册《第5章_多边形面积的计算》小学数学-有答案-单元测试卷(2)
西师版五年级上册《第5章多边形面积的计算》单元测试卷（2）一、画一画1. （1）画一条4厘米长的线段。
1.（2）画一个面积是1平方厘米的正方形。
二、递等式计算递等式计算15+15×16；360÷9×60；102×(200−167)．三、填空．在横线上填上适当的单位名称一架飞机每分钟飞行15千米．一张电脑桌的面积大约有60平方分米．爸爸的身高是17________，奶奶的身高是154________一个网球场的面积大约有240________．一本字典的封面面积大约是1________．2分米2＝________厘米2 800分米2＝________米21米＝________厘米5米2＝________分米2300厘米2＝________分米2 8公顷＝________米2．把一块长6分米，宽4分米的玻璃，裁成边长是2分米的正方形小块，可以裁成________块。
（提示：大面积÷小面积＝块数）把七个边长是3厘米的正方形拼成一个大长方形，那么这个长方形的面积是________平方厘米。
（提示：小面积×它的个数＝大面积）填表格一个长方形的客厅，长6米，宽4米。
（1）它的面积是多少？（2）如果用边长是2分米的正方形瓷砖铺地，需要多少块瓷砖？（提示：大面积÷小面积＝块数）一个木瓜园占地360平方米，平均每棵木瓜占地3平方米。
（1）这个木瓜园一共种了多少棵木瓜？（提示：大面积÷小面积＝棵数）（2）如果每棵木瓜树收木瓜40千克，这个木瓜园一共收木瓜多少千克？参考答案与试题解析西师版五年级上册《第5章多边形面积的计算》单元测试卷（2）一、画一画1.【答案】【考点】直线、线段和射线的认识画指定面积的长方形、正方形、三角形【解析】（1）根据线段的含义：线段有两个端点，有限长，然后画出长4厘米的线段即可。
（2）根据：正方形的面积＝边长×边长，可知画出一个面积是1平方厘米的正方形的边长应画1厘米。
五年级 3 多边形面积 (二)
1、如图，每个小正方形的面积是1平方厘米。 （1）用实线在方格内画出面积是2平方厘米的正方形。 （2）用实线在方格内画出面积是17平方厘米的正方形。
1×1÷2×4 =0.5×4 =2（平方厘米）
1×4÷2×4＋3×3 =+9 =17（平方厘米）
2.画一个面积是5平方厘米的正方形，连接各边中点，可得一个小正方形。 小正方形的面积是（ ）。 A、4cm2 B、3cm2 B、5cm2的一半
小正方形的边长：（96-4×4）÷2÷4=10（厘米） 小正方形的面积：10×10=100（平方厘米） 大正方形的面积：（10+4）×（10+4）=196（平方厘米） 答：大正方形的面积是196平方厘米，小正方形的面积是 100平方厘米。
1、分一分，能感受到组合图形可分成很多基本图形； 拼一拼，能感受到很多基本图形可拼成组合图形。 2、添加两条辅助线比添加一条辅助线无论从寻找需要 的条件还是计算基本图形的面积来说都更复杂，所以尽 量添加最少的辅助线解决问题。在添加一条辅助线的情 况下，还是要转化成自己最熟悉的基本图形，使得在寻 找条件的时候比较简单。 3、堆放的圆木，逐层很有规律，形成了连续自然数， 所以利用梯形面积公式计算根数很方便。
（1+8）×8÷2=36（根）
（3）你有什么发现？ 答：我发现用梯形的面积公式计算圆木的根数与 实际根数相同。
2.从下面梯形，三角形，平行四边形的面积公式变化中，你认为哪个公式 最具代表性，举例算一算再做判断。
梯形面积公式具有代表性
例4 大正方形中的小正方形
如图，大正方形的边长是7厘米，4个相同的长方形的宽是2.5厘米。阴影部 分是一个小正方形，它的面积是多少？
2×25-2÷2×3 =50-3 =47（平方厘米） 答：围成的面积是47平方厘米。
多边形面积计算练习题
多边形面积计算练习题一、基础题1. 计算边长为5的正方形的面积。
2. 一个长方形的长为8cm，宽为6cm，求其面积。
3. 已知三角形的底为10cm，高为8cm，求三角形的面积。
4. 一个等腰三角形的底边长为12cm，腰长为10cm，求其面积。
5. 计算边长为4的等边三角形的面积。
二、进阶题6. 一个梯形的上底为6cm，下底为10cm，高为8cm，求梯形的面积。
7. 已知平行四边形的底为15cm，高为12cm，求平行四边形的面积。
8. 一个菱形的对角线分别为8cm和12cm，求菱形的面积。
9. 计算一个正六边形的面积，其边长为6cm。
10. 一个五边形的边长分别为5cm、7cm、8cm、9cm、10cm，求该五边形的近似面积（可使用海伦公式）。
三、综合题11. 一个梯形和一个三角形的面积相等，梯形的上底为4cm，下底为10cm，高为6cm，求三角形的底和高。
12. 计算一个正六边形和一个等边三角形的面积之和，已知正六边形的边长为8cm，等边三角形的边长为6cm。
13. 一个长方形和一个平行四边形的面积相等，长方形的长为12cm，宽为8cm，求平行四边形的底和高。
14. 已知一个正方形和一个等腰三角形的面积之和为100cm²，正方形的边长为10cm，求等腰三角形的底边长。
15. 计算一个梯形和一个菱形的面积之和，梯形的上底为5cm，下底为10cm，高为8cm，菱形的对角线分别为6cm和8cm。
四、应用题16. 一个花园的形状是梯形，上底为20米，下底为30米，高为15米，计算花园的面积。
17. 一个农田的形状是平行四边形，底边为100米，对应的高为80米，求农田的面积。
18. 一个风筝的形状是菱形，两个对角线的长度分别为40厘米和60厘米，求风筝的面积。
19. 一个篮球场的形状是长方形，长为28米，宽为15米，计算篮球场的面积。
20. 一个湖泊的形状近似为椭圆形，长轴为800米，短轴为600米，求湖泊的面积（可以使用椭圆面积公式近似计算）。
多边形面积练习题及答案
多边形面积练习题及答案一、选择题1. 一个平行四边形的底是8米，高是5米，它的面积是（）平方米。
A. 30B. 40C. 50D. 602. 一个三角形的底是10厘米，高是6厘米，它的面积是（）平方厘米。
A. 30B. 40C. 50D. 603. 一个梯形的上底是4厘米，下底是8厘米，高是5厘米，它的面积是（）平方厘米。
A. 20B. 25C. 30D. 354. 一个圆的半径是3厘米，它的面积是（）平方厘米。
A. 28.26B. 36C. 45D. 545. 一个长方形的长是12米，宽是5米，它的面积是（）平方米。
A. 50B. 60C. 72D. 80二、填空题6. 如果一个平行四边形的面积是60平方米，底是15米，那么它的高是________米。
7. 一个三角形的面积是48平方厘米，底是12厘米，那么它的高是________厘米。
8. 一个梯形的面积是40平方厘米，上底是6厘米，下底是10厘米，那么它的高是________厘米。
9. 一个圆的面积是78.5平方厘米，它的半径是________厘米。
10. 一个长方形的面积是180平方米，长是15米，那么它的宽是________米。
三、计算题11. 计算下列多边形的面积：- 平行四边形：底=10米，高=6米。
- 三角形：底=8米，高=4米。
- 梯形：上底=5米，下底=10米，高=3米。
- 圆：半径=4米。
- 长方形：长=20米，宽=6米。
12. 已知一个平行四边形的面积是100平方米，底是20米，求高。
13. 已知一个三角形的面积是75平方厘米，底是15厘米，求高。
14. 已知一个梯形的面积是150平方厘米，上底是10厘米，下底是20厘米，求高。
15. 已知一个圆的面积是314平方厘米，求半径。
16. 已知一个长方形的面积是360平方米，长是24米，求宽。
四、解答题17. 某学校操场是一个长方形，长是200米，宽是100米。
请计算操场的面积，并说明如果学校要在操场上铺设草坪，需要多少平方米的草坪。
20道多边形面积计算题
20 道多边形面积计算题一、三角形面积计算题1.一个三角形的底是8 厘米，高是6 厘米，求这个三角形的面积。
-解析：三角形面积公式为S = 1/2×底×高。
所以这个三角形的面积为1/2×8×6 = 24 平方厘米。
2.三角形底为12 厘米，高为4 厘米，求面积。
-解析：根据三角形面积公式可得，面积为1/2×12×4 = 24 平方厘米。
3.已知三角形的底是5 厘米，高是7 厘米，求其面积。
-解析：面积为1/2×5×7 = 17.5 平方厘米。
二、平行四边形面积计算题4.一个平行四边形的底是10 厘米，高是5 厘米，求这个平行四边形的面积。
-解析：平行四边形面积公式为S = 底×高。
所以面积为10×5 = 50 平方厘米。
5.平行四边形底为8 厘米，高为6 厘米，求面积。
-解析：面积为8×6 = 48 平方厘米。
6.已知平行四边形的底是12 厘米，高是7 厘米，求其面积。
-解析：面积为12×7 = 84 平方厘米。
三、梯形面积计算题7.一个梯形的上底是4 厘米，下底是8 厘米，高是6 厘米，求这个梯形的面积。
-解析：梯形面积公式为S =（上底+ 下底）×高÷2。
所以这个梯形的面积为（4 + 8）×6÷2 = 36 平方厘米。
8.梯形上底为3 厘米，下底为7 厘米，高为5 厘米，求面积。
-解析：面积为（3 + 7）×5÷2 = 25 平方厘米。
9.已知梯形的上底是6 厘米，下底是10 厘米，高是8 厘米，求其面积。
-解析：面积为（6 + 10）×8÷2 = 64 平方厘米。
四、组合图形面积计算题10.如图，一个由三角形和长方形组成的图形，三角形的底是5 厘米，高是4 厘米，长方形的长是8 厘米，宽是6 厘米，求这个组合图形的面积。
五年级上册多边形面积练习题
五年级上册多边形面积练习题1. 矩形面积计算(1) 小明家的花坛是一个矩形，长是8米，宽是3米。
请计算花坛的面积。
解答：花坛的面积等于长乘以宽，即8米 × 3米 = 24平方米。
所以花坛的面积是24平方米。
(2) 书桌的长是1.2米，宽是0.6米。
请计算书桌的面积。
解答：书桌的面积等于长乘以宽，即1.2米 × 0.6米 = 0.72平方米。
所以书桌的面积是0.72平方米。
2. 正方形面积计算(1) 一块地的边长是5米，这块地是正方形，请计算地的面积。
解答：正方形的面积等于边长的平方，即5米 × 5米 = 25平方米。
所以地的面积是25平方米。
(2) 一块纸的边长是9厘米，这块纸是正方形，请计算纸的面积。
解答：正方形的面积等于边长的平方，即9厘米 × 9厘米 = 81平方厘米。
所以纸的面积是81平方厘米。
3. 三角形面积计算(1) 一个三角形的底边长是6米，高是4米。
请计算三角形的面积。
解答：三角形的面积等于底边长乘以高的一半，即(6米 × 4米) ÷ 2= 12平方米。
所以三角形的面积是12平方米。
(2) 一个三角形的底边长是8厘米，高是5厘米。
请计算三角形的面积。
解答：三角形的面积等于底边长乘以高的一半，即(8厘米 × 5厘米) ÷ 2 = 20平方厘米。
所以三角形的面积是20平方厘米。
4. 其他多边形面积计算(1) 一个梯形的上底长是10厘米，下底长是8厘米，高是6厘米。
请计算梯形的面积。
解答：梯形的面积等于(上底长 + 下底长)乘以高的一半，即[(10厘米 + 8厘米) × 6厘米] ÷ 2 = 54平方厘米。
所以梯形的面积是54平方厘米。
(2) 一个菱形的对角线长度分别为10厘米和8厘米，请计算菱形的面积。
解答：菱形的面积等于两条对角线的长度的乘积的一半，即(10厘米 × 8厘米) ÷ 2 = 40平方厘米。
(优辅资源)人教版五年级上册第六单元《多边形的面积》单元测试卷 (2)
多边形面积单元测试卷一、填一填1、1公顷＝（）平方米 1米＝（）分米 456000平方米=( )公顷5.64公顷=( )平方米 25分米＝（）米 1.2平方米=( )平方厘米12平方米5平方分米=（）平方米=（）平方分米350平方米＝（）公顷＝（）平方分米2、用字母表示三角形面积公式（），用字母表示长方形周长公式（），用字母表示梯形面积公式（），用字母表示正方形面积公式（）。
3、一个三角形的底是3.6分米，高是4.8分米，与它等底等高的平行四边形面积是( )平方米，这个三角形的面积是（）。
4、梯形的上底是10分米，下底是22厘米，高是15厘米，面积是( )平方米。
5、两个完全相同的三角形拼成了一个底是8.5厘米，高是6厘米的平行四边形，这个三角形的底是( )，高是( )，三角形的面积是平行四边形面积的（）6、一个三角形与一个平行四边形面积相等，高也相等，已知三角形的底是20厘米，那么平行四边形的底是（）7、一个梯形的面积是16平方米，上底是30分米，下底是50分米，高是( )分米。
8、平行四边形的底扩大到原来的2倍，高不变，则面积( )倍。
9、一个平行四边形底是12厘米，面积是96平方厘米，它的高是( )10、一个梯形的高4厘米，上底和下底都增加6厘米，面积增加（）二、辨一辨1、两个面积相等的梯形可以拼成一个平行四边形。
（）2、两个三角形的面积相等，它们的形状也一定相同。
（）3、三角形的面积等于平行四边形面积的一半。
（）4、边长是4厘米的正方形，它的周长和面积相等。
（）5、平行四边形的底越大，面积就越大。
（）三、选一选1、一个平行四边形的高有（） A.1条 B.2条 C. 无数条 D.4条2、把一个平行四边形框架拉成一个长方形框架，则周长( ),面积( )；把一个平行四边形沿着高剪开后平移，拼成一个长方形，则周长( ),面积( )。
A.增加B.减少C. 不变D.无法确定四、算一算：3、一种汽车的挡风玻璃近似于一个平行四边形，底1.6米，高0.8米，如果每平方米的钢化玻璃要240元，配这块挡风玻璃要多少元？4、一块梯形麦田，上底是76米，下底是120米，高50米，一共收小麦9310千克，平均每公顷收小麦多少千克？1．平行四边形的面积是480平方分米，底是12米，高是（）cm.2、一个平行四边形，它的高是6cm，高是底的1.2倍，它的面积是（）3、一个平行四边形的面积是90cm2，若它的底和高都扩大2倍，它的面积是（）m2。
小学数学五年级上册新人教版第六单元多边形的面积检测卷(含答案解析)(2)
小学数学五年级上册新人教版第六单元多边形的面积检测卷（含答案解析）(2)一、选择题1．一个三角形与一个平行四边形等底不等高，其面积又相等。
若三角形的高是6厘米，则平行四边形的高是（）厘米。
A. 3B. 1.5C. 6D. 92．下面的四个平行四边形，根据已知条件可以算出面积的是（）。
A. B. C. D.3．如图，每个小方格的面积是1平方厘米，估一估，这个脚印的面积大约是（）平方厘米。
A. 13B. 20C. 35D. 404．一个直角三角形的三条边长分别是9dm，12dm，15dm，这个三角形的面积是（）dm2．A. 108B. 54C. 67.5D. 905．如图所示，把一个长方形分成一个梯形和一个三角形．已知梯形的面积比三角形的面积大18厘米2，那么梯形的上底长为（）厘米．A. 2B. 3C. 4D. 66．一个三角形和一个平行四边形面积相等，底也相等。
如果平行四边形的高是12厘米，三角形的高就是（）厘米A. 6B. 12C. 24D. 367．下图中有（）对面积相等的三角形。
A. 2B. 3C. 48．一堆钢管最上层有14根，最下层有26根。
每层相差1根，共有13层，这堆钢管共有（）根。
A. 260B. 240C. 220D. 2109．一个三角形和一个平行四边形的底和面积都相等，那么三角形的高（）A. 和平行四边形的高相等B. 是平行四边形高的一半C. 是平行四边形高的2倍D. 是平行四边形高的4倍10．一个直角三角形，直角所对的边长是10厘米，其余两边分别是8厘米和6厘米，这个三角形的面积是（）平方厘米。
A. 40B. 30C. 2411．如图，已知A是长方形一边中点，3个三角形的面积比较，（）。
A. 面积相等B. ①<②<③C. ①=②<③12．下图平行线间的三个图形的面积相比较，（）。
A. 平行四边形的面积最大B. 三角形的面积最大C. 梯形的面积最小二、填空题13．在一个直角三角形中，其中一个锐角是a度，另一个锐角是________度。
2024-2025学年苏教版数学五年级上册 第二单元 多边形的面积(含答案)
2024-2025学年苏教版数学五年级上册第二单元多边形的面积一、选择题1．下面的四个平行四边形，根据已知条件，第（）号图形的面积可以算出来。
A．B．C．2．如图，三个图形A、B、C的面积，按从小到大排列是（）。
A．S A<S C<S B B．S C<S A<S B C．S A<S B<S C3．一块平行四边形纸板，面积为56平方厘米，高是8厘米，沿8厘米的高剪开后平移拼成一个长方形，长方形的周长是（）厘米。
A．56B．30C．284．一个三角形，底扩大8倍，高缩小2倍，那么这个三角形的面积（）A．扩大2倍B．扩大8倍C．扩大4倍5．如图中，阴影部分的面积甲（ ）乙．A．大于B．小于C．等于二、填空题6．在下面括号内填上适当的单位名称。
江苏省的面积大约是10万( )。
学校占地面积大约是3( )。
7．一个梯形的上底与下底的和是10厘米，高是4厘米，它的面积是( )平方厘米。
8．一个直角三角形三条边分别是3分米、4分米和5分米，它的面积是( )平方米．9．三角形的底8厘米，高5厘米，面积是( )平方厘米，与它等底等高的平行四边形的面积是( )平方厘米。
10．一个直角梯形的上底是5厘米，如果把它的下底减少2厘米，这个梯形就能变成正方形，原来这个梯形的面积是( )平方厘米。
三、判断题11．一个平行四边形的底增加2 cm，对应的高减少2 cm，这个平行四边形的面积不变．( ) 12．把一张平行四边形纸片剪拼成长方形，面积不变，周长不变。
( )13．如图是三个完全相同的平行四边形，涂色部分的面积都相等。
( )14．如果平行四边形的面积是三角形面积的2倍，那么它们一定等底等高。
( )15．两个三角形的面积相等，它们的形状也一定相同．( )四、计算题16．计算下面图形的面积五、作图题17．下面方格纸的每个小方格的边长都表示1厘米，先在方格纸上以AB为底画一个面积为12平方厘米的梯形，然后在梯形的右面画一个三角形，且三角形的面积和高都与梯形相等。
人教版五年级上册数学 第六单元 多边形的面积 单元测试题2
人教版五年级上册数学第六单元多边形的面积单元测试题一、选择题（本大题共7道小题，每小题3分，共21分）1. 一堆木头最上层有7根，最下层有13根，相邻两层相差一根，这堆木头有（）根。
A．50 B．60 C．70 D．802. 下列说法正确的是（）。
A．含有未知数的式子叫方程。
B． 6.5÷0.9与65÷9的商相等，余数也相等。
C．两个三角形的面积相等，它们的周长就一定相等。
D．在计算小数乘法时，把两个因数变换位置，再乘一遍，可以检验计算对不对。
3. 一个三角形的面积是2140cm，底是20cm，它的高是( )A．7 B．14 C．28 D．394. 一个直角三角形的面积是45平方厘米，其中一条直角边是9厘米，另一条直角边是（）。
A．10厘米B．5厘米 C．2.5厘米 D.4厘米5. 一个平行四边形的底和高分别扩大到原来的2倍，它的面积扩大到原来的（）倍。
A．2 B．4 C．6 D．86. 一块近似三角形的菜地，它的面积大约是160平方米，高约是4米，底约是()A．20米B．40米C．80米D．120米7. 下图是一片银杏叶，下面4个选项中，最接近它面积的是（）。
（每个方格的面积是1）A．20 B．25 C．35 D．30二、填空题（本大题共7道小题，每小题3分，共21分）8. 一堆钢管，最上层有2根，最下层有7根，每相邻两层均相差1根，这堆钢管共有根。
9. 一个梯形的上底是3米，下底是2米，高是2米，这个梯形的面积是；用两个这样的梯形拼成的平行四边形的面积是。
10. 一个三角形的面积是230dm，底边是7.5dm，那么这条底边上的高是dm，与它等底等高的平行四边形的面积是2dm。
11. 观察下图，根据已知信息计算，它的高应该是________cm，面积应该是cm2。
12. 下图中平行四边形的面积是0.48平方米，E是CD的三等分点，三角形FDE的面积是________方米。
13. 一块平行四边形的空地，底是600m，对应的高是350m，这块地的面积是2m，合公顷。
多边形的面积练习题及答案
多边形的面积练习题及答案练习题一：三角形面积计算题目：已知一个三角形的底边长为10厘米，高为6厘米，求该三角形的面积。
解答：根据三角形面积公式，面积 = (底边长× 高) / 2。
代入数值得面积= (10 × 6) / 2 = 30平方厘米。
练习题二：平行四边形面积计算题目：一个平行四边形的底边长为8厘米，高为5厘米，求该平行四边形的面积。
解答：平行四边形的面积公式为面积 = 底边长× 高。
代入数值得面积= 8 × 5 = 40平方厘米。
练习题三：梯形面积计算题目：一个梯形的上底长为4厘米，下底长为8厘米，高为6厘米，求该梯形的面积。
解答：梯形的面积公式为面积 = (上底 + 下底) × 高 / 2。
代入数值得面积= (4 + 8) × 6 / 2 = 18平方厘米。
练习题四：正多边形面积计算题目：一个正六边形的边长为5厘米，求该正六边形的面积。
解答：正六边形可以被划分为6个等边三角形，每个三角形的底边长等于正六边形的边长。
因此，每个三角形的面积= (5 × 5 ×sin(60°)) / 2。
正六边形的总面积= 6 × 每个三角形的面积 = 6× (5 × 5 × √3 / 4) = 75√3 / 2 ≈ 64.95平方厘米。
练习题五：不规则多边形面积估算题目：一个不规则多边形，已知其所有顶点的坐标，如何估算其面积？解答：可以通过将其划分为多个三角形，然后计算每个三角形的面积并求和。
如果顶点坐标已知，可以使用多边形面积公式，即根据顶点坐标计算多边形的面积。
练习题六：圆内接多边形面积计算题目：一个圆的半径为10厘米，求其内接正六边形的面积。
解答：圆内接正六边形的边长等于圆的半径。
因此，正六边形的面积= 6 × (半径× 半径× sin(60°)) / 2 = 6 × (10 × 10 ×√3 / 4) = 150√3 ≈ 259.81平方厘米。
多边形面积练习题及答案
多边形面积练习题及答案多边形面积练习题及答案多边形是几何学中常见的图形，它由若干条线段组成，每条线段称为边，相邻两边的交点称为顶点。
多边形的面积是几何学中的一个重要概念，它表示多边形所占据的平面区域的大小。
在学习多边形面积的过程中，练习题是非常重要的一部分，下面将给出一些多边形面积的练习题及答案，希望能对你的学习有所帮助。
练习题一：计算下列多边形的面积：1. 一个正三角形，边长为5cm。
2. 一个矩形，长为8cm，宽为4cm。
3. 一个正五边形，边长为6cm。
答案一：1. 正三角形的面积可以使用公式S = (边长^2 * √3) / 4来计算，代入边长5cm，得到S = (5^2 * √3) / 4 ≈ 10.83cm²。
2. 矩形的面积可以使用公式S = 长 * 宽来计算，代入长8cm和宽4cm，得到S= 8 * 4 = 32cm²。
3. 正五边形的面积可以使用公式S = (边长^2 * √25 + 10 * √5) / 4来计算，代入边长6cm，得到S = (6^2 * √25 + 10 * √5) / 4 ≈ 61.66cm²。
练习题二：计算下列多边形的面积：1. 一个等边五边形，边长为10cm。
2. 一个正六边形，边长为7cm。
3. 一个梯形，上底长为5cm，下底长为8cm，高为6cm。
答案二：1. 等边五边形的面积可以使用公式S = (边长^2 * √25 + 10 * √5) / 4来计算，代入边长10cm，得到S = (10^2 * √25 + 10 * √5) / 4 ≈ 172.05cm²。
2. 正六边形的面积可以使用公式S = (3 * √3 * 边长^2) / 2来计算，代入边长7cm，得到S = (3 * √3 * 7^2) / 2≈ 91.14cm²。
3. 梯形的面积可以使用公式S = (上底 + 下底) * 高 / 2来计算，代入上底5cm、下底8cm和高6cm，得到S = (5 + 8) * 6 / 2 = 39cm²。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
五年级数学上册期末复习：多边形面积的计算练习题
一、单位换算
（1）把一个平行四边形转化成一个长方形，它的面积与原来的平行四边形（）。
这个长方形的长等于平形四边形的（），宽等于平行四边形的（）。
平行四边形的面积等于（），用字母表示是（）。
（2）一个平行四边形的底为15分米，高为18分米，面积为( )平方分米。
如果一个平行四边
底为12分米，面积为180平方分米，则高为( )分米。
（3）一个平行四边形的底扩大4倍，高缩小2倍，则面积( )；如果它的底缩小3倍，高扩大3倍，则面积( )。
（4）一个长方形木框，长10dm，宽8dm，将它拉成一个平行四边形，面积变( )，这个平行四边形的周长为( )dm。
（5）把一个长8厘米，宽4厘米的长方形框架拉成一个平行四边形，这时面积减少8平方厘米，平行四边形的面积为( )平方厘米，这时平行四边形的高为( )厘米。
三、（三角形）三角形的面积=底×高÷2 S= a h÷2
（1）两个完全一样的三角形能拼成（），所以三角形的面积等于（）。
用字母表示是（）。
（2）一个三角形底是5cm，高是7cm，面积是（）。
（3）一个三角形，它的面积为36平方分米，高为8分米，则它的底为( )分米。
（4）一个三角形的面积是4.8 m2，与它等底等高的平行四边形的面积是（）。
（5）一个三角形的面积为10平方分米，若底扩大2倍，高缩小4倍，则现在的面积为( )平方分米。
（6）一个三角形的面积比与它等底等高的平行四边形的面积少12平方分米，则平行四边形的面积是( )平方分米，三角形的面积为( )平方分米。
（7）一个三角形与一个平行四边形的面积相等，底也相等，如果三角形的高是8米，那么平行四边形的高是( )米；如果平行四边形的高是8米，那么三角形的高是( )米。
（8）一个平行四边形的面积比与它等底等高的三角形面积大48平方厘米，这个三角形的面积是（）平方厘米。
四、（梯形）梯形的面积=（上底+下底）×高÷2 S=（a+b）×h÷2
（1）两个完全一样的梯形能拼（），所以梯形的面积等于（）。
用字母表示是（）。
（2）一个梯形的面积是22平方分米，上、下底之和为11分米，它的高是( )分米。
（3）一个梯形的面积是24平方分米，下底是5分米，高是4分米，上底是( )分米。
（4）一个梯形的面积是42平方米，它的上下底之和与一个平行四边形的底边相等，高与平行四边形的高相等，这个平行四边形的面积是( )平方米。
（5）一块直角梯形的地，它的下底是40米，如果上底增加38米，这块地就变成了正方形，原梯形的面积是( )平方米。
（6）一个梯形的高是6厘米，下底10厘米，如果上底增加7厘米，它就变成了一个平行四边形，这个梯形的面积是( )平方厘米。
五、选择（填上正确答案的序号）
1、下面的四个平行四边形，根据已知条件第( )个平行四边形的面积可以算出。
① ② ③ ④
2、将一个长方形拉成一个平行四边形，面积( )，周长( )，高（ ），底（ ）。
①变大 ②变小 ③不变 ④无法比较
3、能拼成一个平行四边形的两个三角形必须具备( )。
①面积相等 ②形状相同 ③完全一样 ④任意两个均可
4、周长相等的一个正方形，一个长方形，一个平行四边形，( )面积最大。
①正方形 ②长方形 ③平行四边形 ④无法比较 5、梯形ABCD 中，三角形AOD 和三角形BOC 的面积相比，( )大。
①三角形AOD ②三角形BOC ③同样 ④无法比较
6、把一个平行四边形任意分割成两个梯形，这两个梯形的( )总是相等的。
①高 ②面积 ③上、下底的和 ④无法确定
7、一个三角形和一个平行四边形高相等，面积也相等，如果平行四边形的底是6厘米，那么
三角形的底是( )厘米。
①6 ②3 ③12 ④18
8、一个梯形的上底长36dm ，如果补上一块底为64dm ，面积为64dm 2的三角形，就变成了一个
平行四边形，这个梯形的面积是( )。
①20dm 2 ②136dm 2 ③272dm 2 ④68dm 2
9、右图中，甲、乙两点分别为长方形宽的中点，那么图中面积相等的三角形是( )。
①A 、B 、C ②D 、E ③A 、B ④B 、C
10、两个完全一样的等腰直角三角形，可以拼成一个（ ）
①长方形 ②正方形 ③梯形 ④平行四边形
六、判断
1、周长相等的两个平行四边形面积相等。
（ ）
2、面积相等的两个梯形能拼成一个平行四边形。
（ ）
3、平行四边形的底扩大到它的2倍，高缩小到它的一半，则面积不变。
（ ）
4、等底等高的两个三角形，形状不一定相同，但面积一定相等。
（ ）
5、把一个长方形拉成一个平行四边形后，它的面积没有改变。
（ ）
6、三角形的面积大小只与它的底和对应的高有关，与它的形状和位置无关。
（ ）
7、在一个长方形内画一个最大的三角形，这个三角形的面积一定等于长方形面积的一半（ ）
8、两个完全重合的三角形，一定可以拼成一个长方形。
（ ）
9、梯形的面积比平行四边形面积小。
（ ）
10、一个长方形可以划分成两个完全一样的梯形。
（ ）
七、填“＞”、“＜”或“＝”。
①A 的面积( )B 的面积 ②A 的面积( )B 的面积 D C A B O A B C D E 乙 甲。